Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Oct 8;141(44):17838–17846. doi: 10.1021/jacs.9b09036

Ensemble-Based Modeling of the NMR Spectra of Solid Solutions: Cation Disorder in Y2(Sn,Ti)2O7

Robert F Moran †, David McKay †, Paulynne C Tornstrom ‡, Alex Aziz ‡, Arantxa Fernandes †, Ricardo Grau-Crespo ‡,*, Sharon E Ashbrook †,*
PMCID: PMC6900218  PMID: 31591883

Abstract

graphic file with name ja9b09036_0007.jpg

The sensitivity of NMR to the local environment, without the need for any long-range order, makes it an ideal tool for the characterization of disordered materials. Computational prediction of NMR parameters can be of considerable help in the interpretation and assignment of NMR spectra of solids, but the statistical representation of all possible chemical environments for a solid solution is challenging. Here, we illustrate the use of a symmetry-adapted configurational ensemble in the simulation of NMR spectra, in combination with solid-state NMR experiments. We show that for interpretation of the complex and overlapped lineshapes that are typically observed, it is important to go beyond a single-configuration representation or a simple enumeration of local environments. The ensemble method leads to excellent agreement between simulated and experimental spectra for Y2(Sn,Ti)2O7 pyrochlore ceramics, where the overlap of signals from different local environments prevents a simple decomposition of the experimental spectral lineshapes. The inclusion of a Boltzmann weighting confirms that the best agreement with experiment is obtained at higher temperatures, in the limit of full disorder. We also show that to improve agreement with experiment, in particular at low dopant concentrations, larger supercells are needed, which might require alternative simulation approaches as the complexity of the system increases. It is clear that ensemble-based modeling approaches in conjunction with NMR spectroscopy offer great potential for understanding configurational disorder, ultimately aiding the future design of functional materials.

Introduction

The mixing of different elements over specified sites within a crystal lattice, forming a solid solution, offers a powerful and commonly exploited route to engineer the properties of materials. For example, band gap engineering via compositional optimization has been used for several decades to obtain the desired optoelectronic behavior in semiconducting alloys.1 However, the detailed structural characterization of such disordered materials, vital for understanding structure–property relationships, can be extremely challenging, with methods based on Bragg diffraction providing a picture of the structure that is averaged over space and time. While this average picture can be useful in understanding or predicting some selected properties of materials, detailed information on the local atomic environment of individual atoms, which may play an important role in chemical reactivity, is often lost. Nuclear magnetic resonance (NMR) spectroscopy provides a complementary tool for the study of disordered or dynamic systems, with its inherent sensitivity to the atomic-scale geometry through interactions such as the chemical shift.2,3 However, the complexity of the spectral lineshapes obtained for disordered systems hinders the straightforward extraction of structural information, and attention has turned to computation to assist spectral interpretation.4,5 In most cases, this has involved the use of simple substitutions into an ordered parent structure to gain insight into the typical type and magnitude of the changes that are seen in the NMR interaction of interest.4,5 Although this may facilitate a better understanding of the likely effect of disorder on the NMR spectrum, it falls far short of providing the detailed structural picture that is usually desired.

In general, computer simulation is a useful tool for the design of functional solid solutions. However, the computational modeling of site-disordered solids is more challenging owing to configurational complexity, and periodic boundary conditions often cannot be applied directly as in the case of ordered crystals.6 The theoretical investigation of the thermodynamics of disorder and mixing in solid solutions typically involves evaluating the energies of structures within a large configurational space, which becomes affordable by using an effective Hamiltonian that gives the energy as a function of site occupancies, for example using a cluster expansion approach.7−9 The effective interactions are parametrized using density functional theory (DFT) calculations or experimental information. Large supercells and many configurations are normally required to achieve convergence of the configurational entropy and the free energy of the solid solutions. In contrast, when other properties of the solid solution (i.e., those beyond thermodynamics such as electronic behavior) are to be evaluated, the most common approach is to use a single configuration that is representative of the mixed system. For highly ordered solid solutions, the lowest-energy configuration is chosen, whereas for highly disordered systems, a good representative configuration is considered to be the special quasi-random structure (SQS), which mimics the pair correlation function of the fully disordered solid.10

In this work we show that for the prediction of NMR parameters, and interpretation of the complex and overlapped lineshapes that are typically observed in NMR spectra of disordered solids, it is important to go beyond a single-configuration representation and employ configurational ensembles. Such an approach allows the systematic enumeration of all possible chemical environments around a given cation but, unlike the simple “cluster-based” models applied previously,4,5 includes proper consideration of the statistical weights including configurational degeneracy and energetic preference effects. As the evaluation of NMR chemical shieldings is computationally much more expensive than a simple energy evaluation (especially when a cluster expansion is used for the latter), the ensembles are necessarily limited to a cell (or supercell) smaller than those typically used for thermodynamic calculations. However, if the cell is sufficiently large to include the number of neighbors affecting the contributions to the NMR interactions of interest, a robust prediction of the complex NMR spectra can be obtained. Here, we demonstrate this using the Y2(Sn,Ti)2O7 pyrochlore system (studied previously using 89Y, 119Sn and 17O NMR spectroscopy)11−17 as a case study. We show that these calculations allow a clear interpretation of the origin of the features in the NMR spectra of a solid solution, and provide insight into the atomic configurations that are present in the real material, and the importance each has in determining the appearance of the solid-state NMR spectrum. We demonstrate that the combination of NMR spectroscopy and quantum-mechanical simulations that consider configurational probabilities can offer crucial insights into the short-range effects and ordering in solid solutions, which escape most diffraction-based measurements.

Methods

Synthesis and Basic Characterization

Y2(SnxTi1–x)2O7 (x = 0.0 to 1.0 in steps of 0.125) samples were synthesized (in a similar manner to previous work) using a conventional solid-state mixed metal oxide process. Stoichiometric quantities of commercially available Y2O3 (Sigma-Aldrich, 99%), SnO2 (Sigma-Aldrich, 99.9%), and TiO2 (Sigma-Aldrich, 99%) were ball milled (1 h) using ZrO2 balls and acetone/cyclohexanol as the milling medium. The dry powders were then pressed into a pellet, placed in an alumina boat, and heated to ∼1673 K (at 5 K min–1) for 48 h. The pellets were reground and repressed before a second sintering at ∼1673 K for a further 48 h. After cooling (also at 5 K min–1), the samples were assessed for phase purity using a PANalytical Empyrean diffractometer, Cu Kα1 radiation (λ = 1.5406 Å), and an X’celerator linear detector. Patterns were collected over a 2θ angular range of 10–100° with a step size of 0.02° and a step duration of 0.4 s. Samples were shown to be single-phase pyrochlore throughout (see Supporting Information).

Solid-State NMR Spectroscopy

89Y NMR spectra were acquired using a Bruker Avance III 600 MHz NMR spectrometer, equipped with a widebore 14.1 T magnet, at a Larmor frequency of 29.41 MHz. Powdered samples were packed into 4 mm Si3N4 rotors to prevent any 89Y background signal and rotated at 14 kHz, using a 4 mm HX low-γ probe. Spectra were acquired using a spin–echo pulse sequence, with a radiofrequency field strength of ∼22 kHz (π/2 ≈ 11.3 μs) and a recycle interval of 30 s. Although T1 is relatively long for all 89Y resonances, there is little difference in the relative relaxation rates, and spectral intensities accurately reflect the relative site populations even at shorter recycle intervals.13 Chemical shifts are given in ppm relative to the primary reference 1 M aqueous YCl3, measured using a secondary reference compound, Y2Ti2O7, at 65 ppm.12

119Sn NMR spectra were acquired using a Bruker Avance III 400 MHz spectrometer, equipped with a widebore 9.4 T magnet, at a Larmor frequency of 149.2 MHz. Powdered samples were packed into 4 mm ZrO2 rotors and rotated at 14 kHz, using a 4 mm HX probe. Spectra were acquired using a spin–echo, with a radiofrequency field strength of ∼111 kHz (π/2 ≈ 2.25 μs) and a recycle interval of 30 s. Chemical shifts are given in ppm relative to the primary reference (CH3)4Sn, measured using a secondary reference compound, SnO2, at −604.3 ppm.

Calculations

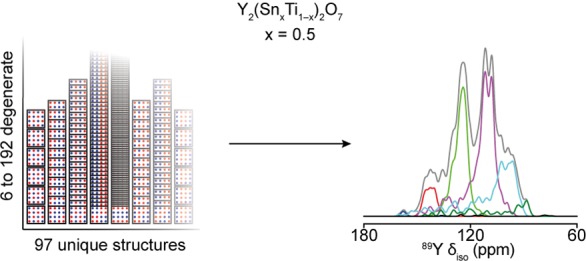
The Site Occupancy Disorder (SOD) program18 was used to generate the set of symmetrically inequivalent configurations for each number k of B-site substitutions in a pyrochlore unit cell Y16B16–kB′kO56. Two configurations are equivalent if there is an isometric transformation that converts one into the other. The transformations considered are simply the symmetry operators of the parent structure (in this case those in the Fd3̅m space group of the cubic pyrochlore structure). The total number of atomic configurations (W) and the number of inequivalent configurations (M) for each pyrochlore composition are listed in Table 1. The total number of configurations is given by simple statistics as

graphic file with name ja9b09036_m001.jpg 1

where N is the number of sites over which substitutions are considered (i.e., 16 for the B sites in the pyrochlore structure) and x = k/N is the molar fraction of substitutions. The geometry of each of the 279 resulting unique structural models was then optimized using the CASTEP DFT code (version 8.0).19,20 DFT calculations were performed using the PBE21 exchange-correlation functional, and core-valence interactions were described by ultrasoft pseudopotentials,22 accounting for scalar relativistic effects using ZORA.23 A planewave energy cutoff of 60 Ry (∼816 eV) was used, with the first Brillouin zone sampled through a Monkhorst-Pack grid24 with a reciprocal space grid spacing of 0.04 2π Å–1. In the geometry optimization all atomic coordinates and unit cell parameters were allowed to vary, with a geometry optimization energy tolerance of 1 × 10–5 eV per atom and an electronic structure energy tolerance of 1 × 10–9 eV per atom used (see Supporting Information). From these energies, thermodynamic properties (enthalpies of mixing, ΔHmix, and free energies of mixing, ΔGmix) were derived in the limit of full disorder and fitted to an asymmetric function using the subregular solid solution model,25 as described in the Supporting Information.

Table 1. Total Number of Atomic Configurations (W) and the Number of Symmetry Inequivalent Configurations (M) for Y2(SnxTi1–x)2O7 Structures in a Single Cubic Unit Cell (with 16 Exchangeable B Sites) Generated Using SOD.

chemical formula x B site NNN W M
Y2Sn2O7 1.0 Sn16 1 1
Y2(Sn0.875Ti0.125)2O7 0.875 Sn14Ti2 120 3
Y2(Sn0.75Ti0.25)2O7 0.75 Sn12Ti4 1820 22
Y2(Sn0.625Ti0.375)2O7 0.625 Sn10Ti6 8008 65
Y2(Sn0.5Ti0.5)2O7 0.5 Sn8Ti8 12 870 97
Y2(Sn0.375Ti0.625)2O7 0.375 Sn6Ti10 8008 65
Y2(Sn0.25Ti0.75)2O7 0.25 Sn4Ti12 1820 22
Y2(Sn0.125Ti0.875)2O7 0.125 Sn2Ti14 120 3
Y2Ti2O7 0.0 Ti16 1 1
total     32 768 279
Open in a new tab

NMR parameters were calculated with CASTEP (version 8.0), using the gauge-including projector augmented wave (GIPAW) approach21,22 to reconstruct the all-electron wave function in the presence of a magnetic field, and the same parameters as in the geometry optimizations. Calculations generate the absolute shielding tensor (σcalc) in the crystal frame, and diagonalization of the symmetric part yields the three principal components σ11calc, σ22calc, and σ33calc. From these, σisocalc = (σ11calc + σ22χαλχ + σ33χαλχ)/3, the magnitude of the anisotropy or span, Ωχαλχ = σ11calc – σ33calc, and the skew, κcalc = 3 (σ22χαλχ – σisocalc)/Ωcalc can be determined. To facilitate comparison to experiment, the corresponding isotropic chemical shift, δisocalc, was determined from σisocalc. See Supporting Information for further details of the referencing methods used in this work. Predicted NMR spectra were simulated for each structural model by representing each value of δisocalc by an individual Gaussian function (with a fixed line broadening of 1 ppm). These spectra were weighted by the corresponding configurational degeneracy of the structural model, before being summed to produce a final spectrum for each composition. In some cases, the spectral intensities were also weighted by the Boltzmann distribution (see Section S2 in the Supporting Information).

Results and Discussion

The A2B2O7 pyrochlore structure is based on a supercell of fluorite (AO2) with one-eighth of the anions removed in an ordered manner, giving an eight-coordinate A site (occupied here by Y3+) and a six-coordinate B site (occupied here by Sn4+ and/or Ti4+), as shown in Figure 1.26−28 For each Y2(SnxTi1–x)2O7 composition (x = 0.0 to 1.0 in steps of 0.125) the set of unique structural models was determined as described above using SOD. As described in the Supporting Information, the thermodynamics of mixing in Y2(Sn,Ti)2O7 were investigated using the subregular solid solution model as a first approximation,25 where a finite enthalpy of mixing, ΔHmix, is determined (and fitted to an asymmetric function, as explained below), but where the entropy of mixing is assumed to be that of the ideal solution, thus eliminating any complications related to the convergence of the calculated entropy with the size of the simulation cell.

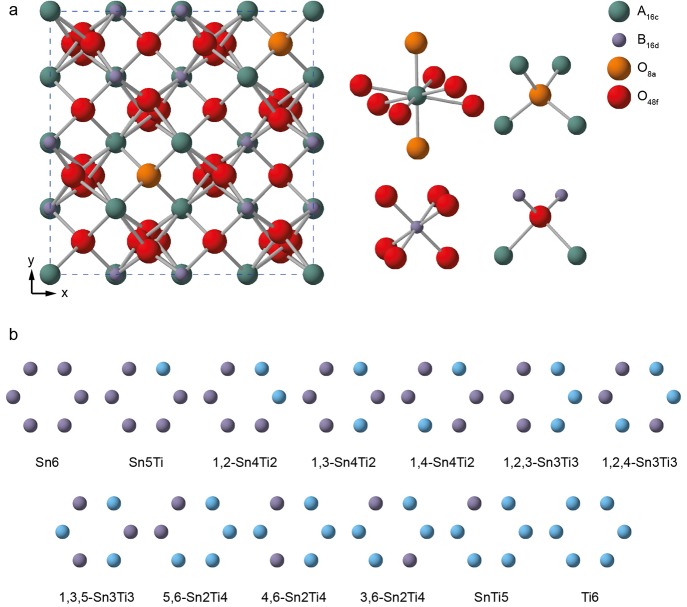
Figure 1.

Figure 1

Open in a new tab

(a) Structure of a typical A2B2O7 pyrochlore, with expansions of the local environments of the Wykoff 16c (A), 16d (B), and 8a and 48f (O) sites. (b) Possible arrangements of Sn and Ti on the six NNN B sites that surround the pyrochlore A and B sites. See the Supporting Information for the numbering scheme used.

Figure 2a shows a plot of ΔHmix for each composition in the limit of full disorder (i.e., the average of the configuration energies weighted only by their corresponding degeneracies).

Figure 2.

Figure 2

Open in a new tab

(a) Enthalpy of mixing (from DFT calculations) in the limit of full disorder (circles) and Guggenheim polynomial fitting using a subregular model (line) for Y2(SnxTi1–x)2O7. (b) Free energy of mixing in the subregular model at 500 K (showing the miscibility gap) and at 1000 K. (c) Phase diagram showing the immiscibility regions where the solid solution is predicted to be metastable with respect to phase separation using the subregular solid solution model.

Values are plotted for each structural model separately in the Supporting Information. The values in Figure 2a can be fitted to obtain an analytical expression using a second-order Guggenheim polynomial;

graphic file with name ja9b09036_m002.jpg 2

giving W0 = 8.88 kJ mol–1 and W1 = 5.42 kJ mol–1. In principle, a better fitting can be achieved using higher-order Guggenheim polynomials, but the improved precision is likely to be irrelevant within the accuracy of the calculations. The enthalpy of mixing is positive and, interestingly, is asymmetric, indicating it is generally easier to substitute Sn into Y2Ti2O7 than to substitute Ti in Y2Sn2O7. This is somewhat surprising, as the ionic radius of Sn4+ (0.69 Å) is greater than that of Ti4+ (0.61 Å),29 and it is often more difficult to substitute a larger ion in a smaller ion site than vice versa.

Figure 2b plots the free energy of mixing (ΔGmix) as a function of temperature. At high temperatures (e.g., 1000 K), the entropic term dominates and the solid solution is predicted to be stable with respect to phase separation. However, at lower temperatures a miscibility gap appears. This corresponds approximately to the region of composition between the two minima x1 and x2 of ΔGmix; that is, a physical mixture of two solid solutions with compositions x1 and x2 has lower free energy than the solid solution with composition x such that x1 < x < x2. Due to the asymmetry, the limits of the miscibility gap do not correspond exactly to the minima of Gmix(x), but to points of intersection with the secant, as shown in Figure 2b. From this, it is possible to create a phase diagram showing the predicted regions of composition/temperature stability of the solid solution (Figure 2c). This shows a significant immiscibility region is predicted below 800 K, where intermediate compositions are expected to be unstable with respect to decomposition into Ti-rich and Sn-rich solids. Experimentally, however, such compositions do exist as solid solutions13,14 (see below), but they are metastable. It should be noted that this analysis is limited by the assumption of the subregular solid solution model, which is expected to overestimate the configurational entropy by assuming ideal mixing. The real system is expected to have lower configurational entropy, and a slightly larger region of immiscibility would be predicted. We have also ignored finite-temperature effects arising from vibrational contributions to the thermodynamics of mixing, which are typically much smaller than configurational effects.30,31 This simplifies the calculations considerably, as we can use the 0 K energies from DFT for the statistical analysis at finite temperature, but this is not expected to substantially affect the results.

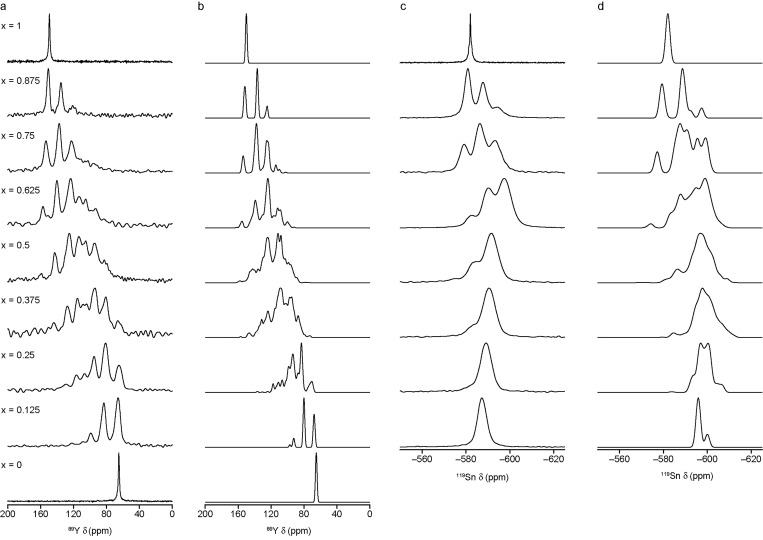
For a specified Y2(SnxTi1–x)2O7 composition, it is possible to predict the corresponding 89Y and 119Sn (I = 1/2) NMR spectra in the limit of full disorder by summing the complete set of spectra predicted for each structural model (after weighting each by the corresponding configurational degeneracy; see above). These predicted spectra are shown in Figure 3, alongside the corresponding experimental spectra. Although 89Y and 119Sn NMR spectra of Y2(SnxTi1–x)2O7 have been published previously,13−15Figure 3 shows new experimental spectra for solid solution compositions that match those used in the calculations.32 It is clear in all cases (and from the powder XRD measurements discussed above) that a pyrochlore solid solution is formed experimentally, rather than the phase separation predicted by the thermodynamic analysis at room temperature, likely reflecting a metastable freezing of the high-temperature disordered distribution, given the high synthesis temperature (∼1673 K). For both nuclei, surprisingly good agreement is seen between the experimental and predicted NMR spectra, with the latter matching well the number and position of the resonances observed in each case. For the calculated spectra, it is possible to determine the contributions from species with different local environments. Variation of the atoms on the six next nearest neighbor (NNN) B sites surrounding the A and B sites produces 13 different local coordination geometries, which are shown schematically (along with the numbering schemes used) in Figure 1c and the Supporting Information.

Figure 3.

Figure 3

Open in a new tab

(a, c) Experimental and (b, d) predicted, assuming the limit of full disorder, (a, b) 89Y and (c, d) 119Sn MAS NMR spectra of Y2(SnxTi1–x)2O7 for x = 0 to 1.

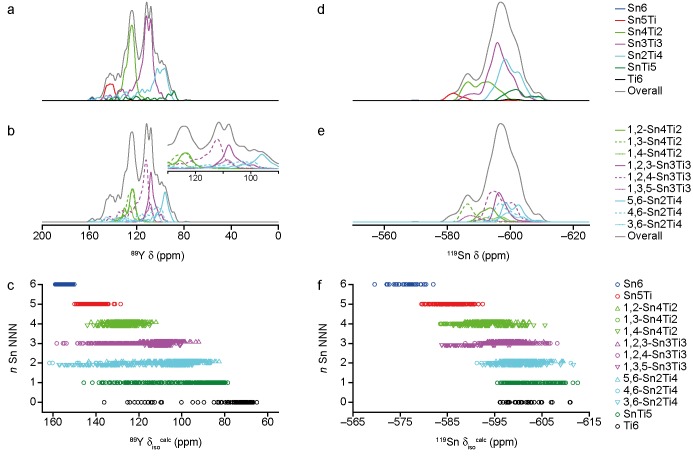
Figure 4a and d show simulated 89Y and 119Sn MAS NMR spectra for Y2SnTiO7 (i.e., x = 0.5), decomposed to show the contributions from species with differing numbers, n, of Sn NNN. (Similar decompositions are shown for all compositions in the Supporting Information). For 89Y (Figure 4a), there is a systematic decrease in the isotropic chemical shift as n decreases, with resolved signals resulting from contributions primarily from Y species with different n. Different arrangements of B site cations (i.e., environments with the same n, but different positions of the Sn/Ti NNN, show typically smaller differences in chemical shift. However, as shown in Figure 4b, these smaller differences account for the pronounced splitting in the resonance at ∼100 ppm (shown expanded in the inset) that was observed, but not explained, in previous work.13,14 It is now clear that this splitting results from the different shifts seen for the 1,2,4-Sn3Ti3 environment (∼5 ppm higher than for 1,2,3-Sn3Ti3 and 1,3,5-Sn3Ti3 environments). However, it can be seen in Figure 4c (where δisocalc values for Y species in all structural models are plotted) and in the spectra shown in the Supporting Information that in most cases there is considerable overlap of the ranges of chemical shift seen for different environments. Therefore, although it may be possible to decompose spectra (and consider integrated intensities of individual resonances, as in previous work13,14) at low Sn and Ti concentrations, for materials with higher levels of disorder this is simply not accurate, with the spectral intensity at any point arising from contributions from species with different n. Figure 4c also shows that as the number of Ti NNN increases (i.e., n decreases), there is significantly more variation in δisocalc for a particular local environment, leading to greater overlap of the spectral lineshapes. This also explains the observation in previous computational work (which modeled disorder simply by varying the number and arrangement of Sn/Ti cations around just one Y (or Sn) cation in the unit cell, in a simple “cluster-like” approach) of unusual values of δisocalc for some species (i.e., values very different from those observed for similar local environments).13,14

Figure 4.

Figure 4

Open in a new tab

Predicted, assuming the limit of full disorder, (a, b) 89Y and (d, e) 119Sn MAS NMR spectra of Y2SnTiO7. (c, f) Plots of (c) 89Y and (f) 119Sn δisocalc as a function of the number of Sn NNN, n, for all Y and Sn species in all SOD-generated structural models.

It is clear from Figure 4c that when more structural models and variations in the longer-range environment are considered, a much larger range of δisocalc is often observed. (For direct comparison, see the Supporting Information for calculations modeling disorder using this “cluster-like” approach, performed with the parameters and version of the code given in the Computational Methods.) Figure 5a reveals that these unusual shifts result from a deviation of the O8a–Y–O8a bond angle away from the value of 180° observed for the ideal pyrochlore structure. However, there is little effect of this distortion (which can be quite significant, at up to 18° in the most extreme cases) on 89Y Ωcalc, as shown in Figure 5b. As shown in the Supporting Information, 89Y Ωcalc depends primarily on the number of Sn NNN, n, and on the mean Y–O8a distance, in agreement with previous work.16

Figure 5.

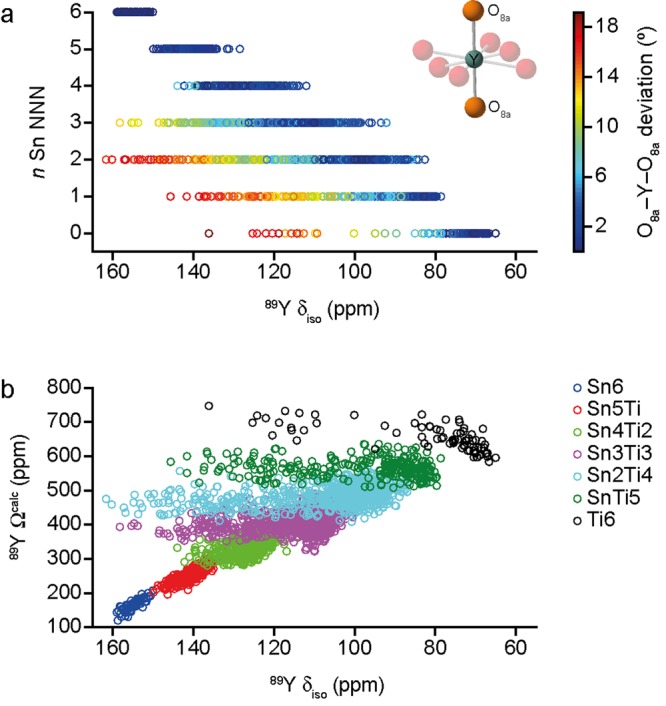
Figure 5

Open in a new tab

(a) Plot of 89Y δisocalc as a function of the number of Sn NNN, n, for all Y and Sn species in all SOD-generated structural models of Y2(SnTi)2O7, with points colored according to the deviation of the O8a–Y–O8a bond angle away from 180°. (b) Plot of 89Y δisocalc against Ωcalc, with points colored according to n.

The decomposition of the predicted 119Sn MAS NMR spectrum of Y2SnTiO7 in Figure 4d and e reveals a significant overlap of contributions from the different NNN arrangements of cations around Sn. As shown in the Supporting Information, a similar level of overlap is seen for most compositions. Figure 4f shows that there is a decrease in 119Sn δisocalc as Ti is substituted onto the NNN B sites,15 but that this decrease is smaller in magnitude as the number of Ti NNN increases. This results, as shown in Figure 3c and d, in increased overlap of the spectral resonances as the level of Ti substitution increases, preventing any accurate decomposition of the 119Sn spectral lineshape and hindering the extraction of detailed information about cation disorder. However, there is generally good agreement between the experimental and predicted spectra, validating the ensemble-based approach used.

The good agreement observed between experimental and predicted NMR spectra suggests there is an essentially random distribution of the B site cations in these materials; that is, the limit of full disorder, where individual subspectra are weighted only by the configurational degeneracy of the corresponding structural model, holds. For comparison, Figure 6 shows 89Y NMR spectra of Y2SnTiO7 simulated with an additional Boltzmann weighting for each subspectrum, determined according to the relative energies of the structural models (as described in the Supporting Information). Spectra have been simulated for temperatures of 298, 500, 1000, and 2000 K, although it should be noted that the earlier thermodynamic analysis predicts theoretically a miscibility gap would exist for this solid solution at lower temperature. At the lower temperatures, increased intensity is seen at the extremities of the spectral range, suggesting the structural models with lower relative energy have more Sn-rich and Ti-rich local environments, i.e., that these models have more clustering of like cations. However, in general, better agreement with the experimental spectrum is seen at the higher temperatures, suggesting that the assumption of the limit of full disorder is reasonable in this system and likely reflects the higher synthesis temperatures used experimentally. It is clear from this analysis that no configurational equilibrium is established at lower temperatures, which is consistent with the prediction above that thermodynamic equilibrium at low temperatures involves phase separation. Movies included in the Supporting Information also show that each simulated Y2SnTiO7 subspectrum is very different, but that only when a large number of these are combined does the spectrum approach that seen experimentally.

Figure 6.

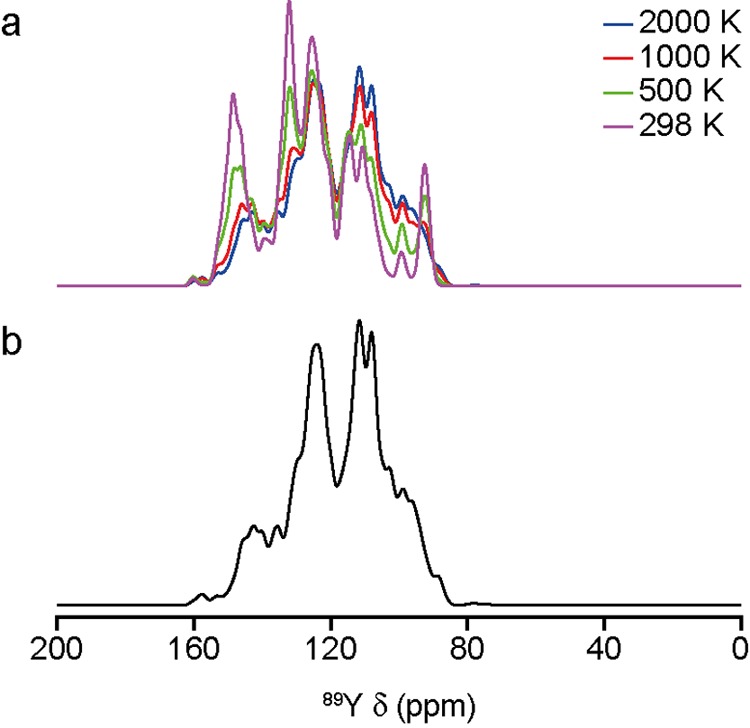
Figure 6

Open in a new tab

(a) Predicted 89Y MAS NMR spectra of Y2SnTiO7, including a Boltzman weighting of the structural models for T = 298, 500, 1000, and 2000 K. For comparison, a similar plot in the limit of full disorder is shown in (b).

It is known that some properties of solid solutions can be evaluated using a single configuration (or SQS, as described above) that best represents the mixed system.10 For Y2SnTiO7, the structural model generated by SOD that is closest to the SQS model has an energy close to that of the ensemble average for this composition and exhibits average numbers of first- and second-nearest neighbor Ti–Ti, Sn–Ti, and Sn–Sn pairs identical to the perfectly disordered structure for this composition. The 89Y MAS NMR spectrum simulated for this structural model is shown in the Supporting Information. Although this spectrum has better agreement with experiment than those for most structural models for this composition (see S6.1 in the Supporting Information), it is clear that it is not possible to reproduce either the summed simulated spectrum (i.e., the full disorder limit) or the experimental NMR spectrum with one “average” structure, illustrating the sensitivity of the NMR parameters to the specific local environment.

Although there is generally good agreement between experimental and simulated spectra, Figure 3 shows that for both 89Y and 119Sn NMR, the agreement is poorer at lower levels of Ti/Sn substitution. For example, when x = 0.875 the number and position of the peaks seen in the simulated 89Y NMR spectra match very well with experiment, but the relative intensities are in poorer agreement, with a Sn6:Sn5Ti:Sn4Ti4 ratio of 1.0:0.7:0.4 seen experimentally and 1.00:1.33:0.33 in the simulated spectrum, as shown in Table 2. For this example, this difference cannot arise from the assumption of full disorder or the need to apply any Boltzmann weighting; only three unique arrangements of atoms are possible within the unit cell for this composition (with gm = 48, 24, and 48), but all have the same number of Y species with 6, 5, and 4 Sn NNN. While applying a Boltzmann weighting might have small effects on the intensities at an exact chemical shift (and therefore the width and shape of the lines in the simulated spectrum), it would not affect the integrated spectral intensities. It is clear that to achieve any better agreement with experiment at these low concentrations it would be necessary to consider disorder on a length scale greater than the unit cell, where all the possible local and longer-range environments are represented. The use of a supercell, however, would be extremely computationally demanding at this level of theory, with even a 1 × 1 × 2 supercell having 346 possible unique arrangements of atoms (35 960 total arrangements) for x = 0.875. The probability of finding Y atoms with n Sn NNN for this extended supercell (taking into account the degeneracies of each structural model) is given in Table 2. These are closer to the relative intensities seen in the experimental spectrum. However, the number of structural models that need to be considered increases significantly when the level of substitution increases, and with the size of the supercell, ensemble modeling and computation quickly become unfeasible.

Table 2. Probability of Finding Y Atoms with n Sn NNN in Different Structural Models of Y2(Sn0.875Ti0.125)2O7a.

NNN environment unit cell 1 × 1 × 2 supercell infinite cell experiment
Sn6 0.3750 0.4157 0.4488 0.48 (5)
Sn5Ti 0.5000 0.4338 0.3847 0.33 (5)
Sn4Ti2 0.1250 0.1356 0.1374 0.19 (5)
Sn3Ti3 0.0000 0.0145 0.0262  
Sn2Ti4 0.0000 0.0004 0.0028  
SnTi5 0.0000 0.0000 0.0002  
Ti6 0.0000 0.0000 4 × 10–6  
Open in a new tab
a

The corresponding data from experiment (Figure 3a, x = 0.875) are shown for comparison.

It is possible to predict the probability of finding Y atoms with n Sn NNN in the limit of an infinite supercell (assuming random disorder) using simple statistics. According to the binomial theorem, the probability (P) of a Y atom having n Sn NNN is given by

graphic file with name ja9b09036_m003.jpg 3

where Ω is the number of possible permutations of the n substitutions on the six surrounding B sites and x denotes the chemical composition. The improved agreement with experiment (seen in Table 2) suggests that disorder is relevant on length scales greater than that of the unit cell. However, such a simple statistical approach is only possible in the limit of full disorder, as a Boltzmann weighting cannot be applied to individual atomic arrangements. Furthermore, comparison to experiment is only possible when well-resolved resonances, which can be easily attributed to a single and specific local environment, can be identified. While this is the case for the 89Y NMR spectrum of Y2(SnxTi1–x)2O7 when x = 0.875, as the Ti content increases, the spectral lineshapes become more complex and more overlapped (as shown in Figure 3), preventing such a simple analysis and comparison. It is also worth noting, for example, that although Figure 6 shows generally better agreement is obtained between experiment and theory at higher temperatures for Y2SnTiO7, this does result in poorer agreement at the highest shifts. While this could indicate some weak preference for clustering or ordering, these differences could also result from the limitations of using a single unit cell. When the spectral overlap is significant, the ensemble approach (even for a single unit cell) is crucial for understanding the contributions to the spectrum, the origin of the spectral lineshapes observed, and the relative importance of different atomic arrangements in the real material. More sophisticated approaches need to be developed that are accurate at both low and intermediate concentrations, possibly based on grand-canonical ensembles where shifts obtained for supercells with different compositions could be combined to model the NMR spectrum at one composition.

Conclusions

While disorder can have a significant impact on the physical and chemical properties of a material, the characterization of disordered solids poses a considerable challenge, for both experiment and computation. The sensitivity of NMR spectroscopy to the atomic-scale environment provides an ideal opportunity for understanding disorder at the local level, rather than relying on a structural picture averaged over space and time. Here, we have shown that ensemble-based modeling can be used to interpret the complex and overlapped spectral lineshapes than often result in disordered materials, providing insight into the structural models likely to be relevant to the real system. Conventionally, in NMR spectroscopy considerable effort is focused on the assignment of signals to specific types of chemical environments. However, it is clear from the results shown here that this is not always possible for complex and disordered solids, with considerable variation in the shifts seen for similar environments and significant overlap of signals resulting from different environments. Indeed, although it is tempting to use this computational work to facilitate spectral assignment, this is, in fact, nonsensical, as the driving force for spectral assignment is to obtain an understanding of the type (and proportion) of species present in order to construct structural models that are consistent with these observations. However, a complete set of structural models is available directly in the ensemble-based modeling approach exploited here, with DFT enabling insight into their relative energies and the NMR parameters associated with different species. Structural insight is obtained by direct comparison to the experimental spectrum, rather than in a two-step process that relies initially on accurate spectral interpretation and analysis. The possession of a complete set of structural models for a system is, however, able to provide an understanding of the origin of the interactions that affect the nuclear spins and, in particular, their dependence on geometric parameters. This fundamental insight will be useful for complex or larger systems, where it may not be possible to generate a complete set of models.

For Y2(Sn,Ti)2O7 we have shown good agreement between predicted and experimental spectra in the limit of full disorder, i.e., where the summed spectrum for a fixed composition contains subspectra that are weighted only by their configurational degeneracy. The inclusion of a Boltzmann weighting confirms best agreement with experiment is obtained for higher temperatures, but highlights that the atomic configurations with lower enthalpy contain more clustering of like atoms. It is also interesting to note that the thermodynamic analysis (using the subregular solid solution model) predicts a miscibility gap in this system at temperatures of <800 K, with the observation of a solid solution experimentally suggesting the materials produced are metastable at room temperature: the high-temperature cation distribution is frozen and diffusion barriers prevent configurational equilibrium at lower temperatures. This analysis also reveals that it is energetically less favorable to substitute the smaller Ti4+ cation into Y2Sn2O7 than vice versa, initially perhaps a surprising observation. However, although the Y2Ti2O7 pyrochlore itself is stable, Ti4+ appears too small to satisfy the bonding requirements of the surrounding oxygens in the Sn-rich material owing to the more covalent nature of the Sn–O bond, which leads to a less flexible structure, as discussed in the Supporting Information.

Although the experimental and predicted spectra show a high level of similarity, the intensity of the spectral resonances is in poorer agreement at low levels of substitution. The restricted number of unique structural models in these cases suggests that disorder should be considered at a length scale greater than that of the ordered unit cell to achieve better agreement with experiment. Although currently computationally demanding in many cases (particularly for the subsequent calculation of NMR parameters), more routine use of supercells may become possible with future advances in hardware or could be possible in cases where there is less significant overlap of the spectral lineshapes and analysis need only consider the number of each type of environment present. As the level of disorder increases, it will, of course, become impossible to generate a “complete set” of structures, and alternative approaches will be required to generate sufficiently large sets of chemically relevant structural models. The approach previously used for glasses, where models were generated using molecular dynamics,4,33 will become increasingly useful in these cases, as will the methods emerging from new machine learning work.34

In conclusion, we have shown that ensemble-based modeling approaches offer great potential for understanding configurational disorder, especially when used in conjunction with experimental NMR spectroscopy. Such an approach does, however, require a change in the mindset of the spectroscopist, moving away from the need for a detailed understanding of every resonance, shoulder or splitting observed in the experimental spectrum, but instead viewing the whole spectrum as the combined result of signals from a set of structural models that can be directly compared to computational predictions. With future developments in hardware and in computational methods, ensemble-based approaches for larger and more complicated systems will become possible, enabling more detailed structural insight and aiding future materials design.

Acknowledgments

The authors would like to thank the ERC (EU FP7 Consolidator Grant 614290 “‘EXONMR’”). S.E.A. would like to thank the Royal Society and Wolfson Foundation for a merit award. We acknowledge support from the Collaborative Computational Project on NMR Crystallography CCP-NC funded by EPSRC (EP/M022501/1) and the UKCP consortium funded by EPSRC (EP/K013564/1). For computational resources we are grateful to the UK Materials and Molecular Modelling Hub, which is partially funded by EPSRC (EP/P020194/1), and to the UK HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202). The research data (and/or materials) supporting this publication can be accessed in refs (32) and (35).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.9b09036.

  • Information on convergence and referencing of DFT calculations, calculation of thermodynamic properties, decomposition of spectral lineshapes, calculations using “cluster-based” models, information on 89Y shielding anisotropy. and simulated subspectra for individual models (PDF)

  • Supporting movie (MP4)

  • (MP4)

The authors declare no competing financial interest.

Supplementary Material

ja9b09036_si_001.pdf (1MB, pdf)
ja9b09036_si_002.mp4 (276.5KB, mp4)
ja9b09036_si_003.mp4 (102KB, mp4)

References

  1. Capasso F. Band-Gap Engineering: From Physics and Materials to New Semiconductor Devices. Science 1987, 235, 172–176. 10.1126/science.235.4785.172. [DOI] [PubMed] [Google Scholar]
  2. Ashbrook S. E.; Dawson D. M.; Griffin J. M.. Solid-State Nuclear Magnetic Resonance Spectroscopy. In Local Structure Characterisation; Bruce D. W., O’Hare D., Walton R. I., Eds.; John Wiley & Sons Ltd, 2014; pp 1–88. [Google Scholar]
  3. Moran R. F.; Dawson D. M.; Ashbrook S. E. Exploiting NMR Spectroscopy for the Study of Disorder in Solids. Int. Rev. Phys. Chem. 2017, 35, 39–115. 10.1080/0144235X.2017.1256604. [DOI] [Google Scholar]
  4. Bonhomme C.; Gervais C.; Babonneau F.; Coelho C.; Pourpoint F.; Azais T.; Ashbrook S. E.; Griffin J. M.; Yates J. R.; Mauri F.; Pickard C. J. First-Principles Calculation of NMR Parameters Using the Gauge Including Projector Augmented Wave Method: A Chemist’s Point of View. Chem. Rev. 2012, 112, 5733–5779. 10.1021/cr300108a. [DOI] [PubMed] [Google Scholar]
  5. Ashbrook S. E.; McKay D. Combining Solid-State NMR Spectroscopy with First-Principles Calculations - a Guide to NMR Crystallography. Chem. Commun. 2016, 52, 7186–7204. 10.1039/C6CC02542K. [DOI] [PubMed] [Google Scholar]
  6. Grau-Crespo R.; Waghmare U. V.. Simulation of Crystals with Chemical Disorder at Lattice Sites. In Molecular Modeling for the Design of Novel Performance Chemicals and Materials; Rai B., Ed.; CRC Press, 2012; pp 299–322. [Google Scholar]
  7. Sanchez J. M.; Ducastelle F.; Gratias D. Generalized Cluster Description of Multicomponent Systems. Phys. A 1984, 128, 334–350. 10.1016/0378-4371(84)90096-7. [DOI] [Google Scholar]
  8. Wu Q.; Bong H.; Song T.; Gao J.; Shi S. Cluster Expansion Method and its Application in Computational Materials Science. Comput. Mater. Sci. 2016, 125, 243–254. 10.1016/j.commatsci.2016.08.034. [DOI] [Google Scholar]
  9. Zunger A.; Wang L. G.; Hart G. L. W.; Sanati M. Obtaining Ising-like Expansions for Binary Alloys from First Principles. Modelling Simul. Mater. Sci. Eng. 2002, 10, 685–706. 10.1088/0965-0393/10/6/306. [DOI] [Google Scholar]
  10. Zunger A.; Wei S. H.; Ferreira L. G.; Bernard J. E. Special Quasirandom Structures. Phys. Rev. Lett. 1990, 65, 353–356. 10.1103/PhysRevLett.65.353. [DOI] [PubMed] [Google Scholar]
  11. Grey C. P.; Dobson C. M.; Cheetham A. K.; Jakeman R. J. B. Studies of Rare-Earth Stannates by l19Sn MAS NMR. The Use of Paramagnetic Shift Probes in the Solid State. J. Am. Chem. Soc. 1989, 111, 505–511. 10.1021/ja00184a017. [DOI] [Google Scholar]
  12. Grey C. P.; Smith M. E.; Cheetham A. K.; Dobson C. M.; Dupree R. 89Y MAS NMR Study of Rare-Earth Pyrochlores: Paramagnetic Shifts in the Solid State. J. Am. Chem. Soc. 1990, 112, 4670–4765. 10.1021/ja00168a007. [DOI] [Google Scholar]
  13. Ashbrook S. E.; Whittle K. R.; Lumpkin G. R.; Farnan I. 89Y Magic-Angle Spinning NMR of Y2Ti2-xSnxO7 Pyrochlores. J. Phys. Chem. B 2006, 110, 10358–10364. 10.1021/jp060844q. [DOI] [PubMed] [Google Scholar]
  14. Reader S. W.; Mitchell M. R.; Johnston K. E.; Pickard C. J.; Whittle K. R.; Ashbrook S. E. Cation Disorder in Pyrochlore Ceramics: 89Y MAS NMR and First-Principles Calculations. J. Phys. Chem. C 2009, 113, 18874–18883. 10.1021/jp906764e. [DOI] [PubMed] [Google Scholar]
  15. Mitchell M. R.; Reader S. W.; Johnston K. E.; Pickard C. J.; Whittle K. R.; Ashbrook S. E. 119Sn MAS NMR and First-Principles Calculations for the Investigation of Disorder in Stannate Pyrochlores. Phys. Chem. Chem. Phys. 2011, 13, 488–497. 10.1039/C0CP01274B. [DOI] [PubMed] [Google Scholar]
  16. Mitchell M. R.; Carnevale D.; Orr R.; Whittle K. R.; Ashbrook S. E. Exploiting the Chemical Shielding Anisotropy to Probe Structure and Disorder in Ceramics: 89Y MAS NMR and First-Principles Calculations. J. Phys. Chem. C 2012, 116, 4273–4286. 10.1021/jp2105133. [DOI] [Google Scholar]
  17. Fernandes A.; Moran R. F.; Sneddon S.; Dawson D. M.; McKay D.; Bignami G. P. M.; Blanc F.; Whittle K. R.; Ashbrook S. E. 17O Solid-State NMR Spectroscopy of A2B2O7 Oxides: Quantitative Isotopic Enrichment and Spectral Acquisition?. RSC Adv. 2018, 8, 7089–7101. 10.1039/C8RA00596F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Grau-Crespo R.; Hamad S.; Catlow C. R. A.; de Leeuw N. H. Symmetry-Adapted Configurational Modelling of Fractional Site Occupancy in Solids. J. Phys.: Condens. Matter 2007, 19, 256201. 10.1088/0953-8984/19/25/256201. [DOI] [Google Scholar]
  19. Pickard C. J.; Mauri F. All-Electron Magnetic Response with Pseudopotentials: NMR Chemical Shifts. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 63, 245101. 10.1103/PhysRevB.63.245101. [DOI] [Google Scholar]
  20. Clark S. J.; Segall M. D.; Pickard C. J.; Hasnip P. J.; Probert M. J.; Refson K.; Payne M. C. First-Principles Methods using CASTEP. Z. Kristallogr. - Cryst. Mater. 2005, 220, 567–570. 10.1524/zkri.220.5.567.65075. [DOI] [Google Scholar]
  21. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 1865–1868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  22. Vanderbilt D. Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism. Phys. Rev. B: Condens. Matter Mater. Phys. 1990, 41, 7892–7895. 10.1103/PhysRevB.41.7892. [DOI] [PubMed] [Google Scholar]
  23. Yates J. R.; Pickard C. J.; Payne M. C.; Mauri F. Relativistic Nuclear Magnetic Resonance Chemical Shifts of Heavy Nuclei with Pseudopotentials and the Zeroth-Order Regular Approximation. J. Chem. Phys. 2003, 118, 5746–5743. 10.1063/1.1541625. [DOI] [Google Scholar]
  24. Monkhorst H. J.; Pack J. D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  25. Ganguly J.Thermodynamics in Earth and Planetary Sciences; Springer-Verlag: Berlin, 2008. [Google Scholar]
  26. Kennedy B. J. Structural Trends in Pyrochlore Oxides. Mater. Sci. Forum 1996, 228, 753. 10.4028/www.scientific.net/MSF.228-231.753. [DOI] [Google Scholar]
  27. Subramanian M. A.; Aravamudan G.; Subba Rao G. V. Oxide Pyrochlores - a Review. Prog. Solid State Chem. 1983, 15, 55–143. 10.1016/0079-6786(83)90001-8. [DOI] [Google Scholar]
  28. Chakoumakos B. C. Systematics of the Pyrochlore Structure Type, Ideal A2B2X6Y. J. Solid State Chem. 1984, 53, 120–129. 10.1016/0022-4596(84)90234-2. [DOI] [Google Scholar]
  29. Shannon R. D. Revised Effective Ionic Radii and Systematic Studies of Interatomie Distances in Halides and Chaleogenides. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1976, A32, 751–767. 10.1107/S0567739476001551. [DOI] [Google Scholar]
  30. Benny S.; Grau-Crespo R.; de Leeuw N. A Theoretical Investigation of α-Fe2O3-Cr2O3 Solid Solutions. Phys. Chem. Chem. Phys. 2009, 11, 808–815. 10.1039/B815907F. [DOI] [PubMed] [Google Scholar]
  31. Ektarawong A.; Simak S. I.; Alling B. First-Principles Prediction of Stabilities and Instabilities of Compounds and Alloys in the Ternary B-As-P System. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 024202. 10.1103/PhysRevB.96.024202. [DOI] [Google Scholar]
  32. Moran R. F.Investigating the Use of First-Principles Calculations for NMR Studies of Disorder in the Solid State, Ph.D. Thesis, University of St Andrews, 2019. [Google Scholar]
  33. Charpentier T.; Menziani M. C.; Pedone A. Computational Simulations of Solid State NMR spectra: A New Era in Structure Determination of Oxide Glasses. RSC Adv. 2013, 3, 10550–10578. 10.1039/c3ra40627j. [DOI] [Google Scholar]
  34. Chaker Z.; Salanne M.; Delaye J. M.; Charpentier T. NMR Shifts in Aluminosilicate Glasses via Machine Learning. Phys. Chem. Chem. Phys. 2019, 21, 21709–21725. 10.1039/C9CP02803J. [DOI] [PubMed] [Google Scholar]
  35. Moran R. F.; McKay D.; Tornstrom P. C.; Aziz A.; Fernandes A.; Grau-Crespo R.; Ashbrook S. E.. Ensemble-Based Modelling of the NMR Spectra of Solid Solutions: Cation Disorder in Y2(Sn, Ti)2O7. Dataset; University of St Andrews Research Portal, 10.17630/47d302a7-1119-47ad-9db3-effe4d3d3bee, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja9b09036_si_001.pdf (1MB, pdf)
ja9b09036_si_002.mp4 (276.5KB, mp4)
ja9b09036_si_003.mp4 (102KB, mp4)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES