Tractography Reproducibility Challenge with Empirical Data (TraCED): The 2017 ISMRM Diffusion Study Group Challenge

Abstract

Background:

Fiber tracking with diffusion-weighted magnetic resonance imaging has become an essential tool for estimating in vivo brain white matter architecture. Fiber tracking results are sensitive to the choice of processing method and tracking criteria.

Purpose:

Phantom studies provide concrete quantitative comparisons of methods relative to absolute ground truths, yet do not capture variabilities because of in vivo physiological factors. Reproducibility does not assess validity of brain connections yet, is still of importance because it describes the variability for an algorithm in group studies. The ISMRM 2017 TraCED challenge was created to fulfill the gap.

Study Type:

Systematic review of algorithms and tract reproducibility study

Subjects:

Single healthy volunteer

Field Strength/Sequence:

3.0 T, two different scanners of the same manufacturer. The multi-shell acquisition included b-values of 1000, 2000 and 3000 s/mm² with 20, 45 and 64 diffusion gradient directions per shell, respectively.

Assessment:

Nine international groups submitted 46 tractography algorithm entries each consisting 16 tracts per scan. The algorithms were assessed using intra-class correlation (ICC) and dice similarity measure.

Statistical Tests:

Containment analysis was performed to assess if the submitted algorithms had containment within tracts of larger volume submissions. This also serves the purpose to detect if spurious submissions had been made.

Results:

7The top five submissions had high ICC & Dice > 0.88. Reproducibility is high within top 5 submissions when assessed across sessions or across scanners: 0.87–0.97. Containment analysis shows that top 5 submissions are contained within larger volume submissions. From the total of 16 tracts as an outcome relatively the number of tracts with high, moderate and low reproducibility are 8, 4 and 4.

Conclusion:

The different methods clearly result in fundamentally different tract structures at the more conservative specificity choices. Data and challenge infrastructure remain available for continued analysis and provide a platform for comparison.

INTRODUCTION

Diffusion weighted magnetic resonance imaging (DW-MRI) is a technique which allows for non-invasive mapping of the human brain’s micro-architecture at milli-metric resolution. Using voxel-wise fiber orientation reconstruction methods, tractography can provide quantitative and qualitative information for studying structural brain connectivity and continuity of neural pathways of the nervous system in vivo. There have been many algorithms, global, iterative, deterministic and probabilistic, that reconstruct streamlines using fiber reconstruction methods. Tractography was conceived[1, 2] using one of the first fiber reconstruction method, diffusion tensor imaging (DTI) [1]. However, DTI has a well-known limitation: it cannot resolve complex fiber configurations [3]. With the advancement in acquisitions protocols allowing for better resolution and higher number of gradient values new methods for reconstruction of local fiber have been developed. These methods are commonly referred to as high angular resolution diffusion imaging (HARDI), e.g., q-ball, constrained spherical deconvolution (CSD), persistent angular structure (PAS) [4–6]. HARDI methods enable characterization of more than a single fiber direction per voxel, but have been often shown to be limited when more than two fiber populations exist per voxel [7–9]. While there is definite gain in sensitivity when using HARDI methods, there remain critical questions of their reproducibility [10].

There have been many validation efforts that aim to assess the anatomical accuracy of tractography. Early studies investigated how well tractography followed large white matter trajectories through qualitative comparisons with dissected human samples [11], or previous primate histological tracings [12]. Later works on the macaque [13] or porcine [14] brains highlighted limitations and common errors in tractography. Recently, the sensitivity and specificity of tractography in detecting connections has been systematically explored against tracers in the monkey [15–17], porcine [18], or mouse [19] brains. The main conclusions drawn from these are (1) that algorithms always show a tradeoff in sensitivity and specificity (i.e. those that find the most true connections have the most false connections) (2) short-range connections are more reliably detected than long-range, (3) connectivity predictions do better than chance and thus have useful predictive power, and (4) tractography performs better when assessing connectivity between relatively large-scale regions rather than identifying fine details or connectivity.

Despite the wide range of validation studies, there have been few reproducibility studies of tractography [20–23]. Rather than ask how right (or wrong) tractography is, we ask how stable are the outputs of these techniques? Because tractography is an essential part of track segmentation, network analysis, and microstructural imaging, it is important that reproducibility is high, otherwise power is lost in group analyses or in longitudinal comparisons. In this study, given a standard, clinically realistic, diffusion protocol, we aim to assess how reproducible tractography results are between repeats, between scanners, and between algorithms.

Publicly organized challenges provide unique opportunities for research communities to fairly compare algorithms in an unbiased format, resulting in quantitative measures of the reliability and limitation of competing approaches, as well as potential strategies for improving consistency. In the diffusion MRI community, challenges have focused on recovering intra-voxel fiber geometries using synthetic data [24] and physical phantoms [20, 25]. Similarly, diffusion tractography challenges [21] have provided insights into the effects of different acquisition settings, voxel-wise reconstruction techniques, and tracking parameters on tract validity by comparing results to ground truth physical phantom fiber configurations [20, 22]. Recently, more clinically relevant evaluations have been put forth. For example, a recent MICCAI challenge benchmarked DTI tractography of the pyramidal tract in neurosurgical cases presenting with tumors in the motor cortex [26]. Towards this direction, the current challenge utilized a large-scale single subject reproducibility dataset, acquired in clinically feasible scan times. This challenge was intended to study reproducibility to describe the limitations for capturing physiological and imaging considerations prevalent in human data and evaluate the newest generation of tractography algorithms.

This paper is organized as follows. First, we present the analysis structure of this challenge to characterize which tracts are the most reproducible. Second, we characterize the variance across the tractography methods by design features and compare the potential containment of tracts on a per algorithm basis.

METHODS

DW-MRI Data Acquisition

Informed consent following Institutional Review Board (IRB) approval, was obtained to conduct this study.

The data were acquired with a multi-shell HARDI sequence on single healthy human subject. The two scanners were both Phillips, Achieva, 3T, Best, Netherlands. These are referred to as scanner ‘A’ and ‘B’. The three shells that were acquired: b=1000 s/mm², 2000s/mm² and 3000s/mm² with 20, 48 and 64 gradient directions respectively (uniformly distributed over a hemi-sphere and independently per shell, this was done in consideration of scanner hardware.). The other parameters were kept consistent for all shells. They are as follows: Delta=~48ms, delta=~37ms, partial fourier=0.77, TE = 99 ms, TR ~= 2920 ms and voxel resolution=2.5mm isotropic. A total of 15 non-weighted diffusion volumes ‘b0’ images interspersed as 5 per shell were acquired. Additionally, for scanner A & B, 5 reverse phase-encoded b0 images and 3 diffusion weighted directions were acquired to aid in distortion correction. The additional 3 diffusion-weighted direction volumes were acquired for ease of acquisition from the scanner. They do not contribute to the pre-processing of the data in any way.

Additionally, a T1-weighted reference image (MPRAGE) was acquired for each session per scanner (4 volumes total). A single volume of T1 was used which was registered to the first session of scanner A where the session had already been registered to the MNI template. This was done using a 6 degree of freedom rigid body registration.

For the initial data release, a technical issue resulted in 5 non-reverse phase-encoded b0 images for scanner A. Note that at the end of the challenge, the scanner ‘A’ data were completely re-acquired for both sessions with 5 reverse phase-encoded b0 images and 3 diffusion weighted directions. These data were released as supplementary material, but not included in the presented challenge data. Following the protocol for tractography in [25], we delineated six tracts cingulum (CNG) Left/Right (L/R), inferior longitudinal fasciculus (ILF) (L/R), inferior fronto-occipital (IFO) (L/R). The mean intra-class correlation (ICC) inter-scanner values for the original challenge data and the updated challenge data were 0.86 and 0.89, respectively. The mean difference between methods was 0.15 in terms of ICC. As expected, the inclusion of full reverse phase encoding for Scanner ‘A’ introduced a small increased in consistency relative to much larger differences between methods.

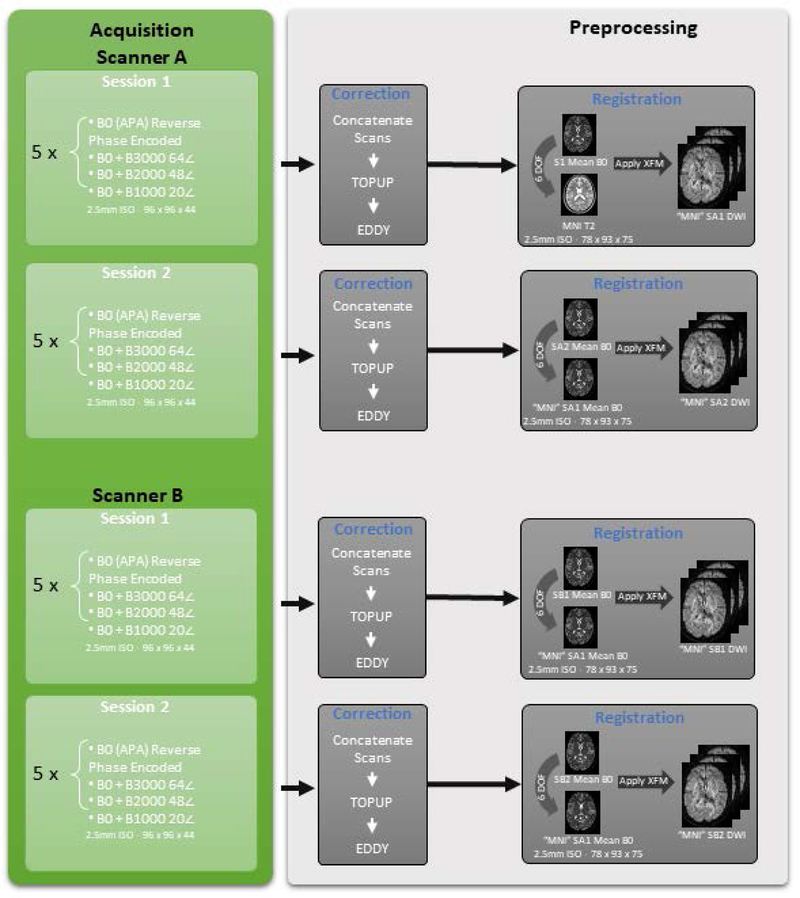
DW-MRI Data Pre-processing as illustrated in Fig 1, the 5 repeated acquisitions from each of the four sessions (two repeated on scanner A and B) were concatenated and corrected with FSL’s eddy and topup [27–29]. Intensity normalization was performed by dividing each diffusion weighted scan by the mean of all non-weighted diffusion volume (B0) per session. The average B0 from scanner A of the first sessions was rigidly (six degrees of freedom) registered [30] to a 2.5 mm T2 MNI template (this was done to ensure resampling from registration was done on both datasets). Next, the average B0 from the scanner A second session was rigidly registered to the average B0 of the registered scanner A first session B0 which had already been registered to the MNI space. Successively, the sessions from scanner B were registered to the sessions of scanner A. The b-vectors were rotated to account for the registration of the DW-MRI data [31].

Figure 1.

The acquisition per session included five repeats of a single b0 and successively at b-values of 3000, 2000 and 1000 s/mm² using 64, 48 and 20 gradient directions respectively. Each session was individually corrected using topup, eddy and then normalized. All the sessions were registered using flirt to the first session of scanner A.

The T1 weighted MPRAGE was rigidly registered to the average registered b0 from the first session of scanner A. This transformation was applied to the T1 maintaining 1 mm isotropic resolution, thus providing a high-resolution segmentation that may be converted into diffusion space by performing a simple down-sampling. Multi-atlas segmentation with non-local spatial STAPLE fusion was used for the segmentation of the T1 volume to 133 different ROI’s [32, 33]. Finally, Multi-atlas CRUISE (MaCRUISE) was used to identify cortical surfaces [34]. These were provided for ease of algorithm implementations.

Challenge Rules and Metrics

For each of the 20 HARDI datasets (5 repetitions x 2 sessions x 2 scanners), participants were asked to submit a tractogram (i.e., “fiber probability membership function”) for each well-modeled fiber structures (uncinate (UNC) [L/R], fornix (FNX) [L/R], genu of the corpus callosum, cingulum (CNG) [L/R], corticospinal tract (CST) [L/R], splenium of the corpus callosum, inferior longitudinal fasciculus (ILF) [L/R], superior longitudinal fasciculus (SLF) [L/R], and inferior fronto-occipital (IFO) [L/R](1)). Each tractogram is a NIFTI volume at the field of view and resolution of the T1-weighted reference space where the floating-point value (32-bit single precision) of each voxel is in [0, 1] and indicates the probability of the voxel belonging to the specified fiber tract. Thus, participants submitted a total of 320 (5 × 2 × 2 × 16) NIFTI volumes using the acquisition of both the scanners. Assessment of fiber fractions was supported (i.e., the sum across all tracts is <=1 with the remainder as background). However, strict probabilities where each voxel may have a high probability of 2 or more fibers with a sum greater than 1 were permitted as well.

Tractograms within a submission were compared based on reproducibility of the tracts (intra-class correlation coefficient (ICC) statistics for continuous values and Dice similarity scores based on maximum probability assignment at 0.5). Intra-session, inter-session, same scanner, and inter-scanner scanner metrics have been reported for quantitative interpretation. The ICC and dice value of unique number of combinations of pairs of repeats were used as data points for violin plots depicting results of intra-session, inter-session and inter-scanner. The unique combinations of repetitions were 40, 50 and 100 respectively for the three levels of reproducibility.

Containment Analysis

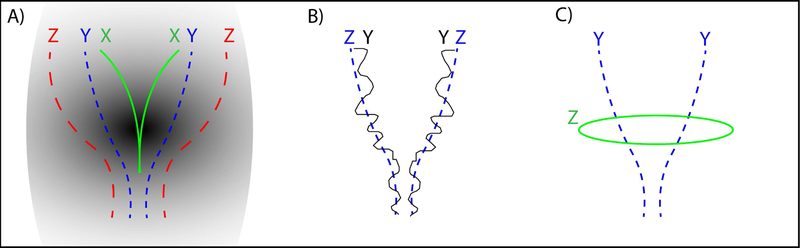
A key question is whether the differences in tractography are driven by different considerations of the volume of the track, i.e., the larger the volume is, the more likely the track may include the underlying true track. For example, it is plausible that a set of tractography methods could see the same underlying probabilistic connection pattern and choose to threshold it based on different preferences for the volume of tracks. If the preference was driving the tractography differences, then tractograms would essentially be able to be nested from smallest to largest. To examine this hypothesis, we define the property containment index (CI) for two tracts where

$$CI\left(A,B\right)=\left\{\begin{array}{c}\left|A\right|=0:1\\ \left|A\right|\ne 0\hspace{0.17em}|and\hspace{0.17em}\left|B\right|=0:0\\ otherwise:\left|A\cap B\right|/\left|B\right|\end{array}\right.$$ (1)

For the purposes of this discussion, we define the tractogram set to be the binary volume resulting at a 0.05 threshold of the mean of all results submitted for each algorithm. A visual understanding of containment index can be observed in Fig 3.

Fig 3.

A) Where the shape X is impeccably contained in Y and Y is contained in Z. The resulting containment CI(Y, X) = 1, CI(Z, X) = 1 and CI(Z, Y) = 1. B) Shape Y is a noisy representation of shape Z where CI(Y, Z) = 0.84. C) Shape Z is different from shape Y in a different orientation and the CI(Z,Y) = 0.17

Then, an optimal ordering (“nesting”) of tractogram entries can be computed by maximizing the containment energy (CE, i.e., sum of CI for all tracts versus the tracts earlier than the one under consideration):

$$\begin{gathered} {\text{argmax}}_{\mathit{o}\in perm\left(1\dots \left|Entry\right|\right)}CE= \\ {\text{argmax}}_{\mathit{o}\in perm\left(1\dots \left|Entry\right|\right)}{\sum }_i^N{\sum }_{{}^{j\le i}}^{N}CI\left(Entry\left\{o_i\right\},Entry\left\{i_j\right\}\right) \end{gathered}$$ (2)

Where perm denotes the permutation operator and Entry is a list of all entered tractograms. Conceptually, this procedure finds the ideal order to stack the tractograms inside each other where the first tract is “most inside” the subsequent ones and the last tract is “most outside” all others. We define <CI> as the average containment index of all nesting for the ordered entries that are smaller than or equal to an entry provides a quantitative way to examine “nesting” (note, this approach includes the self-containment index so that the first entry has a CI of 1). Then, we can see how the nesting holds up from the inner (#’1’) to the outer (#’46’) entry.

Tractography Reconstruction Methods

Team 1

A CSD-based probabilistic streamline tractography [35] seeding from the WM, with a step size of 0.2mm and a maximum deviation angle of 30 degrees (multi-shell data, 20 different datasets). The Tract Querier [36] was used to extract the bundles from anatomical constraints. The processing steps were identically applied to all dataset, without manual intervention any level of the processing. Automatic streamline filtering was applied using COMMIT [37]. The bundle volumes were also post-processed using a distance transform, resulting in weighted volumes with values corresponding to the distance to the closest boundary.

Team 2

Instead of using traditional tractography, which reconstructs every single fiber, the problem is viewed as an image segmentation task. A U-Net is used to segment each fiber bundle. As input features the peaks of the fiber orientation distribution functions were used. As ground truth data for training of the model manual segmentation was performed on the bundles of 30 HCP subjects. The approach is described in more detail in [38].

Team 3

Two shells at b-values of 1000 and 2000 s/mm² were used and the data was upsampled to 2mm isotropic. The tractography approach relies on free water invariant estimation of tensor (FERNET). The free water correction has been adapted from the work described in [39]. FA thresholds of 0.15 and 0.20 were used with angular thresholds of 25 and 35 degrees.

Team 4

The diffusion data ( b=3000 s/mm2) was up-sampled from 2.5mm isotropic to 1mm isotropic. WM mask was computed from the T1-weighted image using FSL FAST [40]. The fiber orientation distribution (FOD) function was estimated using CSD [41] implemented in DiPy [35]. An in-house probabilistic tractography algorithm was used [42]. Tractography parameters were: step size = 0.2 mm, maximal deviation = 20 degrees, number of seeds per voxel = 3. Bundle segmentation was performed using a novel automatic atlas-based bundle segmentation method [43]. The atlas was built from a HCP tractogram using the definition provided by the organisers.

Team 5

A technique for the estimation of the FOD was combined with a more traditional method for tract selection. Specifically, the spherical mean technique (SMT) was used to fit a microscopic compartment model of brain tissue [44] to the pre-processed multi shell diffusion data which subsequently enabled the recovery of the FOD quantitatively using CSD. Resulting FOD’s were used for whole-brain probabilistic tractography. Anatomically constrained tractography and spherical deconvolution informed filtering of tractograms were used to discard spurious tracts. Streamlines belonging to the tracts were selected using both atlas-derived regions (JHU-DTI) and ROI’s manually drawn [45] on track density images.

Team 6

A pipeline was evaluated for diffusion tensor bundle modeling using an atlas-based approach [46], implemented using the Quantitative Imaging Toolkit [47]. First, reference bundles were produced in the IIT tensor atlas consisting of include, exclude, and seed masks, which were deformed to subject space using DTI-TK. The pipeline included denoising using nonlocal means filtering, up-sampling to 1mm³ voxels, weighted-least squares tensor estimation, and streamline integration with step size 1mm, angle threshold 40 degrees, and a FA threshold of 0.15. Fiber bundles were extracted from the streamlines using the atlas masks with outlier rejection and finally discretized to native space voxels.

Team 7

The method described in [48] was augmented into a 2 pass tractography approach. Broad WM waypoints are defined in MNI template space at anatomically significant locations for each fascicle [49]. A deterministic tractography algorithm (based on CSD [50]) generates 500,000 streamlines. These streamlines are filtered by groups of waypoints warped from MNI space into patient space. Waypoints are then refined, only retaining waypoint voxels intersected by at least 1 streamline from each relevant fascicle. 5,000,000 streamlines generated by a CSD based probabilistic tractography algorithm (iFOD2), are filtered by refined waypoints then converted to fiber probability maps for each fascicle.

Team 8

Multi-shell compartment analysis is used on the pre-processed images (v1.0) to compute FODs [51]. Streamlines are computed using the algorithm in [52]. For each of the 20 images, 1.25 million streamlines are obtained using the following parameters: FOD cut-off threshold=0.04, min. length=10mm, max. length=250 mm, step=0.005 mm, σ_T² = 60°, σ_N² = 0.8°, σ_B² =0.8°, σ_K²=0.5, σ_t²=0.25, r=3.75 mm. No post-processing is done. Initially, bundles are obtained by filtering whole brain tractograms with manually drawn ROIs. Final bundles are obtained by removing dangling streamlines. After extracting the bundles, separate binary masks are generated on the 1 mm template.

Team 9

First, a morphological T1-weight image is used to segment the brain (estimate a new mask or tracts identified), identify different structures and different tissues. Then, whole-brain tractography with multi-tissue CSD is performed using four tractography methods. Moreover, multi-tractography-based tracts atlas is exploited to combine four tractography and to reduce the error from individuals tractography algorithms. Fiber bundles with multi-tractography-based tracts atlas were finally automatically segmented with a Tract Querier [36] method. Finally, tracts space will be converted to DWI space by affine transform to mapping tracts to binary images.

RESULTS

Table 1 presents a more detailed technical contribution of each of the works:

Table 1:

The table presents all the hyper-parameters of the different algorithms that were submitted and an overall evaluation of the algorithm in terms of ICC and Dice.

Synapse Submission id	Algorithm ID	ICC	DICE	b-value shells	HARDI/Tensor Model	Step size	Threshold angle	Additional Pre-Processing	Post-Processing
syn8533598	1A	0.7753	0.6364	All shells	CSD	0.2mm	30 degrees	NA	Distance transform of bundle volumes
syn8643780	1B	0.6857	0.6596	All shells	CSD	0.2mm	30 degrees	NA	NA
syn8643793	1C	0.6343	0.6346	All shells	CSD	0.2mm	30 degrees	NA	Distance transform of bundle volumes
syn8648608	1D	0.7707	0.5402	All shells	CSD	0.2mm	30 degrees	NA	Distance transform of bundle volumes
syn8649314	1E	0.6498	0.6508	All shells	CSD	0.2mm	30 degrees	NA	NA
syn8649322	1F	0.6192	0.6197	All shells	CSD	0.2mm	30 degrees	NA	Distance transform of bundle volumes
syn8649611	1G	0.6324	0.6332	All shells	CSD	0.2mm	30 degrees	NA	Automatic spurious fiber removal
syn8649618	1H	0.6494	0.6503	All shells	CSD	0.2mm	30 degrees	NA	Automatic spurious fiber removal
syn8649622	1I	0.6517	0.6526	All shells	CSD	0.2mm	30 degrees	NA	Automatic spurious fiber removal
syn8649650	1J	0.6662	0.6671	All shells	CSD	0.2mm	30 degrees	NA	Automatic spurious fiber removal
syn8649652	1K	0.6616	0.6624	All shells	CSD	0.2mm	30 degrees	NA	Automatic spurious fiber removal
syn8649654	1L	0.6362	0.637	All shells	CSD	0.2mm	30 degrees	NA	Automatic spurious fiber removal
syn8649656	1M	0.7093	0.7103	All shells	CSD	0.2mm	30 degrees	NA	Automatic spurious fiber removal
syn8649658	1N	0.6984	0.6994	All shells	CSD	0.2mm	30 degrees	NA	Automatic spurious fiber removal
syn8555229	2A	0.8506	0.7918	All shells + 30 HCP subjects	CSD + U-net	0.2mm	20 degrees	NA	Spurious Fiber Removal
syn8656474	3A	0.7379	0.7253	b1000 and b2000	Tensor Variant	0.2mm	25 degrees	Data Upsampling	NA
syn8656475	3B	0.6463	0.6341	b1000 and b2000	Tensor Variant	0.2mm	25 degrees	Data Upsampling	NA
syn8662707	4A	0.5285	0.5317	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8662708	4B	0.5822	0.3207	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8662709	4C	0.5881	NaN	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8662710	4D	0.5285	0.5317	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8662711	4E	0.5781	0.3182	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8662712	4F	0.5835	NaN	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8662713	4G	0.5285	0.5317	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8662714	4H	0.5291	0.4932	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8662715	4I	0.5302	NaN	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8662716	4J	0.5285	0.5317	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8662717	4K	0.5596	0.5323	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8662718	4L	0.5616	NaN	b3000	CSD	0.2mm	20 degrees	Data Upsampling	NA
syn8664905	5A	0.9738	0.8231	All shells	CSD	1.25mm	45 degrees	Additional Segmentation	SIFT2
syn8666133	6A	0.7702	0.7708	All shells	Tensor Variant	1mm	40 degrees	Denoising, Upsampling	Outlier Rejection
syn8666134	6B	0.8358	0.5742	All shells	Tensor Variant	1mm	40 degrees	Denoising, Upsampling	Outlier Rejection
syn8666135	6C	0.8171	0.7595	All shells	Tensor Variant	1mm	40 degrees	Denoising, Upsampling	Outlier Rejection
syn8666136	6D	0.817	0.7704	All shells	Tensor Variant	1mm	40 degrees	Denoising, Upsampling	Outlier Rejection
syn8666137	6E	0.8586	0.571	All shells	Tensor Variant	1mm	40 degrees	Denoising, Upsampling	Outlier Rejection
syn8666138	6F	0.8458	0.7646	All shells	Tensor Variant	1mm	40 degrees	Denoising, Upsampling	Outlier Rejection
syn8667007	7A	0.8868	0.6187	b3000	CSD	1.25mm	40 degrees	NA	NA
syn8666587	8A	0.86	0.8672	All shells	Compartment Model	0.005mm	60 degrees	NA	Spurious Fiber Removal
syn8666598	8B	0.8367	0.5166	All shells	Compartment Model	0.005mm	60 degrees	NA	Spurious Fiber Removal
syn8666602	8C	0.8349	0.5287	All shells	Compartment Model	0.005mm	60 degrees	NA	Spurious Fiber Removal
syn8666936	8D	0.8901	0.6409	All shells	Compartment Model	0.005mm	60 degrees	NA	Spurious Fiber Removal
syn8667021	8E	0.8145	0.4983	All shells	Compartment Model	0.005mm	60 degrees	NA	Spurious Fiber Removal
syn8667022	8F	0.8103	0.4773	All shells	Compartment Model	0.005mm	60 degrees	NA	Spurious Fiber Removal
syn8698866	9A	0.6145	0.6015	All shells	CSD	0.2mm	40 degrees	Addtional Segmentation	NA
syn8698867	9B	0.6968	0.6804	All shells	CSD	0.2mm	40 degrees	Addtional Segmentation	NA
syn8698868	9C	0.2703	0.2572	All shells	CSD	0.2mm	40 degrees	Addtional Segmentation	NA

• Team 1, Team 5, Team 6, Team 8 and Team 9 used all three shells of b-values provided in the dataset. Team 2 used all shells with data from an additional 30 subjects from the Human Connectome Project. Team 3 used shells of b-values 1000 and 2000 s/mm². Team 7 and Team 4 only used the shell of b-value 3000 s/mm².

• Additional pre-processing has been used by four teams. Team 4: Data was up-sampled to 1mm isotropic resolution. Team 6 used image de-noising techniques and up-sampled the data to 1.25mm. Team 5 and Team 9 used different styles of segmentation of the data presented for analysis.

• In terms of the fiber detection model, Team 6 and Team 3 used variants of tensor models while the others have used different variants of constrained spherical deconvolution. Notably Team 8 used a compartment analysis model using spherical harmonics.

• Considering the tractography parameters - the range of step sizes that have been used lie between 0.2–1.25mm. Threshold angle lies in the range of 20–40 degrees.

• Single fiber assumptions were considered with the condition of FA > 0.7 by teams Team 1 and Team 4. A notable observation here is that a general assumption was made by Team 6 to reject voxels which were less than 0.15 FA.

• Team 2, Team 6 and Team 8 post-processed the tractography results for removal of spurious fibers by defining different and specific constraints.

• Of note, Team 2 treated the tractography problem as a segmentation problem and developed a U-net which was trained on the HCP data. While Team 9 used a multi-atlas approach to tractography. The other teams used the general approach of probabilistic or deterministic tractography.

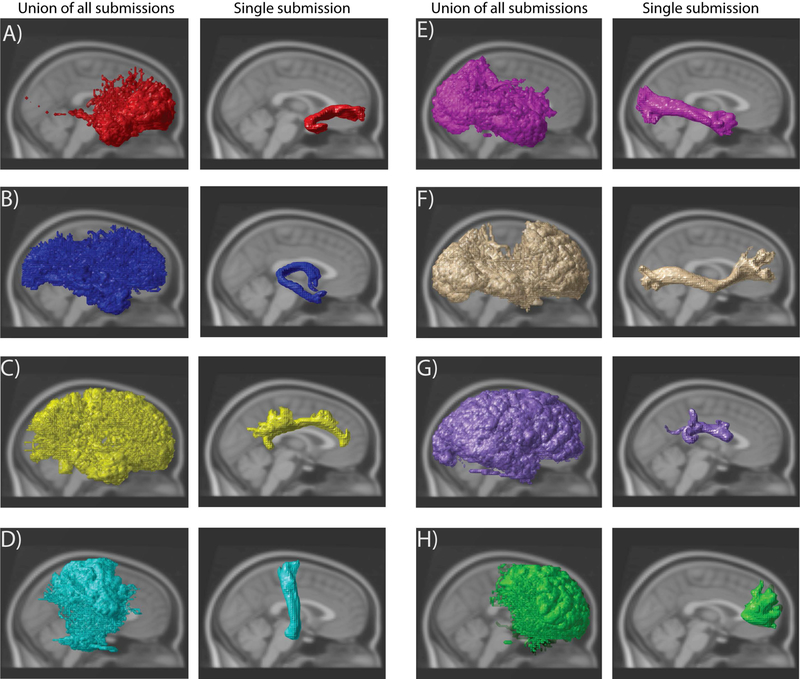
An overlay of all 46 submissions, for all estimated fiber pathways can be observed (Fig 2 Column 1 & 3). Only the left side has been shown as the right side is a similar observation. There are vast differences that can be noticed in the estimated pathways. The volume of the brain occupied by each tract from different submissions varied dramatically. When all 46 submissions are overlaid, tracts occupy 14–53% of the brain volumetrically (average – 34%). Specifically, the union of all entries for FNX (L/R), CNG (L/R), IFO (L/R) and SLF (L/R) cover (30.7, 25.8), (40.9, 37.2), (42.4, 46.1), (50.6, 53.3) respectively, while CST (L/R), ILF (L/R), UNC (L/R) and Fminor and Fmajor cover (23.6, 25.4), (33.4, 33.6), (14.3, 17.4), 44.3 and 34.1. Note that individual submissions appear qualitatively reasonable (Fig 2 Column 2 & 4).

Figure 2.

Left: An overlay of all the 46 submissions from all sessions that were acquired using both scanners per tract Right: An overlay of a single submission using all sessions that were acquired using both scanners per tract A) Uncinate left B) Fornix left C) Cingulum eft D) Corticospinal tract left E) Inferior Longitudinal Fasciculus left F) Inferior Fronto-Occipital Fasciculus left G) Superior Longitudinal Fasciculus left H) Fminor.

The number of algorithmic submission’s team wise are Team 1: 14, Team 2: 1, Team 3: 2, Team 4: 12, Team 5: 1, Team 6: 6, Team 7: 1, Team 8: 6 and Team 9: 3. It can be observed that the ICC range for the set of algorithms on a per team basis does not show a lot of variance. The ICC range of algorithms per team are Team 1 (0.61 – 0.77), Team 4 (0.52 – 0.58), Team 6 (0.77 – 0.85), Team 8 (0.81 – 0.89), Team 9 (0.27 – 0.69), Team 3 (0.64, 0.73), Team 2 (0.85), Team 7 (0.88) and Team 5 (0.97). The teams that submitted more than 3 algorithms show an average difference of 0.1 in terms of ICC.

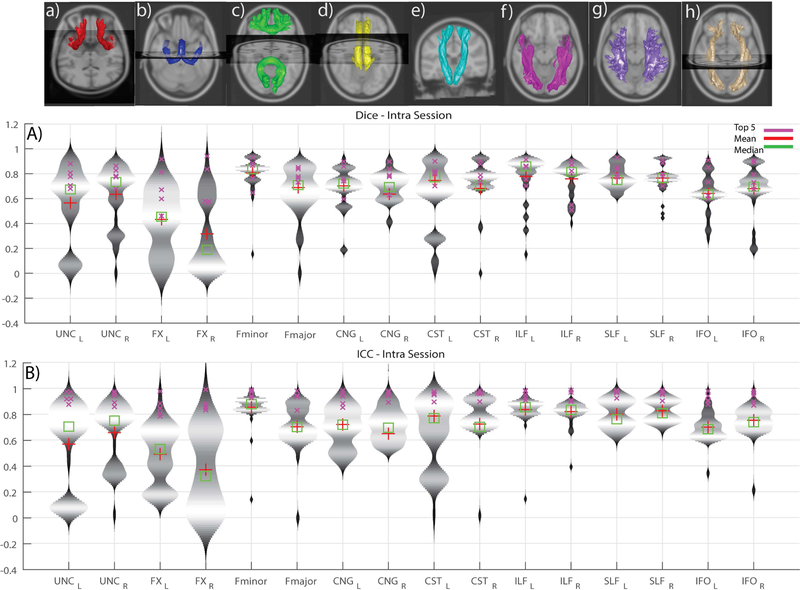
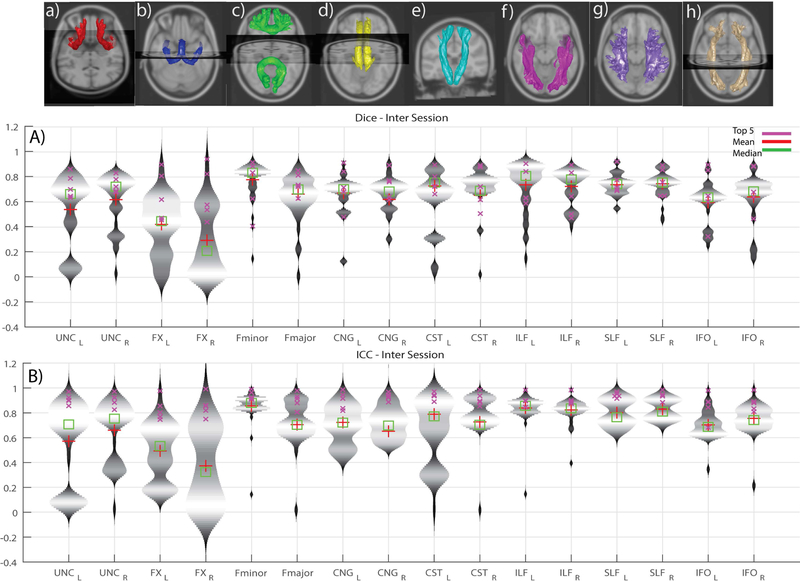
Violin plots (depict the probability density of the data) of ICC and Dice for intra-session reproducibility, inter-session, and inter-scanner measures of reproducibility are presented in Figures 4, 5 and 6, respectively. Since the observations are highly similar in the afore-mentioned figures we only present a detailed comment on Figure 4 which holds true for Figure 5 and 6 as well. This figure helps in identifying the low, moderate and high reproducibility tracts. The intra-session distributions (Figure 4B) across entries for UNC (L/R) and FNX (L/R) are bi-modal with a median of the lower mode less than 0.4 ICC. The CST (L) has a smaller fraction of the entries with ICC less than 0.4, while the remainder of the entries have only a few outlier entries less than 0.4 The inter-session (Fig. 5) and inter-scanner (Fig. 6) distributions were similar, with a slight increase in outlier entries for IFO (L/R). The patterns in the dice were similar when using a quality threshold of less than 0.4 dice.

Figure 4.

Violin plots of intra-session submissions across both the scanners per tract. A) Dice similarity coefficients B) Intra-class correlation coefficients. The top row depicts the median of the top five intra session submissions. The tracts are in the following order (L/R): a) Uncinate b) Fornix c) Fminor & Fmajor d) Cingulum e) Corticospinal tract f) Inferior longitudinal fasciculus g) Superior longitudinal fasciculus h) Inferior fronto-occipital tract

Figure 5.

Violin plots of inter-session submissions across both the scanners per tract. A) Dice similarity coefficients B) Intra-class correlation coefficients. The top row depicts the median of the top five inter session submissions. The tracts are in the following order (L/R): a) Uncinate b) Fornix c) Fminor & Fmajor d) Cingulum e) Corticospinal tract f) Inferior longitudinal fasciculus g) Superior longitudinal fasciculus h) Inferior fronto-occipital tract

Figure 6.

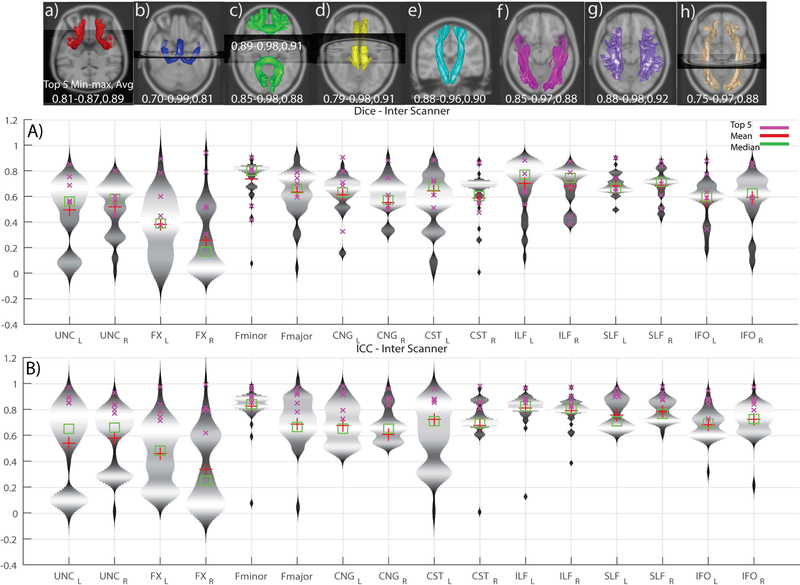
Violin plots of inter-scanner submissions across both the scanners per tract. A) Dice similarity coefficients B) Intra-class correlation coefficients. The top row depicts the median of the top five inter scanner submissions. The tracts are in the following order (L/R): a) Uncinate b) Fornix c) Fminor & Fmajor d) Cingulum e) Corticospinal tract f) Inferior longitudinal fasciculus g) Superior longitudinal fasciculus h) Inferior fronto-occipital tract

We define cutoffs for high, moderate, and low reproducibility on the inter-scanner reproducibility. High reproducibility was defined as a median ICC greater than 0.6 and less than 5% of entries less than 0.4 ICC. Moderate reproducibility was defined as median ICC greater than 0.4 and less than 25% of entries less than 0.4 ICC. Low reproducibility was defined as a median ICC less than 0.4 or more than 25% of entries less than 0.4 ICC. Hence, the high reproducibility tracts were Fminor, CST (/R), ILF (L/R), SLF (L/R) and IFO (L/R). The moderate reproducibility tracts were CST (L), Fmajor, CNG (L/R). The low reproducibility tracts were UNC (L/R) and FNX (L/R). This above is observed when looking at all submissions however when observing the top 5 submissions we see higher reproducibility.

When the analysis is restricted to only the top five submissions, we see a different picture that suggests substantively reproducible methods. The inter-scanner reproducibility among the top 5 entries in ICC (min-max, average) are shown in Fig 6.

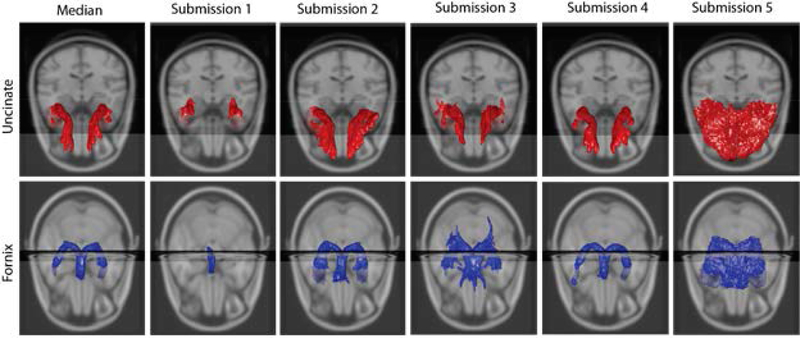
Figure 7 illustrates the top five entries for the tracts with the lowest inter-scanner reproducibility alongside the volumetric median (median per voxel from five submissions) of the top five entries. Qualitatively, the volumetric profiles of the UNC (L/R) and FNX (L/R) are very different across the top five entries. The first submission has small “core” tracts labeled, while the second, third and fifth found much larger spatial extents and the fourth was mid-way between.

Figure 7.

First row shows the median of Uncinate (L/R) and the top five submissions. The second row shows the median and submissions of Fornix (L/R).

DISCUSSION

The most reproducible tracts were Fminor, CST (\R), ILF (L\R), SLF (L\R), IFO (L\R), while the moderately reproducible tracts were Fmajor, CNG (L\R) and CST (\L). Lowest reproducibility tracts are UNC (L\R), FNX (L\R). These tracts have a well-spread/broad probability distribution. Note that the reproducibility of these tracts was maintained across imaging sessions and change of scanner. It is evident that all the algorithms entered are not consistently identifying the same fiber structures given the extreme variance observed. While most of the individual submissions show a reasonable detection of the tracts if observed from a ROI point of view, the difference between tract volumes between methods is quite high.

Previous validation studies have assessed sensitivity and specificity with respect ground truth. For example, comparisons with phantoms, histology, and known anatomy have provided valuable insight into the limitations of tractography [53]. Fibercup shows limitations in terms of tuning of different parameters of tractography [22]. The ISMRM 2015 challenge shows false positives and ambiguity. The 3D Votem challenge shows that sensitivity and specificity are limited. However, rather than anatomical accuracy, this study focuses on the variability of the algorithms themselves, specifically, the volume of the pathways where it was assessed by the containment analysis to assess if there is an ordering for the containment of volumes.

The data acquisition is limited by the acquisitions of two scanners. Alternative approach would be similar to MUSHAC challenge where their ultimate goal was harmonization, but there were multiple datasets across multiple scanners. This study investigated the reproducibility and containment of volume overlap, and did not assess the trajectories of streamlines themselves. For example, streamline density, orientation, and trajectories would provide detailed analysis of the similarities and differences within and across algorithms on the scale of individual voxels.

This study presents a perspective of reproducibility as compared to prior studies which characterize specificity and sensitivity with reproducibility as a limitation. This study shows that reproducibility can be characterized with an indirect estimation of sensitivity and specificity analysis (containment analysis).

However, the study is limited by data acquisition of a single subject. For a better reproducibility validation multi-subject and multi-site (>2) acquisitions would be valuable. Another limitation is that there are quite a few hyper-parameters that can be tweaked for pre and post-processing. In general, the tweaking improves reproducibility but a deterministic study of which combinations maximize reproducibility without tradeoff’s on specificity and sensitivity would be valuable to the diffusion community.

In conclusion, there are 8, 4 and 4 tracts which are depict high, moderate and low reproducibility. The most reproducible algorithms are 5A, 8D, 7A, 6E and 6F as per criteria of ICC. The mentioned algorithms are not an example of a consistent null learning as they all lie with in a nested containment with the largest covered volume.

The 2017 ISMRM TraCED Challenge created a publicly available multi-scanner, multi-scan in-vivo reproducibility dataset and engaged nine groups with 46 algorithm entries. The TraCED Challenge dataset is freely available at www.synapse.org. Consistent with previous studies, reproducibility of tractograms was found to vary by anatomical tract. When viewed across all entries, reproducibility was concerning (ICC <0.5); however, the cluster of top performing methods resulting in reassuringly high results (ICC > 0.85). Variation in performance were seen across processing parameters, but the challenge design did not provide sufficient number of samples to identify uniformly preferred design choices. The key novel finding of this challenge is that variations in tractography methods can be largely attributed to larger/smaller volumetric difference tradeoffs for the larger tracts, especially among methods that are tuned towards volumetrically larger tractograms. Yet, the different methods clearly result in fundamentally different tract structures at the more conservative specificity choices (i.e., volumetrically smaller tractograms). The containment index, containment energy, and containment index framework provide a consistent approach to evaluate the nesting structure tractograms, and the freely available data and results from this challenge can be used to quantify new tractography approaches. There is still room for improvements and innovations in the challenge process itself. For example, combining the knowledge and skillsets of the tractography community with the microstructural community could lead to improvements in phantoms, ground truth evaluations, and potentially unique features that could increase tracking accuracy.

Figure 8.

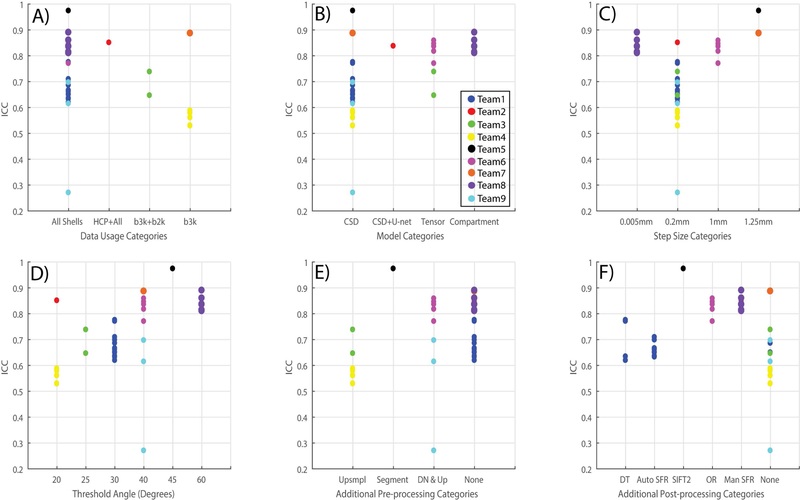
A) Quantifies the number of algorithms that used a specific part of the dataset or added more from other sources. B) Quantifies the usage of HARDI/Tensor methods by different tractography algorithms as a pre-step. C & D) Quantifies the step size and threshold angle parameter for tractography algorithms. E & F) Quantify the number of additional pre-processing and post-processing techniques applied for the tractography algorithms.

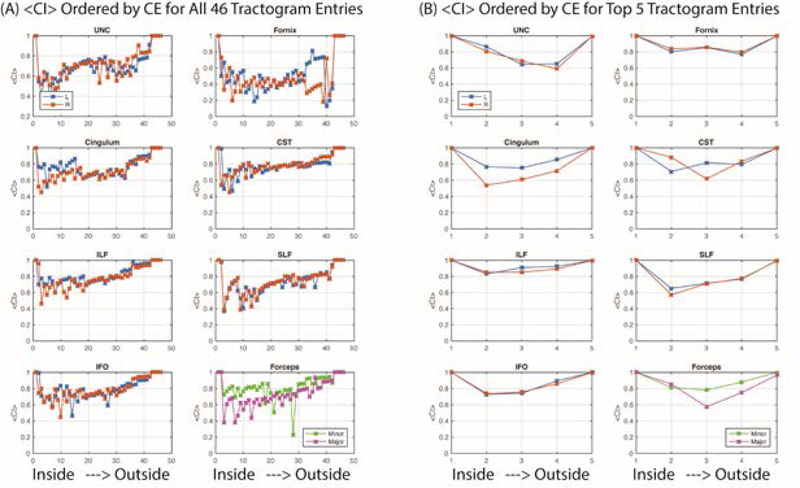
Figure 9.

Ordering entries to minimize containment energy (CE) shows that containment index is generally lower for the volumetrically smaller tractograms (toward “inside” on each subplot) and increases for the larger tractograms (toward “outside” on each subplot). Variations in containment explained the least amount of entry variability for the UNC and Fornix, while the other tracts were more consistent. The containment between all methods (A) were more variable and lower than the containment for the top five methods (B).