Linked-read analysis identifies mutations in single-cell DNA sequencing data

Abstract

Whole-genome sequencing of DNA from single cells has the potential to reshape our understanding of mutational heterogeneity in normal and disease tissues. A major difficulty, however, is distinguishing amplification artifacts from biologically derived somatic mutations. Here, we describe linked-read analysis (LiRA), a method that accurately identifies somatic single nucleotide variants using read-level phasing with nearby germline heterozygous polymorphisms, thereby enabling characterization of mutational signatures and estimation of somatic mutation rates in single cells.

Editorial summary:

LiRA is a method for analyzing single-cell DNA sequencing data that accurately identifies somatic single nucleotide variants using read-level phasing with nearby germline variants, enabling characterization of mutational signatures and estimation of somatic mutation rates in single cells.

Comprehensive profiling of genetic mutations by whole-genome sequencing (WGS) has aided in answering fundamental questions in biology and medicine. Applied to single cells, it has unique potential to reveal genetic variation within an organism at unmatched resolution. With novel protocols for generating single-cell libraries and reduced sequencing costs, large-scale single-cell DNA sequencing studies of genetic variation have now become feasible, utilizing whole exomes^1–3, low-coverage whole-genomes (for copy number analysis)⁴, and, more recently, higher coverage whole-genomes^5,6. Widespread application of single-cell WGS, however, has been hindered by the technical errors associated with whole-genome amplification (WGA) and the lack of computational methods that can properly remove such errors.

There are three main single-cell WGA protocols in use: degenerate oligonucleotide primed PCR (DOP-PCR), multiple annealing and looping based amplification cycles (MALBAC)⁷, and multiple displacement amplification (MDA)⁸. A fourth method, linear amplification via transposon insertion (LIANTI), has been recently described but is not yet widely used⁹. Although DOP-PCR and MALBAC generate reproducible coverage profiles and have been used for detection of large-scale copy number variation^10,11, their coverage is confined to a subset of the genome, and they are characterized by high single-nucleotide error rates (approx. 1 error in 10⁴ bases)¹². For single-cell somatic single nucleotide variant (sSNV) detection, MDA tends to produce the lowest false positive and negative rate, owing to the fidelity of the ϕ29 polymerase (~1 error in 10⁶–10⁷ bases)^12,13, a relatively low allelic dropout rate, and high genomic coverage. As such, MDA has become the most common WGA method in studies aiming to identify sSNVs^10,11.

However, identifying sSNVs in single-cell sequencing data acquired using MDA remains difficult. Despite its relative fidelity, ϕ29 is expected to produce hundreds to thousands of polymerase errors in the first replication of the genome alone. Additionally, genomic DNA may be damaged during cell lysis or other sample preparation steps prior to MDA and may be unfaithfully copied early in amplification. In particular, heat is known to induce cytosine deamination^14–16, and deaminated cytosine created during cell lysis may introduce a substantial burden of artifactual C>T mutation calls. As an exponential amplification process, MDA will cause early errors to propagate. Although these artifacts theoretically will have a lower variant allele fraction (VAF) than expected for an sSNV, high variance in VAF due to allelic dropout and amplification bias may cause a fraction of artifactual calls to reach VAFs comparable to those of true mutations in the final amplification product.

This high level of technical noise has made the validation of putative sSNVs important. Given that MDA consumes the original genome of the cell, past studies have aimed to confirm that candidate sSNVs from individual cells are present in other cells from the same organism. This can be done in bulk tissue using an orthogonal technology such as droplet digital polymerase chain reaction or amplicon sequencing, or by looking for sSNVs that are shared across multiple single cells^5,7. While this strategy is viable for the validation of mosaic or subclonal sSNVs, it cannot validate those detected in only one cell (singletons). This precludes analysis of sSNVs occurring post-mitotically in differentiated single cells, and sSNVs shared by arbitrarily small cell populations.

Here, we present linked-read analysis (LiRA), which applies read-backed phasing with nearby heterozygous germline SNPs to identifying sSNVs in whole-genome sequencing data derived from amplified single-cell genomes. Although the idea of phasing has been used to identify somatic mutations in cancer¹⁷, somatic mosaicism^18–20, and de novo germline mutations²⁰, this is the first method that applies this principle to single-cell data. Also, although leveraging heterozygous variants to improve single-cell variant calling has been previously described and implemented as SCcaller²¹, no existing sSNV caller makes use of read- or mate-pair-backed phasing. By ensuring that candidate mutation calls of interest are consistent with the haplotypes implied by nearby heterozygous germline SNPs, LiRA removes amplification-associated variants and achieves unparalleled specificity.

Results

LiRA aims to provide robust validation for a subset of candidate sSNVs occurring near polymorphic germline heterozygous SNPs (gHets) (Fig. 1a). The key insight underlying LiRA is that false positive calls (FPs) are derived from factors specific to one strand of DNA, while sSNVs, as fixed mutations, are derived from both strands of one chromosome. Single reads as well as mate-pairs covering the genomic positions of a candidate sSNV and the linked locus of a nearby gHet (‘spanning reads’) can distinguish these two scenarios. For example, for a true sSNV occurring on the same haplotype as the linked gHet, every spanning read will contain both the gHet and the sSNV. We call these reads ‘concordant’ (Fig. 1a). In contrast, for a false positive, the set of spanning reads will contain a mixture of reads containing only the gHet and reads containing both the gHet and the sSNV. For FPs derived from DNA damage, the reads containing the reference allele, which we call ‘discordant’ reads (Fig. 1a), originate from the undamaged strand of the same chromosome, and for polymerase errors, from faithfully copied strands of the same chromosome (Fig. 1a,b).

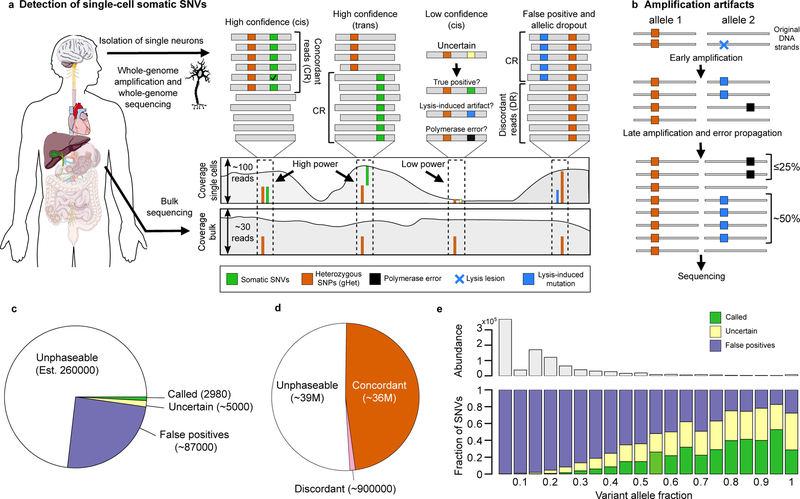
Figure 1 |. Overview of LiRA.

a, Methodology for identifying false positive (FP) somatic SNVs (sSNVs). LiRA analyzes reads and mate-pair reads that cover the positions of an sSNV and a gHet (spanning reads). ‘Concordant’ reads (CR) support the gHet allele (alt/ref in cis/trans) and the sSNV alt call. ‘Discordant reads’ (DR) support the gHet allele but the reference base at the sSNV position. b, Model for how the linked read pattern specific to FPs arises from DNA lesions or polymerase errors. A lesion may be present on and copied from one strand of input DNA (blue), or ϕ29 polymerase may mispair a base (black). Both errors are exponentially amplified. As polymerase errors are introduced after the first round of amplification at the earliest, they are expected to appear in ≤25% of gHet-linked reads, whereas lesion-derived artifacts are expected to appear in ~50%. c, Classification of candidate sSNVs in LiRA. Most sSNV candidates (est. ~260,000, 73%) are too far away from a gHet to be covered by the same read or mate-pair. Over the powered fraction (27%, ~95,000), most (92%, ~87,000) are filtered as false positives due to the presence of at least one discordant read covering the sSNV position and each linked gHet. In the remaining subset, most (63%, ~5,000) do not meet LiRA’s quality thresholds, and 2,980 (37%, 0.8% overall) are reported as LiRA sSNV calls. d, Phasing of gHets. Just under half of gHets are close enough to other gHets to be linked, and only 2% are filtered (erroneously) as false positives. e, Call status of candidate sSNVs in LiRA by variant allele fraction (VAF). Most sSNV candidates are low VAF; LiRA filters almost all low VAF sSNV candidates. As VAF increases, sSNV candidates are more frequently called, but a substantial proportion of high VAF candidates are still false positives.

In LiRA, we first utilize GATK²² to identify as many candidate sSNVs as possible; in principle, any variant caller with high sensitivity could be used in this first step. Candidate sSNVs are identified as any variants that are phased with gHets (any population-polymorphic heterozygous SNV calls made in bulk) and not present in matched bulk sequencing data. We identify sSNVs and gHets that are supported by the same read or mate-pairs, and any sSNVs that are found with any discordant reads are filtered and referred to as ‘LiRA FPs.’ (Supplementary Fig. 1; for a case with multiple gHets linked to an sSNV, see Supplementary Fig. 2).

Application to single-neuron sequencing data.

We applied our method to single neuron data (~45X) from phenotypically normal individuals⁵. We find that a substantial portion of sSNV candidates are close enough to gHet sites to be subjected to LiRA analysis (27% overall, 9–44% in individual cells; Fig. 1c and Supplementary Table 1). Among those identified, 92% are filtered as LiRA FPs (87–96% across cells; Fig. 1c,d and Supplementary Table 1). Applying the same procedure across gHet-gHet pairs, we find that only 2% of gHets are filtered as LiRA FPs (1–4% across cells; Fig. 1d and Supplementary Table 1). This stark difference in results between gHet-gHet and candidate sSNV-gHet pairs suggests that filtering sSNVs by LiRA removes FPs while excluding minimal true variation, and that standard genotypers cannot be used to call sSNVs in single cells without considerable filtering and validation.

After filtering based on the presence of discordant reads, we determine the quality of the remaining variants based on a measure called ‘composite coverage’ (CC), defined as the minimum spanning read depth across bulk and single-cell sequencing data (Supplementary Figs. 1 and 2). As the bulk coverage observed at the same locus increases, it becomes increasingly likely that a candidate sSNV is not a missed germline variant. As single-cell coverage increases, so does confidence that discordant reads are truly absent in the MDA amplification product and not simply missed due to under-sampling. LiRA approaches this issue by finding a CC threshold that controls the estimated false discovery rate (FDR) at a tolerable level (default of 10%). sSNVs with support equal to or greater than the threshold are called, whereas those with sub-threshold support are called as ‘uncertain’ (Fig. 1c,d).

To determine an appropriate threshold, we take advantage of the fact that, in the absence of FPs, the estimated genome-wide sSNV rate should not depend on CC. LiRA first measures the distribution of CC values at all genomic positions linked to any gHet site on both autosomal alleles (Supplementary Fig. 3), and then uses this and the distribution of CC values of sSNV candidates to compute the CC-specific genome-wide sSNV rates (Supplementary Figs. 4 and 5). LiRA then models the observed relationship between the somatic mutation rate and the CC as the mixture of two components: an exponentially decaying error component and an approximately constant true mutation component (Supplementary Figs. 4 and 5). The utility of the model lies in the fact that the fitted true mutation component gives an estimate of the genome-wide sSNV rate, and its value relative to the error component gives an estimate of the FDR at each level of sSNV quality. This information is used to assign FP probabilities to individual mutations, and to ascertain the overall FDR expected across a set of calls at various thresholds.

We found that this procedure identifies many uncertain sSNVs among the candidate set of non-discordant sSNV calls (63% overall, 20–81% across cells; Fig. 1c and Supplementary Table 1). Also, we found that while higher VAF calls are more likely to be called by LiRA, uncertain and LiRA FPs still frequently appear at high VAF values (Fig. 1e). This suggests that read-level phasing by LiRA adds substantial specificity to mutation calling in single-cell sequencing data acquired using WGA.

Importantly, the two-component model used by LiRA is fit for each cell individually, and thus can account for variable artifactual burdens among samples. Instead of choosing a universal cutoff across all cells involved in a study, LiRA chooses a threshold for each such that the FDR is controlled at a specified level. In the Lodato et al.⁵ data, this proved to be an important consideration, as the ratio of errors to predicted true sSNVs (a measure of artifactual burden) varied widely across cells (Supplementary Table 2).

In terms of the genome-wide sSNV rate (Supplementary Fig. 4), we found that LiRA-estimated rates were generally consistent with those found by a previous study²³, which measured the sSNV rate at a subset of genomic loci in the frontal cortex using an orthogonal method that avoided single-cell sequencing or WGA (Supplementary Table 2). This suggests that LiRA accurately accounts for the heterogeneity in power across the genome introduced through MDA-related coverage non-uniformity. Although only a small fraction (Fig. 1c,d) of initial candidate sSNVs are eventually output as LiRA calls, we find that LiRA retains sufficient sensitivity for downstream analysis. For Lodato et al.⁵, we detected an average of 83 sSNVs per cell, which extrapolates to 919 sSNVs per cell genome-wide (Supplementary Table 2).

Comparison to other variant callers.

To confirm the accuracy of LiRA’s sSNV calls, we compared the VAF distribution of LiRA sSNV calls to that of LiRA FPs, LiRA uncertain calls, and gHets (Fig. 2a). True sSNVs should be characterized by a VAF distribution similar to that of gHets, whereas FPs should have lower VAFs, owing to their origin in progressively later rounds of amplification or on one strand of DNA. Accordingly, we found that LiRA calls had a distribution nearly identical to that of gHets, whereas LiRA FPs and, to a lesser extent, LiRA uncertain calls were skewed towards lower VAF values. This remained true when the VAF distributions were split by mutational type (C>A, C>G, C>T, T>A, T>C, T>G) (Supplementary Fig. 6). Overall, these results were consistent with the notion that LiRA distinguishes bona fide fixed heterozygous sSNVs from amplification-induced artifact.

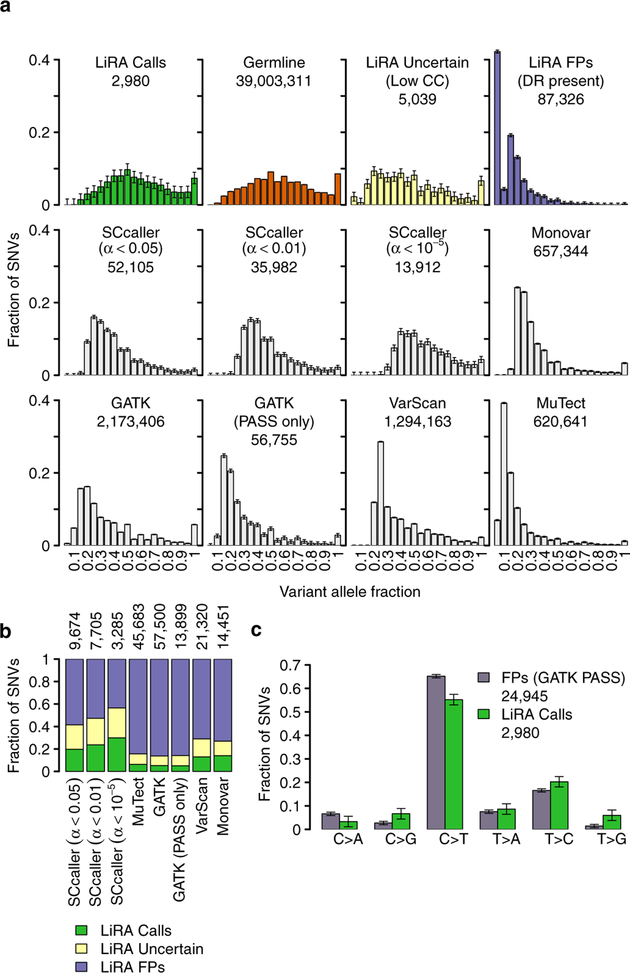
Figure 2 |. Performance of LiRA compared to other calling methods.

a, Comparison of the variant allele fraction (VAF) of LiRA high-confidence calls, uncertain sSNVs, and FPs to germline mutations and other calling methods. LiRA calls have a VAF distribution indistinguishable from that of heterozygous germline polymorphisms, while LiRA uncertain mutations and FPs are moderately and severely skewed towards low VAF values, respectively. Other single-cell variant calling methods also produce VAF distributions skewed towards low VAF values. Accepting only PASS mutations after VQSR in GATK does not change this. In SCcaller, α is the probability that a candidate sSNV is an amplification artifact, and a set of calls is obtained by accepting only those with α less than a user-set threshold. Lowering α mitigates but does not remove skewing towards low VAF values. 99% simultaneous confidence intervals on frequency are shown, and the total number of calls made is listed below each label. b, Call status of sSNVs called by other methods in LiRA. Calls made by single-cell variant calling methods contain many variants filtered as FPs in LiRA. Accepting only PASS mutations after VQSR in GATK does not change this. In SCcaller, lowering α lowers the proportion of the variants identified in LiRA as FPs, but the proportion remains high. 99% simultaneous confidence intervals are shown, and the size of the LiRA-intersection is listed above each bar. c, Comparison of sSNV types between LiRA FPs and LiRA calls. Well-supported LiRA FPs, distinguished as those that are marked as ‘PASS’ by GATK, differ significantly from LiRA calls in mutational spectra. 99% simultaneous confidence intervals are shown.

To compare LiRA to other methods for calling sSNVs, we compared the VAF distribution of LiRA calls to those produced by SCcaller²¹, Monovar²⁴, GATK²², Varscan²⁵, and MuTect²⁶ (Fig. 2a). Unlike the LiRA-derived or germline VAF distribution, calls reported by other variant callers produced VAF distributions skewed towards low VAF calls and inconsistent with the VAF distribution of gHets. As a further comparison, we intersected call sets from each of these packages with phasable sSNV candidates that LiRA could analyze (Fig. 2b). We found that all methods tested had a substantial burden of LiRA FPs, indicating the presence of discordant reads, and uncertain variants (Fig. 2b), suggesting that LiRA achieves a much lower FDR in calling sSNVs from WGA-amplified single cells.

Another validation of LiRA is the comparison of the single-nucleotide substitution types between LiRA sSNV calls and LiRA FPs. High-quality GATK calls (marked with the ‘PASS’ flag) found to be FPs have different mutational frequencies from LiRA calls (P < 10^–5, Fisher’s exact test). The FPs were depleted in C>G, T>A, T>C, and T>G mutations while enriched in C>T and C>A calls (which have been associated with artifactual sSNV calls in previous studies^14–16,27; Fig. 2c). The largest depletion was observed for T>G (~320% higher in LiRA calls), and the largest enrichment was observed for C>A (~50% lower in LiRA calls; Fig. 2c). These results suggest that the two sets originate from different underlying processes. An expanded analysis over trinucleotide context upheld these observations (Supplementary Fig. 7).

Application to cancer genomic data.

A highly specific set of somatic mutations in single neurons obtained by LiRA has allowed us to discover the association between the number of mutations and age, identify the underlying mutational processes, and estimate the rate of mutagenesis²⁸. To investigate its applications to cancer genomics, we analyzed a single-cell exome sequencing dataset of bladder cancer and normal tissues from Li et al.²⁹. This analysis revealed that, when there are a relatively large number of mutations shared across cells (as is the case in cancer), LiRA is able to confidently determine with a small number of reads whether an sSNV is present or absent from a cell. In approaches agnostic to linkage, not detecting a mutation in a cell could be due to dropout or due to the fact that the mutation is really absent. Thus, in previous approaches, calling the status of a cell lacking evidence of an sSNV has involved models in which the likelihood a mutation truly being absent depends on the depth of sequencing at the locus and the overall rate of allelic dropout^24,29. In contrast, with LiRA, we are able to confidently call absence with just one read spanning an sSNV locus and a nearby gHet since, as we have demonstrated over gHets, the rate of errors producing discordant reads is low (Fig. 1d; 98% of linked gHets are linked with only concordant reads).

In the cancer data, LiRA identified a high resolution “scaffold” of sSNVs over which we had confident linked positive and null mutation calls. We then extended this by identifying unlinked mutations that had a pattern of support across cells more associated with a LiRA-identified mutation than was expected by chance (Online Methods). This analysis resulted in identification of several nonsynonymous mutations and one nonsense mutation not found in the original study, in addition to recapitulating the clustering results of Li et al. (Supplementary Fig. 8). The majority of these mutations were also not found by Monovar when this dataset was used in its validation²⁴. Among the new mutations was a nonsynonymous mutation in SYTL3, a gene that has been previously implicated in bladder cancer through its involvement in the Rab pathway via interaction with Rab27³⁰.

Discussion

Our results show that LiRA represents an advance in sSNV calling in single cells, especially with respect to singletons. Whereas existing variant callers produce variants with very high FDRs, LiRA produces a set of high-precision calls that display characteristics of fixed, heterozygous sSNVs. Although there is a limitation of observing the single-cell genome only around gHets, LiRA still produces a sufficient number of accurate calls from which to insights on biological processes can be gathered. In future studies, the utility of LiRA over single-cell sequencing data could be improved further when used in combination with longer reads or synthetic long reads such as those provided by the 10× Genomics platform, greater depth of coverage, or greater heterozygosity in the diploid genome. While the last factor is not easily modifiable over human subjects, in mice or other model organisms crossing distantly related strains may yield very high rates of heterozygosity and greatly improve LiRA’s power.

In theory, there are error modes in amplification that would cause FPs to escape LiRA’s filtering steps. LiRA relies on both strands of a single chromosome being subject to relatively even amplification. If present, strand dropout or severe non-uniformity in strand-specific amplification could cause DNA lesions or polymerase errors to appear as fixed mutations in single-cell sequencing data using LiRA. Shorter or more heterogeneous amplicon sizes in MDA might worsen this effect, as might cell lysis protocols other than the alkaline-based one used previously^5,28. Although we cannot technically rule out strand-dropout, the quality of the two-component model fit across cells (Supplementary Fig. 5) as well as other properties of LiRA calls suggest that this process is of negligible effect size.

Overall, as a new approach to single-cell analysis, LiRA provides a window into the mutational processes within a cell, including rate and characteristics of mutagenesis, leading to new insights into cell aging, lineage, and disease.

Online Methods

Variant calling of candidate somatic single nucleotide variants (sSNVs) and population-polymorphic germline heterozygous sites (gHets).

The GATK Haplotype Caller best practices pipeline²² with default parameters was used to call variants jointly on single cell and bulk sequencing data from each individual. To maximize sensitivity, all variants reported in the output VCF, regardless of the FILTER column flag, were considered. Candidate sSNVs were identified as calls with no alternate-allele supporting reads in bulk and at least one alternate-allele supporting read in a single cell, as specified in the vcf. Polymorphic germline heterozygous sites (gHets) were identified as variants found with nonzero population frequencies in the 1000 genomes database³¹ as annotated in the dbSNP 147 database (available from: http://www.ncbi.nlm.nih.gov/SNP), and called with a ‘0/1’ heterozygous genotype in bulk.

Identification of candidate variants for LiRA analysis.

sSNV-gHet pairs and gHet-gHet pairs that had at least two reads or mate pairs supporting both variant loci were subject to analysis by LiRA. Included reads were required to have maximum mapping quality score (60), to map in a proper pair (SAM flag 2), and to have no indel or base-clipping CIGAR operations.

Read-backed phasing of variant pairs.

In LiRA, the relative phasing of two SNVs, i.e., whether they are derived from the same (cis) or homologous (trans) chromosomes, defines the pattern of alternate (A) and/or ref (R) allele support in discordant and concordant reads (DRs and CRs) spanning the two loci. There are four possible patterns of support (SNV1-SNV2): (R-R, A-R, R-A, A-A). If two SNVs (SNV1 and SNV2) are linked in cis, concordant reads for both SNVs will show A-A, and discordant reads R-A and A-R for SNV1 and SNV2, respectively. Alternatively, if two SNVs are linked in trans, concordant reads will show A-R and R-A, and discordant reads, for both SNVs, will show R-R.

Phasing in LiRA was done by simple majority of counted of reads. SNV1 was linked to SNV2 in cis if the count of A-A reads outnumbered A-R reads, and otherwise was linked in trans.

Filtering non-concordant sSNV candidates and computation of composite coverage.

Following variant phasing, DR and CR read counts were obtained for each variant pair (sSNV-gHet and gHet-gHet) over single-cell data and bulk data. Any sSNV candidate or gHet that was not in a pair that showed complete concordance was filtered, and the composite coverage (CC) was computed over the remaining set.

CC was computed as follows: we first considered each DR-free sSNV-gHet pair, and measured the pairwise-CC as the minimum of the CR count in single cells and the un-mutated haplotype in bulk (for sSNV-gHet pairs) or the CR count in bulk (for gHet-gHet pairs). The un-mutated haplotype in bulk, for a trans linked sSNV-gHet, was R-R, and for a cis-linked sSNV-gHet, R-A.

We then measured the composite coverage as pairwise-CC observed for each sSNV, where a maximum was taken if an sSNV or gHet was linked with multiple gHets.

Power estimation.

For the ref and alt allele of each gHet, we extracted the set of all supporting mate-pair reads from bulk and single cell sequencing data. Then, we measured the minimum coverage between the bulk and single-cell supporting reads at all genomic positions covered by at least two reads in both sets. This gave the hypothetical CC value an sSNV-gHet pair would have received had it occurred at one of the positions covered on the chromosomal haplotype corresponding to the gHet allele under consideration (either ref or alt).

Some positions were close enough to multiple gHets to receive more than one hypothetical CC value on one or both haplotypes. In cases where the gHets themselves could be linked directly in the same reads, to compute an overall value for these sites we took the maximum CC observed across all pairs. However, in cases where a position was close enough to two gHets to be linked with both, but the gHets were too far from each other to be covered by any spanning reads, it was unclear from read data alone which CC values corresponded to the same haplotype. To resolve this, we used SHAPEIT2³² with default parameters on bulk samples for each neuron donor to determine the haplotype of the ref and alt allele of each gHet, and used this information to transform measurements specific to variant alleles (ref/alt) into measurements specific to haplotype.

Overall, this analysis yielded a map between the location of a hypothetical sSNV (genomic position and chromosomal copy) and the composite coverage with which it would have been detected.

Aggregate power calculation.

To calculate the relationship between the estimated somatic mutation rate and composite coverage, we obtained aggregated counts of the total number of loci at which a hypothetical sSNV could have been detected at particular CC values greater than or equal to 2 (P_c, aggregate power). These counts were adjusted to account for two confounding factors: loss of power due to non-artifact driven discordant read observations and loss of power due to the random occurrence of bulk-alternate reads supporting sSNV calls due to technical noise.

To account for the first factor, we reasoned that as composite coverage increases, so should the likelihood that a discordant read will be observed due to technical noise. This would reduce power to detect sSNVs by some amount yet unaccounted for, since SNV pairs with discordant reads are excluded from LiRA in the first step. Our approach to this issue was to measure the rate at which gHet-gHet pairs were observed with discordant reads as a function of CC (d_c) and to adjust aggregate power at each CC value down by the fraction of those we predicted to lose.

To account for the second factor, we predicted that as coverage in bulk sequencing increased, so would the likelihood that bulk reads would support an sSNV because of random sequencing error. We approximated this probability using half the rate at which a third allele is observed in bulk sequencing data at gHets (e.g., a read supporting T at a C/G het. site). We found that this quantity had coverage dependence, but that the relationship was complex and that the rate did not consistently increase with coverage. Because of this, we used a fixed rate (b) computed and applied across all bulk coverage values to adjust P_c.

Overall, the following formula describes the adjustment, which was completed over single-cells individually:

$${\text{P}}_{\text{c}}{}^{\text{adjusted}}=\left(1-\text{b}\right)\left(1-{\text{d}}_{\text{c}}\right){\text{P}}_{\text{c}}{}^{\text{original}}$$

Rate calculation and two-component model.

To obtain estimates of and bounds on the observed somatic mutation rate at different composite coverage values, we used a beta distribution with Jeffrey’s prior: Beta(M_c + 1/2,P_c – M_c + 1/2), where M_c is the number of mutations with composite coverage c and P_c is the adjusted count of the number of loci with power to detect a mutation with composite coverage c. This gave the mutation rate in sSNVs/bp, and we converted this to sSNVs/Gbp by multiplying by 10⁹.

For each cell, we modeled the expected value of this beta distribution, the average somatic mutation rate measured at each value of composite coverage, (M_c + 1/2)/(P_c + 1), as the mixture of an error component (E) and a ‘true mutation’ component (T). The error component we fit had the form:

$$\text{E}\left(c\right)=\text{K}{p}^{\left(c-2\right)};p<1$$

Visually, a decaying exponential appeared to fit the data well at low composite coverage values (Supplementary Fig. 5), consistent with a high burden of FP calls at that level of quality. Theoretically, if we assume an initial burden of K errors per gigabase at c = 2, and that the probability of sampling a concordant read given a variant is truly discordant is p, then the error abundance as a function of composite coverage takes exactly this form.

We found that p = ½ resulted in good fits, and this suggested that the artifacts causing an excess of mutations at low composite coverage values originated from lesions present on the original DNA prior to any amplification. In this scenario, half of reads from the linked germline haplotype (Fig. 1b) are expected to support the artifactual call.

The “true” component T(c) fit by the model was practically constant (Supplementary Fig. 5), but to improve the quality of fitting, was computed using a bootstrapped set of germline variants. The procedure used was as follows:

1. Randomly select a set of germline variants of size equal to the size of the sSNV set for that cell (c ≥ 2) from those found in DR-free gHet-gHet pairs, constraining the loci distance and orientation (cis/trans) distribution to be as close as possible to that observed in the somatic set. The later constraints were chosen because we reasoned that the distance between linked SNVs and the orientation (through alignment-mediated reference bias) almost certainly should affect CC.

2. Compute the rate using P_c and the composite coverage distribution for these sampled gHets.

3. Compute the bootstrap rate B(c) (the “true” component) by averaging over 100 instances.

Overall, the model R(c) = E(c) + T(c) = K₁E(c) + K₂ T(c) was fit using the R function nlm.fit, in which the square error from the beta mean weighted by the inverse beta variance, v_c = var(B(M_c + ½,P_c – M_c + ½))^–1, was minimized:

$$\text{f}\left({\text{K}}_1,{\text{K}}_2\right)=\sum _{\text{c}}{\text{v}}_{\text{c}}{\left({\text{K}}_1\text{E}(\text{c})+{\text{K}}_2\text{T}(\text{c})-\frac{{\text{M}}_{\text{c}}+\frac{1}{2}}{{\text{P}}_{\text{c}}+1}\right)}^2$$

$${\text{v}}_{\text{c}}=\frac{{\left({\text{P}}_{\text{c}}+1\right)}^2\left({\text{P}}_{\text{c}}+2\right)}{\left({\text{M}}_{\text{c}}+\frac{1}{2}\right)\left({\text{P}}_{\text{c}}-{\text{M}}_{\text{c}}+\frac{1}{2}\right)}$$

K₁ and K₂ were constrained to be positive by imposing a large penalty on the objective function for K₁ or K₂ less than 0.

T(c), the expected dependence between CC and observed sSNV rate for true heterozygous mutations, was used to estimate the genome-wide sSNV rate. In the ideal case, T(c) should be constant, but we found that in some cells, especially at high CC values, T(c) was variable, often increasing dramatically in tandem with the observed sSNV rate (e.g., UMB1465–18, UMB1465–47, UMB1465–51, UMB4638–2; Supplementary Fig. 5). At these high CC values, the number of gHet-gHet pairs used to construct T(c), the number of sSNVs, and aggregate power were very low, and we attribute this phenomenon to noise introduced by these low counts in the power adjustment. Thus, to remove this effect, we used the value of the fit T(c) curve at the lowest CC value (K₂T(2)) to estimate genome-wide rate.

To obtain bounds on the genome-wide rate, we sampled our beta model of the observed genome-wide somatic mutation rate Beta(M_c + 1/2,P_c – M_c + 1/2) at each value of c and refit our model on the result 100 times. The bounds we report on the genome-wide somatic mutation rate correspond to the minimum and maximum values of K₂ T(2) obtained over these samples, and as such constitute a 98% confidence interval.

Computation of estimated false discovery rate (FDR) and choosing a threshold for c.

Given the model fit, the estimated false discovery rate (FDR) for the mutations detected was calculated as follows:

1. Compute the FDR as a function of composite coverage:

   • 1.1. FDR(c) = E(c)/[E(c) + T(c)]. This also allowed us to compute, for each value of c, the corresponding Phred quality score (Q) for somatic mutations with that level of support Q = −10log10(FDR(c)).
2. Compute the estimated number of sSNVs (M_c ^(t)) and false positives (M_c ^(e)) as a function of c:

   • 2.1. M_c ^(t) = [(1 - FDR(c)) M_c]
   • 2.2. M_c ^(e) = [(1 - FDR(c)) M_c]
3. Compute the estimated aggregate FDR when thresholding at c_m as:

   $${\text{FDR}}_{\text{agg}}\left({\text{c}}_{\text{m}}\right)=\frac{\sum _{\text{c}\ge {\text{c}}_{\text{m}}}{\text{M}}_{\text{c}}{}^{\left(\text{e}\right)}}{\sum _{\text{c}\ge {\text{c}}_{\text{m}}}\left({\text{M}}_{\text{c}}{}^{\left(\text{e}\right)}+{\text{M}}_{\text{c}}{}^{\left(\text{t}\right)}\right)}$$

   Choose c* as the minimum value c_m such that FDR_agg(c_m) ≤ 0.1.

Somatic variant calling with GATK HaplotypeCaller, SCcaller, Varscan, Monovar, and MuTect.

SCcaller²¹, MuTect²⁶, GATK²², VarScan²⁵, and Monovar²⁴ were used with default parameters to call somatic variants from single cells and bulk control data. For SCcaller, we filtered variants at three different (artifact likelihood)/(heterozygous variant) likelihood thresholds: 10⁻⁵, 0.01, and 0.05, and in all cases we filtered calls to include only sSNVs with allelic fraction ≥ 1/8 (from the SCcaller github page; https://github.com/biosinodx/SCcaller). GATK does not report somatic calls outright but rather reports genotypes and quality metrics for single cells and bulk samples separately. As such, we used the following filters to call somatic variants: ‘0/1’ or ‘1/1’ genotype in a single cell, ‘0/0’ bulk genotype, no supporting reads in bulk, and maximum bulk genotype quality (99). We also analyzed the set of variants meeting these criteria and annotated as ‘PASS’. For Monovar, we filtered raw variants using the procedure described by Zafar et al.²⁴. First, we removed candidate sSNVs with less than 6× coverage or more than 2 alt reads in bulk. Next, we removed sites within 10 bp of each other that were only detected in single cells. Finally, we removed sSNV candidates with <10× coverage and <3 alt reads, and also those with variant allele fraction (VAF) < 10% or VAF < 15% when coverage was between 20 and 100 or over 100, respectively.

Estimation of the abundance of unphasable sSNVs.

An sSNV is considered by LiRA only when there are bulk reads or mate pairs spanning the sSNV position a linked gHEt allele. As such, it is not possible to directly count the total number of sSNV candidates LiRA would analyze if it had power over the entire genome. Instead, we estimate this number by dividing the number of LiRA sSNV candidate by the fraction of GATK somatic calls (PASS only) to which LiRA could be applied.

Analysis of FP and LiRA call sSNV mutation type and trinucleotide context.

FPs were limited to those also called as somatic by our filtering of GATK variant calls and annotated with ‘PASS’ in the VCF filter column. This provided a stronger comparison between FPs and LiRA calls as it removed many sSNV candidates of low quality which had very different VAF, mutation type, and trinucleotide context distributions (data not shown). These excluded calls were likely enriched for errors stemming from sequencing error rather than WGA.

Method for obtaining histogram error bars.

99% confidence intervals for frequencies of SNVs for VAF distribution bins (Fig. 2a–c and Supplementary Fig. 6), mutation type (Fig. 2c), and trinucleotide context (Supplementary Fig. 7), were computed using the multinomialCI function (alpha = 0.01) from the ‘MultinomialCI’ package in R on counts pooled across all cells.

Analysis of Hoang et al.²³ data.

Mutation frequencies for BOTSeq BRA04, BRA05, and BRA06 were obtained from table S9 of Hoang et al.²³ These values were converted into sSNVs/Gbp by multiplying by 10⁹.

Analysis of Li et al.²⁹ bladder cancer exome data.

FASTQ files for 55 bladder cancer cells, 12 normal cells, bulk normal, and 2 bulk cancer samples were downloaded from the NCBI SRA and aligned to GRCh38 using bwa mem version 0.7.17 (r1188)³³. The GATK Haplotype Caller best practices pipeline²² with default parameters was used to call variants jointly on these samples. LiRA was then used to call sSNVs in all single cells relative to the bulk normal sample.

Following analysis by LiRA, sSNVs called as passing or uncertain in any cell were grouped, and the status of each sSNV in each cell was queried. For each sSNV, in cells where no reads covered the sSNV-linked haplotype, no genotype call was made. In cells where at least one read covered the sSNV-linked haplotype and this showed no evidence of the sSNV (the ‘null haplotype’), sSNVs were called as absent. In cells with at least one supporting read for the sSNV (not necessarily spanning a nearby gHet), a call was made. Further, sSNVs were only considered if (i) at least 2 cells showed only the null haplotype (at least 2 spanning reads), (ii) at least 2 cells showed only the sSNV-positive haplotype (at least 2 spanning reads), and (iii) the sSNV was called as passing or uncertain in more cells than it was called as an FP. For a small number of cells, there were FP calls among this set of considered sSNVs, and no genotype call was made in these cases.

To construct an expanded set of calls, a ‘rescue matrix’ of low precision calls was created by considering all remaining sites reported by GATK haplotype caller. Over each single cell, a call was assigned a value of 1 if it had an ALT depth of at least one, zero otherwise. We then performed pairwise fisher tests (of pairwise-complete observations) between the cell calls for sSNVs in the rescue matrix and the cell calls for sSNVs in the set reported by LiRA, aiming to select a set of sSNVs from the rescue matrix that had unexpectedly high correlation in calls over cells with sSNVs reported by LiRA.

To account for multiple hypothesis testing, we first applied a procedure where we computed the minimum possible P-value that could be obtained given the fixed marginals for each pairwise test. If this value was above the Bonferroni threshold at the 0.05 significance level for the number of tests being performed (n, threshold: 0.05/n), it was excluded. Because this lowered the number of tests considered, and thus raised the threshold, we repeated this process until a stable set of tests was obtained (i.e., until all tests in principle could return a significant result).

We then obtained a set of ‘rescued’ sSNVs from the rescue matrix by considering those found to be unexpectedly associated with a LiRA sSNV, controlling FDR < 0.1 by the Benjamini-Hochberg procedure. To verify the validity of this, we performed the same procedure on 100 row-permuted rescue matrices, and found that a nonzero number of sSNVs were rescued only rarely (3/100) under random expectation. In contrast, we found that 57 were rescued over the real data. This set combined with the set of sSNVs (17) reported by LiRA are used in the heatmap presented in Supplementary Figure 8.

Statistics and reproducibility.

We used Fisher’s exact test to compare the distribution of mutation types between LiRA filtered FPs and LiRA calls.

Reporting Summary.

Further information on research design is available in the Life Sciences Reporting Summary published alongside this article.

Data availability.

LiRA was applied to single-neuron and bulk sequencing data collected from the post-mortem brain, heart (UMB1465 and UMB4638), and liver (UMB4643) tissue of three individuals. These data were acquired as part of a previous study⁵ and are available in the NCBI SRA under accessions SRP041470 (UMB1465) and SRP061939 (UMB4638 and UMB4643). The neuron counts by individual were: UMB1465 (16), UMB4638 (10), and UMB4643 (10).

Code availability.

LiRA is available at https://github.com/parklab/LiRA.