Structural and computational examination of the Arabidopsis profilin–Poly-P complex reveals mechanistic details in profilin-regulated actin assembly

Abstract

Profilins are abundant cytosolic proteins that are universally expressed in eukaryotes and that regulate actin filament elongation by binding to both monomeric actin (G-actin) and formin proteins. The atypical profilin Arabidopsis AtPRF3 has been reported to cooperate with canonical profilin isoforms in suppressing formin-mediated actin polymerization during plant innate immunity responses. AtPRF3 has a 37-amino acid-long N-terminal extension (NTE), and its suppressive effect on actin assembly is derived from enhanced interaction with the polyproline (Poly-P) of the formin AtFH1. However, the molecular mechanism remains unclear. Here, we solved the crystal structures of AtPRF3Δ22 and AtPRF3Δ37, as well as AtPRF2 apo form and in complex with AtFH1 Poly-P at 1.5–3.6 Å resolutions. By combining these structures with molecular modeling, we found that AtPRF3Δ22 NTE has high plasticity, with a primary “closed” conformation that can adopt an open conformation that enables Poly-P binding. Furthermore, using molecular dynamics simulation and free-energy calculations of protein–protein binding, along with experimental validation, we show that the AtPRF3Δ22 binds to Poly-P in an adaptive manner, thereby enabling different binding modes that maintain the interaction through disordered sequences. Together, our structural and simulation results suggest that the dynamic conformational changes of the AtPRF3 NTE upon Poly-P binding modulate their interactions to fine-tune formin-mediated actin assembly.

Introduction

Profilins, which are small but abundant cytosolic proteins with a molecule mass of ∼15 kDa, are universally expressed in eukaryotes and regulate actin filament elongation by binding with monomeric actin (G-actin)⁴ and formin proteins. Profilin functions are dynamically regulated to coordinate actin assembly during development and defense mechanisms (1–3), through tuning its intra- and intermolecular associations toward the binding partners (3–5). In Arabidopsis thaliana, five profilin isoforms (AtPRF1–5) share over 70% sequence identity, except for the AtPRF3, which has an extra N-terminal extension (NTE) with 37 amino acids more than the other AtPRFs, which makes AtPRF3 atypical profilin. Global-wide sequences analysis demonstrated that such profilin with additional NTE region is common in a wide range of plant, animal, and fungi species (3). By cooperating with other typical profilin isoforms with positive effect in formin-mediated actin elongation, AtPRF3 plays critical roles in balancing the actin polymerization in support of plant innate immune responses (3).

Formin-mediated actin assembly is one of the two major assembly machineries in plants in generating long actin cables for polarized plant growth and defense mechanism. During actin elongation, profilin transiently associates with the polyproline (Poly-P) of formins to deliver G-actin into the filament growing end and after that released quickly for next rounds of G-actin recruitment (2). However, AtPRF3 binds to AtFH1 Poly-P with a much higher affinity than other AtPRF isoforms, which constrains the dynamic exchange of profilin between the free and Poly-P–bound states (3). Poly-P–bound AtPRF3 conceives negative regulation of actin polymerization and essentially balances the filament assembly with other profilin isoforms during plant innate immunity (3). AtPRF3 NTE contains a highly structurally disordered region that is usually a signaling hub during signal transduction by being post-translational modified and conformationally tuned (6). During pattern-triggered immunity, AtPRF3 was dynamically regulated to protein degradation or synthesis to attenuate formin-mediated actin assembly. However, the molecular basis for understanding the potential conformational regulation of the AtPRF3 NTE is unknown. Studies of the dynamic association of AtPRF3 NTE with formin Poly-P is essential to understand how NTE dynamically regulates profilin activities by modulating its binding states toward Poly-P in plant development and defense mechanisms.

To elucidate the mechanism by which AtPRF3 NTE confers a dynamic but high-affinity binding to Poly-P, we carried out structural studies of the AtPRF2, AtPRF3 and the complex structure with Poly-P. We solved the crystal structures of AtPRF2 both in apo and Poly-P–bound forms, as well as of AtPRF3Δ37 and AtPRF3Δ22, respectively. In vivo functional studies of AtPRF3Δ22 partially recapitulated its negative regulation in actin assembly using yeast reconstitution system by introducing AtPRFs. By integrating both structural studies and mathematical modeling, we found that AtPRF3Δ22 NTE adopts a “closed” conformation and trespasses the Poly-P–binding pocket, which should be able to open upon Poly-P binding. Therefore, we performed the molecule simulation of AtPRF3 NTE in the presence and absence of Poly-P, and the results suggest that AtPRF3 adopts various conformations to modulate the Poly-P binding. Moreover, the NTE in the isolated AtPRF3Δ22 structure likely adopts a “closed” conformation. Our simulation results demonstrated that the NTE evolves dynamically by adopting different interaction modes toward Poly-P, through which an effective Poly-P binding and negative regulation in actin assembly have remained. Taken together, our results suggest that the unique ability of the AtPRF3 NTE by adopting various conformations, which enables precise modulations of actin assembly in defense mechanisms.

Results

AtPRF3 strongly inhibits actin polymerization

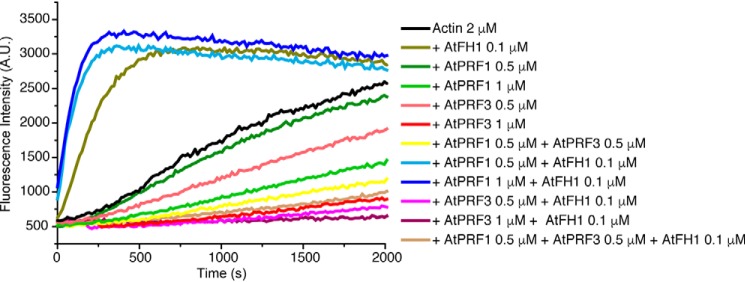
To understand how formin-mediated actin assembly is balanced in the presence of both negative and positive profilin isoforms, we designed a profilin competition assay by comparing the AtFH1-mediated actin assembly in the presence of AtPRF3, AtPRF1, or both. AtPRF3 has a stronger inhibitory effect on spontaneous actin polymerization than AtPRF1 (Fig. 1). A profilin mix of 0.5 μm AtPRF3 and 0.5 μm AtPRF1 results in actin assembly in the middle of 1 μm AtPRF3 and 1 μm AtPRF1, indicating a balanced effect on spontaneous actin assembly using both profilin isoforms. Interestingly, the presence of formin AtFH1 with a coexistence of 0.5 μm AtPRF3 and AtPRF1 at 1:1 ratio showed an overall negative regulation in AtFH1-mediated actin assembly, which is at a similar level of F-actin polymerization by using 0.5 μm AtPRF3 only (Fig. 1). Such inhibition of actin polymerization in the presence of formin strongly indicates the unique function of AtPRF3.

Figure 1.

The competition assay of full-length AtPRF3 to AtPRF1 in AtFH1-FH1FH2COOH (AtFH1)-mediated actin polymerization. 2 μm actin with 3% pyrene-actin was used for actin polymerization assay. The concentration of each protein was indicated.

In vivo reconstitution of AtPRFs in budding yeast

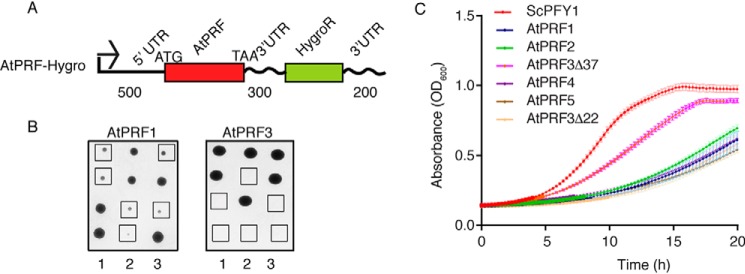
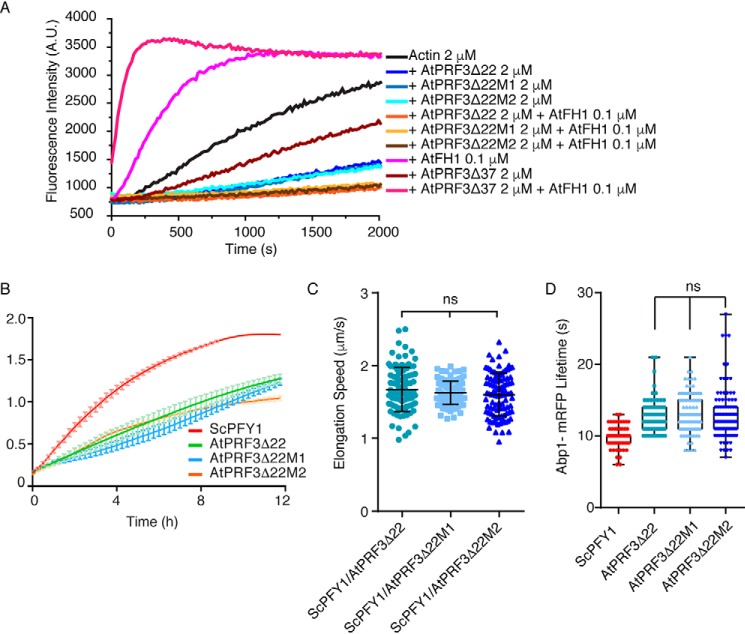
To better understand the unique function of AtPRF3 in vivo, we reconstituted the AtPRF1–5, AtPRF3 truncating the N-terminal 22 amino acids (AtPRF3Δ22), and 37 amino acids (AtPRF3Δ37) in budding yeast by replacing the only profilin ScPFY1 with AtPRF genes, taking advantage of the highly conserved machinery of profilin–formin–actin–mediated actin assembly among eukaryotes. Because haploid deletion mutant pfy1Δ is lethal, we therefore first generated a diploid strain with one ScPFY1 copy replaced by the cgLEU2 gene, ScPFY1/pfy1Δ::CgLEU2. Then the pfy1Δ::CgLEU2 gene was replaced by AtPRFs (Fig. 2A). AtPRFs were transcribed at the ScPFY1 chromosomal locus under the control of the ScPFY1 promoter in haploid. ScPFY1/AtPRF3 diploid showed 2:2 segregation viability, yielding only two viable Hygro⁻ segregants per tetrad (Fig. 2B), which demonstrated that AtPRF3 is a lethal recessive gene and is highly consistent with its strong adverse effects on formin-mediated actin assembly (3). All other segregants with full-length AtPRF isoform genes, AtPRF3Δ37, and AtPRF3Δ22 were viable but showed slower growth than the WT, perhaps because of the in vivo functional difference between yeast and plant profilin (Fig. 2B and Fig. S1A). To perform a direct comparison among all viable AtPRF isoform-expressing stains, we measured yeast growth in liquid culture at 25 °C and found that AtPRF1, AtPRF2, AtPRF3Δ22, AtPRF4, and AtPRF5 yeasts showed growth defect more than AtPRF3Δ37 (Fig. 2C), consistent with lower affinity of AtPRF3Δ37 to Poly-P and positive function in formin-mediated actin assembly (3).

Figure 2.

In vivo reconstitution of AtPRFs in budding yeast. A, constructs of yeast expression cassette for AtPRF isoforms. The lengths of UTRs were indicated. B, tetrad analysis of heterozygous diploid ScPFY1/AtPRF. Haploids expressing AtPRF1 and AtPRF3 were highlighted by squares. C, growth of haploid strains expressing ScPFY1 and AtPRFs on YPD plate at 25 °C for 48 h.

In vivo function analysis of AtPRFs in budding yeast

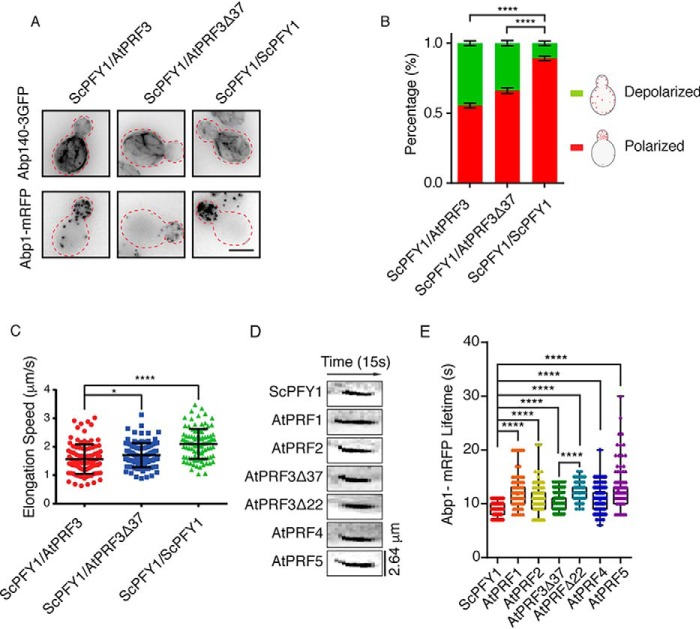
To compare in vivo functions between AtPRF3 and AtPRF3Δ37, we generated heterozygotes diploids ScPFY1/AtPRF3 and ScPFY1/AtPRF3Δ37 expressing actin cable marker Abp140 (Abp140–3GFP) and actin endocytic patch marker Abp1-mRFP. AtPRF3 and AtPRF3Δ37 were expressed normally in diploids, which were detected by anti-Myc antibodies against the N-terminal Myc tags (Fig. S1D). By having the functional allele of ScPFY1, both ScPFY1/AtPRF3 and ScPFY1/AtPRF3Δ37 showed the intact structures of actin cables and patches, although a slight depolarization of Abp1-mRFP was observed (Fig. 3, A and B). To better characterize the mild actin cable defect, we measured the cable elongation rate by following the elongating tip of individual actin cables. ScPFY1/AtPRF3 showed slower cable elongation speed (1.56 ± 0.52 μm/s) compared with that in the ScPFY1/AtPRF3Δ37 (1.71 ± 0.42 μm/s) and ScPFY1/ScPFY1 cells (2.10 ± 0.52 μm/s), respectively (Fig. 3C). We also characterized the in vivo functions of AtPRF isoforms in yeast haploid by examining the actin assembly and actin-mediated endocytosis. Abp1 lifetime records the appearance and disappearance of Abp1 on the plasma membrane that is a sensitive diagnostic approach for investigating endocytosis efficiency (Fig. S1, B and C). An extended lifetime indicates a delayed internalization of the endocytic pit from the plasma membrane. The living cell fluorescence imaging of Abp1 showed a different endocytosis efficiency for each profilin isoform strain (ScPFY1 < AtPRF3Δ37 < AtPRF4 ∼ AtPRF2 < AtPRF1 < AtPRF5 and AtPRF3Δ22) (Fig. 3, D and E).

Figure 3.

In vivo function comparison of AtPRFs in budding yeast. A, maximum intensity Z-projection images of actin cables and patches in heterozygous diploids, ScPFY1/AtPRF3, ScPFY1/ AtPRF3Δ37, and ScPFY1/ScPFY1. Scale bar, 5 μm. B, visual scoring the polarity of actin patches in diploid cells. (6 individual images were analyzed, and more than 200 total yeast cells were classified). C, actin cables motility in heterozygous diploid strains ScPFY1/AtPRF3, ScPFY1/ AtPRF3Δ37, and ScPFY1/ScPFY1 (n = 100 filaments). p values were determined by two-tailed Student's t test assuming equal variances (*, p < 0.05; ****, p < 0.0001). Error bars, S.D. D and E, representative kymographs (D) and lifetimes of Abp1-mRFP patches (E) in the indicated haploids. From left to right, n = 125, n = 120, n = 120, n = 126, n = 147, n = 122, and n = 122 patches used for analysis.

Structural analysis of AtPRF3

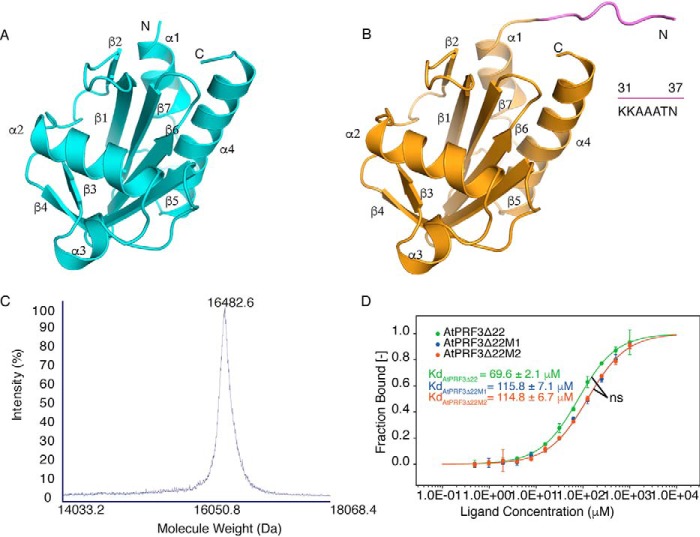
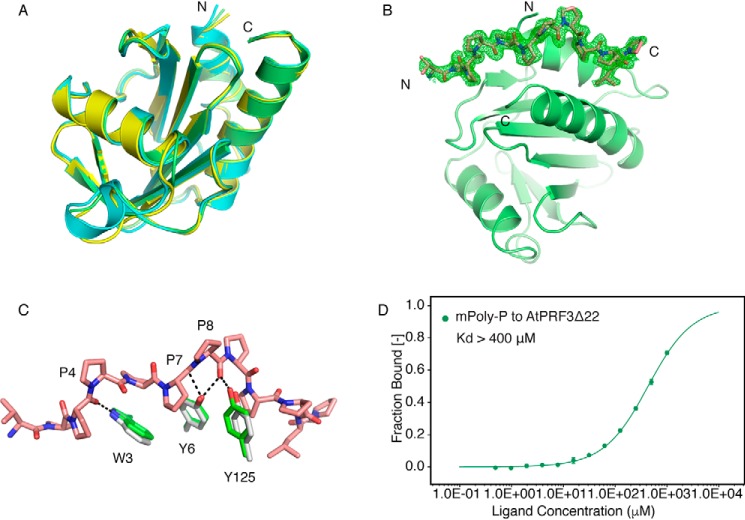
To better understand the functionality of AtPRF3, we solved the crystal structure of AtPRF3Δ37 beyond 1.5 Å resolution. AtPRF3Δ37 is composed of seven anti-parallel β-sheets that are sandwiched by four α-helices (Fig. 4A), demonstrating a canonical profilin fold (1). We also successfully crystallized AtPRF3Δ22, whereas the full-length AtPRF3 was recalcitrant to be crystallized. Eventually, we solved the crystal structure of AtPRF3Δ22 at 3.6 Å resolution by introducing the surface residue mutation AtPRF3Δ22M1 (K33A/K34A/K35A) according to SERP server prediction (7), as well as the additional L136Q mutation AtPRF3Δ22M2 (K33A/K34A/K35A+L136Q) (Fig. S2A). The protein identity of AtPRF3Δ22M2 was verified by MALDI-TOF-MS analysis, which showed the molecular mass of ∼16,482.6 Da, in line with the theoretical molecular mass (16,450.8 Da) (Fig. 4C). To characterize AtPRF3Δ22 mutants, we compared their binding affinities to AtFH1 Poly-P (RVPPPPPPPPPLP) by microscale thermophoresis (MST). The dissociation constant (K_d) values of AtPRF3Δ22, AtPRF3Δ22M1, and AtPRF3Δ22M2 to Poly-P were 69.6 ± 2.1, 115.8 ± 7.1, and 114.8 ± 6.7 μm, respectively, suggesting a negligible effect on binding affinity by the L136Q mutation (Fig. 4D). AtPRF3Δ22 moderately decrease the binding affinity to Poly-P, given the K_d values of 29.6 and 175.6 μm for full-length AtPRF3 and the truncated AtPRF3Δ37, respectively (3). The structure of AtPRF3Δ22M2 showed a protruding N terminus from Lys³¹ to Asn³⁷ (KKAAATN), compared with AtPRF3Δ37 (Fig. 4B). However, we were unable to model the residues 23–30 (QRRSRAKV) because they lack clear electron density. This region Lys³¹–Asn³⁷ does not directly interact with the profilin core domain, appearing to be dynamic. We generated the unbiased F_o − F_c map for all the NTE of 10 chains in the asymmetric unit (Fig. S3, A–J). The main chains of the NTE K31-N37 were well-fitted to the F_o − F_c map. It appears that the AtPRF3Δ22M2 proteins were paired during crystal packing. However, the closest atom distance between the two N termini was 5.0 Å, indicating no direct interaction; therefore crystal packing has little influence on the structural conformation (Fig. S3K).

Figure 4.

Structures and characterization of AtPRF3Δ37 and AtPRF3Δ22. A, crystal structure of AtPRF3Δ37 colored in cyan. B, crystal structure of AtPRF3Δ22 in orange with the extra amino acids (KKAAATN) colored in violet. C, the MALDI-TOF-MS result of AtPRF3Δ22M2 sample for characterizing protein size and integrity. D, thermophoresis binding curves of AtPRF3Δ22, AtPRF3Δ22M1, and AtPRF3Δ22M2 titrated against AtFH1 Poly-P from experiments of three biological replicates. The dissociated constants are shown, respectively. ns indicates no significance between all three sets of affinity data of AtPRF3Δ22, AtPRF3Δ22M1, and AtPRF3Δ22M2.

AtPRF3Δ22 variants have similar in vivo function in budding yeast

To validate the functionality of AtPRF3Δ22M2 used for crystallization, we examined the in vitro biochemical activities of AtPRF3Δ22, AtPRF3Δ22M1, and AtPRF3Δ22M2. Pyrene-actin–based assay showed that both variants inhibit AtFH1-mediated actin assembly, without distinguishable efficacy to AtPRF3Δ22 (Fig. 5A). Haploid stains expressing AtPRF3Δ22, AtPRF3Δ22M1, and AtPRF3Δ22M2 showed similar growth defects by liquid culturing assay at 25 °C (Fig. 5B). Diploid strains ScPFY1/AtPRF3Δ22, ScPFY1/AtPRF3Δ22M1, and ScPFY1/AtPRF3Δ22M2 expressing fluorescent actin cable and patch markers were generated similarly. By tracking the actin cable growing end in time-lapse imaging of Abp140–3GFP, we measured cable elongation speed of ScPFY1/AtPRF3Δ22 (1.67 ± 0.30 μm/s), ScPFY1/AtPRF3Δ22M1 (1.63 ± 0.16 μm/s), and ScPFY1/AtPRF3Δ22M2 (1.60 ± 0.29 μm/s), respectively, in which no functional difference of AtPRF3Δ22M2 was observed (Fig. 5C). In addition, we quantitatively analyzed in vivo endocytosis efficiency of the AtPRF3Δ22 mutants. Consistently, AtPRF3Δ22M1 and AtPRF3Δ22M2 cells showed no significant difference in the Abp1-mRPF lifetime than that of AtPRF3Δ22 (Fig. 5D), supporting the unchanged in vivo endocytosis in AtPRF3Δ22M2 cells when compared with AtPRF3Δ22.

Figure 5.

Functional validation of AtPRF3Δ22 variants. A, kinetic actin polymerization of AtPRF3Δ22, AtPRF3Δ22M1, and AtPRF3Δ22M2 in the presence of AtFH1-FH1FH2COOH (AtFH1). B, thermostatted microplate reader measures the growth of yeast strains expressing AtPRF3Δ22 mutants and WT. C, actin cables motility in heterozygous diploid strains ScPFY1/AtPRF3Δ22, ScPFY1/AtPRF3Δ22M1, and ScPFY1/AtPRF3Δ22M2 (n = 100 filaments). p values were determined by two-tailed Student's t test assuming equal variances (*, p < 0.05; ****, p < 0.0001). Error bars represent S.D. D, lifetimes of Abp1-mRFP patches in the indicated haploids. n = 100 patches used for analysis.

Structural analysis of Poly-P–bound AtPRF2

To better understand how Arabidopsis profilins interact with Poly-P, we determined the crystal structures of AtPRF2 in both apo and Poly-P–bound forms at 2.4 and 1.9 Å resolutions, respectively. The structure of AtPRF2 shares the same fold as that of AtPRF1 and AtPRF3Δ37 with RMS deviation values of 0.41 and 0.40 Å for C-α atoms, respectively (Fig. 6A), suggesting that the overall core structure of Arabidopsis profilin is highly conserved. As for the Poly-P–bound AtPRF2, all of the 13 amino acids except for the first arginine in Poly-P can be modeled (Fig. 6B). The Poly-P is held in a hydrophobic groove formed by the first and the fourth helix of AtPRF2, involving the residues His¹⁰, Trp³³, Leu¹²², Leu¹²⁶, Ser¹²⁹, and Leu¹³¹. Notably, Poly-P binds to AtPRF2 with a 1:1 stoichiometry in a similar way as that of plant pollen allergenic profilin (8). Three key residues (Trp³, Tyr⁶, and Tyr¹²⁵) in AtPRF2 and three essential prolines (Pro⁴, Pro⁷, and Pro⁸) in Poly-P are involved in hydrogen-bond formation (Fig. 6C). To test whether these three prolines contribute to AtPRF3 binding directly, we synthesized the mutated mPoly-P (P4A/P7A/P8A). mPoly-P showed a drastic decrease in binding toward AtPRF3Δ22, with a K_d over 400 μm (Fig. 6D), which validated the importance of the three prolines (Pro⁴, Pro⁷, and Pro⁸) in profilin binding. No significant conformational change of AtPRF2 was observed upon the binding of Poly-P compared with its apo form.

Figure 6.

Structural comparison of AtPRFs and the Poly-P binding. A, crystal structure of AtPRF1 (yellow) (PDB code 3NUL) and AtPRF3Δ37 (cyan) were aligned to AtPRF2 (lime). B, unbiased omit F_o − F_c electron density map (green) contoured at 2.2σ of Poly-P (salmon) bound AtPRF2 (lime). C, the alignment of AtPRF2 to Poly-P–bound AtPRF2. Whereas the Apo structure is shown in gray, the complex structure is colored in green, and the Poly-P is shown in salmon. The residues involved in interaction are labeled, respectively. D, microscale thermophoresis binding curves of the mPoly-P titration curve to AtPRF3Δ22 with the dissociation constant indicated. All the measurements were performed with three biological replicates.

Plasticity of the AtPRF3 NTE revealed by H-REMD

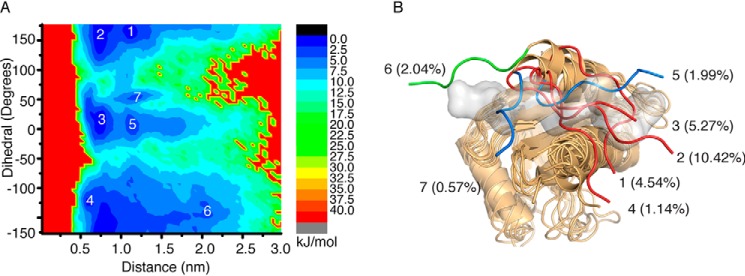
Given that the profilin core of AtPRF2 and AtPRF3 is highly conserved, we compared the structure of AtPRF3Δ22M2 with the Poly-P–bound AtPRF2 and found that Lys³¹–Asn³⁷ residues of AtPRF3Δ22M2 occupied the Poly-P–binding pocket (Fig. S4A). To test whether AtPRF3 NTE is able to open and thereby enable the Poly-P binding, we examined its flexibility using Hamiltonian replica-exchange molecular dynamics (H-REMD) simulations, with L136Q mutation corrected to Leu¹³⁶ during modeling (9). The H-REMD simulation was summarized in the free-energy surface that was shown as a function of the dihedral angle formed by α carbons of the residues Thr³⁶–Ser³⁹ against the center of the mass distance between the NTE and the C-terminal helix (CTH) (Fig. S4B). Seven local minima with representative structures were extracted by geometric clustering, which describes the conformational states of the AtPRF3Δ22M1 (Fig. 7, A and B, and Table S1). Each representative structure of the local minimum was defined as an “open” state if no structural clash was observed between the AtPRF3Δ22M1 and the Poly-P; otherwise, a “closed” state was defined. We found that minimums 1–4 represent closed conformations, whereas minimum 6 represents an open conformation. We consider minimums 5 and 7 to be “semiopen” conformations because a minor structural clash with the Poly-P was observed; thus Poly-P–binding sites were not occluded by AtPRF3Δ22M1. We also used various simulated time from 550 and 650 ns to show that the simulation of NTE is converged (Fig. S4, C and D). The free-energy landscape reveals the dynamic nature of the AtPRF3Δ22M1, which adopts diverse conformations to occlude or accommodate the Poly-P binding, thus fine-tune regulating actin filament assembly.

Figure 7.

Computational simulation analysis of AtPRF3 NTE. A, free-energy surface as a function of dihedral angle formed by α carbons of residues 36–39 (dihedral) of AtPRF3Δ22M2 against center of mass distance between the NTE and C-terminal helix (distance), which describes the conformational space of AtPRF3 NTE. The local minimum is labeled with numbers. B, all the conformations corresponding to the minimum in A of the AtPRF3 NTE are superimposed onto the crystal structure of Poly-P–bound (gray surface) AtPRF2. Seven local minima are indicated. The percentage of each minimum is the ratio between the number of structures in the representative class and the total sampling data.

AtPRF3 NTE might interact with Poly-P in an adaptive mode

Two positive charged clusters, Arg²⁴/Arg²⁵/Arg²⁷ and Lys³¹–Lys³⁵ (particularly the former) in the NTE, could positively be involved in Poly-P binding. To further understand the molecular interactions between the AtPRF3Δ22 NTE and Poly-P, we generated AtPRF3Δ22M3 (R24A/R25A/R27A+K33A/K34A/K35A). AtPRF3Δ22, AtPRF3Δ22M1, and AtPRF3Δ22M3 all showed a marginal difference in Poly-P binding using MST binding assay (Fig. 4D and Fig. S4E). We modeled the Poly-P–bound structure of AtPRF3Δ22 variants by applying the representative structure of AtPRF3Δ22M1 in the open conformation (from minimum 6) with “docked” Poly-P. The Gln²³–Val³⁰ was modeled with an extended and disordered conformation. These conformations of the representative clusters obtained from molecular dynamics simulations and the following geometric clustering analysis were extracted for binding energy calculations using the molecular mechanics–Poisson Boltzmann surface area (MM-PBSA) method (10). For comparison, simulations and binding energy analysis were also performed for the Poly-P–bound AtPRF3Δ37 in which the NTE is absent. AtPRF3Δ22, AtPRF3Δ22M1, and AtPRF3Δ22M3 all showed different contact sites toward Poly-P binding with different contact occupancies (Table 1). Moreover, by calculating the binding energy, the AtPRF3Δ22, AtPRF3Δ22M1, and AtPRF3Δ22M3 clusters showed comparable binding free energy but lower than AtPRF3Δ37 (Table 2). Interestingly, after the simulations were converged, we did not notice any obvious formation of helix structure in NTE, indicating its disordered nature. Considering intrinsically disordered region evolving fast by having low sequence conservation, which enables it to have weak and nonspecific interaction with binding partners, together with molecular dynamic simulations showed that AtPRF3Δ22M1 and AtPRF3Δ22M3 had evolving contact sites toward Poly-P binding, it is very likely that NTE adopts dynamic and nonspecific binding to Poly-P, which is also in agreement with the reported phenomena that peptides with flanked core region could dynamically evolve nonspecific interaction at the binding interface (11).

Table 1.

Contact residues of Poly-P–bound AtPRF3 and their occupancies

Contact occupancy is the ratio of the number of structures (frames) belonging to that particular cluster containing a specific contact (definitions in method section) to the total number of structures (frames) belonging to that cluster.

Cluster	AtPRF3	Poly-P	Type	Occupancy
				%
AtPRF3Δ22–Poly-P	R27-NH2	P9-O	Hydrogen bond	55.8
	K29-O	L12-N	Hydrogen bond	28.3
	K31-NZ	P13-OT1	Electrostatic	33.3
	K31-NZ	P13-OT2	Electrostatic	32.9
AtPRF3Δ22M1–Poly-P	K32-NZ	P13-OT1	Electrostatic	54.6
	K32-NZ	P13-OT2	Electrostatic	54.7
	A34-N	P10-O	Hydrogen bond	25.3
AtPRF3Δ22M3–Poly-P	K31-O	L12-N	Hydrogen bond	26.6
	K31-NZ	P13-OT1	Electrostatic	55.8
	K31-NZ	P13-OT2	Electrostatic	55.2

Table 2.

Calculations of binding free energy using MM-PBSA for Poly-P–bound AtPRF3

The values are given in KJ/mol. The percentage is the ratio of the number of structures (frames) belonging to that particular cluster to the total number of structures we sampled. sasa, solvent-accessible surface area.

Cluster	Percentage	Evdw	Eelec	Epolar	Esasa	Ebinding
	%
AtPRF3Δ22–Poly-P	76.64	−289.099 ± 0.591	−573.063 ± 2.513	606.003 ± 3.075	−34.373 ± 0.055	−290.624 ± 1.140
AtPRF3Δ22M1–Poly-P	82.63	−301.306 ± 0.675	−553.927 ± 2.382	605.557 ± 2.947	−35.945 ± 0.079	−285.674 ± 1.804
AtPRF3Δ22M3–Poly-P	32.05	−276.586 ± 0.861	−575.155 ± 3.003	582.271 ± 3.605	−33.819 ± 0.095	−303.033 ± 1.551
AtPRF3Δ37–Poly-P	100	−200.328 ± 0.346	−287.724 ± 1.276	259.269 ± 1.697	−22.582 ± 0.042	−251.381 ± 0.957

Discussion

Formin FH1 domain effectively increases the profilin-actin concentration at the barbed end to support rapid elongation of actin filament by delivering G-actin to barbed end. During processive elongation, flexible FH1 domain provides transient and frequent collisions between the barbed end and profilin-actin and rapid subsequent disassociation of free profilin from formin and barbed end (12). Both the profilin affinity to Poly-P tracts and the distance between Poly-P tracts and FH2 domain could directly affect the actin transfer efficiency (13). Arabidopsis AtPRF3 demonstrated a high binding affinity toward formin Poly-P, suggesting adverse effects in formin-mediated actin elongation. The AtPRF3 NTE gives the tight binding to Poly-P in a length-dependent manner, whereas the removal of the N-terminal 37 residues entirely reverted its inhibitory effect on actin assembly in vitro (3). Here, the in vitro competition assay validates the inhibitory effect of AtPRF3 on actin polymerization in the presence of AtFH1. Moreover, in vivo yeast reconstitution system fully recapitulated the adverse effects of AtPRF3 NTE in regulating intracellular actin assembly and the viability of the cells. A tight Poly-P binding demonstrated an adverse effect of AtPRF3 that might be derived from the mechanical gating mechanism, such as constraining the rotation or slippage of the FH2 dimer around the F-actin filament for releasing the torsion stress that accumulates during elongation (14, 15).

We used a structural and mathematical modeling approach to study the dynamic interaction between AtPRF3 NTE and Poly-P. The crystal structures of AtPRF3Δ37, AtPRF3Δ22, and Poly-P–bound AtPRF2 disclosed a primary closed conformation of AtPRF3Δ22 NTE at the Poly-P–binding pocket. Geometric clustering revealed that NTE is able to adopt either a closed or an open conformation. Furthermore, by calculating the binding free energy between AtPRF3Δ22 variants and Poly-P and comparing with a parallel calculation of Poly-P–bound AtPRF3Δ37, we showed that the additional contribution of the NTE involves multiple sites. Our structure and simulation data suggest that Poly-P binding by AtPRF3Δ22 is highly modulated through the NTE conformational change. Nevertheless, we could also not exclude the contribution of the first N-terminal 22 residues for Poly-P binding. Such plasticity in AtPRF3 NTE conformation toward Poly-P binding provides an excellent platform to fine-tune the unique negative function of AtPRF3 in regulating actin assembly with other AtPRF isoforms during plant defense responses.

Upon pattern-triggered immunity, the AtPRF3 NTE confers a tunable functional regulation, such as the dynamic modulation of AtPRF3 level through both protein degradation and de novo synthesis, which adjusts the overall balance of profilin-mediated actin assembly (3). In this study, we demonstrated a modulation approach for maintaining AtPRF3 function by tuning its flexible conformation of NTE upon formin Poly-P binding. The N-terminal 22 residues of AtPRF3 are intrinsically disordered in nature that are also usually highly phosphorylated and flexible to adopt conformational changes, which could often be coupled with ubiquitination and protein degradation during signaling transduction (6). Ubiquitination and phosphorylation are highly coupled post-translational modification, which is remarkably enriched on intrinsically disordered region. The potential post-translational modifications on the AtPRF3 NTE might directly modulate its interaction with formin and AtPRF3 activities during immune responses that are worthy of future studies. Furthermore, intrinsically disordered regions play diverse functions in fine-tuning cellular process through regulating protein–protein interactions. Our multiple molecular dynamics simulations, binding free-energy calculations, and biochemical experiments allow us to propose a model that AtPRF3 NTE interacts with Poly-P via dynamic, and nonspecific binding mode. Such adaptive conformations might be able to maintain a continuous interaction between AtPRF3 and formin for the effective negative regulation in F-actin assembly during pattern-triggered immune responses.

Experimental procedures

Yeast strains and plasmid construction

Saccharomyces cerevisiae S288C background strains were used in this study. The manipulation, cultivation, and transformation of yeast strains followed standard methods. Because of the lethality of PFY1 deletion in haploid yeast, one copy of PFY1 gene was deleted by replacing the gene open reading frames with the Candida glabrata LEU2 (CgLEU2) cassettes to generate a PFY1/pfy1Δ::CgLEU2 heterozygote diploid. To produce a strain expressing AtPRF variants, we constructed vectors using the following strategies. Endogenous promoter and terminator of yeast ScPFY1, 500 bp upstream of the start codon and 500 bp downstream of the stop codon of ScPFY1, were constructed into pRS316 vectors harboring Arabidopsis AtPRF variants, respectively. An expression cassette of the hygromycin resistance gene was integrated into the middle of the 500 bp downstream of the ScPFY1 stop codon. Multifragment assembly was performed by Gibson assembly approach (New England BIolabs) to obtain the above constructs. Also, one Myc tag was inserted at the N terminus of AtPRF sequence by Q5 site-directed mutagenesis method (New England BIolabs). The DNA fragments containing ScPFY1 promoter-driven AtPRF expression cassette were transformed into the strain DDY1102, which generates a PFY1/pfy1Δ::AtPRF::HygMX6 heterozygote. PFY1/pfy1Δ::AtPRF::HygMX6 heterozygotes were followed by sporulation to identify the leucine-sensitive but hygromycin-resistant segregants. Genomic C-terminal tagging was performed as previously described. All strains were grown at 30 °C in standard rich medium (YPD) or synthetic medium supplemented with appropriate amino acids unless otherwise specified. Cell growth was determined by either yeast spotting assay on YPD or liquid growth assay using TECAN M200 infinite pro plate reader.

Immunoblotting

Yeast whole-cell extracts were prepared as described previously. In brief, yeast cells at A₆₀₀ of 0.5 in log phase were collected by centrifugation at 2,500 rpm for 3 min at room temperature. Cell pellet was immediately resuspended with 250 μl of 20% TCA, mixed with an equal volume of glass beads (0.5-mm zirconia/silica beads; Biospec), and vortexed by Precellys 24 homogenizer (Bertin Instruments) three times of the 30-s beading with a 1-min interval on ice. Glass beads were washed twice with 250 μl of 5% TCA to maximize protein recovery. The resulting extract was spun at 13,000 rpm for 5 min at 4 °C. The pellet was dissolved in 100 μl of 2× SDS loading buffer (100 mm Tris-HCl, pH 6.8, 4% SDS, 20% glycerol, 0.1% bromphenol blue, 50 mm DTT), neutralized by adding 20 μl of 1 m Tris base, boiled for 5 min, and clarified by centrifugation. Total cell extracts equivalent to 0.4 A₆₀₀ of cells were subjected to immunoblot analysis. Proteins were detected using the primary antibodies, mouse anti-Pgk1 (1:10,000; Invitrogen) and mouse anti-Myc (1:1,000, 9E10). The blots were subsequently scanned using Odyssey IR Imager (LI-COR Biosciences).

Microscopy

Yeast cell imaging was performed essentially as previously described (16). In brief, yeast were grown to log phase in the synthetic media lacking tryptophan at 25 °C, immobilized on concanavalin A–coated coverslips, and then imaged on Leica DMi8 microscopy (Leica Microsystems) that is equipped with a HCX PL APO 100×/1.4 oil objective, ORCA-Flash4.0 LT (Hamamatsu, Japan), and a solid-state Spectra-X light engine (Lumencor) as described. The images were acquired using Metamorph software (Molecular Devices) and processed using ImageJ (National Institutes of Health).

Microscopy image analysis

Fluorescent images of the actin cytoskeleton in budding yeast were evaluated and analyzed using the following criteria. All polarized actin patches indicated by Abp1-mRFP were present in the daughter cell. Depolarized actin patches were present in both the mother cell and daughter cell. For actin cable motility analysis, the Abp140–3GFP movie was taken, actin filament barbed-end elongation was traced by ImageJ (National Institutes of Health), and then filament elongation speed was calculated.

Pyrene actin polymerization assay

Rabbit skeletal muscle actin was purified from rabbit muscle acetone powder (Pel-Freez) as described (17). Monomeric Ca²⁺-ATP-actin was purified by Sephacryl S-300 HR chromatography linked to FPLC system using G buffer (5 mm Tris-HCl, pH 8, 0.2 mm ATP, 0.1 mm CaCl₂, 0.5 mm DTT, 0.1 mm azide). Pyrene-labeled actin was purchased from Cytoskeleton Inc., and prepared followed the manufacture's guide. Polymerization assay was done as previous reported (18). Briefly, 2 μm purified monomeric G-actin (3% pyrene-actin) was mixed with the target proteins and monitored at excitation 365 nm and emission 407 nm at 25 °C in a Cytation 5 cell imaging multimode plate reader (BioTek).

Statistical analysis

All statistical analyses were performed using GraphPad Prism software (GraphPad, San Diego, CA). p values were determined by two-tailed Student's t test assuming equal variances (*, p < 0.05; **, p < 0.01; ***, p < 0.001; ****, p < 0.0001; ns, not significant). MST binding affinity differences were determined by one-way analysis of variance. The error bars indicate the S.D.

Cloning

For the genes encoding AtPRF1 (GenBank^TM accession no. BT000264.1), AtPRF2 (GenBank^TM accession no. AY114048.1), AtPRF3 (GenBank^TM accession no. BT000885.1), AtPRF4 (GenBank^TM accession no. BT024816.1), AtPRF5 (GenBank^TM accession no. DQ653003.1), and ScPRF (GenBank^TM accession no. AAA34861.1) were cloned into a modified vector of pET-21d (+) with an N-terminal His₈ tag and human 3C protease cutting site. The AtPRF3 variants AtPRF3Δ37, AtPRF3Δ22, AtPRF3Δ22M1, AtPRF3Δ22M2, and AtPRF3Δ22M3 were performed by QuikChange mutagenesis followed by sequencing.

Protein expression and purification

All AtPRF variants were transformed into Escherichia coli BL21 (DE3). The bacteria were induced by 0.1 mm isopropyl β-d-thiogalactopyranoside at 16 °C for 16 h for protein expression and harvested by centrifugation at 4,000 rpm for 10 min. The pellet was resuspended in buffer (25 mm HEPES, pH 7.5, 150 mm NaCl, 25 mm imidazole, 10% glycerol), lysed by LM20 microfludizor, and clarified by centrifugation (20,000 rpm) at 4 °C for 1 h. The supernatant was collected, filtered through 0.22-μm filter, and loaded onto a HisTrap FF 5-ml column (GE Healthcare), and the eluted fractions were pooled and dialyzed overnight against buffer (25 mm HEPES, pH 7.5, 150 mm NaCl, 5 mm β-mercaptoethanol) by adding human 3C protease to remove histidine tag. The tag cleaved protein was load onto HiLoad Superdex 75 16/60 (GE Healthcare) pre-equilibrated with buffer (25 mm HEPES, pH 7.5, 150 mm NaCl, 5 mm β-mercaptoethanol). The eluted protein fractions were pooled, concentrated to 20 mg/ml, snap-frozen in liquid nitrogen, and stored in −80 °C for later use. The GST-tagged AtFH1 (1-FH1FH2COOH) was purified as previously described (3).

Crystallization and structure determination

Purified proteins were subjected to crystal screening against crystallization kits from Hampton Research using a sitting-drop method. The final optimized condition for AtPRF3Δ37 was 0.1 m sodium acetate (pH 5.0) and 1.42 m ammonium sulfate with protein concentration of 10 mg/ml. The final optimized condition for AtPRF2 was 0.1 m Tris HCl (pH 8.5) and 2.2 m ammonium phosphate dibasic with a protein concentration of 10 mg/ml. The final optimized condition for AtPRF2 with Poly-P was 0.1 m Bis-tris (pH 7.0) and 2.0 m ammonium phosphate dibasic with protein concentration of 10 mg/ml. The final optimized condition for AtPRF3Δ22 was 0.1 m Tris HCl (pH 7.8) and 0.9 m sodium citrate with a protein concentration of 20 mg/ml. The crystals were harvested by adding 25% glycerol to the mother liquor. The AtPRF2 and AtPRF2 with Poly-P diffraction data were collected using a Rigaku FR-X X-ray generator with a PILATUS3R 300K detector. The AtPRF3Δ37 data sets were collected from the Australia Light Source MX2 beamline. The AtPRF3Δ22 diffraction data set were collected by Swiss Light Source. The data sets were either indexed, integrated, and scaled by HKL 3000 (19) or processed by XDS (20). The structures were solved using the molecular replacement with Phaser in the Phenix suite (21) with 3NUL (Protein Data Bank (PDB) code) as the template structure. The manual model building was done with COOT (22). All the structural figures were generated through PyMOL program (23). The statistics of data collection and structure refinement are listed in Table 3. All the protein structures AtPRF3Δ37, AtPRF3Δ22, AtPRF2, and Poly-P–bound AtPRF2 have been deposited into the PDB with the accession code 6IQF, 6IQK, 6IQI, and 6IQJ, respectively. The multiple sequence alignment was done with ESPript (24).

Table 3.

Data collection and refinement statistics

Structure	AtPRF2	AtPRF2–Poly-P	AtPRF3Δ37	AtPRF3Δ22
PDB code	6IQI	6IQJ	6IQF	6IQK
Wavelength	1.5406	1.5406	0.9537	0.9764
Resolution range	27.7–2.4 (2.48–2.40)	36.77–1.92 (1.991–1.92)	37.96–1.46 (1.509–1.46)	49.24–3.6 (3.729–3.6)
Space group	P 3 2 1	P 21 21 21	C 1 2 1	P 21 21 21
Unit cell	58.68, 58.68, 83.94, 90, 90, 120	51.52, 65.16, 73.53, 90, 90, 90	80.98, 52.86, 32.41, 90, 110.38 90	135.9, 153.37, 196.68, 90, 90, 90
Total reflections	54,868	65,543	143,911	1,315,156
Unique reflections	12,582 (1274)	18,928 (1596)	22,378 (2174)	48,279 (4769)
Multiplicity	4.20	3.50	6.43	27.20
Completeness (%)	99.12 (100.00)	97.37 (84.44)	96.7 (85.3)	99.80 (99.79)
Mean I/σ(I)	25.8 (1.7)	9.3 (2.3)	8.77 (0.88)	5.99 (0.75)
Wilson B-factor	52.38	13.96	25.02	115.08
Rmeas	0.058	0.13	0.077	0.58
CC½	99.7 (73.4)	99.8 (79.3)	99.6 (63.4)	99.1 (27.5)
Reflections used in refinement	12,569 (1274)	18,913 (1596)	22,357 (2166)	48,230 (4763)
Reflections used for Rfree	1168 (96)	929 (72)	1062 (105)	4822 (477)
Rwork	0.2623 (0.3891)	0.1834 (0.2333)	0.1963 (0.4002)	0.3014 (0.4123)
Rfree	0.2968 (0.4503)	0.2183 (0.3123)	0.2156 (0.4381)	0.3469 (0.4396)
Number of non-hydrogen atoms	1969	2447.00	1024.00	11,558
Macromolecules	1950.00	2114.00	975.00	11558
solvent	19	333.00	49.00	0.00
Protein residues	260.00	283.00	130.00	1647
RMS bonds	0.004	0.00	0.01	0.003
RMS angles	0.87	1.03	1.23	0.63
Ramachandran favored (%)	96.09	98.18	96.90	92.34
Ramachandran allowed (%)	3.91	1.82	3.10	7.47
Ramachandran outliers (%)	0.00	0.00	0.00	0.19
Rotamer outliers (%)	0.00	0.00	0.00	0
Clashscore	12.23	2.15	2.58	5.77
Average B-factor	64.83	15.87	30.61	125.61
Macromolecules	64.59	14.38	30.27	125.61
Solvent	89.28	25.32	37.32

Microscale thermophoresis

Binding affinity between profilins and Poly-P (RVPPPPPPPPPLP)/mPoly-P (RVPAPPAAPPPLP) was measured by the MST method. Poly-P peptide was titrated against 20 μm of profilin proteins. Binding reactions were carried out in buffer containing 50 mm Tris, pH 7.4, 150 mm NaCl, 0.05% Tween 20. Samples were loaded into Monolith NT.115 hydrophobic capillaries (Nanotemper Technologies) immediately after preparation to avoid unspecific adsorption. Reaction capillaries were first incubated at 25 °C in the Monolith NT.115 apparatus (Nanotemper Technologies) before measurement. A precise temperature gradient was monitored, while the laser heated glass capillary. The data were collected at 25 °C using the LED power at 5% and IR-Laser power at 20%. The binding curves were fit with initial fluorescence mode in MO analysis software. Data analyses were performed with NTAnalysis (Nanotemper Technologies) (25).

Hamiltonian replica exchange molecular dynamics to sample AtPRF3-NTE

Replica exchange with solute scaling (9), a variant of H-REMD, was performed using Gromacs 5.1.4 (26) with Plumed 2.4 plugin (27). Chain A of the experimentally solved crystal structure of AtPRF3Δ22M2 was used as the initial structure. Lys³¹–Asn³⁷ (KKAAATN) belonging to the NTE were resolved and selected for Hamiltonian Scaling. The Charmm36M (28) force field and Charmm modified TIP3P (29) water model was used for the simulation. The protein was solvated in a cubic box with a distance of 1.2 nm from the box edge. Counter ions were added to neutralize the system. The LINCS (30) algorithm was used to constrain bonds containing hydrogen atoms, enabling a time step of 2 fs. Particle-mesh Ewald (31) was used with a cutoff of 1.2 nm for electrostatics, and a cutoff of 1.2 nm was used for van der Waal's interaction. The temperature of the system was maintained at 300 K using the V-rescale (32) thermostat. Steepest descent energy minimization was performed for 1000 steps to remove any initial bad contacts. A 1-ns equilibration in the Numer of particles, Volume and Temperature ensemble was performed prior to starting the simulation. Ten replicas were used for the simulation, and an effective temperature range of 300–600 K was used to generate the Hamiltonian scaling factors following a geometric progression. This resulted in an average exchange probability of ∼30%. Exchanges were attempted every 2 ps, and the simulation was performed for 550, 650, and 800 ns. Coordinates were saved every 2 ps.

Free-energy surface to describe plasticity of AtPRF3 NTE

Analysis of the simulation was performed on the replica with the unscaled potential energy (effective temperature, 300 K). The first 100 ns of the trajectory was discarded to take into account the effects of initial equilibration. To understand the conformational dynamics of the AtPRF3 NTE, we calculated the potential of mean force and plotted the free-energy surface as a function of the dihedral angle formed by the α-carbons of AtPRF3 residues Thr³⁶–Ser³⁹ against the center of the mass distance between the NTE and the CTH. These reaction coordinates characterized the dynamics of the system and were chosen after detailed observation and analysis of the trajectory. The dihedral angle formed by the α-carbons of residues Thr³⁶–Ser³⁹ characterizes the “hinge” motion of the NTE, whereas the center of the mass distance between the NTE and the CTH is an indicator if the NTE would occlude the Poly-P–binding site. The dihedral angle calculations were done using the gmx_angle tool, whereas the center of mass distance calculations were performed with the gmx_distance tool, both inbuilt into the Gromacs package (26). Two reaction coordinates were illustrated in Fig. S4B. To generate the free-energy surface, the projection was divided into bins, and the counts in each bin were used to calculate its relative free energy by the formula E = −RTln(P_i/P₀). In this formula, P_i refers to the number of counts in each bin, P₀ refers to the count of the most populated bin, R refers to the gas constant, and T refers to the temperature (300 K). To evaluate the convergence of the simulations, we plotted the free-energy surface with different time blocks throughout the simulation and evaluated the conservation of the free-energy surface.

To characterize each minima, we extracted their respective conformations and identified their representative structure through geometric clustering. Clustering of the NTE was performed using the gmx_cluster utility of the Gromacs package, using the GROMOS algorithm with a cutoff of 0.5 nm. To further visualize each representative conformation, we superimposed the representative structure of each minimum onto Poly-P–bound AtPRF2 to evaluate the possibility of a structural clash between the AtPRF3 NTE and the Poly-P, as well as an occlusion of the Poly-P–binding site by the AtPRF3 NTE. The AtPRF3 NTE conformation is considered to be in open state if it does not structurally clash with the Poly-P structure from AtPRF2. To calculate the free-energy difference between closed states and open states of the AtPRF3-NTE, we used the formula F = −RTln(P_closed/P_open), where R is the gas constant, T is the temperature (300 K), and P_closed and P_open represent the number of conformations in the closed states and number of conformations in the open state, respectively.

Model building of Poly-P–bound AtPRF3Δ22

We modeled the QRRSRAKV (Gln²³–Val³⁰) in an extended and disordered conformation on AtPRF3Δ22M1 in open conformation. We superimposed the AtPRF3Δ22 model onto Poly-P–bound AtPRF2 and subsequently extracted the coordinates of the Poly-P together with AtPRF3Δ22. The N-terminal arginine residue was also modeled into Poly-P. To investigate the contribution of NTE to Poly-P binding, we performed additional simulations of AtPRF3Δ22M1 and AtPRF3Δ22M3. To generate the AtPRF3Δ22M3 model, three arginine residues Arg²⁴, Arg²⁵, and Arg²⁷ of AtPRF3Δ22M1 were converted to alanine residues. Prior to simulations setup, the additional AtPRF3Δ22 variant models were subjected to energy minimization in vacuo using a similar energy minimization protocol as the above H-REMD simulations.

Classical molecular dynamics simulations and binding mode analysis of Poly-P–bound AtPRF3Δ22

Classical molecular dynamics simulations were initiated with energy minimization, and equilibration was performed with a protocol similar to described above for the H-REMD simulations. To sample the conformational space of Poly-P–bound AtPRF3Δ22, we performed three repeats of 100-ns production simulations with different initial velocities at 300 K. The last 50 ns of each simulation was extracted and combined for binding mode analysis. We performed geometric clustering by the protein backbone of the combined trajectory using the Gromos algorithm with the gmx cluster tool, using a cutoff of 0.25 nm. The analysis was performed for clusters contributing to more than 15% of the population. The representative structures for each cluster were further analyzed to study the binding modes between AtPRF3Δ22 variants and Poly-P to understand the contribution of the AtPRF3Δ22 NTE to Poly-P binding.

To dissect the interactions between the NTE and Poly-P, contact occupancy was calculated for each cluster of various binding modes. Hydrogen bonds were calculated based on the definition defined by gmx hbond tool. Electrostatic interactions were defined based on the distance between charged residues atoms of the NTE and Poly-P using a cutoff of 0.5 nm. The occupancies were calculated as percentages of the total number of frames belonging to that particular cluster. Contacts with occupancies higher than 25% were included.

Binding free-energy calculations

Using the MM-PBSA (10) method, the binding free energy is defined as E_binding = E_vdw + E_elec + E_polar + E_apolar − TΔS, where E_vdw refers to van der Waal's interaction energy, E_elec refers to electrostatic interaction energy, E_polar refers to polar solvation energy approximated by the Poisson Boltzmann equation, E_apolar refers to the apolar solvation energy approximated using a solvent-accessible surface area model, and ΔS refers to solute entropy. In this case, the entropy was not calculated because the ligand is rigid and similar throughout all the simulations, thus allowing an assumption of similar entropy contributions.

The binding free energy between AtPRF3Δ22 variants and the Poly-P was calculated by extracting frames from each cluster and performing the calculations for each cluster using the g_mmpbsa_ENREF_11 (33) with default parameter settings and bootstrap analysis with 2000 steps to estimate free-energy calculation errors. To allow a meaningful comparison, we set up a parallel system of AtPRF3Δ37 in complex with Poly-P following the similar parameters for comparison.

Author contributions

Z. Q., H. S., Y. Mu, Y. Miao, and Y.-G. G. formal analysis; Z. Q., H. S., J. T. Y. N., Y. Mu, Y. Miao, and Y.-G. G. validation; Z. Q., H. S., J. T. Y. N., Q. M., S.H.K., and Y. Miao investigation; Z. Q., H. S., J. T. Y. N., Y. Mu, Y. Miao, and Y.-G. G. writing-original draft; Z. Q., H. S., J. T. Y. N., Y. Mu, Y. Miao, and Y.-G. G. writing-review and editing; H. S., J. T. Y. N., Y. Mu, Y. Miao, and Y.-G. G. conceptualization; H. S., J. T. Y. N., Y. Mu, Y. Miao, and Y.-G. G. data curation; J. T. Y. N. and Y. Mu software; J. T. Y. N., Y. Mu, Y. Miao, and Y.-G. G. methodology; Y. Mu, Y. Miao, and Y.-G. G. supervision; Y. Mu, Y. Miao, and Y.-G. G. funding acquisition; Y. Mu, Y. Miao, and Y.-G. G. project administration; Y. Miao and Y.-G. G. resources.