Latent cellular analysis robustly reveals subtle diversity in large-scale single-cell RNA-seq data

Abstract

Single-cell RNA sequencing (scRNA-seq) is a powerful tool for characterizing the cell-to-cell variation and cellular dynamics in populations which appear homogeneous otherwise in basic and translational biological research. However, significant challenges arise in the analysis of scRNA-seq data, including the low signal-to-noise ratio with high data sparsity, potential batch effects, scalability problems when hundreds of thousands of cells are to be analyzed among others. The inherent complexities of scRNA-seq data and dynamic nature of cellular processes lead to suboptimal performance of many currently available algorithms, even for basic tasks such as identifying biologically meaningful heterogeneous subpopulations. In this study, we developed the Latent Cellular Analysis (LCA), a machine learning–based analytical pipeline that combines cosine-similarity measurement by latent cellular states with a graph-based clustering algorithm. LCA provides heuristic solutions for population number inference, dimension reduction, feature selection, and control of technical variations without explicit gene filtering. We show that LCA is robust, accurate, and powerful by comparison with multiple state-of-the-art computational methods when applied to large-scale real and simulated scRNA-seq data. Importantly, the ability of LCA to learn from representative subsets of the data provides scalability, thereby addressing a significant challenge posed by growing sample sizes in scRNA-seq data analysis.

INTRODUCTION

Single-cell RNA sequencing (scRNA-seq) quantifies cell-to-cell variation in transcript abundance, leading to a deep understanding of the diversity of cell types and the dynamics of cell states at a scale of tens of thousands of single cells (1–3). Although scRNA-seq offers enormous opportunities and has inspired a tremendous explosion of data-analysis methods for identifying heterogeneous subpopulations, significant challenges arise because of the inherently high noise associated with data sparsity and the ever-increasing number of cells sequenced. The current state-of-the-art algorithms have significant limitations. The cell-to-cell similarity learned by most machine learning–based tools (such as Seurat (4), Monocle2 (5), SIMLR (6) and SC3 (7)) is not always user-friendly, and significant efforts are required for a human scientist to interpret the results and to generate a hypothesis. Several methods require the user to provide an estimation of the number of clusters in the data, and this may not be readily available and many times arbitrary. Furthermore, many methods have a high computational cost that will be prohibitive for datasets representing large numbers of cells. Lastly, although certain technical biases (e.g., cell-specific library complexity) have been recognized as major confounding factors in scRNA-seq analyses (8), despite recent efforts (4,9,10), other technical variations (e.g. batch effects and systematic technical variations that are irrelevant to the biological hypothesis being evaluated) have not received sufficient attention, even though they present major challenges to the analyses (11). Most methods employ a variation based (over-dispersed) gene-selection step before clustering analysis, based on the assumption that a small subset of highly variable genes is most informative for revealing cellular diversity. Although this assumption may be valid in certain scenarios, due to the overall low signal-to-noise ratio in scRNA-seq data, many non-informative genes (such as high-magnitude outliers and dropouts, etc.) are retained as over-dispersed (12). Consequently, it potentially introduces additional challenges for downstream analysis when informative genes are not most variable, which happens when the difference among subpopulations is subtle, or there is a strong batch effect, while most variable genes differ by batch.

We realize that text mining/information retrieval shares many challenges with scRNA-seq, such as data sparsity, low signal-to-noise ratio, synonymy (different genes share a similar function), polysemy (a single gene carries multiple different functions) and the existence of confounding factors. Latent semantic indexing (LSI) is a machine-learning technique successfully developed in information retrieval (13), where semantic embedding converts the sparse word vector of a text document to a low-dimensional vector space, which represents the underlying concepts of those documents. Inspired by LSI’s successes, we developed Latent Cellular Analysis (LCA) for scRNA-seq analysis. LCA is an accurate, robust, and scalable computational pipeline that facilitates a deep understanding of the transcriptomic states and dynamics of single cells in large-scale scRNA-seq datasets. LCA makes a robust inference of the number of populations directly from the data (a user can specify this with a priori information), rigorously models the contributions from potentially confounding factors, generates a biologically interpretable characterization of the cellular states, and recovers the underlying population structures. Furthermore, LCA addresses the scalability problem by learning a model from a subset of the sample, after which a theoretical scheme is used to assign the remaining cells to identified populations.

MATERIALS AND METHODS

Latent cellular states

The input to LC analysis is a gene expression matrix in a gene-cell format, where each column is a cell, and each row is a gene/transcript. In UMI (unique molecular identifier) based platforms, the expression level of a gene in a cell is divided by the total expression in that cell to generate a relative expression matrix (). In read-count based platforms, 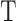can be derived from size factor normalized expression measures. The relative expression matrix is then log-transformed after adding a zero-correction term:

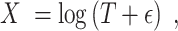where 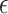is an arbitrarily small number.

We obtain the LC states from a singular value decomposition (SVD) of 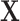(with mean centering and scale normalization).

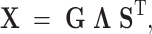where 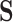is a cell-by-LC states matrix. We note that under certain conditions, 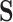is the same as the loading matrix from the principal component analysis (PCA) result of 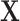(14,15).

Determination of significant LC states

We apply the Tracy–Widom test to associated eigenvalues to determine which LC states are significant (16–18). The LC state associated with the eigenvalue 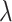is significant if it is significantly different (P  <  0.05) from the Tracy–Widom distribution, with

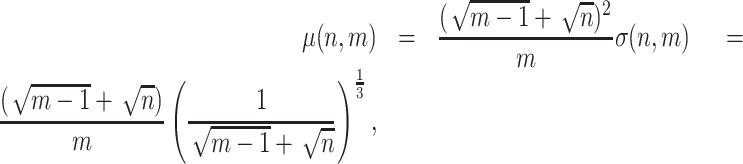where 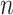is the total number of genes and 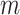is the total number of LC states. We then discard all the LC states that are not significant. Significant LC states were aligned against known technical variations (e.g. cell-specific library complexity and batch information) and states strongly associated with these technical variations were removed, leading to a cell-by-LC states matrix 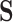with a lower-dimension of candidate LC states that are associated with biological variations.

Distance calculation

Distances between cells in 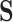(the cell-by-LC states matrix) are calculated using cosine distance:

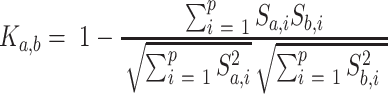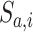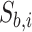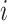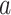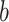where and represent LC state for cells and , and 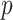is the total number of retained LC states.

Spectral clustering

We perform spectral clustering (19) on the resulted distance matrix to derive a set of candidate clustering models with a range of cluster numbers (i.e. 2–20 by default).

Distance measure in the PC space

The PC space is derived from the cell-gene relative expression matrix (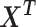, with mean centering and scale normalization), where each cell is projected onto the significant principal components (PCs) determined using the Tracy–Widom test. When known technical variations were strongly associated with significant components, those PCs were further aligned with the technical variations and discarded. Distance between cells was measured by the correlation distance of significant components. When less than three PCs retained, Euclidean distance was used instead. We note that while the construction of LC space and PC space is related, the dramatic difference between the within-cell scaling in the LC space and the within-gene scaling in the PC space results in empirically different data presentations.

The optimal number of clusters and informative cellular states

We rank the candidate clustering solutions (with a different number of clusters) by the silhouette score (20) measured in the PC space. With two or more clusters, the silhouette measures the similarity of an individual to its cluster, as compared to other clusters. For each cell, let 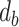be the lowest dissimilarity to any other cluster and let 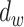be the average dissimilarity to other cells in its cluster. We calculate the silhouette as

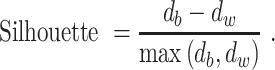We assign a silhouette score of zero for the default solution of one cluster. An end-user may evaluate the top candidate solutions to determine the optimal number of solutions or specify it with a priori biological knowledge.

With the selected number of clusters, we retain LC states that show significant difference among candidate clusters, update the distance matrix, and derive the final clustering solution.

Fast processing of large numbers of cells

We classify unknown cells 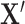efficiently by projecting them into space spanned by the informative LC states learned from a representative sample:

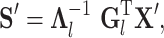where 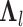is calculated from the original 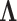by removing those rows and columns that are not associated with the informative LC states, and 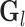is calculated from 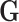by removing those columns that are not associated with the informative LC states. We can then calculate the cosine similarity between 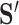and an ‘average’ cell from each cluster and find the cluster with the maximum similarity for each unknown cell.

Simulation of different cell types using Splatter

We used Splatter to simulate single-cell RNAseq data with two cell types. The baseline parameters for Splatter were estimated using a scRNA-seq dataset for 6757 sorted CD44^high Rh41 cells with 13 368 genes. The shape parameter for the mean gamma distribution is 0.393. The rate parameter for the mean gamma distribution is 1.8. The location parameter for the library size log-normal distribution is 9.13. The scale parameter for the library size log-normal distribution is 0.336. The probability that a gene is an expression outlier is 0.014. The location parameter for the expression outlier factor log-normal distribution is 5.69. The scale parameter for the expression outlier factor log-normal distribution is 0.84. Underlying common dispersion across all genes is 0.114. Degrees of freedom for the biological coefficient of variation inverse chi-squared distribution is 19.5. For each simulation, we updated the baseline Splatter parameters to generated individual simulated datasets. We fixed the number of genes to 10,000 genes. For the sample size of 1000 simulated cells, we simulated dataset with the probability of minor cell type at 0.01, 0.05, 0.1, 0.2 and 0.5, and the probability of differentially expressed genes at 0.05, 0.1 and 0.2 making a total of 15 combinations of parameters. For the sample size greater than 4000 simulated cells, we simulated dataset with the probability of minor cell type at 0.005, 0.01, 0.05, 0.1, 0.2 and 0.5, and the probability of differentially expressed genes at 0.05, 0.1 and 0.2 making a total of 18 combinations of parameters. Each parameter combination contains 100 simulations. When the probability of minor cell type was set to 0.005, we further set the location parameter for the differential expression factor log-normal distribution to the default to 1. Batch effects were simulated by setting the number of batches to 2, 3 and 4 with equal size in each batch. For sample size at 10,000, 100,000, 400,000, 1,000,000 and 2,000,000 cells, we generated 100 simulations for each sample size to test scalability. Splatter used a maximum of 2.2 Terabyte memory on an HP Xeon E7-8867v3 DL580 processor to simulated 10,000 genes by 2,000,000 cells; therefore, we did not simulate samples with more than 2,000,000 cells.

Normalized mutual information and adjusted Rand index

We evaluate the performance of clustering against true labels of cells by using normalized mutual information (NMI) (21) and adjusted Rand index (ARI). We use the R package igraph to calculate these metrics (22).

Benchmarking on independently compiled datasets

We benchmarked the performance of LCA with 12–14 clustering algorithms on two additional sets of data: the first is a set of data provided by R package DuoClustering2018 (23), including 12 experiments, ranging from ∼200 to ∼6500 cells. The R package also included the performance statistics of 14 clustering algorithms, including Seurat and SC3. We compared the performance LCA to the 14 algorithms using the wrapper function provided DuoClustering2018. The second compiled set of data (24) included six datasets ranging from ∼1000 to ∼8400 cells and the performance for 12 algorithms, including Seurat and SC3. The R Single-CellExperiment format of datasets was downloaded from https://github.com/bahlolab/cluster_benchmark_data.

Benchmarking on simulations from Splatter

We further benchmarked LCA with SC3 and Seurat in Splatter simulated datasets. For Seurat, we used fifteen different resolutions from (0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3, 1.4, 1.5) and default setting for remaining parameters, which produced 2–10 clusters. The highest NMI was selected for each dataset. For SC3, we ran multiple combinations of different parameters and picked the results with maximum accuracy (NMI). When there were multiple results with the same maximum accuracy, we reported the result with the minimum running time. For the number of clusters used by SC3, we used the number of clusters inferred by SC3 and the true number of clusters. The d_region_min parameter was chosen from (0.01, 0.04), the d_region_max parameter was chosen from (0.07, 0.1), the kmeans_nstart parameter was chosen from (50, 500). Therefore, we evaluated SC3 with 2 × 2 × 2 × 2 = 16 sets of parameters. For batch effect correction, we used two different methods from Seurat: CCA and RegressOut. The performance of batch effect correction for MNN and scmap were tested by piping the results from or to SC3.

Rh41 single-cell dataset

The human alveolar rhabdomyosarcoma cell line Rh41 was grown in culture in a 5% CO₂ incubator in 75-cm² vented flasks containing DMEM medium supplemented with 10% FBS and 2× glutamine until the cells reached 75% confluence at ∼3.6  ×  10⁶ cells. The cells were detached from the flask with 7 ml of 1× citrate saline to which 7 ml of DPBS was added. The cell suspension was then centrifuged at 300  ×  g for 7 min, and the cell pellet was resuspended in 300 μl of blocking buffer (rat IgG/PBS) and incubated on ice for 30 min. An aliquot of 50 μl of the cells in blocking buffer was transferred to a separate tube for the isotype control. The cells were washed with 1 ml of staining buffer (5% BSA/PBS) and centrifuged at 300  ×  g for 5 min. The pellet, which contained ∼3  ×  10⁶ cells, was then incubated with rat IgG2B anti-CD44–Alexa Fluor 488 antibody (R&D Systems) in staining buffer (15 μl antibody + 135 μl of staining buffer) on ice for 30 min. For the isotype control, ∼600,000 cells were incubated with 5 μl of rat IgG2B–Alexa Fluor 488 (R&D Systems, Minneapolis, MN, USA) + 45 μl of staining buffer on ice for 30 min. After the incubation, both sets of cells were collected by centrifugation, washed with 1 ml of staining buffer as described above, and resuspended in staining buffer. Flow cytometric analysis was then used to identify the fractions corresponding to the CD44 ^high and CD44 ^low populations.

For the single-cell experiment, Rh41 cells were grown in culture, harvested, and washed in DPBS as described above. They were then resuspended in PBS/0.2% BSA at a concentration of 1  ×  10⁶ cells/ml. The 10× Genomics Single Cell platform performs 3′ gene expression profiling by poly-A selection of mRNA within a single cell, which uses a cell barcode and UMIs for each transcript. Single-cell suspensions were loaded onto the Chromium Controller according to their respective cell counts to generate ∼6000 partitioned single-cell GEMs (gel bead-in-emulsions). The library was prepared using the Chromium Single Cell 3′ v2 Library and Gel Bead Kit (10× Genomics) in accordance with the manufacturer's protocol. The cDNA content of each sample after cDNA amplification for 12 cycles was quantified, and the quality was checked by high-sensitivity DNA chip analysis on an Agilent 2100 Bioanalyzer (Agilent Technologies, Santa Clara, CA, USA) at a dilution of 1:6. This quantification was used to determine the final library amplification cycles in the protocol, which were calculated out to 12 cycles. After library quantification and a quality check by DNA 1000 chip (Agilent Technologies), samples were diluted to 3.5 nM for loading onto the HiSeq 4000 sequencer (Illumina) with a 2  ×  75-bp paired-end kit, using the following read length: 26 bp Read1 (10× cell barcode and UMI), 8 bp i7 Index (sample index), and 98 bp Read2 (insert). In total, 518 million, 237 million and 154 million reads were obtained for unsorted, CD44^low and CD44^high populations, respectively. The Cell Ranger 2.0.1 Single-Cell Software Suite (10× Genomics) was implemented to process the raw sequencing data from the Illumina HiSeq run. This pipeline performed de-multiplexing, alignment (GRCh38/STAR), and barcode processing to generate gene-cell matrices used for downstream analysis.

After matrix generation, the ribosomal and mitochondria-related genes were filtered out.

Rh41 bulk RNA-seq dataset

Rh41 bulk RNA-seq dataset and its analysis were described in Chen et al. (25).

RESULTS

We started with an overview of the LCA method, followed by a benchmark analysis with more than a dozen commonly used scRNA-seq clustering algorithms in datasets compiled in (23,24). The top performers were further evaluated in large-scale simulation studies to compare their accuracy, scalability, and batch correction. Finally, we analyzed three additional public datasets (26–28) and an Rh41 dataset to demonstrate that latent cellular states efficiently capture hidden biological signals and LCA achieves robust, accurate and scalable performance in real applications.

Overview of the LCA method

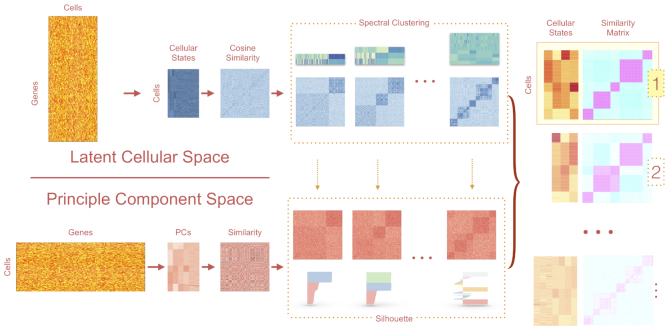
LCA takes a dualistic view of the single-cell gene expression data by decomposing the data matrix into the principal component space (PC space) and latent cellular space (LC space (represented by the gene by cell matrix). In the primary cell-centric LC space, we take the gene by cell expression matrix as input and perform the transcriptome embedding approach to convert the high dimensional matrix into a small vector space with latent cellular states. Similar to latent semantic indexing application for information retrieval (13), the embedding operation condenses important features in the sparse gene expression matrix into an information-dense low-dimensional vector space of latent cellular states, which uncover the underlying biological concepts. LCA bypasses explicit gene selection and performs LC state inference through singular-value decomposition (SVD) of the log-transformed global gene expression matrix (genes in row and cells in column), models known confounding factors (e.g. cell-specific library complexity and batch information), and measures cell-to-cell similarity by the cosine of the angle between the low-dimensional cellular-state vectors. Spectral clustering is employed to derive a set of candidate clustering models with a range of cluster numbers. Meanwhile, in the dual gene-centric PC space (represented by the cell by gene matrix), we decompose the variation of gene expression across cells into low-dimensional principle components, and each gene contributes equally to the total variation in the PC space. By using their expression vectors, cells were projected on to significant components determined by the Tracy–Widom test (16), and cell-to-cell similarity is measured by correlation similarity in the PC space. Finally, LCA retains informative cellular states from the selected clustering model(s) and uses these states to update the final clustering solution(s). Although the ‘optimal model’ is not necessarily the solution with the best numerical score, it should be among the top-ranked models. Therefore, LCA provides users with multiple top-ranked solutions for biology-based evaluations. In summary, LCA employs a heuristic dual-space search approach with a focus on LC states (Figure 1) to provide an analytical scheme for subpopulation structure identification (including the removal of confounding factors, the inference of the number of clusters and informative states, and a mapping function from the expression vector to cluster membership).

Figure 1.

Overview of the workflow of LCA. LCA infers LC states from full expression matrices. Explicit gene filtering is not necessary. LCA converts the raw transcript count data to gene fractions and then performs log transformations. The algorithm features a dual-space model search, generating candidate clustering models based on the cosine similarity matrix in the LC space. Candidate models are then ranked based on the silhouettes measured in the PC space.

Benchmarking of LCA and commonly used scRNA-seq clustering algorithms on independently compiled datasets

We benchmarked LCA with more than a dozen commonly used scRNA-seq clustering algorithms on two independently compiled datasets. The first set included nine publicly available scRNA-seq experiments and three simulations, which is available from the R package DuoClustering2018 (23). A systematic performance evaluation of LCA against the results of 14 included clustering algorithms suggested that LCA, SC3, and Seurat were the top performers (Supplementary Results, Supplementary Figure S1). The second set included one ‘gold standard’ 10× Genomics data, generated from the mixture of three cell lines, and several ‘silver standard’ 10× data from peripheral blood mononuclear cells (24). Again, LCA, Seurat and SC3 out-performed the remaining 10 methods tested on that sets of data (Supplementary Table S1).

Benchmarking of LCA, Seurat and SC3 in simulation datasets

Because LCA, Seurat, and SC3 consistently outperformed other algorithms in both independently compiled datasets, we performed extensive benchmark experiments (33 300 datasets) in simulated dataset using the splatter (29) package. We also ran LCA with the 1000 most variable genes (LCA-top1k) to evaluate the effects of gene filtering in LCA analysis. Moreover, we attempt different parameter settings to optimize the consistency with the ground truth for both Seurat and SC3. Specifically, for SC3, we run eight different parameter settings to infer the number of clusters and selected the cluster number that is closest to the ground truth. We then include an additional eight settings with the true number of clusters specified when comparing the accuracy in cluster membership and report the highest NMI achieved among all 16 models. For Seurat, we ran 15 different settings of the resolutions parameter and reported the results with the highest NMI.

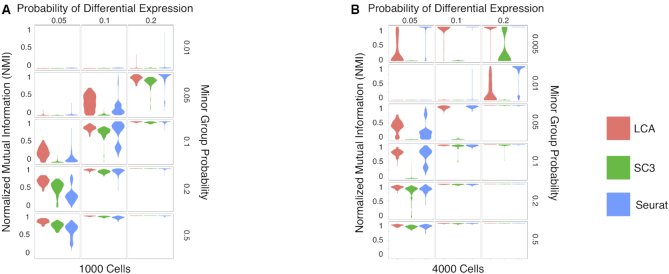
Our extensive simulations demonstrated that even with dataset-specific, ground-truth based optimizations, LCA outperformed LCA-top1k, Seurat and SC3 in terms of both the number of cluster inference and accuracy in cluster membership (Table 1, Figure 2 and Supplementary Table S2). LCA inferred the correct number of clusters in 68.2% of simulated datasets, significantly higher than LCA-top1k (51.9%, P < 2.2 × 10⁻¹⁶ [proportion test]), Seurat (36.6%, P < 2.2 × 10⁻¹⁶ [proportion test]) and SC3 (41.4%, P < 2.2 × 10⁻¹⁶ [proportion test], excluding SC3 runs with the true number of clusters specified). We used normalized mutual information (NMI [14], 1 for perfect matching) to quantify the clustering accuracy. Similar to the adjusted Rand index (ARI) used in (23,24), NMI is a commonly used measure in comparison of clustering algorithms (30,31). LCA achieved an average NMI of 0.721 across all the simulated scenarios, significantly higher than those from LCA-top1k (0.623, P < 2.2 × 10⁻¹⁶ [Wilcoxon signed-rank test]), Seurat (0.614, P < 2.2 × 10⁻¹⁶ [Wilcoxon signed-rank test]) and SC3 (0.627, P < 2.2 × 10⁻¹⁶ [Wilcoxon signed-rank test]). Importantly, in challenging but separable datasets (where at least one algorithm achieved an NMI < 0.7 and at least one algorithm achieved NMI > 0.8), LCA (average NMI = 0.801) significantly outperformed LCA-top1k (0.666, P < 2.2 × 10⁻¹⁶ [Wilcoxon signed-rank test])), Seurat (0.759, P < 2.2 × 10⁻¹⁶ [Wilcoxon signed-rank test]) and SC3 (0.482, P < 2.2 × 10⁻¹⁶ [Wilcoxon signed-rank test]), suggesting that LCA have better power in revealing subtle differences among different cell types.

Table 1.

Overview of the performance of LCA vs. Seurat and SC3 on simulated datasets

Methods	Average NMI (%)	Average run-time (s)
LCA	72	203
LCA-top1k	62	41
Seurat	61	61
SC3	63	640

Figure 2.

Benchmarking of LCA against Seurat and SC3 on simulated datasets. (A) Clustering accuracy by LCA, Seurat, and SC3 was compared using NMI on 1000 simulated cells by Splatter: the probability of differential expression ranges from 0.05 to 0.2, and the probability of minor group ranges from 0.01 to 0.5. Each combination of simulation parameters contained 100 randomly generated samples. (B) Clustering accuracy by LCA, Seurat, and SC3 on 4000 simulated cells.

Scalability to large-scale datasets

LCA’s implementation renders exceptional scalability, which is an attractive feature for scRNA-seq analysis of an ever-increasing number of cells. LCA can derive a cell subpopulation structure by using a relatively small representative set (training cells) sampled from the full data. LCA provides mathematical formulae with which to project the remaining cells (testing cells) directly to the inferred low-dimensional LC space, after which individual cells are assigned to the subpopulation with the best similarity. Consequently, LCA runs at a low level of computational complexity. SC3 provides similar functionality by training on a subset of cells and project remaining cells based on the learned model. Seurat does not support the functionality at the moment, and it has difficulty in running large dataset (running time jumped from 1 minute for a 1000-cell dataset to 10.8 h for a dataset with 100,000 cells. Jobs for datasets with 400,000 cells or more did not complete in a day.

We first compared the accuracy of clustering between the training cells (5–25% of 4000-cell datasets) and the remaining testing cells in simulated models (Supplementary Figure S2). As expected, the accuracy of the clustering model improved with the increase of training cells. Strikingly, LCA achieved comparable accuracies between training and testing cells in all models evaluated.

We then compared the scalability of LCA to SC3 in large datasets simulated by Splatter, from 5000 cells to 2,000,000 cells. We trained both LCA and SC3 on a random subset of 1000 cells from tested datasets, then predicted cell types on full test datasets using trained models. LCA is more efficient than SC3 across all sample sizes tested (Supplementary Table S3). The mean running time for 400,000 cells is 37 min for LCA, compared to 63 minutes for SC3 (P  <  2.2  ×  10⁻¹⁶ [Wilcoxon signed-rank test]), with a slightly increased memory footprint (29.1 Gb for LCA versus 27.2 Gb for SC3, P = 2.6  ×  10⁻¹⁶, [Wilcoxon signed-rank test]). In datasets with 1,000,000/2,000,000 cells, LCA used an average of 60/118 min, respectively. SC3 runs failed for datasets larger than 400,000 cells.

Batch-effect correction

Batch effects represent a major analytical challenge in large scale OMICS studies. LCA addresses the challenge by aligning batch effects and other known technical variations (e.g. the difference in library complexity for individual cells) with a small set of inferred LC states, which are excluded in further analysis (Supplementary Figure S3). We compared its performance with four state-of-art algorithms: Seurat CCA (4), Seurat RegressOut (4), MNN batch-effect correction (9) and scmap(10) in 12,000 splatter simulated datasets with batch effects (2–4 batches evaluated). Seurat provides two ways to handle batch effects by regress out the batch effect (Seurat-RegressOut) and by aligning between batches through canonical correlation analysis (Seurat-CCA). Again, we applied Seurat-RegressOut and Seurat-CCA with 15 different resolutions and reported the highest NMI for each test dataset. We applied MNN batch correction (implemented in the R scran package), followed by SC3 clustering (MNN-SC3, with 16 different settings). For scmap, we ran SC3 in one batch to infer cell types (with 16 different settings), followed by scmap to project cells from other batches (SC3-scmap). For each simulated dataset, the model achieving the highest NMI with the ground-truth is reported for Seurat-RegressOut, Seurat-CCA, MNN-SC3 and SC3-scmap. LCA outperformed other pipelines in cluster membership inference (Figure 3, Supplementary Table S4).

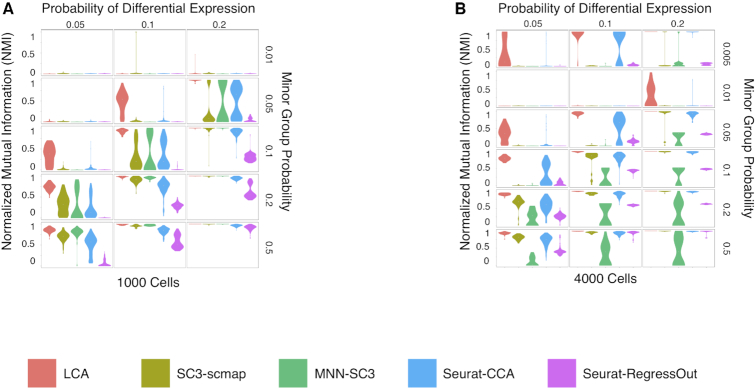
Figure 3.

Benchmarking of LCA against Seurat-CCA, Seurat-RegressOut, MNN-SC3, and SC3-scmap on simulated datasets with two equal-size batches. (A) Clustering accuracy by LCA, Seurat-CCA, Seurat-RegressOut, MNN-SC3 and SC3-scmap was compared using NMI on 1000 simulated cells by Splatter: the probability of differential expression ranges from 0.05 to 0.2, and the probability of minor group ranges from 0.01 to 0.5. Each combination of simulation parameters contained 100 randomly generated samples. (B) Clustering accuracy on 4000 simulated cells.

LCA achieved an average clustering accuracy of 0.68 across all simulated datasets, significantly higher than those from Seurat-RegressOut (0.21, P < 2.2 × 10⁻¹⁶ [Wilcoxon signed-rank test]), Seurat-CCA (0.52, P < 2.2 × 10⁻¹⁶ [Wilcoxon signed-rank test]), MNN-SC3 (0.29, P < 2.2 × 10⁻¹⁶ [Wilcoxon signed-rank test]) and SC3-scmap (0.42, P < 2.2 × 10⁻¹⁶ [Wilcoxon signed-rank test]). Similar to datasets without batch effects, LCA achieved near perfect performance in easy-to-separate cases and substantially improved the accuracy in challenging scenarios.

Application of LCA on additional publicly available datasets

By using publicly available large-scale scRNA-seq datasets collected on various popular scRNA-seq platforms, we demonstrated that LCA robustly identified LC states of biological importance and produced parsimonious and accurate models that were highly consistent with biological knowledge.

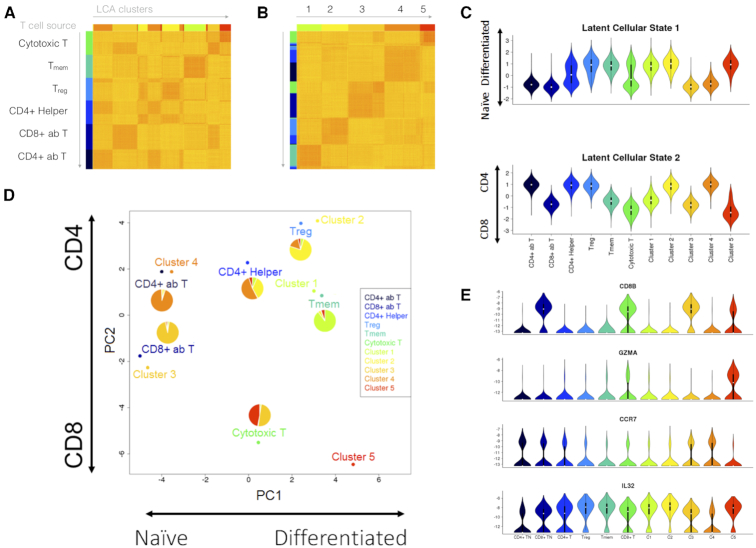
Using the GemCode platform (10× Genomics, Pleasanton, CA), Zheng et al. generated reference scRNA-seq transcriptomes for subpopulations of peripheral blood mononuclear cells (PBMCs) purified via well-established cell surface markers (26). Subsets of the data have been included in both benchmark studies (23,24). To better understand the potential intra-population heterogeneity, we generated a purified T-cell dataset (representing 55,000 cells) by pooling the CD4+ T-helper (CD4+ helper), CD4+/CD25+ regulatory T (T_reg), CD4+/CD45RO+ memory T (T_mem), CD4+/CD45RA+/CD25- naïve T (CD4+ ab T), CD8+ cytotoxic T (cytotoxic T) and CD8+/CD45RA+ naïve cytotoxic T (CD8+ ab T) cell subpopulations. We inferred the cellular states and subpopulation structure by using 10% and 25% of the full dataset, and we assigned the remaining cells to one of the inferred subpopulations. We evaluated the top three models for both runs, which were the 3-population, 4-population and 5-population models. Despite a 9.6-fold difference in running time, both the 3-population and 5-population models from the two runs achieved high consistency (NMI  =  0.87 and 0.84, respectively). Although the 4-population models differed between runs, they represented two different subpopulation-merging orders from the 5-population model to the 3-population model. We selected the 5-population model learned from 25% cells (with 19 LC states) for further biological inference. Whereas the purified T_mem, CD4+ ab T and CD8+ ab T cells contained cells mostly from a single subpopulation (Clusters 1, 3 and 4, respectively), different levels of heterogeneity were detected in the remaining purified populations (T_reg, CD4+ helper and cytotoxic T), especially the CD4+ helper, and cytotoxic T cells (Figure 4A, B). Given the single surface-marker settings in the purification of CD4+ helper and cytotoxic T cells, it is not surprising that we found substantial heterogeneity in them. Nevertheless, LCA inferred a parsimonious subpopulation structure in this large dataset. We selected representative genes encoding surface markers, transcription factors, and secreted effector molecules for 19 usual T-cell subsets (https://docs.abcam.com/pdf/immunology/t_cells_the_usual_subsets.pdf) and derived a PCA projection of the six purified populations and five inferred clusters based on the average population/cluster expression level of individual marker genes (Figure 4D). The first PC largely described the differentiation status, and the second PC represented the difference between the CD4+ subsets and CD8+ subsets. As expected, Clusters 3 and 4 were found next to the CD8+ ab T and CD4+ ab T cells. Cluster 1 was found near the T_mem population. Cluster 2 consisted mostly of T_reg cells and a smaller fraction of CD4+ helper cells that was located adjacent to the T_reg population. Both the CD4+ helper and cytotoxic T-cell populations were split approximately equally between naïve and differentiated cells and were spotted between their corresponding naïve clusters (Cluster 3 for CD8+ cells and Cluster 4 for CD4+ cells) and differentiated clusters (Clusters 1 and 2 for CD4+ cells and Cluster 5 for CD8+ cells). Analysis of selected genes validated the separation of naïve and differentiated cells in the CD4+ helper and cytotoxic T cells (Figure 4E). An evaluation of the first LC state inferred from the full expression data revealed a striking approximation to the expected distribution of naïve and differentiated cells in both purified populations and inferred clusters. Similarly, the second LC state recaptured the CD4+ and CD8+ difference in the dataset (Figure 4C). These results not only revealed the substantial heterogeneities among several ‘purified’ T-cell subpopulations but also showed that LCA identified LC states of biological importance and consequently produced a parsimonious and accurate model that was highly consistent with biological knowledge.

Figure 4.

Investigation of PBMC heterogeneity by using LCA. We applied LCA to data from Zheng et al. (26) for 55 000 cells representing a combination of six sorted T-cell populations. LCA identified five cell populations with biologically meaningful LC states. (A) Cell distance matrix, sorted by source ID. (B) Cell distance matrix, sorted by LCA clustering results. (C) The first LC state captured the difference between the naïve and differentiated T cells, whereas the second LC state captured the difference between the CD4+ and CD8+ cells. (D) LCA further revealed heterogeneity in the CD4+ helper T cells and CD8+ cytotoxic T cells. (E) Expression profiles of selected genes across naïve and differentiated cells in the CD4+ helper and cytotoxic T cells.

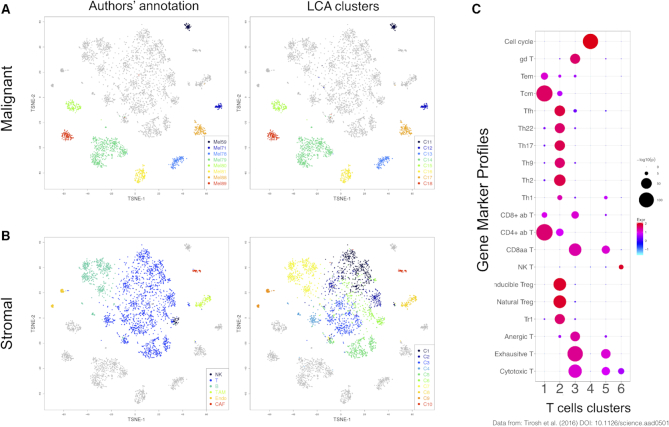
We evaluated the performance of LCA in a second dataset published by Tirosh et al. (27), who employed a stepwise approach to analyze separately the malignant and stromal cells of 19 melanoma tumors captured on the C1 Fluidigm platform. We applied those authors’ cell-selection criteria (27) to generate a dataset with 1169 malignant cells from eight tumors and 2588 nonmalignant (stromal) cells. LCA inferred 18 clusters with 53 LC states (Figure 5). Malignant cells dominated eight clusters, which were further separated by the patient origin of the tumors (Figure 5A). Among the stromal cells, distinct clusters were identified for B cells, macrophages, cancer-associated fibroblasts, and endothelial cells (Figure 5B). Moreover, LCA divided tumor-infiltrating T cells and natural killer cells into six clusters, which was concordant with the supervised analysis of T cells based on surface markers by Tirosh et al. (27). Using the pre-defined marker genes for T-cell subsets and MKI67 for cell-cycle activities, we revealed the characteristics of these T-cell populations (Figure 5C). Cluster 1 was enriched for naïve CD4+ cells, whereas Cluster 2 harbored mostly T_reg and T_FH cells. Although Clusters 3 and 5 both had enriched signatures for cytotoxic T and exhaustive T cells, Cluster 3 had greater signal strength in both signatures, consistent with the reported high correlation between exhaustion markers and cytotoxic markers (27). Cells in active cell cycles were grouped in Cluster 4, which showed unique enrichment of MKI67 expression. Lastly, natural killer cells and T cells with weak cytotoxic activity and no exhaustion signatures were found in Cluster 6. As a comparison, we applied SC3 to the same data, which resulted in an estimation of 43 clusters. Although SC3 clustering of malignant cells was consistent with the separation by patient, accuracy in the stromal component was lower than with LCA (Supplementary Table S5). These results demonstrate the power of LCA to reveal subtle diversities in different subpopulations of tumor-infiltrating T cells in the presence of strong transcriptomic variations among malignant cells (from different patients) and various stromal cells from different lineages (cancer-associated fibroblasts, macrophages, B cells, and endothelial cells).

Figure 5.

Reanalysis of melanoma cellular data (27) with LCA. We applied LCA to 1169 malignant cells from eight tumors and to 2588 stromal cells. LCA identified 18 clusters with a clear biological interpretation. LCA further revealed subtle diversity among the infiltrating T cells. (A) t-SNE (t-Distributed stochastic neighbor embedding) plot of the clustering results for malignant cells, contrasting the LCA results and original results. (B) t-SNE plot of the clustering results for stromal cells, contrasting the LCA results and original results. (C) Enrichment of gene markers in T-cell clusters.

We further evaluated LCA’s performance in handling large-scale datasets from heterogeneous sources by combining a scRNA-seq dataset of ∼1.3 million embryonic day 18 murine brain cells collected on the Chromium Single Cell 3′ v2 platform (10x Genomics, Pleasanton, CA) (https://support.10xgenomics.com/single-cell-gene251expression/datasets/1.3.0/1M_neurons, the 10× E18 dataset) with a dataset of ∼5500 embryonic day 17 murine cerebellum cells collected on the GemCode platform (the Carter E17 dataset) (28), By training on a randomly sampled subset with 2000 cells from the 10× E18 dataset and 2000 cells from the Carter E17 dataset, LCA revealed a 24-cluster pattern after modeling global differences between the experiments. The remaining cells were projected to the 24-cluster structure. The projected cells have a similar cluster distribution fractions with the training dataset and share the same expression profiles of marker genes identified for individual clusters in the training subset (Figure 6), which supports the accuracies of the cluster membership projection. The entire procedure (including data loading, model generation on the training set and projection of the whole set) utilized 4.65 CPU hours and 30.1 Gb memory on an HP Xeon E7-8867v3 DL580 processor. The data provider for the E18 dataset reported a 22-cluster pattern using a random subset of 20 000 cells with ∼350 CPU hours and ∼300 Gb memory usage (http://go.10xgenomics.com/l/172142/2017-06-09/bsylz/172142/31729/LIT000015_Chromium_Million_Brain_Cells_Application_ Note_Digital_RevA.pdf, downloaded on 11 November 2018). This example demonstrated LCA’s efficiency and scalability in large-scale scRNA-seq data.

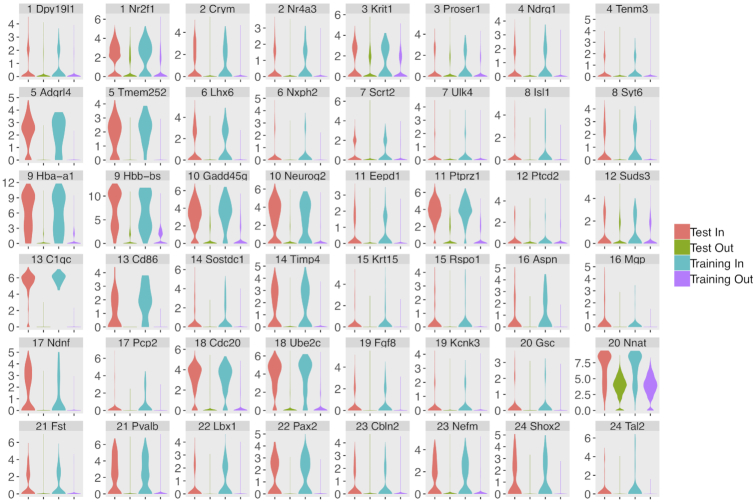
Figure 6.

LCA analysis of a large combined dataset including 1.3 million embryonic day 18 murine brain cells collected on Chromium Single Cell 3′ v2 kits (10× Genomics, Pleasanton, CA), and ∼5500 embryonic day 17 murine cerebellum cells collected on the GemCode platform (the Carter E17 dataset). Expression profiles of marker genes were shown in violin plot for each individual cluster.

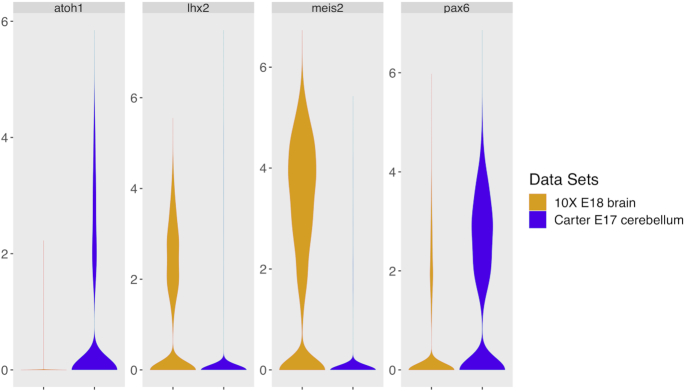
Although glutamatergic neurons were enriched in both datasets, there were substantial design differences between them (i.e. mouse strain, embryonic age, tissue isolation protocol, and single-cell library construction protocols, etc.), which produced distinct neuron subtype enrichment. Specifically, the 10× E18 dataset largely consisted of glutamatergic cerebellar nuclei (CNs, identified by expression of Meis2 and Lhx2) while the granule neuron progenitors (GNP) and/or granule neurons (marked by Atoh1 and Pax6) were highly enriched in the Carter E17 dataset (Figure 7). Despite these substantial differences, LCA identified several rare cell subpopulations that were shared between the experiments: erythrocytes (C9, marked by Hba-a2, 0.33 and 0.88% of cells in the Carter E17 dataset and 10× E18 dataset, respectively), endothelial precursors (C5, marked by Pecam1, 1.30% and 1.07%), microglia (C13, marked by Ly86, 0.65% and 0.39%) and meninges (C16, marked by Vtn, 1.56% and 0.91%). These results showed LCA’s power in accounting technical differences and identifying rare cell subpopulations in real datasets from heterozygous sources.

Figure 7.

LCA identified specific cell clusters between the 1.3 million embryonic day 18 murine brain cells collected on Chromium Single Cell 3′ v2 kits (10× Genomics, Pleasanton, CA), and ∼5500 embryonic day 17 murine cerebellum cells collected on the GemCode platform (the Carter E17 dataset). The 10× E18 dataset largely consisted of glutamatergic cerebellar nuclei (CNs, identified by expression of Meis2 and Lhx2) while the granule neuron progenitors (GNP) and/or granule neurons (marked by Atoh1 and Pax6) were highly enriched in the Carter E17 dataset.

LCA revealed a less-differentiated, stem-like cancer cell subpopulation in a dataset despite strong batch effects

LCA groups cells based on orthogonal LC states aligned with major differences among cells, which enables control of technical variations (e.g. batch effects) without an explicit need for gene filtering. We evaluated the efficiency of batch effect removal in a cancer cell dataset and further experimentally validated the subpopulations revealed by LCA. Rhabdomyosarcoma is the most common soft-tissue tumor in children and has two major histologic subtypes with different genomic landscapes: PAX3/PAX7-FOXO1 fusion–positive alveolar rhabdomyosarcoma (FP-ARMS) and fusion-negative embryonal rhabdomyosarcoma (ERMS) (32). LCA identified two subpopulations in a scRNA-seq dataset for Rh41 cells (a commonly used human PAX3-FOXO1 FP-ARMS cell line). The CD44 gene, which encodes a commonly used cell surface marker with great prognostic and therapeutic potential (33,34), appeared at the top of the differentially expressed genes (DEGs) of the two subpopulations (Supplementary Figure S4A). Flow cytometry confirmed a bimodal expression pattern of CD44 in Rh41 cells (Supplementary Figure S4B). We first used bulk RNA-seq to profile unsorted populations and CD44^high and CD44^low subpopulations sorted by fluorescence-activated cell sorting. In addition to the differences among the sorted CD44^high, CD44^low and unsorted populations, the analysis revealed strong batch effects. Specifically, samples in Batch 1 and those in Batches 2 and 3 were separated on the first PC, whereas the biologically different populations (the unsorted population and sorted subpopulations) were separated on the second PC (Supplementary Figure S4C). We collected scRNA-seq data for the unsorted populations in Batch 1 and the sorted CD44^high and CD44^low subpopulations in Batch 2. The libraries were sequenced at different depths for the three samples. The median numbers of UMIs captured per cell were 8278, 6678 and 12,850 for the CD44^high subpopulation, CD44^low subpopulation, and unsorted population, respectively (Kruskal-Wallis rank sum test, P  <  2.2  ×  10⁻³⁰⁸). With both batch effects and biological difference among cell populations, LCA inferred five clusters, with cells in Batch 1 being represented by Clusters 1 and 2 and cells in Batch 2 being grouped in Clusters 3 to 5 (Supplementary Figure S4D). Similarly, SC3 inferred a 12-cluster structure. Consistent with the strong batch effects observed in bulk RNA-seq analysis, when required to infer a two-cluster model, both LCA and SC3 achieved a perfect separation based on the batch information (NMI  =  1 and 0.99, respectively). Next, we modeled batch effects through LCA, Seurat-CCA and MNN-SC3. LCA identified that the first LC state was significantly associated with the batch information (P  <  2.2  ×  10⁻³⁰⁸) (Supplementary Figure S4E). Upon excluding this state, LCA retrieved an optimal structure with two clusters, where 73.4% (4961/6757) and 96.1% (6733/7005) cells profiled in the sorted CD44^high/CD44^low subpopulations were clustered into Clusters 1 and 2, respectively (Figure 8A). After MNN normalization, we evaluated 16 SC3 models with different configurations (like what we did in the simulation studies) and selected a 2-cluster model achieving the highest NMI between the two sorted populations. In the selected MNN-SC3 model, 85.9% of CD44^high cells were found in Cluster 1, which also contained 51.1% of CD44^low cells. For Seurat-CCA result with highest NMI among 15 different resolution parameters, 90.1% of CD44^high cells were found in Cluster 1, which also contained 48.9% of CD44^low cells; Cluster 2 contained 3.7% of CD44^high cells and 51.5% of CD44^low cells; while a small Cluster 3 contained 2.1% of CD44^high cells and 0.09% of CD44^low cells. To further validate the clustering result, we evaluated the consistency of identified DEGs between the inferred clusters with 1709 DEGs identified between sorted CD44^high and CD44^low subpopulations (log₂FC ≥ 1, FDR ≤ 0.05, FPKM ≥ 1 in at least one subpopulation, Supplementary Table S6). NBID, a single cell DE analysis (25) identified 1054/1174/604 DEGs (log₂FC ≥ 1, FDR ≤ 0.05, TPM ≥ 3 in at least one subpopulation) in the LCA, Seurat-CCA (comparing Clusters 1 and 2 only), and MNN-SC3 models (with batch-effects correction), of which 614/627/291 matched the DEGs found between the sorted subpopulations (F₁ score = 0.4444/0.4350/0.2516), respectively. This analysis further supported LCA’s superior performance compared to Seurat-CCA and MNN-SC3 with knowledge-based optimization.

Figure 8.

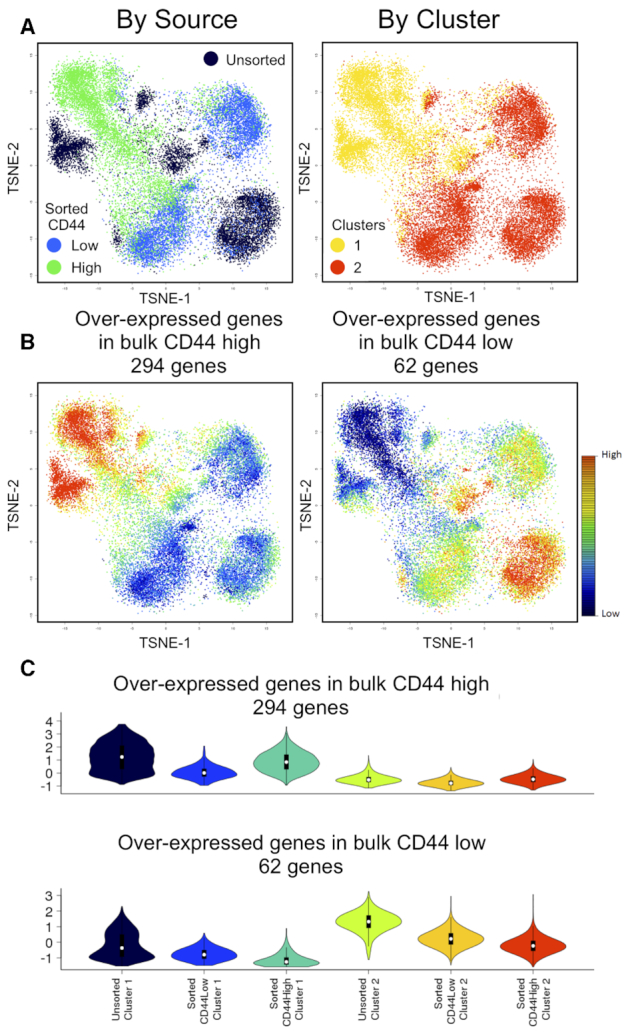
LCA analysis of Rh41 cells, correcting for batch effects. (A) t-SNE plots of clustering results, colored according to source ID or cluster ID. (B) Cellular expression patterns of DEGs identified in bulk RNA-seq. (C) Violin plot of expression patterns of DEGs from bulk RNA-seq in cells classified by source and cluster ID.

Although the inferred LCA model revealed a relatively pure cell population in the sorted CD44^low subpopulation, 26.6% cells from the CD44^high subpopulation were grouped in the same cluster with CD44^low cells (Cluster 2). We evaluated the transcriptomic signature of these cell groups (Cluster 1 cells from sorted CD44^high subpopulation, Cluster 1 cells from sorted CD44^low subpopulation, Cluster 2 cells from sorted CD44^high subpopulation and Cluster 2 cells from sorted CD44^low subpopulation) by DEGs identified in bulk RNA-seq Of 1709 DEGs, 356 were captured in at least 10% of the cells in one sequenced population or inferred cluster. As expected, Clusters 1 and 2 had higher average expression levels of genes overexpressed in the sorted CD44^high and CD44^low subpopulations, respectively (Figure 8B). Importantly, Cluster 2 cells from the sorted CD44^high subpopulation had significantly lower expression level for those DEGs overexpressed in the bulk CD44^high subpopulation than did either Cluster 1 cells from the sorted CD44^high subpopulation (P  <  2.2  ×  10⁻³⁰⁸ [Mann–Whitney test]) or Cluster 1 cells from the sorted CD44^low subpopulation (P  =  7.5  ×  10⁻⁷¹ [Mann–Whitney test]). Analysis of DEGs overexpressed in the bulk CD44^low subpopulation showed the same pattern (Figure 8C). These results suggested that Cluster 2 cells in the sorted CD44^high subpopulation more closely resembled CD44^low cells. Moreover, the differential expression pattern was essentially captured by the first LC state after modeling the batch effects (Spearman correlation coefficient  =  −0.90, P < 2.2  ×  10⁻³⁰⁸), confirming the biological importance of the inferred LC states.

Of the three established molecular markers (TFAP2B, MYOG and NOS1) for FP-ARMS (35), TFAP2B and MYOG were overexpressed in the sorted CD44^low subpopulation (Supplementary Table S6). Moreover, known PAX3-FOXO1 target genes were significantly enriched in DEGs overexpressed in the CD44^low subpopulation (Supplementary Table S7). These results suggest that the CD44^high subpopulation represents a less-differentiated, stem-like cell subpopulation. Although the exact mechanism by which the distinct subpopulations develop warrants further investigation, we conclude that LCA controls technical variations and reveals reliable transcriptome-based heterogeneity.

DISCUSSION

The rapid technological advance in scRNA-seq platforms has inspired a tremendous explosion of data-analysis methods for identifying heterogeneous subpopulations. Most methods employ a gene-selection step before clustering analysis, based on the assumption that a small subset of highly variable genes is useful for revealing cellular diversity. Although this assumption is valid in most scenarios and reduces the data dimensionality, it potentially excludes genes that are informative for separating subpopulations with subtle diversity. Also, in datasets with strong batch effects, it may result in a small set of retained genes being dominated by batch effects. Moreover, several methods require the user to provide an estimation of the number of clusters in the data, and this may not be readily available.

LCA bypasses the gene selection, learns biologically informative cellular states directly from the raw gene expression matrix, reduces potential technical variations, and measures the cell-to-cell distance by using cosine similarity in the low-dimensional and informative cellular-state space in a data-driven and unsupervised fashion. Cosine similarity has been widely used in information retrieval and text mining to reveal the relation between text documents, a process that shares many similarities with scRNA-seq analysis (36). However, when simultaneously inferring the number of clusters and the informative LCs that support the cluster separation, optimization in the LC space alone potentially risks in model overfitting, a common concern in statistical and machine learning (37). LCA addresses this challenge by employing a dual-space search strategy from empirical observations that (i) the true cell population structure (higher intra –cluster cell-cell similarities than inter-cluster similarities) pertains in both the LC space and the PC space and (ii) albeit presented at a higher level, the noises in the PC space are empirically uncorrelated with those in the LC space (Supplementary Figure S5). Therefore, LCA derives candidate models in the LC space (where the separation is strong), followed by model evaluation in the PC space. Furthermore, LCA provides a mathematical solution for assigning new cells to inferred clusters in a model learned from a subset of cells, a capability that is urgently needed to handle the ever-increasing sample sizes in scRNA-seq. We have demonstrated through extensive simulation and the use of large-scale scRNA-seq datasets that LCA is an efficient, scalable, and robust clustering algorithm that outperforms other tools without the explicit need for gene selection or an estimation of the number of clusters in the data.

DATA AVAILABILITY

The Rh41 scRNA-seq dataset and bulk RNA-seq dataset generated during the current study have been deposited in the Gene Expression Omnibus (GEO) under accession number GSE113660. The functions used for the data analysis are included in the single_cell_LCA package, which can be installed from Bitbucket (https://bitbucket.org/scLCA/single_cell_lca).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Cancer Institute of the National Institutes of Health [P30CA021765]; American Lebanese Syrian Associated Charities (ALSAC). Funding for open access charge: ALSAC.

Conflict of interest statement. None declared.