A spatially explicit model of muscle contraction explains a relationship between activation phase, power and ATP utilization in insect flight

Summary

Using spatially explicit, stochastically kinetic, molecular models of muscle force generation, we examined the relationship between mechanical power output and energy utilization under differing patterns of length change and activation. A simulated work loop method was used to understand prior observations of sub-maximal power output in the dominant flight musculature of the hawkmoth Manduca sexta L. Here we show that mechanical work output and energy consumption (via ATP) vary with the phase of activation, although they do so with different phase sensitivities. The phase relationship for contraction efficiency (the ratio of power output to power input) differs from the phase relationships of energy consumption and power output. To our knowledge, this is the first report to suggest that ATP utilization by myosin cross-bridges varies strongly with the phase of activation in muscle undergoing cyclic length changes.

Introduction

Over the past several decades, studies of insect flight have attempted to understand how the aerodynamics of wing motions determine the forces and energy required to power flight. Much of this effort focused on the engineering aspects of wing motions, using approaches that include detailed and elegant reconstruction of wing motions in scale models (for a review, see Sane, 2003), theoretical and computational aspects of flapping flight (Hedrick and Daniel, 2006), measurements of wing motions, and the subsequent patterns of fluid motion. Processes such as wake capture, delayed stall, wing rotation and potential unsteady fluid dynamic flow have all been implicated as important factors affecting the timing and magnitude of wing muscle forces generated during flight. These factors contribute to the overall energy requirements, as well as underlying control mechanisms, for insect flight.

A variety of physiological experiments complemented these engineering studies of flight. For example, direct measurement of metabolic gas exchange (Dickinson and Lighton, 1995; Ellington, 1985), as well as the in vivo timing and magnitude of muscle activity, have been used to assess the power output in insect flight (Tu and Daniel, 2004). A unifying approach pioneered by Josephson (Josephson, 1985; Josephson, 1989) measured the temporal patterns of muscle force and the associated changes in muscle length to quantify mechanical work generated by muscle. This work loop method relates the timing of muscle activation, relative to its length change, to the overall mechanical power output. Presumably, the power required for flight, as estimated by the host of aerodynamic studies, agrees with the power measured by these physiological methods.

Hawkmoths, among the largest insect fliers, power their flight with two sets of synchronously activated muscles connected to the thorax. The dorso-longitudinal muscles (dlm) compress the thorax in the antero-posterior axis to power the wing downstroke while the dorso-ventral muscles (dvm) compress the thorax in the orthogonal plane to power the wing upstroke. Work loop analyses of the dlm showed a strong phase dependence of muscle mechanical power output that was consistent with prior findings for insect muscles (Josephson, 1997). Enigmatically, however, the physiological (in vivo) dlm phase of activation generated only 40% of the maximal realizable power (max=100 W kg^–1) (Tu and Daniel, 2004).

Operating at sub-maximal power seems advantageous, assuming that the physiological phase of activation affords ample power reserves required for maneuvering flight. Therefore, any additional energy required for turns, elevations and accelerations becomes available by simply shifting activation phases to produce higher mechanical power output. With no clear evidence that the phase of activation affects the energy derived from myosin cross-bridge ATPase activity, we have a paradoxical situation: muscles operating at phases generating sub-maximal power would operate inefficiently unless ATPase rate varies with phase.

Because neuro-muscular control of locomotion inextricably links multiple levels of organization (from protein forces to aerodynamic forces), the dynamics and kinetics of protein level processes affect organ and organism function. This paper attempts to resolve the above paradox, drawing on a series of molecular models of muscle contraction (Daniel et al., 1998; Chase et al., 2004; Tanner et al., 2007) to examine the coupled relationship between activation phase, mechanical work and ATP utilization. Specifically, we ask whether the mechanics and kinetics of myosin cross-bridges lead to a phase-dependent ATPase behavior at the sarcomeric level. Our simulations show that mechanical power output (work) and ATP utilization (energy input) depend upon phase of activation (each having different sensitivities to phase). These results also show that some phases maximizing work do so at large energy costs (high ATPase rates). Combining our computational results with prior experimental studies (Tu and Daniel, 2004) shows that physiological phases of activation generating sub-maximal power output may do so more efficiently (by optimizing the ratio of mechanical power output to ATPase rate).

Materials and methods

The spatially explicit computational model used for these work loop analyses follows structural, kinetic and mechanical analyses described more fully in a series of prior studies (Daniel et al., 1998; Daniel and Tu, 1999; Chase et al., 2004; Tanner et al., 2007). These modeling studies incorporated a half-sarcomere-length lattice of compliant thick and thin filaments to determine the mechanics and energetics of force generation in muscle. A recent advancement for these models included kinetics for calcium activated thin filaments (Tanner et al., 2007). This refinement permits simultaneous control of activation and muscle length, while assessing force, work and energy consumption. Here we briefly review elements of the models and indicate how we modified prior approaches to generate work loop predictions for muscle.

Geometry and mechanics

Rather than specifically modeling the details of Manduca sexta flight muscle per se, we focus on examining how phase of activation may influence the energetics of contraction. The model is based on geometry of a half-sarcomere consisting of four thick and eight thin filaments packed in a hexagonal array (Tanner et al., 2007). Each thick filament bears 120 myosin cross-bridges arranged in a two-start helix. Cross-bridges directly face thin filaments bearing 90 binding sites per filament. These geometries reflect those used in previous spatially explicit models (Chase et al., 2004; Tanner et al., 2007) and generally approximate the cross-bridge and binding site pattern observed in striated muscle. As no published accounts of the myofilament ultrastructure from Manduca flight muscle exist, this geometric model serves as an approximation for the thick and thin filament arrangement.

Estimates of the myofilament mechanical properties are layered upon the geometric arrangement described above (Daniel et al., 1998; Chase et al., 2004; Tanner et al., 2007). Each cross-bridge has a spring constant (k_xb) of 5 pN nm⁻¹, somewhat stiffer than the values reported in the literature from single molecule studies, but more consistent with recent estimates from cellular experiments (Howard, 2001; Piazzesi et al., 2002; Linari et al., 2007). Thick and thin filament spring constants (k_m and k_a, respectively) were set at 6060 and 5230 pN nm⁻¹ for resting (unbound) thick and thin filament lengths of 14.3 and 12.3 nm, respectively, consistent with parameter values used in previous studies (Daniel et al., 1998; Chase et al., 2004; Tanner et al., 2007).

Kinetics of cross-bridges and calcium activation

Ca²⁺-binding proteins regulate the binding of force-generating motor proteins (cross-bridges) within this myofilament network. The kinetics of these two coupled protein systems are described with a three-state [Ca²⁺]-sensitive, thin-filament regulatory cycle coupled to a three-state cross-bridge cycle (for details, see Tanner et al., 2007). Briefly, the thin-filament regulatory states (Fig. 1A) describe Ca²⁺ binding to troponin (a transition from state T₁ to T₂), which triggers movement of tropomyosin (into state T₃) and exposes myosin-binding sites along the thin filament (McKillop and Geeves, 1993; Xu et al., 1999; Pirani et al., 2006). Transition rates for the thin filament kinetics are as specified elsewhere (Tanner et al., 2007), with the exception of the rates describing Ca²⁺ dissociation from the thin filament (r_t,21 and r_t,31, which were set to 100 s⁻¹; Fig. 1A). These modified rates produced faster relaxation dynamics to simulate the time-course of a Manduca twitch more effectively (Tu and Daniel, 2004). The second order rates associated with activating troponin are functions of intracellular [Ca²⁺].

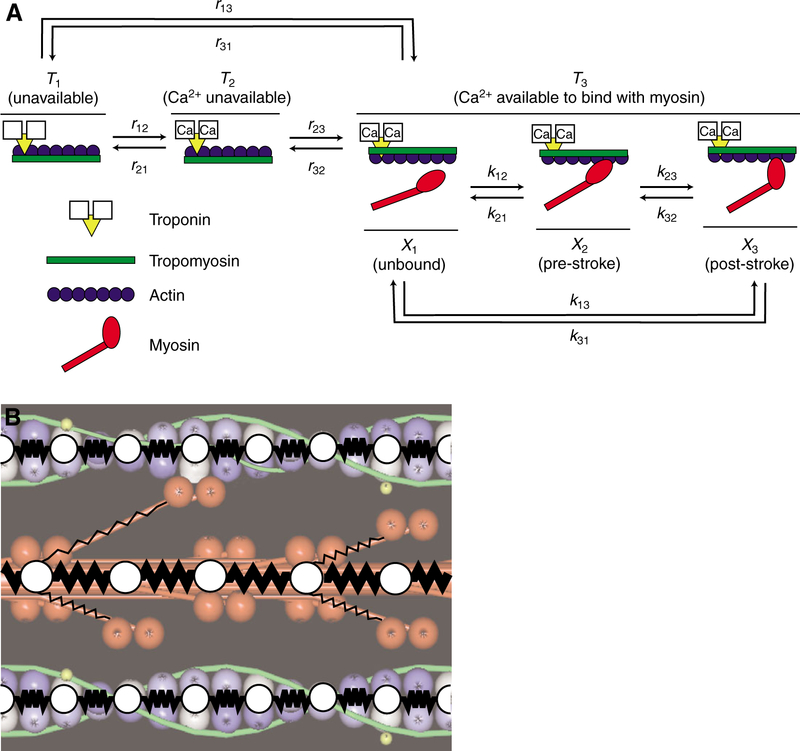
Fig. 1.

(A) Kinetics of thin filament regulation and cross-bridge cycling, modeled as coupled three-state cycles. Transition rates (k_ij) between cross-bridge states (X₁–X₃) are strain dependent. Transition rates (r_ij) between thin filament states (T₁–T₃) explicitly encode spatial information about troponin binding Ca²⁺ and tropomyosin movement. B) We simulated force production in a network of linear springs, using spring constants for thick filaments (k_m), thin filaments (k_a) and cross-bridges (k_xb). Thick and thin filament nodes (white circles between springs) represent modeled points from which cross-bridges extend from the thick filament backbone or actin binding sties along the thin filament where cross-bridges. At each time step, Monte-Carlo methods simulate likelihoods of Ca²⁺ regulated cross-bridge attachment to thin filaments, then forces balance about each node throughout the filament lattice.

Cross-bridge states are represented as an unbound (state X₁) or weakly bound, non-force bearing state, and two states where cross-bridges were bound and bear relatively low (state X₂) versus high (state X₃) strain (Fig. 1A). The X₂ state represents a conformation preceding the mechanical transition often referred to as the power stroke, and the X₃ state a conformation following the power stroke. Concomitant with each mechanical state is a biochemical state representing the cyclical hydrolysis of ATP, release of inorganic phosphate (P_i) and ADP, and binding of another ATP to dissociate a myosin cross-bridge from the thin filament. The energetically and chemo-mechanically coupled thick filament transition rates are distortion dependent.

We summarize these two kinetic processes by a set of coupled differential equations that are solved by Monte-Carlo simulation. The governing equations for each interaction between a cross-bridge and a potential thin filament binding site are described with three states of thin filament activation (T₁, T₂, T₃) and three states associated with the cross-bridge cycle (X₁, X₂, X₃):

$$\begin{array}{l}\frac{\text{d}{X}_1}{\text{d}t}=X_1{T}_3\left(-k_{12}-k_{13}\right)+X_2\left(k_{21}\right)+X_3\left(k_{31}\right)\\ \frac{\text{d}{X}_2}{\text{d}t}=X_1{T}_3\left(k_{12}\right)+X_2\left(-k_{23}-k_{21}\right)+X_3\left(k_{32}\right)\\ \frac{\text{d}{X}_3}{\text{d}t}=X_1{T}_3\left(k_{13}\right)+X_2\left(k_{23}\right)+X_3\left(-k_{31}-k_{32}\right)\\ \frac{\text{d}{T}_1}{\text{d}t}=T_1\left(-r_{12}-r_{13}\right)+T_2\left(r_{21}\right)+T3X_1\left(r_{31}\right)\\ \frac{\text{d}{T}_2}{\text{d}t}=T_1\left(r_{12}\right)+T_2\left(-r_{21}-r_{23}\right)+T3X_1\left(r_{32}\right)\\ \frac{\text{d}{T}_3}{\text{d}t}=T_1\left(r_{13}\right)+T_2\left(r_{23}\right)+T3X_1\left(-r_{31}-r_{32}\right),\end{array}$$ (1)

where the transition rates r_ij and k_ij are specified more fully elsewhere (Tanner et al., 2007). The equations describing interactions between these two protein systems are coupled by the interaction between unbound cross-bridges (X₁) and available binding sites (T₃). The availability of binding sites is regulated by Ca²⁺ binding to troponin. The system of equations above can be further reduced to four equations with:

$$\sum _{i=1,3}{T}_i=1\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\sum _{i=1,3}{X}_i=1.$$ (2)

As described more fully elsewhere (Daniel et al., 1998; Tanner et al., 2007), we implement an instantaneous force balance for a system of linear springs that characterize each cross bridge, thin filament and thick filament (Fig. 1B). The total force generated by the half-sarcomere is determined by the number of attached cross-bridges and their local distortion. The force on each thick filament is proportional to the distortion of the spring element closest to the M-line (Δx–x_rest) times the thick filament spring constant (k_m). Similarly, the force on each thin filament is proportional to the distortion of the spring element closest to the Z-disk (Δy–y_rest) times the thin filament spring constant (k_a). The total force borne by the model half-sarcomere (F_T) is the sum of the forces for all four thick and eight thin filaments, respectively:

$$F_{\text{T}}=\sum _1^4{k}_{\text{m}}\left(\Delta x_i-x_{\text{rest}}\right)=-\sum _1^8{k}_{\text{a}}\left(\Delta y_i-y_{\text{rest}}\right).$$ (3)

Controlling motion and activation

Initial half-sarcomere length (L₀) was 1200 nm (Tanner et al., 2007), from which sinusoidal length oscillations varied the length (L) as a function of time (t): L(t)=–Acos(2πft)+L₀, where f represents wing beat frequency for the hawkmoth (f=25 Hz). Length oscillated at amplitudes (A) of 30 and 15 nm per half-sarcomere, yielding normalized peak-to-peak strain amplitudes (ϵ=2A/L₀) of 0.05 and 0.025. The frequencies and amplitudes of length change were chosen to be close to those values reported previously (Tu and Daniel, 2004).

The modeled activation pulse represents a Ca²⁺ transient within the cell (following a neural stimulus) that leads to muscle contraction, or twitch (in Manduca and other insects there is a one-to-one correspondence between evoked potential and muscle twitch forces). This activation transient was modeled with a square wave of binary amplitude, representing intracellular [Ca²⁺] of 10⁻⁴ or 10⁻⁹ mol l⁻¹ for activated or inactivated contraction, respectively. While the actual temporal pattern of [Ca²⁺] is more likely represented as a skewed Gaussian function, this simple square wave provided a sufficient model for probing phase relationships and duty cycle. Two parameters determined the duration of this wave: period (P), set to 40 ms (=1/f); and duty cycle (δ_Ca), the fraction of P that [Ca²⁺]=10^–4 mol l^–1.

Following with the experimental work loop analysis of Tu and Daniel (Tu and Daniel, 2004), raw phase (ϕ) equals zero when the onset of force generation and muscle lengthening are co-incident in time. To adjust their phases accordingly, Tu and Daniel (Tu and Daniel, 2004) measured the temporal delay between external stimulus and muscle force generation (Δt_ep was ~8 ms). Several processes may contribute to this delay, including the timing of Ca²⁺ release from the sarcoplasmic reticulum and subsequent diffusion into the cytosol. As we do not know the actual transient, we simulated a number [Ca²⁺] transients by changing their duty cycle (δ_Ca) and phase (ϕ_Ca). We used three values for δ_Ca: 0.1, 0.2 and 0.5, each representing an increasing duration of activation (4, 8 and 20 ms, respectively). To compensate for the variable square wave duration affecting phase of activation, we adjusted the Ca²⁺ sensitive phase of activation (ϕ_Ca) with respect to muscle lengthening: ϕ_Ca=ϕ–δ_Ca/2. This adjustment aligned the center of the [Ca²⁺] activation pulse with the onset of muscle lengthening (when ϕ=0) even though the duration of activation changes with δ_Ca. Consistent with the experimental work loop analysis (Tu and Daniel, 2004), these simulations examine the relationship between work output and phase of activation.

Implementation

Full details about the simulation algorithm are described elsewhere (Tanner et al., 2007). Briefly, simulations were implemented in Matlab (The MathWorks, Natick, MA, USA) using the Matlab distributed computing engine on a 16 node IBM cluster running Linux. Thin filament and cross-bridge kinetics were stochastically driven using a uniform random number generator and state transitions were accepted using Monte Carlo algorithms. Simulations at each parameter set ran for 10 s using time steps of 1 ms, yielding 250 work loops. At each time step in the simulation we record force, ATP utilization, and kinetic state of thin filament binding sites and cross-bridges. Average values were calculated from 245 individual work loop cycles, as the initial five ‘start up’ cycles were omitted from averaging.

Results

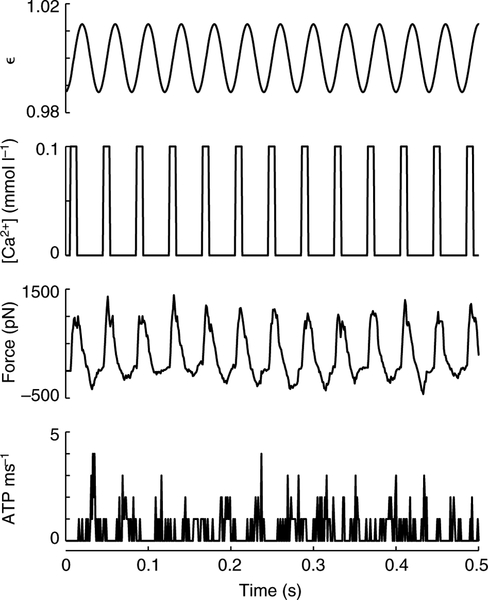
Simulations of simultaneous periodic calcium activation and muscle length change result in an oscillating, twitch-like force response as well as an oscillating pattern of ATP consumption (Fig. 2). Interestingly, the force response was shifted in phase with respect to the Ca²⁺ activation transient, and ATP utilization was further phase shifted relative to force. At these particularly high activation rates [relative to those in Tanner et al. (Tanner et al., 2007)] cross-bridges remained bound after the Ca²⁺ activation transient ended. These results largely followed from temporal delays associated with thin filament de-activation, cross-bridge binding (force generation) and cross-bridge cycling (ATP consumption).

Fig. 2.

Work loop simulations oscillated muscle length and intracellular Ca²⁺ concentration as a function of time, while monitoring force and ATP utilization. These panels show the initial half second of a simulation where muscle strain amplitude (ϵ, normalized peak to peak) was 0.025 and the Ca²⁺ transient had a 0.2 duty cycle (δ_Ca) at a 0.033 phase of activation (ϕ_Ca). Force and ATP utilization were calculated at each time step (dt=1 ms). Our standard mechanical parameters apply to these simulations: k_xb=5, k_a=5229 and k_m=6060 pN nm⁻¹ (Tanner et al., 2007).

A parametric plot of force against strain (known as the work loop) shows positive work output (=548 pN nm, Fig. 3). In simulations described more fully below, work output for our half-sarcomere model ranges between 200 and 1500 pN nm (0.2–1.5 aJ). It is interesting to compare mass specific power output (W kg⁻¹) for these simulation results to whole muscle measurements. Taking our average predicted work output to be approximately 1000 pN nm per cycle and a cycle period of 40 ms (f=25 Hz), the corresponding power output equals 2.5×10⁻¹⁷ W. Our model half-sarcomere is 1200 nm long, 70 nm high and 80 nm wide, corresponding to a volume of 6.7×10⁶ nm³ (Tanner et al., 2007). With a density of 1000 kg m⁻³, this would lead to a mass of 6.7×10⁻¹⁸ kg and specific power output of approximately 4 W kg⁻¹. Over the full set of simulations, we would predict a range of 1–6 W kg⁻¹ for specific power output. These predictions are less than the operating power output of 45 W kg⁻¹ reported previously (Tu and Daniel, 2004), but well within the range of power output values reported (−20 to 80 W kg⁻¹).

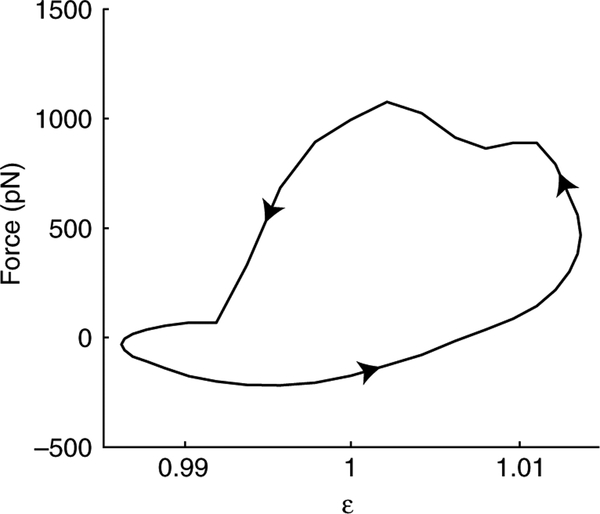
Fig. 3.

Each simulation (10 s long) produced 250 work loops, constructed from the phase portrait of force and muscle strain over any single oscillation period (40 ms). This work loop is the average phase portrait for the simulation shown in Fig. 2. The counter-clockwise direction (arrows) denotes positive work output (548.6±46.6 pN nm, mean ± s.d., N=245 work loops).

Our simulations used lower strain amplitudes than in the earlier experiments (Tu and Daniel, 2004). This constraint followed from a computational limitation in which we were restricted to time steps greater that those required for large amplitude strains. Because strain strongly determines predicted power output values, we rescaled predictions with the assumption that the filament lattice is linearly elastic. This assumption allows us to compare simulation results with experiments via normalizing power output to the square of strain amplitude (ϵ²). This calculation yields predicted values ranging from 1860 to 2640 W kg⁻¹ (ϵ=0.05) and 1190 to 4761 W kg⁻¹ (ϵ=0.025) for mass-specific power output per ϵ² (Fig. 4A). These values are similar to estimates of power output for Manduca at the measured physiological strain (ϵ=0.09 yields about 5000 W kg⁻¹ ϵ⁻²) (Tu and Daniel, 2004). Thus, our half-sarcomere model predicts physiological levels of mechanical work and power, previously measured in whole muscle studies.

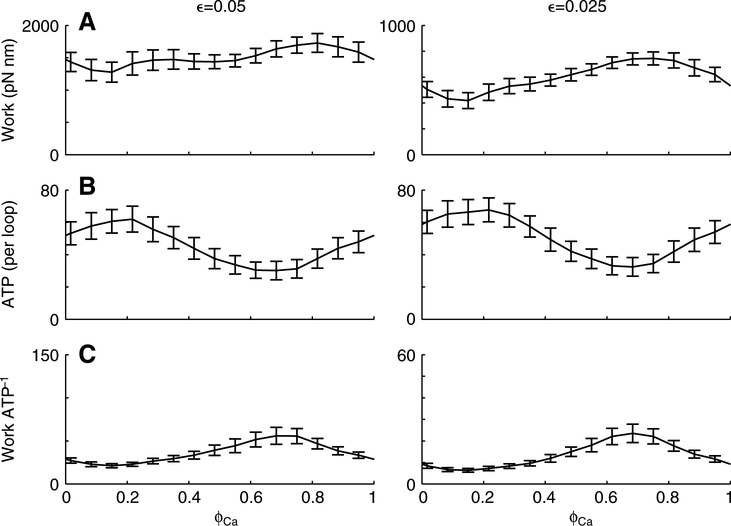
Fig. 4.

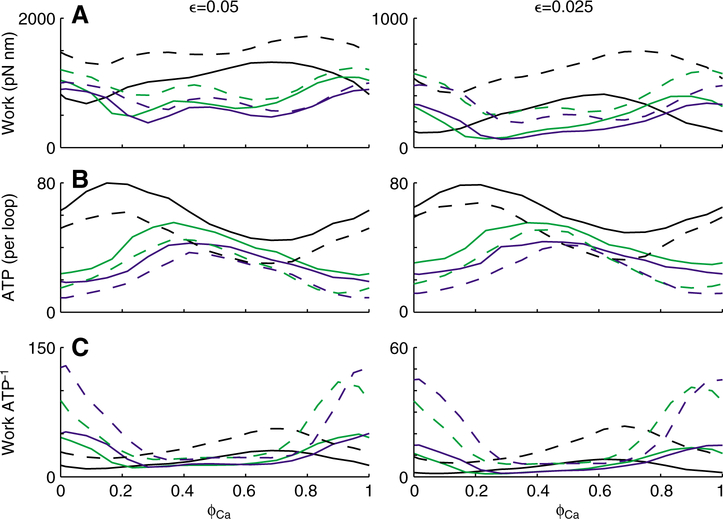
Work and ATP utilization vary with respect to the phase of Ca²⁺ activation (ϕ_Ca). Data points (connected with a line) represent average values (mean ± s.d.) from 245 individual work loops at a duty cycle (δ_Ca) of 0.5. The ϕ_Ca values producing maxima and minima varied for work (A) and ATP (B), therefore yielding a unique ϕ_Ca that maximized efficiency (ratio of work to ATP; C). Strain amplitude ϵ was 0.05 (left) and 0.025 (right), and primarily affected work magnitude. Note the difference in ordinate scales between the left and right panels in A and C when ϵ=0.05 versus 0.025. Mechanical parameters for the filaments and cross-bridges are listed in Fig. 2.

For two levels of strain (0.025 and 0.05) we note a clear phase dependence of both mechanical work output and ATP utilization rate (Fig. 4). While there appears to be a stronger phase dependence for work at the lower strain amplitude (Fig. 4A, right), this is an artifact of different ordinate scales between the two panels in Fig. 4A. The resultant mechanical work per ATP (Fig. 4C), a proxy for contractile efficiency (sensu Kushmerick and Davies, 1969), also depends on phase of activation. While these efficiencies show a very similar phase dependence, the magnitudes remains highly strain dependent (with different ordinate scales between the two panels, Fig. 4C). At both levels of strain, the peak value for mechanical work output, ATP use and efficiency all occur at different phases. Thus, muscles operating at phases that may maximize work may do so at some considerable reduction in efficiency. Adjusting phase of activation could modulate the muscle function, moving the performance from high power output to high efficiency.

Although mechanical work output depends on activation phase, this response is influenced by compliance of the filament network and duty cycle (δ_Ca) of calcium activation. The effects of these parameters are summarized in Fig. 5, where we simulated work loops at three different duty cycles (0.1, 0.2 and 0.5) and two levels of filament compliance (the standard values listed above and one tenth the standard values). Under these standard filament conditions (at either strain), decreasing duty cycle leads to decreased mechanical work output and ATP use (broken lines in Fig. 5). Decreasing duty cycle also shifted the phase maximizing mechanical work output and ATP use. These phase shifts differed between mechanical work output and ATP use and their sensitivities varied with strain. The correlation between decreasing δ_Ca and decreased ATP use follows directly from the smaller fraction of time during which cross-bridges may cycle each period. Because duty cycle yields different phase sensitivities between work output and ATP use, the ratio of these two (efficiency) resulted in even a greater (and unique) sensitivity to phase as duty cycle decreased.

Fig. 5.

Duty cycle and filament stiffness influence how work and ATP vary with respect to phase of activation (ϕ_Ca). Similar to Fig. 4, lines represent mean work (A), ATP (B) and efficiency (C) values; however error bars are not shown. Duty faction (δ_Ca) varied between 0.1 (blue), 0.2 (green) and 0.5 (black). Broken lines represent our standard mechanical parameters for the filaments and cross-bridges, listed in Fig. 2. Therefore, the mean data shown in Fig. 4 correspond to the grey broken lines shown here in Fig. 5. Solid lines represent a more compliant filament lattice, where both k_a and k_m were simultaneous scaled by a factor of 0.1 (k_xb did not change). As in Fig. 4, note the difference in ordinate scale between the left and right panels in A and C when ϵ=0.05 (left) versus 0.025 (right).

Under these standard filament conditions (at either strain), decreasing duty cycle shifted the phase maximizing mechanical work output and ATP use (broken lines in Fig. 5). Interestingly, the range of mechanical work output across all phases was unchanged by duty cycle (at standard filament conditions). In contrast, decreasing duty cycle decreased the maximal ATP use value as well as the range of ATP (broken, colored lines in Fig. 5). The correlation between greater ATP use and increased δ_Ca follows directly from the greater fraction of time during which cross-bridges may cycle each period. Furthermore, decreasing duty cycle leads to greater sensitivity of efficiency to phase.

In general, increasing filament compliance (the thick and thin filaments becoming more flexible) decreased work output and increased ATP use (solid lines, Fig. 5), compared to standard filament conditions. These observations agree with prior results showing that cross-bridge cycling rate increases with increased cross-bridge binding via greater filament movement (compliant realignment of binding sites) (Daniel et al., 1998; Tanner et al., 2007). As with the standard filament conditions (at either strain), decreasing duty cycle shifted the phase maximizing mechanical work output and ATP use (solid lines, Fig. 5). Interestingly, the range of mechanical work output across all phases was unchanged by duty cycle (different from the standard filament condition results). In contrast with these mechanical work output results, decreasing duty cycle decreased the maximal ATP use value and the shift in this peak (toward higher phases at lower duty cycles) became more pronounced for the more compliant filament values. Lower values for work with greater ATP utilization (for these more compliant myofilament values versus standard values) result in lower efficiency at the more compliant filament values. The sensitivity of efficiency to phase is also lower when filament compliance increases. Together, these results demonstrate that the coupled relationship between filament compliance, duty cycle and activation phase determines the energetics of muscle contraction.

Discussion

The phase dependence of mechanical power output predicted by our model is consistent with the studies of whole muscle function (e.g. Josephson, 1985). However, to our knowledge, no prior study has shown that myosin cross-bridge ATPase rates vary with phase of activation. In this regard, our simulations show three key features: (1) mechanical power output and power input (ATP consumption rate) both vary with phase, but their respective maxima occur at different phases (Figs 4, 5); (2) therefore the maximum efficiency of contraction (the ratio power output to power input) occurs at yet a third, distinct phase (Figs 4, 5); and (3) the specific phases leading to maximum power output, minimum energy consumption or maximum efficiency vary with the duty cycle of activation and the filament lattice compliance (Fig. 5). Moreover, our simulation results suggest that these changes in muscle function could occur over relatively small adjustments in phase of activation.

The notion that efficiency and power may not share a phase relationship has not been a central focus of muscle functional studies, possibly because there has not been a compelling case made for changes in ATPase rate (and thus efficiency) with activation phase. There is good evidence, however, that these metrics should co-vary. A trade-off between power and efficiency was shown in dogfish muscle (Curtin and Woledge, 1996), and a modified Hill model (Lichtwark and Wilson, 2005) demonstrated the co-variance of efficiency and power output during oscillatory length changes over a range of frequencies.

Periodic length changes produce periodic velocity changes. With strong evidence that ATPase rate varies with shortening velocity, we might expect the energy consumption to depend on phase. Despite these observations, no one has proposed a molecular mechanism that would explain the co-variance of phase and energetics. Our simulations show that some phases of activation may be more advantageous for the efficiency of contraction, whereas other phases may lead to higher levels of power output. Thus one reason moths may operate at a phase of activation leading to sub-maximal power output (Tu and Daniel, 2004) may reside in the potential trade-off between power and efficiency with respect to phase. As suggested (Tu and Daniel, 2004), operating at sub-maximal power output affords power reserves for use in extreme behaviors such as escape, load carrying, or take-off. However, this only makes sense if ATP consumption also varies with phase, so that sub-maximal power output reduces energy consumption rate.

The relationship between power and efficiency is complicated by the strong dependence of these parameters on duty cycle (Fig. 5). Very short duty cycles lead to lower mechanical power output and lower ATP use. At the same time, the phases producing peak power output and peak ATP use increase with decreasing duty cycle (each with different sensitivities to phase; Fig. 5). One component of this process that we have not considered is the possible correlation between short duty cycles (at a given frequency) and the energetics of Ca²⁺ pumping into the sarcoplasmic reticulum of flight muscle. Hence, short duty cycles may require greater ATP use simply because the faster rates at which Ca²⁺ sequestering must occur become energetically expensive. Adding these ATP costs at decreased duty cycles may yield more similar values of ATP use per oscillatory cycle, thereby further amplifying the differences in efficiency of muscle contraction (work/ATP) shown in Fig. 5.

Filament compliance also affected the magnitudes of power output and power input (Fig. 5). Interestingly, the phases at which these components generate their respective maxima and minima are somewhat independent of the mechanical properties of the myofilament lattice. Our result showing higher ATP use with greater filament compliance is consistent with previous work (Daniel et al., 1998; Daniel and Tu, 1999; Tanner et al., 2007). Thus, these basic mechanical characteristics may underlie varied performance in muscles among diverse taxa. The extent to which the mechanical properties of filaments vary among species is not well understood, although the lattice geometry (myofilament ultrastructure) varies considerably (Hoyle, 1983). To our knowledge studies of the mechanical properties of isolated filaments and cross-bridges have focused on vertebrate striated muscle.

Combining our existing ability to calculate work loops from measured force and length changes (Tu and Daniel, 2004) with simultaneous measurements of oxygen consumption and carbon dioxide production allows one to measure the phase dependence of power and efficiency relationships in synchronous insect flight muscle. While instantaneous measurements of ATPase activity in muscle during oscillatory length changes and concomitant phase changes may be challenging, the relatively poor capacity of insect flight muscle for anaerobic metabolism allows one to use oxygen consumption as a proxy for ATP use. As shown previously (Tu and Daniel, 2004), work loop preparations are stable for a sufficiently long time to facilitate this experimental approach (approximately 1 h).