Abstract
Sensorimotor control during overt movements is characterized in terms of three building blocks: a controller, a simulator, and a state estimator. We asked whether the same framework could explain the control of internal states in the absence of movements. Recently, it was shown that the brain controls the timing of future movements by adjusting an internal speed command. We trained monkeys in a novel task in which the speed command had to be controlled dynamically based on the timing of a sequence of flashes. Recordings from the frontal cortex provided evidence that the brain updates the internal speed command after each flash based on the error between the timing of the flash and the anticipated timing of the flash derived from a simulated motor plan. These findings suggest that cognitive control of internal states may be understood in terms of the same computational principles as motor control.
Introduction
Theories of embodied cognition posit an intimate link between mental states and how we move our body. Compelling theoretical arguments have advanced the hypothesis that movements are controlled through the interaction of three building blocks 1–5 (Figure 1a): a controller that drives the body, a simulator that simulates movements to predict future states, and an estimator that updates state variables. Considering the common challenges that the dynamic control of motor and cognitive states face 6, we set out to test whether the regulation of cortical dynamics supporting anticipation and planning can be similarly understood in terms of the interplay between a controller, a simulator, and a state estimator.
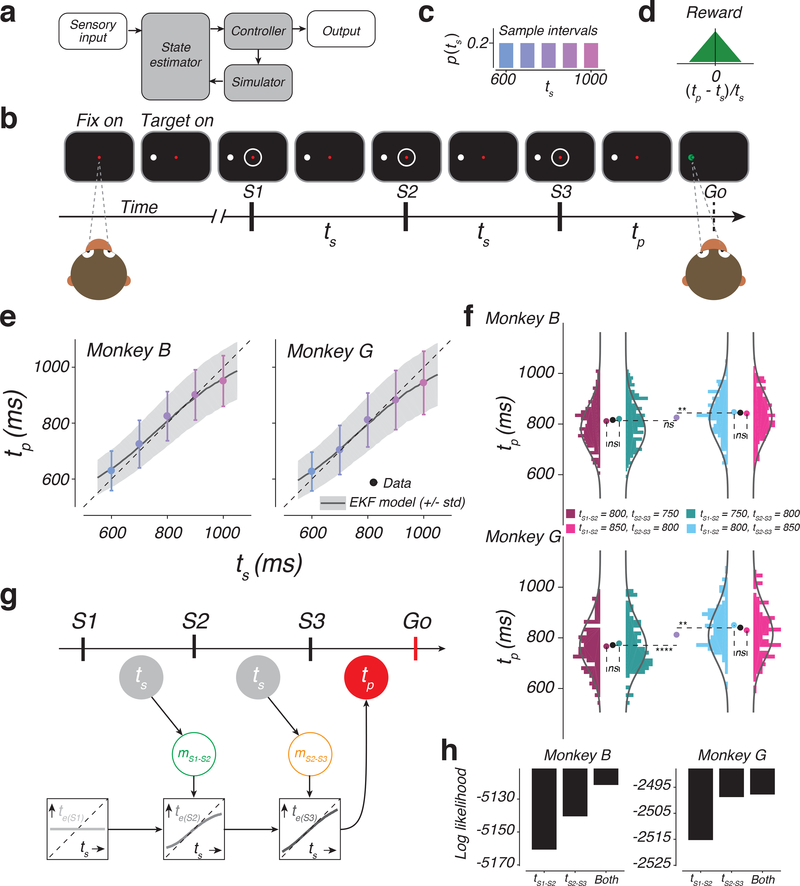
Figure 1. The 1-2-3-Go task, behavior, and a sequential updating model.
a) Internal-model based control. The controller drives the output. In the presence of delays and variability, the output control would benefit from a simulator and a state estimator. The simulator predicts the output and the estimator integrates the prediction with sensory inputs to update the controller. b) Sequence of events during a trial of 1-2-3-Go. The monkey fixates a central spot (Fix on). After the presentation of a saccadic target (Target on), three isochronous flashed annuli (S1, S2, and S3) are presented around the fixation point. The animal measures the sample interval (ts), between consecutive flashes and aims to produce a matching interval (tp) after S3 (Go). c) Sample interval distribution, p(ts). Across trials, ts was randomly drawn from a discrete uniform prior distribution with 5 values ranging between 600 and 1000 ms. d) Reward schedule. Maximum reward was delivered for tp=ts. Reward amount decreased linearly to zero with increasing relative error (|(tp - ts)/ts|). e) Produced interval (tp) as a function of sample interval (ts). tp increased monotonically with ts (mean: colored circles; standard deviation: error bars; monkey B: n = 1412, 1326, 407, 1336, 1326 total trials for ts = 600, 700, 800, 900, and 1000 ms, respectively; monkey G: n = 699, 724, 243, 685, 643 trials for ts = 600, 700, 800, 900, 1000 ms, respectively). Responses were biased toward the median ts and away from the unity line (dashed). Black traces and gray shadings are the mean and standard deviation predicted by the Extended Kalman Filter (EKF) model fit to the behavior. f) Analysis of behavior under the four cue conflict conditions. Histograms show the distribution of tp in different cue conflict conditions (colors) for the two animals (top and bottom). Monkey B: n = 215, 216, 224, and 206 trials (left to right). Monkey G: n = 117, 83, 111, and 104 trials (left to right). Solid lines are the predicted distribution under the EKF model. Pairs of nearby histograms (e.g., tS1-S2 = 800 ms, tS2-S3 = 750 ms versus tS1-S2 = 750 ms, tS2-S3 = 800 ms) correspond to conflict conditions with the same mean ts. Colored circles show the mean tp for different cue conflict conditions. Black circle shows the mean tp across conflict conditions with the same mean ts. Purple circles corresponds to the mean tp for tS1-S2 = tS2-S3 = 800 ms trials. Dashed lines are added to aid comparison between mean values (ns: not significant; **: p < 0.01; ****: p < 0.0001; two-sided t-test). g) The EKF model. At the time of S1, the model uses the mean of the prior as its initial estimate of ts (te(S1): light gray). At S2, the model derives an updated estimate (te(S2): medium gray) by applying a nonlinear function to the difference between te(S1) and the current measurement, denoted mS1-S2 (green). At S3, the model further updates the estimate (te(S3): dark gray) by applying the same nonlinearity to the difference between te(S2) and the second measurement, denoted mS2-S3 (orange). The model uses te(S3) as its final estimate, and produces tp (red), which is corrupted by production noise (see Online Methods, Supplementary Figure 1). Open and filled circles correspond to unobserved and observable variables, respectively. h) Log likelihood of different variants of the EKF model that either use tS1-S2, or tS2-S3, or both. Larger values indicate more support for a given model. n = 861 and 415 total trials for monkeys B and G, respectively. See also Supplementary Figure 1.
To address this problem, we leveraged a recent finding in monkeys regarding how the brain controls movement initiation time. When animals are instructed to initiate a movement after a delay, neural responses in multiple brain areas evolve toward a movement-initiation state at a speed that is inversely proportional to the delay 7,8,9; i.e., faster for shorter intervals and slower for longer intervals. Moreover, similar to how movements are controlled by motor commands 10, the speed with which neural responses evolved over time was controlled by an internally-generated “speed command” 8.
From the perspective of control, initiating a movement based on an instructed delay and in the absence of feedback is relatively straightforward; it only requires an open-loop system driven by the desired speed command. The natural next question is how such speed command may be controlled in a closed-loop fashion in the presence of sensory feedback. To address this question, we developed a novel timing task in which the speed command controlling movement initiation time had to be adjusted based on uncertain and discrete sensory cues. As noted in the motor control literature, to integrate uncertain and delayed sensory feedback, the system would benefit from establishing a simulator and an estimator (Figure 1a). Accordingly, we asked whether closed-loop control of an internally-generated speed command could be explained in terms of augmenting the open-loop control with a simulator and an estimator.
Results
1-2-3-Go task
In the 1-2-3-Go task (Figure 1b), animals had to attend three flashes presented around the fixation point (S1, S2, and S3), and subsequently initiate a delayed saccade to a target (Go). On every trial, the inter-flash interval, which we refer to as the sample interval (ts), was drawn from a fixed prior distribution (Figure 1c). Animals had to estimate ts from measurements of the S1-S2 and S2-S3 intervals and produce an S3-Go interval (tp) that closely matched ts. Animals received reward when the relative error (|(tp - ts)/ts|) was below an adaptively controlled threshold (see Online Methods). The magnitude of reward decreased linearly with relative error (Figure 1d).
Animals integrate prior knowledge with multiple measurements
Animals learned to time their saccade based on ts (Figure 1e). Using linear regression (tp = bts+c), we verified that, for both animals, tp increased with ts (monkey B: b = 0.82 +/− 0.01 [95% CI], t(5806) = 8.51 × 103; p < 0.001; monkey G: b = 0.81 +/− 0.02 [95% CI], t(2293) = 3.84 × 103; p < 0.001; two tailed t-test). The variability of tp also increased with ts as evidenced by the regression slope relating standard deviation of tp to ts (100 resamples of the data; monkey B: b = 0.04 +/− 0.002 [95% CI], t(498) = 782.52, p < 0.001; monkey G: b = 0.11 +/− 0.003 [95% CI], t(498) = 1.84 × 103, p < 0.001). This increase in variability is consistent with scalar variability 11 during time interval reproduction tasks 12,13.
In the presence of behavioral variability, an ideal observer would reduce variability by taking into account the prior statistics of ts 7,14,9. This was evident in animals’ behavior from systematic biases of tp (“BIAS”, see Online Methods) toward the prior mean (monkey B: BIAS=30.35 +/− 1.27 ms [mean +/− std], t(99) = 23.97, p < 0.001; monkey G: BIAS=29.89 +/− 1.54 ms [mean +/− std], t(99) = 19.37, p < 0.001; two tailed t-test), and by the less-than-unity regression slope relating tp to ts (monkey B: t(5806) = −1877, p < 0.001; monkey G: t(2993) = −987.8966, p < 0.001; two tailed t-test).
An ideal observer would additionally improve accuracy by combining information from measurements of both the S1-S2 and S2-S3 intervals 12. This was also evident in the animals’ behavior based on a subset of conflict trials for ts=800 ms condition in which either the S1-S2 interval, tS1-S2, or S2-S3 interval, tS2-S3, was made 50 ms longer or shorter. We analyzed the conflict trials to distinguish between three hypotheses: (H1) monkeys only relied on tS1-S2, (H2) monkeys only relied on tS2-S3, or (H1,2) monkeys used both intervals. When either tS1-S2 or tS2-S3 was 850 ms, the average tp was significantly longer than when both intervals were 800 ms (Figure 1f, light blue for tS2-S3; one tailed t-test; Monkey B: t(629) = 2.95, p = 0.002; Monkey G: t(352) = 3.51, p < 0.001; pink for tS1-S2; one tailed t-test; Monkey B: t(611) = 2.17, p = 0.015; Monkey G: t(345) = 1.51, p =0.066). This indicated that animals used both tS1-S2 and tS2-S3 and rejected both H1 and H2. Moreover, the change in average tp was statistically indistinguishable between the two conflict conditions (two tailed t-test; Monkey B: t(428) = −0.62, p = 0.531; Monkey G: t(213) = −1.54, p = 0.125) suggesting that animals combined the two measurements with comparable weights. Together, these results confirm that animals combined the two measurements.
A sequential updating model for the 1-2-3-Go task
Recently, we found that human performance on this task was better captured by a near-optimal sequential updating model than an optimal Bayesian model 12. This model, which we refer to as the Extended Kalman Filter (EKF), functions as follows (Figure 1g; Supplementary Figure 1c): 1) At S1, the estimated interval, te(S1), is set to the mean of the prior. 2) At S2, the model integrates the first measurement, denoted mS1-S2, with the prior to compute an updated estimate, te(S2). To do so, EKF, updates te(S1) by a nonlinear function of error between te(S1) and mS1-S2 (see Online Methods). (3) At S3, the model repeats this process to integrate the second measurement, mS2-S3, with the prior and mS1-S2 and compute the final estimate, te(S3). After S3, the model produces tp, which is te(S3) plus signal dependent production noise.
We found that the pattern of responses in monkeys was also more accurately captured by the EKF model (Figure 1e, curves) compared to an optimal Bayesian model (Supplementary Figure 1). We also used EKF to substantiate that animals integrated both measurements. We compared the log likelihood of the data given three variants of the EKF based on H1, H2, and H1,2, respectively. The EKF that relied on both measurements was more likely than the other two variants (Figure 1h). Further, EKF fitted to trials without conflict was able to capture the distribution of tp in conflict trials (Figure 1f, curves). Based on these results, we concluded that monkeys integrated the prior with the two measurements using a sequential updating strategy exemplified by EKF.
Speed control in the 1-2-3-Go task
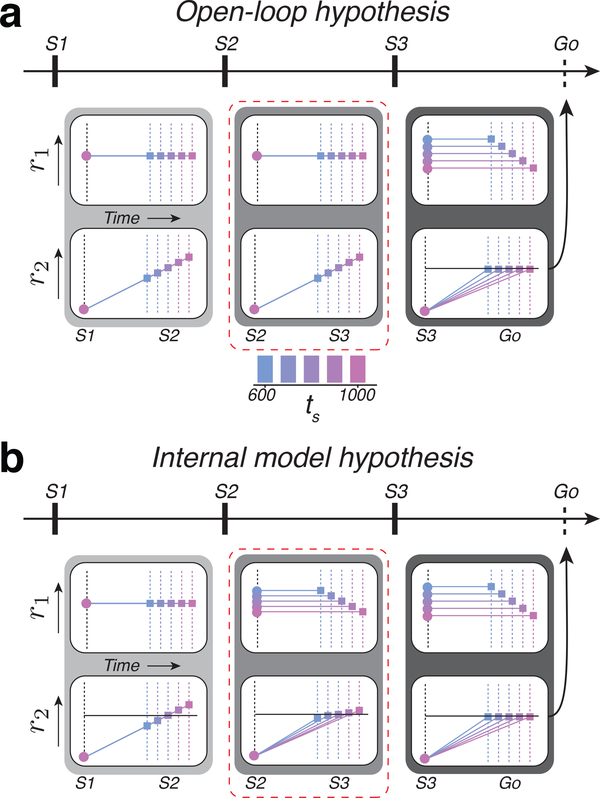
Previous work in monkeys has shown that the brain controls movement initiation time by setting a speed command that determines how fast neural trajectories in the cortico-basal ganglia system evolve toward a movement-initiation state (i.e., “threshold”) 8. Building on this finding, we considered two hypotheses regarding how the brain might control movement initiation time in the 1-2-3-Go task. One hypothesis, which we refer to as the open-loop hypothesis, is that the brain integrates the prior with the two measurements (mS1-S2 and mS2-S3) to compute the final estimate, te(S3), which in turn determines the speed of neural trajectories in the S3-Go epoch. A key prediction of this hypothesis is that neural activity in the S1-S2 and S2-S3 epochs should be similar and reflect explicit measurements of time intervals. Moreover, activity patterns in the first two epochs should be qualitatively different from that in the third epoch in which the responses would evolve with different speeds depending on the animal’s final estimate. The predictions of this hypothesis can be illustrated using a toy model. Let us assume that the brain tracks time by accumulating ticks from a clock. Since the first two epochs are associated with measurement of the interval, we would expect some neurons to carry signals reflecting a fixed clock, and others to exhibit ramping activity with a fixed slope (Figure 2a, left and middle). In the third epoch, however, signals would change qualitatively such that the clock speed and the slope would correspond to the animal’s estimate (Figure 2a, right).
Figure 2. Predictions of the open-loop and internal model hypothesis in the 1-2-3-Go task.
a) Activity profile of two hypothetical populations, r1 and r2, under the open-loop hypothesis. Predictions are shown for each of the three epochs. r1 provides the clock and r2 integrates the clock to track elapsed time. During both the first and second epochs (light and medium gray boxes), the clock signal is independent of ts. Therefore, r2 at S2 or S3 represent the measured interval (different colored squares). These measurements set the clock speed (output of r1) according to te(S3), and, as a consequence, r2 ramps to threshold (horizontal black line) at a rate that depends on ts from S3 to Go (dark gray box). b) Activity profile under the internal model hypothesis. r1 and r2 represent the control signal and simulation, respectively. During the first epoch (light gray box), the r1 population supplies a constant speed command according to the mean of the prior. The r2 population integrates this speed command and produces ramping activity that terminates at different points depending on the sample interval, ts (different colored squares). The difference between the terminal point of r2 and the predicted terminal point based on the mean of the prior (horizontal line) provides an error that allows r1 to encode an interval-dependent speed command in the subsequent epoch (medium gray box, top). The corresponding r2 population integrates the updated speed to generate ramping activity whose slope varies with ts (bottom). The same process is repeated in the third epoch (dark gray box). Dashed red line highlights the key differences between the two hypotheses.
The other hypothesis, which we refer to as the internal model hypothesis, is that the brain implements a closed-loop control system similar to the EKF model, in which feedback is used to update estimates sequentially from te(S1) at S1 to te(S2) at S2 to te(S3) at S3. To implement this strategy, the brain has to additionally establish a simulator and an estimator. The simulator would run after each flash to predict the next flash, and the estimator would update the speed based on the prediction error at the time of the next flash.
We used the inverse relationship between interval estimate and speed of neural trajectories to formulate a set of concrete predictions under the internal model hypothesis: 1) After S1 and before S2, the speed of neural trajectories should reflect the initial estimate, te(S1). 2) After S2 and before S3, the speed command and the speed with which responses evolve should be inversely proportional to te(S2). 3) After S3, the speed should be adjusted to reflect te(S3). Note that the key difference between the open-loop and internal model hypotheses is the nature of signals in the S2-S3 epoch. According to the open-loop hypothesis, responses in this epoch reflect an interval measurement regardless of the duration of the interval in the S1-S2 epoch. In contrast, the internal model hypothesis predicts that responses in the S2-S3 epoch evolve with different speeds depending on the animal’s estimate after S2 (te(S2)). The predictions of the two hypotheses for the other two epochs (S1-S2 and S3-Go) are identical.
The predictions of this hypothesis can also be demonstrated using the clock-accumulator toy model (Figure 2b). In the first epoch, the clock speed and the slope of the ramping activity would be fixed and reflect te(S1) (Figure 2b, left). The second and third epoch, in contrast, would represent a simulated motor plan (S2-S3) and an actual motor plan (S3-Go). Accordingly, both the level of activity of neurons that encode the clock speed, and the slope of the neurons generating ramping activity would be interval-dependent (Figure 2b, middle and right). Specifically, in S2-S3 and S3-Go, the speed and the slope should be inversely proportional to te(S2) and te(S3), respectively.
Single-neuron signatures of the internal model hypothesis
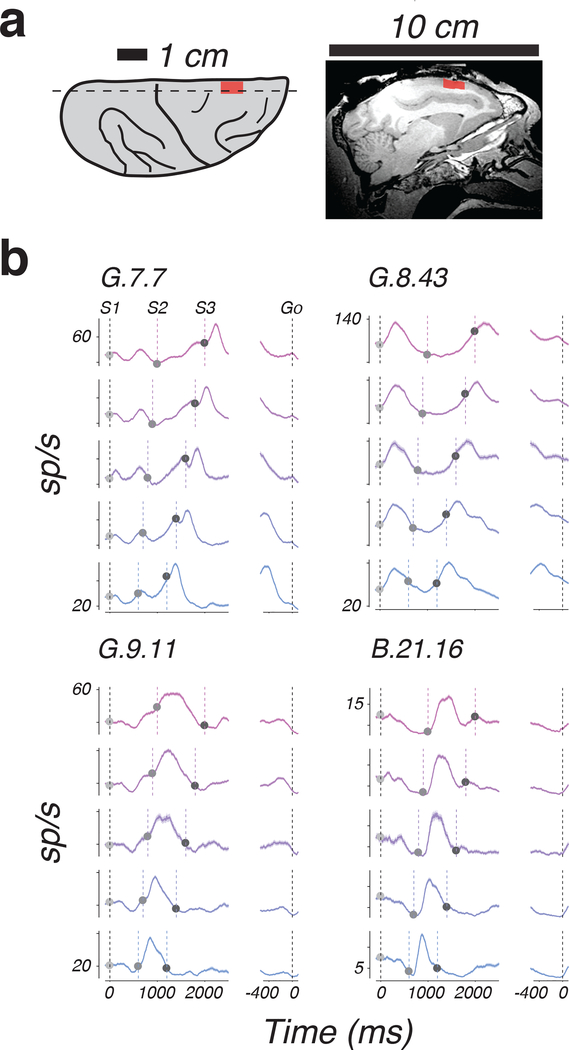
We recorded neural activity (N=63 and 118 in monkeys B and G, respectively) in the dorsomedial frontal cortex (DMFC; Figure 3a) including the supplementary eye field (SEF), the dorsal region of the supplementary motor area (SMA), and pre-SMA. Our choice of recording areas was motivated by previous work showing a central role for DMFC in sensorimotor timing 15–18. We targeted the same region of DMFC where we previously observed the inverse relationship between time and speed 7,8,9.
Figure 3. Example response profiles of individual DMFC neurons during 1-2-3-Go task.
a) Recording locations. Left: illustration of the dorsal aspect of the right hemisphere, showing major sulci (black lines) and the location of recordings across monkeys (red). Right: Magnetic resonance image showing a sagittal section (dashed line, Left) of the right hemisphere in monkey G; mean across two image acquisitions with similar results. Red indicates the rostral-caudal extent of recordings. b) Average response profiles for 4 example neurons aligned to S1 (left) and Go (right) sorted according to ts (colors). Shading indicates standard errors. Vertical dashed lines indicate flash and saccade times. Trial number for ts = 600, 700, 800, 900, and 1000 ms: G.7.7 – 185, 206, 72, 193, and 148; G.8.43 – 156, 169, 51, 138, and 133; G.9.11 – 178, 172, 49, 157, and 151; B.21.16 – 210, 168, 47, 176, and 173.
DMFC responses were modulated throughout the trial and had heterogeneous profiles that were typically distinct across the three epochs (Fig. 3b). Our main interest was to evaluate the neural data in terms of the open-loop and internal model hypotheses. To do so, we analyzed the activity of 115 well-isolated neurons with respect to the aforementioned predictions of those hypotheses (Fig. 2b).
Temporal scaling across individual neurons
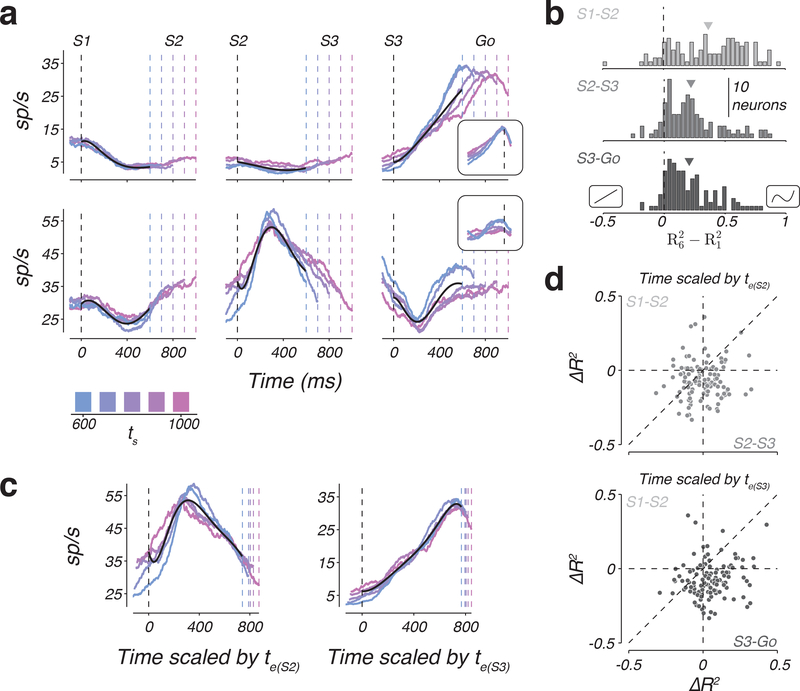
Temporal scaling predicts that response profiles across ts would become more similar after undoing the temporal scaling. This was most conspicuous for the small subset of neurons with a ramp-like response profile for which the slope of the ramp had an inverse relationship to ts (Figure 4a, top right). However, consistent with previous findings 8,19,20, a majority of neurons had non-monotonic firing rate profiles, and were better fit by higher-order polynomials (see Online Methods; Supplementary Figure 2). For example, cross-validated 6th order polynomials explained 40.86%, 24.42%, and 20.34% more variance than cross-validated 1st order polynomials in the S1-S2, S2-S3, and S3-Go epochs, respectively (Figure 4b).
Figure 4. Temporal scaling of non-monotonic firing rates across individual DMFC neurons.
a) Firing rates of two example neurons (rows) as a function of task epoch (columns) for different values of ts (colors). Black lines are the fit of a 6th order polynomial to the first 600 ms of each epoch and neuron. From left to right, firing rates were aligned to S1, S2, and S3 flashes, respectively (black dashed line). Colored dashed lines represent the time of the subsequent flash. Insets: firing rates aligned to Go (black dashed line). b) Histograms of the difference in the fraction of variance explained, R2, between the 6th and 1st order polynomial fit to the data. Negative and positive values correspond to neurons that favored the 1st and 6th order polynomial, respectively. Insets on the negative and positive sides of the abscissa illustrate example 1st and 6th order polynomials. Arrows indicate the mean of the distributions. Different gray levels correspond to different task epochs. c) Example scaled temporal responses. Left: firing rate of the second neuron in panel a during the S2-S3 epoch, temporally scaled by the animals’ estimate in the S2-S3 epoch. The estimate was inferred from the model fits to the behavior. Right: firing rate profile for the S3-Go epoch of the first neuron in panel a temporally scaled by the animals’ estimate in the S3-Go epoch. Black lines show the 6th order polynomial that best fit the scaled data. Dashed lines as in panel a, but appropriately scaled. d) Scatter plot showing the change of explanatory power (ΔR2) of the 6th order polynomial fit to the scaled versus unscaled data across neurons. Top: ΔR2 in the S2-S3 epoch compared to the S1-S2 epoch. Bottom: ΔR2 in the S3-Go epoch compared to the S1-S2 epoch. Vertical and horizontal dashed lines indicate ΔR2 = 0 and the diagonal in the unity line. See also Supplementary Figures 2 and 3.
To assess the presence of temporal scaling for every neuron, we normalized response profiles in time according to the animal’s estimates (i.e. te(S2) and te(S3) for the S2-S3 and S3-Go epochs, respectively; Figure 4c), and asked whether a polynomial fit to the normalized response profiles would explain more variance (R2) than a polynomial of the same order fit to original data (see Online Methods). We used the difference between the explanatory powers of the two polynomial fits (ΔR2) as our metric of the degree of scaling. We also computed the same metric in the S1-S2 epoch as a benchmark since we were certain that there was no temporal scaling in this epoch (the animal did not yet know ts). Here, we show the result for a 6th order polynomial, which was sufficiently complex to describe the temporal responses across DMFC population (Supplementary Figure 2).
The degree of scaling in the S3-Go epoch was consistently stronger than the S1-S2 epoch (Figure 4d, bottom; one-tailed Wilcoxon, Z = 7.08, p < 0.001). Importantly, the same was true in the S2-S3 epoch (Figure 4d, top; one-tailed Wilcoxon; Z = 4.62; p < 0.001), and the results remained unchanged independent of the degree of the polynomial used to assess scaling. In fact, scaling was evident even when the polynomial order was chosen to maximize R2 for unscaled data (Supplementary Figure 3). Therefore, we concluded that responses in both S2-S3 and S3-Go were temporally stretched in accordance with ts. These observations provide evidence that 1) signals in the S3-Go epoch are governed by a speed-dependent motor plan consistent with previous work on motor timing 8,21, and 2) responses in the S2-S3 epoch also exhibited temporal scaling despite the fact that they were not associated with a motor plan. The latter observation suggests that activity in the S2-S3 epoch is predictive of the upcoming flash, and therefore provides evidence in support of the internal model hypothesis and against the open-loop hypothesis.
Speed command across individual neurons
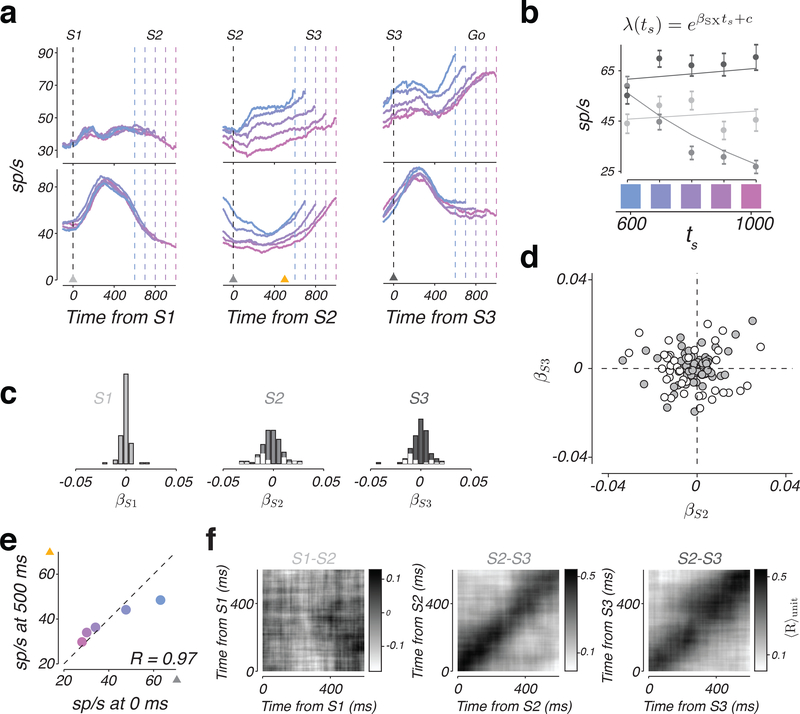
A neuron could be a candidate for providing the hypothesized speed command if its response in the S2-S3 and S3-Go epochs were to vary systematically with ts (Figure 2b). In our population, the firing rate of many neurons was modulated by ts in either S2-S3 or S3-Go epochs (Figure 5a). To quantify this observation rigorously, we fit a linear-nonlinear-Poisson (LNP) model to the spike count data (Figure 5b, lines; see Online Methods). This yielded a parameter, βSX (with X = 1, 2, or 3) that we used to quantify the degree to which firing rate depended on ts at the time of each flash. At S1, neurons cannot logically encode ts since the animal has not yet measured ts. Accordingly, βS1 across the population was distributed tightly around zero (Figure 5c, left), and was not significant for any of the neurons. βS2 and βS3 were distributed more broadly and were significant for 27 and 20 of the neurons, respectively (Figure 5c, middle and right, white bars; see Online Methods). However, the degree of sensitivity to ts at S2 and S3 were unrelated across the population (Figure 5d; R2 = 0.0013, p = 0.70).
Figure 5. A representation of the sample interval by individual DMFC neurons.
a) Top: Firing rate of two example neurons with the same format as in Figure 4a. Triangles indicate time points of analysis in panels b and e. b) The relationship between ts and firing rates +/− standard error (circles and error bars; n = 30 trials for each ts, sampled with replacement from test data set) at S1, S2, and S3 for the example neuron in panel a (bottom row). Firing rates were computed from spike counts within a 150 ms window centered on S1 (light gray), S2 (medium gray), and S3 (dark gray). Lines are fits of the linear-nonlinear-Poisson (LNP) model (functional form shown on top). c) Histogram showing the sensitivity of individual neurons at the time of each flash to ts. Sensitivity values (βS1, βS2, and βS3) were derived from the LNP model fits as shown for an example neuron in panel b. White bars include neurons for which LNP provided a superior fit to a constant firing rate model (see Online Methods). d) Scatter plot of sensitivity to ts at S3 versus S2 across the population based on βS2 and βS3 parameters. White circles represent neurons that were significantly tuned to ts at either S2 or S3. e) Pearson’s correlation coefficient between firing rates, conditioned on ts, at the time of S2 (x-axis) and 500 ms afterwards (y-axis) for the example neuron in a (middle column, bottom row). Mean values for the 0 ms time point were found from a random selection of half the total trials (n = 156, 169, 51, 138, and 133 for ts = 600, 700, 800, 900, and 1000 ms, respectively); mean values for the 500 ms time point were found from the remaining trials. f) Average correlation between firing rates, conditioned on ts, computed for different pairs of time points. The average is taken across all individual neurons (n = 115). Left, middle, and right correspond to the analysis performed at time points relative to S1, S2, and S3, respectively. See also Supplementary Figures 4, 5, 6, and 7.
We next asked whether single neurons had an invariant representation of ts throughout each epoch. Invariant encoding of ts would predict high and persistent correlation between spike counts at pairs of time points within each epoch. To test this prediction, we quantified spike count correlations for each neuron as a function of ts across all pairs of time points within the first 600 ms after the onset of each epoch (e.g., Figure 5e), and constructed a 2D map of average correlations across ts. In both S2-S3 and S3-Go epochs, average correlations exhibited a diagonal structure indicating that correlations were high for nearby time points and weak for points farther apart (Figure 5f). These results provide evidence against an invariant representation of ts in the S2-S3 or S3-Go epochs at the level of individual neurons. This conclusion was further supported by an analysis using the LNP model (Supplementary Figure 4). Note that although single neurons did not encode ts invariantly, we were able to readily decode ts from the population activity over the entire S2-S3 and S3-Go epochs (Supplementary Figure 5–7).
Population response in DMFC exhibits hallmarks of the internal model hypothesis
Single-neuron analyses were consistent with some of the predictions of the internal model hypothesis. However, four considerations motivated us to further analyze the responses at the level of population. First, single neurons that exhibited temporal scaling had non-monotonic response profiles (Figure 4b), and thus could not unambiguously predict the upcoming event. We reasoned that this ambiguity might be resolved at the population level. Second, single neurons whose firing rate encoded ts and thus could serve as a control signal did so transiently (Figure 5f). However, at the level of population, responses carried a persistent representation of ts that was present for the entire S2-S3 or S3-Go epochs (Supplementary Figures 4–7). Third, since our experiment did not include any dynamic stimuli or ongoing movement between consecutive flashes, the observed patterns of activity likely emerge from recurrent interactions, and therefore, may be more interpretable if analyzed at the population level. Fourth, we wanted to exploit the additional statistical power afforded by the population analysis to ask whether the speed command and the simulated motor plan reflected ts or the animal’s internal estimate of ts (te(SX)).
As a first step, we performed principal component analysis (PCA) to identify the dominant modes of response from S1 to Go. Projections of neural activity onto the first 3 PCs as a function of ts revealed a set of highly structured neural trajectories with two notable features. First, neural trajectories had a persistent representation of ts after S2 (Figure 6a). This suggests that, unlike single neurons, the population activity in DMFC carries a ts-dependent signal that could serve as a speed command. Second, neural trajectories were highly similar in form and terminated in nearby states at the time of S3 and Go irrespective of the duration of ts. This observation implied that the speed at which different trajectories evolve had an inverse relationship to ts, which is what is expected from a predictive process anticipating the next event.
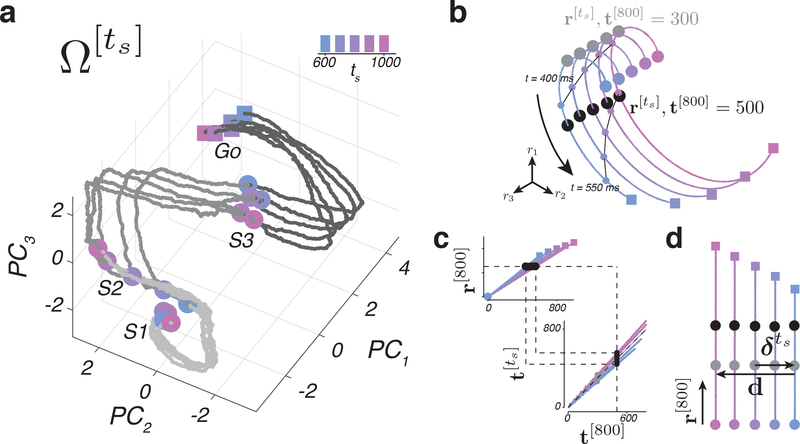
Figure 6. Neural trajectories and a technique for analyzing their kinematics.
a) Neural trajectories plotted in a subspace spanned by the first three principal components (PCs) computed from patterns of activity of n = 181 units across time, from S1 to Go. Circles indicate state at S1, S2, or S3 and squares denote state 100 ms before the correct tp for each ts. (b-d) Schematic illustration of KiNeT. b) Simulated neural trajectories generated under the internal model hypothesis and embedded in three-dimensional space by a nonlinear transformation. Gray and black markers correspond to the set of states, , nearest to r[800] at t[800] = 300 ms and t[800] = 500 ms, respectively. Small circles connected by thin black lines are states on the trajectories at 400 ms or 550 ms after the starting point. c) The time required for to reach , denoted , depends on the speed along each trajectory (top). Using this relationship, we can map to t[800] for each trajectory (bottom). Black points illustrate for t[800] = 500 ms. The application of KiNeT on with different speeds is illustrated by the dashed lines. Gray points illustrate for t[800] = 300 ms. d) KiNeT to infer the relative positions of trajectories. Each colored line represents the trajectories corresponding to different values of ts unraveled into two dimensions using KiNeT (panels b and c). KiNeT provides an estimate of the distance between and Ω[800] at different time points. is a vector that connects corresponding states on and Ω[800]. d is a vector that connects corresponding states on the first and last trajectories. Distance was measured by the projection of on d. Black and gray circles correspond to the nearby states as in panel a. See also Supplementary Figures 8 and 9.
Analysis of relative speed and distance of neural trajectories
When a set of neural trajectories are structured as in our experiment, it is possible to estimate their relative distance and speed using a recently developed analysis known as KiNeT 7. We have described KiNeT in detail in the Online Methods section. Here, we use an analogy to describe the key idea. Imagine that we want to measure the speed of a set of runners running in parallel tracks along a winding road. If we draw a line connecting nearby points along the tracks, the time at which each runner reaches that line would be inversely proportional to their speed. We can also estimate the distance between tracks from the relative position of runners when they reach that line. KiNeT applies the same logic to estimate relative distances and speeds of a set of winding neural trajectories (see Online Methods).
Let us denote the neural trajectory associated with a specific value of ts by (Figure 6a). We designated Ω[800] as the reference trajectory, and defined t[800] as the vector of time points along Ω[800] (e.g., a vector containing 0, 1, …, 800). Next, for every neural state along Ω[800], denoted r[800], we found the nearest neural state on the remaining trajectories, denoted (Figure 6b), and defined as the vector of time points when activity reached (Figure 6c). Finally, we quantified the distance between and Ω[800], denoted , using the vector connecting and r[800], and the speed of relative to Ω[800] () based on the values of relative to t[800] (see Online Methods).
DMFC population activity is governed by speed-dependent predictive dynamics
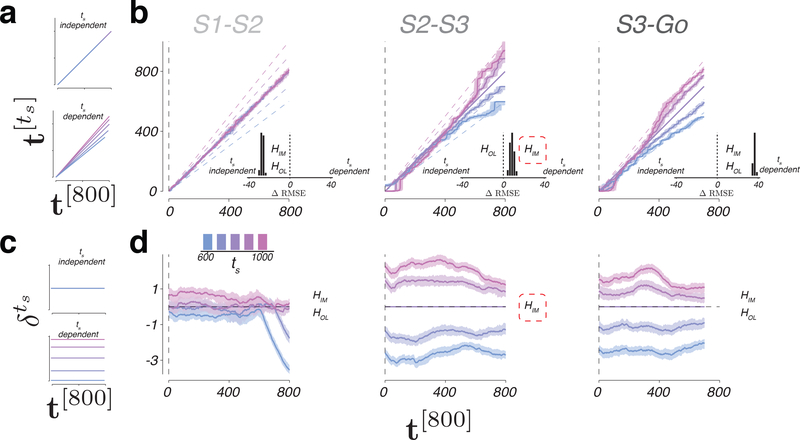
We first formulated the predictions of KiNeT for the open-loop and internal model hypotheses. For both hypotheses, the speed in the S1-S2 epoch should not depend on ts (Figure 7a, left top). Accordingly, in the first epoch, should be identical to t[800] irrespective of ts. However, the two hypotheses make different predictions for the S2-S3 epoch. According to the open-loop hypothesis, the computation in the S2-S3 epoch is similar to the S1-S2 epoch. Therefore, for the open-loop hypothesis, should remain identical to t[800] irrespective of ts (Figure 7a, upper). In contrast, the internal model hypothesis predicts that activity in the S2-S3 epoch is predictive and, therefore, the speed exhibits an inverse relationship to ts (Figure 7a, lower). Therefore, should increase faster than t[800] for slower trajectories and vice versa. In the S3-Go epoch, both hypotheses predict that the speed would depend on ts, and therefore the relationship between and t[800] should depend on ts (Figure 7a, lower). Therefore, the key prediction that differentiates between the two hypotheses is whether or not activity in the S2-S3 epoch is predictive, or equivalently, whether the relationship between and t[800] depends on ts.
Figure 7. Relative speed and distance between neural trajectories during 1-2-3-Go.
a) ts-independent (top) or ts-dependent (bottom) representation of speed. b) Speed of each neural trajectory, , compared to the speed of the reference trajectory, Ω[800]. Colored lines show the progression of elapsed time on as a function of elapsed time on Ω[800] (t[800]) for different ts. Shadings indicate median +/− 95% confidence intervals computed from n = 100 bootstrap resamples. Unity line corresponds to no difference in speed. Dashed lines represent the expected relationship between and t[800] under the internal model hypothesis for an observer with perfect knowledge of ts. Insets: difference in RMSE under the assumption of ts-independent speed (left of zero) versus ts-dependent speed (right of zero). In S1-S2 epoch, both the open-loop and internal hypotheses (HOL and HIM) predict ts-independent speed; ts-dependent predictions were based on fits of EKF to behavior. In S2-S3 epoch, HOL predicts ts-independent speed, and HIM predicts ts-dependent speed; the data supports HIM (red dashed line). In S2-S3 epoch, both hypotheses predict ts-dependent speed. c) ts-independent (top) or ts-dependent (bottom) representation of the speed command. d) Distance between nearby states on and Ω[800] as a function of time. Horizontal dashed line corresponds to overlapping trajectories. The data supports HIM (red dashed line). Shadings indicate median +/− 95% confidence intervals computed from n = 100 bootstrap resamples. See also Supplementary Figures 10, 11, and 12.
KiNeT provided clear evidence in support of the internal model hypothesis. In the S1-S2 epoch, did not exhibit any systematic relationship to ts; i.e., the slope of as a function of t[800] was not statistically different from one (Figure 7b left; two tailed t-test; ts = 600: t(99) = 0.1225, p = 0.9028; ts = 700: t(99) = −0.3136, p = 0.7545; ts = 900: t(99) = −0.5884, p = 0.5576; ts = 1000: t(99) = 0.7642, p = 0.4466; Figure 7a left). Accordingly, in the S1-S2 epoch was better explained by ts-independent model than a ts-dependent model (Figure 7b, left inset; one-tailed t-test, t(99) = −22.4067, p < 0.001). In the S2-S3 epoch, values of increased faster than values of t[800] for longer ts (Figure 7b middle; one-tailed t-test; ts = 900: t(99) = 5.3862, p < 0.001; ts = 1000: t(99) = 9.1030, p < 0.001) and slower for shorter ts (one-tailed t-test; ts = 600: t(99) = −14.4431, p < 0.001; ts = 700: t(99) = −9.6668, p < 0.001; Figure 7b, middle). This indicates that in the S2-S3 epoch was ordered according to ts, consistent with the internal model hypothesis (Figure 7b, middle inset; one tailed t-test, t(99) = 4.1760, p < 0.001). The organization of with respect to t[800] in the S3-Go epoch was also consistent with adjustments of speed depending on ts (Figure 7b right; one tailed t-test, t(99) = 35.2322, p < 0.001). These results are consistent with DMFC responses reflecting a simulated and an actual motor plan in the S2-S3 and S3-Go epochs, respectively.
DMFC population activity reflects an interval-dependent speed command
The open-loop and the internal model hypothesis also make distinct predictions regarding the representation of a ts-dependent speed command. The open-loop hypothesis predicts a ts-independent speed command in the first two epochs (Figure 7c, top) and a ts-dependent signal in the third epoch (Figure 7c, bottom). The internal model hypothesis, in contrast, predicts a ts-dependent signal in both the second and third epochs (Figure 7c, bottom). Qualitative examination of supported the internal model hypothesis: neural states evolved along parallel trajectories in both the S2-S3 and S3-Go epochs and were systematically organized in neural state space in accordance with ts (Figure 6a). To examine this organization quantitatively, we measured the distance between each and Ω[800] as a function of time after using KiNeT (see Online Methods; Figure 6d).
In the first epoch, trajectories were highly overlapping and there was no significant distance between Ω[700] and Ω[900] (Figure 7d, left; one tailed t-test; t(99) = 0.4796, p = 0.6325), the two test trajectories. In contrast, in the S2-S3 (Figure 7d, middle) and S3-Go epochs (Figure 7d, right), test trajectories were systematically separated according to ts (one tailed t-test; S2-S3: t(99) = 8.2495, p < 0.001; S3-Go: t(99) = 6.2927, p < 0.001; see Online Methods). Moreover, the magnitude of was nearly constant between consecutive flashes as evidenced by the slope of the regression line relating to t[800], which was less than 0.1% of the offset in both epochs. These observations indicate that population responses in DMFC harbor a representation of ts throughout the S2-S3 and S3-Go epochs, consistent with the internal model hypothesis.
We performed a number of additional analyses to verify the robustness of our results. For example, the preceding results were based on the application of KiNeT to the first 10 PCs derived from activity within each epoch, which captured more than 90% of variance (Supplementary Figures 8 and 9). However, the same results were found when we applied KiNeT to PCs of activity across the three epochs (Supplementary Figure 10). Moreover, all results were consistent across the two animals (Supplementary Figure 11). We also tested KiNeT on responses aligned to the time of saccade to ensure that results in the S3-Go epoch were not due to an averaging of firing rates across trials of different durations (due to different saccade times; Supplementary Figure 12). Finally, we note that the systematic modulations of the relative distance and speed with ts in the S2-S3 and S3-Go epochs cannot be a simple artifact of applying KiNeT to complex spatiotemporal responses as we found no evidence for ts-dependent speed in the S1-S2 epoch despite the presence of complex non-monotonic response profiles.
Linking behaviorally-relevant computations to internal models
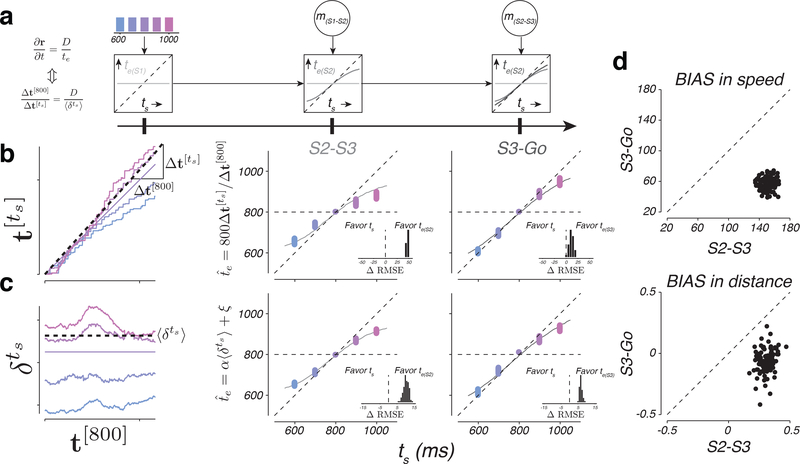
Results of KiNeT provided evidence for the presence of a speed command driving a simulated motor plan during the S2-S3 epoch, and an actual motor plan in the S3-Go epoch. However, according to the internal model hypothesis, the speed command and the simulation have to be guided by an estimator. Therefore, we predicted that and should reflect the animal’s internal estimate of ts, and not the experimentally controlled ts. To test this prediction, we used the fits of EKF to the behavior to infer the animal’s internal estimates immediately after S1, S2, and S3 – te(S1), te(S2), and te(S3). According to EKF, te(S1) is equal to the mean of the prior (Figure 8a, left), te(S2) follows ts but is biased toward the prior mean (Figure 8a, center), and te(S3) follows ts with less bias than te(S2) (Figure 8a, right).
Figure 8. Speed and distance between neural trajectories reflect animals’ internal estimates.
a) Interval estimates derived from EKF model (same format as in Figure 1g). b) Interval estimate inferred from the speed of neural trajectories as a function of ts. Left: the procedure for inferring for each ts. The colored traces show as a function of t[800] for a random draw from the bootstrap distribution (see Online Methods). To infer for each ts, we measured the slope of the regression line relating to and then scaled the slope by the duration of the reference interval (800 ms). The dotted line is the regression slope for ts=900 ms. Middle and right: as a function of ts inferred from the speed of neural trajectories in the S2-S3 and S3-Go epochs. The colored dots show multiple estimates of derived from bootstrapping (n=100). The solid curves show interval estimates derived from EKF model fits (te(S2) in the middle panel and te(S3) in the right panel). Unity indicates perfect estimates of ts and the horizontal line represents the mean of the prior. Insets: difference in RMSE between models that assume that the speed of neural trajectories reflects ts versus te(S2) (middle) or te(S3) (right). Positive values indicate neural data more accurately captured by EKF. c) The value of inferred from the distance between neural trajectories as a function of ts. Left: the procedure for inferring for each ts. The colored traces show as a function of time for a random draw from the bootstrap distribution (see Online Methods). We inferred for each ts using a linear transformation of the average distance . The dotted line shows the average distance, , for ts=900 ms. Middle and right: as a function of ts inferred from the distances between neural trajectories in the S2-S3 and S3-Go epochs (same format as panel b). Insets: differences in RMSE between models assuming the distances of neural trajectories reflect ts versus te(S2) (middle) or te(S3) (right). d) Comparison of the degree of BIAS in speed (top) and distance (bottom) during the S2-S3 and S3-Go epochs. Dashed lines are unity. See also Supplementary Figure 13.
We leveraged these prior dependent biases to ask whether the speed of different neural trajectories was ordered according to ts (no bias) or te(SX) (biased) as prescribed by EKF. Since speed is inversely proportional to time, we used KiNeT to restate this question as follows: does more accurately correspond to ts or te? We converted to an inferred estimate, , by multiplying the slope of the regression line relating to t[800] (; Figure 8b, left) by the reference interval of 800 ms (see Methods). Clearly, exhibited the biases observed in te(S2) and te(S3) during S2-S3 and S3-Go epochs, respectively (Figure 8b, center and right panels). This relationship was not explained by the monotonic relationship between te with ts, as the organization of neutrally-derived was far better predicted by the animal’s estimates than ts (Figure 8b, insets, see Online Methods).
We also asked whether the ts-dependent position of neural trajectories that provide a correlate of the speed command reflected te more accurately than ts. To test this, we asked whether average distances between neural trajectories within each epoch were more accurately captured by the experimentally-controlled ts or by the behaviorally-inferred te in that epoch (see Methods). Again, we found that the distances between trajectories were more similar to te(S2) and te(S3) than ts (Figure 8c, center and right). These observations suggest the neural correlates of both the speed command and the predictive dynamics associated with the simulated motor plan correspond to the animal’s estimates (see Supplementary Figure 13 for individual animals). In other words, changes in neural activity after each flash reflect the estimation process prescribed by EKF.
A final prediction of the internal model hypothesis is that the speed and distance of neural trajectories ought to reflect the integration of each new measurement. This integration was clearly evident during the transition from S1-S2 to S2-S3 epoch: speeds and distances were independent of ts before S2, and were systematically organized according to ts after S2. To assess whether a similar integration was evident during the transition from S2-S3 to S3-Go epoch, we returned to the predictions of the EKF model (Figure 8a). According to the model, both te(S2) and te(S3) exhibit a systematic bias towards the mean of the prior distribution, but the overall bias is smaller in the S3-Go epoch (Figure 8a, right) 12. To examine whether this pattern was present in neural trajectories, we compared the bias in both the speeds and distances of neural trajectories in the S2-S3 and S3-Go epochs (see Online Methods). The analysis of speeds provided clear evidence that biases were larger during the S2-S3 epoch than during the S3-Go epoch (Figure 8d, top). We also measured the degree of bias in the distance between neural trajectories. Because neural trajectories in the S2-S3 and S3-Go epochs were analyzed using PCs derived from activity in their respective epochs, a direct comparison of the distances was not warranted. Therefore, we computed the bias based on relative distances within each epoch (see online Methods). Again, results indicated that the degree of bias was larger during the S2-S3 epoch than the S3-Go epoch (Figure 8d, bottom). These observations validated our hypothesis that DMFC responses reflected animal’s estimate in accordance with sequential updating after both S2 and S3 flashes.
Discussion
Our results demonstrate that internal models can be used to understand the algorithm the brain uses to control internally generated cortical activity patterns in the absence of overt movements. This is an important finding as it indicates that the internal model hypothesis, advanced by decades of research on sensorimotor function 5,22–26 and motor control 4,10,27–29, may also be used to understand how the brain controls mental states that are not observable.
A prominent result from our analysis of individual neurons was the heterogeneity of responses. A few neurons exhibited characteristics consistent with a speed command (i.e., control signal) and predictive dynamics (i.e., simulation), but the responses of most neurons reflected a mixture of both. This motivated a complementary analysis across the population, which led to three important findings. First, the distance between neural trajectories provided evidence for the presence of a persistent speed command consistent with the output of a controller. Second, the speed with which trajectories evolved through time revealed a predictive process consistent with the output of a simulated motor plan in the S2-S3 epoch, and an ongoing motor plan in the S3-Go epoch. Third, the speed information inferred from neural activity reflected the sequential updating consistent with the output of an underlying estimator.
Although the activity in DMFC was consistent with the computations associated with the controller, simulator and estimator, we do not know whether and how DMFC might implement these computations. We previously established that inactivation of the DMFC interferes with time interval production 8. Given that active and simulated motor plan rely on similar dynamics, it is possible that DMFC also contributes to both 30. However, the tight interaction between DMFC and other cortical and subcortical areas 31–35, suggests that other brain areas are also involved.
Our previous work on a simple time production task suggests that the speed command in DMFC may originate in thalamus 8. It is therefore possible that the speed command in the 1-2-3-Go task is also driven by a tonic thalamic input. The source of the speed command in the thalamus has not been identified. One possibility is the dentate nucleus of the cerebellum that trans-thalamically drives DMFC 36–38, and is thought to support interval timing in non-motor tasks 39–42. This interpretation is consistent with experimental and modeling work suggesting a role for ascending cerebellar signals in driving cortical dynamics 43. However, if the speed command is indeed provided by the cerebellum, then performing sequential updating as in the 1-2-3-Go task will have to engage the entire cortico-cerebellar loop so that the command can be updated in the cerebellum depending on the state of the simulated motor plan in cortical circuits.
More generally, since the generation of simulated and actual motor plans involves recurrent interactions among neurons, making definite statements about the nature of the control signal is difficult. Dynamical system can generate task-dependent dynamics either through adjustment of initial conditions or via direct inputs 7,44. In our work, we interpreted the presence of the persistent ts-dependent signals across the population as a persistent control signal. However, it is also possible that this persistent signal results from setting the initial conditions of the system. Consistent with this interpretation, trajectories associated with the S1-S2 and S2-S3 epochs terminated at different states, providing a potential substrate for using initial conditions as the control signal. If so, we would need to reinterpret the action of the control signal as being mediated through initial conditions. Exerting control through initial conditions instead of a tonic input does not change our conclusions with respect to understanding the control of dynamics in terms of internal models but points to a different underlying implementation.
We also do not know how DMFC alone or through interactions with other brain areas implements an estimator. The function of the estimator is to use the state of the simulated motor plan at the time of feedback to update the speed command. Since the establishment of a suitable estimator demands learning and optimization 5,10,45, a likely substrate for establishing an estimator could be synaptic learning of the recurrent connections in various cortical areas including DMFC. The key requirement for estimation is to have a network that can adjust its responses to inputs (e.g., flashes) in a state-dependent manner (i.e., the state of the simulated plan). Recent theoretical work suggests that this computation is well within the capacity of recurrent neural networks 7,46,47,9, and can be mediated through suitable connectivity 48. If so, alternations of neural states right before the flash using precise perturbation techniques should lead to specific errors in updating.
Finally, our findings regarding the implementation of a simulated motor plan at the level of cortical population activity highlights the possibility of a novel mechanism for performing predictive computations. Theoretical considerations have long noted the computational advantages of predictive information processing 49, and computational models have hypothesized a number of possible mechanisms for its implementation in cortical microcircuits 50. Our work provides evidence for a novel mechanism for generating top down predictions afforded by population-level latent dynamics of cortical networks.
Online Methods
Methods
Experiments involved in-vivo extracellular recording of neural activity from the dorsomedial frontal cortex (DMFC) of two awake, behaving male monkeys (Macaca mulatta) trained to perform the 1-2-3-Go behavioral task. During experimental sessions, monkeys were seated comfortably in a dark and quiet room. Stimuli and behavioral contingencies were controlled using MWorks (https://mworks.github.io/). Visual stimuli were presented on a frontoparallel 23-inch Acer H236HL monitor at a resolution of 1920 × 1080 at a refresh rate of 60 Hz. Eye positions were tracked with an infrared camera (Eyelink 1000; SR Research Ltd, Ontario, Canada) and sampled at 1 kHz. All experimental procedures conformed to the guidelines of the National Institutes of Health and were approved by the Committee of Animal Care at Massachusetts Institute of Technology. Randomization and blinding were not applicable at the level of subjects, as animals were not assigned to experimental groups. However, trials and conditions for each animal were randomized. When warranted, data analyses were subjected to blinding using cross-validation.
Task and stimuli
Each trial began with the presentation of a central fixation point (FP; circular, red, 0.5 deg diameter). Following fixation (with delay selected from a uniform hazard, minimum = 100 ms, mean = 400 ms), a saccadic target (circular, white, 1.5 deg diameter) was presented 10 deg to the left or right of FP. Afterwards (uniform hazard, minimum = 500 ms, mean = 1000 ms), three flashed visual stimuli (S1, S2 and S3) were presented. Each flash was presented for 100 ms as an annulus around FP (white, inside diameter = 2.5 deg, outer diameter = 3 deg). The time between consecutive flashes was fixed within a trial and was drawn at random from a discrete uniform prior distribution across trials (Figure 1c; 5 values, minimum = 600 ms, maximum = 1000 ms). We refer to the time between flashes as the sample interval, ts. Monkeys had to maintain fixation until after S3 within an electronic window around FP (7 deg diameter). After S3, monkeys had to proactively initiate a saccade to the saccadic target to produce an interval equal to ts. The produced interval, tp, was measured as the time between S3 and when animal’s eye entered an electronic window (7 deg diameter) around the saccadic target. Early fixation breaks (before 200 ms post S3) or extremely long production times (tp > ts + 1000 ms) were considered ‘aborted trials’ and were discarded. We additionally removed ‘outlier’ trials whereby the value of tp was more than three standard deviations from the mean tp for a given ts. Animals received trial-by-trial visual feedback on the magnitude and sign of error by a visual stimulus (circular, 0.5 deg diameter) presented immediately after the saccade along the line connecting FP to the saccadic target. The magnitude of the relative error (|tp-ts|/ts) was represented by the distance of the feedback stimulus to the saccadic target, and positive (negative) errors were associated with locations farther away (closer to) the FP. When the magnitude of the relative error was smaller than a threshold, both the saccadic target and the feedback stimulus turned green and the animal received juice reward. The magnitude of the reward decreased linearly with the magnitude of the relative error (Figure 1d). If the relative error was larger than the threshold, the target stimulus and analog feedback remained white and no reward was delivered. Performance was evaluated according to the relative error (as opposed to absolute error) to accommodate the scalar variability of time interval production 11. Reward threshold was initialized at 0.15 at the start of every session and was adjusted adaptively and on a trial-by-trial basis in one-up one-down fashion with a fixed increment/decrement of 0.001 for unrewarded/rewarded trials, respectively. With this scheme, animals received reward on approximately 50% of the trials.
We quantified the animal’s overall bias as the root-mean square of bias for each ts:
| (1) |
where is the mean tp across trials of the i-th sample interval .
Bayesian integration model of behavior
We developed a Bayesian observer model for the 1-2-3-Go task based on a model that was used previously to account for behavior in a timing task with a single measurement interval 12,14,51. The model computed the posterior of ts from the prior, p(ts), and the likelihood function, λ(m|ts), from two independent measurements mS1-S2 and mS2-S3, and used the mean of the posterior (shown with angle brackets) as the final estimate, eS3-Go:
| (2) |
| (3) |
Where represents the Bayes–least–squares estimator of ts. The likelihood function for each measurement was modeled based on the assumption that the measurement is subject to zero-mean Gaussian noise whose standard deviation scales with ts according the Weber fraction wm (Supplementary Figure 1a).
| (4) |
Finally, we assumed that the production interval, tp, is subject to zero-mean Gaussian noise whose standard deviation scales with eS3-Go according the Weber fraction wp (Supplementary Figure 1a). To fit the model to animals’ behavior, we augmented the model by an offset term, b, to account for stimulus- and prior-independent biases observed in responses as follows:
| (5) |
Extended Kalman filter (EKF) model of interval estimation
Following our previous efforts to model human behavior in a similar task, we developed an updating model of interval estimation that approximates the fully Bayesian estimate 12. The model implements a sequential updating scheme akin to the Kalman filter 52. According to EKF, at S1, the estimated duration is the mean of the prior distribution:
| (6) |
At the time of S2, the observer combines the measurement of the S1-S2 interval, mS1-S2, with eS1-S2 to generate a new estimate, eS2-S3:
| (7) |
with kS2 = 1. f* is a nonlinear function based on the Bayesian model after one measurement, . At the time of S3, the model combines the new measurement, mS2-S3 with eS2-S3 to generate a final estimate of ts
| (8) |
with kS3 = 0.5. This final estimate is used to guide production, with noise in the production phase described by equation (5). See also Supplementary Figure 1.
Model fitting
We used a maximum likelihood procedure to fit the Bayesian and EKF models to the data. Assuming tp are conditionally independent across trials, the log likelihood of model parameters can be formulated as:
| (9) |
where the superscripts denote trial number. We found the parameters that maximize equation (9) with a constrained optimization function.
We used the fitted model to additionally infer the expected value of the animal’s estimate after each of the S1, S2, and S3 flashes, which we denote by te(S1), te(S2), and te(S3), respectively. Because the only information available to the animal after S1 is the prior distribution, p(ts), te(S1) was set to the prior mean. We derived te(S2) and te(S3) by averaging the EKF estimates (eS2-S3 and eS3-Go, respectively) across measurements for each ts.
Cue conflict trials
To test whether animals integrated both measurements, 33% of the trials with ts = 800 ms were modified such that either S1-S2 or S2-S3 were made either 50 ms longer or shorter. We verified that animals used both measurements in two ways. First, we tested whether tp was biased in direction expected under the integration hypothesis, and whether the magnitude of bias depended on which epoch was jittered. Second, we asked which of three models best explained the behavior in the cue conflict trials: (1) monkeys used both mS1-S2 and mS2-S3 to guide production, (2) monkeys used mS1-S2 only, or (3) monkeys used mS2-S3 only. All three models had the same parameters (wm, wp, b). We used a maximum-likelihood procedure to fit the models to the data without conflict and compared the likelihood of the conflict data under each model.
Analysis of DMFC data
Electrophysiological recordings were made by one or two 16- or 24- channel laminar V-probes (Plexon Inc.; Dallas Texas, USA) through craniotomies located above the dorsomedial frontal cortex (DMFC). In total, we analyzed neural activity from 16 recording sessions, 12 from monkey B and 4 from monkey G. We targeted the region of interest using the following procedure. We started by gathering anatomical information about the regions of DMFC associated with the supplementary eye field (SEF) 31,53–55 and presupplementary area (preSMA) 55,56 using previous studies in rhesus macaques. We compiled information about reported stereotactic coordinates, histological plots and MRI scans to identify the general region of interest. We then sampled DMFC starting from the center of the identified region and move outward a quasi-systematic fashion looking for regions with strong modulation during any epoch of the task. Neural activity in monkey B was recorded from between 0.5 mm to 2.9 mm lateral of the midline and 2.2 mm posterior to 8.1 mm anterior of the genu of the arcuate sulcus. Neural activity in monkey G was recorded from between 0.9 mm to 4.6 mm lateral of the midline and 1.8 mm to 9.3 mm anterior of the genu of the arcuate sulcus. Because the targeted recording sites were defined anatomically, we conservatively refer to the recorded region as DMFC. This anatomically defined region potentially comprised of the functionally defined areas referred to as SEF, preSMA, and dorsal SMA (i.e., outside the medial bank). Data was stored using a Blackrock Cerebus Neural Signal Processor (Blackrock Microsystems; Salt Lake City, USA) and analyzed offline using custom code in MATLAB (R2017a, The MathWorks Inc., Natick, MA, 2000).
Single- and multi-unit activity was extracted from band-pass filtered voltage traces by an initial threshold crossing followed by spike sorting. We used the following procedure for spike sorting: 1) We used a Gaussian mixture model to cluster waveforms on each channel that crossed a threshold. Let us assume that the data was best fit by a Gaussian mixture model with N clusters. 2) We used the fitted model to generate surrogate samples from each of the N clusters. 3) We used maximum likelihood to classify the surrogate samples (i.e., which cluster were they sampled from). 4) For each cluster, we used the classification results to quantify the probability of assigning surrogate samples from other clusters as originating to the current cluster, which we refer to as probability of false alarm, PFA. Note that the ground truth for the surrogate samples was known. 5) We only accepted units as well-isolated if surrogate samples from the corresponding cluster were associated with PFA < 0.05.
The spiking data for each neuron was first smoothed over time using a 150 ms boxcar, after alignment to different events in the task (i.e., S1, S2, S3 and Go). Trial by trial data was then conditioned on ts to measure PSTHs and perform PCA. We assigned all conflict trials to the ts = 800 ms condition for these analyses. Population analyses were based on all 181 units collected across the 16 individual recording sessions, after excluding units with poor signal to noise or that were unmodulated by the task. Single unit analysis was based on 115 well isolated units. No statistical methods were used to pre-determine sample size but our sample size are similar to those reported in previous publications 7,15,16. Supplementary analysis was performed on units from each monkey separately.
To characterize the firing rate profiles over time, we fit a polynomial of order n to the mean firing rates across ts calculated using a random half of the trials without replacement. We assessed the goodness of fit by measuring the correlation coefficient between the expected firing rate, based on the polynomial fit, and the mean firing rate calculated from the left-out trials. We also assessed polynomial fits to temporally scaled firing rates using the same procedure.
To assess the degree of stationarity in the encoding of ts by individual neurons we first assigned the trial-by-trial spike counts into two groups at random (without replacement). For each group, we calculated the firing rate as a function of time and ts, r1(t,ts) and r2(t,ts). We calculated the correlation coefficient between the firing rates at two different time points, r1(t’,ts) and r2(t”,ts), across ts. We performed this analysis for each combination of times, t’ and t”, with t’ and t” between 0 and 600 ms relative to the onset of the epoch of interest. We used the resulting matrix of correlation coefficients to assess the degree of similarity in firing rates as a function of ts at different time points. This procedure enables us to measure similarity without making assumptions about the exact nature of encoding of ts.
Linear-Nonlinear-Poisson (LNP) model
Neural encoding of ts by individual neurons was also assessed by fitting an LNP model to spike count data at t = 0, 100, 200, 300, 400 or 500 ms following each flash (S1, S2 and S3). We modeled spike count data as a nonhomogeneous Poisson process with a ts-dependent rate function as follows:
| (10) |
With β(t) parameterizing the sensitivity of the neuron to ts at time t. The probability of a given spike count on a particular trial is:
| (11) |
To fit the parameters of the model and assess goodness of fit, we split the data into training and validation sets, designating every other trial as training data. We fit the model by maximizing the log likelihood of model parameters given ts and the observed spike count, rni(t), of the nth neuron across i=1,..,M training trials at time t:
| (12) |
We assessed the significance of sensitivity to ts by comparing the LNP model with the ts-dependent rate function (above) to another model with a ts-independent rate function:
| (13) |
We compared the models using Bayesian information criterion (BIC) and took BIC>10 in favor of the ts-dependent model as evidence for significant sensitivity to ts.
Decoding ts using the LNP model
We used the LNP model fits to the training data to compute the maximum likelihood estimate of ts, , on validation trial i, assuming the firing of the N neurons is conditionally independent:
| (14) |
| (15) |
We assessed decoding performance by calculating the correlation coefficient between the actual and decoded values of ts. We also considered the performance of a decoder that assumes the representation of ts is stationary following each flash. To do so, we held β(t) at the value fit at the time of S1, S2, or S3 for decoding ts during the S1-S2, S2-S3, and S3-Go epochs, respectively.
Principal component analysis (PCA)
To perform PCA, we averaged spike times by a 150 ms boxcar filter and used the square root of spike counts to reduce the effect of Poisson noise on analyses 57. Data from each unit was then trial-averaged and z-scored by removing the mean and normalizing by the standard deviation calculated across time and conditions. Finally, z-scored data over time was arranged in a data matrix to perform PCA, with rows of the data matrix concatenating data across time and ts condition and columns corresponded to units collected across the 16 individual recording sessions. To visualize activity patterns from S1 to Go (Figure 6a) within a single coordinate system, we applied PCA to neural activity from S1 to Go. We also performed PCA on activity within each epoch.
Kinematic analysis of neural trajectories (KiNeT)
We developed an analysis technique to infer the relative position and speed of multiple low-dimensional neural trajectories based on the organization of sets of points along those trajectories. KiNeT can be broken down to the following 6 steps: 1) Choose a subspace to perform the analysis. In our case, we focused on the projection of the neural activity onto the first 10 PCs, which captured more than 93% of variance in the data. 2) Designate one of the trajectories as a reference trajectory. In our case, we designated the median ts (800 ms) as the reference. 3) Sample the reference trajectory at a given time resolution and compute a vector of associated time points. In our case, we used a time resolution of 1 ms and denoted the resulting vector of time points by t[800]. 4) For each element of t[800], find the corresponding neural state vector on Ω[800], r[800]. The set of state vectors was arranged in a matrix, R[800], with each column associated with a time point in t[800]. 5) For each neural state in R[800], find the nearest point (minimum Euclidean distance) on all the other (non-reference) trajectories. This provides a corresponding matrix of states on each non-reference trajectory, which we denoted by (the superscript is a reference to the trajectory associated with ts). 6) Find the time when the neural state reaches each state in . This furnishes a corresponding set of times, which we denoted by . The four arrays, t[800], R[800], , and can then be used to evaluate the relative geometry and speed of the neural trajectories.
We estimated the relative position of neural trajectories by measuring the distance between each and the corresponding reference state r[800] along the direction defined by the local vector connecting r[1000] to r[600]. Mathematically, this is equivalent to finding the projection of the difference vector onto the base vector, d = r[1000]−r[600], according to . Repeating the process for each state in results in a scalar quantity for each point in t[800]. The result of this analysis was robust to the choice of the base vector so long as it captured the dimension along which trajectories differed (e.g., the base vector cannot be orthogonal to the difference vectors).
Confidence intervals for the various hypotheses tested by the KiNeT analysis were computed by resampling the data 100 times. To assess the significance of our distance metric, we compared the bootstrap distribution of for ts = 700 and 900 ms, the two values of ts that were held out of the distance metric. Significance was computed by a t-test.
Comparison of KiNeT results to behavior
The time it takes for the state variable to reach a point in is inversely proportional to the speed with which it changes with time. Using this relationship and denoting the speed of the reference and non-reference trajectories by V[800] and , we approximated the relative speed, by ; i.e., the slope of the regression line relating to t[800] that passes through the origin.
We also asked whether used by the simulator was governed by the experimentally controlled ts or the EKF estimate, te, inferred from the animal’s behavior (Figure 8b). These two possibilities can be written in terms of the following two hypotheses, respectively:
| (16) |
| (17) |
Rearranging, and exploiting the inverse relationship between speed and time, we can write:
| (18) |
| (19) |
We evaluated these hypotheses by comparing the RMSE under the two hypotheses.
We asked whether relative position of neural trajectories was organized in neural state space according to the experimentally controlled ts or the EKF estimate, te, inferred from the animal’s behavior (Figure 8c). Using a linear model, we asked whether the relative position was more directly associated with ts or te:
| (20) |
| (21) |
Where is the average of over all t[800]. We evaluated these hypotheses by fitting the parameters α and ξ under the two hypotheses and compared the goodness of fit using RMSE.
To determine if the second interval was integrated into the speed of the population response, we compared the overall bias in estimated from speeds during S2-S3 and S3-Go. We measured the overall bias as:
| (22) |
with i indexing the sample interval.
We also used the average distance between trajectories to test whether animals integrated the second measurement. The sigmoidal bias observed in behavior predicts that the inter-trajectory distances should exhibit a compressive nonlinearity; i.e. distances between consecutive trajectories should become smaller for ts values that are farther away from the middle values of 800 ms. We inferred the bias in each epoch from the average inter-trajectory distances using the following formulation:
| (23) |
In this formulation, positive values reflect the presence of the aforementioned compressive nonlinearity. Since the integration of the second measurement should reduce this nonlinearity, we asked whether the BIAS computed based on Equation 23 was smaller in the S3-Go epoch relative to the S2-S3 epoch.
Statistics
The significance of the differences in slope from zero or unity of the linear model fit to animal behavior was assessed by a two tailed t-test (Figure 4e). We tested the increase in variance with tp by resampling the data 100 times with replacement to generate an estimate of the variance in each associated with each ts. We then fit a linear model to the data and tested the significance of the difference from zero with a two tailed t-test. The significance of the BAIS in behavior was determined by resampling to generate 100 estimates of the statistic followed by a two tailed t-test. Determination of the significance of differences in responses to different conflict conditions was determined by one tailed t-tests (Figure 2f). Significance of the difference in the degree of scaling of individual neuron responses between task epochs was assessed with one tailed Mann-Whitney-Wilcoxon test for equal medians (Figure 4d). For population analyses (Figures 7 and 8), we tested statistical significance by resampling trials to generate 100 bootstrap estimates of the statistic of interest. A t statistic, estimated from the mean and standard deviation of the bootstrap distribution, was then used to perform either one or two tailed sample tests depending the assumptions associated with the test of interest. For all t-tests, assumptions of normality were not formally tested.
Supplementary Material
Acknowledgements
M.J. is supported by NIH (NINDS-NS078127), the Sloan Foundation, the Klingenstein Foundation, the Simons Foundation, the McKnight Foundation, the Center for Sensorimotor Neural Engineering, and the McGovern Institute.
Footnotes
Competing financial interests statement
The authors declare no conflicting interests.
Reporting Summary
Further information on research design and analyses is available in the Life Sciences Reporting Summary.
Data availability statement
The data that support the findings of this study are available at the following URL: TBD
Code availability statement
Standalone code including custom analyses used for generating the plots in the paper are provided at the following URL: TBD
References
- 1.Wolpert DM & Ghahramani Z Computational principles of movement neuroscience. Nat. Neurosci 3 Suppl, 1212–1217 (2000). [DOI] [PubMed] [Google Scholar]
- 2.Todorov E Optimality principles in sensorimotor control. Nat. Neurosci 7, 907–915 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Scott SH Optimal feedback control and the neural basis of volitional motor control. Nat. Rev. Neurosci 5, 532–546 (2004). [DOI] [PubMed] [Google Scholar]
- 4.Shadmehr R & Krakauer JW A computational neuroanatomy for motor control. Exp. Brain Res 185, 359–381 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wolpert DM, Ghahramani Z & Jordan MI An internal model for sensorimotor integration. Science 269, 1880–1882 (1995). [DOI] [PubMed] [Google Scholar]
- 6.Ito M Opinion - Control of mental activities by internal models in the cerebellum. Nat. Rev. Neurosci 9, 304–313 (2008). [DOI] [PubMed] [Google Scholar]
- 7.Remington ED, Narain D, Hosseini EA & Jazayeri M Flexible Sensorimotor Computations through Rapid Reconfiguration of Cortical Dynamics. Neuron 98, 1005–1019.e5 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang J, Narain D, Hosseini EA & Jazayeri M Flexible timing by temporal scaling of cortical responses. Nat. Neurosci 21, 102–110 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sohn H*, Narain D*, Meirhaeghe N*, Jazayeri M (2019). Bayesian computation through cortical latent dynamics. Neuron pii: S0896 6273(19)305628. doi: 10.1016/j.neuron.2019.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shadmehr R & Mussa-Ivaldi FA Adaptive representation of dynamics during learning of a motor task. J. Neurosci 14, 3208–3224 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gallistel CR & Gibbon J Time, rate, and conditioning. Psychol. Rev 107, 289–344 (2000). [DOI] [PubMed] [Google Scholar]
- 12.Egger SW & Jazayeri M A nonlinear updating algorithm captures suboptimal inference in the presence of signal-dependent noise. Sci. Rep 8, 12597 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Acerbi L, Wolpert DM & Vijayakumar S Internal representations of temporal statistics and feedback calibrate motor-sensory interval timing. PLoS Comput. Biol 8, e1002771 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jazayeri M & Shadlen MN A Neural Mechanism for Sensing and Reproducing a Time Interval. Curr. Biol 25, 2599–2609 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kurata K & Wise SP Premotor and supplementary motor cortex in rhesus monkeys: neuronal activity during externally- and internally-instructed motor tasks. Exp. Brain Res 72, 237–248 (1988). [DOI] [PubMed] [Google Scholar]
- 16.Mita A, Mushiake H, Shima K, Matsuzaka Y & Tanji J Interval time coding by neurons in the presupplementary and supplementary motor areas. Nat. Neurosci 12, 502–507 (2009). [DOI] [PubMed] [Google Scholar]
- 17.Kunimatsu J & Tanaka M Alteration of the timing of self-initiated but not reactive saccades by electrical stimulation in the supplementary eye field. Eur. J. Neurosci 36, 3258–3268 (2012). [DOI] [PubMed] [Google Scholar]
- 18.Merchant H, Pérez O, Zarco W & Gámez J Interval tuning in the primate medial premotor cortex as a general timing mechanism. J. Neurosci 33, 9082–9096 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Merchant H, Zarco W, Pérez O, Prado L & Bartolo R Measuring time with different neural chronometers during a synchronization-continuation task. Proc. Natl. Acad. Sci. U. S. A 108, 19784–19789 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Murakami M, Vicente MI, Costa GM & Mainen ZF Neural antecedents of self-initiated actions in secondary motor cortex. Nat. Neurosci 17, 1574–1582 (2014). [DOI] [PubMed] [Google Scholar]
- 21.Merchant H & Averbeck BB The computational and neural basis of rhythmic timing in medial premotor cortex. J. Neurosci (2017). doi: 10.1523/JNEUROSCI.0367-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Franklin DW & Wolpert DM Computational mechanisms of sensorimotor control. Neuron 72, 425–442 (2011). [DOI] [PubMed] [Google Scholar]
- 23.Kawato M, Furukawa K & Suzuki R A hierarchical neural-network model for control and learning of voluntary movement. Biol. Cybern 57, 169–185 (1987). [DOI] [PubMed] [Google Scholar]
- 24.Angelaki DE, Shaikh AG, Green AM & Dickman JD Neurons compute internal models of the physical laws of motion. Nature 430, 560–564 (2004). [DOI] [PubMed] [Google Scholar]
- 25.Sommer MA & Wurtz RH Influence of the thalamus on spatial visual processing in frontal cortex. Nature 444, 374–377 (2006). [DOI] [PubMed] [Google Scholar]
- 26.Desmurget M & Grafton S Forward modeling allows feedback control for fast reaching movements. Trends Cogn. Sci 4, 423–431 (2000). [DOI] [PubMed] [Google Scholar]
- 27.Sabes PN The planning and control of reaching movements. Curr. Opin. Neurobiol 10, 740–746 (2000). [DOI] [PubMed] [Google Scholar]
- 28.Todorov E & Jordan MI Optimal feedback control as a theory of motor coordination. Nat. Neurosci 5, 1226–1235 (2002). [DOI] [PubMed] [Google Scholar]
- 29.Sommer MA & Wurtz RH A pathway in primate brain for internal monitoring of movements. Science 296, 1480–1482 (2002). [DOI] [PubMed] [Google Scholar]
- 30.Cadena-Valencia J, García-Garibay O, Merchant H, Jazayeri M & de Lafuente V Entrainment and maintenance of an internal metronome in supplementary motor area. Elife 7, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shook BL, Schlag-Rey M & Schlag J Primate supplementary eye field. II. Comparative aspects of connections with the thalamus, corpus striatum, and related forebrain nuclei. J. Comp. Neurol 307, 562–583 (1991). [DOI] [PubMed] [Google Scholar]
- 32.Shook BL, Schlag-Rey M & Schlag J Primate supplementary eye field: I. Comparative aspects of mesencephalic and pontine connections. J. Comp. Neurol 301, 618–642 (1990). [DOI] [PubMed] [Google Scholar]
- 33.Picard N & Strick PL Motor areas of the medial wall: a review of their location and functional activation. Cereb. Cortex 6, 342–353 (1996). [DOI] [PubMed] [Google Scholar]
- 34.Schall JD Visuomotor Areas of the Frontal Lobe in Extrastriate Cortex in Primates (eds. Rockland KS, Kaas JH & Peters A) 527–638 (Springer US, 1997). [Google Scholar]
- 35.Matelli M, Luppino G & Rizzolatti G Architecture of superior and mesial area 6 and the adjacent cingulate cortex in the macaque monkey. J. Comp. Neurol 311, 445–462 (1991). [DOI] [PubMed] [Google Scholar]
- 36.Asanuma C, Thach WR & Jones EG Anatomical evidence for segregated focal groupings of efferent cells and their terminal ramifications in the cerebellothalamic pathway of the monkey. Brain Res. 286, 267–297 (1983). [DOI] [PubMed] [Google Scholar]
- 37.Lynch JC, Hoover JE & Strick PL Input to the primate frontal eye field from the substantia nigra, superior colliculus, and dentate nucleus demonstrated by transneuronal transport. Exp. Brain Res 100, 181–186 (1994). [DOI] [PubMed] [Google Scholar]
- 38.Prevosto V, Graf W & Ugolini G Cerebellar Inputs to Intraparietal Cortex Areas LIP and MIP: Functional Frameworks for Adaptive Control of Eye Movements, Reaching, and Arm/Eye/Head Movement Coordination. Cereb. Cortex 20, 214–228 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kunimatsu J, Suzuki TW, Ohmae S & Tanaka M Different contributions of preparatory activity in the basal ganglia and cerebellum for self-timing. Elife 7, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ashmore RC & Sommer MA Delay activity of saccade-related neurons in the caudal dentate nucleus of the macaque cerebellum. J. Neurophysiol 109, 2129–2144 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ohmae S, Uematsu A & Tanaka M Temporally specific sensory signals for the detection of stimulus omission in the primate deep cerebellar nuclei. J. Neurosci 33, 15432–15441 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Narain D, Remington ED, Zeeuw CID & Jazayeri M A cerebellar mechanism for learning prior distributions of time intervals. Nat. Commun 9, 469 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gao Z et al. A cortico-cerebellar loop for motor planning. Nature (2018). doi: 10.1038/s41586-018-0633-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Remington ED, Egger SW, Narain D, Wang J & Jazayeri M A Dynamical Systems Perspective on Flexible Motor Timing. Trends Cogn. Sci 22, 938–952 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Berniker M & Kording K Estimating the sources of motor errors for adaptation and generalization. Nat. Neurosci 11, 1454–1461 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Mante V, Sussillo D, Shenoy KV & Newsome WT Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chaisangmongkon W, Swaminathan SK, Freedman DJ & Wang X-J Computing by Robust Transience: How the Fronto-Parietal Network Performs Sequential, Category-Based Decisions. Neuron 93, 1504–1517.e4 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Mastrogiuseppe F & Ostojic S Linking Connectivity, Dynamics, and Computations in Low-Rank Recurrent Neural Networks. Neuron 99, 609–623.e29 (2018). [DOI] [PubMed] [Google Scholar]
- 49.Friston K The free-energy principle: a unified brain theory? Nat. Rev. Neurosci 11, 127–138 (2010). [DOI] [PubMed] [Google Scholar]
- 50.Rao RPN & Ballard DH Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci 2, 79–87 (1999). [DOI] [PubMed] [Google Scholar]
Methods-only references
- 51.Jazayeri M & Shadlen MN Temporal context calibrates interval timing. Nat. Neurosci. 13, 1020–1026 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Stengel RF Optimal control and estimation. (Dover Publications Inc., 1994). [Google Scholar]
- 53.Schlag J & Schlag-Rey M Evidence for a supplementary eye field. J. Neurophysiol 57, 179–200 (1987). [DOI] [PubMed] [Google Scholar]
- 54.Huerta MF & Kaas JH Supplementary eye field as defined by intracortical microstimulation: connections in macaques. J. Comp. Neurol 293, 299–330 (1990). [DOI] [PubMed] [Google Scholar]
- 55.Fujii N, Mushiake H & Tanji J Distribution of eye- and arm-movement-related neuronal activity in the SEF and in the SMA and Pre-SMA of monkeys. J. Neurophysiol 87, 2158–2166 (2002). [DOI] [PubMed] [Google Scholar]
- 56.Matsuzaka Y, Aizawa H & Tanji J A Motor Area Rostral to the Supplementary Motor Area (Presupplementary Motor Area) in the Monkey: Neuronal Activity During a Learned Motor Task. Journal of Neurophysiology 68, 653–662 (1992). [DOI] [PubMed] [Google Scholar]
- 57.Yu BM et al. Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity. J. Neurophysiol 102, 614–635 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.