Reducing temperature errors in transcranial MR-guided focused ultrasound using a reduced-field-of-view sequence

Abstract

Purpose:

To reduce temperature errors due to water motion in transcranial MR-guided focused ultrasound (tcMRgFUS) ablation.

Theory and Methods:

In tcMRgFUS, water is circulated in the transducer bowl around the patient’s head for acoustic coupling and heat removal. The water moves during sonications that are monitored by MR thermometry, which causes it to alias into the brain and create temperature errors. To reduce these errors, a two-dimensional excitation pulse was implemented in a gradient-recalled echo thermometry sequence. The pulse suppresses water signal by selectively exciting the brain only, which reduces the imaging FOV. Improvements in temperature precision compared to the conventional full-FOV scan were evaluated in healthy subject scans outside the tcMRgFUS system, gel phantom scans in the system with heating, and in 2×-accelerated head phantom scans in the system without heating.

Results:

In vivo temperature precision (standard deviation of temperature errors) outside the tcMRgFUS system was improved 43% on average, due to the longer TR and TE of the reduced-FOV sequence. In the phantom heating experiments, the hot spot was less distorted in the reduced-FOV scans, and background temperature precision was improved 59% on average. In the accelerated head phantom temperature reconstructions, temperature precision was improved 89% using the reduced-FOV sequence.

Conclusion:

Reduced-FOV temperature imaging alleviates temperature errors due to water bath motion in tcMRgFUS, and enables accelerated temperature mapping with greater precision.

Introduction

Transcranial magnetic resonance imaging-guided focused ultrasound (tcMRgFUS) is a non-invasive ablative surgical technique which is FDA-approved for the treatment of essential tremor [1] and Parkinsonian tremor, and is under development for other applications including neuropathic pain, obsessive compulsive disorder, and brain tumors [2]. During tcMRgFUS treatment, ultrasound energy is delivered from a hemispherical transducer through the skull to a specific location within the brain, without affecting tissue outside the target. The primary role of MRI during MRgFUS treatments is to provide images with soft tissue contrast for targeting, and to provide real-time temperature measurements in the target tissue using the proton resonance frequency- (PRF-) shift method.

tcMRgFUS temperature imaging uses a real-time single-slice gradient echo 2DFT scan oriented in the axial, coronal, or sagittal planes, and temperature maps are calculated from the phase shift between a baseline (pre-heating) image and each image acquired during heating. However, the precision of the temperature maps is degraded in multiple ways by the presence of the water bath that couples acoustic energy from the transducer to the head, and is circulated between sonications to cool the skull. First, the water bath prevents the use of local imaging coils, so the body coil is used for transmit and receive, which provides relatively low image SNR and consequently low temperature precision [3]. Second, the water bath requires a large imaging FOV (usually 28 cm) to prevent it aliasing into the brain. Even with the large imaging FOV, the water bath’s motion within an image acquisition (3.3 seconds/image) causes it to alias in the phase encode dimension, which creates phase errors that vary in both space and time and reduce temperature precision. This effect is most pronounced at the beginning of a sonication, when water circulation has just been switched off but the water continues to move due to its remaining inertia. Water motion continues throughout the 15–30 second sonication, and the ultrasound can cause additional water motion during sonications. While there is ongoing research into doping and other methods to eliminate the water bath signal, these will not be clinically available in the near future, since a solution must be found that is non-toxic, does not modify the speed of sound, can be circulated and maintains water’s capacity for removing heat from the skull, does not lower the acoustic cavitation threshold, and can be obtained in the large volumes required to fill the transducer and cooling and degassing circuits.

This work describes the use of an RF pulse to reduce temperature errors in tcMRgFUS by suppressing water bath signal on either side of the head, which reduces the imaging FOV in the phase-encoded dimension. There are two common RF pulse-based approaches to eliminate unwanted signals that would otherwise alias into a volume of interest. The first is outer volume suppression, wherein one or more spatially-selective RF pulses are applied to produce 90 degree excitations of unwanted tissue regions followed by crusher gradients to eliminate the tissue’s longitudinal magnetization immediately prior to the imaging excitation and readout [4–8]. In tcMRgFUS, outer volume suppression is limited by the very low transmit efficiency and large $B_1^{+}$ inhomogeneities inside the transducer and water bath. The second approach which is immune to $B_1^{+}$ errors is a two-dimensional excitation that selectively excites only the region of interest, within the slice of interest [9–11]. In this work, a two-dimensional excitation was implemented in the pulse sequence that is used clinically for tcMRgFUS temperature monitoring. The resulting sequence was compared to the conventional full-FOV scan in healthy subjects outside the transducer, in gel phantoms in the transducer with FUS heating, and in a head phantom in the transducer without FUS heating but with k-space undersampling.

Methods

Pulse Design and Imaging Sequences

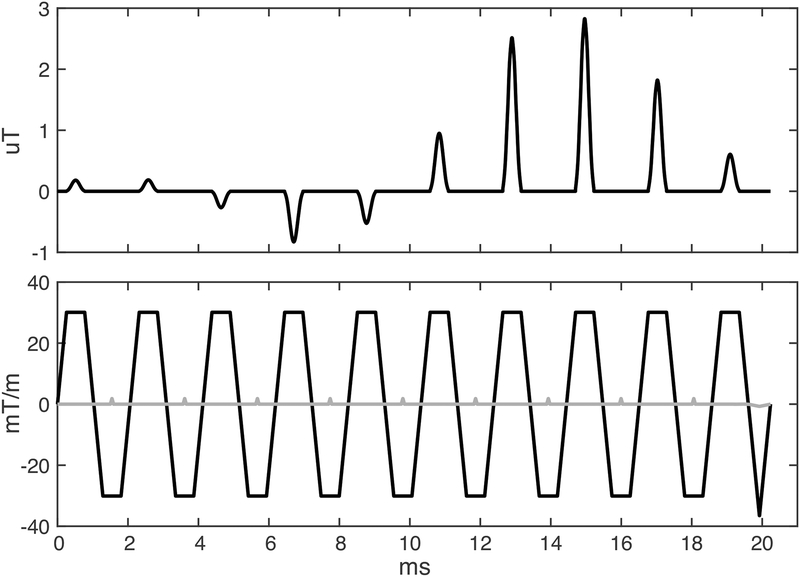
A two-dimensional RF pulse was implemented in the RF-spoiled gradient-recalled echo 2DFT sequence (fgre) used clinically for PRF-shift thermometry in the brain, on a GE Discovery MR750T 3T scanner (GE Healthcare, Waukesha, WI, USA) equipped with an Insightec ExAblate Neuro 650 focused ultrasound system (Insightec Ltd, Tirat Carmel, IL). Figure 1 plots the pulse’s RF and gradient waveforms. The pulse was designed by duplicating the original sequence’s time-bandwidth product 2 slice-select RF pulse waveform 10 times, and multiplying each copy by its corresponding position in a minimum-phase space-bandwidth product 4 small-tip-angle RF envelope, which was designed using the Shinnar-Le Roux algorithm [12]. The subpulses were aligned with the positive plateaus of a repeating z-gradient trapezoid without ramp sampling, which traced out a flyback trajectory. G_y phase encode blips were centered with each z-gradient rewinder. A bipolar version of the pulse was also implemented but the flyback trajectory was used for all experiments due to its robustness to gradient and timing errors, as discussed below. The default slab width was 100 mm, and the distance between slab repetitions was 250 mm. The slab width and the distance between slab repetitions were adjusted as needed for each scan by scaling the phase encode blips. The position of the slab was also controlled by adjusting a linear phase ramp across the subpulses. The gradient trapezoids were designed for minimum duration, subject to peak gradient amplitude and slew rate limits of 40 mT/m and 120 mT/m/ms, and each had an amplitude of 30 mT/m and a duration of 1.032 ms, for a total pulse duration of 20.24 ms. All scans used a 3 mm slice thickness and a 30 degree flip angle. The TE/TR of the full-FOV sequence were 13/25.6 ms, and the TE/TR of the reduced-FOV sequence were 17.3/43.9 ms. The full image FOV in each case was 280 × 280 mm, with a 256 × 256 reconstructed matrix size. The full-FOV scan measured 128 phase encode lines, and had a scan time of 3.29 seconds/image. The readout bandwidth was 5.68 kHz. Thirty time points were measured in every scan.

Figure 1:

Two-dimensional RF pulse and gradient waveforms. The z (slice) gradient is plotted in black, and the y (phase) gradient is plotted in grey. The RF pulse is scaled for a flip angle of 30 degrees, and the gradient is scaled for a slice thickness of 3 mm, which were the values used in all scans in this study. The y-gradient is scaled for a slab thickness of 100 mm.

In Vivo Temperature Precision

The conventional and reduced-FOV scans are expected to have different PRF-shift temperature precision due to the reduced-FOV sequence’s longer TR (which increases image SNR) and its reduced phase encoding (which lowers image SNR). To compare the scans, images were acquired in axial, coronal, and sagittal planes during free breathing in a healthy volunteer outside the water bath, with approval of the Institutional Review Board at the University of Virginia. The subject’s head was supported inside a head birdcage coil, but the body coil was used for imaging since it is used for all scans with the transducer. The reduced-FOV scans used slab widths of 120 mm (axial and coronal) and 200 mm (sagittal), and encoded y-FOV’s of 168 mm/60% (axial and coronal) and 196 mm/70% (sagittal). The resulting scan times were 3.37 seconds/image (axial and coronal) and 3.93 seconds/image (sagittal). PRF-shift temperature maps were calculated by the hybrid single-baseline and referenceless method [13] using the first image in the time series as the baseline, and a zeroth order referenceless phase polynomial to remove dynamic phase shifts due to scanner drift and respiration [14]. Since temperature errors can be positive or negative, the hybrid method’s non-negative temperature change constraint was not enforced in these calculations.

Gel Phantom FUS Heating

To compare the full- and reduced-FOV in a scan with FUS heating, a hemispherical gel phantom was placed in the Insightec system and sonicated while imaging in axial and sagittal planes. The phantom was a vendor-provided tissue-mimicking hemispherical quality assurance gel phantom with an 8-cm diameter and an acoustic absorbance of 0.005 Np/mm at 650 kHz. A coronal experiment was omitted since, due to circular symmetry of both phantom and transducer, the geometry was the same as the sagittal experiment. Sonications were started 15 seconds after the scans started, and lasted 30 seconds at 15 Watts acoustic power. The Insightec system managed water in the same manner as in a human surgery: the system automatically circulated, cooled, and degassed water between sonications and switched off circulation at the start of each scan. Due to the phantom’s small size, the reduced-FOV scans used slab thicknesses of 70 mm (axial and sagittal), and encoded y-FOV’s of 182 mm/65% (axial) and 210 mm/70% (sagittal). The resulting scan times were 3.65 seconds/image (axial) and 4.21 seconds/image (sagittal). PRF-shift temperature maps were calculated by the hybrid single baseline and referenceless method [13] using the second image in the time series as the baseline, and a zeroth order (constant) referenceless phase polynomial to remove dynamic phase shifts due to scanner drift.

Accelerated Head Phantom Precision

Several methods to accelerate brain temperature scans by k-space undersampling have been proposed to increase the volume or number of slices that can be imaged without decreasing frame rate [15–18]. However, these methods all rely on temporal redundancies in the data, which are obscured by unpredictable water motion [19]. Hence, eliminating water bath signal in the undersampled dimension may improve undersampled temperature precision. To evaluate improvements in temperature precision with the reduced-FOV scan and 2× k-space undersampling, full- and reduced-FOV axial scans were acquired in an anthropomorphic head phantom [20] in the transducer with the water bath filled but without heating. The reduced-FOV scan used a slab width of 110 mm and an encoded y-FOV of 168 mm/60%, for a scan time of 3.37 seconds/image. The second time point images were reconstructed as baselines and subsequent data were retrospectively uniformly undersampled in the left-right/phase-encoded dimension by a factor of 2, to achieve effective scan times of 1.65 seconds/image (full-FOV) and 1.69 seconds/image (reduced-FOV). PRF-shift temperature maps were reconstructed using the k-space hybrid algorithm [18] with a zeroth order (constant) referenceless phase polynomial. The algorithm reconstructs temperature maps from undersampled k-space data by fitting the hybrid single baseline and referenceless image model directly to the data. Since temperature errors can be positive or negative, the k-space hybrid method’s non-negative temperature change constraint was not enforced in these calculations. As in the phantom heating experiments, the Insightec system automatically managed water circulation and switched it off at the start of each scan.

Data Availability

Data and MATLAB code to generate Figures 2–5 in this paper is available at https://bitbucket.org/wgrissom/rfov_brain_thermo/.

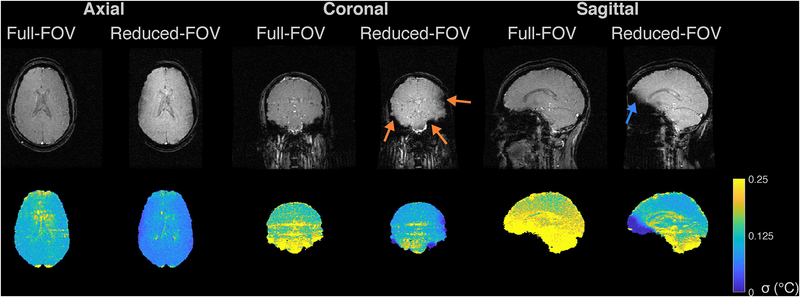
Figure 2:

In vivo temperature precision. The top row shows the magnitudes of the baseline (first time point) images, in three planes for the full- and reduced-FOV sequences. The second row shows corresponding through-time temperature standard deviation maps. The orange arrows in the coronal reduced-FOV image point to regions of signal loss where off-resonance caused the brain tissue to fall out of the two-dimensional pulse’s passband, and the blue arrow points to a region of signal loss in the sagittal image.

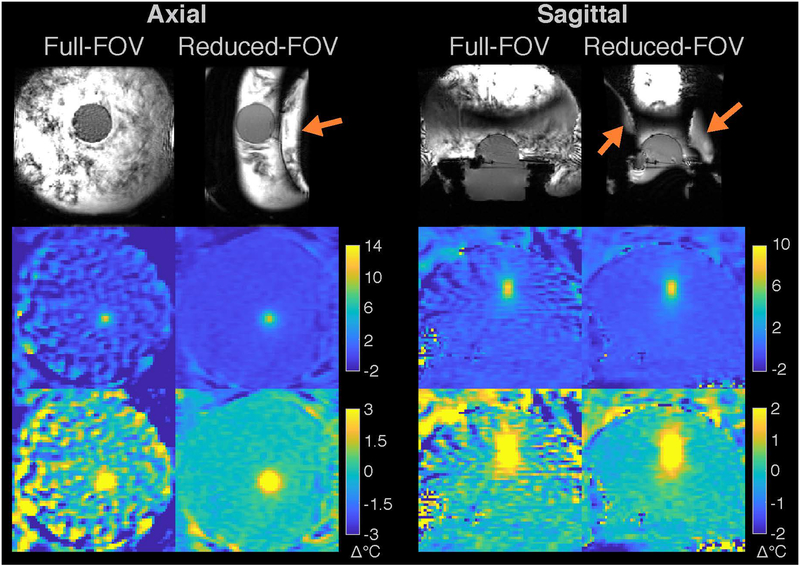
Figure 5:

Head phantom results. The top row shows the magnitudes of the fully-sampled baseline (second time point) images, for the full-FOV and reduced-FOV sequences. The second row shows temperature maps reconstructed by the k-space hybrid method from the k-space data of the first point in the time series (immediately after the baseline), which was uniformly 2x-undersampled in the left-right/phase-encoded dimension. The third row shows through-time temperature standard deviation maps.

Results

In Vivo Temperature Precision

Figure 2 shows magnitude images and through-time temperature standard deviation maps for the three slice orientations and the full-FOV and reduced-FOV sequences. The reduced-FOV magnitude images had a higher peak signal (approximately 30% higher) than the full-FOV images due to their longer TR. In the coronal and sagittal orientations, off-resonance caused tissue in a few regions at the edge of the brain to fall out of the two-dimensional pulse’s passband, which reduced flip angles (indicated by arrows). Through-time temperature standard deviation maps are shown in the bottom row of the figure inside a tissue mask which was the same for both scans. The reduced-FOV sequence generally had lower temperature errors, especially in the midbrain which is the target of essential tremor treatment. The temperature standard deviations taken over both space and time within voxels with non-zero estimated temperatures were 0.18 °C (full-FOV) and 0.12 °C (reduced-FOV) for the axial case, 0.32 °C (full-FOV) and 0.19 °C (reduced-FOV) for the coronal case, and 0.44 °C (full-FOV) and 0.21 °C (reduced-FOV) for the sagittal case. Approximating that temperature signal-to-noise ratio is proportional to TR, the square root of the number of phase encodes, and $TE\cdot e^{-TE/T_2^{*}}$ [3] where $T_2^{*}\approx 45$ ms in brain tissue, we expect a reduction in temperature standard deviation of 37% (axial and coronal) and 42% (sagittal) with the reduced-FOV scan. In the above results the standard deviations were reduced by 35% (axial), 41% (coronal), and 53% (sagittal). The hybrid reconstruction suppressed temperatures in voxels with signal amplitude less than 5% of the maximum image amplitude, which led to low displayed through-time temperature standard deviations in regions of signal loss in the coronal and sagittal reduced-FOV images. These were usually regions where the full-FOV image also had high temperature standard deviations, indicating that precise temperature measurement is not possible in those regions with either scan. These voxels were left out of the overall standard deviation calculations reported above, which were calculated using voxels that had significant signal in both full-FOV and reduced-FOV images, across all time points. Supporting Information Video S1 shows temperature error maps for each time point, which reflect that for both scans, most of the temporal variations were due to respiration and CSF pulsation, which affected both scans similarly. Supporting Information Figure S1 shows through-time mean temperature maps for each scan. The time- and space-averaged temperatures were all smaller than 0.01 °C.

Gel Phantom FUS Heating

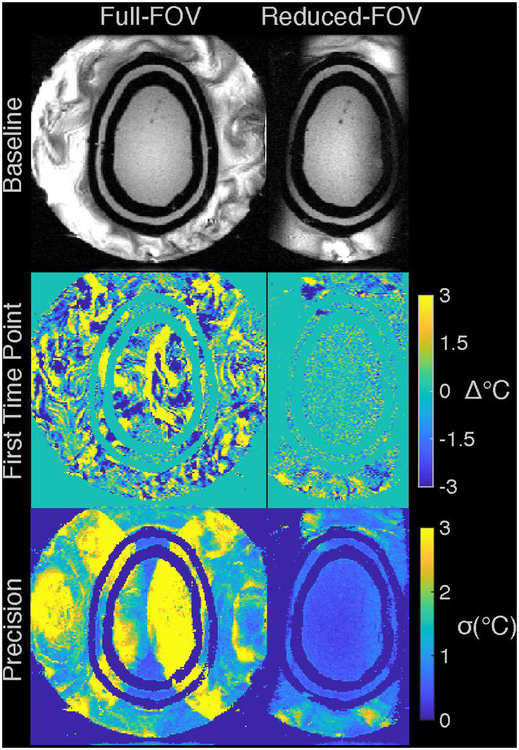
Figure 3 shows axial and sagittal phantom baseline images and zoomed-in temperature maps at peak heat. The reduced-FOV pulse successfully excited the phantom region in both cases, but due to the relatively narrow slab width (70 mm) the pulse also excited the outer edges of the water bath, which were prevented from aliasing into the phantom by appropriate adjustment of the phase encoding FOV (orange arrows). The full-FOV temperature maps contained large spatially-varying errors of more than 3 °C due to water aliasing, which were absent from the reduced-FOV maps. The aliasing also distorted the hot spots, which were more symmetric in the reduced-FOV maps. Supporting Information Figure S2 plots profiles through each dimension of the hot spots in each orientation at peak heat. The full-width-at-half-maximums of the axial profiles were 4.5 mm (full-FOV x), 3.7 mm (full-FOV y), 4.6 mm (reduced-FOV x), 4.5 mm (reduced-FOV y), and the full-width-at-half-maximums of the sagittal profiles were: 5.1 mm (full-FOV y), 8.6 mm (full-FOV z),4.7 mm (reduced-FOV y), 8.2 mm (reduced-FOV z). The true widths are unknown but the x- and y-widths were more consistent for the reduced-FOV scan (4.5–4.7 mm) than for the full-FOV scan (3.7–5.1 mm).

Figure 3:

Temperature maps measured in a gel phantom during FUS heating. The top row shows the magnitudes of the baseline (second time point) images for the full- and reduced-FOV sequences, in axial and coronal slice orientations. The reduced-FOV pulse successfully excited the phantom region in both cases, but also excited the outer edge of water bath due to the narrow 70 mm slab width, which was prevented from aliasing into the phantom by appropriate adjustment of the phase encode FOV (orange arrows). The second row shows temperature maps zoomed-in to the phantom at peak heat, and the third row shows the same maps with windowing adjusted to better visualize background temperature errors.

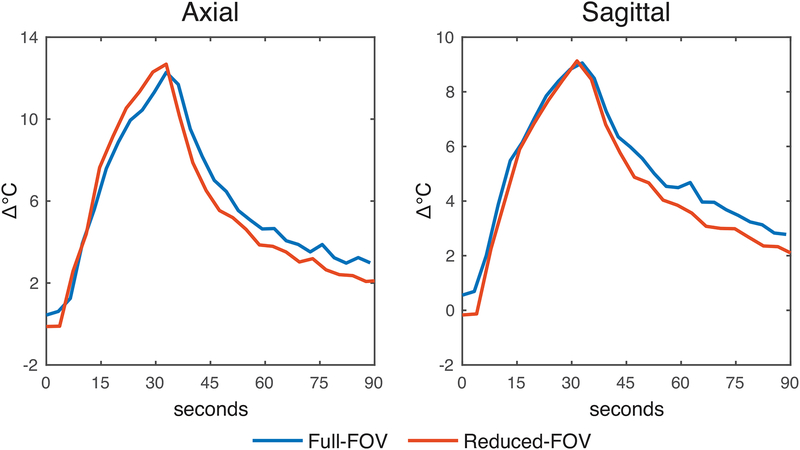
Supporting Information Figure S3 shows through-time temperature standard deviation and mean temperature error maps calculated from separate scans without heating. From those scans the temperature standard deviations over space and time were measured to be 1.2 °C (full-FOV) and 0.41 °C (reduced-FOV) for the axial case, and 0.56 °C (full-FOV) and 0.27 °C (reduced-FOV) for the sagittal case. Following the same temperature signal-to-noise ratio calculations as for the in vivo case, we expect temperature standard deviations to be 39% (axial) and 42% (sagittal) smaller with the reduced-FOV scan. Here, due to the water bath motion the measured reductions were larger: 66% (axial) and 52% (sagittal). The full-FOV mean temperature errors have a wide range due to water motion artifacts in the baseline images. Time- and space-averaged temperatures were all smaller than 0.01 °C. Figure 4 plots temperature versus time in the voxel with highest heating for each scan and slice orientation; in each slice orientation the voxel was in the same location in the full- and reduced-FOV maps. The peak temperatures largely agree though there is an apparent positive bias in the full-FOV curves before and after heating, which is likely due to biases from water motion artifacts in the baseline image. The reduced-FOV curves are also qualitatively smoother. Supporting Information Figure S4 plots temperature errors in the same voxels in the no-heating scans. The axial full-FOV curve contains larger swings than the reduced-FOV scan near the beginning of the scan when water is moving the most, and the sagittal full-FOV curve contains larger swings throughout the scan.

Figure 4:

Temperature versus time in the voxels with highest heating, which were in the same location between the full- and reduced-FOV maps for each slice orientation.

The above results indicate that the full-FOV temperature maps are biased over the scan duration by water motion artifacts in the baseline images that are especially large at the beginning of the scan, soon after water circulation has been switched off. Later in the scan, the water motion slowed but continued to contribute errors that gradually diminished. The second images in the time series were used as the baseline images when calculating these temperature maps; Supporting Information Figure S5 shows that using the first image in the time series (immediately after stopping circulation) causes temperature biases that completely obscure the full-FOV hot spot. Water suppression in the reduced-FOV scan largely eliminated these errors, regardless of which image was used as the baseline.

Accelerated Head Phantom Precision

The first row of Figure 5 shows fully-sampled full- and reduced-FOV baseline image magnitudes. In this scenario with a more realistic head size and slab width, the water bath edges were not excited. The second row shows temperature error maps reconstructed from uniformly 2x-undersampled data for the first time point in the series, immediately after the baseline image, and the third row shows through-time temperature standard deviation maps. Supporting Information Video S2 shows temperature error maps for all time points in the series. The full-FOV maps show that immediately after the baseline image there are large signal changes in the water bath that alias into the brain. In contrast, the reduced-FOV temperature maps had small errors throughout the time series. In the anterior and posterior brain regions where the water bath did not alias into the brain, the full-FOV temperature errors and standard deviations were similar to the reduced-FOV values. Temperature standard deviations over space and time in the phantom brain region were 6.21 °C (full-FOV) and 0.69 °C (reduced-FOV). Following the same temperature signal-to-noise ratio calculations as for the in vivo and gel phantom cases, we expect temperature standard deviation to be 37% smaller with the reduced-FOV scan. Here, due to the water bath motion and its aliasing the measured reduction was a larger 89%. Supporting Information Figure S6 shows through-time mean temperature maps for each scan. Mean temperature errors over space and time in the phantom brain region were 1.2 ° for the full-FOV scan, and 0.072 ° for the reduced-FOV scan.

Discussion

The experimental results in this work showed that a two-dimensional RF pulse can be used to suppress water bath signals on either side of the head during tcMRgFUS, which improves temperature precision by preventing moving water from aliasing into the brain and interfering with heating-induced phase shifts. The in vivo results showed that temperature precision was improved inside the brain (43% on average) in the reduced-FOV scans, including regions targeted by tcMRgFUS treatment, which was likely due to the longer TR and TE of the reduced-FOV sequence. There were some regions around the periphery of the brain where signal was lost because the tissue’s off resonance caused it to shift out of the pulse’s passband. However, these regions also coincided with regions of poor temperature precision in the full-FOV scan. The TE starting time was determined by the isodelay of the minimum phase envelope used in the pulse; finer control over the TE starting time could be achieved using a more flexible pulse design as in Ref. [21]. The in vivo scans used the first image in the time series as the baseline. Clinically, since it takes time for the long-T₁ water bath signal to stabilize, the first image is discarded and the second image is used as the baseline, as was done in the phantom experiments here. However, since the water was absent in the in vivo scans, we found that using the first baseline instead of the second led to no signficant differences in our results. In the gel phantom heating experiments, the hot spots appeared more symmetric than in the conventional scans, and temperature curves in the voxel with peak heating appeared smoother. In the absence of heating in the gel phantom, the background temperature precision was improved 59%. Since a typical head is larger than the gel phantom used in these experiments, the space-averaged improvement with reduced-FOV may be somewhat less in vivo, though the reduction in maximum errors should be similar. Finally, the anthropomorphic head phantom temperature reconstructions showed that the reduced-FOV scan is more amenable to acceleration by k-space undersampling than the conventional scan, and that 2×-undersampled temperature precision was improved 89%. In addition to the k-space hybrid method we used for these undersampled reconstructions, suppressing the time varying water bath signal should also improve the quality of other temperature reconstructions that rely on temporal redundancies in the data, including temporally constrained reconstruction [15], model-predictive filtering [16], and Kalman filtering [17, 22]. While this work was based on the original single-echo thermometry scan that is used by many tcMRgFUS sites, the two-dimensional RF pulse should also be compatible with the multiecho scan that has more recently become available, and suffers less blurring in the frequency encode dimension due to chemical shift. Since the multiecho and single-echo scans use the same phase encoding, the improvements in temperature precision should be similar, but this remains to be validated. The pulse may also enable water circulation to be left on during sonications to improve cooling.

Presently the main limitation of the reduced-FOV sequence is the long duration of the RF pulse, which increased the sequence’s minimum TR and TE compared to the conventional excitation, and made it sensitive to off-resonance. This long duration was principally a consequence of the flyback design, which was chosen to avoid poor stopband suppression that we observed using a bipolar design, which we believe was due to eddy currents with a spherical-type spatial dependence that were induced by the slice-select gradients in the conductive transducer bowl. Our bipolar design had a duration of 11 ms (9 ms shorted than flyback). The flyback and bipolar stopband suppressions were identical outside the transducer, so it is possible that bipolar pulses could be used in future transducer designs that support less eddy currents [23]. The pulse duration could also be reduced using ramp sampling without increasing slew rate or max gradient strength [24], but this may result in slice profile distortion requiring gradient calibration, and was beyond the scope of this work. The pulse duration could also be shortened on more recent scanners with higher slew rates. Finally, it may be possible to shorten the pulse by removing a few subpulses (i.e. reducing the distance between passband replicas) so long as the edges of the slab replicas sit outside the water bath, which has a width of approximately 320 mm at its widest point. Combined with the reduced phase encoding, a shorter pulse could make the scan short enough that imaging additional slices would not significantly increase the current 3.3 seconds/image frame rate. The subpulses could also be replaced with multiband pulses, to implement simultaneous multislice thermometry [25].

Conclusions

Reduced-FOV temperature imaging using a two-dimensional excitation pulse alleviates temperature errors due to water bath motion, and enables accelerated temperature mapping with greater precision. In practice it will be most effective when used in axial and coronal slice orientations, where the water bath occupies a large portion of the FOV in the phase-encoded dimension.

Supplementary Material

Supp VideoS1

Supporting Information Video S1: In vivo temperature error maps. The top row shows the magnitude images, in three planes for the full- and reduced-FOV sequences. The second row shows corresponding temperature error maps.

Supp VideoS2

Supporting Information Video S2: Temperature maps reconstructed from the head phantom by the k-space hybrid method from the k-space data of each point in the time series (starting immediately after the baseline), which were uniformly 2x-undersampled in the left-right/phase-encoded dimension. Note the larger colorbar range compared to the first time point maps shown in the second row of Figure 5.

Supp figS1-6

Supporting Information Figure S1: Through-time mean in vivo temperature error maps. The time-and space-average temperatures were all smaller than 0.01 °C.

Supporting Information Figure S2: Temperature profiles through the hot spot at peak heat, for the axial and sagittal phantom heating experiments shown in Figures 3 and 4.

Supporting Information Figure S3: Through-time temperature standard deviation and mean temperature error maps for axial and sagittal full- and reduced-FOV gel phantom scans without heating.

Supporting Information Figure S4: Gel phantom temperature errors versus time in the same voxels as Figure 4, from a scan acquired without FUS heating.

Supporting Information Figure S5: Temperature maps measured in a gel phantom during FUS heating, using the first image in the time series (immediately after water flow has been shut off) as the baseline image, rather than the second image as in Figure 3. The top row shows the magnitudes of the baseline (second time point) images for the full- and reduced-FOV sequences, in axial and coronal slice orientations. The second row shows temperature maps zoomed-in to the phantom at peak heat, and the third row shows the same maps with windowing adjusted to better visualize background temperature errors.

Supporting Information Figure S6: Through-time mean temperature error maps for the undersampled head phantom experiment. The time- and space-averaged temperature error overs the phantom’s brain region were 1.2 ° for the full-FOV scan, and 0.072 ° for the reduced-FOV scan.