Remarks on the design and analyses of longitudinal studies for cancer patients with anorexia and weight loss

Abstract

Longitudinal data serve an important role in understanding the cancer anorexia weight loss syndrome and in testing interventions to palliative and treat patients who develop this syndrome. The element of time and the interrelatedness of data points define longitudinal data and add to the richness of this type of data. However, longitudinal data can also give rise to non‐random, missing data that can lead to flawed conclusions. This paper discusses these issues and suggests practical considerations for design and analysis of longitudinal cancer anorexia weight loss studies.

Introduction

Longitudinal data—perhaps more so than any other type of data—provide rich depth of content. However, these data also pose a risk for drawing inaccurate conclusions. The element of time serves to define longitudinal data but also leads to this perilous juxtaposition of informative content and risk for generating faulty conclusions if the collection of such data is poorly designed and/or analyses are poorly conducted. One of the biggest challenges with a longitudinal study is to ensure that outcome measures are collected for all patients at all pre‐specified time points. Longitudinal data that focus on cancer anorexia and weight loss are particularly vulnerable to inaccurate interpretation because of missing data. In this context, a focused discussion of longitudinal data, such as that offered here, attempts to lead to sounder longitudinal trial designs and more thoughtful and accurate data interpretation.

Why are longitudinal studies that target cancer anorexia and weight loss especially at risk for yielding inaccurate conclusions? The answer rests in the complexity of this syndrome.1, 2 Cancer anorexia and weight loss is a multidimensional syndrome that arises in over 50% of patients with advanced, incurable malignancies. Loss of appetite with accompanying reduced caloric intake, weight loss, preferential attrition of lean as opposed to adipose tissue, diminished patient functionality, compromised effects of antineoplastic therapy, and increased chemotherapy toxicity—all in conjunction with poor survival—characterize this syndrome. This complexity is synonymous with patient morbidity and mortality, both of which make it difficult for patients to adhere at times to all aspects of an interventional clinical trial. Further, this deleterious complexity is further exacerbated by the fact that no intervention, including attempts at caloric repletion, yields complete and total therapeutic improvement. At best, palliative measures with hormonal therapies, for example, progestational agents, improve appetite but have no favourable impact on patients' physical functionality, global quality of life, or survival. In this context, longitudinal data serve an essential role, enabling us to test with rigor palliative and therapeutic interventions that target this syndrome.

Longitudinal data: a definition and examples

Longitudinal data are composed of repeated measures, where outcomes are assessed at multiple time points for each patient. Time can be expressed linearly (as is typically the case), logarithmically, or in a number of equally scaled methods. Quantitative data are the most frequently generated type of outcome data in cancer anorexia weight loss clinical trials—for example, with body weight scores, patient‐reported questionnaire items from validated questionnaires that are scored and summed, or computerized tomography‐based measures of area of muscle at the L3 vertebra. Longitudinal data can also be used to qualitatively assess a change of the target outcome over time, the so‐called time‐to‐event outcome—for example, patients' time‐to‐weight loss at a certain level from baseline (5% or 10%) or overall survival. Although time‐to‐event outcomes are a type of longitudinal data, they are often handled differently and are analysed using survival analysis techniques. This review focuses on only repeated measures longitudinal data.

Although thoughtfully designed prospective longitudinal studies, where real‐time monitoring mechanisms are in place to minimize missing data, are preferred, previously gathered longitudinal data can also be assessed in a retrospective manner. This approach offers the obvious advantages of enabling research questions to be answered in an efficient, low‐cost manner. However, managing missing data can be an issue with fleetingly fewer mechanisms in place over time to make amends to capture such data. Our group has used this design to explore whether agents that might dually target the growth of the cancer and target muscle wasting pathways should be further investigated specifically for the treatment of cancer anorexia and weight loss. For example, earlier preclinical studies had identified the ubiquitin‐proteasome system as a key pathway for cancer‐induced muscle wasting.3, 4 Subsequently, the proteasome inhibitor, bortezomib, was entered into clinical testing as an antineoplastic agent. Our group capitalized on a previously completed trial that examined bortezomib as an antineoplastic agent for the treatment of pancreas cancer patients. Focusing on 45 patients who had received bortezomib as monotherapy for cancer treatment, we reassessed weight and quality of life data that included appetite scores from the Functional Assessment of Cancer Therapy‐Colorectal (FACT‐C) to screen whether bortezomib merited further study for the cancer anorexia and weight loss syndrome. We reported slight increases in weight and stable appetite, although, of note, results were reported with caution because of high dropout rates. The extent and severity of adverse events, such as peripheral neuropathy, dissuaded us from testing bortezomib further for the treatment of cancer anorexia and weight loss. As a second example, our group examined veliparib, an inhibitor of poly (ADP‐ribose) polymerase.5, 6, 7 A host of studies, including some in animal models, suggests that poly (ADP‐ribose) polymerase inhibitors give rise to increased mitochondrial function, increased NAD(+) muscle content, and increased SIRT1 activity, all of which appear to culminate in weight gain in tumour‐bearing animal models. Using this same approach of reanalysing longitudinal data, we observed that among 60 cancer patients, only one had achieved our a priori threshold of success of 10% weight gain above baseline at any time point while on veliparib. However, the weight gain observed in this sole patient was not composed of muscle but rather abdominal ascites, as seen on computerized tomography scan. Admittedly, the use of this efficient, low‐cost, retrospective assessment of prospectively gathered data enabled us to draw only tentative conclusions about bortezomib and veliparib, but this approach prompted us to channel our clinical research efforts in other directions. Figure 1

Figure 1.

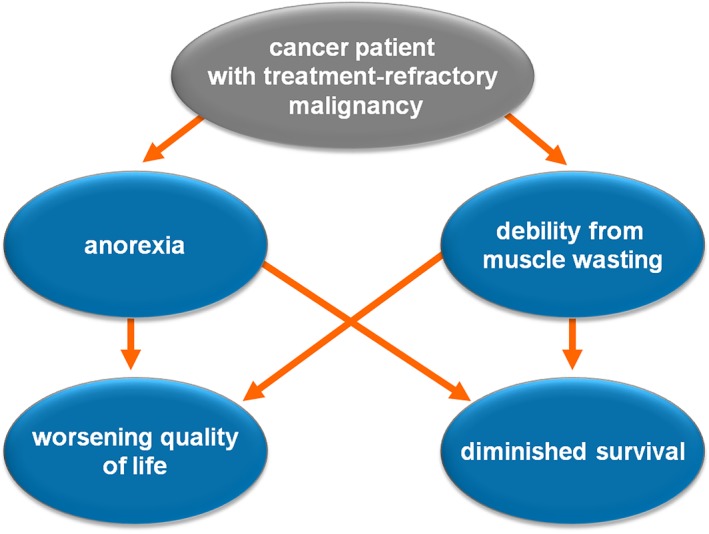
Overview of the cancer anorexia weight loss syndrome. The cancer anorexia weight loss syndrome is multidimensional in nature and associated with a decline in quality of life and survival.

To further define longitudinal data, it should be distinguished from cross‐sectional data. The latter can also be obtained at different time points, but the key distinction between longitudinal and cross‐sectional data is that the former consist of a series of interrelated measurements from the same set of patients over time whereas cross‐sectional data are collected using different sets of patients at different time points. This key aspect of interrelatedness offers several advantages, namely, an ability to assess change in outcomes over time, an ability to adjust for variability in outcome data between patients, and an overall need for fewer patients when designing a clinical study (Table 1). In contrast, compared with cross‐sectional data, longitudinal data also offer disadvantages. These include the need to incorporate within the study design longer follow‐up, which, of course, carries with it more effort and greater expense; a more complex study design; and the challenge of contending with missing data that can arise from patients' choosing not to participate in some aspects of the study or dropping out of the study all together. Of parenthetical note, the critical importance of these distinctions raises the point that investigators should denote on graphical renditions of their data whether their data are in fact longitudinal vs. cross sectional (Figure 2). Despite the challenges of longitudinal data, in certain situations, no type of data other than longitudinal data enables investigators to examine whether an intervention truly yields clinical therapeutic efficacy.

Table 1.

Advantages of longitudinal vs. cross‐sectional data

Longitudinal	Cross‐sectional
Allows for assessment of change over time	Shorter/no follow‐up
Adjusts for variability between individuals	Fewer challenges in dealing with missing data
Requires fewer patients	Simpler study design and analyses

Figure 2.

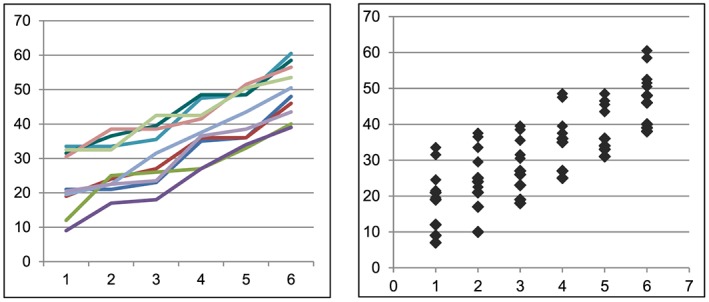
Denoting longitudinal vs. cross‐sectional data. Upon inspection, it is impossible to tell which graph represents longitudinal data (the reader's left) and which represents cross‐sectional data (the reader's right). The important distinctions between these data types underscore the need to denote data type—whether longitudinal or cross sectional—on graphed data.

Missing data

At a recent scientific meeting where results from an interventional trial for patients with the cancer anorexia and weight loss syndrome were presented, the speaker offered the following, directly quoted observation from the podium: ‘Many patients died before they could benefit from our intervention.' Without question, this statement evokes further comment. First, in patients who suffer from the cancer anorexia and weight loss syndrome, shortened survival is an unfortunate but integral aspect of this syndrome. Hence, to claim that patients would have benefited from an intervention had they only lived longer is an oxymoron. Second, the aforementioned statement illustrates the frustration and tragedy associated with the cancer anorexia and weight loss syndrome. Antineoplastic therapy is aimed at prolonging life in the setting of an acceptable toxicity profile, and palliative therapy is aimed at mitigating symptoms. In effect, truly effective treatment of the cancer anorexia and weight loss syndrome must do both, setting the bar that defines success extremely high and generating disappointment on the part of investigators on the seemingly unreachable height of that bar. This situation also underscores further the importance of thinking through how best to manage the problematic issue of missing data that often plague longitudinal data.

This issue of missing data is perhaps the most challenging and most critical one that comes into play in designing and interpreting results from cancer anorexia and weight loss trials. Illustrative of this challenge is a trial from Barber and others, where these investigators clearly acknowledged this bias, noting ‘there might be a bias to overestimate the overall efficacy …'—thereby making it easier to discuss this trial critically in the current paper.8 To summarize, in 1999, Barber and others reported on a single arm cancer anorexia weight loss trial that tested an omega‐3 fatty acid product in patients with advanced pancreas cancer. Twenty patients were assessed at baseline, 3 weeks, and 7 weeks. By 3 weeks, the sample size had dropped to 18 patients; and, by 7 weeks, it had dropped to 13 patients. Yet the investigators' data described stability of anthropometric measurements (change in mid‐arm muscle circumference and change in triceps skinfold thickness); stability of change in percentage of total body water and fat mass, as assessed with bioelectrical impedance; and stability of appetite. At 7 weeks, these investigators also reported on an improvement in weight (p=0.033), an improvement in change in lean body mass, as assessed by bioelectrical impedance (p=0.0047), and an improvement in Karnofsky scores from baseline (p=0.046). Overall, the use of this omega‐3 fatty acid product was viewed favourably and, per their recommendation, merited further testing.

It remains unclear how the data from the seven patients who had dropped out at 13 weeks were handled. It does not appear that these dropouts were included in the analyses; one might wonder if different study conclusions might have been reached had the data from these dropouts been handled in a highly conservative manner to suggest that these patients were doing especially poorly from a cancer anorexia and weight loss standpoint. In addition to the high dropout rate, potential issues with the study conclusions are that they are based on an extremely small sample size with no adjustment for the multiple outcomes comparisons where the P‐values are at best marginal. The handling of dropout is even more important with such small sample sizes. Since the publication of this trial, several hundred cancer patients have been enrolled in clinical trials, which have tested this same agent, only to yield results that demonstrate no clinical advantage with omega‐3 fatty acid for the treatment of cancer anorexia and weight loss.9, 10 Now, this hindsight of many years suggests a need to implement consistent, well‐defined approaches to handling missing data in cancer anorexia and weight loss trials.

Missing data fall into two categories: those that are absent intermittently and those that are absent at one visit and then at all subsequent time points. Patients who yield the latter type of missing data are called ‘dropouts'. Although it is difficult to construct statistical models to look for patterns of missing values in intermittently missing data, intermittently missing data pose less of a challenge because they can be easier to recover; these patients have in fact returned for a reassessment at a later date, thus providing opportunities to discern what had occurred during the time point of absent data. Thus, an acceptable approach to deal with intermittently missing data that remain missing is to impute data from shoulder visits. Although inevitably some potential for bias exists even with such an imputation plan, this approach is viewed as acceptable and associated with a lesser risk of giving rise to misleading trial results.

In contrast, missing data from dropouts pose greater concerns for bias. This issue of patient dropout is not trivial. In our review of interventional trials that have targeted cancer anorexia and weight loss, only one study reported a near‐zero dropout rate within 4–6 weeks of trial initiation; most reported dropout rates between 10% and 30%.11, 12 Although dropout rates likely vary based on the patient trial eligibility criteria and other trial‐related factors, these percentages are by no means trivial and are capable of swaying trial conclusions. Dropout data are often never able to be recovered, and they provide an ever‐lingering concern that they might not be occurring at random but instead are directly confounding the trial's outcome data; therefore, under these circumstances, it becomes difficult to know how to impute missing data in a manner congruent with what actually happened to the patient after his or her cessation of trial participation. Some investigators suggest taking the last value of the outcome of interest and carrying it forward. Others contend that this carry forward approach overshoots the outcome of interest in a more favourable, biased manner.13 Instead, these more conservative investigators contend that such missing data should be imputed with the maximally unfavourable outcome value possible—for example, a zero value of appetite, a zero value of functionality, or a zero value of lean tissue measurement on scans—particularly given the highly negative ramifications of the cancer anorexia and weight loss syndrome. One might argue, however, that imputation methods should be specific to the entity being studied. For example, a patient who drops out of a trial for nausea and vomiting may do so because he has had absolutely no nausea and vomiting and no longer has an interest in completing a study requirement; in contrast, a patient with the cancer anorexia weight loss syndrome may dropout for a totally opposite reason: the syndrome may be overwhelming to the point that completing a study requirement is no longer possible. In essence, managing dropouts in cancer anorexia and weight loss trials remains problematic, and, although imputation of data can be used, it should not create a false sense of security with respect to the completeness of a data set.

Although advanced statistical methods such as imputation, mixture data, or dynamic inverse modelling13, 14, 15, 16 have been developed for analysis of longitudinal data when missing data are thought to be confounded with the outcome measures, there is no truly reliable way to recover the missing outcome measures. The validity of the results from these methods is based on untestable assumptions.13, 14 For retrospective studies, this is the best one can do. However, for prospective clinical trials, the best approach is to design the trial with great care to minimize the likelihood of missing data to help ensure that, when the issue of missing data does arise, these data are missing in a truly random manner. First, focusing data collection at only the time points necessary to address the study objectives and to only those items most relevant to the study question can reduce patient burden and lessen missing data. Previous studies have suggested that the greater the burden of questionnaire completion—as indicated in part by the length of the questionnaires and time necessary for a patient to complete them—the less likely a patient will continue to adhere to questionnaire completion.17 Second, among cancer patients who are suffering from anorexia and weight loss, the prognostic effect of this syndrome is such that capturing data early on is especially important. Along these lines, one strategy might entail acquiring outcome data at a greater frequency early on during the trial—for example, request questionnaire completion at home on a weekly basis during the first 6 weeks of trial participation. In the event, a patient does drop out shortly after enrolment, at least some data remain available to assess the outcomes of interest. Third, if a randomized trial design is being used, it makes sense to attempt to include stratification factors that attempt to balance dropout rates of a serious nature across study arms. Fourth, incorporating an intention‐to‐treat analysis makes sure that patients who had enrolled in the trial but had dropped out are nonetheless contributing to trial conclusions and not biasing results in an unrealistically favourable or unfavourable manner as a result of their omission from the analyses. Finally, analyses plans should include a priori, detailed sensitivity analyses aimed at identifying whether patient dropout had been truly random or instead reflective of an unanticipated or uncaptured source of bias. One does not know what one does not know. Regression models that incorporate specific covariates to reveal a pattern of dropout are an important aspect of checking for bias—even when the study team has no reason to suspect bias. When it does appear as if dropouts arose in a non‐random manner, this situation is suggestive of a flawed element in the study design and is thought to be impossible to repair fully after the trial has been full accrued. The only option at that point is to report results objectively and call for confirmatory studies.

Importantly, it should be noted that the aforementioned points of caution are not intended to stifle or curtail the exploration of novel ideas. This syndrome is in need of novel therapeutic strategies. For example, Antoun and others provided innovative and provocative evidence that a multikinase inhibitor, in this case sorafenib, is associated with muscle wasting.18, 19 Relying upon an 800+ patient, randomized, placebo‐controlled trial in patients with renal cell carcinoma, these investigators examined computerized tomography scans at the L3 vertebral level among 48 sorafenib‐treated patients and 32 placebo‐exposed patients, reported on cross‐sectional muscle area on those scans, and compared muscle area between earlier‐assigned trial arms (sorafenib vs. placebo) as per the original trial. Such comparisons led to the provocative conclusion that ‘patients with renal cell carcinoma have a high prevalence of advanced muscle wasting and that muscle loss is specifically exacerbated by sorafenib'. Admittedly, when one considers the non‐random arm assignment within this substudy (as opposed to the original study) and the resulting potential for bias within the longitudinal data set used for this substudy—for example, dropouts occurred prior to the acquisition of a computerized tomography scan (thus, potentially biasing results related to those who had a scan), a very small subgroup of the total trial population was the focus of this substudy for reasons that are not entirely clear, and higher dropout rates likely occurred with placebo in a non‐random fashion based on the fact that sorafenib turned out to yield an improvement in cancer progression‐free survival as well as trends in favour of improved overall survival—all three points of which might prompt one to question whether it was truly the sorafenib that had this deleterious effect on muscle or whether it was some other, unidentified confounding factor at work. The point here is that as investigators continue to strive for perfection in designing rigorous longitudinal studies, along the way, they must continue to ask provocative questions (as was performed in the study referenced here), report their results and interpretations of findings, and invite confirmatory studies, as appropriate.

Analysis methods

Many different analytic methods can be used with longitudinal data, including simple analyses using the average of outcome measures over time or the area under the longitudinal plot of outcomes over time; repeated separate analyses of change from baseline to post‐baseline time points; transition models, that is, changes between consecutive time points; or comprehensive regression methods using marginal models or mixed effects models to even more complex modelling using imputation or mixture models (Table 2). Analysis methods are intricately tied to study objectives, study designs, and the level and mechanism of missing data. The literature on analysis and handling of missing data in longitudinal studies spans across many areas of research from clinical trials to psychological research to behaviour therapy.13, 14, 15, 16, 20, 21, 22

Table 2.

General analysis approaches for longitudinal data

Method	Explanation of methodology	Missing data	Pros	Cons
Simple analyses	Compare the mean outcome across multiple time points between groups or compare the area under the longitudinal plot of outcome measures between groups	Completely random	Simple and well‐established methodology	Require complete data, cannot assess effect of time on outcome
Transition models	Compare response changes between consecutive time points between groups	Completely random	Simple analysis	Require complete data, cannot formally assess effect of time on outcome, cannot determine overall effect of treatment
Marginal models	Regression model to assess treatment effect average over the population over time and can adjust for other covariates in the models	Completely random	Flexible regression models, can adjust for other covariates, can accommodate missing data if it is missing completely at random	Assume that data are missing completely at random, population average interpretation
Mixed effects models	Regression model to assess treatment effect within each individual over time and can adjust for other covariates	Random	Flexible regression models, can model differential treatment effect over time, can accommodate missing data with less stringent assumptions	Assume that data are missing at random
Imputation (simple or multiple)	Missing values are imputed based on various assumptions	Not random	Flexible models to fill in missing outcome measures, complete data set with imputed values can be used in any methods used for complete data	Require careful considerations of assumptions used for imputation
Mixture (pattern) models	Overall treatment effects are estimated as an average of effects from the mix of different dropout patterns	Not random	Flexible and require less stringent missing data mechanism	Based on unverifiable assumptions, require careful considerations for model assumptions

Prior to analysing a data set, missing data need to be scrutinized. To focus exclusively on patients who have a complete trajectory of follow‐up is inefficient and potentially fosters biased conclusions. Instead, analyses should be undertaken after the data set is critically analysed in a two‐step manner. First, the extent of missing data should be assessed. Do only a handful of cases have missing data? Do most cases have some missing data? Do all cases have most of their data missing? The greater the data void, the greater the concern for flawed conclusions. Second, Rubin introduced taxonomy on the extent of randomness to characterize missing data, providing the categories of ‘missing completely at random', ‘missing at random', and ‘missing not at random', which together are illustrative of the spectrum of randomness of missing data.23 This taxonomy is relevant when choosing which model might be most relevant for data analyses. However, if missing data are clearly non‐random, the concern for drawing flawed conclusions is heightened, regardless of model choice.

Statistical modelling has sought to lessen the problematic nature of both the extent of missing data and the extent of non‐randomness of missing data (Table 2). Research in statistical modelling of longitudinal data has entailed the study of artificially generated data sets that are manipulated, fit into statistical models, and then reassessed for goodness of fit—all in an effort to negotiate the problematic nature of missing data and non‐random missing data and to draw meaningful, nonbiased conclusions from the data.24, 25, 26, 27 A variety of models have been generated, and some of these major ones appear in Table 2. These models align with the three categories of missing data.

In studies where there are no missing data or where data are missing completely at random, simple analyses comparing the mean outcomes across multiple time points, or the area under the longitudinal plot of outcome across time points using complete data can be used, but they cannot assess the outcome measures over time. Another approach is using separate transition models that rely heavily on previous measurements and again limit the ability to formally assess the outcome measures over time. This class of model again requires complete data; moreover, it attenuates the response from an intervention because of its reliance on prior data outcomes, thus making it less than optimal to use to analyse data from an interventional trial for the cancer anorexia and weight loss syndrome. The use of repeated measures analyses restricted to complete data has limited use in cancer anorexia and weight loss trials, where missing data are almost inevitable in view of the debility and risk for early demise observed in patients with this syndrome. Another method, the marginal models with generalized estimating equations,28 is more flexible than the simple analysis and transitional models and allows evaluation of treatment effect over time. However, this method assumes that data are missing completely at random, a situation that creates a tall order that frequently cannot be met.

A method that is more flexible and can accommodate some missing data better than all the aforementioned models is the linear mixed effects models. The mixed effects models offer the greatest flexibility that allows for modelling both the effect of time and treatment on a specific outcome. These models also allow for an assessment of the interaction between time and the treatment intervention. Another major advantage of the mixed effects model is its ability to handle missing data. Unlike other analysis methods discussed earlier that work best when there are no missing data or only appropriate when one is fairly certain that the data are missing completely at random, the mixed effects models require a less stringent assumption about missing data. Specifically, mixed effects models can be used when the reason for missingness can be traced back to baseline factors or to previous outcome measures. These advantages of linear mixed models make them a preferred method for analysis of longitudinal data. For most well‐designed interventional studies for the cancer anorexia weight loss syndrome, this model seems the most apt.

More sophisticated analysis methods such as imputation and mixture models are available when missing data are correlated to the outcome of interest and cannot be traced back to baseline characteristics or previous outcome measures. Again, as alluded to earlier, these methods rely on unverifiable assumptions. Therefore, the validity of study conclusions remains a concern when the data are missing in a non‐random manner.

Conclusion

Longitudinal data offer the greatest promise to enable us to better understand the cancer anorexia weight loss syndrome and identify the best therapeutic/palliative interventions. There is a vast literature across many research areas.13, 14, 15, 16, 20, 21, 22, 28 This review provides remarks on practical considerations when designing and analysing longitudinal cancer anorexia weight loss trials. Careful study design coupled with careful data analyses and reporting are essential, but, importantly, no degree of scrutiny, thoughtful analyses, or creative modelling can remedy a flawed trial design that has generated a large quantity of non‐random missing data. Furthermore, ignoring missing data or failing to report that data are missing can lead to flawed conclusions.

Conflict of interest

None declared.

Le‐Rademacher J. G., Storrick E. M., and Jatoi A. (2019) Remarks on the design and analyses of longitudinal studies for cancer patients with anorexia and weight loss, Journal of Cachexia, Sarcopenia and Muscle, 10, 1175–1182. 10.1002/jcsm.12480.