SSEThread: Integrative threading of the DNA-PKcs sequence based on data from chemical cross-linking and hydrogen deuterium exchange

Abstract

X-ray crystallography and electron microscopy maps resolved to 3–8 angstroms are generally sufficient for tracing the path of the polypeptide chain in space, while often insufficient for unambiguously registering the sequence on the path (i.e., threading). Frequently, however, additional information is available from other biophysical experiments, physical principles, statistical analyses, and other prior models. Here, we formulate an integrative approach for sequence assignment to a partial backbone model as an optimization problem, which requires three main components: the representation of the system, the scoring function, and the optimization method. The method is implemented in the open source Integrative Modeling Platform (IMP) (https://integrativemodeling.org), allowing a number of different terms in the scoring function. We apply this method to localizing the sequence assignment within a 199-residue disordered region of three structured and sequence unassigned helices in the DNA-PKcs crystallographic structure, using chemical crosslinks, hydrogen deuterium exchange, and sequence connectivity. The resulting ensemble of threading models provides two major solutions, one of which suggests that the crucial ABCDE cluster of phosphorylation sites cannot undergo intra-molecular autophosphorylation without a conformational rearrangement. The ensemble of solutions embodies the most accurate and precise sequence threading given the available information.

1. Introduction

Building atomic models into medium resolution (~4–8 Å) electron density maps, generated from electron microscopy and/or X-ray crystallography is an important component of macromolecular modeling of large complexes. A number of tools exist for fitting backbone models into low-resolution electron density maps. However, for many structures, the assignment of sequence to these backbone models is ambiguous. Atomic models can be computed by rigidly or flexibly fitting previously determined atomic structures of fragments (Baker et al., 2011) or larger units of structure (Baker et al., 2011; DiMaio et al., 2015; Lindert et al., 2012; Terwilliger et al., 2018; Tjioe et al., 2011; Wang et al., 2015; Woetzel et al., 2011) onto backbone models or only utilizing sidechain fit to the original low-resolution density map. (Chen and Baker, 2018) These methods, however, are not able to benefit from other biophysical information, exhaustively sample potential threading solutions and do not report the uncertainty (precision) of the resulting models. To improve the accuracy and inform the precision of a threading assignment, a method that can sample and rank alternative threading assignments based on any source of structural information is required.

To fill this need, we developed a general method within the integrative structure modeling (ISM) framework. ISM is generally used to build structural models from varied biophysical data and prior information. The modeling problem is formulated as a computational optimization where input information about the system is encoded into a scoring function that evaluates candidate models proposed by structural sampling. Here, a model encodes the threading of the sequence to a set of given structural coordinates. Alternative models are sampled using a Monte Carlo scheme whose Metropolis criterion relies on a scoring function dependent on various types of information about the system. The threading assignment may not be unambiguous. Therefore, our method also reports uncertainty in the sequence-structure assignment. The method is benchmarked on a set of small crystal structures with computed distance restraints, secondary structure propensities, and selenomethionine anomalous scattering sites. This method is implemented in our open source Integrative Modeling Platform (IMP) package (https://integrativemodeling.org). (Russel et al., 2012)

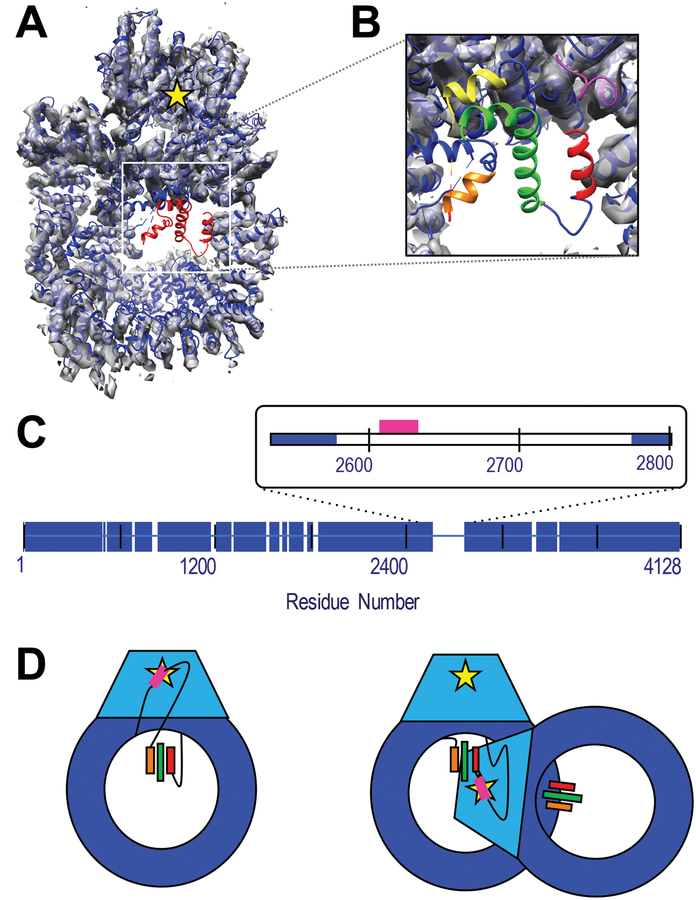
We illustrate the method by threading three previously unassigned helices in the structure of human DNA-PKcs defined by X-ray analysis at 4.6 Å (PDB 5LUQ; (Sibanda et al., 2017)) [Figure 1], based on chemical crosslinks, hydrogen deuterium exchange data, sequence connectivity, and statistical potentials. DNA-PKcs is a very large protein kinase that is proposed to be allosterically regulated through an extended scaffold DNA, Ku 70/80 and various cofactors such as the nuclease Artemis in the non-homologous end-joining (NHEJ) pathways of double stranded DNA break repair (Sibanda et al., 2017). While the majority of the sequence was assigned manually using aromatic and selenomethionine anchoring, three regions in the density map that are clearly helical remain unassigned to sequence. The helices are posited to reside in a 199-residue “disordered” region that contains the phosphorylation sites of the ABCDE cluster, found between residues 2609–2638, crucial to regulation of DNA-PKcs-DNA-Ku interactions (Dobbs et al., 2010; Hammel et al., 2010; Jette and Lees-Miller, 2015; Uematsu et al., 2007), possibly through allosteric regulation (Sibanda et al., 2017), a critical step in the NHEJ pathway (Ding et al., 2003). While these sites are known to be autophosphosphorylated (Block, 2004), it is unknown whether kinase activity is performed within the same chain (intra-molecular) or in the adjacent chain (inter-molecular) of the synaptic complex. Should the ABCDE cluster be in or near the three unassigned helices, it would preclude intra-molecular kinase activity from this configuration as these helices are 50–70 Å from the kinase site; [Figure 1D]. Thus, reducing the uncertainty in the sequence localization of the ABCDE cluster could provide insight into the nature of this phosphorylation event.

Figure 1: Structure of DNAPKcs and identification of unassigned helices.

A) The crystal structure of human DNA-PKcs (5LUQ) is shown in blue cartoon. Red cartoon identified the residues with only C_α coordinates assigned. The structure has been fitted to the 4.4 Å resolution EM map, (grey volume), (Sharif et al., 2017) which shows no density in the unassigned region. The yellow star indicates the position of the kinase active site. B) Zoom-in of unassigned region highlighting the three helices identified by DSSP as red, green and orange. The pink and yellow cartoon identifies the structured and assigned residues immediately N- and C-terminal of the disordered domain. C) Blue bars identify residues with both structure and sequence identification in the crystal structure. The inset highlights the 199-residue disordered region of interest in this study. The sector corresponding to the ABCDE cluster of phosphorylation sites (residues 2609–2638) is identified in pink. D) Cartoon representation of DNA-PKcs with the kinase domain in light blue and kinase active site as a yellow star. Potential threading arrangements that include a long linker between the ABCDE cluster (pink) and unassigned helices (colored bars) could allow an intra-molecular autophosphorylation event (left), while localization on or near the ordered helices would require a conformational change or inter-molecular autophosphorylation mechanism (right). Panels A and B were generated in part using VMD. (Humphrey et al., 1996)

We apply integrative threading to localizing the three unassigned helices of DNA-PKcs within the 199-residue disordered region by collecting and using chemical crosslinking and hydrogen-deuterium exchange information along with physics- and knowledge-based restraints. The results show that the critical autophosphorylation residues may exist close to the observed helical density, well out of range of the kinase site. This finding suggests that this region of DNA-PKcs may undergo a conformational rearrangement prior to phosphorylation or that it proceeds via an inter-molecular autophosphorylation.

2. Materials and Methods

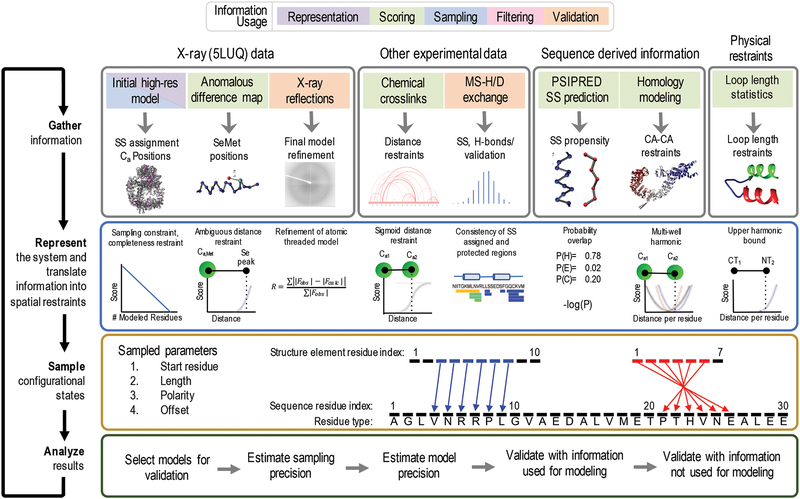
Integrative structure determination (ISD) proceeds in four steps [Figure 2]. (Alber et al., 2008, 2007; Kim et al., 2018; Russel et al., 2012) First, input information about the system is gathered, including experimental data and prior information (physical theories, statistical preferences, and other prior models). Second, the system is represented in a manner that allows for useful interpretation of the model, sufficiently efficient sampling, and convenient translation of input information into spatial restraints. Third, alternative models are sampled and potentially filtered to find those models that sufficiently satisfy the input information (if any). Finally, the uncertainty of these models is estimated to properly qualify their interpretation.

Figure 2: Four stages of integrative threading of DNA-PKcs using IMP:SSEThread.

The full integrative threading protocol proceeds through four stages. In stage 1, we gather all information about the system that we wish to use and decide at which stage of modeling we will apply it. In stage 2, we define a representation that includes the degrees of freedom we wish to assess and translate the information from stage 1 into spatial restraints [Section 2.2.2]. In stage 3, we sample alternative threading models using a Monte Carlo approach, using the scoring function from stage 2 as a guide [Section 2.2.3]. Finally, in stage 4 we assess the set of models generated in stage 3 by filtering those models that satisfy the input information, estimating the sampling and modeling precision as well as validating the models by both data used for modeling and data not used for modeling (orange boxes in stage 1).

2.1. Gathering Information

2.1.1. Backbone model

We began by identifying segments of unassigned sequence with contiguous secondary structure longer than three residues using the secondary structure dictionary DSSP (Joosten et al., 2011). This assignment resulted in the identification of distinct secondary structure elements, denoted herein as SEs, including alpha-helices of at least three residues and others. For each residue in a SE, the X-ray model provides the coordinates of the C_α atom, although it does not identify its residue type.

2.1.2. Sequence

The sequence of amino acid residues informs the likely distance between the pair of residues at each end of a disordered loop connecting two SEs.

2.1.3. Secondary structure and disorder propensities

The secondary structure propensity for each residue in DNA-PKcs was calculated using PSI-PRED (Buchan et al., 2013) and the propensity for disorder determined using DISOR-PRED (Jones and Cozzetto, 2015), based on its sequence.

2.1.4. Distance-per-residue of loops

A statistical potential for loop-length was extracted from the DINGO-PCS algorithm, in which this potential aided protein structure determination from pseudo-contact shift data by paramagnetic NMR spectroscopy (Pilla et al., 2017). This potential was extracted from a set of 63,864 domains as defined by the CATH 3D structural database (Sillitoe et al., 2015). Specifically, the S100 dataset of CATH 3D, which contains exclusively 3D structures without sequence redundancy. The domains were further divided into super-secondary structural motifs (Smotifs) (Fernandez-Fuentes et al., 2010) from which the loop-length statistical potential was derived. An elemental Smotif is defined as a pair of regular secondary structure elements connected by a loop; the two types of secondary structure element include the β-Strands and helices (α-helices, 3₁₀-helices, and Π-helices). By this definition, there are only four basic types of Smotifs, including helix-loop-helix, sheet-loop-sheet, helix-loop-sheet, and sheet-loop-helix. The STRIDE program (Frishman and Argos, 1995) was used to define the secondary structure elements for all CATH domains. For each loop length (≤ 30 residues) in each of the four different Smotif types, the statistical potential is defined by the mean and standard deviation of the C_α-C_α Euclidian distances between the C-terminal residue of the first secondary structure element and the N-terminal residue of the adjoining secondary structure element (Table 1).

Table 1:

Distance-per residue values for secondary-structure bounded loops

Loop length	Helix-loop-helix (Mean)	Helix-loop-helix (SD)	Sheet-loop-sheet (Mean)	Sheet-loop-sheet (SD)	Sheet-loop-helix & helix-loop-sheet (Mean)	Sheet-loop-helix & helix-loop-sheet (SD)
1	3.81	0.027	3.81	0.027	3.809	0.067
2	3.036	0.284	3.19	0.313	3.137	0.278
3	2.836	0.397	1.846	0.293	2.818	0.361
4	2.511	0.441	1.607	0.469	2.482	0.418
5	2.275	0.483	1.274	0.419	2.154	0.45
6	2.178	0.499	1.14	0.474	1.928	0.448
7	2.026	0.504	1.139	0.49	1.749	0.455
8	1.876	0.537	1.198	0.505	1.67	0.436
9	1.835	0.534	1.177	0.447	1.531	0.452
10	1.669	0.538	1.115	0.501	1.428	0.438
11	1.658	0.545	1.029	0.475	1.377	0.416
12	1.666	0.507	1.048	0.479	1.282	0.407
13	1.625	0.494	0.935	0.417	1.261	0.402
14	1.53	0.468	0.91	0.451	1.203	0.411
15	1.445	0.447	0.908	0.416	1.135	0.405
16	1.374	0.428	0.85	0.373	1.045	0.381
17	1.292	0.439	0.83	0.395	1.004	0.378
18	1.212	0.415	0.852	0.47	1.02	0.373
19	1.164	0.432	0.849	0.418	0.977	0.36
20	1.133	0.392	0.761	0.36	0.928	0.372
21	1.049	0.382	0.722	0.349	0.865	0.338
22	1.043	0.38	0.742	0.359	0.834	0.322
23	1.074	0.401	0.684	0.312	0.811	0.308
24	0.977	0.381	0.677	0.302	0.756	0.285
25	0.965	0.38	0.611	0.281	0.761	0.289
26	0.938	0.317	0.587	0.279	0.749	0.296
27	0.868	0.328	0.596	0.264	0.777	0.298
28	0.824	0.304	0.565	0.259	0.74	0.294
29	0.805	0.318	0.576	0.346	0.655	0.286
30	0.788	0.273	0.532	0.257	0.648	0.208

The mean and standard deviation of the distance-per-residue for loops based on number of residues and bounding secondary structure element was determined from the CATH S100 database as described in [2.1.4]. Helix-loop-helix and sheet-loop-sheet values were computed using 1,668,774 and 614,152 Smotif elements, respectively. Sheet-loop-helix and helix-loop-sheet observations were combined, with a total of 1,416,244 Smotif elements (702,557 sheet-loop-helix and 713,687 helix-loop-sheet) used to compute the values.

2.1.5. Chemical cross-linking

Full-length DNA-PKcs was purified from human cells as previously described (Goodarzi and Lees-Miller, 2004) and prepared to a concentration of 0.7 μM in 20mM HEPES pH 7.5, 75mM KCl, 5mM MgCl₂, and 0.5mM DTT. In separate experiments, the protein was crosslinked with DSS (disuccinimidyl suberate) (Creative Molecules Inc.), DSG (disuccinimidyl glutarate) (Creative Molecules Inc.), and BS(PEG)₅ (PEGylated bis(sulfosuccinimidyl)suberate, Thermo Scientific Inc.). Multiple concentration ratios of crosslinker to protein were prepared for each to improve the sampling of crosslinkable sites. Crosslinking proceeded at 37°C for 30 minutes with shaking, except BS(PEG)₅, which was conducted at 30°C. Crosslinking reactions were quenched by adding ammonium bicarbonate to a final concentration of 50 mM. Samples were digested overnight at 37°C with trypsin, using 1:30 enzyme-to-substrate ratio (w/w). To further enrich for crosslinked peptides, some digests were reconstituted in SEC (size exclusion chromatography) mobile phase (30% acetonitrile, 0.1% FA (formic acid)) and separated on a Superdex Peptide PC 3.2/30 column (GE Healthcare Inc.). All samples and SEC fractions were reconstituted in 0.1% FA prior to mass spectrometric analysis, on a nanoLC-Orbitrap Velos (Thermo Scientific Inc.). Samples were loaded on a 10cm × 75μm self-packed picotip column (Aeris Peptide XB-C18, 3.6 μm particle size, Phenomenex). Separation was achieved using a 30-minute gradient (5–60%) of mobile phase B (97% acetonitrile with 0.1% formic acid) at 300 nl/minute. The Velos was operated in positive ion mode, using a high/high configuration where MS resolution was set at 60,000 (400–2000 m/z) and MS² resolution at 7500. Up to ten of the most abundant ions were selected for fragmentation using higher energy collisional dissociation (HCD), rejecting charge states 1 and 2, and using a normalized collision energy of 40%. Crosslinks were identified using the Mass Spec Studio crosslinking plug-in. (Sarpe et al., 2016)

2.1.6. Hydrogen-deuterium exchange

Kinetics data from Sheff J.G. et al were mined to determine the protection factors for peptides in the central cavity of DNA-PKcs (Sheff et al., 2017). To distinguish structured from unstructured peptides, we calculated an average exchange rate constant k_HX from timecourse data (0.5, 1, 5, 15 and 60 min) and referenced these values against the calculations of rate constants for the corresponding unstructured peptides according to the equation S_SSEThread = S_SS + S_LL + S_XL + S_Tem + S_Com + S_SeMet, where P_f represents the averaged protection factor for a given peptide i, k_ch the averaged exchange rate for the unstructured form of the peptide, calculated according to (Bai et al., 1993), and k_HX the measured average exchange rate constant for peptide i. For the purposes of this study, a peptide was considered to be highly structured if log (P_f) > 1.

2.2. Representing the system and translation information into spatial restraints

Some of the gathered information is used to define the representation of the model, the choice of which defines the variables that are fit to input information; a set of values of these variables (parameters) comprises the model. For example, an atomic model is represented by Cartesian coordinates of its atoms. In general, the system is represented in a manner that allows useful interpretation of the model, sufficiently efficient sampling, and convenient translation of input information into spatial restraints.

2.2.1. System Representation

Here, each unassigned secondary structure element (Section 2.1.1; SE) is defined by four variables that map it to specific residues in the sequence: 1) Start Residue, defining the first residue in the sequence to which the SE is mapped, 2) Length, the number of residues in the sequence overlapping with the SE, 3) Offset, the index of the first SE residue that is assigned to the sequence, and 4) Polarity, which defines the direction of the mapping between the SE and the sequence [Figure 4].

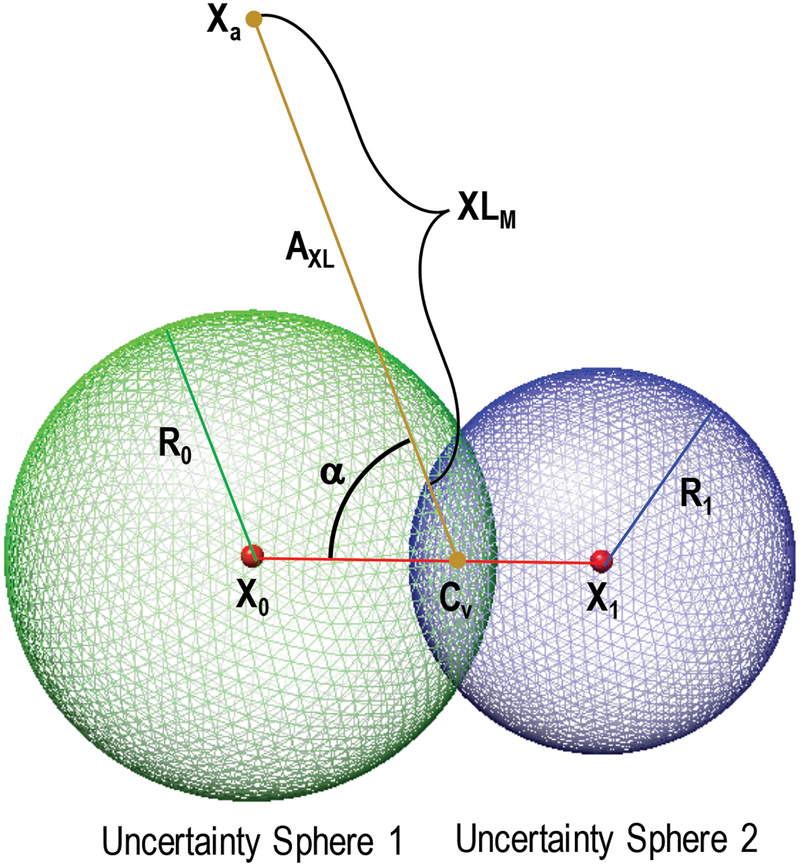
Figure 4: Formulation of crosslinking restraint for unstructured residues.

Schematic of the evaluation of the model crosslinking distance, XL_M, for a single unstructured residue between residues with coordinates at X₀ and X₁ and a structured residue at coordinate X_A. See Section 2.2.2.3 for a complete description of the evaluation of XL_M.

2.2.2. Spatial restraints

With the representation in hand, we can now use some of the input information to define the spatial restraints that comprise the scoring function. The relative importance of each piece of information in the scoring function is determined by the magnitude of the difference between the scores for good and poor fitting models. The restraints, including their weights, should be defined so as to not over- or under-utilize a given piece of information (Adams et al., 1997; Brunger et al., 1999). Here, we develop restraints to have similar contributions to the overall score in the neighborhood of the global optimum.

2.2.2.1. Secondary structure restraint

The secondary structure restraint is computed by comparing the secondary structure assignment in the input X-ray structure with the secondary structure propensity computed from the input sequence. The restraint is calculated for those residues in the sequence that are mapped to SEs in the model. The restraint on residue i in the sequence reflects the difference between the DSSP secondary structure assignment of the SE and the PSIPRED secondary structure propensity for the mapped sequence: S(M|PSIPRED)_i = −log(PSIPRED(SS(M)_i), where the PSIPRED score, S(M|PSIPRED)_i, for a residue, i, is defined as the negative log of the PSIPRED probability, PSIPRED(SS(M)_i), of the DSSP assigned secondary structure, (SS(M)_i, for that residue. The total secondary structure score, S_SS, is the sum of the scores for all SE-assigned residues in the model, S_SS = ∑ −log(PSIPRED(SS(M)_i).

2.2.2.2. Loop length restraint

A restraint on the Cartesian distance between the C- and N-termini of sequentially adjacent SEs is computed from the statistical preferences for end-to-end loop distance in a representative set of known protein structures: S_LL = K_LLR(d_M - n_r(δ(n_r, s) + σ(n_r, s)))², where the loop length score, S_LL, is evaluated based on the distance observed from the model, d_M, and the number of residues between the terminal residues, n_r. δ(n_r,s) and σ(n_r,s) are the distance and standard deviation of the distance per residue based on the number of residues and terminal secondary structure elements (s) as described in Section 2.1.4. The harmonic constant, k_LLR, is determined by trial-and-error, with values from 0.5–1.0 / Ų providing values for this restraint that are comparable to the other information-based scores.

2.2.2.3. Crosslinking restraint

A crosslinking restraint on a pair of residues reflects the observation of a crosslink between those residues. Each observation of MS-linked peptides was converted into a harmonic upper-bound on the restraint distance: S_XL,i = k_xl(XL_M,i - XL_0,i)², where the score for an individual crosslink, S_XL,i, is evaluated based on the crosslink distance observed from the model, XL_M,I and the length of the experimental crosslinking reagent plus side chain lengths, XL_0,i. The harmonic constant, k_xl, is found to be effective between values of 0.1–1 / Ų, with a value of 0.5 used herein. When XL_M,I < XL_0,i, the score is evaluated as zero. For a crosslink with both residues in structured domains, XL_M,i is evaluated as the distance between the two C_α coordinates from the evaluated model.

To evaluate an observed crosslink where one or both crosslinked residue(s) have unknown position(s), we compute the distance from the edge of the volume of uncertainty containing the unstructured residue(s). The volume of uncertainty of a residue is defined as a sphere centered at the nearest structured residue(s) with a radius that depends on the number of residues between the positioned residue and the cross-linked residue (Section 2.1.4). For those unstructured crosslinked residues with only one adjacent positioned residue (and thus, on an N- or C-terminal tail), the volume of uncertainty is defined simply as this sphere with radius, R₀, and center C_v located at the coordinate of the adjacent positioned residue, X₀. The evaluated model restraint distance, XL_M,i, of a crosslink between this residue and a positioned residue at point X_a is simply the minimum distance between the point X_a and the sphere of uncertainty: XL_M,i = ‖X₀ - X_a‖ - R₀.

For a residue in a loop bounded by two SEs, the volume of uncertainty is defined as the intersection between the two sphere volumes whose centers are at the coordinates of positioned residues, X₀ and X₁, and whose radii are R₀ and R₁, respectively [Figure 4]. The center of the volume, C_v, is defined as the center of the circle defined by the intersection of the two spheres. The coordinate, C_v can be determined from the sphere parameters along the vector X₀→X₁ as follows: $C_v= X_0+\frac{1}{2}*\frac{\left(R_0^2-R_1^2\right)}{2{‖X_0-X_1‖}^2}*(X_0-X_1)$. We then define a crosslinking vector, A_xl, as the vector between the centers of uncertainty volumes for each endpoint (a structured endpoint will have no uncertainty volume and A_xl is determined from the structured coordinate). The evaluated model restraint distance, XL_M,i, is then evaluated as the magnitude of A_xl minus an uncertainty distance, U, for each volume: XL_M,i = ‖A_xl‖ - U₁ - U₂. The uncertainty distance for a sphere intersection volume is determined by subtracting the distance from C_v to the edge of the sphere cap along the crosslinking vector, A_xl. This is evaluated as: $U= -d*\text{sin}\left(\propto \right)+\sqrt{d^2*\left({\text{sin}\left(\propto \right)}^2-1\right)}+R^2$, where α is the angle between the vector defined by (X₀ - X₁) and A_xl and d is the distance between the sphere center and the volume center, d = ‖X − C_v‖.

For cases where the uncertainty sphere centered at one structured endpoint envelops the uncertainty sphere at the other endpoint (R₁ > |X₀ - X₁| - R₀), then the crosslink model distance is calculated the same as for a residue in a terminal loop described above.

The total crosslinking score, S_XL, is then the sum over all N individual crosslinking terms in a dataset, $S_{XL}=\sum _{i=1}^N{S}_{XL,i}$.

This method trades a small amount of accuracy for significantly increased efficiency. Evaluating the true minimum distance between volumes of uncertainty comprising sphere caps requires numerical integration of the volumes, which is computationally expensive (we estimate about 50-fold slower than the described algorithm, depending on the size of the volumes and desired accuracy). As this restraint in its current form is generally the rate-limiting step in scoring function evaluation, any increased complexity would hinder the ability of IMP:SSEThread to quickly score and sample alternative states.

2.2.2.4. Template-based restraint

Template-based restraints on the modeled sequence were imposed based on its alignment to related template structures using the standard comparative modeling formalism implemented in MODELLER (Sali and Blundell, 1993). Specifically, each restraint is a cubic spline fitted to a weighted sum of multiple Gaussian functions, where each Gaussian function accounts for one template structure; the mean of the Gaussian is equal to the template distance, while the corresponding standard deviation and weight reflect the local sequence similarity to the modeled sequence. For a template-based restraint based on N templates, the total score of this contribution, S_Tem, is the sum of the negative log of each individual Gaussian: $S_{Tem}=\sum _{i=1}^N{S}_{XL,i}$

2.2.2.5. Structure completeness restraint

Our representation allows for the length of the SEs to change, thus, some coordinates from the initial model may not be applied to the threading models. We implement a restraint to encode our belief that the observed residues are there, by imposing a linear score on the length of each SE. This penalty is applied as 4 times the difference between the number of coordinates in the SE, X_SE, and the SE length key, L_SE. The structure completeness score, S_SC, is evaluated over all N SEs as: $S_{SC}=\sum _{SE=1}^{N}4*(L_{SE}-X_{SE})$.

2.2.2.6. Selenomethionine anomalous scattering restraint

Anomalous scattering peaks from SeMet substituted X-ray data provide a spatial restraint for the localization of methionine residues, however the mapping of a methionine residue to a specific peak is usually ambiguous. Here, a restraint is applied to each observed anomalous peak center, X_Se,i. The distance between X_Se,i and each positioned methionine C_α atom, X_Met,j, is calculated and the smallest distance used to evaluate the restraint, which is formulated as an upper harmonic restraint with center at 3.5 angstroms (the approximate distance between the C_α and SG atoms in methionine): S_SeMet,i = k_SeMet(‖X_Se,i - X_Met,j‖ - 3.5)². The harmonic spring constant, k_SeMet, is set to 2 / Ų. For systems with multiple anomalous peaks, we ensure that each methionine can only satisfy one anomalous peak restraint by first satisfying the restraint with the smallest X_Se,I to X_Met,j distance and removing all distances to this specific X_Met,j from the remainder of the anomalous restraints. The total selenomethionine restraint score is the sum over all N selenomethionine anomalous scattering peaks: $S_{\mathit{SeMet}}={\sum }_{i=1}^N{S}_{\mathit{SeMet},i}$.

2.2.2.7. Combined IMP:SSEThread scoring function

The combined scoring function for IMP:SSEThread consists of the sum of all individual components described above:

$$S_{\mathit{SSEThread}}= S_{SS}+S_{LL}+S_{XL}+S_{Tem}+S_{Com}+S_{\mathit{SeMet}}$$

Any additional scoring terms defined in IMP, such as FRET (Bonomi et al., 2014), SAXS (Schneidman-Duhovny et al., 2013), and pairwise statistical potentials (Dong et al., 2013), may also be included. In addition, weights may be applied to individual scores in case certain terms appear to be under- or over-valued.

2.2.3. Sampling

Sampling must explore the values of the four variables describing each SE comprising the model. The goal is to find those models that score well given the scoring function defined above.

The sampling space depends on the number of unassigned residues, lengths of the unassigned regions, and the number of SEs. For systems with small disordered regions and few SEs, the space can be effectively enumerated.

For models that cannot be enumerated, we implemented a stochastic Monte Carlo scheme (Metropolis and Ulam, 1949). Each independent Monte Carlo sampling is initiated with a random allowed value for the starting residue and polarity for each SE; the length was set to the number of residues in each SE and the offset set to zero. Next, a series of random moves of five types are applied before evaluation of the Metropolis criterion (Metropolis et al., 1953) with the “temperature” fixed at a value of 5 (chosen by trial and error), using the scoring function defined above as the “energy function”. In each Monte Carlo step, five discrete moves are considered for each SE in the system. First, the start residue of that SE can shift up or down by an integer number of residues chosen at random from a range (−5 to 5 utilized here); 2) the length can shift up or down by one (not to exceed the total number of coordinates in the SE); 3) the offset can shift up or down by one, subject to the constraints of the length parameter and number of coordinates; 4) the polarity of the SE is multiplied by −1; 5) The start residue of this SE is exchanged with that of another random SE. Typically, ten to twenty independent Monte Carlo runs are executed.

2.2.4. Analysis

The resulting model ensembles generated by sampling must be analyzed to ensure sampling exhaustiveness (for those analyzed by random sampling methods), filtered to include only those models that satisfy the input information and clustered to assess the precision of the model and potential multiple solutions.

Sampling precision, defined as the smallest clustering threshold that produces clusters proportional to the size of the two (or more) sets of independent input ensembles, is assessed using a modified form of the method developed for structural models (Viswanath et al., 2017). In this embodiment, the distance between two models is assessed using the sum of the difference of the sequence number assigned to each SE residue divided by the total number of SE residues, resulting in a measure similar to RMSD, but for residue numbers. The precision of each SE in each cluster is then assessed by computing the standard deviation of the start residue for that SE over all models in that cluster.

2.3. Benchmark System

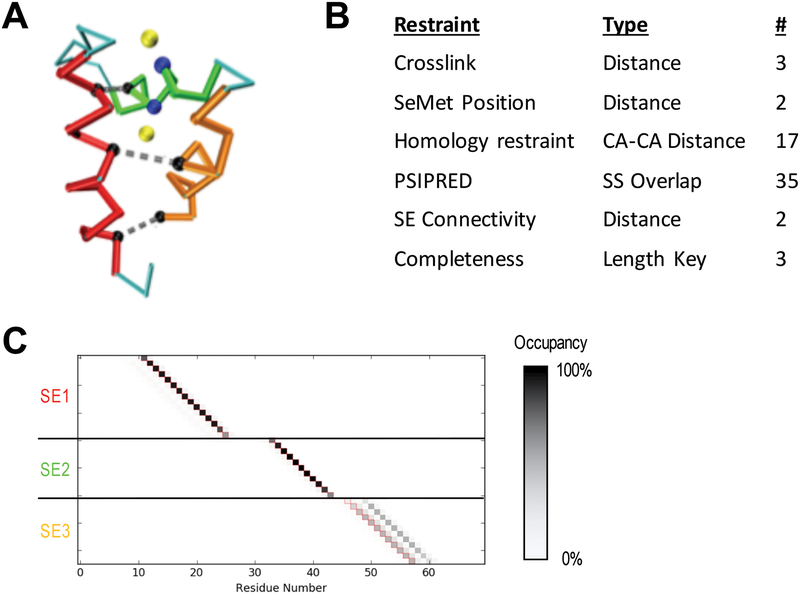
A benchmark system was used to test the algorithm and assess sampling parameters. The PHD domain of human MLL5 (PDB 2LV9) contains three helices in a single globular domain [Figure 5]. Three simulated distance restraints of 8 angstroms were generated between three sets of residue pairs: (4, 47), (11, 40) and (15, 29). Additionally, selenomethionine restraints were applied at the site of the SG atoms of the two methionine residues (30, 32). End-to-end distance restraints and a secondary structure restraint was also applied.

Figure 5: Simulated benchmark results.

A) C_α trace of the human MLL5 PHD domain (PDB 2LV9) showing the three identified SEs (red, green, orange), distance restraints used (grey dashed lines connecting black residues), and SeMet restraints (yellow atoms are anomalous peaks and blue atoms are the corresponding Methionine C_αs). B) Table of restraints for SE localization using IMP:SSEThread. C) Residue occupancy of the top 5000 threading models following enumeration of all possible states. Each box represents the mapping of a residue in sequence (X-axis) to a coordinate in a structure element (Y-axis). A black box indicates that 100% of the top models map the corresponding residue to the structure element coordinate. SE3 shows multiple threading possibilities that are equally likely. The correct threading solution is indicated by the red outline of the boxes.

Three structural elements were generated of 15, 11 and 12 residues, corresponding to each of the three helices and the set of possible models enumerated.

2.4. Integrative threading of DNA-PKcs

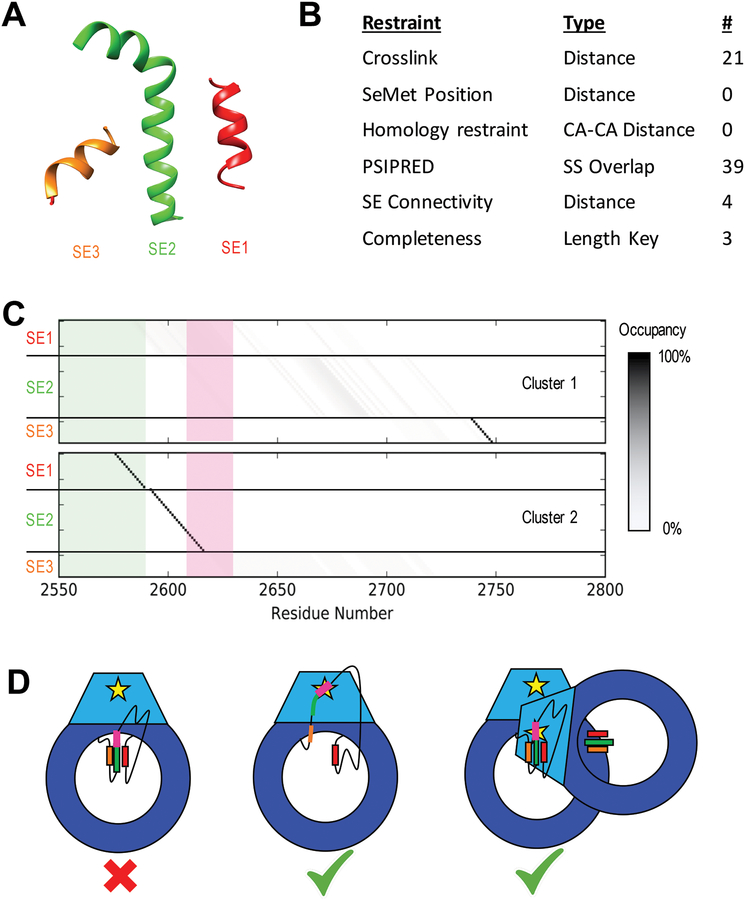
The crystal structure of DNA-PKcs contains a region of electron density that has been fitted with a poly-alanine model. DSSP secondary structure assignment identified three distinct helices of 14, 25, and 10 residues, which were modeled as SEs [Figure 6A]. The 199-residue disordered region of DNA-PKcs (2576 to 2774) was considered for threading these SEs. Twenty-one crosslinks (5 DSS, 6 DSG, and 10 BS(PEG)5) were observed with at least one endpoint in the disordered region, resulting in one crosslinking restraint each [Section 2.2.2.3]. In addition, 39 PSIPRED residue secondary structure restraints [Section 2.2.2.1], three completeness restraints [Section 2.2.2.5] and four loop length restraints [Section 2.2.2.2] were also imposed [Figure 6B].

Figure 6: Results of DNA-PKcs threading.

A) Cartoon models of the three unassigned helices assigned as SEs in the DNA-PKcs crystal structure in space relative to each other (Figure 1A). B) Table of restraints utilized for SE localization using IMP:SSEThread. C) Residue occupancy of the two clusters of models identified from the top 500 threading models following enumeration of all possible start residues values. Each box represents the mapping of a residue in sequence (X-axis) to a coordinate in a structure element (Y-axis). A black box indicates that near 100% of the top models map that residue in sequence to that structure element coordinate. The green shadow highlights residues identified by hydrogen exchange as being partially protected. Cluster 1 shows a high specificity for SE3 near residue 2740 with SE1 and SE2 highly variable. Cluster 2 localizes SE1 and SE2 with high precision and has SE3 disordered. The threading solutions for SE1 and SE2 also match the HDX data, which suggest some local order in these regions. The ABCDE cluster (pink) is unlocalized in Cluster 1, while it occurs at the N-terminal end of SE2 in Cluster 2, highly constraining its position in space. D) Cartoon models of potential autophosphorylation mechanisms for the ABCDE cluster of DNA-PKcs based on Cluster 2 models. The intra-molecular mechanism (left) is not supported by this model, as the ABCDE cluster (pink) in SE2 (green) cannot interact with the kinase site (yellow star). The helices could potentially unravel (center), allowing the cluster to interact with the kinase site on the same chain. Alternatively, the other DNA-PKcs molecule in the synaptic complex could position itself to perform an inter-molecular autophosphorylation (right).

Unfortunately, no suitable template structures were found for the 199-residue disordered sequence of DNA-PKcs, and no methionine peaks are observed near the unassigned helices, so we were not able to include a template-based restraint or methionine restraint as originally hoped.

Sampling was performed by enumeration of start residue values for each of the three SEs, constrained by the residues in the disordered domain (2576–2774), disallowing overlaps in SE residues and loops shorter than two residues. The polarity key was fixed to result in left-handed helices only. This enumeration resulted in 2.86M alternative threading models that were divided into 64 subsets and evaluated in parallel on 64 2.2GHz Intel Xeon Silver 4114 CPUs, requiring a total of approximately 400 hours of CPU time. The top 5000 scoring models were clustered by K-means clustering as implemented in the Python library scikit-learn (Pedregosa et al., 2011), producing two clusters of models.

3. Results and Discussion

3.1. Benchmarking

We started by benchmarking our method on a modeling problem that is similar in type and scope to the application of integrative threading to a region of DNA-PKcs, namely threading three helices in the context of a globular domain whose structure is known. Threading of the benchmark provided unambiguous localization of first two of the three SEs to their exact locations in the structure [Figure 4C]. The C-terminal SE is localized to within 3 residues, with two major populations: one at the correct location and one three residues N-terminal. This displacement corresponds to approximately a single helical turn, which places the residues of the helix on the same side of the helix but shifted up one turn. This displacement allows the short distance restraints between helix 1 and helix 3 to be satisfied, illustrating both the lack of precision resulting from a relatively small amount of input information and the ability of our method to enumerate all solutions consistent with this information, including the correct configuration.

3.2. Structural mass spectrometry data

An extensive set of crosslinks was obtained from the application of three different crosslinkers (DSS, DSG and BSP) to DNA-PKcs. For the central cavity, we identified 21 high confidence long-range crosslinks (defined as spanning sites at least 100 residues apart) with one of the two crosslinked sites residing within the disordered region (Figure S1A). An inspection of the solution hydrogen exchange data for this region revealed that structured elements appear to penetrate into this nominally disordered region (Figure S2B). Most notably, there is a strongly structured segment from 2576 to 2586 at the C-terminus of the region, and another from 2764 to 2774 on the N-terminal end. The intervening sequence may adopt secondary structural elements, but the resolution of the kinetics measurements suggests these would be highly dynamic.

3.3. Sequence localization of the unassigned helices in DNA-PKcs

DNA-PKcs modeling revealed two distinct clusters of models, each one of which satisfies a subset of the input data: Cluster 1, comprising 61% of the good scoring models, satisfies all restraints except for the two connectivity restraints between SE1-SE2 and SE2-SE3. In contrast, Cluster 2 satisfies all connectivity restraints, while violating five crosslinking restraints (a crosslink restraint is violated when the distance between the model evaluated distance is greater than 5 Å longer than the length of the crosslinker plus side chains). Cluster 1 places the SE3 helix between residues 2740 and 2754, with a precision of 10.3 residues, while the SE1 and SE2 helices are not well localized. In contrast, Cluster 2 shows the SE1 and SE2 helices in adjacent series from residues 2577–2590 and 2594–2619, with precisions of 2.3 and 3.8 residues, respectively, with the SE3 helix not localized [Figure 6C].

Hydrogen exchange data show that the sequence assignment of SE1 predicted in Cluster 2 overlaps with the N-terminal area observed to have a moderate-to-high degree of protection [3.2], while the localized SE3 helix of Cluster 1 is not observed as protected [Figure 6C]. The parsimony between Cluster 2 and the HDX data, along with the good scoring models of Cluster 1 violating physics-based connectivity restraints is a small indication that Cluster 2 is the more relevant model. In addition, the lack of localization of SE1 and SE2 in Cluster 1 results in little insight into the spatial localization of the ABCDE cluster [Figure 6C, pink], precluding any further interpretation.

Should Cluster 2 be the correct threading model, this would place the critical phosphorylation sites of the ABCDE cluster in or just N-terminal of SE2. In the DNA-PKcs structure, this would put them 40–50 Å from the kinase site of that molecule, indicating that these residues are either activated by an inter-molecular autophosphorylation event, or a conformational change involving unraveling of these helices is required for phosphorylation to be performed by the same chain [Figure 6D].

In general, the lack of certainty in the output models (here, the existence of two instead of one cluster and the ambiguous placement of some helices in each cluster) can result from the lack of input information and modeling errors, which, in turn, include errors in the scoring function, sampling, and representation of the system. The precision of the scoring function could be improved by adding terms for additional crosslinking data and hydrogen exchange data. The accuracy of the scoring function might be improved by more objective relative weighting of the restraints relative to each other (e.g., via Bayesian data likelihoods and noise models (Bonomi et al., 2014; Molnar et al., 2014; Saltzberg et al., 2017)). Even though the sampling of alternative discrete threadings is exhaustive by construction, it may still be necessary to sample alternative models at higher resolution to find accurate structures. For example, it may be necessary to shift the helix positions slightly or distort the helices, which would, in turn, allow for artifacts in the crystal structure, such as the helical segments observed in the crystal not existing in the same position or conformation under the conditions of the crosslinking experiments. The representation of the system could be made more detailed by allowing for multi-state behavior and/or including side chains, which would, in turn, allow scoring of excluded volume and nonbonded interactions (currently, these considerations are satisfied by a residue-level model by construction because the sequence is threaded on the fixed X-ray structure).

Even though integrative threading of DNA-PKcs has not yet produced a complete and precise model, it did allow an increased understanding of the system given the current information. It also provides a framework for incorporating more information into the modeling, should it become available.

3.4. Potential applications of IMP:SSEThread

By implementing the SSEThread method in IMP, a number of additional, already implemented scoring function terms can be conveniently added to the IMP:SSEThread method, if the corresponding data are available; for example, pairwise statistical potentials (Dong et al., 2013), SAXS (Schneidman-Duhovny et al., 2012), NMR, electron density (Velazquez-Muriel et al., 2012) and FRET (Bonomi et al., 2014). Similarly, additional scoring function terms that do not yet exist in IMP and would be useful for SSEThread could easily be implemented; for example, scoring a threading model by converting it into an atomic model followed by its assessment against an input electron density map. In addition, for large sampling problems, IMP’s existing message passing DOMINO algorithm (Lasker et al., 2009) and stochastic sampling methods, such as various implementations of the Monte Carlo scheme, could be used instead of the enumeration applied for DNA-PKcs. Estimates of sampling precision by stochastic methods can also be immediately applied. (Viswanath et al., 2017) Finally, implementation in IMP will allow hybrid threading/structural modeling, where the threading assignment is sampled along with the positions of the residues (e.g. disordered residues or loops) and evaluated against a single scoring function, similarly to the MOULDER algorithm. (John and Sali, 2003)

3.5. Availability of software

SSEThread is implemented as a module of IMP (IMP.threading), which is freely available at https://integrativemodeling.org under the GNU Lesser general Public License. The input and output files for the benchmark and DNA-PKcs are available at https://github.com/salilab/SSEThread. In addition, the integrative model of DNA-PKcs and modeling protocols are deposited in the PDB-dev repository (Vallat et al., 2018), accession code PDBDEV_000000XX.

4. Conclusion

We describe a method, IMP:SSEThread, to represent, sample, and assess alternative threadings of a sequence into a given backbone model, based on multiple types of input information. By implementing the method in IMP, threading models can be evaluated by custom scoring functions already available in IMP. We have applied this method to reducing uncertainty in the sequence localization of three unassigned helices in the DNA-PKcs crystal structure, gaining insight into the nature of the autophosphorylation mechanism and potentially guiding more informative future experiments.

Supplementary Material

Supplemental Figure 1

Figure S1. Information from Mass Spectrometry. A) Identified crosslinks with one end terminating in the 199 residue disordered region (yellow box). Red are DSS crosslinks, blue are BS(PEG)₅ crosslinks, and green DSG crosslinks. B) Hydrogen-deuterium exchange data of peptides around and spanning the 199 residue disordered region (yellow box). Each black bar is a unique peptide. Peptides with a log(protection factor) below 1 (red dotted line) were considered to have no measurable protection. Panel A was generated using xVis. (Grimm et al., 2015)

Figure 3: Relationship between structure element keys and threading model.

A SE defines a secondary structure designation, a set of C_α coordinates and four keys that map these coordinates to residues in the primary sequence. SE1 defines the C_α coordinates of ten residues of a helix and the set of four keys map the six blue coordinates onto sequence. The start residue, 4, denotes that the threaded sequence begins at residue four, the length, 6, means six total coordinates from the SE are assigned, a polarity of 1 assigns the coordinates in advancing order and an offset of 2 begins from coordinate 3 in the structure element. SE2 shows a similar assignment, beginning at residue 21; however, the polarity of −1 flips the assignment, such that the last assigned coordinate in the SE is threaded to the sequence at residue 21 and the remainder of the SE is assigned backwards.