A Fast and Accurate Method for Genome-wide Scale Phenome-wide G × E Analysis and Its Application to UK Biobank

Abstract

The etiology of most complex diseases involves genetic variants, environmental factors, and gene-environment interaction (G × E) effects. Compared with marginal genetic association studies, G × E analysis requires more samples and detailed measure of environmental exposures, and this limits the possible discoveries. Large-scale population-based biobanks with detailed phenotypic and environmental information, such as UK-Biobank, can be ideal resources for identifying G × E effects. However, due to the large computation cost and the presence of case-control imbalance, existing methods often fail. Here we propose a scalable and accurate method, SPAGE (SaddlePoint Approximation implementation of G × E analysis), that is applicable for genome-wide scale phenome-wide G × E studies. SPAGE fits a genotype-independent logistic model only once across the genome-wide analysis in order to reduce computation cost, and SPAGE uses a saddlepoint approximation (SPA) to calibrate the test statistics for analysis of phenotypes with unbalanced case-control ratios. Simulation studies show that SPAGE is 33–79 times faster than the Wald test and 72–439 times faster than the Firth’s test, and SPAGE can control type I error rates at the genome-wide significance level even when case-control ratios are extremely unbalanced. Through the analysis of UK-Biobank data of 344,341 white British European-ancestry samples, we show that SPAGE can efficiently analyze large samples while controlling for unbalanced case-control ratios.

Introduction

Most complex diseases, such as type 2 diabetes and cancers, have an etiology influenced by genetic variants, lifestyles, and environmental factors. Besides their marginal effects, the gene-environment interaction (G × E) also plays an important role for complex diseases and is worthy of comprehensive investigation. Identifying G × E effects is particularly important for personalized and stratified prevention and treatment. However, compared to identifying genetic marginal effects, more samples and detailed environmental exposure information are required in order to identify G × E effects, and this limits the possible discoveries.^{1, 2, 3, 4, 5, 6, 7, 8, 9}

The advances in genotyping technologies and electronic health records (EHRs) make it possible to genotype hundreds of thousands of samples and identify a large number of traits.^{10, 11, 12, 13, 14, 15} For example, UK Biobank includes 500,000 genotyped samples and more than 1,000 phenotypes and exposures from ICD billing codes, web surveys, and lab measurements.¹⁶ Through genome-wide × phenome-wide association analysis, these massive datasets have resulted in a considerable number of new genetic associations across different phenotypes, and the associations could provide evidence for pleiotropy or shared pathways for disease pathogenesis.^{17, 18, 19} All these motivate the development of genome-wide scale phenome-wide G × E study (PheWIS).

Currently, however, no scalable statistical methods exist for a genome-wide scale G × E study of thousands of phenotypes in large biobanks. For the analysis of genetic marginal effects, the score test has provided fast computation. In contrast to Wald and likelihood ratio tests, the score test does not require us to fit the model under the alternative hypothesis. Score tests use the parameter estimates under the null hypothesis to calculate test statistics and p values. Because the null model for marginal genetic effects does not include genetic variants, for a single phenotype, score tests require fitting one null model only and use it for the genome-wide tests.^20,21 However, for the analysis of G × E, because the null model includes genetic variants to adjust for genetic marginal effects, the same trick cannot be used. Score tests for G × E need to fit a separate model for each variant, which results in tens of millions of model fittings, like Wald and likelihood ratio tests.²² For example, suppose that fitting a single model takes ∼1.7 s (as in Supplementary Methods in the Supplemental Data: a standard logistic regression with 400,000 samples and five covariates); in that case, fitting 20 million models would take more than 1 year. Although more optimized tools such as CGEN²³ and GxEScan²⁴ have been developed, because these tools mainly implement the Wald test, the computation burden is still very high.

Alternatively, a two-step procedure which screens out variants based on marginal genetic associations can be used instead.^{25, 26, 27, 28, 29, 30} However, because this approach excludes a majority of variants in the screening step, it can miss potential G × E and cannot generate genome-wide summary statistics of G × E; these summary statistics can be useful resources for phenome-wide analysis, for meta-analysis, or as a validation dataset.^{31, 32, 33} Another possible two-step procedure is a case-only (CO) analysis for screening followed by a case-control test to validate the association.^{34, 35, 36} This is a computationally efficient approach, especially when case-control ratio is low. However, as shown in our simulation studies, CO analysis can be less powerful than case-control analysis for a cohort study design. In addition, when the gene-environment independence assumption is violated, CO analysis can be biased.⁵

Given that the data are collected in large cohorts, unbalanced case-control ratios are commonly observed. For example, most binary phenotypes in UK Biobank (1,431 out of 1,688; 84.8%) have case-control ratios lower than 1:100.¹⁵ These unbalanced case-control ratios will result in incorrect type I error rates. For the genetic marginal effect test, saddlepoint approximation (SPA) has been used to control the type I error rates in such situations.^{12, 13, 14, 15,37} However, the effect of case-control imbalance for the G × E analysis has not been well studied.

In this paper, we propose a SaddlePoint Approximation implementation of G × E analysis (SPAGE), a fast and accurate method that is scalable for a genome-wide scale single-variant G × E analysis and is well calibrated for controlling type I error rates even under unbalanced case-control ratios. The proposed method fits a genotype-independent logistic model only once for the genome-wide analysis and then uses a conditional expectation to exclude the marginal genetic effect. The SPA, instead of normal approximation, is used to calibrate p values so that type I error rates can be controlled under unbalanced case-control ratios. The method is valid for analyzing both hard-called genotypes and imputed dosage values. Through simulation studies and applications to UK Biobank data of 344,341 unrelated samples from white British participants, we demonstrate that SPAGE is computationally feasible, can control type I error rates, and is sufficiently powerful to identify several G × E signals for a number of diseases including chronic airway obstruction (CAO), cardiac dysrhythmias (CDR), and hyperlipidemia (HLD).

Material and Methods

Logistic Regression Model and Score Statistics

For a single-variant test, we consider the following logistic model $H_{\text{Θ}}$:

$$\text{logit}\left({\mu }_i^{\text{Θ}}\right)=X_i^T{\beta }_X+E_i{\beta }_E+G_i{\beta }_G+G_i{E}_i{\beta }_{G\times E},i=\mathrm{1,2},\dots ,N,$$

where ${\mu }_i^{\text{Θ}}=\mathrm{Pr}\left(Y_i=1|X_i,G_i,E_i\right)$ is the probability of a binary phenotype (e.g., disease status) $Y_i=1$ for subject i, conditional on the covariates, genotypes, and an environmental factor. We let $X_i$ denote a $p\times 1$ vector of covariates including the intercept; $G_i$ the hard-called genotypes $\left(G_i=0,1,2\right)$, genotypes $\left(G_i=0,1\right)$ following a dominant or recessive model,³⁸ or dosage values of the genetic variant to be tested;$E_i$ the environmental factor of interest; ${\beta }_X$ a $p\times 1$ coefficient vector corresponding to covariates; ${\beta }_G$ the marginal genetic effect; ${\beta }_E$ the marginal environmental effect; and ${\beta }_{G\times E}$ the G × E effect. N is the total number of all samples. Suppose that covariates matrix X, genotype vector G, and G × E interaction vector $G_E$ are

$$X=\left(\begin{array}{cc}{X}_1^T& E_1\\ ⋮& ⋮\\ X_N^T& E_N\end{array}\right),G=\left(\begin{array}{c}{G}_1\\ ⋮\\ G_N\end{array}\right),G_E=\left(\begin{array}{c}{G}_1{E}_1\\ ⋮\\ G_N{E}_N\end{array}\right),$$

then the matrix form of the model $H_{\text{Θ}}$ is $\text{logit}\left({\mu }^{\text{Θ}}\right)=X\alpha +G{\beta }_G+G_E{\beta }_{G\times E}$ where $\alpha ={\left({\beta }_X^T,{\beta }_E\right)}^T$.

Under the model $H_{\text{Θ}}$, we are interested in testing for the marginal G × E effect. The classic score test first fits the null model $H_0:{\beta }_{G\times E}=0$ to estimate $\left({\hat{\alpha }}^{H_0},{\hat{\beta }}_G^{H_0}\right)$, and then calculates ${\hat{\mu }}^{H_0}={\text{logit}}^{-1}\left(X{\hat{\alpha }}^{H_0}+G{\hat{\beta }}_G^{H_0}\right)$ and uses $S^{H_0}=G_E^T\cdot \left(Y-{\hat{\mu }}^{H_0}\right)$ as a test statistic with a mean of zero. Because the null models $H_0$ vary for different variants, this strategy requires a separate model fitting for each variant, which is computationally expensive for a genome-wide analysis.

Instead of fitting the null model $H_0$, we fit a genotype-independent model, $H_c:{\beta }_G={\beta }_{G\times E}=0$, to estimate ${\hat{\alpha }}^c$, and then we calculated ${\hat{\mu }}^c={\text{logit}}^{-1}\left(X{\hat{\alpha }}^c\right)$ as the estimated probability of being a case under the model $H_c$. Suppose that W is an $N\times N$ matrix with ${\hat{\mu }}_i^c\left(1-{\hat{\mu }}_i^c\right)$ as the i^th diagonal element, and

$$\tilde{G}=G-X{\left(X^{T}WX\right)}^{-1}{X}^{T}WG,{\tilde{G}}_E=G_E-X{\left(X^{T}WX\right)}^{-1}{X}^{T}W{G}_E,$$

are covariate-adjusted vectors in which covariate effects are projected out from genotype and G × E interaction vectors, respectively. We propose a test statistic $S=\left({\tilde{G}}_E^T-\lambda {\tilde{G}}^T\right)\cdot \left(Y-{\hat{\mu }}^c\right)$, where $\lambda ={\tilde{G}}_E^{T}W\tilde{G}/{\tilde{G}}^{T}W\tilde{G}$. In Appendix A, we use Taylor expansion to show that S approximates $S^{H_0}$, and the variance of $S$, $Var\left(S\right)$, is approximated by $\left({\tilde{G}}_E^T-\lambda {\tilde{G}}^T\right)W\left({\tilde{G}}_E-\lambda \tilde{G}\right)$.

Using statistic $S$ to approximate $S^{H_0}$ greatly reduces the computation time because $S$ requires fitting the genotype-independent model $H_c$ only once for a genome-wide analysis. However, because the approximation is based on Taylor expansion around $\left(\alpha ={\hat{\alpha }}^c,\beta =0\right)$, it can provide inaccurate results when the marginal genetic effect is large. To avoid possible inflated type one error rates caused by an inaccurate approximation, we use a hybrid strategy to determine the appropriate test statistic. We first conduct a standard score test to test for the marginal genotype effect by using score test statistic $S_G=\tilde{G}\cdot \left(Y-{\hat{\mu }}^c\right)$. If the score test p value is greater than a pre-selected cutoff $\epsilon$, we use $S$ as the test statistic. Otherwise, we estimate ${\hat{\mu }}^{H_0}$ and calculate $S^{H_0}$ as the test statistic. This hybrid strategy is a pragmatic compromise between efficiency and accuracy. We set the cutoff $\epsilon =0.001$ in simulation studies and real data analyses.

For the subset of variants whose marginal genetic effect p value $<\epsilon$, we use a method developed by Dey et al. to calculate $S^{H_0}$. Instead of fitting the model $H_0$, this method estimates the genetic effect ${\hat{\beta }}_G^{H_0}$ based on score statistics $S_G$ while adjusting for covariates.³⁹ Compared to the Firth’s method, this method reduces the computational complexity from O(Nk²+k³) to O(N), where k is the number of non-genetic covariates. In this paper, we first use this method to estimate the marginal genetic effect ${\hat{\beta }}_G^{H_0}$. Then we update ${\hat{\alpha }}^{H_0}={\hat{\alpha }}^c-{\left(X^{T}WX\right)}^{-1}{X}^{T}WG{\hat{\beta }}_G^{H_0}$ and estimate ${\hat{\mu }}^{H_0}={\text{logit}}^{-1}\left(X{\hat{\alpha }}^{H_0}+G{\hat{\beta }}_G^{H_0}\right)$ and $S^{H_0}=G_E^T\cdot \left(Y-{\hat{\mu }}^{H_0}\right)$.

The hybrid strategy above is different from the conventional two-step methods. The two-step methods only calculate G × E p values of the variants whose marginal genetic effect p values are below the threshold, but the proposed approach obtains G × E p values across the whole genome regardless of their marginal genetic effects. Compared to the constrained marginal G × E test under a constrained model ${\beta }_G=0$, the proposed test statistic adjusts for the marginal genetic main effect (see Appendix A).

p Value Calculation with Saddlepoint Approximation

The classical likelihood-based test approximates the null distribution of statistics $S$ through the use of a normal distribution with a mean $E\left(S\right)$ and a variance $Var\left(S\right)$. The normal approximation works well when the statistic $S$ is near the mean of the distribution, but it performs poorly at the tails, especially when the underlying distribution is highly skewed, such as in an unbalanced case-control setting. In this situation, SPA performs well because higher moments can be incorporated. Because our test statistic can be written as a weighted sum of mean adjusted $Y_i$ given ${\hat{\mu }}_i^c$,

$$S=\sum _{i=1}^N\left({\left({\tilde{G}}_E\right)}_i-\lambda {\tilde{G}}_i\right)\cdot \left(Y_i-{\hat{\mu }}_i^c\right)$$

and $Y_i\sim \text{Bernoulli}\left({\hat{\mu }}_i^c\right)$, the entire cumulant-generating function (CGF) of $S$ is

$$K\left(t\right)=\sum _{i=1}^N\text{log}\left(1-{\hat{\mu }}_i^c+{\hat{\mu }}_i^c{e}^{{\text{Δ}}_{i}t}\right)-t\sum _{i=1}^N{\text{Δ}}_i\cdot {\hat{\mu }}_i^c,$$

where ${\text{Δ}}_i={\left({\tilde{G}}_E\right)}_i-\lambda {\tilde{G}}_i$. The distribution of $S$ at the observed statistic $s$ can be approximated by $\mathrm{Pr}\left(S<s\right)\approx \tilde{F}\left(s\right)=\text{Φ}\left\{\omega +1/\omega \cdot \text{log}\left(\nu /\omega \right)\right\}$, where $\omega =\text{sgn}\left(\hat{t}\right)\sqrt{2\left(\hat{t}s-K\left(\hat{t}\right)\right)},\nu =\hat{t}\sqrt{K\text{'}\text{'}\left(\hat{t}\right)}$, $\hat{t}$ is the solution to the equation $K^{\text{'}}\left(\hat{t}\right)=s$, and $\text{Φ}$ is the distribution function of a standard normal distribution. When the testing is based on the classic score statistic $S^{H_0}$, i.e., marginal genetic effect p value $<\epsilon$, we can simply follow the SPA proposed by Dey et al.¹²

Implementation Details and Approaches to Reducing Computation Time

Because the normal approximation behaves well near the mean of the distribution, we can use it to obtain the p values when the observed score statistic lies close to the mean of 0.¹² We apply the normal approximation to obtain a p value if the absolute value of the observed score statistic $\left|S\right|<r\sigma$, where $\sigma =\sqrt{Var\left(S\right)}$ and $r$ is a pre-specified value. For example, we use $r=2$ in our simulation studies and real-data analyses. When $\left|S\right|\ge r\sigma$, we use the SPA to obtain calibrated p values in tail areas. Because using the normal approximation takes less time than using the SPA, this approach also reduces the computation time.¹²

Similar to the fastSPA method¹² designed for genetic marginal effects, the SPA method requires only $O\left(N\right)$ computations and can be further decreased to $O\left(m\right)$ computations, in which $m$ is the number of non-zero elements in $G$. Since $N\times \left(p+1\right)$ matrix $X{\left(X^{T}WX\right)}^{-1}$ can be pre-calculated, and matrix $W$ is diagonal, the calculations of $\tilde{G}$ and ${\tilde{G}}_E$ require $O\left(pN\right)$ multiplications. Given $\tilde{G}$ and ${\tilde{G}}_E$, the calculations of the score statistics $S$ and the corresponding variances $Var\left(S\right)$ take $O\left(N\right)$ multiplications. Hence, the total computation complexity is still $O\left(pN\right)$.

Numeric Simulations

We carried out extensive simulation studies to evaluate computation time, type I error rates, and powers of SPAGE. Three case-control ratios were considered: balanced (case:control = 1:1), moderately unbalanced (case:control = 1:9), and unbalanced (case:control = 1:99). For each choice of case-control ratios, a binary phenotype for individual $i$ was simulated from the following logistic model:

$$\text{logit}\left[\mathrm{Pr}\left(Y_i=1\right)\right]={\alpha }_0+0.5X_{1i}+0.5X_{2i}+0.5E_i+G_i{\beta }_G+{\left(G_E\right)}_i{\beta }_{G\times E}$$ (1)

where a binary covariate $X_{1i}$ was simulated following a Bernoulli(0.5) distribution, a continuous covariate $X_{2i}$ was simulated following a standard normal distribution, an environmental factor $E_i$ was simulated following a standard normal distribution, and a genotype $G_i$ was simulated following a binomial$\left(2,p\right)$ distribution where $p$ is the minor allele frequency (MAF). Parameters ${\beta }_G$ and ${\beta }_{G\times E}$ are log odds ratios of the marginal genetic effect and the G × E effect, respectively. Intercept ${\alpha }_0$ was chosen to correspond to the given case-control ratio.

To evaluate computation time in realistic scenarios, we randomly sampled MAFs from the MAF distribution in the UK-Biobank dataset and then simulated 10,000 variants with ${\beta }_G={\beta }_{G\times E}=0$. Two scenarios were considered in order to compare computation time for different methods. First, we fixed the sample size at 400,000 and increased the total number of covariates from 5 to 30. Then, we fixed the number of covariates at 15 and increased the sample size from 10,000 to 400,000. Besides the two covariates $X_{1i}$ and $X_{2i}$ in Equation (1), the other covariates were simulated following a standard normal distribution. We compared the computation time of six different tests: Wald test for the logistic regression that fits a complete model for each variant (Wald), Firth’s penalized likelihood ratio test (Firth’s test), the normal-approximation-based test (SPAGE-NoSPA), the fast SPA-based test with a standard deviation threshold $r=2$ (SPAGE), the constrained maximum likelihood method (CML) implemented in R package CGEN (version: 3.18.0), and the CO approach implemented in GxEScan (version: 1.0). As the same as CO, CML assumes the gene-environment independence. The CO approach in GxEScan uses a polytomous logistic regression to adjust for covariates. We modified the core codes (C in CGEN and C++ in GxEScanR) to suppress the unnecessary parts so that we can accurately record the computation time of CML and CO.

To evaluate type I error rates under the null model ${\beta }_{G\times E}=0$, we fixed the sample size at 50,000 and simulated ${10}^9$ variants of which 99.9% had no marginal genetic effect and the other 0.1% had marginal genetic effects with an odds ratio of 1.4. This corresponds to having 1,000 causal variants in an analysis with one million variants. We compared empirical type I error rates of Wald, Firth’s test, SPAGE-NoSPA, and SPAGE at significance levels $\alpha =5\times {10}^{-5}$ and $5\times {10}^{-8}$. In addition, we also evaluated SPAGE when the marginal genetic odds ratio ranged from 1.1 to 1.5. Due to the heavy computational burden, it is practically impossible to perform Wald and Firth’s test ${10}^9$ times. Following Dey et al.,¹² we performed a hybrid approach in which we used Wald and the Firth’s test to calculate p values only when the SPAGE p values were smaller than $5\times {10}^{-3}$.

To evaluate powers under the alternative model, we fixed the sample size at 50,000, considered a wide range of $\left({\beta }_G,{\beta }_{G\times E}\right)$, and simulated ${10}^5$ variants for each choice of $\left({\beta }_G,{\beta }_{G\times E}\right)$. We compared the empirical powers of SPAGE, Wald, and Firth’s tests at significance levels $\alpha =5\times {10}^{-5}$ and $5\times {10}^{-8}$. We also evaluated CML and empirical Bayes (EB) implemented in CGEN. Note that all datasets were simulated following a cohort study design.

Application to UK Biobank Data

To illustrate the performance in a real-data application, we applied the proposed methods to UK Biobank. Environmental factors and phenotypes were defined based on UK Biobank field ID (FID) and PheWAS codes (PheCodes), respectively.^{12,13,15,16,18,40} We selected 79 pairs of environmental factors and phenotypes (see Table S3) including five environmental factors: smoking status (FID: 20116), vigorous physical activity (FID: 904), moderate physical activity (FID: 804), gender (FID: 31), and alcohol intake frequency (FID: 1558). More details about these environmental factors can be seen in Supplementary Methods in the Supplemental Data.

We randomly selected 344,341 unrelated samples from white British participants and restricted our analysis to markers directly genotyped or imputed by the Haplotype Reference Consortium (HRC)⁴¹ panel due to quality control issues of non-HRC markers reported by UK Biobank. Approximately 28 million markers with minor allele counts (MAC) $\ge$ 20 and imputation info scores > 0.3 were used in the analysis. For each binary phenotype, we further removed markers with less than five minor alleles in the cohort of cases.

We incorporated the first four principal components plus birth year, gender, and the environmental factor of interest as covariates to fit null models. Smoking status was encoded to numeric variables of 0, 1, and 2 to represent never, former, and current smoker, respectively. Vigorous and moderate physical activities were encoded to categorical variables ranging from 0 to 7 based on the number of days per week the individual exercised for 10+ minutes. Alcohol intake frequency was encoded to categorical variables ranging from 1 (daily or almost daily) to 6 (never). When fitting a null model, we considered the physical activities and alcohol intake frequency as categorical variables in order to avoid inaccurate type I error rates because most complex diseases were not additively affected by these variables.⁴² On the other hand, when calculating G × E interaction vector $G_E$, we considered the physical activities and alcohol intake frequency as numeric variables in order to avoid testing with multiple degrees of freedom. We applied the SPAGE-NoSPA and SPAGE methods to the genome-wide analyses for all 79 pairs of environmental factors and phenotypes, and we used Wald and Firth’s test for only one pair of alcohol and colorectal cancer. In addition, we also used Wald and Firth’s test for all variants identified by SPAGE method at a significance level of $5\times {10}^{-8}$.

Results

Comparison of Computation Time

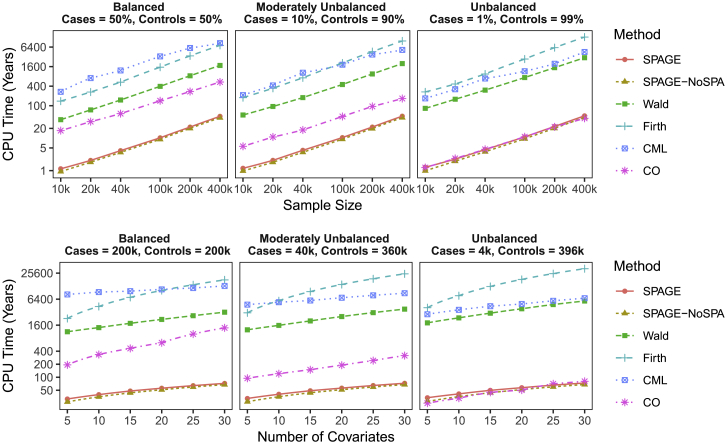
The projected computation time for testing 1,500 phenotypes across 20 million variants via different methods is presented in Figure 1 and Table S1, which shows that SPAGE performed 72–439 times faster than Firth’s test and 33–79 times faster than Wald test. CO took similar time as SPAGE did when the case-control ratio was 1:99, and both were much faster than CML. This is because CO uses case samples only, but CML uses both case and control samples. For example, in an unbalanced case-control setup of 4,000 cases and 396,000 controls, when analyzing 20 million variants across 1,500 phenotypes while adjusting for 15 covariate variables, Firth’s test, Wald test, and CML would require 13,032, 3,010, and 4,517 CPU years, respectively, whereas SPAGE and CO would require only 48.7 and 40.9 CPU years. Hence, SPAGE and CO required 18 days and 15 days (without data reading) on a cluster with 1,000 CPU cores, but Firth’s test, Wald, and CML needed 12.96, 3, and 4.5 years, respectively. Interestingly, when case-control ratio was 1:9, SPAGE was 3.5 times faster than CO (47.57 versus 166.34 CPU years), although CO used only 10% of samples. This may be due to the fact that the model fitting of a polytomous regression is generally slow. Both Wald and Firth’s test took more time when case-control ratio was more unbalanced. This is because the regression took more iteration steps to get a converged parameter estimation (see Supplementary Methods in Supplemental Data).

Figure 1.

Projected Computation Time (CPU Years) for Testing 1,500 Phenotypes across 20 Million Variants

The time is projected based on a simulated dataset with 10,000 variants. For example, suppose that it takes α h to analyze 10,000 variants; then the projected computation time for 20 million variants would be 2,000 × α h. The computation is performed on a CPU of an Intel(R) Xeon(R) E5-2680 v3 @ 2.50GHz processor. Three case-control ratios: balanced with 50% cases and 50% controls, moderately unbalanced with 10% cases and 90% controls, and unbalanced with 1% cases and 99% controls. Minor allele frequencies are sampled from a minor allele frequency distribution of the UK Biobank dataset.

Type I Error Simulation Results

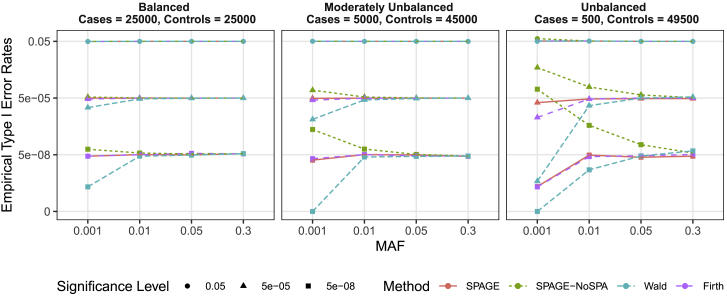
The results of empirical type I error rates based on ${10}^9$ simulated variants with ${\beta }_{G\times E}=0$ are presented in Figure 2 and Table S2. Note that 0.1% of variants (${10}^6$ variants) were simulated with nonzero ${\beta }_G$ = $\text{log}\left(1.4\right).$Under balanced and moderately unbalanced case-control ratios, SPAGE and Firth’s test controlled type I error rates regardless of common, low-frequency, or rare variants. Meanwhile, Wald had deflated type I error rates and SPAGE-NoSPA had inflated type I error rates, especially when testing rare variants with a MAF of 0.001. Under an unbalanced case-control ratio, Wald and SPAGE-NoSPA had more deflated and inflated type I error rates, respectively, while SPAGE and Firth could still control type I error rates reasonably well.

Figure 2.

Empirical Type I Error Rates of SPAGE, SPAGE-NoSPA, Wald, and Firth Tests

Empirical type I error rates were estimated based on 10⁹ simulated variants, of which 99.9% had no marginal genetic effect and the other 0.1% had marginal genetic effects with an odds ratio of 1.4. From left to right, the plots consider case-control ratios of 25,000:25,000 (balanced), 5,000:45,000 (moderately unbalanced), and 500:49,500 (unbalanced).

The results of empirical type I error rates based on ${10}^6$ simulated variants with ${\beta }_G\ne 0$ are presented in Figure S1. If the hybrid strategy was not used to adjust for statistics (denoted as RAW SPAGE and RAW SPAGE-NoSPA), as an increase in marginal genetic effect ${\beta }_G$, the type one error rates of p values increased slowly but constantly. Meanwhile, in these situations, the hybrid strategy provided a better type I error rates control.

Power Simulation Results

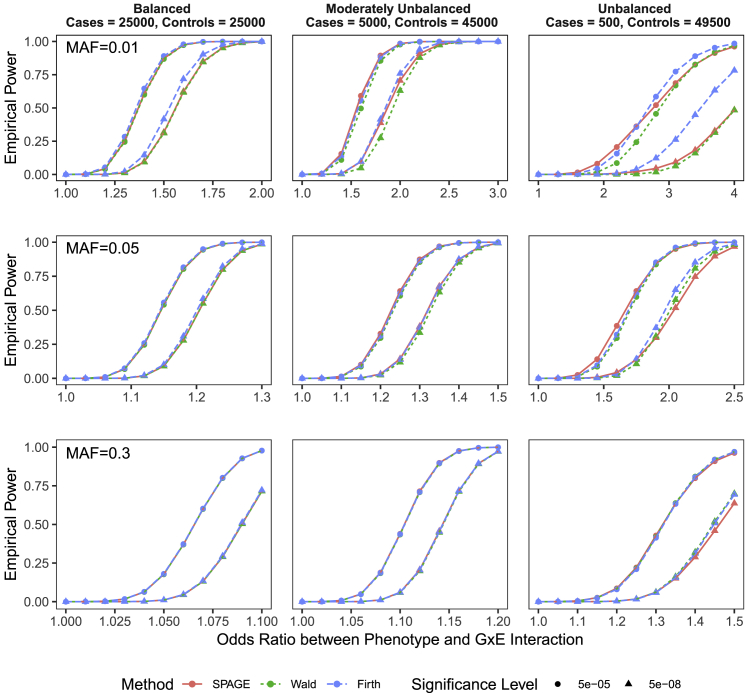
Next, we compared the empirical powers of SPAGE, Wald, Firth’s test, CML, CO, and EB. Because SPAGE, Wald and Firth’s test are all based on a prospective likelihood, the empirical powers of these three methods were similar (see Figure 3 and Figure S2). Only when we tested low-frequency or rare variants under an unbalanced case-control ratio, Firth’s test was more powerful than SPAGE; both of these were more powerful than Wald. Although more powerful, Firth’s test and SPAGE still required very a large effect size to detect a low-frequency or rare variant in G × E analysis; this result is not commonly observed in a practical application.

Figure 3.

Power Comparison of SPAGE, Wald, and Firth Tests

Empirical powers were estimated based on ${10}^5$ simulated variants with ${\beta }_G=0$ and ${\beta }_{G\times E}\ne 0$. From top to bottom, the plots show empirical powers when testing variants with MAFs of 0.01, 0.05, and 0.3. From left to right, the plots consider case-control ratios of 25,000:25,000 (balanced), 5,000:45,000 (moderately unbalanced), and 500:49,500 (unbalanced). Round points are for powers at $\alpha =5\times {10}^{-5}$ and triangle points are for powers at $\alpha =5\times {10}^{-8}$.

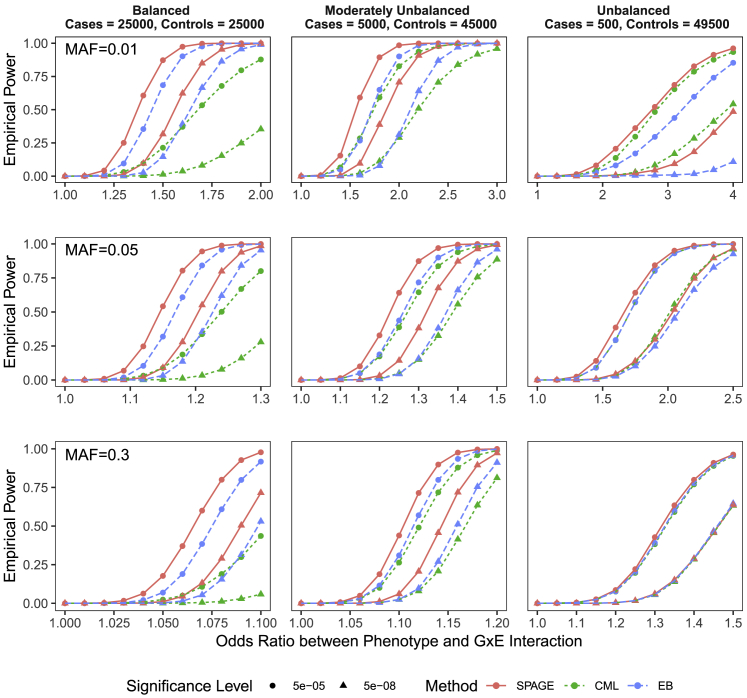
The results of power comparisons of SPAGE, CML, and EB are presented in Figure 4 and Figure S3. Interestingly, the power of SPAGE was generally larger than that of CML and EB. The differences among SPAGE, CML, and EB depended on the case-control ratio, e.g. the prevalence of disease in the cohort. When the case-control ratio was 1:1 or 1:9, SPAGE was more powerful than CML regardless of minor allele frequencies and effect sizes. When the case-control ratio was 1:99, the powers of CML, EB, and SPAGE were similar. The advantage of SPAGE over CML and EB was mainly due to the fact that the data are from a cohort study design instead of a case-control study design. Figure S4 compared empirical powers of SPAGE, CML, and EB methods under different study designs. Under a case-control study design, CML and EB were more powerful than SPAGE, and under a cohort study design, SPAGE was more powerful than EB and CML. We do not show CO because it had a nearly identical power as CML. When testing low-frequency or rare variants with moderate or high G × E effects, CO was generally unstable, especially when case-control ratio was 1:99 (see Figure S5). In terms of powers (assuming G-E independence), under a case-control study design, we still recommend CML and EB methods, and under a cohort-based study design, we recommend the SPAGE method.

Figure 4.

Power Comparison of SPAGE, CML, and EB Tests

Empirical powers were estimated based on ${10}^5$ simulated variants with ${\beta }_G=0$ and ${\beta }_{G\times E}\ne 0$. From top to bottom, the plots show empirical powers when testing variants with MAFs of 0.01, 0.05, and 0.3. From left to right, the plots consider case-control ratios of 25,000:25,000 (balanced), 5,000:45,000 (moderately unbalanced), and 500:49,500 (unbalanced). p values of CML (constrained maximum likelihood) and EB (empirical Bayes) were calculated via an R package CGEN. Round points are for powers at $\alpha =5\times {10}^{-5}$ and triangle points are for powers at $\alpha =5\times {10}^{-8}$.

Application to UK Biobank Data

We applied the proposed SPAGE to UK Biobank to analyze 79 combinations of environmental factors and phenotypes. Under a genome-wide level $\text{α}=5\times {10}^{-8}$, 34 significant G × E signals were identified (see Table S4 for a complete list). Under a Bonferroni corrected threshold $5\times {10}^{-8}/79=6.33\times {10}^{-10}$, there was one signal (rs1906609, p = 1.42$\times$10⁻¹², environmental exposure is gender, and phenotype is CDR) left. Since some phenotypes are strongly correlated, the Bonferroni correction would be over-conservative. Three combinations are highlighted: smoking status and CAO (8,701 cases and 314,750 controls), vigorous physical activity and HLD (27,622 cases and 299,859 controls), and gender and CDR (20,754 cases and 320,152 controls). The complete genome-wide summary statistics for all 79 combinations can be found on our website (see Web Resources).

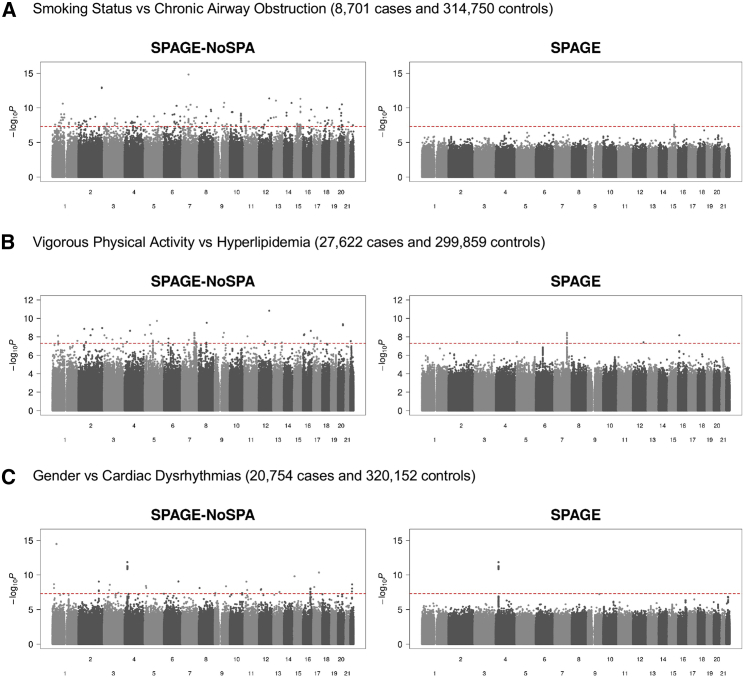
The Manhattan plots (Figure 5) and the QQ-plots (Figure S6) showed that SPAGE-NoSPA produced a large number of potentially spurious associations for G × E association analyses, especially when testing low-frequency and rare variants, whereas the p values of SPAGE closely followed a uniform distribution. Under a significance level $\text{α}=5$ × ${10}^{-8}$, we identified several G × E signals. The top SNPs and a complete list of SNPs whose p values less than $5$ × ${10}^{-8}$ are presented in Table 1 and Table S5, respectively. For each of the top SNPs, the overall and stratified associations of phenotype × genotype and phenotype × environmental factors are presented in Figure 6 and Figure S7, respectively. In addition, we reported the p values of Wald and Firth’s test for the top SNPs. For common and low-frequency variants, the p values of Wald and Firth’s test were similar to the p value of SPAGE, and for rare variants, the p values of Wald were larger than the p values of SPAGE and Firth’s test. For the pair of Alcohol × Colorectal Cancer, QQ-plots and Manhattan plots of Wald and Firth’s test can be seen in Figure S8, from which we can see that the Wald test was conservative when testing low-frequency and rare variants, and p values of the Firth’s test closely followed a uniform distribution. These results are consistent with the simulation results.

Figure 5.

Manhattan Plots for Three Combinations of Environmental Factors and Phenotypes from UK Biobank

The left panels show Manhattan plots based on SPAGE-NoSPA and the right panels show Manhattan plots based on SPAGE. The red line represents the genome-wide significance level $\alpha =5\times {10}^{-8}$.

Table 1.

Top SNPs Identified from UK Biobank G × E Analyses

Environ. Factor	Phenotype	RSID	CHR	Imputation Info	MAF	p Value (G effect)∗	p Value (SPAGE)	p Value (Firth)	p Value (Wald)	Func.refGene	Gene.refGene
Smoking status	chronic airway obstruction	rs55781567	chr15	1	0.3343	7.76E-12	2.87E-08	2.55E-08	2.64E-08	UTR5	CHRNA5
Gender	cardiac dysrhythmias	rs1906609	chr4	0.99	0.1612	3.06E-68	1.42E-12	9.12E-13	1.11E-12	intergenic	PITX2; C4orf32
Vigorous physical activity	hyperlipidemia	rs10950866	chr7	0.99	0.4230	0.2568	3.64E-09	3.82E-09	3.75E-09	intronic	DNAH11

^∗p value of the marginal genetic effect

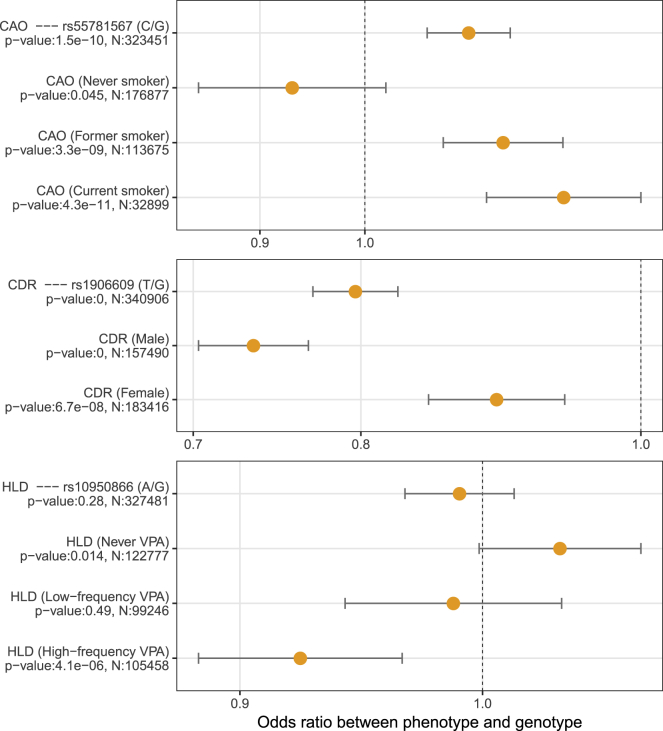
Figure 6.

Associations between Phenotypes and Top SNPs

p values and odds ratios (with 99% confidence interval) were calculated from the Firth’s test. Note that p = 0 means that the Firth’s test p value < 1$\times$10⁻¹⁰⁰. N is the sample size. CAO, chronic airway obstruction; CDR, cardiac dysrhythmias; HLD, hyperlipidemia; CRC, colorectal cancer; VPA, vigorous physical activity; Never VPA: 0 days/week VPA; Low-frequency VPA: ≤2 days/week VPA; High-frequency VPA: >2 days/week VPA.

In the analysis of CAO, we identified a significant G × E effect of smoking status and a variant rs55781567 in CHRNA5 (MIM: 118505). The allele G of the variant rs55781567 is a risk allele in the whole population, and its risk effect will increase significantly for smoker. Smoking is an important risk factor to the CAO, and CHRNA5 is well known to be associated with the smoking behavior and some smoking-related diseases such as chronic obstructive pulmonary disease.^{43, 44, 45} In the analysis of CDR, we identified a significant G × E effect of gender and a variant rs1906609 near PITX2 (MIM: 601542). The allele G of the variant rs1906609 is a protective allele in the whole population (p < 1$\times$10⁻¹⁰⁰), and its effect in males (p < 1$\times$10⁻¹⁰⁰) is significantly larger than that in females (p = 6.7$\times$10⁻⁸). The gene PITX2 plays an important role in cardiac development and diseases, and the incidence of cardiac arrhythmias is known to be different for males and females.^46,47 In the analysis of HLD, we identified a significant G × E effect of vigorous physical activity and a variant rs10950866 in DNAH11 (MIM: 603339). This variant is not significantly associated with HLD in the whole population (p = 0.28), but its G allele is a protective allele for people who take vigorous exercise more than two days per week (p = 4.1$\times$10⁻⁶). The gene DNAH11 has been reported to be associated with serum lipid levels.^48,49

Discussion

In this paper, we have proposed SPAGE, an accurate and scalable method to perform a genome-wide scale phenome-wide G × E analysis for binary phenotypes in large cohorts. SPAGE can adjust for covariates and accurately calibrate p values regardless of minor allele frequencies even in extremely unbalanced case-control settings. Through extensive numerical studies, we have demonstrated that SPAGE can perform 33–79 times faster than the Wald test and 72–439 times faster than the Firth’s test while retaining similar powers and well-controlled type I error rates. Because SPAGE is based on a prospective likelihood method, the genotype-environment independence assumption is not required. The UK Biobank data analysis illustrates that SPAGE can identify G × E signals while controlling for type I error rates, even for binary phenotypes with a small number of cases and a large number of controls.

The current G × E approaches need to fit a null model or a complete model, both of which require adjusting for genotypes separately for each variant. Our method fits a genotype-independent logistic model only once across a genome-wide analysis and then uses a hybrid strategy to exclude marginal genetic effects from the G × E effect. This strategy greatly reduces the computation time so that it is computationally feasible for SPAGE to analyze a large cohort. To calibrate p values, we utilize the SPA when the test statistics deviate from the mean value by more than a pre-specified standard-derivation threshold. Here, we follow the recommendation of Dey et al. to use a threshold of two.¹² Both simulations and application to UK Biobank data showed that the SPA (i.e, SPAGE) performs better than the normal approximation (i.e, SPAGE-NoSPA), so we recommend using SPAGE.

The three commonly used methods for G × E analysis include case-control, CO (or CML), and EB approaches.⁵ Of these, the powers of the case-control approaches increase as the control group size increases. Following a cohort study design, large biobanks collect far more controls than cases for most diseases. In this situation, as a case-control approach, SPAGE can be more powerful than the other methods while remaining computationally efficient. A case-only approach can be a scalable method if the number of cases is moderate or small. However, because the case-only approach requires the gene-environment independence assumption, it cannot be as robust as SPAGE.

Several two-step approaches have been proposed to improve the efficiency of G × E analysis. However, if the screening step is to test the marginal genetic effect or gene-environment independence, it could miss some potential G × E and cannot generate the genome-wide summary statistics. As an accurate and scalable solution, the proposed SPAGE can calculate the genome-wide summary statistics of G × E, which can be of great value for the G × E community. First, phenome-wide G × E analysis can utilize the G × E statistics across multiple phenotypes to provide evidences for pleiotropy. Second, meta-analysis can use the G × E statistics across different studies to improve the power. Third, the genome-wide summary statistics can also facilitate a two-stage discovery-validation study.

Family relatedness is commonly observed in large biobank datasets. To adjust for the sample relatedness, a generalized linear mixed model (GLMM) is widely used.^{50, 51, 52} BOLT-LMM and SAIGE methods used several optimization strategies so that the GLMM could be computationally feasible for large cohorts.^15,52 In the future, we plan to extend the current method to a genome-wide scale G × E analysis with related samples. Another future research area of interest is to design an accurate and fast algorithm to identify rare variants with G × E effect based on gene- or region-based multiple-variant tests.

In summary, we have proposed an accurate and scalable method for genome-wide scale phenome-wide G × E analysis. Large-scale biobanks can be great resources for identifying G × E effects across the genome-wide scale. Our SPAGE method provides a scalable solution for this large-scale problem and contributes to finding novel G × E effects of complex disease. All of our tests are implemented in an R package SPAGE.

Declaration of Interests

The authors declare no competing interests.

Published: November 14, 2019

Appendix A. The Approximation of ${\mathit{S}}^{{\mathit{H}}_0}$

A naive approach is to use $S_{G\times E}^c=G_E^T\cdot \left(Y-{\hat{\mu }}^c\right)$ to approximate $S^{H_0}$ and then to test the G × E marginal effect ${\beta }_{G\times E}=0$. However, this strategy ignores the main genetic effect on phenotype and is only valid under a constrained model ${\beta }_G=0$. To better approximate $S^{H_0}$, we adjust for the main genetic effect by deducting $\lambda {\tilde{G}}^T\cdot \left(Y-{\hat{\mu }}^c\right)$. From the first-order Taylor expansion,

$$\begin{array}{l}{\hat{\mu }}^{H_0}={\text{logit}}^{-1}\left(X{\hat{\alpha }}^{H_0}+G{\hat{\beta }}_G^{H_0}\right)\approx {\text{logit}}^{-1}\left(X{\hat{\alpha }}^c\right)+W\left(X{\hat{\alpha }}^{H_0}-X{\hat{\alpha }}^c+G{\hat{\beta }}_G^{H_0}\right)\\ ={\hat{\mu }}^c+W\left(X{\hat{\alpha }}^{H_0}-X{\hat{\alpha }}^c+G{\hat{\beta }}_G^{H_0}\right).\end{array}$$

$$\text{since}{X}^T\left(Y-{\hat{\mu }}^c\right)=X^T\left(Y-{\hat{\mu }}^{H_0}\right)=0,$$

$$0=X^T\left({\hat{\mu }}^{H_0}-{\hat{\mu }}^c\right)\approx X^{T}WX\left({\hat{\alpha }}^{H_0}-\hat{\alpha }\right)+X^{T}WG{\hat{\beta }}_G^{H_0},$$

$$\begin{array}{l}\text{from}\text{which},{\hat{\alpha }}^{H_0}-\hat{\alpha }\approx -{\left(X^{T}WX\right)}^{-1}{X}^{T}WG{\hat{\beta }}_G^{H_0}.\text{Thus},{\hat{\mu }}^{H_0}-{\hat{\mu }}^c\text{can}\text{be}\\ \text{approximated}\text{as}{\hat{\mu }}^{H_0}-{\hat{\mu }}^c\approx W\left(X{\hat{\alpha }}^{H_0}-X\hat{\alpha }+G{\hat{\beta }}_G^{H_0}\right)\approx W\tilde{G}{\hat{\beta }}_G^{H_0}\text{and}\end{array}$$

$$\begin{array}{l}S=\left({\tilde{G}}_E^T-\lambda {\tilde{G}}^T\right)\cdot \left(Y-{\hat{\mu }}^{H_0}+{\hat{\mu }}^{H_0}-{\hat{\mu }}^c\right)\\ =\left({\tilde{G}}_E^T-\lambda {\tilde{G}}^T\right)\cdot \left(Y-{\hat{\mu }}^{H_0}\right)+\left({\tilde{G}}_E^T-\lambda {\tilde{G}}^T\right)\cdot \left({\hat{\mu }}^{H_0}-{\hat{\mu }}^c\right)\\ \approx \left({\tilde{G}}_E^T-\lambda {\tilde{G}}^T\right)\cdot \left(Y-{\hat{\mu }}^{H_0}\right)+\left({\tilde{G}}_E^T-\lambda {\tilde{G}}^T\right)\cdot W\tilde{G}{\hat{\beta }}_G^{H_0}\\ =\left({\tilde{G}}_E^T-\lambda {\tilde{G}}^T\right)\cdot \left(Y-{\hat{\mu }}^{H_0}\right)=G_E^T\cdot \left(Y-{\hat{\mu }}^{H_0}\right)=S^{H_0}\end{array}$$

The above equation also implies that $E\left(S\right)\approx E\left(S^{H_0}\right)=0$. We assume that the weight matrix $W$ changes slowly with respect to the conditional mean (following Breslow and Clayton⁵³), then our estimate of the variance of S is $Var\left(S\right)\approx \left({\tilde{G}}_E^T-\lambda {\tilde{G}}^T\right)W\left({\tilde{G}}_E-\lambda \tilde{G}\right)$.

Web Resources

• CGEN R package, https://bioconductor.org/packages/release/bioc/html/CGEN.html

• Genome-wide summary statistics, https://www.leelabsg.org/resources

• GxEScan R Package, https://github.com/USCbiostats/GxEScanR

• OMIM, https://www.omim.org

• SPAGE R package, https://github.com/WenjianBI/SPAGE

• UK Biobank, https://www.ukbiobank.ac.uk/