Single-Stranded DNA Translocation Recordings Through Solid-State Nanopores on Glass Chips at 10-MHz Measurement Bandwidth

Abstract

Accurate and low-cost analysis of biomolecules is important for many applications. This work seeks to further improve the measurement bandwidths achievable with solid-state nanopores, which have emerged as an important platform for this analysis. We report single-stranded DNA translocation recordings at a bandwidth of 10 MHz copolymers of 80 (C₂₀A₂₀C₂₀A₂₀), 90 (C₃₀A₃₀C₃₀), and 200 (C₅₀A₅₀C₅₀A₅₀) nucleotides through Si nanopores with effective diameters of 1.4–2.1 nm and effective membrane thickness 0.5 – 8.9 nm. By optimizing glass chips with thin nanopores and by integrating them with custom-designed amplifiers based on complementary metal-oxide-semiconductor (CMOS) technology, this work demonstrates detection of translocation events as brief as 100 ns with a signal-to-noise ratio exceeding seven at a measurement bandwidth of 10 MHz. We also report data robustness and variability across 13 pores of similar size and thickness yielding a current blockade between 30 and 60 % with a mean ionic current blockade (ΔI) of ~ 3 to 9 nA and a characteristic dwell time of ~ 2 to 21 ns per nucleotide. These measurements show that characteristic translocation rates are at least ten times faster than previously recorded. We detect transient intra-event fluctuations, multiple current levels within translocation events, and variability of DNA-translocation-event signatures and durations.

Graphical Abstract

Nanopores are emerging as a versatile platform for studying various biomolecules, such as DNA, providing single-molecule detection, high-throughput, and real-time feedback. In the case of DNA sequencing, nanopores offer the promise of long read lengths and reduced cost.^1–10 Successful nanopore systems for DNA sequencing to date are based on tracking the real-time operation of enzymes operating on a strand of DNA through protein nanopores. In this context, MspA pores in lipid bilayer membranes with ratcheting polymerases have been used to sequence individual DNA nucleotides.⁴

Solid-state nanopore platforms offer an alternative to protein pores, delivering higher signal levels, diameter tunability, and stability. These higher signal levels translate into the ability to achieve better temporal resolution when coupled to optimized electronics,^6–10 which we address in this work. Higher temporal resolution holds the promise of enzymeless, free-running nanopore sequencing when sufficient bandwidth performance can be achieved and if the entropy associated with the DNA motion during translocation can be controlled and reduced. This also benefits enzyme-ratcheting approaches by reducing error rates associated with the temporal stochasticity of enzyme dynamics.

Use of optimized CMOS transimpedance amplifiers has previously been shown to yield faster nanopore recordings.^7,8 In such high-bandwidth measurements, the overall capacitance of the chip, amplifier, and wiring combine with the input-referred voltage noise of the amplifier to determine the total input-referred current noise. Decreasing either of these components helps reduce the overall noise in the recordings. For DNA detection, nanopore diameters, similar to single-stranded DNA (ssDNA) cross-sectional size (~ 1.2 nm), and thin pores, approaching atomic levels comparable to nucleotide spacing (~ 0.3 nm), are optimal.^9–15 Although there is no consensus on the rate of free-running DNA translocation through nanopores, estimated by dividing the total translocation time by the number of nucleotides, speeds of > 10 nts/μs have been reported for silicon based nanopores with similar experimental conditions of buffered KCl solutions, pore diameters < 2 nm, pore thicknesses < 5 nm, and bias voltages up to 1V.^7,8,16 The translocation speed has traditionally been reduced by choosing higher viscosity solutions, heavier ions, or by lowering the solution’s temperature, at the cost of slowing down detection and limiting the size of detectable molecules.^8,9,16–19

In this Letter, we report data from ssDNA translocation recordings from 13 pores at measurement bandwidths up to 10 MHz. Each pore records ~ 10² to 10³ events, and at 10-MHz bandwidth, we detect events and features within an event as short as 100 ns. This capability is achieved by combining custom-designed CMOS amplifiers, glass (fused silica) chips with SiN_x membranes with sub-1 pF to 2 pF capacitance, and 1.4-nm-to-2.1-nm-effective-diameter Si pores with an effective thickness 0.5 to 8.9 nm. While previous work focused on optimizing the chip^20–23 or the amplifier^6,7 separately, optimization of all experimental parts simultaneously (amplifier, membrane, interconnects) is necessary to achieve the results presented here. The membrane capacitance and input capacitance of the amplifier are comparable in our study. We measure time traces of the ionic current for ssDNA from 80 to 200 nucleotides (nts) in length -- poly(dA)₂₀poly(dC)₂₀poly(dA)₂₀poly(dC)₂₀, poly(dC)₃₀poly(dA)₃₀poly(dC)_30, and poly(dA)₅₀poly(dC)₅₀poly(dA)₅₀poly(dC)₅₀. The 20- to 50-nucleotide-long homopolymer segments used here have lengths of 6–15 nm (nucleotide separation is ~ 0.3 nm),¹ designed to be comparable or longer than the pore thicknesses. Pores were drilled in amorphous silicon/SiO_x membranes produced from a local, multi-step thinning of silicon nitride (SiN_x) membranes by reactive ion etching, followed by focused electron beam etching in the scanning transmission electron microscope.²⁴ We report events with signal-to-noise ratios over 7 at 10 MHz with event durations as short as 100 ns.

Results and Discussions

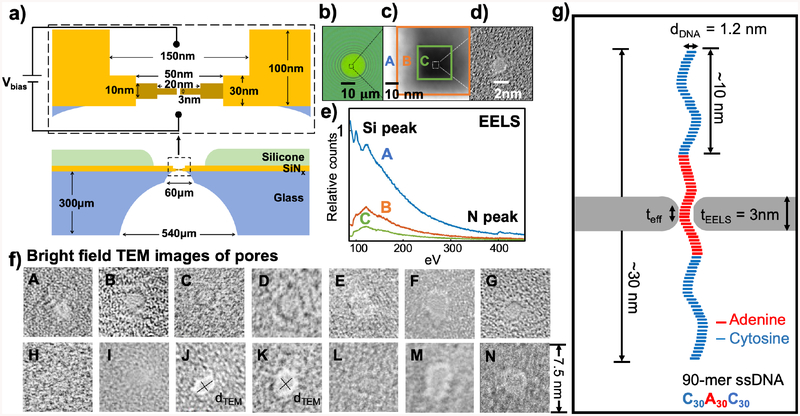
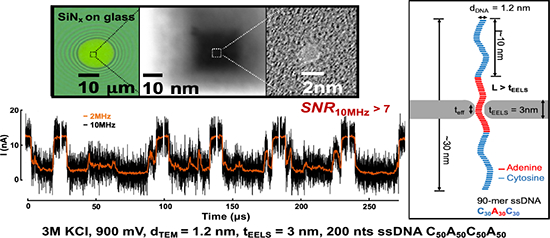
Figure 1a shows a representative cross-section of the nanopores studied in this work. When a bias voltage is applied across two electrolyte solution chambers separated by a dielectric membrane containing a nanopore, ssDNA is driven through the nanopore, blocking the baseline ionic current. This current block can be measured by a sensitive amplifier. To make small-diameter and thin pores within low-capacitance membranes, we fabricate fused-silica (glass) substrates (Figure 1a) instead of using a conventional silicon substrate to suspend the silicon nitride membrane.^7,8 These 300-μm-thick glass chips were especially designed for high-bandwidth experiments to reduce the chip capacitance below 1 pF,^21–23 exposing a circular region of the silicon nitride membrane with a diameter of 10 to 30 μm (Figure 1b). A 30-nm-thick, 150 × 150 nm² region is then produced in this silicon nitride membrane with electron beam lithography and reactive ion etching. Finally, pore diameters and thickness were optimized for ssDNA measurements using a thinning and drilling procedure developed previously on Si substrates.^7,24 The 200-kV focused electron beam was rastered within a 50 × 50 nm² region at high beam current until the thickness decreased from ~ 30 nm to 10 nm. We then scanned over a smaller region of 20 × 20 nm² with a slightly lower beam current to ensure precise control of the thickness to as thin as 1 nm (Figure 1c).²⁴ Molecular dynamics simulations performed previously showed that amorphous silicon membranes can be stable down to 0.7 nm thick,²⁴ consistent with our observations. The adjustment of the TEM beam current is achieved by changing the condenser lens and apertures. The pore is drilled at the thinnest area by holding the beam position fixed at a desired spot for a few seconds resulting in pores < 2 nm in diameter as shown in Figure 1d. The narrow nanopores allow only single-file ssDNA translocation, as the nanopore diameter is only ~ 0.2 to 0.9 nm wider than ssDNA.

Figure 1.

Glass (fused-silica) chips with small and thin solid-state pores. a) Schematics of measurement setup and cross-sectional view of the glass chip and the solid-state pore. b) Circular, 20-μm diameter, suspended SiN_x window on top of fused-silica (glass) substrate. c) High-angle annular dark-field (HAADF) image of thin a-Si/SiO₂ membrane geometry. Labelled “A” is the area that was thinned down to 30 nm by reactive ion etching (RIE) etching. Labelled “B” is the area that was thinned using STEM techniques down to ~10 nm.²⁴ Labelled “C” is the area of the second thinning step where we thin down the membrane to 3 to 8 nm, calibrated by electron energy loss spectroscopy (EELS). d) A bright field (BF) image of nanopore that is drilled in the thinnest region C in part c). e) The EELS spectrum of the respected region in part c). The N peak is completed depleted when a nanopore is drilled. The Si peak is used to monitor the thickness of the thin membrane. Region C has roughly 0.1 relative counts with respect to region A, translating to 3 nm thickness.²⁴ f) BF images of nanopores measured in this work. The TEM diameter (d_TEM) is measured as shown as examples in Pore J and Pore K of elliptical and circular pores. g) The schematics of single-stranded DNA translocation through a nanopore shown to scale with dimension specified.

Figure 1e shows the whole scanning TEM (STEM) thinning process where membrane thickness is monitored and calibrated simultaneously from the electron energy loss spectroscopy (EELS) spectrum. Due to the charging on these glass chips the beam could be moving slightly; therefore, manual correction of positions is required when the beam does not stay in a desired position. Because of the lighter atomic weight of N (=14) compared to Si (=28) atoms, the rate of N atoms being sputtered is faster, resulting in an amorphous silicon membrane by the time it reaches the desired thickness of several nanometers. The EELS spectrum shows that at this stopping thickness, there is no more N peak at ~ 400 eV. The atoms are sputtered from the top and from the bottom resulting in a double-sided, trench-like pore geometry best depicted by Figure 1a. The amorphous silicon is known to naturally oxidize after exposure to air after being taken out of the TEM chamber, resulting in the membrane turning into a-Si/SiO_x; the nanopore shape and size were checked subsequently and remained unchanged in TEM images after the pores were exposed to air and imaging was repeated. Figure 1f shows the TEM bright-field images of nanopores used here, labeled from A to N. The image contrast is weak because the membranes are locally only about one nanometer thick, comparable to the thickness of 2D materials and in contrast to the typical image contrast of thicker SiN_x pores.²⁴ Figure 1g shows an illustration to scale of a 90 nts poly(dC)₃₀poly(dA)₃₀poly(dC)₃₀ ssDNA translocating through a pore with dimensions comparable to those used in this study.

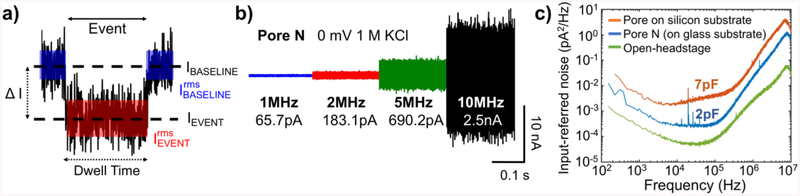
Figure 2a summarizes the relevant signal and noise levels of a typical translocation event. Before and after the event, the average ionic current in the open pore state is denoted as I_BASELINE. The noise in this baseline current, ${\text{I}}_{\text{BASELINE}}^{\text{rms}}$, is the root-mean-square input-referred current noise of the open-pore signal without the presence of translocating DNA. I_EVENT is defined as the mean current value during an event with ΔI = I_BASELINE − I_EVENT. The rms current noise within an event is denoted by ${\text{I}}_{\text{EVENT}}^{\text{rms}}$.

Figure 2.

Translocation event parameters, noise, and noise comparison of glass and silicon chips. a) Schematic of a typical event of ssDNA translocation through a nanopore, taken from Pore F, with important parameters labelled. I_BASELINE, and I_EVENT are taken to be the mean value. The blue box represents the noise in the baseline, ${\text{I}}_{\text{BASELINE}}^{\text{rms}}$, and the red box represents the noise within the event ${\text{I}}_{\text{EVENT}}^{\text{rms}}$. b) Concatenated time trace of a 20-ms-long, 0 mV baseline measurement of Pore N. Each section corresponds to the same trace filtered using a digital four-pole Bessel filter to cutoff frequencies of 1 MHz, 2MHz, and 5 MHz, respectively. The 10 MHz trace has no extra filtering except the effect of an analog four-pole Bessel filter while recording. Corresponding ${\text{I}}_{\text{BASELINE}}^{\text{rms}}$ values are shown below the filtering frequency. c) Input-referred current noise (PSD) for the open-headstage configuration of the amplifier (green), PSD for Pore N on the glass chip (blue), and the PSD for a pore on the silicon chip from Shekar et al. (orange) with chip capacitances of 2 pF and 7 pF, respectively.

In order to observe small changes in the ionic current, increasing signal-to-noise ratio (SNR) is important. We define SNR as $\Delta \text{I}/{\text{I}}_{\text{BASELINE}}^{\text{rms}}$. At sufficiently high bandwidths, ${\text{I}}_{\text{BASELINE}}^{\text{rms}}$ is given by the equation $I_{\mathit{\text{BASELINE}}}^{\mathit{\text{rms}}}(B)=\left(\frac{2\pi }{\sqrt{3}}\right)B^{3/2}C{v}_n$,²⁵ where B is the bandwidth of measurement, v_n is the input-referred voltage noise of the amplifier, and C is the total capacitance at the input of the amplifier and typically consists of the chip capacitance C_chip, the wiring capacitance, C_w, and the capacitance of the amplifier C_amp. Improvements in SNR can be obtained by decreasing ${\text{I}}_{\text{BASELINE}}^{\text{rms}}$ and increasing ΔI.

To estimate I_BASELINE, we use a simple cylindrical resistor model²⁶ of the pore surrounded by the top and bottom ionic hemispheres (access regions), where $R_{\mathit{\text{pore}}}=\frac{4t_{\mathit{\text{eff}}}}{\sigma \pi d_{\mathit{\text{eff}}}{}^2}$, and including the contribution of the access regions, $R_{\mathit{\text{access}}}=\frac{1}{2\sigma d_{\mathit{\text{eff}}}}$, resulting in

$$I_{\mathit{\text{BASELINE}}}=V_{\mathit{\text{bias}}}\sigma {\left(\frac{4t_{\mathit{\text{eff}}}}{\pi d_{\mathit{\text{eff}}}{}^2}+\frac{1}{d_{\mathit{\text{eff}}}}\right)}^{-1},$$

where σ is the conductivity of solution, t_eff is the effective nanopore thickness, and d_eff is the effective nanopore diameter. The current blocked by DNA translocating through the pore can be estimated by

$$\Delta I=\sigma V_{\mathit{\text{bias}}}\left({\left[\frac{4t_{\mathit{\text{eff}}}}{\pi d_{\mathit{\text{eff}}}^2}+\frac{1}{d_{\mathit{\text{eff}}}}\right]}^{-1}-{\left[\frac{4t_{\mathit{\text{eff}}}}{\pi \left(d_{\mathit{\text{eff}}}^2-d_{\mathit{\text{dna}}}^2\right)}+\frac{1}{\sqrt{d_{\mathit{\text{eff}}}^2-d_{\mathit{\text{dna}}}^2}}\right]}^{-1}\right),$$

where V_bias is the applied transmembrane voltage and d_dna is the cross-sectional width of ssDNA. The signal, ΔI, is maximized when the pore diameter approaches the width of DNA and when the nanopore thickness is minimized.

Translocation rates of single-stranded DNA molecules through solid-state nanopores with similar parameters as this work have been reported to be as fast as 1 μs/nt, with studies suggesting significantly faster rates of up to 100 ns/nt.^7,8,16 It is important to note that these per nucleotide translocation rates are rough estimates from the total translocation times measured, using strong assumptions of uniform translocation speeds, and that the start and end of events correspond to DNA entering and leaving the pore. These timescales suggest that single nucleotide detection will require a measurement bandwidth of at least 10 MHz.

Our measurement hardware performs antialiasing filtering at 10 MHz, samples the data at 40 million samples per second (MSps). We further filter the data to lower bandwidths as required, using a digital approximation of a fourth-order low-pass Bessel filter. We also filter some of the datasets with wavelet filters, which have been shown to improve SNR based on the pulse-like nature of the signal waveforms.²⁷ Nanopores on low-capacitance, glass chips with SiN_x membranes are integrated with a CMOS amplifier with an input capacitance of 3.25 pF, v_n of 3.15 nV/√Hz, and a maximum recording bandwidth of 10 MHz.⁷ Figure 2b shows the integrated input-referred noise for Pore N, d_TEM = 1.6 nm and t_EELS = 3 nm, measured in 1M KCl, ${\text{I}}_{\text{BASELINE}}^{\text{rms}}$ is 65.7 pA_rms, 183.1 pA_rms, 690.2 pA_rms, and 2.5 nA_rms at 1 MHz, 2 MHz, 5 MHz and 10 MHz, respectively. Figure 2c shows the power spectral density (PSD) of the open headstage of the amplifier, the noise spectrum for Pore N, and, for comparison, the best previous results obtained using the same amplifier using nanopores on membranes lacking the glass passivation described above.⁷ The reduced capacitance provided by the glass chips reduces the noise power across the entire frequency range by more than a factor of two. At the full 10 MHz bandwidth, the integrated noise decreases by 40 %, from 4.2 nA_rms to 2.5 nA_rms. Table 1 quantifies the improvements demonstrated in this work by comparing this data with previous high-bandwidth measurement efforts.

Table 1.

Summary and comparison of the recent high-bandwidth DNA translocation recordings at 1 MHz and higher bandwidth.

Year/Reference	2012 Rosenstein. et al.6	2015 Balan et al.21	2016 Shekar et al.8	2019 This work
Pore material	SiNx	SiNx	a-Si/SiOx	a-Si/SiOx
Substrate material	Silicon	Fused-silica	Silicon	Fused-silica
Pore thickness	10 nm	100 nm	~ 3 nm	~ 3 nm
Pore diameter	4 nm	4 nm	< 2 nm	< 2 nm
vn	$5.3\text{\hspace{0.17em}nV}/\sqrt{\text{Hz}}$	$1\text{\hspace{0.17em}nV}/\sqrt{\text{Hz}}$	$3.15\text{\hspace{0.17em}nV}/\sqrt{\text{Hz}}$	$3.15\text{\hspace{0.17em}nV}/\sqrt{\text{Hz}}$
Camp	2.15 pF	20 pF	4 pF	~3.25 pF
Cpore	6 pF	1 pF	~10 pF	1–2 pF
ΣC	8.15 pF	21 pF	14 pF	4–5 pF
Highest bandwidth of translocations reported	1 MHz (dsDNA)	1 MHz (dsDNA)	5 MHz (ssDNA)	10 MHz (ssDNA)
Input-referred noise at 1 MHz bandwidth	155 pA rms	110 pA rms	128 nA rms	65 nA rms

We performed short ssDNA translocation experiments with these glass chips containing a-Si/SiO_x nanopores with TEM-measured diameters from 0.9 nm to 2.4 nm, pore A to M. The bright-field TEM images of the pores are shown in Figure 1f. Membrane thicknesses from 3 to 8 nm were measured by EELS.²⁴ Experiments were performed in buffered salt solutions of 1 M or 3 M KCl at pH = 8, measured conductance to be 11.8 S/m for 1 M and 30.6 S/m for 3 M, and transmembrane bias voltages up to 900 mV. Ionic current time traces for a fixed voltage were measured for 10-minute periods or longer after introduction of 1 μL of 200 nM ssDNA to the solution. At 40 MSps and with 12-bit quantization, data are generated at a rate of 60 MB/s, presenting challenges for real-time nanopore data analysis. We split the data into several one-second-long segments for subsequent analysis.

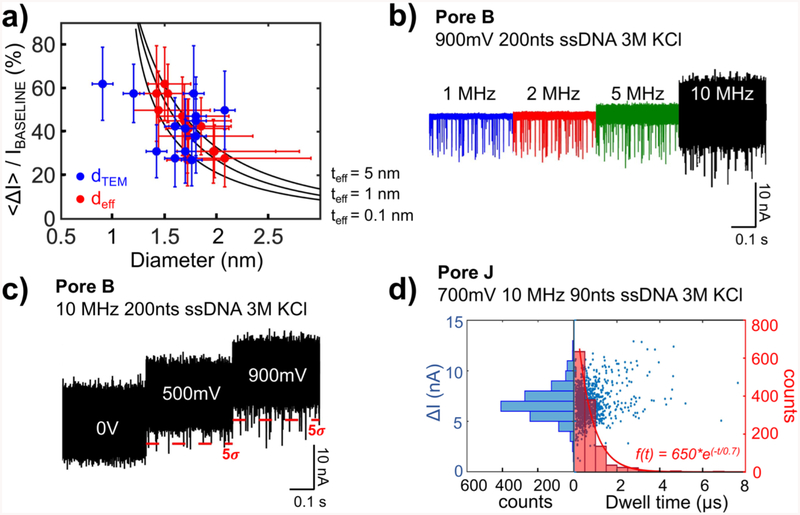
Table 2 shows results at a 2 MHz filter bandwidth, sorted in the order of decreasing average current blocked percentage, < ΔI >/I_BASELINE. For these 13 pores, the pore diameter measured from TEM images (d_TEM) ranges from 0.9 to 2.4 nm, while the membrane thickness determined from EELS (t_EELS) varies from 3–8 nm. < ΔI >/I_BASELINE is as high as ~ 60%. We calculate an effective diameter (d_eff) and effective thickness (t_eff), from the measured open pore current I_BASELINE and the current blockade ΔI, using the cylindrical model for nanopore conductance described previously.²⁶ Figure 3a and Table 2 summarize the results of our analysis. The error bars in Figure 3a for d_eff and t_eff originate from the variance in ΔI, which propagates through the calculations. Figure 3a shows the blockade percentage < ΔI >/I_BASELINE as a function of d_eff, and d_TEM, as red and blue circles, respectively. For pores that are not circular (for example, “Pore J” in Figure 1f), d_TEM is approximated by taking the area of the pore and calculating a diameter of a circle with the same area. The solid black lines are the calculated blockade percentages as a function of d_eff, for t_eff = 5 nm, 1 nm and 0.1 nm.

Table 2.

Summary of nanopore parameters and translocation statistics extracted from data from all thirteen a-Si/SiO_x nanopores measured at room temperature with filtering at 2 MHz using an “8-sigma threshold” to define events. d_TEM is measured from TEM images as illustrated in Figure 1f. t_EELS is the thickness measured from the EELS spectrum. d_eff and t_eff are the effective diameters and thicknesses calculated using a simple cylindrical model for nanopore conductance (Eq. 1 and Eq. 2). τ_dwell are the characteristic dwell times for ssDNA molecules obtained by fitting the event time histograms by an exponential function, and rates are the characteristic dwell times divided by the number of nucleotides. For the 13 pores we presented here, the baseline current increased within 10% of the starting open-pore current within a 10-minute time interval. *Note that for Pore D, the calculated t_eff is negative, and we set t_eff to be 0 to obtain an approximate d_eff value.

Pore	dTEM (nm)	deff (nm)	tEELS (nm)	teff (nm)	Voltage (mV)	KCl (M)	τdwell (μs)	IBASELINE (nA)	< ΔI > (nA)	$\frac{<\Delta I>}{I_{BASELINE}}$	< G > (nS)	< ΔG > (nS)	ssDNA (nts)	rate (ns/nt)
A	0.9	1.5	3	8.9	900	3	1.2	4.8	3.0	0.62	5.4	3.3	200	5.8
B	1.2	1.5	3	3.6	900	3	3.0	10.6	6.1	0.58	11.7	6.8	200	14.8
C	1.6 × 2	1.4	3	0.5	500	3	0.8	14.8	8.5	0.58	29.6	17.0	200	4.2
D	1.8 × 2.4	1.4*	3	0*	400	3	0.5	18.1	9.0	0.50	45.2	22.5	200	2.3
E	1.8	1.7	3	3.3	900	3	1.0	13.1	6.2	0.47	14.6	6.9	80	13.1
F	1.8	1.7	3	2.6	900	3	2.0	15.8	7.1	0.45	17.6	7.9	200	10.0
G	1.6	1.9	3	4.2	900	3	1.5	13.4	5.6	0.43	14.8	6.2	90	16.3
H	1.7	1.7	3	2.1	900	3	1.1	19.0	7.9	0.42	21.1	8.8	200	5.4
I	1.8	1.7	5	0.9	900	1	1.4	10.8	4.1	0.38	12.0	4.6	90	15.6
J	1.2 × 1.7	2.0	8	2.3	700	3	0.8	17.1	5.3	0.31	24.4	7.6	90	9.1
K	1.7	2.0	8	1.9	700	3	0.5	19.0	5.8	0.31	27.1	8.3	90	5.3
L	1.6	2.1	3	2.3	900	1	0.7	9.2	2.6	0.28	10.2	2.8	90	7.9
M	1.4 × 2.2	1.7	5	1.5	900	1	1.9	8.7	3.5	0.27	9.6	3.9	90	20.9

Figure 3.

ssDNA translocation data analysis up to 10 MHz. a) The % of <ΔI>/IBASELINE plotted as a function of the nanopore diameter, where red circles are d_eff and the blue circles are d_TEM. The solid lines are calculated using cylindrical model for effective thickness of 5 nm, 1 nm and 0.1 nm. b) Concatenated time traces of 0.4 s-long recordings of 200 nt ssDNA through Pore B at 900 mV bias. The traces are filtered using a 4-pole Bessel filter to 1 MHz, 2 MHz, 5 MHz bandwidths, and also shown are the 10 MHz unfiltered data. All data recorded at 40 MSps. c) Concatenated time trace of 200 nt ssDNA translocation recordings 10 MHz through Pore B at bias voltages of 0, 500, and 900 mV. The dotted red line is the 5-sigma threshold used to define detectable events. There are many events surpassing the 5-sigma threshold at as low as 500 mV bias voltage. d) Dwell-time vs amplitude scatter plot (points) and histograms (bars) of ~ 1000 translocation events at 10 MHz frequency of 90 nts ssDNA through Pore J at 700 mV bias voltage. The red curve represents an exponential fit to the dwell-time histogram.

There is a small difference between d_TEM and d_eff up to ± 0.6 nm (Table 2). This difference can be attributed to several factors, including the fact that some of our pores are not perfectly circular, that their shapes and dimensions can change slightly after being taken out of vacuum and immersed into the aqueous salt solution, and that the d_eff calculation does not consider the charge on the pore wall. Across all the pores used in this study, the estimated d_eff = 1.4 – 2.1 nm, and t_eff = 0 – 8.9 nm. Note that for Pore D, the calculated t_eff is negative, and we set its t_eff to be 0 to obtain an approximate d_eff value. Pore clogging can happen during measurements. However, we prevent the clogging by applying a voltage of opposite polarity. This reversed voltage repels the DNA from the pore and the baseline current returns to its original open-pore current value. We observed that clogging happens at a frequency of roughly once per minute. The increase of the open pore current during the measurement was also observed. For example, Pore F exhibited an increase of open pore current, I, from 15.9 nA to 16.7 nA within the first 2 minutes of the measurements at 900 mV in 3 M KCl. This translates to a 5% increase in baseline current, and an increase of about 0.05 nm in pore diameter, assuming an unchanged pore thickness.

One of the benefits of using solid-state pores is the ability to apply higher bias voltages than in protein pore systems, increasing current signal levels and enabling high bandwidth measurements.^7,8 The higher noise in high bandwidth measurements requires us to drive the voltage as high as 900 mV to have sufficient signal-to-noise to detect individual events. Event recognition is performed with simple thresholding at multiples of $\sigma =I_{\mathit{\text{BASELINE}}}^{\mathit{\text{rms}}}$, and chose thresholding of 5σ to reduce false events at 10 MHz (see Section 1 in Supplementary Information). Nanopores here record only electrical signals and there is no direct visualization of how exactly the DNA passes through the pore. However, when ssDNA goes through the pore under these conditions, it typically blocks the amount of current close to what is calculated from the simple resistor model and such events can be attributed to translocations.²⁴ For example, if the DNA blocks the pore completely, the current blockade should be 100%. On the other hand, when the blockade of current is much smaller, this means that the DNA has either not gone through the pore, or that the DNA has passed through the pore too quickly that we observe artificially attenuated current due to the lack of time resolution by the experimental setup. Such shallow current blockades are not included in the analysis as we have chosen the threshold to be 5σ of the baseline signal for 10 MHz data, and 8σ of the baseline signal for 2 MHz data. Therefore, most events recorded have measured value very close to the predicted value when DNA blocks the pore (see Table 2) and are therefore consistent with the fact that they correspond to DNA passage through the pore. For the smallest pore (Pore A), we achieve an average ΔI/I_BASELINE over 60%, which corresponds well to the ssDNA width of 1.2 nm translocating through a nanopore of diameter 1.4 nm. A simple geometrical estimate based on the ratio of ssDNA-to-nanopore cross-sectional areas yields a comparable value of 1.2²/1.4² ~ 73%.

Figure 3b shows current time traces for “Pore B” at 1 MHz, 2 MHz, and 5 MHz, and 10 MHz bandwidths, with ssDNA translocation events clearly distinguishable at 10 MHz. Figure 3c shows time traces at 0 V, 500 mV and 900 mV biases at 10 MHz from the same pore. One of the benefits of using solid-state pores is the ability to apply higher bias voltages than in protein pore systems, increasing current signal levels. Event recognition is performed with simple thresholding at multiples of $\sigma =I_{\mathit{\text{BASELINE}}}^{\mathit{\text{rms}}}$, and we chose thresholding of 5σ to reduce false events (see Section 1 in Supplementary Information). The 5σ current levels are indicated in Figure 3c as red dotted lines. Only events with durations longer than 100 ns and less than 100 μs are considered true events. The upper bound serves to exclude long events that we hypothesize correspond to situations when ssDNA molecules get stuck in the pore. These comprise on average ~ 7% of the total number of events, and the highest percentage, up to ~ 20%, is observed for the smallest pores, d_eff ~ 1.4 nm. Smaller diameter pores and longer analytes, in general, should result in higher percentages of longer events, and we observe a weak correlation within the range of our diameters. (1.4 nm - 2.1 nm) and DNA lengths (80nts – 200nts) (see Section 2 in Supplementary Information). The lower bound for event duration detection is set to be twice the rise time of the four-pole Bessel filter. The four-pole Bessel filter has a rise time associated with the cut-off frequency chosen, with the rise time at 10 MHz being about 50 ns. Events shorter than twice this time would be attenuated in current magnitude and temporally distorted and are not considered here. Therefore, we do not record events shorter than 100 ns, because we cannot resolve them due to the limit of our setup. The scatter plot of 1251 events over the 5s threshold at 10-MHz bandwidth from “Pore J” and the corresponding histogram of dwell time and event depth are plotted in Figure 3d, for an applied voltage of 700 mV. The characteristic dwell time τ_dwell is calculated by fitting the dwell time distribution to the exponential function $A{e}^{-t/{\tau }_{\text{dwell}}}$ as shown as the red curve in the right panel.¹⁷ The fit equation for the dwell time is f(t) = 650*e^(−t/0.7) and R-square value is 0.98 indicating an appropriate fit. At the same 5s threshold, the number of events recorded per second at 10 MHz bandwidth is smaller than the number of events recorded from the same traces filtered to lower bandwidth because of the increase in noise with bandwidth and the corresponding decrease of SNR. For example, “Pore J” produces approximately 1850 events at 2 MHz compared to 1251 events at 10 MHz over the same three-second measurement window. Increasing the filtering bandwidth from 2 MHz to 10 MHz increases < ΔI > from 3.1 nA to 6.8 nA, as fewer small amplitude events are captured, and decreases the characteristic dwell time from 1.1 μs to 0.7 μs (see Section 3 in Supplementary Information). At 10 MHz, we record current changes more accurately without attenuation for shorter events, detect short events that would have been missed at lower bandwidths, and have a higher temporal resolution for the events detected.

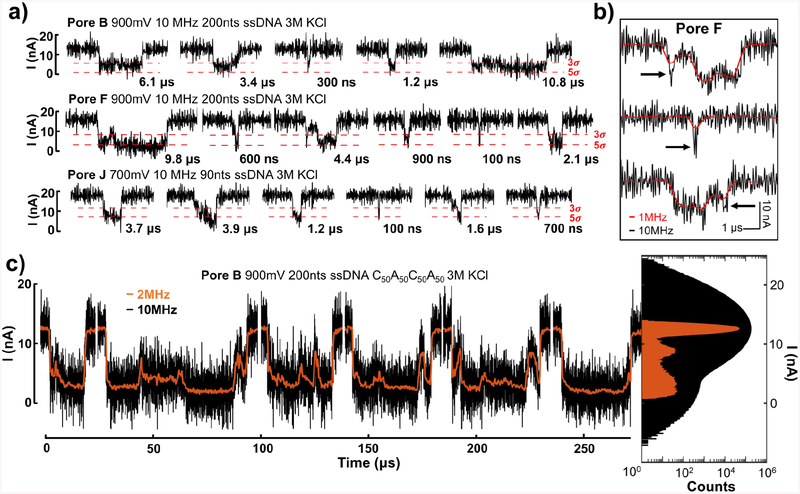
For pores with the highest SNRs, we resolve translocation events at 10 MHz. Figure 4a shows representative translocation events from “Pore B”, “Pore F” and “Pore J” with durations as short as 100 ns. In Figure 4b, for comparison, we show some representative events also filtered to 1 MHz bandwidth; the 10-MHz bandwidth is clearly required to resolve many of the events detected. In particular, the transient current features at 10 MHz, indicated by arrows, are highly attenuated at 1 MHz.

Figure 4.

ssDNA translocation events at 10 MHz measurement bandwidth and comparison with data filtered at 1 MHz and 2 MHz. a) Sample events of unfiltered 10 MHz data containing translocation events of various durations from several pores (Pore B, Pore F and Pore J) and conditions as indicated. The events are as short as 100 ns. Only the events that surpass the 5-sigma thresholds are shown here, and the 3-sigma and 5-sigma threshold lines are marked by the red dashed lines. b) Example events from Pore F demonstrating short events and short features within the events that are missed or greatly attenuated in magnitude, indicated by arrows, at 1 MHz (red), but detectable at 10 MHz (black). c) The concatenated traces of selected events with dwell times over 10 μs from Pore B at bandwidth of 10 MHz (black) and 2 MHz (orange) are shown in the left panel. The right panel is the all-points histograms of a one-second-long current trace with 155 events from which 6 selected events to the left are chosen. The black histogram is for the data taken at 10 MHz and the orange histogram is for the same data set but filtered down to 2 MHz.

In Figure 4c, we show concatenated traces of selected events of 200 nts poly(dA)₅₀poly(dC)₅₀poly(dA)₅₀poly(dC)₅₀ from “Pore B” that have durations between 10 μs – 100 μs, at both 10 MHz and 2 MHz bandwidths. For Pore B, 38% of events have dwell time between 10 μs and 100 μs. We also observe structure within these events. Some events maintain fairly constant current values within the event, while others show switching levels and bumps (see Section 4 in Supplementary Information). A few recent studies claimed identification of homopolymer blocks with solid-state nanopores. Goto et al. fabricated 5-nm-thick SiN nanopores with calculated diameters down to 2 nm and showed that in CsCl solution, triblock DNA copolymers, poly(dA)₅₄poly(dC)₃₃poly(dT)₃₃ and poly(dG)₃₃poly(dA)₅₄poly(dT)₃₃, exhibit trimodal distributions in all-point histograms.²⁸ They attributed these peaks to signals from homopolymer blocks. This identification was made in the histograms showing current distributions, but not within translocation events. We note that peaks in histograms are not sufficient proof of homopolymer block differentiation. For example, in Figure 4c while we also observe a two-level all-points histogram corresponding to two current levels visible within the events on the left, this apparent two-level structure in the individual events does not correspond to the number or order of homopolymer blocks, nor is it consistent from event to event. Yamazaki et al. claimed poly(dA) and poly(dC) detection within the same DNA strand with a ~ 1.4-nm diameter SiN nanopore with effective thickness ~ 1.8 nm as calculated from pore current, by observing two distinct current levels in selected events comprising ~19% of total number of recorded events.²⁹ The signal was attributed to the unzipping of dsDNA through the nanopore with the calculated diameter smaller than the dsDNA diameter, and the two current levels were attributed to differences in the helical secondary structure of poly(dA) and poly(dC). Here, unfortunately, there are no consistent current levels that can be visually attributed to homopolymer segments, even when the data are denoised using wavelets (see Sections 5 and 6 in Supplementary Information). In the all-point histograms shown in Figure 4c, when we filter to 2 MHz to reduce the baseline noise, we observe several distinct peaks in the current distributions suggesting these transient current features within an event could reflect movements and reorientations of ssDNA above and inside the pores,^30,31 but more modeling work is needed to understand their origin.³¹

To quantify the transient fluctuations, we calculate the magnitude of current fluctuations due to the presence of ssDNA in and around the pore as $I_{\mathit{\text{DNA}}}^{\mathit{\text{rms}}}=\sqrt{{\left(I_{\mathit{\text{EVENT}}}^{\mathit{\text{rms}}}\right)}^2-{\left(I_{\mathit{\text{BASELINE}}}^{\mathit{\text{rms}}}\right)}^2}$, If one assumes a ΔI between adenine (A) and cytosine (C) of ~ 1 nA,⁸ one would expect current fluctuation due to this size difference in our segmented 90 nts poly(dC)₃₀poly(dA)₃₀poly(dC)₃₀ ssDNA homopolymer translocation events to be approximately 0.5 nA_rms (see Section 7 in Supplementary Information). Instead we find ${\text{I}}_{\text{DNA}}^{\text{rms}}$ on the order of 1.5 nA_rms, suggesting that these fluctuations reflect more than just nucleotide differences. For pores where diameter is comparable to thickness, the access resistance is comparable to the resistance of the pore itself.²⁸ Across the 13 pores measured, R_pore/(2R_access) ranges from 0.5 to 7.5, where R_pore ranges from 10 MΩ to 160 MΩ. For smaller values of this ratio, the change of R_access by the presence of the DNA also contributes to the measured translation event.^6,7,24,30,31 The entropy of the ssDNA also contributes to ${\text{I}}_{\text{DNA}}^{\text{rms}}$ and obfuscates more sequence-determined current traces. ssDNA entropy exceeds that of dsDNA, the more common analyte in previous solid-state nanopore studies, due to the much shorter persistence length of ssDNA compared to dsDNA.³² As illustrated in Figure 1g, the ssDNA outside the pores can possess various configurations and movements in the access region that will contribute to ${\text{I}}_{\text{DNA}}^{\text{rms}}$.

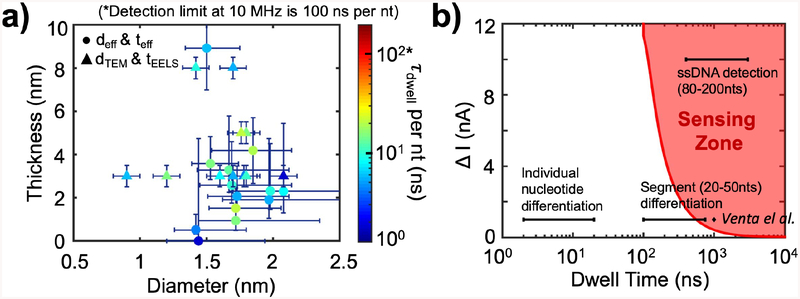
To evaluate whether a temporal resolution of 100 ns is sufficient to resolve the DNA sequence at the translocation speeds measured in this study, we plot the characteristic dwell time per nucleotide, τ_dwell/nt (characteristic dwell time for the molecule divided by the number of nucleotides) as a function of t_eff and d_eff for the pores used in this study in Figure 5a. Here, we assume a constant DNA speed to estimate the dwell time per nucleotide, and we record τ_dwell/nt between 2 and 21 ns/nt across the pores studied, which is 5 to 50 times shorter than what is resolvable at 10 MHz bandwidth. The shaded red area in Figure 5c, marked as the “sensing zone”, is the region of ΔI and τ_dwell corresponding to events that can be detected with our measurement system. Specifically, for a feature to be detected by the amplifier, its dwell time has to be longer than the minimum temporal resolution determined by the measurement bandwidth, and the signal ΔI should be more than at least five times the noise ${\text{I}}_{\text{BASELINE}}^{\text{rms}}$ at the measurement bandwidth.

Figure 5.

Characteristic dwell times for all pores vs. pore diameters and thicknesses, and the ssDNA ionic signal, ΔI, vs. dwell time, τ_dwell, parameter space. a) Characteristic dwell time per nucleotide (τ_dwell per nt) plotted as a function of the nanopore diameter and thickness for all pores. d_eff and t_eff are marked as circles, and d_TEM and t_EELS are marked as triangles in the graph. The time detection limit of a 10 MHz amplifier is 100 ns per nt, above which our 10 MHz amplifier could accurately report a signal from each nucleotide. The blue vertical and horizontal lines represent errors in thickness and diameter, described in the text. DNA used are 90–200 nts long ssDNA, salt solutions are 1 M or 3 M KCl, and biased voltages are from 400 – 900 mV, as listed in Table 2. b) The red curve is the minimum current blockade (ΔI) for translocation events as a function of dwell time to surpass the 5s threshold, which we define as the minimum requirement for an event to be detected by the 10 MHz amplifier; Hence, the red area represents the 10 MHz 5-sigma “Sensing Zone”. As seen from the red shaded region, for large ΔI, the minimum detection time is 100 ns; as ΔI decreases, the minimum detection time increases to about 500 ns at ΔI = 1 nA. The detection of ssDNA (ΔI = 10 nA, τ_dwell = 0.4 – 3μs), homopolymer segment (20–50 nts) differentiation (ΔI = 1 nA, τ_dwell = 0.1 – 0.8 μs), and individual nucleotide differentiation (ΔI = 1 nA, τ_dwell = 2 – 20 ns) are marked as black horizontal line segments on the graph, and only the right end of the “segment (20–50 nts) differentiation” line overlaps with the “sensing zone”. The ΔI from Venta et al.⁷ for 30-nucleotides-long ssDNA homopolymers with similar pores is marked as the diamond on the graph for reference.

Several important benchmarks in the ΔI - τ_dwell parameter space are marked in Figure 5c as “ssDNA detection”, “Individual nucleotide differentiation”, and “Segment differentiation.” “ssDNA detection” requires ΔI on the order of 10 nA at 1 V bias in 1 M KCl and a characteristic τ_dwell range from 0.5 to 3 μs for 80 to 200 nts ssDNA, as measured, well within the sensing zone of our detector. We observed a difference in the characteristic translocation time of ssDNA molecules that differ in length for pores similar in dimensions. For example, in Pore E & Pore F, d_eff = 1.7 nm for both pores and the thickness, t_eff, for Pore E is 3.3 nm and for Pore F is 2.6 nm, respectively. The molecules used in Pore E are 200 nts ssDNA, and Pore F are 90 nts ssDNA. The τ_dwell for Pore E was 1 μs and for Pore F was 2 μs, which scaled roughly with the ssDNA length used in the two experiments. (see Table 2). “Individual nucleotide differentiation” requires ΔI on the order of 1 nA at 1 V bias^8,9,28 in 1 M KCl as does “Segment differentiation” for homopolymer sequences from 20 to 50 nts long.^8,9,28 Individual nucleotide sensing is completely outside the sensing region for detection but long homopolymer sequences can be detected⁸ as indicated in Figure 5b. Efforts of slowing down DNA translocation speed such as reducing temperature or changing salt solutions from KCl to LiCl have been proposed.^16,17 Here, we find that these two approaches came at the expense of SNR at a given bandwidth. Experiments with Pore C were conducted at approximately 4 °C and at 25 °C (room temperature). The characteristic translocation dwell time increased from 0.8 to 1.0 μs at lower temperature, but ΔI was reduced from 8.5 to 4.3 nA. The translocation dwell time only slightly increased at this lower temperature, but we sacrificed the SNR due to reduced I and ΔI. We also performed experiments with 1M and 3 M LiCl solution. These solutions were previously observed to slow down translocation by a factor of 10 in ~ 20-nm-diameter SiN pores.¹⁷ With the same experimental conditions as in this previous study, but with much smaller diameter nanopores, we did not detect any translocation events. These results are summarized in Sections 8 in Supplementary Information. Other methods for slowing down as performed previously may also be beneficial to resolve bases, in combination with the improved high-bandwidth setup.^8,9,16–19

Conclusions

In conclusion, we present a nanopore recording system able to record translocation events at 10 MHz bandwidths by combining a custom CMOS amplifier, ~ 1pF capacitance nanopore chips, and small and thin a-Si/SiO_x pores. We detect events with durations as short as 100 ns. This work establishes the robustness of ultrathin a-Si pores for ssDNA measurements and the overall consistency between the ionic current data recorded from similar pores in the diameter range of 1 to 2 nm. We observe intra-event fluctuations and multiple levels within the events, and study the variability of current vs. time signatures within the events. However, we cannot identify or articulate any characteristic features within events that can be attributed to the repeated DNA homopolymer sequences, such as distinct current levels for repeated poly(dA) and poly(dC). We attribute this to high R_access ~ R_pore in these devices and to the entropy of ssDNA. To understand and deconvolve these various contributions to the ionic signal in a regime when d_eff ~ t_eff ~ 1 to 2 nm, further modeling and advanced data analysis tools for large data sets are needed. Approaches to reduce this entropy through geometric or electrostatic control will be important to achieve further progress.

Methods

The low-stress 100 nm thick SiNx membrane is supported by a 3 mm in diameter circular glass (fused-silica) chip of thickness of 300 μm, with a circular window of 20 – 30 μm in diameter. The SiN_x membrane is thinned down by reactive ion etching and TEM (JOEL 2010 F) to a thickness of 3 nm for nanopore drilling. Before experiments, the nanopore chip is cleaned and wetted using a hot piranha solution for 5 minutes and rinsed by DI water.

The glass chip is secured with Kwik-cast, a silicone layer that we apply around the SiN membrane to separate electrolyte solutions and as an additional insulating layer that reduces capacitance, on PDMS cells and is separated into two chambers containing a salt solution composed of 1 M or 3 M KCl buffered to pH 8 using 10 mM Tris-HCl with 1 mM EDTA. Bias voltages between 0 mV and 900 mV are applied across the nanopore through Ag/AgCl electrodes. Experiments are carried out using a custom CMOS-integrated nanopore (CNP) amplifier⁸ to apply a voltage bias and measure the current through the nanopore simultaneously. The data are recorded using a custom-designed data acquisition board and software at 40 MSps and filtered using a digital approximation of a four-pole low-pass Bessel filter. The output of the amplifier is subjected to boosting filters to restore flat frequency response up until 10 MHz.⁸ Single-stranded DNA of specific segments and lengths indicated are ordered from IDT (Integrated DNA Technologies, Inc.) and made into stock solution of 20 μM and stored in the freezer. In each DNA translocation experiments, 200 nM of ssDNA in desired salt solution is made, and 1 μL of solution is added to the cis chamber of the PDMS cell. Data analysis is done in custom-made programs in Matlab (MathWorks, Natick, MA, USA).