Abstract
Electronic Health Records (EHR) contain extensive patient data on various health outcomes and risk predictors, providing an efficient and wide-reaching source for health research. Integrated EHR data can provide a larger sample size of the population to improve estimation and prediction accuracy. To overcome the obstacle of sharing patient-level data, distributed algorithms were developed to conduct statistical analyses across multiple clinical sites through sharing only aggregated information. However, the heterogeneity of data across sites is often ignored by existing distributed algorithms, which leads to substantial bias when studying the association between the outcomes and exposures. In this study, we propose a privacy-preserving and communication-efficient distributed algorithm which accounts for the heterogeneity caused by a small number of the clinical sites. We evaluated our algorithm through a systematic simulation study motivated by real-world scenarios and applied our algorithm to multiple claims datasets from the Observational Health Data Sciences and Informatics (OHDSI) network. The results showed that the proposed method performed better than the existing distributed algorithm ODAL and a meta-analysis method.
Keywords: distributed computing, heterogeneity, median, meta-analysis, multi-site analysis, surrogate likelihood
1. Introduction
Real-world data, including Electronic Health Records (EHR) data, claims data, and many others, have become a major source for medical and health research. In particular, EHR systems have been increasingly implemented across the nation to investigate various research questions in the last few decades [1–4]. EHR data contain various patient health data collected routinely at the point of care including diagnosis, medications, procedures, imaging, clinical notes, etc. Researchers conclude that the meaningful use of the data relies on the successful integration of clinical information from multiple centers [5]. The multicenter study provides researchers a larger sample size of the population to improve the estimation and prediction accuracy, which can also contribute to accelerating knowledge discovery and enhancing the generalizability of scientific findings [6].
A few successful networks have been founded and have become beneficial to multicenter research. For example, the Observational Health Data Sciences and Informatics (OHDSI) consortium was founded (https://ohdsi.org/) for the primary purpose of developing open-source tools that could be shared across multiple sites. OHDSI developed the OMOP Common Data Model [7] for data standardization. This tool enables each site to convert a variety of datasets into a common format. It also allows a single script to be shared and ran across sites without the alteration of format. The standardization procedure decreases the probability of translation error when converting a database into another format and increases the efficiency of data analysis. Another example is the National Pediatric Learning Health System (PEDSnet) that contains data from eight of the nation’s largest pediatric health systems [8]. This network comprises clinical information from millions of children and provides increasing opportunities for multicenter pediatrics research.
In multicenter research, privacy protection is a major challenge of data sharing [9]. In many situations, it is not feasible to share patient-level information, especially for important clinical outcomes and demographic information. Thus, some EHR-based studies have been done to develop the models to share and integrate patient information with privacy-preserving feature [10–14]. Currently, the state-of-the-art method for multicenter logistic regression without sharing patient-level information is to conduct a meta-analysis, which fits a logistic regression model separately within each site and reports the point estimates and standard errors of the odds ratios, and obtain a combined result through a weighted average. For example, a treatment pathway study [15], a birth season – disease risk study [15, 16] and several pharmacovigilance studies [17] have been successfully conducted in such fashion within the ODHSI consortium.
In addition to meta-analysis, distributed algorithms have been recently developed to decompose computational tasks into multiple components. Each component is computed in parallel at a single site and patient-level information is not required to be transferred across sites. For example, an algorithm called WebDISCO (a Web service for distributed Cox model learning) was developed to fit the Cox proportional hazard model distributively by Cox [18], and Wu et al. developed a distributed algorithm for conducting logistic regressions, named GLORE (Grid Binary LOgistic Regression). Both algorithms have been successfully deployed to the pSCANNER consortium [9, 19]. However, as acknowledged by the investigators, the GLORE and WebDISCO are known as iterative algorithms that require iterative information transfer across the sites until convergence is reached. These two methods could be time-consuming and communication-intensive in practice. To address these issues, Duan et al. proposed a non-iterative privacy-preserving distributed algorithm to perform logistic regressions (termed as ODAL) [15], which utilizes the patient-level data from one site and aggregated information from other sites. The accuracy and efficiency of the ODAL method were proved to be comparable to the pooled patient-level datasets through a wide spectrum of settings in practice.
However, one common limitation for all of the aforementioned distributed algorithms is that they all assume that the data from different sites are homogeneous. This assumption is often impractical in biomedical studies. Specifically, data from different study sites within a distributed research network are often heterogeneous due to various reasons. For example, different coding, labeling systems might be used in different sites, which lead to different data structures. In this case, substantial mapping work is required through methods such as the OMOP Common Data Model [7] to unify the data structure and coding system to make the data sources interoperable. Furthermore, heterogeneity might also be caused by different patient population and hospital-level effects due to intrinsic differences in geographical locations and variations in clinical operations, etc., which can result in the overall distribution of the data in each site to be different. In this paper, we assume the structure of the data is unified while the distributions of the data are heterogeneous.
One motivating example is the PEDSnet, a National Pediatric Learning Health System [8], for facilitating multi-institutional data integration, cohort discovery, and advanced analytics that enables rapid learning. The PEDSnet consortium includes eight hospitals and health systems across the nation, such as the Children’s Hospital of Philadelphia, Cincinnati Children’s Hospital, Seattle Children’s Hospital. There is a substantial difference in patient characteristics as well as clinical practices across these hospitals. Another example is our recent collaboration with the Janssen Research and Development at Johnson & Johnson, where we are interested in integrating drug safety signals from five massive medical claims/electronic health records databases. There is also a substantial heterogeneity across these five databases.
In general, ignoring heterogeneity across the sites could lead to biased estimates of the associations between exposures and outcomes [21, 22]. It is critically important to develop robust methods for data integration that can account for the heterogeneity in the data across sites. To this end, in this paper, we attempt to develop a simple yet effective privacy-preserving distributed algorithm for fitting logistic regression within heterogeneous health systems without sharing patient-level data. The key idea is to modify the ODAL algorithm [20] by communicating robust summary statistics that are less sensitive to the existence of “outlying studies”. Through simulation studies and real data analysis using databases from the Janssen Research, we found that our new algorithm, which we refer to as the “robust-ODAL” method, is substantially more robust to the outlying studies and produces less biased estimates than the current ODAL method and traditional meta-analysis method.
2. Method
In this section, we introduce the proposed robust-ODAL method. Simulation studies are performed to compare the method with state-of-the-art methods in terms of estimation bias.
2.1. Proposed Algorithm
Suppose we have data stored in K different clinical sites. We assume the majority of the K sites (hereafter referred to as Group 1) are relatively homogeneous, and a small number of sites (hereafter referred to as Group 2) are considered heterogeneous in terms of the patient population, clinician population, data quality, etc. (illustrated in Fig. 1). We are interested in integrating the estimates from the majority of the K sites. However, a challenge for such data integration is that the identification of which sites belonging to the majority of sites is unknown. To handle this type of heterogeneity and keep the algorithm to be entirely data-driven, we propose the following distributed algorithm by strengthening the algorithm in Duan et al. (2019) [20].
Fig. 1.
Among K sites, a small number of the sites are considered heterogeneous taking into the factors of the patient population, clinician population, data quality, etc., compared with other relatively homogeneous sites.
Specifically, denote Y to be a binary outcome and x to be a p-dimensional predictor, which contains the exposures of interest and potential confounders to be adjusted in a regression model. Suppose that we have N observations from K different clinical sites in total and the jth clinical site contains nj observations. Let (xij, Yij) denotes the ith observation in the jth clinical site. Under the assumption of a logistic regression model, the log-likelihood function for the combined data can be written as
| (1) |
In the distributed algorithm, we assume that the individual patient-level information is not allowed to be transferred across the sites. Thus, LN(β) cannot be obtained directly by integrating all patient-level data. Suppose we only have access to the data stored in a local site (hereafter referred to as Site 1) and Site 1 belongs to Group 1 (i.e., the majority of studies). The log-likelihood at Site 1 can be written as
| (2) |
With the given initial value , we can construct the following surrogate likelihood function based on the local likelihood function and borrow aggregated information from other sites, i.e.,
| (3) |
where and is the first gradient of the jth site.
The term is essentially the sample-size weighted average of the first-order gradients obtained from the sites. Under the homogenous assumption that data are identically and independently distributed across sites, is used to correct the shape of around the initial value . However, if the data from the sites in Group 2 have a different distribution from the data in Group 1, will be influenced by Group 2 and be different from , leading to biased estimation of the regression parameters.
In order to reduce the bias caused by the heterogeneous sites in Group 2, instead of taking the mean of the first-order gradients across sites, we propose to simply take the element-wise median of across sites, which is known to be more robust to potential outliers. The new proposed surrogate likelihood function can be written as
| (4) |
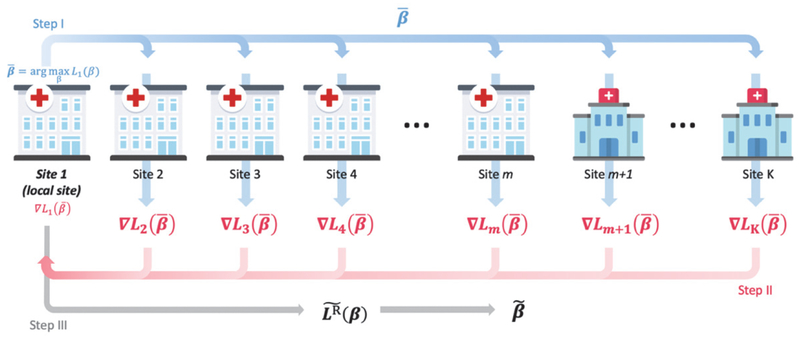
where . In Equation (4), L1(β) and can be obtained using data from Site 1; can be computed once we obtain each from all sites. Notably, the intermediate quantity contains only aggregated information and has the dimension being the same as the parameter β. An illustration of the method is provided in Figure 2. The robust-ODAL estimator can be obtained by maximizing the objective function in equation (4):
Fig. 2.
Illustration of the robust-ODAL method. I: Using data from Site 1 (i.e., local site) to estimate the local estimator , and transfer to other sites. II: Intermediate term is evaluated at each site and transfer back to Site 1. III: With and L1(β), we obtain the surrogate function and the robust-ODAL estimator is obtained by maximizing the surrogate function (4).
Regarding the initial value , a natural choice of is the maximum likelihood estimator of the local likelihood L1(β). A detailed algorithm is outlined below.

2.2. Simulation Design
To evaluate the empirical performance of the proposed robust-ODAL algorithm and compare with existing algorithms ODAL and meta-analysis, we conducted extensive simulation studies. To cover a wide spectrum of practical settings, we set the total number of sites, K = 10 or 50, the sample size of each site was randomly sampled from a discrete Uniform distribution on (750, 1250). In addition, to mimic the assumption that a small number of the sites were outlying studies, we considered 10% or 20% of the sites being in Group 2. In other words, there were 1 (or 2) out of 10 sites and 5 (or 10) out of 50 sites in Group 2, being substantially different from the majority group (Table 1).
Table 1:
Sizes of Groups 1 and 2 when the total number of sites K = 10 and 50
| Total number of sites | Size of Group 1 | Size of Group 2 |
|---|---|---|
| K= 10 | 9 (90%) | 1 (10%) |
| 8 (80%) | 2 (20%) | |
| K= 50 | 45 (90%) | 5 (10%) |
| 40 (80%) | 10 (20%) |
We considered a setting where a binary outcome was associated with two risk factors, (x1, x2), where x1 represented a continuous confounder and x2 was a binary exposure of interest (such as medication usage). The binary outcome Y (e.g., presence/absence of an adverse event) was generated from a Bernoulli distribution, with the conditional probability specified by the following logistic regression model,
where logit(p) = log{p/(1 - p)}, β1 and β2. were the coefficients of x1 and x2. respectively, and β0 was the intercept, characterizing the prevalence of the outcome Y.
The choice of the parameter values was motivated by the empirical distributions of data in the real application. We simulated the continuous covariate variable to mimic the empirical distribution of BMI. Besides, the binary covariate variable was generated to mimic the prevalence of the risk factors in the real data (e.g., Hypertensive disorder). Table 2 specifies the distributions for generating the risk factors (x1, x2). Specifically, the distribution of x1 for each study site within Group 1 was a normal distribution with mean α1 and variance of 1, where this study-specific mean α1 was drawn from a uniform distribution on [−0.25, 0.25]. Such setup allowed for both within-study variation (with a variance of 1) and between-study variation (over a range between −0.25 to 0.25). In addition, the study sites within Group 1 were relatively homogeneous because the between-study variation is ¼ of the within-study variation.
Table 2:
Distributions of variables x1 and x2 in simulation studies
| Covariates | Group 1 | Group 2 |
|---|---|---|
| x1 (confounder) | Normal (−0.25 ~ 0.25, 1) | Normal (2, 0.5) |
| x2 (parameter of interest) | Bernoulli (0.25 ~ 0.35) | Bernoulli (0.7) |
In contrast, the predictor x1 in Group 2 was generated from a normal distribution with the mean of 2 and the variance of 0.5. Such specification mimicked a setting with outlying studies of substantially different distribution in mean and variance in Group 2, compared to Group 1.
Following a similar rationale, we generated predictor x2 in Group 1 from a Bernoulli distribution with probability equal to α2, where α2 ranged from 0.25 to 0.35. For Group 2, x2 was generated from a Bernoulli distribution with probability equal to 0.7. This setup was mimicking a setting that medication is less commonly prescribed in the majority of clinical sites (with a probability of prescribing as 0.25~0.35), whereas the medication is very commonly prescribed (with a probability of 0.7) in the outlying sites due to difference in clinical practice. For example, 6-mercaptopurine has been less commonly prescribed for treating pediatric Crohn disease at the Children’s Hospital of Philadelphia (with a probability of prescribing of 23%), but is commonly prescribed at the Boston’s Children’s Hospital (with a probability of prescribing of 80%) [23, 24, 25].
To cover a wide spectrum of practical scenarios, we considered both common and rare outcomes. The prevalence for the common disease was set at 37% (mimicking Type 2 diabetes) and for the rare disease was set at 0.8% (mimicking the prevalence of AMI which is around 1% in the real data), which corresponded to the values of β0 equal to −0.5 and −4.8 respectively (Table 3).
Table 3:
Values of coefficients in heterogeneous setting one and two
| Outcome | Setting One | Setting Two | ||||||
|---|---|---|---|---|---|---|---|---|
| β2 | β2 | |||||||
| Common | −0.5 | 1.0 | −1.0 | −0.5 | −1.0 | 1.0 | 1.8 | −1.0 |
| Rare | −6 | −4.8 | −6 | |||||
As illustrated in Table 3, we conducted simulation studies under two different settings to mimic two types of heterogeneity. In setting one (left part of Table 3), we assumed there exists heterogeneity only in the distribution of covariates while the disease prevalence and the coefficients (i.e., log odds ratio) of the covariates were the same across all sites. In setting two (right part of Table 3), we assumed not only the distributions of variables were different but also the disease prevalence and the coefficients (i.e., log odds ratio) of the covariates across the sites were different.
3. Results
In this section, we present the simulation results under different settings to compare three methods: meta-analysis, ODAL, and robust-ODAL. We also show the data evaluation results with three methods using the data from the Janssen Research and Development at Johnson & Johnson.
3.1. Simulation Results
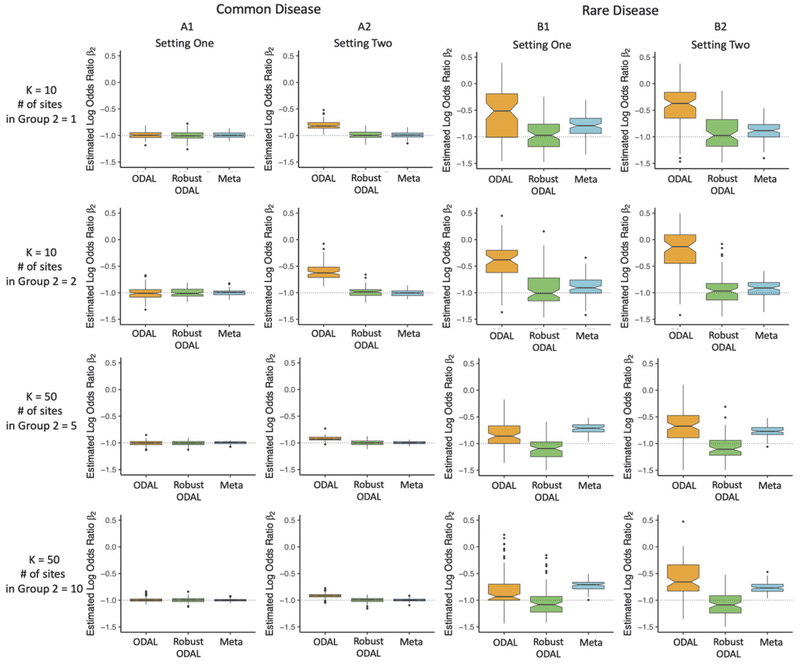
Fig. 3 presents the estimations of β2, the parameter of interest. We compared the estimators of ODAL, robust-ODAL, and meta-analysis when the number of sites is 10 (upper two panels) or 50 (lower two panels) for common disease (A1 and A2) and rare disease (B1 and B2).
Fig. 3.
Simulation results of K = 10 and K = 50 for setting one and setting two with common disease prevalence (37%) and rare disease prevalence (0.8%). Setting one: heterogeneity only exists in the distribution of covariates while the disease prevalence and the coefficients of the covariates are the same across all sites. Setting two: distributions of variables, disease prevalence, and coefficients of the covariates are all different across the sites.
The box plots in panel A1 and B1 are the simulation results for setting one where variables x1 and x2 are heterogeneous across the sites and the values of disease prevalence and coefficients are the same across all of the sites. The box plots in panel A2 and B2 are the results for setting two, where the distributions of variables, disease prevalence, and β1’s are different in Group 1 and 2.
The y-axes in the box plots present the values of estimated log odds ratio for β2 under 100 times iterations and the x-axes are three models to compare: ODAL (yellow), robust-ODAL (green), and meta-analysis (blue). The solid black segment in each box shows the median of the estimates, and the boundaries of the colored boxes give the interquartile ranges for the estimates.
Common disease:
Setting one shows that when the heterogeneity only exists in the distributions of variables, the ODAL, the robust-ODAL, and the meta-analysis perform similarly when the outcome is common (panel A1 in Fig. 3). Setting two presents that when the heterogeneity exists in variables, disease prevalence, and the coefficient of the confounder, estimates with the robust-ODAL method have smaller bias than those using ODAL (panel A2 in Fig. 3) and have similar performance with the meta-analysis.
Rare disease:
Setting one shows that when the heterogeneity only exists in the distributions of variables when the disease is rare, the robust-ODAL performs better than both ODAL and meta-analysis (panel B1 in Fig. 3). A similar conclusion can be made under setting two (panel B2 in Fig. 3). Compared with setting one, the results show that the robust-ODAL performs much better than ODAL in setting two.
To summarize, when the disease is common, the robust-ODAL performs better than (e.g., in setting two) or at least similar (e.g., in setting one) compared to the ODAL; the robust-ODAL performs similar to meta-analysis. When the outcome is rare, the robust-ODAL is more accurate in estimating the association between the outcome and exposure than both ODAL and meta-analysis.
3.2. Data Evaluation
We applied the robust-ODAL method to study the risk factors of acute myocardial infarction (AMI) in a population with pharmaceutically-treated major depressive disorder using data from five insurance claims databases in the Janssen Research and Development at the Johnson & Johnson. The databases have been converted to the OMOP Common Data Model [7]. The outcome, AMI, was defined as the occurrence of the respective diagnosis codes in an inpatient or emergency room setting. We restricted the first occurrence per patient. The summaries of patients’ characteristics of the five sites are listed in Table 4
Table 4.
Characteristics of the five claims datasets at the Janssen Research and Development at Johnson & Johnson.
| Dataset | CCAE | JMDC | MDCD | MDCR | Optum |
|---|---|---|---|---|---|
| Number of subjects | 64,222 | 1,976 | 59,861 | 69,164 | 62,348 |
| Median Age | 43 | 42 | 35 | 71 | 47 |
| % of Female | 69.21 | 36.69 | 73.82 | 68.08 | 69.68 |
| Number of outcomes | |||||
| Acute myocardial infarction (AMI) | 155 | 2 | 438 | 1,207 | 360 |
| % of AMI | 0.24 | 0.10 | 0.73 | 1.75 | 0.58 |
| % of Obesity | 7.15 | 0.71 | 16.54 | 6.71 | 9.62 |
| % of Alcohol dependence | 7.15 | 1.01 | 16.54 | 6.71 | 9.62 |
| % of Hypertensive disorder | 20.81 | 14.37 | 31.80 | 57.70 | 32.96 |
| % of Major depressive disorder | 4.17 | 3.88 | 3.55 | 3.16 | 3.34 |
| % of Type 2 diabetes mellitus | 7.49 | 2.83 | 14.63 | 21.83 | 12.71 |
| % of Hyperlipidemia | 20.96 | 19.23 | 22.00 | 43.21 | 33.85 |
The full names of the five claims datasets are CCAE (IBM MarketScan® Commercial), JMDC (Japanese Medical Data Center), MDCD (IBM MarketScan® Medicaid), MDCR (IBM MarketScan® Medicare) and Optum (Optum© De-Identified Clinformatics).
The risk factors we included in the logistic model include: obesity, alcohol dependence, hypertensive disorder, major depressive disorder, type 2 diabetes, and hyperlipidemia [26,27], i.e.,
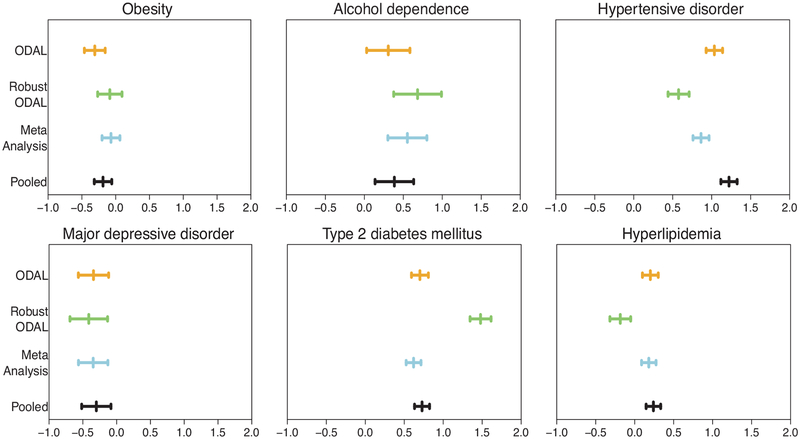
Figure 4 shows the estimated log odds ratios as well as the 95% confidence intervals for six risk factors from four different methods. One direct observation is that there is a substantial difference between the ODAL estimates and estimates from our proposed robust-ODAL algorithm. For most of the risk factors, ODAL provides the point estimates of the log odds ratio closer to the pooled analysis. However, comparing the distributions of the data at the five claims databases, it is highly likely that the data stored in JMDC are very different from the other sites as it is a Japanese database while others are all from the US. Among the four US sites, MDCR tends to have older patients and therefore has a higher prevalence of AMI, hypertensive disorder, Type 2 diabetes, and Hyperlipidemia. Thus, data are heterogeneously distributed across the five datasets, and JMDC and MDCR are likely more different from the other three sites. As a consequence, it is believed that fitting a joint logistic regression model across all sites might lead to bias as it ignores the difference between the sites. And the estimates from the pooled analysis are possibly biased. Our proposed robust-ODAL algorithm is designed to account for such heterogeneity and as a result, it is shown to have the widest confidence interval, which properly reflects the potential impact of heterogeneity.
Fig. 4.
Comparison between the log odds ratio estimates from the ODAL (yellow), robust-ODAL (green), meta-analysis (blue), and pooled analysis (black) with data from OHDSI network for AMI as the outcome and CCAE as the local site.
4. Discussion
Motivated by the critical need for data integration that can account for heterogeneity across clinical sites, we proposed a simple yet effective privacy-preserving distributed algorithm for logistic regressions. Our algorithm is designed to provide an estimator of multi-site logistic regression that is robust to the presence of outlying studies. The proposed robust-ODAL requires to transfer the same aggregated information as the original ODAL. However, the robust-ODAL is shown to have higher accuracy, compared to the ODAL, in practical settings where the data are not independently and identically distributed. In addition, the robust-ODAL also outperforms traditional meta-analysis with less bias in settings with rare diseases.
There are several advantages of the proposed algorithm compared to the existing distributed algorithms. First, compared to the iterative algorithms such as GLORE and WebDISCO [9,18,19], robust-ODAL does not require iterative communication across the sites, reducing the communication cost and the amount of administrative efforts. Secondly, implementation of the robust-ODAL only requires the access of individual patient-level data in a single clinical site. Only aggregated information is transferred from other sites to construct the surrogate likelihood function which avoids sharing patient-level information. Thirdly, compared to the ODAL, the robust-ODAL produces substantially less biased estimates of regression coefficients.
However, the proposed method has a few limitations. First, compared to the original ODAL algorithm, the robust-ODAL is preferred if there exist potential outlying clinical sites. When the data are considered to be relatively homogeneous, the ODAL method is preferred. Secondly, based on the real data application, it suggested that the total number of clinical sites might affect the performance of the proposed method. When the total number of sites is small, the robust-ODAL may not perform well because the median is more sensitive (with larger variation) when the number of sites is small. Thirdly, the proportion of the outlying sites among all the sites also makes an impact on the proposed method. In this paper, we assume there exists a small proportion of outlying sites among all the sites. However, when the proportion is large, other methods should be considered.
Our current investigation can be extended in several aspects. First, since currently we only have access to this data, we plan to apply this method to other datasets in the future. Secondly, we plan to develop methods to integrate other types of outcomes, including continuous, categorical, and time-to-event data. The integration of evidence from statistical models such as Cox proportional hazard models poses unique challenges due to the need for communicating risk sets across sites. Finally, we have been developing an open-source software R package for the direct implementation of our methods in distributed research networks. We believe that our algorithm can be a good complement to the existing distributed algorithms for better facilitating data integration across health systems while accounting for heterogeneity across clinical sites.
Acknowledgments
This work is supported by in part by the University of Pennsylvania, and National Institutes of Health grants1R01LM012607, 1R01AI130460, and the Commonwealth Universal Research Enhancement Program grant from the Pennsylvania Department of Health.
References
- 1.Center for Devices and Radiological Health. Real-World Evidence to Support Regulatory Decision-Making for Devices. FDA Med Bull. www.fda.gov/regulatory-information/search-fda-guidance-documents/use-real-world-evidence-support-regulatory-decision-making-medical-devices [Google Scholar]
- 2.Center for Drug Evaluation and Research. Submitting Documents Using Real-World Data and Real-World Evidence. FDA Med Bull. www.fda.gov/regulatory-information/search-fda-guidance-documents/submitting-documents-using-real-world-data-and-real-world-evidence-fda-drugs-andbiologics-guidance [Google Scholar]
- 3.Center for Drug Evaluation and Research. Use of Electronic Health Record Data in Clinical Investigations. FDA Med Bull. www.fda.gov/regulatory-information/search-fda-guidance-documents/use-electronic-health-record-data-clinical-investigations-guidance-industry [Google Scholar]
- 4.Sherman RE, Anderson SA, Dal Pan GJ, Gray GW, Gross T, Hunter NL, et al. Real-World Evidence - What Is It and What Can It Tell Us? N Engl J Med. 2016;375: 2293–2297. [DOI] [PubMed] [Google Scholar]
- 5.Bowens FM, Frye PA, Jones WA. Health information technology: integration of clinical workflow into meaningful use of electronic health records. Perspect Health Inf Manag. 2010;7: 1d. [PMC free article] [PubMed] [Google Scholar]
- 6.Friedman CP, Wong AK, Blumenthal D. Achieving a nationwide learning health system. Sci Transl Med. 2010;2: 57cm29. [DOI] [PubMed] [Google Scholar]
- 7.Overhage JM, Ryan PB, Reich CG, Hartzema AG, Stang PE. Validation of a common data model for active safety surveillance research. J Am Med Inform Assoc. 2012;19: 54–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Forrest CB, Margolis PA, Bailey LC, Marsolo K, Del Beccaro MA, Finkelstein JA, et al. PEDSnet: a National Pediatric Learning Health System. J Am Med Inform Assoc. 2014;21: 602–606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wu Y, Jiang X, Kim J, Ohno-Machado L. Grid Binary LOgistic REgression (GLORE): building shared models without sharing data. J Am Med Inform Assoc. 2012;19: 758–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Seol Kwangsoo, et al. Privacy-preserving attribute-based access control model for XML-based electronic health record system. IEEE Access 6 (2018): 9114–9128. [Google Scholar]
- 11.Kho Abel N., et al. Design and implementation of a privacy preserving electronic health record linkage tool in Chicago. Journal of the American Medical Informatics Association 225 (2015): 1072–1080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Huang Lu-Chou, et al. Privacy preservation and information security protection for patients’ portable electronic health records. Computers in Biology and Medicine 399 (2009): 743–750. [DOI] [PubMed] [Google Scholar]
- 13.Sahi Muneeb Ahmed, et al. Privacy preservation in e-healthcare environments: State of the art and future directions. IEEE Access 6 (2017): 464–478. [Google Scholar]
- 14.Dubovitskaya Alevtina, et al. A cloud-based ehealth architecture for privacy preserving data integration. IFIP International Information Security and Privacy Conference Springer, Cham, 2015. [Google Scholar]
- 15.G, Ryan PB, Duke JD, Shah NH, Park RW, Huser V, et al. Characterizing treatment pathways at scale using the OHDSI network. Proc Natl Acad Sci U S A. 2016;113: 7329–7336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Boland MR, Shahn Z, Madigan D, Hripcsak G, Tatonetti NP. Birth month affects lifetime disease risk: a phenome-wide method. J Am Med Inform Assoc. 2015;22: 1042–1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Katzan IL, Rudick RA. Time to integrate clinical and research informatics. Sci Transl Med. 2012;4: 162fs41. [DOI] [PubMed] [Google Scholar]
- 18.Cox DR. Regression Models and Life-Tables In: Kotz S, Johnson NL, editors. Breakthroughs in Statistics: Methodology and Distribution. New York, NY: Springer New York; 1992. pp. 527–541. [Google Scholar]
- 19.Ohno-Machado L, Agha Z, Bell DS, Dahm L, Day ME, Doctor JN, et al. pSCANNER: Patient-centered scalable national network for effectiveness research. J Am Med Inform Assoc. BMJ Publishing Group; 2014;21: 621–626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Duan R, Boland MR, Moore JH, Chen Y. ODAL: A one-shot distributed algorithm to perform logistic regressions on electronic health records data from multiple clinical sites. Pac Symp Biocomput. 2019;24: 30–41. [PMC free article] [PubMed] [Google Scholar]
- 21.Liang KY. Extended Mantel-Haenszel estimating procedure for multivariate logistic regression models. Biometrics. 1987;43: 289–299. [PubMed] [Google Scholar]
- 22.Wu H-DI. Effect of Ignoring Heterogeneity in Hazards Regression In: Balakrishnan N, Nikulin MS, Mesbah M, Limnios N, editors. Parametric and Semiparametric Models with Applications to Reliability, Survival Analysis, and Quality of Life. Boston, MA: Birkhäuser Boston; 2004. pp. 239–250. [Google Scholar]
- 23.Forrest CB, Crandall WV, Bailey LC, et al. Effectiveness of anti-TNFα for Crohn disease: research in a pediatric learning health system. Pediatrics 2014; 134(1): 37–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Antunes O, Filippi J, Hébuterne X, Peyrin-Biroulet L. Treatment algorithms in Crohn’s–Up, down or something else? Best Practice & Research Clinical Gastroenterology 2014; 28(3): 473–83. [DOI] [PubMed] [Google Scholar]
- 25.Lee YS, Baek SH, Kim MJ, Lee YM, Lee Y, Choe YH. Efficacy of early infliximab treatment for pediatric Crohn’s disease: a three-year follow-up. Pediatric Gastroenterology, Hepatology & Nutrition 2012; 15(4): 243–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Anand SS, Islam S, Rosengren A, Franzosi MG, Steyn K, Yusufali AH, et al. Risk factors for myocardial infarction in women and men: insights from the INTERHEART study. Eur Heart J. 2008;29: 932–940. [DOI] [PubMed] [Google Scholar]
- 27.Lanas F, Avezum A, Bautista LE, Diaz R, Luna M, Islam S, et al. Risk factors for acute myocardial infarction in Latin America: the INTERHEART Latin American study. Circulation. 2007;115: 1067–1074. [DOI] [PubMed] [Google Scholar]