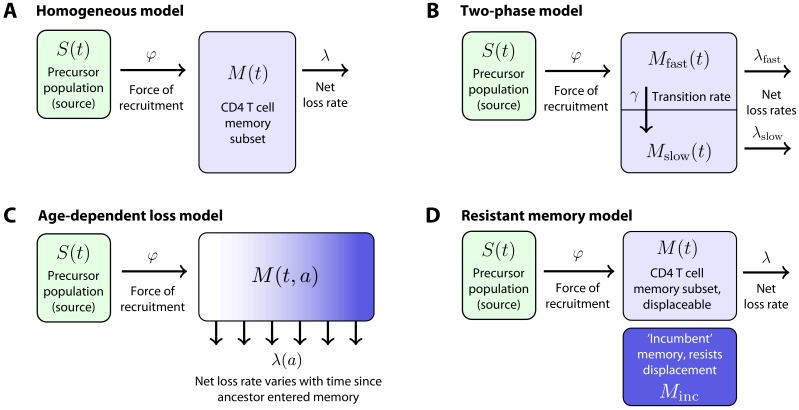
Figure 2. Models of the generation and maintenance of memory CD4⁺ T cell subsets in adult mice.

(A) New cells from a precursor (source) population of size $S(t)$ flow in to a homogeneous memory subset $M(t)$ at total rate $\phi S(t)$. The force of recruitment $\phi$ is approximately the daily probability that any given cell from the source will be recruited into memory, multiplied by an expansion factor. This memory population may self-renew through division and be lost through death or differentiation and is continually supplemented by cells from the source. We assume that the net loss rate (loss minus division) is a constant, $\lambda$. (B) In a two-phase model of memory, new cells are recruited at rate $\phi S(t)$ into a population $M_{\text{fast}}(t)$ that has a high net loss rate ${\lambda }_{\text{fast}}$ and so is replaced by donor cells relatively quickly. These cells transition into a slower subset $M_{\text{slow}}(t)$ at constant rate $\gamma$ and are then lost at net rate ${\lambda }_{\text{slow}}<{\lambda }_{\text{fast}}$. (C) The age-dependent loss model; here, the net loss rate of memory is a continuous function of cell 'age' $a$, defined as the time since a cell or its ancestor entered the memory pool. The model tracks the evolution of the population density of memory T cells of age $a$ at host age $t$, $M(t,a)$. (D) The resistant memory model invokes a subpopulation of ‘incumbent’ memory cells which are presumed to be established early in life, stable in numbers, and not replenished from the source population. As in the homogeneous model, the source feeds a compartment of 'displaceable’ cells, with net loss rate $\lambda$.