Mid-Holocene Northern Hemisphere warming driven by Arctic amplification

Analyses of a mid-Holocene climate model ensemble and paleo-proxies reveal that the mid-Holocene Northern Hemisphere was warm.

Abstract

The Holocene thermal maximum was characterized by strong summer solar heating that substantially increased the summertime temperature relative to preindustrial climate. However, the summer warming was compensated by weaker winter insolation, and the annual mean temperature of the Holocene thermal maximum remains ambiguous. Using multimodel mid-Holocene simulations, we show that the annual mean Northern Hemisphere temperature is strongly correlated with the degree of Arctic amplification and sea ice loss. Additional model experiments show that the summer Arctic sea ice loss persists into winter and increases the mid- and high-latitude temperatures. These results are evaluated against four proxy datasets to verify that the annual mean northern high-latitude temperature during the mid-Holocene was warmer than the preindustrial climate, because of the seasonally rectified temperature increase driven by the Arctic amplification. This study offers a resolution to the “Holocene temperature conundrum”, a well-known discrepancy between paleo-proxies and climate model simulations of Holocene thermal maximum.

INTRODUCTION

Since the end of the last ice age around 12,000 years ago, warming climates have led to the development of agriculture and the rise of human civilization. This important period is referred to as the Holocene geological epoch (1). During the early-mid Holocene, Northern Hemisphere (NH) summer solar insolation was anomalously strong, causing the Holocene thermal maximum (HTM) from around 9000 to 5000 years before present (1, 2). Pronounced warming at high latitudes, including Greenland, Western Arctic, and Northern Europe, has been associated with the HTM (3–6). Proxy data indicate that mid-Holocene Arctic sea ice cover was likely reduced relative to the present (7–9).

The Arctic temperature is closely related to the global mean temperature in equilibrium climate states (10), and Arctic warming has been directly linked to warming of the extratropical ocean (11, 12). Therefore, it is reasonable to assume that the NH was probably warmer during the HTM than during the preindustrial era, at least in the NH extratropics (30°N-90°N). However, this analogy does not account for the seasonal changes in solar radiation during the HTM: Because the stronger summer solar heating was compensated by weaker winter insolation, the annual mean insolation anomalies were relatively small (13) and the annual mean HTM temperatures are difficult to estimate (2, 6). In addition, in a climate model simulation, the annual mean mid-Holocene temperature in the northern extratropics (30°N-90°N) was found to be slightly lower than that of the preindustrial climate (14).

In this study, we investigate the annual mean temperature during the mid-Holocene warm period using a suite of climate model simulations. We show that the response of the NH annual mean temperature to mid-Holocene insolation is closely tied to the degree of Arctic amplification simulated in these models. Specifically, we show that the NH temperature anomalies are strongly correlated with Arctic surface temperature and sea ice cover anomalies. In other words, climate models simulating warmer NH climate exhibit much larger Arctic amplification and sea ice loss than others. In these warm models, summer Arctic sea ice loss persists into winter and increases the mid- and high-latitude temperatures throughout the season. We further show that the northern high-latitude temperatures reconstructed from paleo-proxy data agree better with these warm models’ estimates. This comparison suggests that during the mid-Holocene, the climate system underwent an Arctic-amplified warming response to the more pronounced seasonal cycle of insolation and that the persistence of sea ice loss into winter led to an annual mean warming of the NH. In addition, our findings resolve a previously highlighted discrepancy between Holocene temperature reconstructions derived from paleo-proxy data versus climate models (14–16), coined the “Holocene temperature conundrum” (14, 15); this discrepancy vanishes in models that simulate a strong Arctic amplification response to mid-Holocene insolation.

RESULTS

Arctic and global temperature anomalies in climate models

To assess the climate response to the amplified seasonal insolation forcing during the HTM, we examined the mid-Holocene climate simulated by 13 climate models. Of 13 models, 11 were obtained from the Paleoclimate Modeling Intercomparison Project phase 3 (PMIP3), while the remaining 2 simulations were conducted by the authors for the purpose of this study (see Methods). The mid-Holocene, which was about 6000 years BP, belongs to the late period of the HTM and is one of the benchmark periods of the PMIP3 (6).

Figure 1A shows the globally averaged mid-Holocene temperature anomalies relative to the preindustrial climate from the 13 model simulations. A majority of climate models simulate a colder mid-Holocene relative to the preindustrial climate, which is qualitatively consistent with a recent model study (14) showing that the global mean temperature may have increased from the HTM to the present. However, the annual mean NH extratropical temperatures averaged over 30°N-90°N show generally warm anomalies: 9 of the 13 models simulate a warmer mid-Holocene than the preindustrial NH climate (Fig. 1C). Note that the northern extratropics is the key region where the proxy-based reconstruction (15) shows the largest warm anomalies during the HTM. The three warmest climate models, CNRM-CM5 (Coupled Climate Model version 5), CESM1-CAM5 (Community Atmospheric Model version 5), and MRI-CGCM3, exhibit more than 0.3 K warming in the mid-Holocene NH. In contrast, NCAR-CCSM4, which was used in (14), exhibits a 0.25 K cooling in the mid-Holocene. For reference, 1 SD of the annual mean temperature variations averaged in NH extratropics is less than 0.2 K (estimated from preindustrial simulations).

Fig. 1. Global and Arctic surface temperature simulated by 13 climate models.

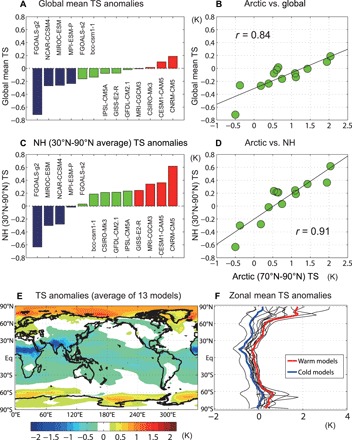
(A and C) The mid-Holocene surface temperature (TS) anomalies (differences between 6 ka and 0 k) of 13 different climate models, averaged (A) globally (90°S-90°N) and (C) in the NH extratropics (30°N-90°N). (B and D) Multimodel relationships between surface temperature anomalies (B) in the Arctic (70°N-90°N) versus the global average and (D) in the Arctic versus the NH extratropics. (E) The annual mean surface temperature anomalies averaged across the 13 models. (F) The zonal mean surface temperature anomalies as a function of latitude in all 13 models (black lines) and averaged across the 4 warmest (red line) and 4 coldest (blue line) models.

The multimodel mean temperature anomalies exhibit a pattern of warming at high latitudes and cooling in the tropics (Fig. 1E), and this pattern is generally consistent with the annual mean insolation anomalies (fig. S1). However, the individual models simulate a wide range zonal mean temperature anomalies (Fig. 1F), and these intermodel temperature differences render the multimodel average mid-Holocene temperature anomaly statistically insignificant (17). The composite maps of surface temperature averaged over the four warmest and the four coldest models show that the warmest models simulate an enhanced polar warming, especially in the Arctic (red line in Fig. 1F and fig. S2). Over Europe, a slight warming (Fig. 1E) and more pronounced warming (fig. S2) appear in the averages of 13 models and the 4 warmest models, respectively, which is consistent with multiple proxy records (6, 18, 19), but no such warming is distinguishable in the coldest model average (fig. S2).

The warmest models exhibit less tropical cooling (red line in Fig. 1F), which is consistent with previous model findings (20) that the degree of Arctic amplification is correlated with tropical temperature anomalies in both past and future climates. Tropical sea surface temperature (SST), despite its relatively small variations, is known to affect the Arctic amplification through poleward energy transport (21). Additional idealized climate model experiments (see Methods) indicate that the tropical SST cooling drives moderate cooling in the southern extratropics (30°S-50°S), where the cooling signal persists throughout the season (fig. S3). However, the seasonal surface temperature anomalies show that the NH cooling is not seasonally persistent; the tropics and extratropics experience slight warming in autumn and early winter (fig. S3). In NH, the tropical SST cooling drives extratropical cooling in late winter, spring, and summer (from around February to August), especially over the western North Pacific, where SSTs decrease by more than 0.5 K. On the contrary, the tropical SST warming in autumn and early winter is followed by an extratropical warming, especially in the Arctic (fig. S3), likely due to the tropical-extratropical teleconnection in response to tropical heating in boreal winter (22). In summary, the tropical SST cooling in mid-Holocene certainly contributes to decreasing temperature in the subtropics and mid-latitudes, which is consistent with the finding in (20). However, the annual mean tropical SST cooling can slightly warm the Arctic, suggesting that the weakened tropical SST cooling in the warm models is not driving the Arctic amplification in those models.

Consistent with previous modeling studies, our idealized tropical cooling experiments indicate that the local radiative forcing and the associated feedbacks in the Arctic are more important than teleconnections from the tropics in explaining polar amplification in both the Arctic (23) and Antarctic (24). Recent studies further indicate that the Arctic warming can increase extratropical SSTs (11, 12), which can, in turn, accelerate the Arctic warming (12). Moreover, the Arctic sea ice loss can increase tropical SSTs via ocean dynamical processes and air-sea interaction (25, 26). Figure 1B shows that the intermodel spread in global mean temperature is well correlated with that in Arctic temperature with a correlation coefficient of 0.84, which is statistically significant (P < 0.01). The correlation between the Arctic and the northern extratropics is even larger, r = 0.91 (Fig. 1D). This result implies that the uncertainty in Arctic temperature response to the mid-Holocene insolation forcing explains more than 80% of the variance in the NH temperature responses across the 13 climate models examined here. The multimodel regression line also indicates that the Arctic warming is about 3.5 times stronger than that of the northern extratropics. These robust relationships (r = 0.84 and 0.91) suggest that the degree of Arctic amplification plays a key role in setting the mid-Holocene global temperature, especially in the northern extratropics.

Seasonal temperature anomalies in the warmest versus coldest models

What drives such a large intermodel difference in Arctic temperature responses (Fig. 1, B and D)? The zonal mean time-latitude Hovmöller plots of surface temperature show that high-latitude (60°N-85°N) warming in summer persists into winter in the four warmest models (Fig. 2A), whereas the summer warming does not persist in the four coldest models (Fig. 2B). These results appear robustly in the case when the second and third warmest/coldest models are chosen for the Hovmöller plots of surface temperature (fig. S4), verifying that the seasonally persistent high-latitude warming is a general feature of warm models rather than an average artifact associated with the extremely warm model, CNRM-CM5. These results indicate that the key difference between the warmest and the coldest models is the magnitude of summer heating and its persistence into winter.

Fig. 2. Surface temperature and Arctic sea ice responses.

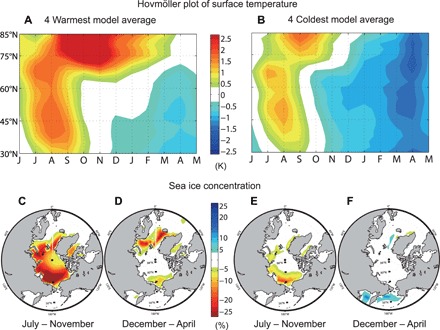
(A and B) Zonally averaged, latitude-time Hovmöller plots of surface temperature anomalies in (A) the four warmest models and (B) the four coldest models. The abscissa is time (months) and the ordinate is latitude. Arctic sea ice concentration (SIC; %) anomalies in (C and D) the four warmest models and (E and F) the four coldest models, averaged in (C and E) July to November and (D and F) December to April.

It is likely that the seasonally persistent Arctic warming in the warmest models (e.g., CNRM-CM5 and CESM1-CAM5) is the outcome of various climate feedbacks associated with Arctic sea ice loss (27). In the warmest models, Arctic sea ice concentration (SIC) in summer-autumn decreases by 30 to 35% over wide areas of the Arctic relative to the preindustrial climate (Fig. 2C), and these SIC anomalies persist into winter and early spring over the marginal ice zone (Fig. 2D), indicative of delayed refreezing and reduced ice growth (28). This autumn-winter sea ice loss is accompanied by increases in heat transfer from the Arctic Ocean to the atmosphere, primarily through turbulent heat fluxes (fig. S5), further contributing to the Arctic amplification via the cloud radiative feedback (28–30). Moreover, the near-surface temperature inversion in the cold season confines the warming to the surface (30), and the associated weakening of temperature inversion can contribute to the Arctic amplification (23). Last, the paleo calendar effect (31) may also affect the degree of Arctic amplification in autumn and winter.

The winter SIC anomalies, although smaller than those of summer-autumn, strongly influence mid-latitude climate (32), partly because the reduction of winter SIC is accompanied by reduced ice thickness (33). In the coldest models, however, the summer-autumn SIC anomalies are small, generally within 10% (Fig. 2E), and do not persist into winter (Fig. 2F). In the absence of the Arctic sea ice loss, the northern mid- and high latitudes are anomalously cold (Fig. 2B) because of the weaker winter insolation in the mid-latitudes and the sub-Arctic (fig. S1). Several paleo-proxy records suggest that the eastern Canada and the Atlantic sector of the Arctic experienced a substantial reduction in sea ice cover during the HTM (8, 9), lending support to the anomalies simulated by the warmest models. However, it is still unclear whether there was a basin-wide reduction of Arctic SIC (34).

Rectification of seasonal temperature by Arctic sea ice loss

Because the Arctic sea ice loss is generally confined to latitudes higher than 70°N (Fig. 2, C and D), the causality between the sea ice loss and the mid-latitude warming (Fig. 2A) remains elusive. While the degree of Arctic amplification is somewhat constrained by tropical SSTs in past climates (20), recent modeling studies indicate that Arctic warming can increase extratropical and tropical SSTs (11, 12, 25, 26). To better quantify the climatic responses to the mid-Holocene Arctic sea ice loss, we performed idealized climate model experiments (see Methods) using CESM1-CAM5, the second warmest model (see Fig. 1, A and C). A series of simulations show that the impact of Arctic sea ice loss is not limited to high latitudes but extends to warming of the mid-latitudes (Fig. 3, A and D). The zonal mean, time-latitude Hovmöller plot of surface temperature (Fig. 3A) shows that the Arctic sea ice loss can substantially increase the sub-Arctic (60°N-70°N) temperature by around 1.0 K and that these anomalies extend southward to around 50°N. Although the Arctic sea ice loss is most pronounced in summer and autumn (Fig. 2C), the associated mid-high latitude warming is largest in autumn and winter (Fig. 3A). This result supports a previous modeling study (35) that the wintertime high-latitude temperature in mid-Holocene is controlled by the enhanced summer insolation.

Fig. 3. Disentangling the impacts of Arctic sea ice loss and insolation forcing.

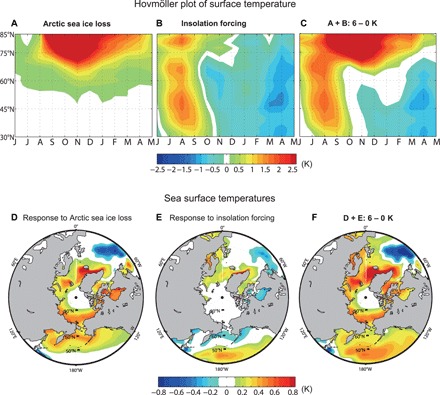
Surface temperature responses to mid-Holocene (A and D) Arctic sea ice loss, (B and E) insolation forcing, and (C and F) total forcing (sum of sea ice loss and insolation). (A to C) Zonally averaged, latitude-time Hovmöller plots of anomalous surface temperature and (D to F) the annual mean SST anomalies. In (A) to (C), the abscissa is time (months) and the ordinate is latitude.

In contrast, the direct insolation forcing does not contribute to the rectification of seasonal temperature but amplifies the seasonal cycle; the zonal mean surface temperature anomalies rapidly increase in summer-autumn but quickly subside in late autumn and become negative in winter (Fig. 3B). The seasonal temperature response of CESM1-CAM5 to the total forcing (the sum of sea ice loss and insolation forcing; Fig. 3C) exhibits seasonally persistent high-latitude warming, which is similar to that of the warmest models (Fig. 2A). These results indicate that the reduced summer SIC anomalies persisting into winter in the warmest models (Fig. 2, C and D) contribute to the Arctic amplification through radiative feedback (28–30) and possibly through lapse rate feedback (23).

How does the Arctic sea ice loss increase the mid-latitude temperature? Climate model simulations consistently indicate that the projected Arctic sea ice decline is followed by extratropical ocean warming (11, 12) that enhances the impact of sea ice loss on mid-latitude climate (12). Consistent with previous studies, Fig. 3D shows that Arctic sea ice loss increases the annual mean SSTs over the North Pacific and the Nordic Seas by more than 0.5 K. This extratropical ocean warming, resulting from the Arctic sea ice loss (Fig. 3D), is generally stronger than that of the direct insolation forcing (Fig. 3E), especially in the sub-Arctic regions. The Arctic sea ice loss also produces a localized ~0.5 K decrease in SSTs in the central North Atlantic, but this localized Atlantic cooling signal is masked under a zonal average (Fig. 3A).

Evaluation of climate models against proxy data

Evaluating the climate model simulations against reconstructed proxy data is one of the key purposes of PMIP (18). While the simulated temperatures differ widely from one another (Fig. 1, A and C), they are well correlated with the degree of Arctic amplification (Fig. 1, B and D). This strong intermodel correlation could provide a quantitative framework via which to estimate global-scale temperatures from the reconstructed proxy data in the high latitudes. To evaluate the model simulations, we used four different proxy datasets:

(1) Bartlein data

This is a pollen-based dataset assembled by a PMIP working group (36). This dataset has 2° ×2° spatial resolution and is based on 148 proxy stations in high latitudes (higher than 60°N) mostly over land (Fig. 4B). To quantitatively compare these proxy data with model simulations, the same grids covered by the proxy data are selected in the climate models (Fig. 4C). Both proxy data (Fig. 4B) and the warm model average (Fig. 4C) exhibit anomalously warm temperatures over Fennoscandia, where proxy data are most abundant. However, regional-scale temperature variations are much larger in paleo-proxy data than climate model simulations (6). Because of the large spatial temperature variations in proxy data, the spatial correlation coefficients between the proxy data and the models are generally low (see Table 1), although 6 of 13 climate models exhibit statistically significant correlations (P < 0.05).

Fig. 4. Evaluating the climate models against paleo-proxy data.

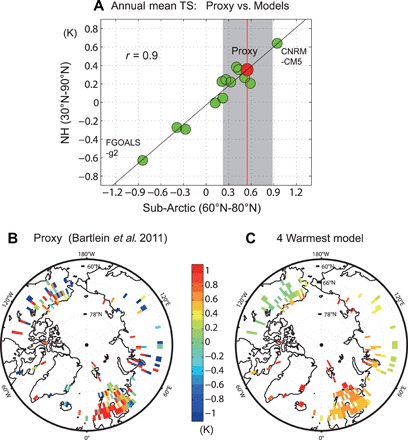
(A) Relationship between mid-Holocene surface temperature anomalies in the sub-Arctic (60°N-80°N), averaged over the grid points at which paleo-proxy data are available (abscissa), and the entire NH extratropics (30°N-90°N) (ordinate). The green dots are from the 13 climate model simulations examined in this study, and the red dot is from the paleo-proxy data. The gray shading superposed on the red dot indicates a 95% confidence interval range for the paleo-proxy data, bootstrapped via Monte Carlo simulation. Sub-Arctic surface temperature anomalies (B) reconstructed from the paleo-proxy data and (C) simulated by the four warmest climate models over the grid points at which the paleo-proxy estimates are available.

Table 1. The spatial correlation coefficient of the annual mean temperature anomalies between paleo-proxy data (37) and the individual climate model.

The second and third columns indicate the correlation coefficient and statistical significance, respectively. Statistically significant values, higher than 95% (p < 0.05), are in boldface.

Climate models (from the warmest to coldest)	Correlation coefficient	Statistical significance
CNRM-CM5 (warm)	0.12	86%
CESM1-CAM5 (warm)	0.05	46%
MRI-CGCM3 (warm)	0.19	98%
GISS-E2-R (warm)	0.08	62%
IPSL-CM5A-LR (median)	0.20	98%
GFDL-CM2.1 (median)	0.10	76%
CSIRO-Mk3-6-0 (median)	0.25	99.7%
BCC-CSM-1 (median)	0.15	93%
FGOALS-s2 (median)	0.24	99.6%
MPI-ESM-P (cold)	0.17	95%
NCAR-CCSM4 (cold)	0.19	98%
MIROC-ESM (cold)	−0.09	72%
FGOALS-g2 (cold)	0.14	89%

Annual mean temperature anomalies averaged over the selected grids are plotted in the abscissa of Fig. 4A. The intermodel temperature difference ranges up to 1.8 K and this is about 30% smaller than that in the Arctic [about 2.5 K as shown in Fig. 1 (B and D)]. Although spatially sparse grids are averaged, these grid-averaged temperatures are well correlated with temperatures averaged in the entire NH extratropics (Fig. 4A). The average of proxy-based temperature anomaly is 0.56 K (red dot in Fig. 4A), which is similar to those of the relatively warm climate models such as CESM1-CAM5 and MRI-CGCM3. The uncertainty range for the high-latitude proxies, derived via Monte Carlo simulation, is from 0.25 to 0.88 K of warming (gray shading in Fig. 4A). This uncertainty range, when using the sensitivity range suggested by the model spread, corresponds to an NH extratropical warming range of 0.12 to 0.6 K and that both the coldest and warmest models provide useful information to generate this empirical fit.

(2) Sundqvist data

This dataset, compiled from previously published Holocene proxy records in northern high latitudes (37), provides 93 proxy stations for the temperature data reconstructed from various proxies such as pollen, oxygen isotopes in ice cores, dinocysts, chironomids, and diatoms. While the number of stations is smaller than that of Bartlein data (36), the temperature records were reconstructed not only from land but also from the Arctic and sub-Arctic oceans. Consistent with Fig. 4, the average value proxy-based reconstruction of temperature anomalies is similar to those of the warm models (Fig. 5A). This uncertainty range of this proxy dataset (gray shading in Fig. 5A) ranges from 0.38 to 0.92 K, which corresponds to an NH extratropical warming range of 0.12 to 0.42 K.

Fig. 5. Validating against multiple paleo-proxy datasets.

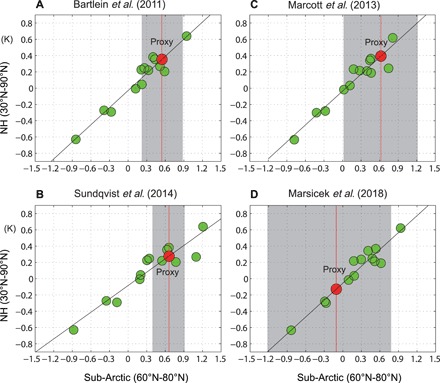
Relationship between surface temperature anomalies in the sub-Arctic (60°N-80°N), averaged over the grid points at which paleo-proxy data are available (abscissa), and the entire NH extratropics (30°N-90°N) (ordinate). Paleo-proxy data are from (A) Bartlein et al. (36), (B) Sundqvist et al. (37), (C) Marcott et al. (15), and (D) Marsicek et al. (16). The green dots are from the 13 climate model simulations examined in this study, and the red dots are from the paleo-proxy data. The gray shading superposed on the red dot indicates a 95% confidence interval range for the paleo-proxy data, bootstrapped via Monte Carlo simulation. (A) is identical to Fig. 4A.

(3) Marcott data

More comprehensive Holocene temperature variations covering the entire globe can be found in proxies compiled in (15), which shows a distinct warming in HTM. While this proxy dataset can be directly used for assessing the Holocene temperature conundrum, there are only 13 stations covering the northern high latitudes. Therefore, the uncertainty range of the average temperature estimated for this proxy dataset is large, ranging from around 0 to 1.2 K (gray shading in Fig. 5C). The average value of these 13 proxies for the mid-Holocene era (5500 to 6500 BP) is about 0.6 K, which is similar to those of the warm models, supporting the estimations from Bartlein data (36) and Sundqvist data (Figs. 4A and 5A) (37).

(4) Marsicek data

We also examined the most recent paleo-proxies, which estimated the Holocene temperature variations from subfossil pollen across North America and Europe using a modern analog technique (16). The annual mean temperatures of this Marsicek data exhibit long-term warming throughout the Holocene until around 2000 years ago, which directly contradicts the findings in (15). Because these proxies focus on the mid-latitudes, there are only around 18 stations covering the northern high latitudes. The average temperature anomaly derived from these 18 stations is about −0.1 K, and the associated NH temperature anomaly is −0.15 K (Fig. 5D), indicating that the NH annual mean temperature in mid-Holocene could have been lower than the preindustrial climate. However, the uncertainty range of these proxies (gray shading in Fig. 5D) covers the entire model spread, except the warmest model (CNRM-CM5), so it is difficult to reconcile this proxy dataset (16) with the other three proxy datasets (15, 36, 37).

In summary, three of four paleo-proxy datasets (Figs. 4A and 5, A and B) indicate that the NH extratropics may have been warmer during the mid-Holocene than in the preindustrial era and that the proxy-based estimation of NH annual mean temperature is generally within the range of model simulations. This suggests that the apparent discrepancy between temperature reconstructions from paleo-proxy data (15) and simulated mid-Holocene temperature (14) may be attributable to intermodel variations in the degree of simulated Arctic amplification.

DISCUSSION

In this study, we examined 13 climate models that simulate widely varying annual mean temperature responses in the NH extratropics and found that these temperature anomalies are strongly correlated with the degree of Arctic amplification. The models that exhibited the strongest annual mean NH warming and Arctic amplification in response to mid-Holocene insolation also simulated pronounced summer warming anomalies that persisted into winter. Idealized climate model perturbation experiments using CESM1-CAM5 exhibit a similar warming anomaly in response to an isolated loss of Arctic sea ice, indicating that the response of Arctic sea ice to mid-Holocene insolation is a key discriminator between the models’ NH temperature responses. However, a caveat remains in applying our single model (i.e., CESM1-CAM5) results to all the other climate models. The Arctic sea ice cover during the HTM was likely smaller than the preindustrial climate, as shown by proxy records (8, 9), which is consistent with a substantial Arctic warming in the mid-Holocene. Unfortunately, the pan-Arctic reconstruction of mid-Holocene Arctic sea ice cover is not available (34). As an alternative means of evaluating the model results, we used high-latitude (higher than 60°N) temperature reconstructions and found that the proxy-based temperature anomalies were close to those of the climate models that simulated a warmer NH mid-Holocene.

Our results indicate that climate models simulating stronger rectified temperature increases, and more pronounced Arctic sea ice loss, are closer to the proxy-based temperature reconstructions and therefore simulate the mid-Holocene climate with greater fidelity. Combined with paleo-proxy temperature records, this suggests that during the mid-Holocene, changes in insolation induced an Arctic amplification response and sea ice retreat and resulted in an annual mean NH warming. Our findings also resolve the apparent discrepancy between climate model simulations and paleo-proxy records (14): This discrepancy is absent in models that simulate a stronger Arctic amplification response to mid-Holocene insolation, which more closely reproduce the average temperature anomalies derived from paleo-proxies.

Last, this finding has implications for the projection of future climate change. Climate models simulating more Arctic sea ice loss in response to the mid-Holocene insolation generally exhibit higher sensitivities to an increased CO₂ concentration (38). Therefore, our results suggest that the projected Arctic sea ice decline will likely to be faster than the multimodel ensemble mean prediction.

METHODS

Multimodel simulations (PMIP3)

The mid-Holocene, around 6000 years BP, is a benchmark period of the PMIP3. These simulations are designed to test the climate models’ responses to the enhanced seasonal insolation forcing, a key characteristic of the HTM. The primary difference between the mid-Holocene and the preindustrial climate simulations is the orbital forcing. Mid-Holocene CO₂ concentration, aerosols, ice sheets, and topography are the same as those of the preindustrial climate simulation. We evaluated the surface temperature and SIC fields by examining the differences between PMIP3 mid-Holocene and phase 5 of the Coupled Model Intercomparison Project (CMIP5) preindustrial simulations. A list of the PMIP3-CMIP5 models, their atmosphere and ocean resolutions, and averaging periods (in years) used for analysis are provided in Table 2.

Table 2. Summary of the PMIP3 simulations and two additional climate model simulations conducted for the purpose of this study.

The fourth and fifth columns indicate the averaging periods (years) for the preindustrial (0 ka) and the mid-Holocene (6 ka) simulations, respectively. References for these PMIP3 models can be found in (39).

PMIP3 models	Atmosphere resolutions (lat × lon lev)	Ocean resolutions (lat × lon lev)	0 ka (years)	6 ka (years)
BCC-CSM-1	T42 L26	360 × 232 L40	500	100
NCAR-CCSM4	0.9° × 1.25° L26	320 × 384 L60	1050	300
CNRM-CM5	T127 L31	362 × 292 L42	850	200
CSIRO-Mk3-6-0	T63 L18	192 × 192 L31	500	100
FGOALS-g2	2.81° × 2.81° L26	360 × 196 L30	700	685
FGOALS-s2	1.67° × 2.81° L26	360 × 196 L30	501	100
GISS-E2-R	2.0° × 2.5° L40	288 × 180 L32	1200	100
IPSL-CM5A-LR	1.875° × 3.75° L39	182 × 149 L31	1000	500
MIROC-ESM	2.8° × 2.8° L80	256 × 192 L44	630	100
MPI-ESM-P	T63 L47	256 × 220 L40	1150	100
MRI-CGCM3	TL159 L48	364 × 368 L51	500	100
Additional models	Atmosphere resolutions	Ocean resolutions	0 ka (years)	6 ka (years)
CESM1-CAM5	0.9° × 1.25° L26	gx1v6 L60	250	250
GFDL-CM2.1	2.0° × 2.5° L24	360 × 384 L50	150	150

Two additional climate model simulations

To improve the robustness of our analyses of the PMIP3 ensemble, we performed two additional simulations using NCAR CESM1.2.1 (40) and GFDL (Geophysical Fluid Dynamics Lab) CM2.1 (41). For each model, we performed both mid-Holocene and preindustrial climate simulations, configured and forced in the same way as the existing PMIP3 simulations.

(1) NCAR CESM1.2.1

The atmospheric component of NCAR CESM1.2.1 is the CAM5 with 30 vertical levels, and the ocean component is the Parallel Ocean Program version 2 with 60 vertical levels. The land and sea ice components are the Community Land Model version 4 and the Los Alamos sea ice model version 4, respectively. We integrated this model using a horizontal grid spacing of approximately 1° (f09g16). The root mean square errors of sea ice extent and volume between CESM1-CAM5 and observations are one of the lowest (42) among 49 climate models that have participated in CMIP5.

(2) GFDL CM2.1

We also used the CM2.1, which was developed at the GFDL. The atmospheric model (AM2.1) uses a Lagrangian finite-volume dynamical core, with a 2.5° longitude × 2° latitude and 24 vertical levels. The ocean component is the Modular Ocean Model (MOM) (MOM5.1 in this study), which consists of 50 vertical levels, a constant zonal resolution of 1°, and a meridional resolution varying from 0.33° at the equator to 1° close to the poles. The land and sea ice components are the land model version 2.1 based on the Land Dynamics Model and the Sea Ice Simulator. We performed simulations of approximately 200 years in duration for both the mid-Holocene and preindustrial climates.

Idealized climate model perturbation experiments

(1) NCAR CESM1.2.1

This is the second warmest model in simulating the mid-Holocene climate and exhibits a relatively strong Arctic warming (Fig. 1). We used this model to test the impact of Arctic sea ice loss on extratropical temperature. To distinguish the climatic responses to sea ice loss and anomalous insolation forcing in the mid-Holocene, we performed three different model simulations:

(1) 0 k: Preindustrial control simulation (335-year duration);

(2) 6 ka: Mid-Holocene climate simulation (315-year duration);

(3) 6 ka with 0 k sea ice: Mid-Holocene climate with sea ice albedo is increased to 0.91 (316-year duration).

These are the same simulations used in (39). While (39) focused on the atmosphere and ocean circulation responses to sea ice loss, this study focuses on how the seasonal cycle of insolation led to the annual mean warming in the mid-Holocene. For the “6 ka with 0 k sea ice” simulation, the mid-Holocene forcing is branched off at year 31 of the preindustrial run, except that the albedo of sea ice is increased globally, and throughout the year, from 0.73 to 0.91 to reflect more sunlight, while the snow albedo over sea ice is not changed. Recent studies (12, 43) also used this method (changing sea ice albedo) to identify the impact of Arctic sea loss. The increased ice albedo simulation maintains the Arctic sea ice cover by reflecting anomalously strong 6 ka summer insolation, keeping SIC anomalies within 5% of the preindustrial simulation in summer and autumn. A more detailed description of these idealized model experiments is given in (39).

The contributions of Arctic sea ice loss and direct insolation anomalies to mid-Holocene climate, relative to the preindustrial, can be separated as follows:

(1) The contribution of Arctic sea ice loss: (6 ka) − (6 ka with 0 k sea ice)

(2) The contribution of insolation forcing: (6 ka with 0 k sea ice) − (0 k)

In each simulation, we performed analysis using the last 250 years.

(2) GFDL CM2.1

This model’s global and northern extratropical temperature responses to the mid-Holocene insolation forcing are close to the multimodel averages being neither too warm nor too cold (Fig. 1, A and C). Similar to the multimodel averages, this model also exhibits a pattern of warming in the high latitudes and cooling in the tropics (fig. S3). To isolate the impact of this tropical SST cooling on global temperature, especially on the Arctic amplification, we performed an idealized mid-Holocene climate experiment, in which the tropical (30°S-30°N) SSTs were continuously restored to those of the preindustrial climate. These simulations are summarized as follows:(1) 6 ka: Mid-Holocene climate simulation (208-year duration);(2) 6 ka with 0 K tropical SSTs: Mid-Holocene climate with tropical SSTs are restored to those of 0 K with a restoring time scale of 5 days (180-year duration).

The contributions of the tropical SST cooling to mid-Holocene climate can be separated as the difference between these two simulations:

The contribution of tropical SST cooling: (6 ka) − (6 ka with 0 k tropical SSTs).

In each simulation, we performed analysis using the last 150 years. The simulation results are presented in fig. S3.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/12/eaax8203/DC1

Fig. S1. Mid-Holocene insolation anomalies.

Fig. S2. Surface temperature anomalies simulated by climate models.

Fig. S3. Testing the impact of mid-Holocene tropical cooling using CM2.1.

Fig. S4. Same as Fig. 2 except for the second and third warmest/coldest model composites.

Fig. S5. Autumn-winter surface heat fluxes in the Arctic.