Abstract
Heterogeneous environments, such as mountainous landscapes, create spatially varying selection pressure that potentially affects several traits simultaneously across different life stages, yet little is known about the general patterns and drivers of adaptation in such complex settings. We studied silver fir (Abies alba Mill.) populations across Switzerland and characterized its mountainous landscape using downscaled historical climate data. We sampled 387 trees from 19 populations and genotyped them at 374 single-nucleotide polymorphisms (SNPs) to estimate their demographic distances. Seedling morphology, growth and phenology traits were recorded in a common garden, and a proxy for water use efficiency was estimated for adult trees. We tested whether populations have more strongly diverged at quantitative traits than expected based on genetic drift alone in a multi-trait framework, and identified potential environmental drivers of selection. We found two main responses to selection: (i) populations from warmer and more thermally stable locations have evolved towards a taller stature, and (ii) the growth timing of populations evolved towards two extreme strategies, ‘start early and grow slowly' or ‘start late and grow fast', driven by precipitation seasonality. Populations following the ‘start early and grow slowly' strategy had higher water use efficiency and came from inner Alpine valleys characterized by pronounced summer droughts. Our results suggest that contrasting adaptive life-history strategies exist in silver fir across different life stages (seedling to adult), and that some of the characterized populations may provide suitable seed sources for tree growth under future climatic conditions.
Subject terms: Evolutionary genetics, Quantitative trait, Stable isotope analysis, Forest ecology
Introduction
Phenotypic differences between populations may reflect neutral, adaptive, and/or plastic processes (Kawecki and Ebert 2004). Neutral processes often lead to phenotypic differentiation between populations at the species’ range edges, where populations are small and isolated (e.g., Hampe and Petit 2005; Kawecki 2008). The relative importance of adaptation and plasticity ultimately depends on the degree of environmental heterogeneity and the dispersal ability of the species (Via and Lande 1985; Sultan and Spencer 2002, Chevin and Lande 2010; Polechova 2018). Local adaptation is likely to establish when the spatial scale of environmental variation is greater than the dispersal ability of the species, while plasticity is likely to be favoured with a fine-scale environmental variability and/or in the presence of long-distance gene flow.
Forest trees have large effective population sizes, species ranges that span large spatial scales, a long life-span and a predominantly outcrossing mode of reproduction (Petit and Hampe 2006). Long-distance gene flow is also common in forest trees and its role in adaptation has been recognized (Kremer et al. 2012). These characteristics largely favour plasticity, which has been illustrated by multi-site common garden trials, for example for growth (e.g., Rehfeldt et al. 2002) or phenology (e.g., Vitasse et al. 2010; De Kort et al. 2016); see further references in Kremer et al. (2012). Nevertheless, local adaptation is also common in forest trees, with ample evidence for adaptive divergence along continuous environmental clines, such as those created by latitude or distance to the sea in the boreal zone, or altitudinal gradients in the temperate zone (Savolainen et al. 2007; Alberto et al. 2011; Lind et al. 2018).
While adaptation has been extensively studied along environmental gradients, much less is known about its general patterns and drivers in heterogeneous environments. Indeed, populations across heterogeneous landscapes may display rapid and often non-predictable changes in genetic diversity and trait divergence (Yeaman and Jarvis 2006). Mountainous regions of the Northern Hemisphere often create such heterogeneous landscapes for many species. Here, post-glacial recolonization not only traced the climatic niche, but was also constrained by topography, creating complex patterns in species distributions and demography (Hewitt 1999). Environmental drivers of adaptation in mountain ranges can go undetected with coarse-scale climate data (e.g., Austin and Van Niel 2011; Ruosch et al. 2016). The development of many fine-scale environmental data sets provides new opportunities to study adaptation across mountainous landscapes (e.g. Karger et al. 2017; Hengl et al. 2017). It is also increasingly recognized that spatial heterogeneity in climate in mountainous landscapes represents an important spatial buffer in response to climate change (e.g., Ackerly et al. 2010).
The phenotypic signature of spatially varying selection across populations can be assessed using QST, a measure of genetic differentiation between populations (Whitlock 2008). Comparing QST with divergence at neutral genetic markers (FST) provides a means for identifying locally adapted populations (Whitlock 2008; Whitlock and Guillaume 2009). In principle, a comparison of QST to FST controls for demography, but insufficiently so, because the complex history of potentially numerous populations cannot be adequately represented by FST. This issue has been widely recognized and alternative solutions have been suggested (e.g. Chenoweth and Blows 2008, Martin et al. 2008). The most complete approach has been proposed by Ovaskainen et al. (2011), which uses a statistically more powerful and biologically more meaningful null hypothesis: it accounts for the neutral demographic distances among all populations to derive a null expectation of trait divergence (see applications in e.g., De Kort et al. 2016; Schäfer et al. 2018). Furthermore, most past studies assessed traits in isolation from each other and focus on traits that are likely affected by the studied environmental gradient. The method of Ovaskainen et al. (2011) can be used to assess adaptive divergence on multiple traits at a time, thus potentially identify adaptive life-history strategies.
Most evidence for adaptive divergence in forest trees comes from seedling traits measured in common garden experiments. Although multiple seedling traits can be used to identify adaptive life-history strategies, it is difficult to assess if results are transferable to natural populations (e.g., Neale and Kremer 2011). Indeed, trees have a long life span with two characteristic life-history stages, seedling and adult, where different selection pressures and physiological processes are operating (Petit and Hampe 2006). Connecting these two life stages is essential because seedling mortality has the largest impacts on the structure and function of future forests, while the death of big trees causes the longest lasting carbon losses (McDowell et al. 2013). Tree breeders have long known that seed or seedling traits are often poor predictors of adult traits in field conditions (e.g., Resende et al. 2012), with some exceptions, e.g., wood traits (Gaspar et al. 2008) or seed size in pines (Zas and Sampedro 2015). Measures of adult growth traits in-situ may also be uninformative when they are affected by management practices and competition, even if this effect is less pronounced for shade-tolerant species, such as silver fir (Kunstler et al. 2011). In contrast, carbon isotope discrimination, δ13C, may represent a suitable trait for adult trees. δ13C is related to the intrinsic water-use efficiency, a measure of relative water loss per molecule carbon acquired in the leaf, and has been advocated as a proxy for drought tolerance (Farquhar et al. 1989). In vascular plants, δ13C is to a large extent genetically determined (Dawson et al. 2002), and several important quantitative trait loci (QTL) have been identified in forest trees (Brendel et al. 2002, 2008). Further, for example, in Picea mariana, δ13C was highly negatively genetically correlated to growth, while being less environmentally sensitive than growth, thus the authors suggested this trait for indirect selection for growth (Johnsen et al. 1999). Overall, δ13C is one of the key traits for understanding the genetics of drought tolerance (Moran et al. 2017).
Here, we study adaptive divergence patterns in populations of silver fir (Abies alba Mill.) across a highly heterogeneous mountainous landscape. We asked whether populations have developed adaptive life-history strategies in response to local climatic conditions that are consistently present from the seedling to adult stage, while controlling for demographic distances between populations. Seedling morphology, growth and phenology were recorded in a common garden on half-sib families. We hypothesized that traits most likely do not evolve independently, thus we used a multi-trait quantitative genetic approach to identify correlated responses to selection. Adult δ13C was measured in-situ on unrelated individuals, and was used to correlate the populations’ mean water use efficiency in the field with the populations’ mean life-history strategies in seedlings. We developed a set of fine spatial scale historical climate variables to identify potential drivers of locally adapted life-history strategies. Finally, we estimate the evolutionary potential in seedling quantitative traits to assess the future of silver fir populations in Switzerland.
Material and methods
Study system
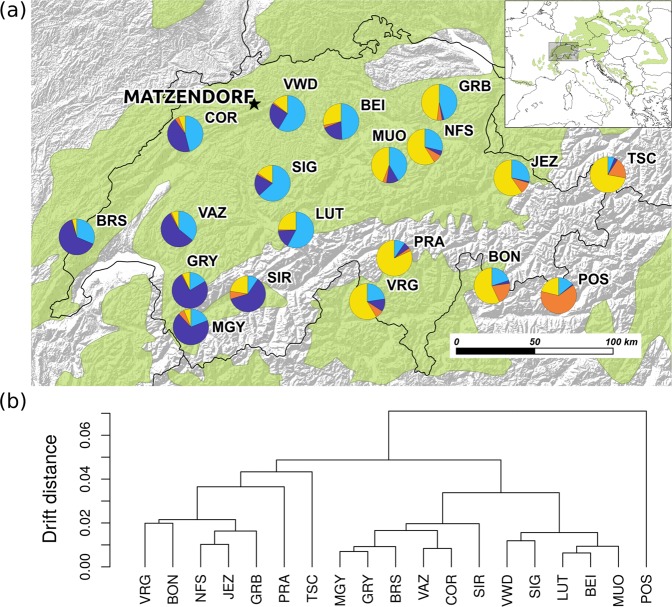
Silver fir is an ecologically and economically important European conifer. It can likely tolerate episodes of drought due to its deep rooting system (e.g., Lebourgeois et al. 2013; Vitali et al. 2017) and its high tolerance to bark beetle attacks (Wermelinger 2004). We selected 19 putatively autochthonous silver fir populations across a highly heterogeneous Alpine region across the Swiss Alps, Pre-Alps, Central Plateau and Jura Mountains (Fig. 1a, Supporting Information Fig. S1 and Table S1). The selection was based on various data sources, including the national register of seed stands (NKS, for autochthony/allochthony information), national forest inventory (NFI, for the distribution of silver fir and stand histories), the long-term forest ecosystem research (LWF), and after consulting forest experts. In 2009, seeds were collected from three trees, and in 2013 and 2016, needles were sampled from 19 to 22 adult trees per population (total of 387 trees), including the previously sampled trees. A minimum distance of 100 m was respected between the sampled trees to minimize the risk of collecting closely related trees (e.g., parent-offspring or sibs). Note that it is common practice to sample adult trees with only 20 m (Mosca et al. 2012) or 37 m (Roschanski et al. 2016) minimum distance for population samples.
Fig. 1.
(a) Geographic location of the silver fir (Abies alba Mill.) populations indicated by a summary of the STRUCTURE results with K = 4. Each pie shows the average coancestry of the sampled, on average, 20 individuals from the 19 populations from the four assumed genetic clusters. Matzendorf indicates the common garden location. Population names are abbreviated using three letter codes; see full names in Table S1. (b) Drift distances between populations as estimated with the admixture F-model (AFM). Coancestry between populations is the mean of the posterior means from 10 independent Markov chains. Distances were calculated from the posterior mean coancestry matrix to draw the dendrogram
Based on palynological evidence, it is likely that the Swiss range of silver fir was colonized from south to north after the Last Glacial Maximum. The species most likely reached the southern slopes of the Alps between 10 and 9 kyr BP and the northern slopes between 8 and 5 kyr BP (van der Knaap et al. 2005; Liepelt et al. 2009; Ruosch et al. 2016). Range-wide patterns of chloroplast and mitochondrial DNA variation (Liepelt et al. 2002) and isozyme data (Burga and Hussendörfer 2001) from extant silver fir populations suggest that the Swiss Alps were colonized from a single ancestral refugial population situated in the Central and/or Northern Apennines, even though the potential contribution of eastern refugial populations cannot be excluded.
Adult tree data
All adult trees were genotyped at 374 single-nucleotide polymorphism (SNP) loci originating from three different sources. Our aim was to estimate demographic distances between populations, so we attempted to select principally neutral markers. First, we used 220 out of 267 SNPs from Roschanski et al. (2016): we excluded the 25 SNPs that coded for non-synonymous mutations and 22 others where we had more than 10% missing data. Second, we selected 110 new putatively neutral SNPs from the transcriptome assembly of Roschanski et al. (2016), based on respective values of Tajima’s D between 2 and −2 and dN/dS between 0.9 and 1.1, and with low LD with the existing 220 SNPs (r2 < 0.1 and p-value > 0.05). However, only 25 of these SNPs were successfully genotyped, most likely because the primer sequences were not specific enough (results not shown). Third, we selected 149 SNPs from the control panel of Mosca et al. (2012) that had less than 5% missing data in that study. Of these, 129 SNPs were successfully genotyped. Both DNA isolation and genotyping using KASP arrays was performed using the all-inclusive service from LGC Genomics (Middlesex, UK).
Ten of the adult trees per population were measured for δ13C. Needles were sampled in spring 2016 for 2015 grown needles. Approximately 80 mg freeze-dried needle material was milled in 2 ml polypropylene tubes equipped with a 5 mm glass ball at 30 Hz for 4 min. Subsamples of approximately 5 mg needle powder were combusted in an elemental analyzer (Flash EA by Thermo Finnigan, Bremen, Germany) coupled to an isotope ratio mass spectrometer (Delta XP by Thermo Finnigan, Bremen, Germany) by a Conflo II interface (Thermo Finnigan, Bremen, Germany).
Seedling common garden data
In April 2010, from three mother trees per population (subsequently called families) approximately 2000 seeds were sown in open-air nursery beds at the Swiss Federal Research Institute WSL in Birmensdorf, Switzerland (47°21′42″N, 8°27′22″E, 550 m a.s.l.). Families and populations were not replicated or randomized in the nursery because the soil was well mixed and the terrain was mostly flat, but the position of each family was recorded to check and control for spatial auto-correlation (see Supplementary Methods S1). In spring 2012, at least 12 randomly selected viable seedlings per family were transplanted to an open experimental field site near Matzendorf, a former pasture on a south facing slope (20–24% incline) in the Swiss Jura Mountains (47°19′35″N, 7°36′42″E, 1090 m a.s.l.). Seedlings were planted at 30 × 40 cm spacing, provenances and families were randomized across 16 blocks. Both the nursery and common garden locations were within the natural range of silver fir. Note that the data presented here were part of a larger experiment involving more species and populations, see Frank et al. (2017b) for more details.
Phenotypic measurements used herein were performed during the fourth and fifth growing seasons, in 2013 and 2014 respectively. The 2013 measures and Terminal Bud Break 2014 were published in Frank et al. (2017b); see also Supplementary Methods S1. Traits analysed herein included Terminal Bud Break (2013 and 2014, variable names capitalized hereafter) and Lateral Bud Break (2013) defined as the Julian date when the membrane below bud scales was broken and the first green needles became visible, Growth Cessation (2013) defined as the date when 95% of terminal leader height growth was achieved, Maximum Growth Rate (2013) calculated as the first derivative of the growth curve fitted to 5–17 height measures recorded during the growing season following the procedure proposed in Frank et al. (2017b), Growth Duration (2013) defined as time from Terminal Bud Break to Growth Cessation, Height (2013 and 2014) defined from the ground surface to the uppermost bud base, and Diameter (2013 and 2014) at 2 cm above ground surface. The latter two were measured after Growth Cessation. For clarity, we call Height and Diameter morphology traits, Maximum Growth Rate and Duration growth traits, and Terminal/Lateral Bud Break and Growth Cessation (equivalent to bud set) phenology traits. In total, we analyzed 880 observations. All traits were normally distributed, or could be approximated with a normal distribution in the case of discrete traits, and correlated with one another to a varying extent (Supporting Information Fig. S2).
Environmental data
We used downscaled historical climatic data to characterize environmental differences among populations. In order to obtain the closest representation of the climate of the period when the current populations were established, we used data from 1 January 1901 to 31 December 1978. The choice of this period was justified by two facts: (i) no observation-based climate data go back further in time, and (ii) starting from approximately 1980, the temperature time series are overwhelmed by the effect of global warming (Harris et al. 2014). We used statistical downscaling using the delta method (Hay et al. 2000) to obtain 1 km grid scale monthly minimum, maximum and mean temperature, and total precipitation fields for this period. The reference climatic data set was the 0.5° resolution CRU TS v. 4.01 data (20 September 2017 release, Harris et al. (2014)) available for the 1 January 1901–31 December 2016 period, while the downscaling was based on the overlapping period (i.e., 1 January 1979–31 December 2016) with the 1 km resolution CHELSA data (Karger et al. 2017). Further, soil available water capacity (AWC) was obtained at a 250 m resolution from the Soilgrids data base (Hengl et al. 2017).
We calculated the 19 bioclimatic variables (Booth et al. 2014) using the R package dismo (Hijmans et al. 2017), two potential evapotranspiration (PET) indices and four standardized precipitation-evapotranspiration index (SPEI) variables using the R package SPEI (Beguería and Vicente-Serrano 2017), two indicators of late frost, and the self-calibrated Palmer’s drought severity index or scPDSI (Wells et al. (2004), Table 1). SPEI and scPDSI were summarized as measures of drought severity and frequency across the full monthly time series (Table 1). All climatic variables were considered as raw values or as deviations from the common garden environment in Matzendorf (based on the CHELSA data for the period of 1 January 1979–31 December 2013). However, the two ways of calculating the climate led to the same conclusions (results not shown), so we present results with the raw variables only for ease of interpretation.
Table 1.
Geography and environmental variables calculated for the period of 1 January 1901–31 December 1978 from monthly mean, minimum and maximum temperature and total precipitation (CRU TS v. 4.01 data (Harris et al. 2014) downscaled using CHELSA (Karger et al. 2017)), and available water capacity (AWC, Soilgrids data base, Hengl et al. (2017))
| Variable | Description | Mean | (Min., Max.) |
|---|---|---|---|
| Geography | |||
| Long | Longitude (degrees N) | 8.3 | (6.2, 10.5) |
| Lat | Latitude (degrees E) | 46.7 | (46.1, 47.3) |
| Elev | Elevation (m a.s.l) | 1062.2 | (481, 1602.5) |
| Slope | Slope (%) | 40 | (0, 70) |
| Standard bioclimatic indexes | |||
| bio.1 | Annual mean temperature | 6.1 | (3.1, 9.3) |
| bio.2 | Mean diurnal range (Mean of monthly Tmax–Tmin)) | 8.9 | (8.6, 9.2) |
| bio.3 | Isothermality (bio.2/bio.7) (*100) | 23.9 | (23.2, 24.6) |
| bio.4 | Temperature Seasonality (standard deviation *100) | 663.7 | (636.4, 676.9) |
| bio.5 | Max temperature of warmest month | 24.2 | (21, 27.4) |
| bio.6 | Min temperature of coldest month | −13 | (−15.8, −10) |
| bio.7 | Temperature annual range (bio.5-bio.6) | 37.2 | (36.2, 37.9) |
| bio.8 | Mean temperature of wettest quarter | 9.5 | (−2.6, 17.7) |
| bio.9 | Mean temperature of driest quarter | −1.7 | (−6.1, 3.9) |
| bio.10 | Mean temperature of warmest quarter | 16.8 | (13.8, 20) |
| bio.11 | Mean temperature of coldest quarter | −6 | (−8.5, −3.3) |
| bio.12 | Annual precipitation | 1176.4 | (505.6, 1690.9) |
| bio.13 | Precipitation of wettest month | 281 | (128.1, 432.6) |
| bio.14 | Precipitation of driest month | 4 | (0.4, 9.1) |
| bio.15 | Precipitation seasonality (coefficient of variation) | 50 | (46, 55.3) |
| bio.16 | Precipitation of wettest quarter | 641.2 | (274.2, 1024.7) |
| bio.17 | Precipitation of driest quarter | 55.6 | (24.5, 83.7) |
| bio.18 | Precipitation of warmest quarter | 277.3 | (156, 442.9) |
| bio.19 | Precipitation of coldest quarter | 222.7 | (65.6, 452.7) |
| Drought | |||
| AWC | Available water capacity | 163.9 | (147.7, 184.5) |
| PET.thorn | Mean annual PET (Thornthwaite) | 43.8 | (37.3, 51.8) |
| PET.harg | Mean annual PET (Hargreaves) | 52.6 | (47.3, 59.4) |
| SPEI.m1 | Number of month with SPEI < −1 | 162 | (144, 178) |
| SPEI.m2 | Number of month with SPEI < −2 | 13.8 | (7, 22) |
| SPEI.q5 | 5% quantile of SPEI | −1.6 | (−1.6, −1.5) |
| SPEI.q1 | 1% quantile of SPEI | −2.1 | (−2.2, −1.9) |
| scPDSI.m3 | Number of month with scPDSI < −3 | 42.6 | (29, 53) |
| scPDSI.m4 | Number of month with scPDSI < −4 | 9.6 | (2, 14) |
| scPDSI.q5 | 5% quantile of scPDSI | −3.2 | (−3.4, −2.8) |
| scPDSI.q1 | 1% quantile of scPDSI | −4.5 | (−4.9, −4.1) |
| Late frost | |||
| late.frost | Min temperature of the first month of the year with mean temperature > 5 °C | 1.7 | (1.4, 2) |
| late.frost2 | Min temperature of May | 4.7 | (1.5, 8.2) |
PET potential evapotranspitation, scPDSI Palmer’s Drought Severity Index, SPEI standardized precipitation-evapotranspiration index
Statistical analysis
We used the statistical framework developed by Ovaskainen et al. (2011) and Karhunen et al. (2014) with slight modifications. Briefly, this methodology integrates genetic, phenotypic and environmental data to test if trait differentiation measured in a common garden experiment reflects local adaptation, while accounting for past demography inferred from supposedly neutral molecular marker data, and to identify potential environmental drivers. The three steps of this analysis were (i) inference of the demography, (ii) estimation of the additive genetic trait values in a supposed ancestral population and contrasting these with their equivalents in the contemporary populations, and (iii) assessing if the deviations of additive genetic trait values from the ancestral values can be explained by environmental variation. We detail these steps in the following paragraphs (see also Supporting Information Fig. S1 for an overview).
First, we estimated the coancestry matrix (i.e., drift distances) between all pairs of populations from variation in SNP allele frequencies assuming an admixture F-model (AFM) and using a Metropolis-Hastings algorithm implemented in the R package RAFM (Karhunen and Ovaskainen 2012). Further, we compared the posterior mean coancestry matrix against that estimated using the Bayesian clustering algorithm implemented in the software STRUCTURE v.2.3.4 (Falush et al. 2003). See details of the demographic inference in Supplementary Methods S2.
Second, we used the method of Ovaskainen et al. (2011) to test if the estimated additive genetic trait values of the contemporary populations have diverged more from the ancestral value than expected by genetic drift only. We used a slightly modified version of the R package driftsel (Karhunen et al. 2013) that co-estimates the ancestral variance-covariance matrix (GA), the ancestral mean additive genetic trait values and the effect of covariates (i.e., the fixed effects), and the population effects (i.e., deviations from the ancestral mean) using a Bayesian mixed-effects animal model. This model is different from a classical animal model (reviewed in Kruuk et al. (2008)) in that it accounts simultaneously for the family structure of the common garden (i.e., the pedigree) and the drift distances (i.e., the demography) previously estimated from genetic marker data. In Ovaskainen et al. (2011) a single statistic, the S-statistic, is calculated to evaluate the overall evidence for selection across all populations. S = 0.5 indicates consistency with neutrality, S = 0 implies a match with purifying, and S = 1 with diversifying selection. In this study, we also assess to what extent the particular populations deviate from their neutral expectation (see Supplementary Methods S3 for details).
We tested all traits individually and all pairwise combinations between traits measured in the same year. Seed weight and block of the common garden were included as covariates. We ran three independent Markov chains of the Bayesian animal model using a burn-in of 50,000 iterations followed by 30,000 iterations for estimation for single traits, and a burn-in of 70,000 iterations followed by 30,000 iterations for estimation for trait pairs, both with a thinning interval of 20. The three independent chains converged to similar optima and led to the same conclusions concerning the signature of selection for the single-trait and two-trait analysis (potential scale reduction factor for the S-statistic ranged between 0.99 and 1.1 across all traits). However, with more than two traits the convergence was no longer optimal, so we did not consider these higher order trait interactions.
Third, we attempted to identify the potential environmental drivers of adaptive divergence between populations. We used the H*-test, which can be viewed as a standardized version of the H-test developed by Karhunen et al. (2014) (see Supplementary Methods S3 for more details). To avoid a multiple testing burden of 34 environmental variables (Table 1), we performed a Principal Component Analysis (PCA) on the standardized and scaled variables. The first five axes explained 84% of the variance, thus we performed a H*-test for each of these PC axes only. The variables with the highest loadings on each of the PC axes were the following: PC1: bio.2 (Mean Diurnal Range) and Elevation, PC2: bio.10 (Mean Temperature of the Warmest Quarter) and PET.harg, PC3 and 4: none, PC5: bio.8 (Mean Temperature of the Warmest Quarter) and bio.15 (Precipitation seasonality). See Supporting Information Table S2 for the loadings of all environmental variables on the first five PC axes. The novel methodological aspects detailed in Supplementary Methods S3, i.e. the procedure to evaluate adaptive divergence at each population, and the H*-test are now implemented in the R package driftsel1.
For a comparison with the Ovaskainen et al. (2011) approach, we also performed a classic QST − FST test using the bootstrap procedure described in Whitlock and Guillaume (2009) implemented in the R package QstFstComp (Gilbert and Whitlock 2015)2. We considered a one-tailed test, because we were interested in testing for adaptive divergence only, thus QST being significantly greater than FST.
Finally, the resemblance between the family members measured in the common garden experiment can also be exploited to estimate the evolutionary potential of the studied traits. Two commonly used measures of evolutionary potential are the heritability (h2 = VA/VP) and the additive genetic coefficient of variation (CVA = σA/M) (Mittell et al. 2015), where VA is the additive genetic variance and σA is its square-root, VP is the total phenotypic variance and M is the trait mean. CVA is dimensionless, independent of other sources of variance, thus has been advocated for comparisons between traits (Houle 1992, Hansen et al. 2011).
Results
Population history
The STRUCTURE analysis and the estimated drift distances among populations using AFM indicated the presence of two main clusters that correspond to Eastern and Western Swiss populations (Fig. 1). In addition, the population POS did not belong to either of these two groups, which is plausible given its isolated geographic location on the south side of the Swiss Alps (Fig. 1). The posterior mean global FST across the 19 populations based on the coancestry matrix was 0.0184 (95% credible interval: 0.0167, 0.0202). In contrast, FST estimated with the Whitlock and Guillaume (2009) approach was 0.0056 (95% confidence interval: 0.0051, 0.0061). Both methods show that FST is small, which reflects recent divergence between Swiss populations (approximately 200 generations if we assume a colonization 8 kyr BP and a generation time of 40 years) and ongoing gene flow due to long-distance dispersal. Further, FST from driftsel is likely lower because driftsel explicitly models the demographic distances between populations, and it is less sensitive to the level of polymorphism in marker loci (Karhunen and Ovaskainen 2012). Demographic distances between populations estimated using RAFM or the software STRUCTURE were similar; the highest similarity between the two was achieved for K = 4 in STRUCTURE (Mantel statistic of 0.891, which is similar to deviations between different chains of AFM; see Supplementary Methods S2 for more details).
Adaptive trait divergence across all populations
Similar degrees of adaptive divergence were revealed using the S-test of Ovaskainen et al. (2011) and classic QST − FST comparison (Whitlock and Guillaume 2009) across traits (Table 2). Using either of the methods, the strongest signature of selection was observed for seedling Height followed by the Bud Break traits, then for Growth Duration and Diameter. Traits measured both in 2013 and 2014 revealed similar signatures of selection, but in the QST − FST test Terminal Bud Break was only marginally significant in 2014. Maximum Growth Rate and Cessation showed no evidence of adaptive divergence in either of the tests due to their high within-population variance (Table 2).
Table 2.
Evidence of adaptive divergence across 19 Swiss silver fir (Abies alba Mill.) populations using the QST − FST test of Whitlock and Guillaume (2009) and the S-test of Ovaskainen et al. (2011)
| Trait | QST − FST test | S-test | Evolvability | |||
|---|---|---|---|---|---|---|
| QST | 2.5% | 97.5% | p-value | S | CVA | |
| Height 2013 | 0.18 | 0.05 | 0.42 | 0.003 | 1.00 | 0.100 |
| Height 2014 | 0.29 | 0.11 | 0.59 | 0.002 | 1.00 | 0.153 |
| Diameter 2013 | 0.09 | 0.00 | 0.29 | 0.044 | 0.92 | 0.161 |
| Diameter 2014 | 0.08 | 0.00 | 0.23 | 0.042 | 0.83 | 0.153 |
| Terminal Bud Break 2013 | 0.15 | 0.01 | 0.64 | 0.054 | 0.94 | 0.021 |
| Terminal Bud Break 2014 | 0.18 | 0.04 | 0.57 | 0.025 | 0.86 | 0.021 |
| Lateral Bud Break 2013 | 0.12 | 0.02 | 0.35 | 0.020 | 0.96 | 0.020 |
| Maximum Growth Rate 2013 | 0.06 | −0.02 | 0.28 | 0.133 | 0.67 | 0.184 |
| Growth Duration 2013 | 0.25 | 0.05 | 0.96 | 0.035 | 0.93 | 0.097 |
| Growth Cessation 2013 | 0.23 | −2.62 | 2.75 | 0.081 | 0.54 | 0.004 |
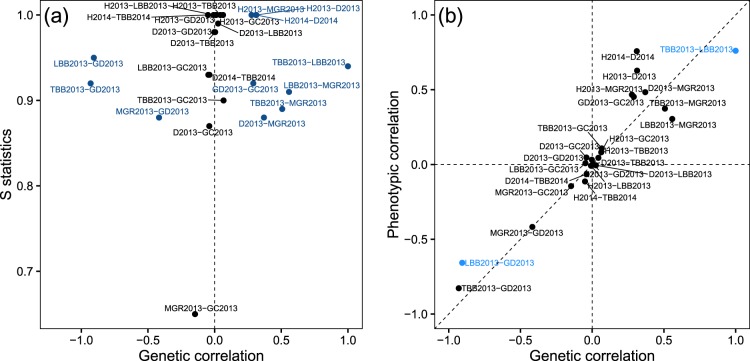
Several trait pairs showed a signature of selection using the S-test, mostly those that already did so in the single-trait analysis (Fig. 2a). We extracted the genetic correlations between traits from the posterior mean ancestral G-matrix (GA), and assessed if the 95% credible interval included zero (Fig. 2a, Supporting Information Table S3). Trait pairs that involved Height had the highest S statistics, but their genetic correlations did not differ from zero. Bud break often had high genetic correlations with growth traits and also high S values. The lowest S was observed between the Maximum Growth Rate and Growth Cessation (Fig. 2a). We used a standardized Mantel test following Cheverud (1988) to compare the phenotypic variance-covariance matrix (P-matrix) with GA. The null hypothesis is no association between genetic and phenotypic matrices. The test was averaged across the posterior distribution of GA. Five trait pairs had significantly different GA and P-matrices (Mantel-test, p > 0.05), but only two had rg different from zero (Supporting Information Table S3): Terminal and Lateral Bud Break, and Terminal Bud Break and Growth Duration. These two trait pairs were more strongly genetically correlated than expected based on the phenotypes (Fig. 2b). The posterior mean rg was at its maximum value for Terminal and Lateral Bud Break, which is likely due to developmental constraints. Further, Terminal Bud Break and Growth Duration also had a 38% higher genetic than phenotypic correlation (Fig. 2b).
Fig. 2.
(a) The strength of selection acting on a given pair of traits measured using the S statistics of Ovaskainen et al. (2011), and the genetic correlation between them estimated from the ancestral G-matrix (see Supplementary Methods S3 for formulae). Points and trait names in blue indicate trait pairs with genetic correlations significantly different from zero. (b) Phenotypic and genetic correlations between trait pairs estimated from the P- and the ancestral G-matrix. Points and trait names in blue indicate trait pairs with genetic correlations significantly different from zero and different from phenotypic correlations. The trait abbreviations for 2013 are as follows: H2013: Height 2013, D2013: Diameter 2013, TBB2013: Terminal Bud Break 2013, LBB2013: Lateral Bud Break 2013, MGR2013: Maximum Growth Rate 2013, GD2013: Growth Duration 2013, GC2013: Growth Cessation 2013, and with identical letter codes for 2014
Adaptive life-history strategies of particular populations
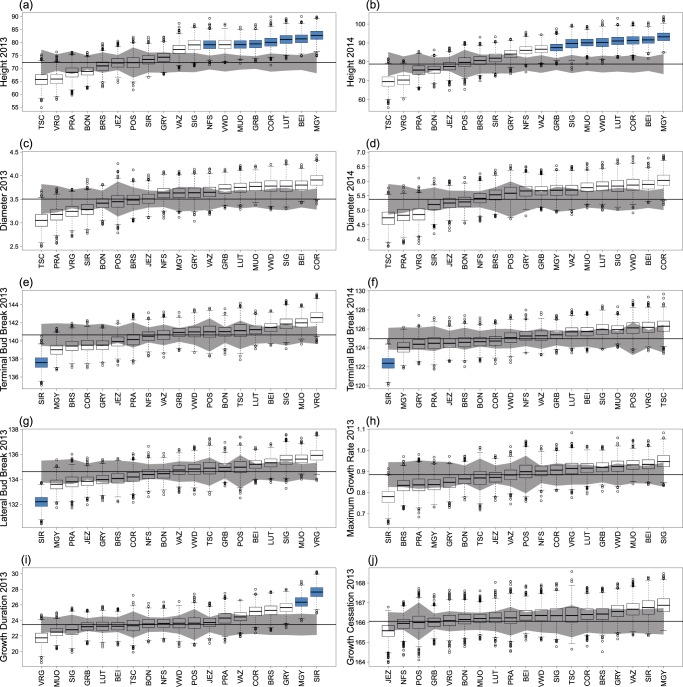
Unusual trait divergence at several populations contributed to the overall signature of selection using the S-test. Figure 3 shows, for each trait, how much each population diverged from the ancestral mean and if this divergence is more than expected by drift. The highest number of populations with adaptive divergence was observed for Height (Fig. 3a, b): seven (in 2013) and eight (in 2014) out of 19 populations deviated from their neutral expectations. All these outlier populations evolved towards a higher mean height and no populations have been selected for reduced height. The S-test revealed also a signature of selection for Diameter (Table 2), however, none of the particular populations showed unusual divergence (Fig. 3c, d). Yet, since there was a strong genetic correlation between Height and Diameter, the same populations showed the largest Diameter as for Height (Fig. 3a–d). The signature of selection on bud break traits was dominated by divergence in one population (SIR) that had unusually early bud break (Fig. 3e–g). Similarly, for Growth Duration, unusually longer growth duration was detected in two populations only, SIR and MGY (Fig. 3i).
Fig. 3.
Adaptive divergence for each trait separately. (a)–(j) Panels show the estimated ancestral additive mean trait value (horizontal line), the amount of trait divergence from this mean that is expected based on drift (gray envelop), and the estimated posterior distribution of the additive trait values for each population (boxes). Blue boxes indicate strong evidence of selection at the particular population. Populations are ordered on each panel according to their additive trait values
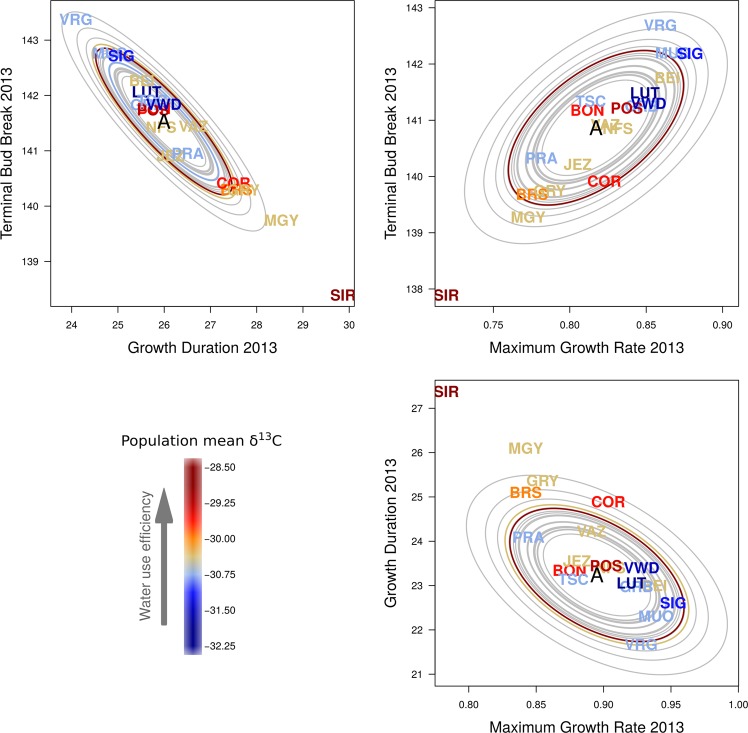
In the two-trait analysis, the correlated evolution of Bud Break, Growth Duration and Rate of particular populations became even more apparent (Fig. 4). SIR and MGY still showed a signature of selection, but at the opposite end of the trait space, and population VRG evolved towards late Terminal Bud Break and shorter Growth Duration. These patterns can be interpreted as contrasting life-history strategies. SIR and MGY followed a “start early and grow slowly” strategy, i.e., they burst buds early, and then grow for a long time at a low rate, while at the other end of trait space, population VRG followed a “start late and grow fast” strategy, i.e., bursts buds late, but then grows fast for a short period of time (Fig. 4).
Fig. 4.
Correlated adaptive divergence in a two-trait space between Terminal Bud Break, Growth Duration and Maximum Growth Rate. Colors indicate a proxy for water use efficiency, mean δ13C of ten adult trees per population. Less negative δ13C indicate higher water use efficiency. The capital letter A in the middle of the ellipses indicates the estimated ancestral additive mean trait value. Ellipses represent the median amount of trait divergence that is expected based on drift for each population (null hypothesis). Population codes (3 letters) represent the median of the posterior distribution of the additive trait values for each population. Populations with strong evidence of selection using the S-test are highlighted with an ellipse in color (identical to that of the population code). Ellipses of populations that do not deviate from drift are shown in gray
Phenology and growth traits’ posterior mean additive genetic trait values were significantly correlated with δ13C in adult trees measured in-situ (2013 Terminal Bud Break, r = −0.54, p-value = 0.033; 2014 Terminal Bud Break r = −0.5, p-value = 0.055; 2013 Lateral Bud Break r = −0.56, p-value = 0.025, 2013 Maximum Growth Rate r = −0.53, p-value = 0.041; 2013 Growth Duration r = 0.53, p-value = 0.037). The correlations with the phenology–growth complex were such that the “start early and grow slowly” seedling strategy had, on average, higher water use efficiency in adults, while the “start late and grow fast” seedling strategy low water use efficiency in adult trees (Fig. 4). In contrast, the other traits were not correlated with mean δ13C (absolute value of r < 0.25 and p-value > 0.58). p-values were corrected for multiple testing using the method of correction for non-independent tests (Cheverud 2001); see all additive trait value-mean δ13C correlations in Supplementary Information Fig. S3.
Environmental drivers
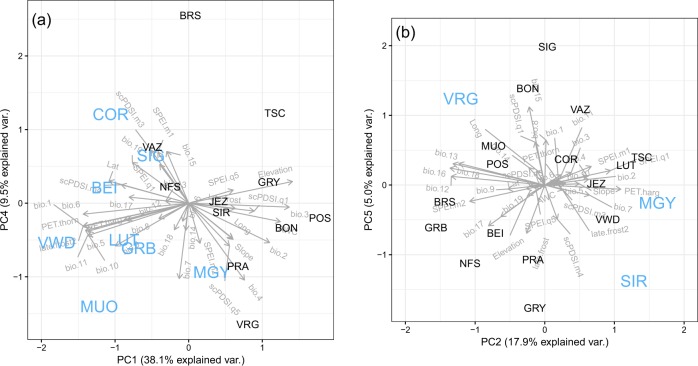
Environmental PC axes explained a non-zero proportion of the trait divergence for most traits, but the highest correlations (>90%) were obtained for Height, Lateral Bud Break and Growth Duration (Table 3). Notice that, not surprisingly, these traits showed a signature of selection with the S-tests (Table 2 and Fig. 3). For each of these traits a particular aspect of the environment mattered. For Height, and also for Diameter to some extent, environmental PC axis 1 showed the highest correlations with trait divergence (Table 3). The raw environmental variables that had the highest loadings on PC1 were variables related to the mean and variance in temperature, such as Annual Mean Temperature (bio.1), Elevation, Potential Evapotranspiration (PET.thorn), Late frost (late.frost2), or Isothermality (bio.3) (see the list of top ten variables in Table S2). Figure 5a shows the full environmental space defined by PC1 and PC4, which was the second most important axis for Height: populations that evolved towards a taller stature are situated in the warmer and more thermally stable part of the climatic space.
Table 3.
H*-test for the first five principal components of the environmental variables listed in Table 1 for each trait
| Trait | PC1 | PC2 | PC3 | PC4 | PC5 |
|---|---|---|---|---|---|
| Height 2013 | 92 | 62 | 35 | 74 | 41 |
| Height 2014 | 94 | 60 | 33 | 73 | 42 |
| Diameter 2013 | 88 | 45 | 31 | 66 | 40 |
| Diameter 2014 | 78 | 42 | 29 | 67 | 45 |
| Terminal bud break 2013 | 12 | 84 | 32 | 68 | 94 |
| Terminal bud break 2014 | 23 | 82 | 30 | 35 | 88 |
| Lateral bud break 2013 | 17 | 80 | 16 | 47 | 95 |
| Maximum growth rate 2013 | 51 | 70 | 31 | 49 | 86 |
| Growth duration 2013 | 08 | 92 | 56 | 70 | 93 |
| Growth cessation 2013 | 20 | 73 | 55 | 33 | 44 |
| Cumulative variance | 38 | 56 | 70 | 79 | 84 |
H* and the cumulative variance explained by each PC axes are expressed as percentages. For each trait, the highest H*-value is highlighted in bold. The variables with the highest loadings on each of the PC axes are the following: PC1: bio.02 (Mean Diurnal Range) and Elevation, PC2: bio.10 (Mean Temperature of the Warmest Quarter) and PET.harg, PC3 and 4: none, PC5: bio.08 (Mean Temperature of the Warmest Quarter) and bio.15 (Precipitation Seasonality)
Fig. 5.
Principal component (PC) analysis of the environmental variables listed in Table 1 with populations (three letter codes) highlighted in blue if they showed evidence of selection in the S-tests for 2013 or 2014 Height (a) and for Terminal Bud Break, Maximum Growth Rate and Duration (b). Each panel shows the environmental space with the first two PC axes that had explained the highest amount of variance using the H*-test, which were PC 1 and 4 for 2013 or 2014 Height, and PCs 2 and 5 for Bud Break and Growth Duration
For the phenology–growth complex, PC axes 2 and 5 had the highest correlations with trait divergence (Table 3). The environmental variables with the highest loadings on these axes were principally variables related to the mean and variance in precipitation, such as Annual Precipitation (bio.12), Precipitation Seasonality (bio.15), Precipitation of Wettest Quarter (bio.16) (see the list of top ten variables in Table S2). Thus, the “start early and grow slowly” seedling strategy of SIR and MGY, together with their high water use efficiency as adult trees (Fig. 4), has potentially evolved as a response to the low yearly total amount of precipitation (755 mm in SIR and 801 mm in MGY) and low precipitation seasonality (Fig. 5b). At the other end of the trait space, the climate of population VRG is characterized by high levels of yearly total precipitation (1621 mm) and ample winter snow as reflected by its higher precipitation seasonality (Fig. 5b).
Evolutionary potential
We found the highest potential for evolution in three growth traits: Maximum Growth Rate, Growth Duration and Diameter, while spring phenology showed the lowest potential for evolution (Table 2). Estimating the additive genetic variance across the 19 populations and 57 families (three families per population) involves the assumption that the additive genetic variance is constant across the sampling area. We tested this hypothesis using the larger data set used by Frank et al. (2017b) involving 4107 observations from 91 populations and 259 families. We found that estimates of CVA were not strongly affected by the reduction in sample size, and h2 and CVA were similar across three main geographic regions of Switzerland (Supplementary Methods S1), suggesting that our sample size was sufficient to estimate the evolutionary potential across the 19 populations.
Discussion
Are there general patterns of adaptation across a heterogeneous environment?
In this study, we found evidence for locally adapted life-history strategies across a heterogeneous Alpine landscape. The high number of populations leveraged the power of classical QST − FST tests and led to similar global conclusions as the S-test of Ovaskainen et al. (2011) (Table 2). However, using our novel methodology, we were also able to identify adaptive life-history strategies in a multi-trait space and pinpoint which populations show a signature of adaptive divergence (Ovaskainen et al. (2011) and Supplementary Methods S3). In particular, we identified two groups of correlated characters whose evolution could be driven by particular environmental cues. First, our results suggest that the two morphological characters, Height and Diameter, evolve in a correlated manner, and that warmer and more thermally stable environments select for larger stature (Fig. 5a). Second, we identified a phenology-growth trait complex that may evolve in response to precipitation. Populations from areas characterized by generally low levels of precipitation and drought evolved to start the growing season early and then grow slowly, and also to have a high water use efficiency (Figs. 4 and 5b). These populations, SIR and MGY, originate from a dry inner Alpine valley of Switzerland, the Rhône Valley. Further, the other Rhône Valley populations, GRY and BRS, and populations from other areas of Switzerland with a similar climate, such as the Rhine valley (JEZ) and Ticino (PRA) are also the closest in the phenology-growth trait space to SIR and MGY (Figs. 1 and 4). In contrast, VRG, situated in a valley characterized by ample precipitation, evolved towards a “start late and grow fast” strategy. Again, independent data from adult trees corroborated our findings in that, VRG, and other populations from humid sites, such as GRB and MUO, had a low water use efficiency (Fig. 4).
The length of the annual development cycle of temperate trees is constrained between two opposing forces: maximizing the length of the vegetative season while avoiding late frost and summer drought. This life-history trade-off is particularly important in mountainous environments, where the length of the growing season is often limited by late snow or compromised by summer drought in dry, inner Alpine valleys. Our study region is relatively small, and limited to one part of the Alpine range. However, the correlation between the phenology-growth life-history trade-off in seedlings and water use efficiency in adults provides independent evidence for this trade-off (Fig. 4), and supports the existence of a general pattern of adaptation across a mountainous landscape. Thus, we speculate that the phenology-growth life-history trade-off may be more general across other mountainous regions and provide a testable prediction in other mountain ranges and species.
Why are some traits under selection and not others?
Demonstrating selection for taller stature in a tree is not surprising because tall stature has numerous fitness advantages. Taller seedlings/young trees have access to more light and can out-compete their neighbors, and high stature in mature trees can facilitate pollen and seed dispersal (Petit and Hampe 2006). Interestingly, at least some of the populations that appear to have been selected for larger stature (Fig. 3a, b) are located in the Swiss Plateau, where the effect of forest management cannot be fully excluded (e.g., Bürgi and Schuler 2003). Since tree height is also a key trait from an economical point of view, there is a possibility that the observed patterns are, in part, a result of artificial selection for height.
A long-standing hypothesis in evolutionary biology is that traits belonging to the same functional and/or developmental group are genetically more integrated than traits with different functions or developmental origins (Berg 1960; Pigliucci and Preston 2004). Several empirical studies found evidence that there is greater genetic and phenotypic character integration within suites of functionally or developmentally related traits than between them, e.g., within or between floral vs. vegetative traits in plants (Waitt and Levin 1998; Baranzelli et al. 2014). Here, we found two trait pairs with an ancestral G-matrix that was significantly different from the P-matrix, and in both cases the genetic correlation was significantly higher than the phenotypic correlation. First, between Terminal and Lateral Bud Break the genetic correlation was one, which illustrates a complete character integration (Fig. 2b). Second, between Terminal Bud Break and Growth Duration (Fig. 4), which suggests that, at the physiological and molecular level, spring phenology and growth are strongly linked.
There is overwhelming evidence of adaptive clines for bud set (a proxy for growth cessation) in many forest tree species, including conifers, but none in Abies species (Alberto et al. 2013). Consistently, in this study, Growth Cessation did not show evidence of adaptive divergence. The explanation may lie in the deterministic bud development of Abies species (Cooke et al. 2012). They produce terminal buds during the summer at the tip of each leading branch shoot and remain dormant during the following winter. Each bud contains a preformed stem unit composed of internodes and leaf primordia that will grow to branches and photosynthesizing needles, respectively, during the following growing season.
Potential limitations and caveats
Adaptive trait divergence may be a result of local adaptation or adaptive phenotypic plasticity (Merilä and Hendry 2014). To tell these two apart, one has to measure trait values of a particular genotype across different environments. Common garden studies of forest trees often observe site-specific effects for growth or phenology, indicative of adaptive plasticity (Alberto et al. 2013). For example, Santos-del Blanco et al. (2013) found a growth-reproduction trade-off in Pinus halepensis, with trees in high stress sites investing more in reproduction and trees in low stress sites investing more in vegetative growth. Here, we only had a single common garden and the relocation to Matzendorf did not affect all provenances the same way. Thus, we could not distinguish between local adaptation and adaptive plasticity. Nevertheless, even if plasticity is known to play an important role in explaining phenotypic differences, the signature of adaptive divergence is often confirmed across all tested common garden sites (e.g., Rodríguez-Quilón et al. 2016).
Plasticity could have also caused the observed spatial variation in δ13C measured in adult trees in-situ. It appears that the importance of plastic and genetic factors is species specific even among conifers. For example, in Pinus sylvestris, Santini et al. (2018) suggested that plastic, and not genetic, responses dominate the inter-population variability in water use efficiency, even though, admittedly they did not have progeny information. In contrast, Voltas et al. (2008) reported large genetic differences among populations in Pinus halepensis using a common garden trial. δ13C is also prone to temporal, year-to-year, fluctuations because it integrates the photosynthetic activity through the period the tissue was synthesized, which is a single growing season. While measures of δ13C are often correlated across years (e.g., Chevillat et al. 2005), environment can also have an effect (e.g., Rinne et al. 2015). For example, a temporal increase in water use efficiency due to anthropogenic CO2 and N fertilization have been reported across different forest tree species across Europe (Saurer et al. 2014). Finally, spatial variation, notably latitudinal and altitudinal trends, in δ13C have long been demonstrated (Körner et al. 1991). However, it is often difficult to pinpoint single environmental variables across regional or continental spatial scales that explain the variation in δ13C (Leonardi et al. 2012). Thus, we estimated that any attempts for environmental corrections of the population mean δ13C would lack a solid basis.
Common garden studies that use seeds from wild populations may provide inaccurate estimates of population differentiation, particularly for early traits, due to environmental maternal effects (Bossdorf et al. 2005). Quantitative genetic studies that control for genetic and/or epigenetic maternal effects in forest trees are still rare (Alberto et al. 2013). Although there is evidence for long-lasting effects of seed size in Pines (Zas and Sampedro 2015; Surles et al. 1993), such effects are less obvious in other conifers (St. Clair and Adams 1991). Nevertheless, we controlled for the average seed weight of the families in the Bayesian animal model (see also Supplementary Methods S1), which is, admittedly, just one component of the maternal effects. More recently, the role of epigenetic ‘memory' effects has been demonstrated in forest trees (Prunier et al. 2016). For example, a common garden transplantation experiment of Norway spruce and European larch found that the previous year’s environment and provenance contributed to the current year’s bud break phenology (Gömöry et al. 2015). Similar effects could have played a role in our experiments, however, all populations experienced the same year-to-year environmental fluctuations.
The design of the common garden study suffers from three potential limitations. First, for height, the results might be sensitive to non-randomization in the nursery (see Supplementary Methods S1). Seedlings were likely stressed from the replanting from the nursery to the common garden location in 2012, which may still be detectable in 2013 Height (Supplementary Methods S1), and, in 2014, a frost event in March damaged some seedlings. However, even with this new stress, the evidence for adaptive trait differentiation was almost identical to that in 2013 (Fig. 3). Second, we had phenotypic observations from three families per population, which is rather low. Nevertheless, using the full phenotypic data set of Frank et al. (2017b) across 91 populations, we were able to combine populations from nearby regions, thereby increasing the number of families to 5.3 families per population, on average. We found that estimates of evolutionary potential and also QST were extremely similar to those obtained from three families (Supplementary Methods S1). Third, we estimated the evolutionary potential, in particular, the evolvability, across many populations, thereby assuming that the additive genetic variance is constant across the study region. Laboratory experiments have shown that the G-matrix can change in response to drift or selection, but maybe not in the wild (Delahaie et al. 2017). To test this hypothesis, we estimated the h2 and CVA separately for the three main climatic regions as defined by foresters. We found that the evolutionary potential was similar across the three regions (Supplementary Methods S1), suggesting that the assumption of constant additive genetic variance across Swiss populations is acceptable. Overall we found that CVA was much more robust to any of the three above-cited issues than h2, in agreement with previous studies (Houle 1992; Hansen et al. 2011).
Practical implications and the future of silver fir in the study area
Silver fir has been identified as a conifer with great ecological and economic potential for the future because of its high tolerance to bark beetle attacks (Wermelinger 2004), and because it may cope well with drought stress (Lebourgeois et al. 2013; Vitali et al. 2017; Frank et al. 2017a). Nevertheless, silver fir may already be threatened in some Mediterranean areas, where die-back events have been documented (Cailleret et al. 2014), or in Southwestern Europe, where reduced growth has been reported (Gazol et al. 2015). In this study, we found that silver fir was able to evolve to a taller stature in warm and thermally stable regions, such as the Swiss Plateau. Indeed, positive effects of climate warming have been observed in temperate forest trees, where warming enhanced growth (Gazol et al. 2015). Since height, diameter and growth rate have the highest evolvability and strongest signature of selection among the studied traits (Table 2), we may speculate that some populations will respond with enhanced growth. However, the predicted pace of climate change is much faster than it has been during post-glacial expansion/re-colonization, thus assisted migration may provide a practical solution to overcome this rapid rate of change (Aitken and Bemmels 2016). Based on our results, populations of the Rhône and Rhine Valleys could provide drought tolerant seed sources for future plantations in other parts of Switzerland.
Data archiving
SNP and δ13C data have been submitted to Dryad (10.5061/dryad.s205vd8).
Supplementary information
Acknowledgements
We thank all members of the ADAPT project that provided the phenotypic data for this study, especially Aline Frank, Caroline Heiri and Peter Brang, and to the leader of the EADAPT project, Andrea Kupferschmid, who provided the height and diameter data for 2014. The project was funded by a research grant from the Center for Adaptation to a Changing Environment (ACE) at the ETH Zurich. KC was supported by an ACE fellowship and by a Marie Skłodowska-Curie fellowship (FORGENET). We thank Kristian Ullrich for help with the SNP selection, and Dirk Karger with extracting the climatic data from the data bases. The contribution of several field and lab workers was necessary for the sample collection and preparation for DNA extraction and genotyping, in particular, we thank Catherine Folly, René Graf, and Olivier Charlandie. We thank Annika Ackermann (Grassland Isolab, ETH Zurich), who performed the stable isotope measures, and Fabian Deuber for sample preparation.
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version of this article (10.1038/s41437-019-0240-0) contains supplementary material, which is available to authorized users.
References
- Ackerly D, Loarie S, Cornwell W, Weiss S, Hamilton H, Branciforte R, Kraft N. The geography of climate change: implications for conservation biogeography. Divers Distrib. 2010;16:476–487. [Google Scholar]
- Aitken SN, Bemmels JB. Time to get moving: assisted gene flow of forest trees. Evol Appl. 2016;9:271–290. doi: 10.1111/eva.12293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alberto F, Bouffier L, Louvet JM, Lamy JB, Delzon S, Kremer A. Adaptive responses for seed and leaf phenology in natural populations of sessile oak along an altitudinal gradient. J Evol Biol. 2011;24:1442–1454. doi: 10.1111/j.1420-9101.2011.02277.x. [DOI] [PubMed] [Google Scholar]
- Alberto FJ, Aitken SN, Alía R, et al. Potential for evolutionary responses to climate change - evidence from tree populations. Glob Change Biol. 2013;19:1645–1661. doi: 10.1111/gcb.12181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Austin MP, Van Niel KP. Improving species distribution models for climate change studies: variable selection and scale. J Biogeogr. 2011;38:1–8. [Google Scholar]
- Baranzelli MC, Sérsic AN, Cocucci AA. The search for Pleiades in trait constellations: Functional integration and phenotypic selection in the complex flowers of Morrenia brachystephana (Apocynaceae) J Evol Biol. 2014;27:724–736. doi: 10.1111/jeb.12341. [DOI] [PubMed] [Google Scholar]
- Beguería Santiago, Vicente-Serrano Sergio M., Reig Fergus, Latorre Borja. Standardized precipitation evapotranspiration index (SPEI) revisited: parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. International Journal of Climatology. 2013;34(10):3001–3023. [Google Scholar]
- Berg R. The ecological significance of correlation pleiades. Evolution. 1960;14:171–180. [Google Scholar]
- Booth TH, Nix HA, Busby JR, Hutchinson MF. Bioclim: the first species distribution modelling package, its early applications and relevance to most current maxent studies. Divers Distrib. 2014;20:1–9. [Google Scholar]
- Bossdorf O, Auge H, Lafuma L, Rogers WE, Siemann E, Prati D. Phenotypic and genetic differentiation between native and introduced plant populations. Oecologia. 2005;144:1–11. doi: 10.1007/s00442-005-0070-z. [DOI] [PubMed] [Google Scholar]
- Brendel O, Le Thiec D, Scotti-Saintagne C, Bodénès C, Kremer A, Guehl JM. Quantitative trait loci controlling water use efficiency and related traits in Quercus robur L. Tree Genet Genomes. 2008;4:263–278. [Google Scholar]
- Brendel O, Pot D, Plomion C, Rozenberg P, Guehl JM. Genetic parameters and QTL analysis of δ13C and ring width in maritime pine. Plant Cell Environ. 2002;25:945–953. [Google Scholar]
- Burga CA, Hussendörfer E. Vegetation history of Abies alba Mill. (silver fir) in Switzerland–pollen analytical and genetic surveys related to aspects of vegetation history of Picea abies (L.) H. Karsten (Norway spruce) Veg Hist Archaeobot. 2001;10:151–159. [Google Scholar]
- Bürgi M, Schuler A (2003) Driving forces of forest management-an analysis of regeneration practices in the forests of the Swiss Central Plateau during the 19th and 20th century. For Ecol Manage 176:173–183
- Cailleret Maxime, Nourtier Marie, Amm Annabelle, Durand-Gillmann Marion, Davi Hendrik. Drought-induced decline and mortality of silver fir differ among three sites in Southern France. Annals of Forest Science. 2013;71(6):643–657. [Google Scholar]
- Chenoweth SF, Blows MW. QST meets the G matrix: The dimensionality of adaptive divergence in multiple correlated quantitative traits. Evolution. 2008;62:1437–1449. doi: 10.1111/j.1558-5646.2008.00374.x. [DOI] [PubMed] [Google Scholar]
- Cheverud JM. A comparison of genetic and phenotypic correlations. Evolution. 1988;42:958–968. doi: 10.1111/j.1558-5646.1988.tb02514.x. [DOI] [PubMed] [Google Scholar]
- Cheverud JM. A simple correction for multiple comparisons in interval mapping genome scans. Heredity. 2001;87:52–58. doi: 10.1046/j.1365-2540.2001.00901.x. [DOI] [PubMed] [Google Scholar]
- Chevillat Véronique S., Siegwolf Rolf T.W., Pepin Steeve, Körner Christian. Tissue-specific variation of δ13C in mature canopy trees in a temperate forest in central Europe. Basic and Applied Ecology. 2005;6(6):519–534. [Google Scholar]
- Chevin LM, Lande R. When do adaptive plasticity and genetic evolution prevent extinction of a density-regulated population? Evolution. 2010;64:1143–1150. doi: 10.1111/j.1558-5646.2009.00875.x. [DOI] [PubMed] [Google Scholar]
- Cooke JE, Eriksson ME, Junttila O. The dynamic nature of bud dormancy in trees: environmental control and molecular mechanisms. Plant Cell Environ. 2012;35:1707–1728. doi: 10.1111/j.1365-3040.2012.02552.x. [DOI] [PubMed] [Google Scholar]
- Dawson TE, Mambelli S, Plamboeck AH, Templer PH, Tu KP. Stable isotopes in plant ecology. Annu Rev Ecol Syst. 2002;33:507–559. [Google Scholar]
- De Kort H, Vander Mijnsbrugge K, Vandepitte K, Mergeay J, Ovaskainen O, Honnay O (2016) Evolution, plasticity and evolving plasticity of phenology in the tree species Alnus glutinosa. J Evol Biol 29:253–264 [DOI] [PubMed]
- Delahaie B, Charmantier A, Chantepie S, Garant D, Porlier M, Teplitsky C. Conserved G-matrices of morphological and life-history traits among continental and island blue tit populations. Heredity. 2017;119(2):76–87. doi: 10.1038/hdy.2017.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falush D, Stephens M, Pritchard JK. Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics. 2003;164:1567–1587. doi: 10.1093/genetics/164.4.1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farquhar GD, Ehleringer JR, Hubick KT. Carbon isotope discrimination and photosynthesis. Annu Rev Plant Biol. 1989;40:503–537. [Google Scholar]
- Frank A, Howe GT, Sperisen C, Brang P, Clair JBS, Schmatz DR, Heiri C. Risk of genetic maladaptation due to climate change in three major European tree species. Glob Change Biol. 2017;23:5358–5371. doi: 10.1111/gcb.13802. [DOI] [PubMed] [Google Scholar]
- Frank A, Sperisen C, Howe GT, Brang P, Walthert L, Clair JBS, Heiri C. Distinct genecological patterns in seedlings of Norway spruce and silver fir from a mountainous landscape. Ecology. 2017;98:211–227. doi: 10.1002/ecy.1632. [DOI] [PubMed] [Google Scholar]
- Gaspar Maria João, Louzada José Luís, Silva Maria Emília, Aguiar Alexandre, Almeida Maria Helena. Age trends in genetic parameters of wood density components in 46 half-sibling families ofPinus pinaster. Canadian Journal of Forest Research. 2008;38(6):1470–1477. [Google Scholar]
- Gazol A, Camarero JJ, Gutiérrez E, et al. Distinct effects of climate warming on populations of silver fir (Abies alba) across Europe. J Biogeogr. 2015;42:1150–1162. [Google Scholar]
- Gilbert KJ, Whitlock MC. QST − FST comparisons with unbalanced half-sib designs. Mol Ecol Resour. 2015;15:262–267. doi: 10.1111/1755-0998.12303. [DOI] [PubMed] [Google Scholar]
- Gömöry D, Foffová E, Longauer R, Krajmerová D. Memory effects associated with early-growth environment in Norway spruce and European larch. Eur J For Res. 2015;134:89–97. [Google Scholar]
- Hampe A, Petit RJ. Conserving biodiversity under climate change: the rear edge matters. Ecol Lett. 2005;8:461–467. doi: 10.1111/j.1461-0248.2005.00739.x. [DOI] [PubMed] [Google Scholar]
- Hansen TF, Pélabon C, Houle D. Heritability is not evolvability. Evol Biol. 2011;38:258. [Google Scholar]
- Harris I, Jones P, Osborn T, Lister D. Updated high-resolution grids of monthly climatic observations–the CRU TS3.10 Dataset. Int J Clim. 2014;34:623–642. [Google Scholar]
- Hay LE, Wilby RL, Leavesley GH. A comparison of delta change and downscaled GCM scenarios for three mountainous basins in the United States. J Am Water Resour Assoc. 2000;36:387–397. [Google Scholar]
- Hengl T, de Jesus JM, Heuvelink GB, et al. SoilGrids250m: Global gridded soil information based on spring2018@DE!machine learning. PLoS One. 2017;12:e0169748. doi: 10.1371/journal.pone.0169748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hewitt GM. Post-glacial re-colonization of european biota. Biol J Linn Soc. 1999;68:87–112. [Google Scholar]
- Hijmans RJ, Phillips S, Leathwick J, Elith J, Hijmans MRJ (2017) Package ‘dismo’. Circles. 9:1–68
- Houle D. Comparing evolvability and variability of quantitative traits. Genetics. 1992;130:195–204. doi: 10.1093/genetics/130.1.195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnsen Kurt H, Flanagan Lawrence B, Huber Dudley A, Major John E. Genetic variation in growth, carbon isotope discrimination, and foliar N concentration inPicea mariana: analyses from a half-diallel mating design using field-grown trees. Canadian Journal of Forest Research. 1999;29(11):1727–1735. [Google Scholar]
- Karger DN, Conrad O, Böhner J, et al. Climatologies at high resolution for the Earth’s land surface areas. Sci Data. 2017;4:170122. doi: 10.1038/sdata.2017.122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karhunen M, Merilä J, Leinonen T, Cano JM, Ovaskainen O. driftsel: An R package for detecting signals of natural selection in quantitative traits. Mol Ecol Resour. 2013;13:746–754. doi: 10.1111/1755-0998.12111. [DOI] [PubMed] [Google Scholar]
- Karhunen M, Ovaskainen O. Estimating population-level coancestry coefficients by an admixture F model. Genetics. 2012;192:609–617. doi: 10.1534/genetics.112.140871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karhunen M, Ovaskainen O, Herczeg G, Merilä J. Bringing habitat information into statistical tests of local adaptation in quantitative traits: A case study of nine-spined sticklebacks. Evolution. 2014;68:559–568. doi: 10.1111/evo.12268. [DOI] [PubMed] [Google Scholar]
- Kawecki TJ. Adaptation to marginal habitats. Annu Rev Ecol Evol Syst. 2008;39:321–342. [Google Scholar]
- Kawecki TJ, Ebert D. Conceptual issues in local adaptation. Ecol Lett. 2004;7:1225–1241. [Google Scholar]
- Körner C, Farquhar G, Wong S. Carbon isotope discrimination by plants follows latitudinal and altitudinal trends. Oecologia. 1991;88:30–40. doi: 10.1007/BF00328400. [DOI] [PubMed] [Google Scholar]
- Kremer A, Ronce O, Robledo-Arnuncio JJ, et al. Long-distance gene flow and adaptation of forest trees to rapid climate change. Ecol Lett. 2012;15:378–392. doi: 10.1111/j.1461-0248.2012.01746.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruuk Loeske E.B., Slate Jon, Wilson Alastair J. New Answers for Old Questions: The Evolutionary Quantitative Genetics of Wild Animal Populations. Annual Review of Ecology, Evolution, and Systematics. 2008;39(1):525–548. [Google Scholar]
- Kunstler G, Albert CH, Courbaud B, et al. Effects of competition on tree radial-growth vary in importance but not in intensity along climatic gradients. J Ecol. 2011;99:300–312. [Google Scholar]
- Lebourgeois F, Gomez N, Pinto P, Mérian P. Mixed stands reduce Abies alba tree-ring sensitivity to summer drought in the Vosges mountains, Western Europe. Ecol Manag. 2013;303:61–71. [Google Scholar]
- Leonardi S, Gentilesca T, Guerrieri R, et al. Assessing the effects of nitrogen deposition and climate on carbon isotope discrimination and intrinsic water-use efficiency of angiosperm and conifer trees under rising CO2 conditions. Glob Change Biol. 2012;18:2925–2944. doi: 10.1111/j.1365-2486.2012.02757.x. [DOI] [PubMed] [Google Scholar]
- Liepelt S, Bialozyt R, Ziegenhagen B. Wind-dispersed pollen mediates postglacial gene flow among refugia. Proc Natl Acad Sci USA. 2002;99:14590–14594. doi: 10.1073/pnas.212285399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liepelt S, Cheddadi R, de Beaulieu JL, et al. Postglacial range expansion and its genetic imprints in Abies alba (Mill.)—A synthesis from palaeobotanic and genetic data. Rev Palaeobot Palynol. 2009;153:139–149. [Google Scholar]
- Lind BM, Menon M, Bolte CE, Faske TM, Eckert AJ. The genomics of local adaptation in trees: Are we out of the woods yet? Tree Genet Genomes. 2018;14:29. [Google Scholar]
- Martin G, Chapuis E, Goudet J. Multivariate QST − FST comparisons: A neutrality test for the evolution of the G matrix in structured populations. Genetics. 2008;180:2135–2149. doi: 10.1534/genetics.107.080820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDowell NG, Ryan MG, Zeppel MJ, Tissue DT. Feature: Improving our knowledge of drought-induced forest mortality through experiments, observations, and modeling. New Phytol. 2013;200:289–293. doi: 10.1111/nph.12502. [DOI] [PubMed] [Google Scholar]
- Merilä J, Hendry AP. Climate change, adaptation, and phenotypic plasticity: the problem and the evidence. Evol Appl. 2014;7:1–14. doi: 10.1111/eva.12137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mittell EA, Nakagawa S, Hadfield JD. Are molecular markers useful predictors of adaptive potential? Ecol Lett. 2015;18:772–778. doi: 10.1111/ele.12454. [DOI] [PubMed] [Google Scholar]
- Moran E, Lauder J, Musser C, Stathos A, Shu M. The genetics of drought tolerance in conifers. New Phytol. 2017;216:1034–1048. doi: 10.1111/nph.14774. [DOI] [PubMed] [Google Scholar]
- Mosca E, Eckert AJ, Di Pierro EA, Rocchini D, La Porta N, Belletti P, Neale DB. The geographical and environmental determinants of genetic diversity for four alpine conifers of the European Alps. Mol Ecol. 2012;21:5530–5545. doi: 10.1111/mec.12043. [DOI] [PubMed] [Google Scholar]
- Neale DB, Kremer A. Forest tree genomics: growing resources and applications. Nat Rev Genet. 2011;12:111–122. doi: 10.1038/nrg2931. [DOI] [PubMed] [Google Scholar]
- Ovaskainen O, Karhunen M, Zheng C, Arias JMC, Merilä J. A new method to uncover signatures of divergent and stabilizing selection in quantitative traits. Genetics. 2011;189:621–632. doi: 10.1534/genetics.111.129387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petit RJ, Hampe A. Some evolutionary consequences of being a tree. Annu Rev Ecol Evol Syst. 2006;37:187–214. [Google Scholar]
- Pigliucci M, Preston KA. Phenotypic integration: studying the ecology and evolution of complex phenotypes. Oxford, UK: Oxford University Press; 2004. [Google Scholar]
- Polechová Jitka. Is the sky the limit? On the expansion threshold of a species’ range. PLOS Biology. 2018;16(6):e2005372. doi: 10.1371/journal.pbio.2005372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prunier J, Verta JP, MacKay JJ. Conifer genomics and adaptation: at the crossroads of genetic diversity and genome function. New Phytol. 2016;209:44–62. doi: 10.1111/nph.13565. [DOI] [PubMed] [Google Scholar]
- Rehfeldt GE, Tchebakova NM, Parfenova YI, Wykoff WR, Kuzmina NA, Milyutin LI. Intraspecific responses to climate in Pinus sylvestris. Glob Change Biol. 2002;8:912–929. [Google Scholar]
- Resende M, Munoz P, Acosta J, et al. Accelerating the domestication of trees using genomic selection: accuracy of prediction models across ages and environments. New Phytol. 2012;193:617–624. doi: 10.1111/j.1469-8137.2011.03895.x. [DOI] [PubMed] [Google Scholar]
- Rinne KT, Saurer M, Kirdyanov AV, Bryukhanova MV, Prokushkin AS, Churakova O, Siegwolf RT. Examining the response of needle carbohydrates from Siberian larch trees to climate using compound specific δ13C and concentration analyses. Plant Cell Environ. 2015;38:2340–2352. doi: 10.1111/pce.12554. [DOI] [PubMed] [Google Scholar]
- Rodríguez-Quilón I, Santos-del Blanco L, Serra-Varela MJ, Koskela J, González-Martínez SC, Alía R. Capturing neutral and adaptive genetic diversity for conservation in a highly structured tree species. Ecol Appl. 2016;26:2254–2266. doi: 10.1002/eap.1361. [DOI] [PubMed] [Google Scholar]
- Roschanski AM, Csilléry K, Liepelt S, et al. Evidence of divergent selection for drought and cold tolerance at landscape and local scales in Abies alba Mill. in the French Mediterranean Alps. Mol Ecol. 2016;25:776–794. doi: 10.1111/mec.13516. [DOI] [PubMed] [Google Scholar]
- Ruosch M, Spahni R, Joos F, Henne PD, van der Knaap WO, Tinner W. Past and future evolution of Abies alba forests in Europe - comparison of a dynamic vegetation model with palaeo data and observations. Glob Change Biol. 2016;22:727–740. doi: 10.1111/gcb.13075. [DOI] [PubMed] [Google Scholar]
- Santini F, Ferrio J, Heres AM, et al. Scarce population genetic differentiation but substantial spatiotemporal phenotypic variation of water-use efficiency in Pinus sylvestris at its western distribution range. Eur J Res. 2018;137:863–878. [Google Scholar]
- Santos-del Blanco L, Bonser S, Valladares F, Chambel M, Climent J. Plasticity in reproduction and growth among 52 range-wide populations of a Mediterranean conifer: adaptive responses to environmental stress. J Evol Biol. 2013;26:1912–1924. doi: 10.1111/jeb.12187. [DOI] [PubMed] [Google Scholar]
- Saurer M, Spahni R, Frank DC, et al. Spatial variability and temporal trends in water-use efficiency of european forests. Glob Change Biol. 2014;20:3700–3712. doi: 10.1111/gcb.12717. [DOI] [PubMed] [Google Scholar]
- Savolainen O, Pyhäjärvi T, Knürr T. Gene flow and local adaptation in trees. Annu Rev Ecol Evol Syst. 2007;38:595–619. [Google Scholar]
- Schäfer MA, Berger D, Rohner PT, et al. Geographic clines in wing morphology relate to colonization history in New World but not Old World populations of yellow dung flies. Evolution. 2018;72:1629–1644. doi: 10.1111/evo.13517. [DOI] [PubMed] [Google Scholar]
- St Clair J, Adams W (1991) Effects of seed weight and rate of emergence on early growth of open-pollinated Douglas-fir families. For Sci 37:987–997
- Sultan SE, Spencer HG. Metapopulation structure favors plasticity over local adaptation. Am Nat. 2002;160:271–283. doi: 10.1086/341015. [DOI] [PubMed] [Google Scholar]
- Surles Scott E., White Timothy L., Hodge Gary R., Duryea Mary L. Relationships among seed weight components, seedling growth traits, and predicted field breeding values in slash pine. Canadian Journal of Forest Research. 1993;23(8):1550–1556. [Google Scholar]
- Van der Knaap W, van Leeuwen JF, Finsinger W, et al. Migration and population expansion of Abies, Fagus, Picea, and Quercus since 15000 years in and across the Alps, based on pollen-percentage threshold values. Quat Sci Rev. 2005;24:645–680. [Google Scholar]
- Via S, Lande R. Genotype-environment interaction and the evolution of phenotypic plasticity. Evolution. 1985;39:505–522. doi: 10.1111/j.1558-5646.1985.tb00391.x. [DOI] [PubMed] [Google Scholar]
- Vitali Valentina, Büntgen Ulf, Bauhus Jürgen. Silver fir and Douglas fir are more tolerant to extreme droughts than Norway spruce in south-western Germany. Global Change Biology. 2017;23(12):5108–5119. doi: 10.1111/gcb.13774. [DOI] [PubMed] [Google Scholar]
- Vitasse Y, Bresson CC, Kremer A, Michalet R, Delzon S. Quantifying phenological plasticity to temperature in two temperate tree species. Funct Ecol. 2010;24:1211–1218. [Google Scholar]
- Voltas Jordi, Chambel María Regina, Prada María Aránzazu, Ferrio Juan Pedro. Climate-related variability in carbon and oxygen stable isotopes among populations of Aleppo pine grown in common-garden tests. Trees. 2008;22(6):759–769. [Google Scholar]
- Waitt DE, Levin DA. Genetic and phenotypic correlations in plants: a botanical test of Cheverud’s conjecture. Heredity. 1998;80:310–319. [Google Scholar]
- Wells N, Goddard S, Hayes MJ. A self-calibrating Palmer drought severity index. J Clim. 2004;17:2335–2351. [Google Scholar]
- Wermelinger Beat. Ecology and management of the spruce bark beetle Ips typographus—a review of recent research. Forest Ecology and Management. 2004;202(1-3):67–82. [Google Scholar]
- Whitlock MC. Evolutionary inference from QST. Mol Ecol. 2008;17:1885–1896. doi: 10.1111/j.1365-294X.2008.03712.x. [DOI] [PubMed] [Google Scholar]
- Whitlock MC, Guillaume F. Testing for spatially divergent selection: comparing QST to FST. Genetics. 2009;183:1055–1063. doi: 10.1534/genetics.108.099812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeaman S, Jarvis A. Regional heterogeneity and gene flow maintain variance in a quantitative trait within populations of lodgepole pine. Proc R Soc Lond, Ser B. 2006;273:1587–1593. doi: 10.1098/rspb.2006.3498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zas R, Sampedro L. Heritability of seed weight in maritime pine, a relevant trait in the transmission of environmental maternal effects. Heredity. 2015;114:116. doi: 10.1038/hdy.2014.76. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
SNP and δ13C data have been submitted to Dryad (10.5061/dryad.s205vd8).