Graphical abstract
Keywords: Cellular polarity, Rho family of GTPases, Adhesion size, Molecularly explicit spatiotemporal model, Stochastic simulations, Hysteresis and bistability, ROCK inhibitor, βPIX-dependent Rac activation
Abstract
Cell migration is a tightly-regulated process that involves protein gradients formed by the Rho family of GTPases, including Rho and Rac. The front (rear) of cells is generally characterized by higher active Rac (Rho) and lower active Rho (Rac) concentrations. Protein clusters, called adhesions, that anchor cells to their external environment have been shown to be dynamic and small (stable and large) at the cell front (rear), forming the force-transmission points necessary for persistent movement. Differences in adhesion sizes and dynamics have been linked to gradients in Rac and Rho activity. Here, we study the effects of Rac activation and gradients in Rac and Rho concentrations and activities on cellular polarity and adhesion size using mathematical and experimental approaches. The former is accomplished by expanding an existing reaction-diffusion model to a 2D domain utilizing stochastic dynamics. The model revealed that a hysteresis between the induced/uninduced states (corresponding to higher/lower Rac concentrations, respectively) along with Rac and Rho activation gradients, generated by chemical cues, were vital for forming polarity. Experimentally, the induced state was generated by increasing the cellular βPIX (a Rac-GEF) level and/or decreasing ROCK (a Rac-GAP effector protein) activity with Y-27632 (a ROCK-inhibitor). In agreement with the simulations, our results showed that cells with elevated RacGTP migrated faster, indicating more robust cellular polarization. However, the directionality of cells was not changed significantly, suggesting that external and/or internal physical or chemical cues were needed. Complementing the faster migration observed, adhesions were smaller, generating the phenotype expected with the induced state.
1. Introduction
Cell migration drives many essential biological processes, such as embryonic development, wound healing and inflammation, and is also central in many pathological conditions, including neurological disorders and cancer metastasis [15]. It requires the recruitment of many proteins to cell-matrix adhesion complexes and proteins that play a central role in regulating cell signalling, such as the adaptor protein paxillin. Cell signalling leads to the activation of downstream processes necessary for protein activation and expression. The former allows for cohesive movement of the cell through the coordination of the cytoskeleton and the regulation of both adhesions and cellular morphology [62]. Under physiological conditions and in the absence of soluble external cues, the initial signal for adhesion formation and cell migration is the activation of integrins through binding to specific extracellular matrix (ECM) proteins [11]. For example, in Chinese Hamster Ovary (CHO-K1) cells, integrin cell surface receptors and ECM substrate interaction occurs by binding to a conserved arginine-glycine-aspartic acid-serine (RGDS) sequence in fibronectin [1]. As a result of this initial binding, integrin receptors are activated, causing rearrangement of the cytoskeleton to promote changes in cell morphology followed by cell migration [70], [16]. Initially, localized actin polymerization and branching at the cell front causes the membrane to protrude [70], [16]. This process is then accompanied by the assembly of macromolecular complexes known as adhesions at this leading edge [70], [16]. The adhesions behave as traction points to pull the cell against the ECM while actin-mediated contractions around the rest of the cell allow for the translocation of the nucleus and organelles to the front of the cell [70], [16]. As the adhesions at the rear of the cell disassemble, the tail of the cell retracts such that the cell advances forward [70], [47], [16].
All of these aspects of cell migration are regulated by signalling pathways involving the Rho subfamily of the Ras superfamily of small GTP-binding proteins, which include Rac, Cdc42 and Rho [23]. These small GTPases are critical for activating signalling molecules involved in regulating actin polymerization, adhesion dynamics and cell polarity [49], [23]. Rac1 (Rac) is typically involved in actin polymerization at the leading edge, which allows for the formation of lamellipodia and controls adhesion formation [41]. Similar to Rac, Cdc42 regulates the organization of actin and adhesions but in specialized membrane protrusions, known as filopodia [41]. Finally, RhoA (Rho) promotes actin organization into stress fibers, adhesion assembly, and tail retraction at the rear of the cell [41], [67]. To execute these functions in the cell, the Rho GTPases transition between a GDP-bound inactive form (RacGDP and RhoGDP) and a GTP-bound active form (RacGTP and RhoGTP), and the switch between the two forms is regulated by intracellular GTPase-inactivating proteins (GAPs) and proteins with guanine-exchange factor (GEF) activity, respectively [23], [48], [66]. In the GTP-bound active state, these Rho family proteins mediate their effects on cell migration and adhesion dynamics by activating their respective effector proteins.
Multiple proteins are recruited to regulate adhesion dynamics and the protein paxillin has been found to play an important role in this process [9], [30]. For instance, paxillin has previously been shown to bind to vinculin, another focal adhesion protein, to regulate its spatial localization in the adhesion, as well as recruit other proteins to adhesions through a variety of tyrosine and serine phosphorylation sites [61], [56], [40]. The phosphorylation of paxillin at serine 273 (S273) in the leucine-aspartic acid rich (LD4) domain is a key regulator of adhesion dynamics and cell migration [40], [57]. Phosphorylation of S273 is mediated by p21-activated kinase (PAK1), a serine-threonine kinase that is also a Rac effector protein [55], [42], [40], [57]. Notably, this modification of S273 significantly increases the binding affinity between paxillin and the trimolecular, GIT1-βPIX-PAK1 complex at adhesions, promoting rapid adhesion dynamics and increased cell motility [40], [57]. βPIX recruitment to adhesions through this complex likely facilitates local Rac activation at adhesions since βPIX is a Rac-GEF [31], [40], [57]. Knowing that both PAK1 and βPIX interact with Rac, it has been suggested that the localization of these proteins at adhesions enhances cell protrusion and migration through the maintenance of a high, local concentration of active Rac at adhesions in protrusive regions of the cell [40].
Although these Rho GTPases have been shown to have defined functions and activities in cell migration, in most biological systems, there also exists crosstalk between the pathways regulated by these proteins. This crosstalk can lead to mutual activation or antagonism, depending on the cellular context and extracellular conditions [60], [13]. For instance, Tsuji et al. [60] showed that Rho can both activate and inhibit Rac, depending on which Rho-dependent signalling pathway is predominantly favoured in the cell. Specifically, they showed that completely inhibiting Rho signalling in lysophosphatidic acid (LPA)-induced Swiss-3T3 fibroblasts led to the inhibition of Rac activation because mDia1, a Rho effector protein which also promotes Rac activation, was suppressed [60]. However, selectively inhibiting Rho-associated coiled-coiled containing protein kinase (ROCK), which is another effector of Rho, led to an increase in Rac activation and, consequently, promoted cell spreading, cell migration and focal complex formation [60].
A way to understand the complex inner workings of cells is by taking experimental observations and developing a mathematical model that reproduces the results obtained experimentally. The relationship between Rac and Rho has been previously investigated mathematically using molecularly explicit models [27], [28], [57]. By assuming mutual inhibition between Rac and Rho, these models exhibited bistability with a hysteresis in their dynamics, a phenomenon in which two steady states of the system can coexist [29], [7], [4]. This behaviour indicates that cells can attain one of two (stable) steady states within a given parameter regime, depending on the initial concentrations of the proteins under consideration and on the history of the protein concentrations within the cell. The hysteresis of such systems allows for verification through experiments by varying key parameters of the model that can be targeted chemically. The models of Rac and Rho interaction can be refined by experimentation that quantifies protein concentrations after changing external or internal cues. Our aim in this study was to explore if the hysteresis obtained in [57] persists in the presence of stochasticity and diffusion in a 2D domain, and if so, determine whether it could generate cellular polarity.
One biochemical mechanism by which we hypothesized that Rho and Rac could antagonize each other’s respective functions was through the regulation of Rac-GEF activation. This activation could be suppressed through inhibition of βPIX (a Rac-GEF) activity [57] or suppression of Rho activity (and thus cell contractility) with a Rho-associated protein kinase (ROCK) inhibitor. ROCK has been reported to mediate both modes of RacGTP suppression. RhoGTP first binds to ROCK to activate it, and the resulting complex either suppresses βPIX (depicted by the green, dashed line in Fig. 1), decreasing the levels of RacGEFs, or phosphorylates FilGAP (a Rac-GAP) (depicted by the red, dashed line in Fig. 1), increasing the levels of Rac-deactivating species [50], [22], [39]. Here, we experimentally demonstrated that suppression of Rho signalling through selective inhibition of ROCK using a small molecule inhibitor, Y-27632, led to migratory phenotypes consistent with higher Rac activity. The mathematical simulations we performed revealed a propensity for the Rho/Rac signalling system to attain the induced state (more active Rac, higher migration speeds), once Rac activation was increased, and to remain in this state even once Rac activation was reduced significantly. Experimentally, elevations in active RacGTP concentration was induced by simultaneously overexpressing βPIX-mCherry and pharmacologically inhibiting ROCK, resulting in increased cell migration without any effect on intrinsic directionality. This observation appeared to agree with the outcomes of the model which showed that increasing Rac activation led to a global increase in RacGTP without producing the polarization required for enhanced directionality. Interestingly, ROCK-inhibition did not significantly alter βPIX localization at adhesions, but the results suggest that local βPIX activity is likely increased. In turn, ROCK-inhibition led to cells having decreased paxillin localization at adhesions and exhibiting smaller adhesion complexes, reminiscent of higher Rac and lower Rho activity.
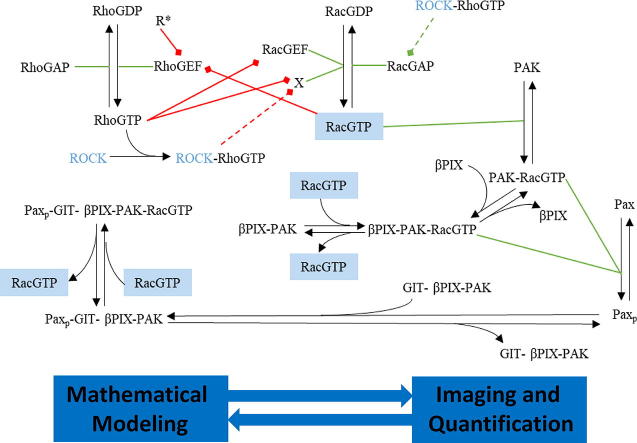
Fig. 1.
Diagram illustrating the interaction between the different proteins involved in cellular motility. Chemical reactions are represented by black arrows, green lines indicate catalysis of a reaction by a specific protein, and red arrows signify inhibition of a protein’s catalytic activity. The dashed lines show plausible mechanisms by which our experimental manipulations could have influenced the biochemical pathways. ROCK is written in blue text to emphasize that it was the target in the experiments. Briefly, the activation/inactivation of the two members of the Rho family of GTPases, Rac and Rho, are regulated by Rac-GEF/Rac-GAP and Rho-GEF/Rho-GAP, respectively, while ROCK activates Rac-GAP. Rac and Rho also mutually inhibit each other’s activation through inhibiting their respective GEFs. Activated Rac activates PAK which in turn induces paxillin phosphorylation at Serine 273 (S273). Phosphorylated paxillin then binds to the protein complex GIT-βPIX-PAK, where βPIX is a Rac-GEF (i.e., can induce Rac activation). Thus, according to this diagram, PAK and βPIX act upstream and downstream of paxillin phosphorylation and Rac activation, respectively. The RacGTP is in blue boxes to indicate that active Rac comes from the same protein pool. Finally, X = [βPIX], [βPIX-PAK], [βPIX-PAK-RacGTP], [GIT-βPIX-PAK], [Paxp-GIT-βPIX-PAK], [Paxp-GIT-βPIX-PAK-RacGTP] (i.e. the set of all protein complexes containing βPIX), whereas (i.e., the set of protein complexes containing RacGTP). (For interpretation of the references to the colours in this figure legend, the reader is referred to the web version of this article.)
In brief, here are the main highlights of this study:
-
•
Cellular polarity (and hence directionality) did not form spontaneously when simulating a stochastic spatiotemporal model of Rac, Rho and paxillin in a 2D domain representing a randomly moving CHO-K1 cell. This result of the simulation was verified experimentally by inhibiting ROCK in these cells, which was previously shown to increase directionality in fibroblasts [59]. Although polarity was not formed, hysteresis was still preserved by the model.
-
•
Imposing activation gradients on the 2D domain of the model produced polarity in a manner similar to that observed experimentally.
-
•
Experimentally inhibiting ROCK led to phenotypes similar to those seen following Rac hyperactivation, including increases in cell motility speeds and a reduction in adhesion size.
-
•
Cells treated with Y-27632 also had decreased localization of paxillin at adhesions but increased association between βPIX and paxillin, as predicted by the model.
2. Methods
2.1. Mathematical model and simulations
2.1.1. Model formalism
We adopted the same spatiotemporal model presented in [57] (see Fig. 1), which was originally developed from the experimental findings of [40]. This molecularly explicit model consists of six equations governing the dynamics of the following key proteins: inactive Rho or RhoGDP, active Rho or RhoGTP, inactive Rac or RacGDP, active Rac or RacGTP, unphosphorylated paxillin and paxillin phosphorylated at serine residue 273 (S273). Other proteins involved in the dynamics of this system include p21-Activated Kinase 1 (PAK), G protein-coupled receptor kinase InteracTor 1 (GIT) and beta-PAK-Interacting eXchange factor (βPIX). The main assumptions of this model are (see Fig. 1):
-
1.
Active PAK mediates the phosphorylation of paxillin at S273, allowing the protein complex GIT-βPIX-PAK to subsequently bind to it [40].
-
2.
Rac and Rho activation and inactivation are mediated by GTPase-specific Guanine Exchange Factors (GEFs) and GTPase-specific GTPase-Activating Proteins (GAPs), respectively [49], [12].
-
3.
Rac and Rho mutually inhibit each other through the inhibition of each other's Rho- and Rac-GEFs, respectively [12], [25], [26], [43].
-
4.
Active Rac (RacGTP) activates PAK by forming the intermediate PAK-RacGTP, while βPIX and its intermediates can act as Rac-GEFs [31], [42], [3].
For the remaining set of model assumptions, see [57].
Rescaling the concentrations of the key proteins Rho, Rac and paxillin (Pax) by their total corresponding concentrations within the cell, we obtain
| (1) |
where
and
The fraction of total active Rac (including RacGTP and RacGTP-containing complexes) is given by
whereas the fraction of total phosphorylated paxillin (including Paxp and Paxp-containing complexes) is given by
Based on the assumptions listed above and the rescaling in Eq. (1), we obtain the following equations for the model
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where is the ratio of total active PAK (PAK-RacGTP and all complexes containing it)-to-total PAK concentrations, given by
and
with
The first terms in Eqs. (2), (3) represent the inhibition of Rho activation by active Rac (through Rac-GEF), the second terms signify Rho inactivation (occurring at a constant rate), and the third terms depict the diffusion of active and inactive forms of Rho. Similarly, the first terms in Eqs. (4), (5) represent the inhibition of Rac activation by active Rho (through Rho-GEF), the second terms denote Rac inactivation (occurring at a constant rate), and the third terms designate the diffusion of active and inactive forms of Rac. Finally, the first and second terms in Eqs. (6), (7) describe the phosphorylation and dephosphorylation of paxillin, respectively, while the third terms describe their diffusion. The terms and represent the feedback loops involving PAK, RacGTP and Paxp (along with their complexes) and result from the quasi-steady state assumptions imposed on various intermediates as well as other proteins, including GIT, βPIX and PAK. Specifically, represents the role of active PAK complexes (assumed at steady state) in driving Rac activation, Rho inactivation and paxillin phosphorylation [40], while (which is a function of ) represents the role of βPIX in Rac activation as a Rac-GEF through the feedback loop involving GIT-βPIX-PAK binding to paxillin (see Fig. 1). For more details about how these terms are derived, please see the Supplementary Materials of [57].
In the absence of diffusion (i.e, by setting , for ) and by applying quasi-steady state approximation, the model can be further simplified to a system of three ordinary differential equations [57], given by
| (8) |
| (9) |
| (10) |
where
is the total concentration of active Rac (RacGTP and all complexes containing it), rescaled by the total concentration of Rac, and
is the total concentration of phosphorylated paxillin (Paxp and all complexes containing it), rescaled by the total concentration of paxillin. For the full derivations of the model, please see [57] and its Supplementary Material. Model parameters are listed in Table 1.
Table 1.
Model parameters are as specified and references used to obtain the parameter values are provided in [57].
| Parameter | Description | Value | Unit | References |
|---|---|---|---|---|
| Cell length | μm | [29] | ||
| Rho activation rate | s−1 | [45], [46] | ||
| Rho inactivation rate | s−1 | [45] | ||
| Rho level at half-maximal inhibition | Unitless | [45], [51], [46] | ||
| Basal Rac activation rate | s−1 | Estimated, [57] | ||
| Additional Rac activation rate | s−1 | Estimated, [57] | ||
| Rac level at half-maximal inhibition | Unitless | [45], [51], [46] | ||
| Rac inactivation rate | s−1 | Estimated, [57] | ||
| Ratio of total PAK-to-total Rac | Unitless | Estimated, [57] | ||
| Affinity constant for PAK-RacGTP binding | Unitless | [58], [32], [29] | ||
| Association constant for GIT-βPIX binding | s−1 | [53] | ||
| Association constant for βPIX-PAK binding | s−1 | [31] | ||
| Association constant for Paxp-GIT binding | s−1 | Estimated,[57] | ||
| Maximum paxillin phosphorylation rate | s−1 | [56] | ||
| Scaled level of paxillin at half-maximum activation | Unitless | [56] | ||
| Paxillin dephosphorylation rate | s−1 | [56] | ||
| Hill coefficient; level of cooperativity | Unitless | [32], [29] | ||
| Concentration of GIT | μM | [34], [54] | ||
| Concentration of βPIX | μM | [34], [54] | ||
| Total concentration of PAK | μM | Estimated, [57] | ||
| Total concentration of paxillin | μM | [34], [54] | ||
| Diffusion coefficient of active Rho | μm2/s | [8] | ||
| Diffusion coefficient of inactive Rho | μm2/s | [8] | ||
| Diffusion coefficient of active Rac | μm2/s | [8] | ||
| Diffusion coefficient of inactive Rac | μm2/s | [8] | ||
| Diffusion coefficient of phosphorylated paxillin | μm2/s | [10], [5] | ||
| Diffusion coefficient of unphosphorylated paxillin | μm2/s | [10], [5] |
2.1.2. Stochastic simulations
Like many other cellular processes, cell migration is stochastic in nature. This stochasticity is apparent at the cellular level in the seemingly random directional changes that CHO-K1 cells undergo and is due to noisy molecular processes which can be observed when using fluorescent biosensors for Rac and Rho [2], [69], [21], [35]. In a well-mixed setting, the dynamics of these processes are described rigorously at the microscopic level by the Chemical Master Equation [18], which can be extended to a spatial setting as the Reaction Diffusion Master Equation (RDME) [14]. While it is possible to simulate this system using a set of stochastic partial differential equations with appropriate noise terms, this approach has been shown to produce solutions that are qualitatively different from realizations of the RDME when the reaction propensities are nonlinear (as is the case with the model presented here) [17]. Thus, we have opted to incorporate stochasticity in the model through the use of the Spatial Stochastic Simulation Algorithm (SSSA, a spatial variant of the Gillespie Algorithm) in order to produce realizations of the RDME [19], [14].
In the implementation of the SSSA using Eqs. (2), (3), (4), (5), (6), (7), we considered the dynamics of the six proteins: active/inactive Rho, active/inactive Rac and phosphorylated/unphosphorylated paxillin. These proteins were distributed uniformly over a 2D square domain, divided into a by matrix. The total copy number of protein molecules in the cell for both Rho and Rac was estimated to be 2,250,000, whereas the initial copy number of paxillin molecules was estimated to be 690,000. These values were obtained from model parameters presented in [57]. Here, we have reduced these copy numbers by a factor of 10 to decrease computation time. In order to verify the validity of this approach, a simulation was done with the estimated copy number of molecules and no qualitative differences were observed (results not shown). The stochastic simulations were performed step-by-step, based on the following set of conditions/decisions:
1. The six species of proteins could undergo 34 different possible reactions, which included:
-
I.
Rac inactivation (RacGTP to RacGDP).
-
II.
Rac activation (RacGDP to RacGTP).
-
III.
Rac complexing (formation\de-formation of [PAK-RacGTP], [βPIX-PAK-RacGTP], [Paxp-GIT-βPIX-PAK-RacGTP]).
-
IV.
Rho inactivation (RhoGTP to RhoGDP).
-
V.
Rho activation (RhoGDP to RhoGTP).
-
VI.
Paxillin S273 dephosphorylation (Paxp to Pax).
-
VII.
Paxillin S273 phosphorylation (Pax to Paxp).
-
VIII.
Paxillin complexing (formation\de-formation of [Paxp-GIT-βPIX-PAK], [Paxp-GIT-βPIX-PAK-RacGTP]).
-
IX.
Four directional movements within the 2D domain for each of the six-protein species (24 possible reactions).
2. Reaction propensities were calculated for each of the eight reactions in I-VIII based on Eqs. (8), (9), (10) that govern the temporal dynamics of the system (assuming matter is conserved). The resulting coefficients were then multiplied by the total amount of their respective proteins, as done in [64]. For example, to calculate the propensity for the conversion of inactive Rho to active Rho, the coefficient representing the activation rate , found in the first term of Eq. (8), was multiplied by the total number of inactive Rho proteins within a given lattice square. Likewise, the propensity of the conversion from active to inactive Rho was calculated by multiplying the inactivation coefficient in Eq. (8) with the number of active Rho proteins in a given lattice square. The same was done to quantify the number of proteins for (in)active Rac and (un)phosphorylated paxillin. This process is then repeated for every lattice square in the domain.
3. Diffusion of proteins was modelled in a similar way, with the propensity for diffusion in a given direction determined by multiplying the rate, , by the number of molecules in that lattice square (where D is the diffusion coefficient and h is the length of a lattice square). This process is repeated for all allowed directions of movement.
4. Reactions governing the formation of complexes involving Rac and paxillin were assumed to be instantaneous (leading to the nonlinearities in Eqs. (2), (3), (4), (5), (6), (7)). These instantaneous reactions were implemented within the framework of the SSSA by repeatedly performing appropriate complexation reactions (with a time increment of zero) every time a (non-instantaneous) reaction changed the propensity of these (instantaneous) reactions. This was done by randomly choosing a (complexing or de-complexing) reaction according to the probability of forming a complex. For active Rac, this probability of forming a complex is given by
while for phosphorylated paxillin, it is given by
where
and and are the concentrations of complexes formed by active Rac and phosphorylated paxillin, respectively.
When a non-instantaneous reaction changed either the Rac or paxillin concentration in a lattice square, these probabilities were used to choose one of the relevant instantaneous reactions 50 times before a non-instantaneous reaction was allowed to occur. The choice of 50 iterations was found to be sufficiently large enough to obtain no qualitative changes in the simulation when more iterations were added.
5. In the presence of Rac/Rho activation rate gradients, the propensity of each protein (e.g. Rac) was calculated using a gradient in the activation parameter (e.g. ) such that it linearly decreased along each row (e.g. ). The propensity in a specific lattice square was calculated using the corresponding activation rate constant along the row.
6. For generating the hysteresis, we varied the maximum phosphorylation rate () linearly over time. For example, for a total reaction time of 100 time units and a hysteresis ranging between s−1, we would set
This ensured that the value of increased linearly with reaction time. When the time variable reached half the total reaction time (50 s), we redefined the equation for so that it decreased linearly from to .
2.1.3. Software
Numerical simulations and bifurcation analysis were performed using MATLAB (MathWorks, Natick, MA) and xppauto (a freeware available at http://www.math.pitt.edu/~bard/xpp/xpp.html). Steady state expressions for intermediate complexes were previously derived using Wolfram Mathematica (Wolfram, Champaign, IL). All codes required for reproducing the stochastic simulations are available online [72].
2.2. Cell culture, plasmid transfection and drug treatments
Chinese Hamster Ovary K1 (CHO-K1) cells stably expressing G. gallus paxillin-EGFP were maintained in DMEM cell culture media containing low-glucose plus L-glutamine, 110 mg/L sodium pyruvate and pyridoxine hydrochloride (ThermoFisher Scientific, 11885–084). Media were supplemented with 10% vol/vol fetal bovine serum (FBS) (ThermoFisher Scientific, 10082–147), 1% vol/vol 100X non-essential amino acids (ThermoFisher Scientific, 11140–050), 1% penicillin–streptomycin (ThermoFisher Scientific, 10378–016), and 25 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) (ThermoFisher Scientific, 15360–080). CHO-K1 cells stably expressing paxillin-EGFP were provided by Rick Horwitz at the University of Virginia. Cells were only allowed to reach 70–80% confluency to maintain the exponential phase of growth. For every passage, cells were split using 0.05% trypsin-EDTA (Thermofisher Scientific, 25200–056).
Plasmids of βPIX fused with mCherry were constructed as previously described in [57]. Transient transfections were conducted in CHO-K1 cells stably expressing paxillin-EGFP that were grown to 70–80% confluence in cell culture media. In phenol red-free and reduced serum 1X OptiMEM media (Thermofisher Scientific, 11058201), 1 µg of βPIX-mCherry plasmid and 2.5 µL of Lipofectamine 2000 (Thermofisher Scientific, 11668–027) were incubated in separate tubes for 5 min at room temperature. The plasmid and Lipofectamine were then combined in the same tube and incubated for 20 min at room temperature. Cell culture media was replaced with Opti-MEM media to which the plasmid DNA and Lipofectamine 2000 solutions were added. Five hours following transfection, Opti-MEM media were replaced by regular culture media. The cells were plated on fibronectin coated 35-mm glass-bottom dishes 24 post-transfection for all the experiments. All live-cell experiments described below were performed on live cells seeded on fibronectin-coated glass-bottom dishes (Word Precision Instruments, FD-35). Fibronectin-coated dishes were prepared prior to seeding the cells by incubating overnight at 4 °C with a solution of 2 µg/mL of human plasma fibronectin (Sigma Aldrich, F-0895) diluted in phosphate buffered saline (PBS). The plates were washed three times the following day with PBS after which cells were plated and incubated overnight at 37 °C to properly settle.
A 5 mM stock solution of ROCK inhibitor Y-27632 (Selleckchem, S1049) was prepared in double distilled water (ddH2O) and stored at −20 °C. For inhibition studies, the stock solution was diluted in media to treat the cells with a final concentration of 20 µM of the inhibitor. For control treatments, an equal volume of double distilled water was added to media.
2.3. Cell migration and persistence experiments
CHO-K1 cells stably expressing paxillin-EGFP alone or transfected with βPIX-mCherry were imaged in transmitted light illumination on an automated inverted Zeiss AxioObserver microscope (Carl Zeiss, Jena, Germany) using a 20X/0.80 Plan-Apochromat objective lens and a 16 ms exposure time on an Axiocam 506 monochrome CCD camera. A stage-top environmental control chamber kept the cells at 37 °C and 5% CO2 throughout the live-cell experiments (Live Cell Instruments, Seoul, Korea). For cells transfected with βPIX-mCherry, fluorescence images were collected using an X-Cite 120 LED light source and FS15 (TRITC) filter cube just prior to time-lapse imaging as a reference for tracking transfected cells.
For the ROCK inhibition studies, cells were allowed to migrate and were imaged with transmitted light every 2 min for 3 h, after which they were treated with 20 µM of Y-27632. One hour post-treatment, the same cells were imaged for another 3 h. The raw time-lapse images were loaded in MetaXpress 5.0 (Molecular Devices Inc., SunnyVale, CA). The “track points” application was used to track cells by clicking on the centre of each call in a semi-automated way (automatic frame advance). The tracked data was logged and exported into Microsoft Excel. For each cell, the instantaneous speed between each tracked frame was first calculated by measuring the distance moved by the cell between two frames and then divided by 2 min. The average cell speed was determined by averaging the instantaneous speed between each tracked frame over the 3 h. The persistence measurement of each cell’s trajectory was calculated as a ratio of the net displacement over the total track distance over the 3 h. Speed and directionality analyses and Rose plots were obtained by using a published custom Excel macro [20].
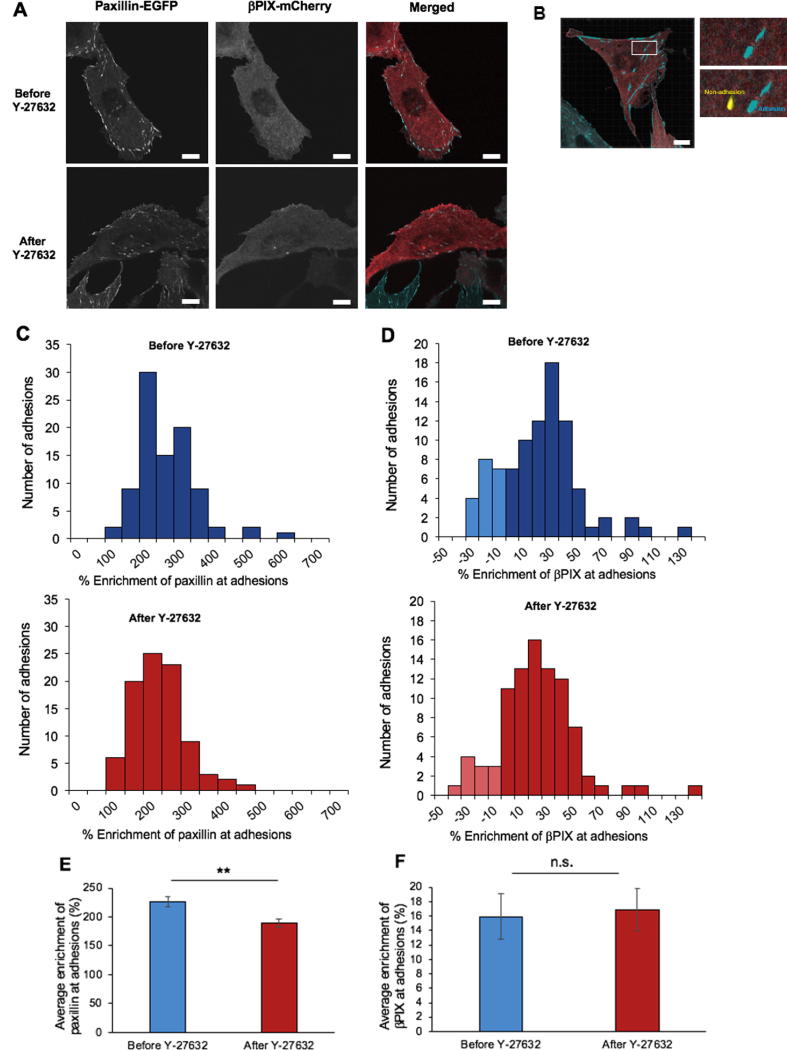
2.4. Quantification of protein intensity at adhesions
Cells co-expressing paxillin-EGFP and transiently transfected βPIX-mCherry with or without treatment for 1 h with 20 µM Y-27632 were fixed with 4% para-formaldehyde (PFA) for 15 min at room temperature, washed with PBS three times and left in PBS overnight at 4 °C. The untreated and treated cells were imaged the next day on the Zeiss LSM 710 confocal laser scanning microscope, equipped with a 63X/1.4NA Plan-Apochromat oil immersion objective lens. Sequential imaging of paxillin-EGFP and βPIX-mCherry was done using 1% of the 488 nm line of a 25 mW Argon-Ion laser and 1% laser power from the 561 nm 20 mW diode-pumped solid state (DPSS) laser, respectively, and each pixel was exposed for 3.15 µs. The acquired images were 1024-by-1024 pixels with a pixel size of 0.088 µm. A built-in 488/561 beam splitter was used to collect the images, capturing light from 493 to 550 nm for EGFP and 584 nm to 674 nm for mCherry. Imaris 9.3.1 software (Bitplane, Switzerland) was used to perform quantitative analysis of adhesion intensity in the acquired images. The “surface” application was used to generate a surface to detect individual adhesions in the cells. A reference non-adhesion surface was generated manually by copying adhesion surfaces to areas beside each selected adhesion. The mean intensity of paxillin-EGFP and βPIX-mCherry in the adhesions and non-adhesion regions were extracted to measure the relative % enrichment of the proteins in adhesions as follows: % enrichment = (Fadhesions − Fnon-adhesion)/Fnon-adhesion, where F represents the average fluorescence intensity. The histogram function in Microsoft Excel was used to generate distributions of protein localization for all conditions.
2.5. Total internal fluorescence reflection (TIRF) microscopy
A TIRF microscope (Spectral Applied Research, Richmond Hill, Toronto) attached to a Leica inverted DMI6000B microscope (Leica Microsystems, Wetzler, Germany) with a Leica Plan ApoChromat 63×/NA 1.47 TIRF oil immersion objective lens was used. The platform incorporated a 488 nm diode laser and a 561 nm diode-pumped solid-state laser (Spectral Applied Research) and was equipped with two Flash 4 sCMOS Cameras (Hamamatsu, Hamamatsu City, Japan). A 100-Watt X-Cite 120 LED (370–700 nm) light source was used for visualization of fluorescent proteins by eye. The platform was integrated with MetaMorph 7.1 image acquisition software (Molecular Devices Inc.) and custom-designed TIRF controls (Quorum Technologies Inc., Guelph, ON). Cells plated on fibronectin-coated 35 mm glass-bottom dishes were placed in a stage-top live cell instrument chamber maintained at 37 °C under a 5% CO2 humidified environment (Live Cell Instruments, Seoul, Korea). For all imaging, the TIRF penetration depth was set to 80 nm using the MetaMorph software. To monitor adhesion size, the 488 nm diode laser was set at 20% laser intensity with laser pulsing set such that the laser was only on 1% of the time using the Quorum Flicker device, so the effective laser intensity was 0.2%. The exposure time was set to 5 s. Images of paxillin-EGFP at adhesions were acquired using the prism-based TIRF system and an EGFP emission filter (ET 525/50 nm). In cells co-expressing paxillin-EGFP and βPIX-mCherry, doubly-labelled cells were identified by eye and were imaged on the TIRF microscope using the 488 nm laser to capture paxillin-EGFP fluorescence intensity at adhesions.
2.6. Adhesion intensity measurements
The adhesions in background-subtracted images were found using the surfaces function in Imaris. Surfaces were created using the following settings on the creation wizard. “Track surfaces over time” was selected, and a smoothing filter was applied with the “Surface Area Detailed Level” of 0.25 μm. The “Sphere Diameter” used to perform background subtraction was also 0.25 μm. Adhesions close in location were identified as separate using “Split Touching Objects” with a “Seed Points Diameter” of 0.70 μm. Some additional noise was removed by applying a “Quality” filter with the threshold of 2.65. If a surface had the centre pixel intensity below this value, it was not considered an adhesion. To prevent erroneous linking of adhesions between frames, the “Autoregressive Motion” algorithm was chosen and a “Maximum Distance” that a presumed adhesion could travel between frames was set at 0.35 μm. Lastly, if a surface was not found in 4 consecutive frames, the track was terminated. Any track lasting fewer than 4 frames (40 s) was not used in further analyses. The intensity values of the generated “surfaces” (which corresponded to adhesions) were exported as a CSV file and imported into MATLAB (MathWorks, Natick, MA). The intensity values reported are the maximum sum intensities the adhesions reached over their respective lifetimes (where the sum intensity is the sum of the intensity units of each pixel corresponding to the adhesion).
2.7. Statistical tests
All experiments were performed in at least three, independent trials and analyzed with Microsoft Excel. Statistical significance of all data generated from the experiments was determined by two-tailed Student’s t-tests. The t-test for the adhesion parameter (intensity sum) was performed on the percentage change (i.e. the ‘before’ condition value was 100%, and the ‘after’ condition value was the ratio of the ‘after’ condition value to the ‘before’ condition value multiplied by 100%) rather than the raw values, due to the inherent variability between cells. P-values less than 0.05 were considered statistically significant.
3. Results
3.1. Stochastic simulations in the absence of a gradient
It has been previously shown that, in the deterministic case, the temporal dynamics of the six key proteins (active/inactive Rac, active/inactive Rho, and phosphorylated/unphosphorylated paxillin described by Eqs. (8), (9), (10)) could produce bistability [57], a phenomenon in which two steady states can coexist. In this system, bistability consisted of two branches of steady states, one of which was the induced state with elevated active Rac and reduced active Rho, while the other was an uninduced state with elevated active Rho and reduced active Rac. The deterministic spatiotemporal model given by Eqs. (2), (3), (4), (5), (6), (7), on the other hand, was also shown to produce polarity in a 1D domain [57]. While these deterministic approaches robustly produce bistability and/or polarity, the molecular events underlying Rac and Rho biochemical pathways are intrinsically stochastic in nature [2], [69], [21], [35]. This situation raises the question of whether localized activations of Rac or Rho can lead to qualitatively different patterns of biochemical activity compared to the deterministic case. For example, can they produce a spontaneous change in the direction of cellular polarization, as is seen in CHO-K1 cells, without the effect of chemokines?
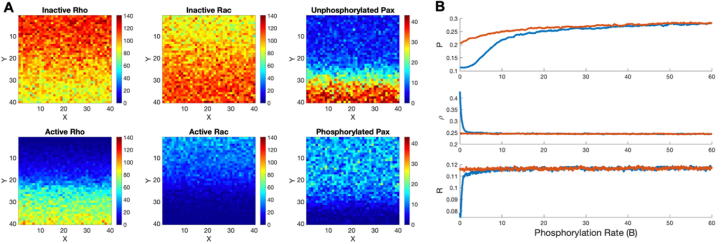
To further explore the role of Rac and Rho in generating bistability and polarity in the presence of stochasticity, we simulated Eqs. (8), (9), (10) using the SSSA over a square 2D domain, where both protein reactions and diffusions were considered (see Methods Section). Starting with uniformly distributed concentrations of these proteins over the entire 2D domain of the cell, with the inactive (active) form of Rac (Rho) and unphosphorylated form of paxillin taken to be at much higher (lower) level than the active (inactive) and phosphorylated forms (Fig. 2), the heat-maps at steady state obtained after 25 time units displayed an overall elevation in the active form of the protein Rac and an elevation in phosphorylated paxillin throughout the cell (Fig. 3A). The results obtained, however, did not generate any spontaneous increase in localized activity manifested as small regions of elevated activated Rac () and/or phosphorylated paxillin () or cellular polarization with a large-scale gradient in any of the proteins of interest. This was mainly due to the fact that there was large disparity between the propensity for diffusion and chemical reactions. The results obtained thus suggest that a biochemical or physical cue or a pre-existing gradient must be present to produce such outcomes.
Fig. 2.
Heat-maps of the 2D square domain showing the initial state of a simulated cell. The six key proteins (active/inactive Rho, active/inactive Rac and phosphorylated/unphosphorylated paxillin) were considered, while setting the remaining proteins to steady state. The simulated cell is a square lattice with an integer number of Rho, Rac and paxillin molecules residing in each lattice square. Heat-maps of the initial number of these proteins per lattice square, colour-coded according to the colour-bar to the right of each panel, show the spatially-uniform initial condition of our simulations. Simulations were initiated from a state with a lower level of inactive/active Rac/Rho and phosphorylated paxillin compared to active/inactive Rac/Rho and unphosphorylated paxillin (i.e. near the uninduced steady state).
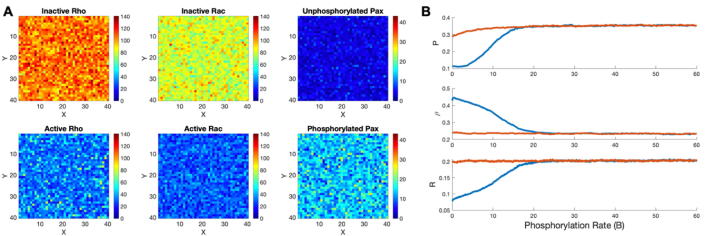
Fig. 3.
Spatiotemporal dynamics of the model in a 2D square domain representing the cell in the absence of a gradient. (A) Heat-maps of inactive/active Rac, inactive/active Rho and unphosphorylated/phosphorylated paxillin at steady state (at the end of the simulation), as indicated by the legend in each panel, in the absence of gradients in Rac and Rho activation rates. The heat-maps were colour-coded according to the colour-bar to the right of each panel. (B) Averaged total number of phosphorylated paxillin (top), active Rho (middle) and active Rac (bottom) molecules over the entire 2D domain in the absence of gradients in Rac and Rho activation rates. The model exhibits a hysteresis, a hallmark of bistability, consisting of non-coinciding jumps between two co-existing states representing the induced (high active Rac/low active Rho) and uninduced (low active Rac/high active Rho) states, depending on where the simulations were initiated. Blue/orange lines correspond to model responses when maximum paxillin phosphorylation rate, , was increased/decreased while starting the simulations from the uninduced/induced state. Although the model exhibits bistability at the whole-cell level, stochastic dynamics were insufficient to produce polarity in the absence of a gradient in reaction rates. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Interestingly, plotting the average levels of active Rac (), Rho () and paxillin () from 2D simulations as a function of the maximum paxillin phosphorylation rate () produced a hysteresis for all three proteins (Fig. 3B). The hysteresis was generated by linearly increasing the value of from 0 s−1 to 60 s−1, starting the cell in the uninduced state (blue line). At the half-way point in the simulation, when the cell has reached the induced state (orange line), was decreased linearly back to 0 s−1. We note that, during this time, all of the chemical reaction rates were increased such that effectively acts as a parameter for the system rather than a time-dependent quantity. The fact that the blue and orange lines do not coincide in Fig. 3B was indicative of a hysteresis. Indeed, the blue line exhibited a right-shifted jump for all proteins, while the orange line exhibited either a left-shifted jump in paxillin (top panel) or no jump at all in active Rho and Rac (bottom two panels, respectively). In other words, the system was biased towards the uninduced state.
Hysteresis is a hallmark of bistability. It suggests that either one of the two steady states, the induced and uninduced states, can be attained, depending on the initial concentrations or numbers of proteins present in this system. As previously demonstrated [12], [57], such behaviour was mainly due to the mutual inhibition exerted by active Rho on Rac and active Rac on Rho. In the case of paxillin, however, bistability (or hysteresis) was less pronounced and smaller in range compared to that exhibited by Rac and Rho (compare Fig. 3B top with middle and bottom panels), consistent with previous observations [57].
3.2. Stochastic simulations in the presence of a gradient
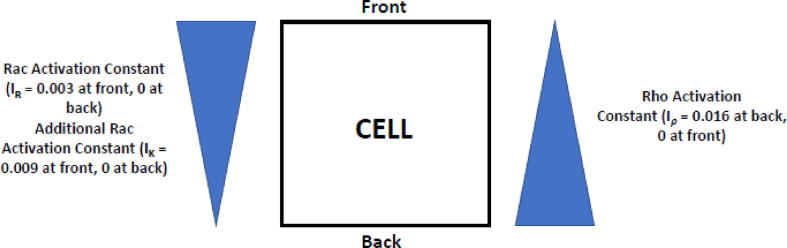
Due to the absence of polarity in the simulations performed previously, we repeated the same analysis but imposed a linear gradient from the “front” to the “back” of the cell on three activation parameters: basal Rac activation rate (decreasing from to s−1), additional Rac activation rate (, decreasing from to s−1) and Rho activation rate (, increasing from to s−1) vertically along the 2D domain while keeping it constant in the horizontal direction (See Fig. 4). These gradients would simulate a cell moving downward or upward based on the plots shown in Fig. 5A. In the first set of simulations, we kept the remaining parameters constant throughout the cell as before (i.e., as in Fig. 3A). The goal of these simulations was to mimic the physiological effects of chemical cues, such as chemotaxes that can drive protein activity gradient formation across the cell and cause it to move in a given direction, polarize or localize proteins to a specific area. The linear gradients introduced were strong enough to produce heat-maps with cellular polarization in all proteins under consideration (Fig. 5A). Outcomes of these simulations were very similar to those observed experimentally for active Rac [57], confirming its role in inducing an increase in cellular motility. These simulations highlight the importance of external cues, such as chemical (chemotaxes) or mechanical (durotaxis), to drive protein activity gradients, resulting in cellular polarity in motile cells.
Fig. 4.
Schematic showing how the linear gradient in Rac and Rho activation rates is imposed on the 2D domain representing the cell. The range of values for the activation rates are provided in the legends.
Fig. 5.
Spatiotemporal dynamics of the model in a 2D square domain representing the cell in the presence of a gradient. (A) Heat-maps of inactive/active Rac, inactive/active Rho and unphosphorylated/phosphorylated paxillin at steady state (after 500 time units), as indicated by the legend in each panel, in the presence of gradients in Rac and Rho activation rates as indicated by Fig. 4. The heat-maps were colour-coded according to the colour-bar to the right of each panel. (B) Averaged total number of phosphorylated paxillin (top), active Rho (middle) and active Rac (bottom) molecules over the entire 2D domain in the presence of a gradient in Rac activation rate only. Blue/orange lines correspond to model responses when maximum paxillin phosphorylation rate, , was increased/decreased while initiating the simulations from the uninduced/induced state. Notice here that the hysteresis is less pronounced (compared to that in Fig. 3B) and that there is no jump from the uninduced to the induced state. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Our results also revealed that the model could still produce a hysteresis but within a limited range with respect to the maximum phosphorylation rate of paxillin, . The hysteresis was manifested as a jump from the uninduced to the induced state when increasing (Fig. 5B, blue line) and a lack of it when decreasing (Fig. 5B, orange lines). As before, the jump was obtained by starting the simulations from the uninduced state, whereas there was no jump when starting from the induced state (Fig. 5B). Similar results were obtained with a gradient in Rho activation rate only, Rac activation rate only or in combination with the gradient in Rac inactivation rate (results not shown).
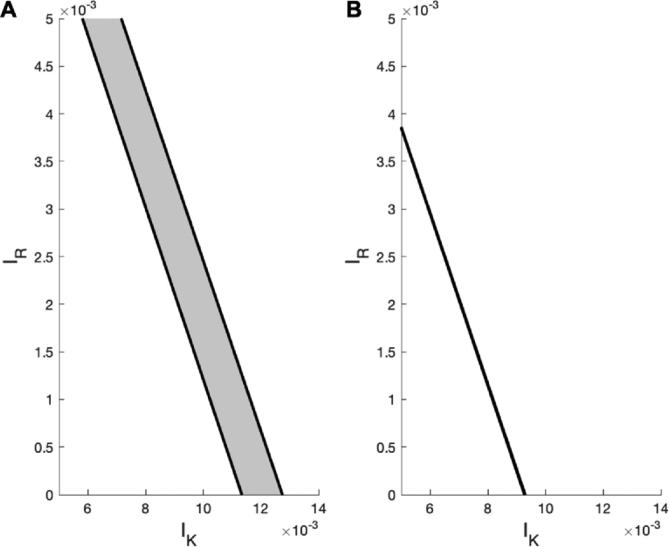
As indicated by our previous results, the presence of hysteresis was a consequence of the bistable nature of the model described by Eqs. (8), (9), (10). In the presence of activation gradients, however, the range of the hysteresis was less pronounced (i.e., smaller in range) and generally more left-shifted compared to that obtained in the absence of such gradients (compare Fig. 3B with Fig. 5B). This result was due to the narrow bistable regime formed towards the front of the cell, limiting the areas of the cell that can be found in both the induced and uninduced state (see Fig. 6), causing the jump to occur earlier and be less pronounced (compare Fig. 5B with Fig. 3B). The lack of downward jump from the induced to the uninduced state in Fig. 3B, middle and bottom, and Fig. 5B was mainly due to the closeness of the left threshold (i.e., the fold) of the bistable switch to zero, as suggested in a previous study [57].
Fig. 6.
Regimes of coexistence (bistability) between the induced and uninduced states when varying the activation rates, demonstrating the model’s sensitivity to the parameter . The gray region (bounded by two black lines) corresponds to the bistable regime in which both of these states coexist, whereas the white regions correspond to the monostable regimes in which either the induced (above the gray region) or uninduced (below the gray region) state exists. Notice that decreasing the value of from (A) s−1 to (B) diminishes the regime of bistability until it becomes almost negligible.
3.3. Inhibition of ROCK led to increased cell migration speeds
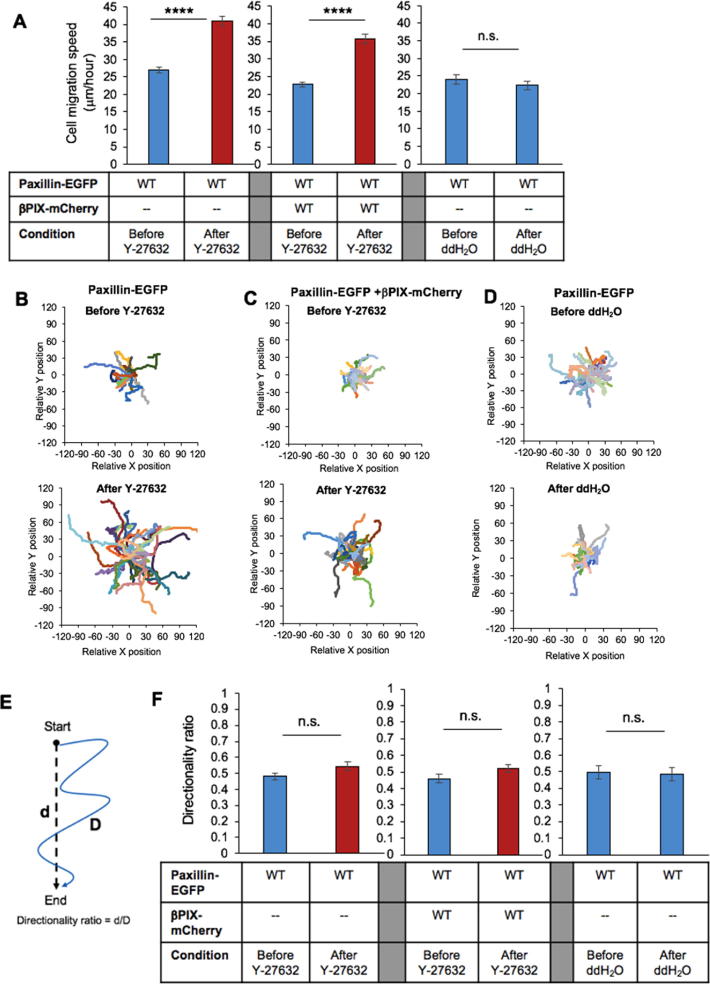
We sought to explore whether indirectly increasing Rac activity by inhibition of ROCK (inactivation of Rac-GAP leaving more Rac in the GTP bound active state), one effector protein of Rho, could lead to increased cell migration speeds or changes in intrinsic directionality. CHO-K1 cells were imaged at 20X magnification with transmitted light for 3 h prior to the addition of 20 µM Y-27632 for 1 h followed by an additional 3 h of imaging. Cells expressing paxillin-EGFP moved with an average speed of 27 µm/h but sped up to 41 µm/h following Y-27632 treatment (Fig. 7A, Video 1 and 2). This increase in cell speed was quite apparent from Rose plots of individual cell tracks (Fig. 7B). Overexpression of βPIX-mCherry in paxillin-EGFP expressing cells did not impact cell speed (23 µm/h) or the response to ROCK-inhibition (36 µm/h, Fig. 7A, 7C). This indicates that there are no obvious βPIX overexpression artifacts, causing more rapid cell migration, but rather βPIX GEF activity is highly regulated in the cell. These results suggest that ROCK-inhibition may suppress ROCK antagonism on βPIX activity (represented by the red dashed line in Fig. 1), allowing βPIX activity to increase, thus increasing Rac activation. To ensure the observed changes were specifically due to the addition of the Y-27632 inhibitor, control experiments were executed by incubating cells after an addition of ddH2O to the culture media instead of concentrated ROCK inhibitor solution. The control cells did not demonstrate any changes in migration speed or track shape or duration (24 µm/h versus 22 µm/h, Fig. 7A, 7D).
Fig. 7.
Suppression of Rho signalling through ROCK-inhibition leads to an increase in cell migration but not intrinsic cell directionality. Cell speed and directionality were calculated from time lapse images acquired with transmitted light microscopy before treatment and 1-hour post-treatment with 20 µM of the ROCK inhibitor or ddH2O. (A) Average cell speed of CHO-K1 cells expressing paxillin-EGFP or co-expressing paxillin-EGFP and βPIX-mCherry before (blue) and after (red) treatment with Y-27632 or ddH2O. Rose plots of migration tracks of CHO-K1 cells (B) expressing paxillin-EGFP, (C) co-expressing paxillin-EGFP and βPIX-mCherry before (top panels) and 1 h after (bottom panels) addition of Y-27632, or (D) control paxillin-EGFP expressing cells before (top panel) and after addition of ddH2O (bottom panel) in culture media. For the Rose plots, each cell track starts at the 0,0 position. (E) Visual representation of how the directionality ratio was assessed from a cell’s migratory track, where d represents the net distance and D represents the total cumulative distance travelled by a cell along the entire track distance. (F) Cell directionality ratios of CHO-K1 cells expressing paxillin-EGFP or co-expressing paxillin-EGFP and βPIX-mCherry before and after treatment with Y-27632 or ddH2O. Error bars are standard errors of the means. Four stars correspond to (****) p < 0.0001. n = 60–70 cells in total from 3 independent experiments. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Localized Rac activation has been implicated as a positive regulator in migration and in maintaining increased cell directionality during migration, although in different contexts [6], [40], [68]. The directionality index is a measure of persistence along one direction (i.e. straightness) in the path of a migratory cell and represents a ratio of the net displacement of the cell (direct distance from the initial to the final position) to the total distance the cell travelled along its trajectory (blue line, Fig. 7E). The ratio yields a value between 0.0 and 1.0, with smaller numbers representing more random cell movement and higher numbers representing a more persistent migration path. Although cells migrated faster after ROCK-inhibition, the cell movement for all cases was random and did not show any evidence of changes in intrinsic directionality under any condition tested (Fig. 7E, 7F). The control cells also showed no changes in cell migration persistence in any one direction (Fig. 7E, 7F). Thus, ROCK-inhibition and the presumed increases in Rac activation did not contribute to nor obstruct the cells’ preferred intrinsic direction of cell migration.
3.4. ROCK-inhibition alters the localization of paxillin but not βPIX at adhesions
Adhesions are the fundamental protein sub-structures that control communication between the cell and ECM, and their molecular composition is important in regulating cell migration. Even though βPIX plays a significant role in cell migration, unlike paxillin, it does not localize at high levels at adhesions but rather remains diffuse across the cell (Fig. 8A) [44]. The relative enrichment of both paxillin-EGFP and βPIX-mCherry in adhesions was determined quantitatively by comparing the intensity in each adhesion to the intensity in a region of the cell adjacent to the adhesion (i.e. non-adhesion area) (Fig. 8A, 8B). While paxillin was always highly localized in adhesions, with a relative enrichment of 2–6-fold (Fig. 8C, top, blue panel), βPIX was only modestly enriched in adhesions with an average of 10–40% enrichment, and an occasional enrichment in non-adhesion areas (Fig. 8D, top, blue panel). This observation is consistent with previous work from our group [44]. Cells co-expressing paxillin-EGFP and βPIX-mCherry were then treated with 20 µM Y-27632 for 1 h, and the relative enrichment of each of the proteins was measured (Fig. 8C and 8D, bottom, red panels). Upon treatment with ROCK inhibitor, the mean enrichment of paxillin decreased significantly in adhesions from 230% to 190% (Fig. 8E), but there was no change in the % enrichment of βPIX-mCherry in adhesions (16%, Fig. 8F). Thus, Rho-dependent ROCK signalling promotes either paxillin recruitment to adhesions or more stable paxillin-binding in adhesions, which allows adhesions to grow. It is more likely that the latter is the case because our dynamic binding experiments show that mutants of paxillin that cannot be phosphorylated at paxillin S273 show longer binding in adhesions [44]. βPIX localization at adhesions did not change with inhibition of ROCK signalling. According to our model, however, it was hypothesized that, under physiological conditions, Rho-mediated activation of ROCK would lead to the inhibition of the βPIX GEF activity (red, dashed line in Fig. 1). Thus, although ROCK-inhibition did not affect βPIX localization to adhesions, it presumably affected its activity.
Fig. 8.
Inhibition of ROCK results in decreased paxillin-EGFP localization without affecting βPIX-mCherry localization at adhesions. (A) Laser scanning confocal images of CHO-K1 cells co-expressing paxillin-EGFP and βPIX-mCherry before and after 1-hour treatment with 20 µM Y-2763. (B) Imaris surface generation on adhesions. Higher magnification insets show adhesion surfaces (blue) and an adjacent non-adhesion surface (yellow). The relative enrichment of paxillin-EGFP (C) and βPIX-mCherry (D) at adhesions without (top, blue panels) or with (bottom, red panels) 1-h of treatment with 20 µM Y-27632. Negative enrichment values denote a higher concentration of the proteins in non-adhesion areas and are represented by lightly-shaded histogram bars. Average enrichment of (E) paxillin-EGFP and (F) βPIX-mCherry at adhesions before and after Y-27632 treatment. Error bars are standard errors of the means. n = 80–90 adhesions from at least 12–15 cells in total from three, independent experiments. Two stars correspond to (**) P < 0.01. Scale bars are 10 µm. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
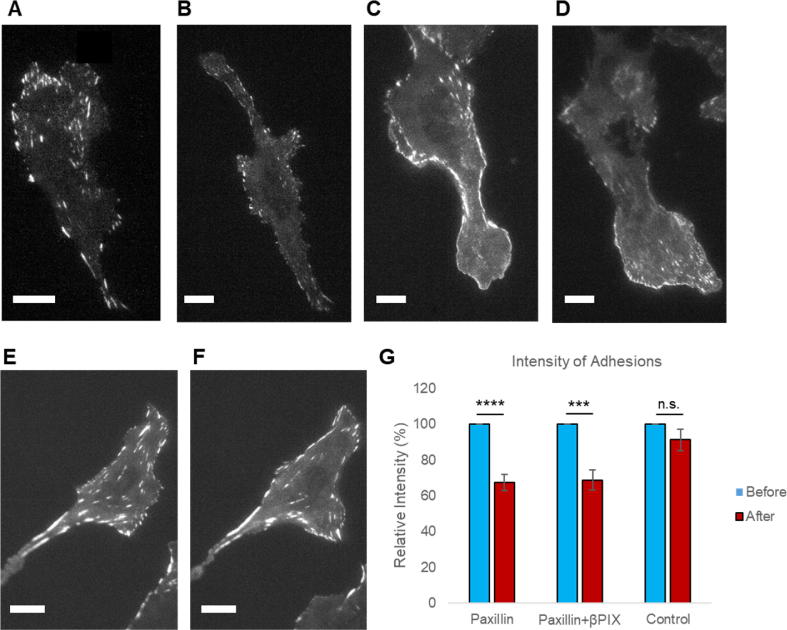
3.5. Adhesions do not grow in size when ROCK is inhibited
We next investigated how adhesions behave when the induced state was promoted. Faster cell migration and decreased enrichment of paxillin at adhesions following ROCK-inhibition led us to hypothesize that adhesions would also be more dynamic and would remain as smaller, nascent structures and not increase in size following ROCK-inhibition. Paxillin-EGFP-containing adhesions were imaged in single cells using TIRF microscopy before and after a 1-h treatment with Y-27632. Imaging the same cells before and after ROCK-inhibition allowed for a direct comparison of adhesion sizes (measured by total intensity of paxillin-EGFP), while removing some dependence on cell-to-cell variation. Fig. 9 shows representative images of one cell expressing paxillin-EGFP before and after treatment with Y-27632 (panels A and B, respectively), one cell expressing paxillin-EGFP (fluorescence shown) and βPIX-mCherry (fluorescence not shown) before and after treatment with Y-27632 (panels C and D, respectively) and one cell expressing paxillin-EGFP in control conditions (panels E and F, respectively). The total intensity of each adhesion, rather than the area, was measured as an indication of the number of proteins in the adhesion, since many adhesions were beyond the resolution of the microsope. The cells expressing paxillin-EGFP had adhesions with an intensity of 9,000 ± 600 arbitrary units (A.U.) before treatment and a 30% decrease to 6,300 ± 100 A.U. after Y-27632 treatment (Fig. 9G). A similar decrease in intensity of 38% was observed in cells with elevated βPIX concentrations, which had adhesions with intensities of 13,100 ± 200 A.U. before and 8,200 ± 100 A.U. after the inhibition of ROCK (Fig. 9G). Control cells, treated with the addition of ddH2O, did not demonstrate any significant changes in adhesion intensity (Fig. 9G). Thus, ROCK-inhibition led to smaller adhesions (Fig. 9B, D), indicating that ROCK is a key player in protein localization to adhesions and adhesion growth and stabilization.
Fig. 9.
Paxillin-EGFP signal intensity in adhesions decreases upon the addition of a ROCK inhibitor. TIRF images of a representative CHO-K1 cell expressing: (A, B) paxillin-EGFP acquired before (A) and after (B) treatment with Y-27632, (C, D) paxillin-EGFP in cells also transfected with βPIX-mCherry (not shown) acquired before (C) and after (D) treatment with Y-27632, and (E, F) paxillin-EGFP acquired before (E) and after (F) the addition of ddH2O (control). Scale bars are 10 µm. (G) The average intensity of adhesions within cells before and after treatment with Y-27632 or ddH2O (control). Nine cells from at least three independent experiments were averaged in the Y-27632 treatment and ten cells, from four different experiments, were averaged in the control. There were a total of 2104 adhesions before Y-27632 treatment and 1784 adhesions after for the paxillin-EGFP cells, 4772 adhesions before treatment and 4510 adhesions after for the paxillin-EGFP and βPIX-mCherry cells, and 5873 adhesions before treatment and 6315 adhesions after for the control cells. Statistical significance was calculated using a t-test on the percentage change (relative change of the after condition to the before condition) and is indicated by stars, with four stars (****) indicating P < 0.0001 and three stars (***) corresponding to P < 0.001. Error bars represent standard errors of the means.
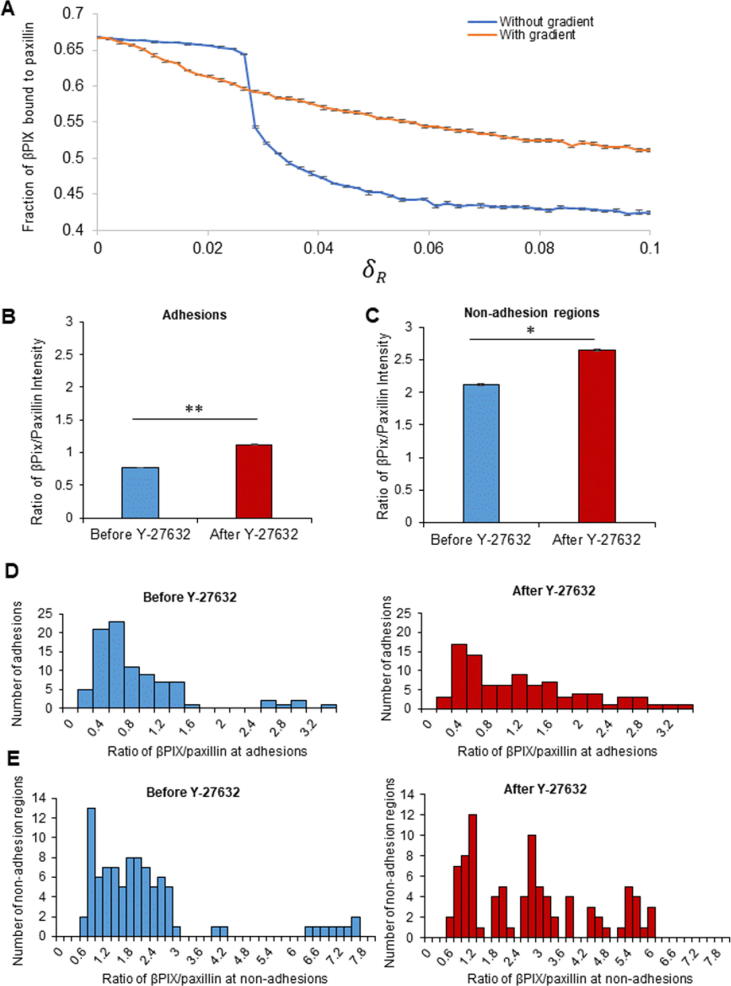
3.6. βPIX binds strongly to paxillin in the cell after ROCK-inhibition
When assessing how the Rac inactivation rate affects the ratio of paxillin-bound βPIX to the total level of βPIX using the spatiotemporal model, our results revealed that decreasing this rate leads to an increase in the ratio of paxillin-bound βPIX-to total βPIX when averaged over 10 simulations (Fig. 10A, blue line). Imposing the gradient defined by Fig. 4 produced similar results, but the increase in the ratio was less steep (Fig. 10A, orange line). Experimentally, Rac inactivation was induced by treatment of CHO-K1 cells with 20 µM of Y-27632. Based on data shown in Fig. 8, this treatment led to a significant increase in the ratio of βPIX to paxillin intensity in both adhesions and non-adhesion regions of the cell (Fig. 10B, 10C). This observation is supported by the shifts in the distribution of the ratio of βPIX/paxillin towards higher values after ROCK-inhibition (Fig. 10D, 10E). An increase in the ratio of the intensity of βPIX to paxillin indicates that, even though there are less paxillin molecules present in the adhesions, the paxillin that is present at adhesions is likely active and bound to βPIX. The fact that the ratio of paxillin/βPIX is also higher in areas outside of adhesions suggests the proteins may be in a complex that is active and ready to bind adhesions once a binding site is available.
Fig. 10.
Inhibition of ROCK leads to increased βPIX localization with paxillin. (A) Fraction of paxillin-bound βPIX to total βPIX levels as a function of Rac inactivation rate (δR), calculated by averaging over 10 simulations, 4000 s each, in the absence (blue) and presence (orange) of the gradient defined in Fig. 4. The ratio of the average intensity of βPIX to paxillin was assessed at (B) adhesions and (C) non-adhesion regions of the cell before and after treatment with 20 µM of Y-27632 for 1 h. n = 89–90 adhesions from at least 12–15 cells. Two stars (**) correspond to P < 0.01, one star (*) corresponds to P < 0.05. The distribution of the ratio of βPIX to paxillin at (D) adhesions and (E) non-adhesion regions before (left, blue panels) and after (right, red panels) treatment with 20 µM Y-27632 for 1 h. Error bars represent the standard errors of the means. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
4. Discussion
The crucial role of Rac/Rho activation and paxillin phosphorylation in inducing cellular polarity has been previously highlighted [57]. A deterministic model, identical to the one described by Eqs. (2), (3), (4), (5), (6), (7), was developed, to show that in the absence of diffusion, the system exhibits bistability consisting of an induced and uninduced state. The induced (uninduced) state represented the steady state of the system with elevated (reduced) active Rac and reduced (elevated) active Rho. In the presence of diffusion over a 1D domain, polarity was formed when a gradient in the initial paxillin concentration or in the maximum paxillin phosphorylation rate was imposed. This generated a phenomenon, called wave-pinning [38], [37], in which the front of the wave remains fixed in time. In this study, we sought to further investigate, experimentally and mathematically, how activated Rac (along with its intermediates) affects the dynamics of this system based on the mechanism proposed in Fig. 1 [57].
The complex interactions Rac has with other proteins, particularly with Rho, within a very stochastic environment that is also subject to cellular heterogeneity, render cell polarization challenging to study. For instance, deterministic mathematical models suggest that asymmetry in Rac and/or Rho activation rates is necessary to induce cellular polarization while global changes in Rac/Rho activation are only likely to influence overall migration speed [38], [57]. However, experimental evidence also suggests that inhibition of ROCK activity at the whole-cell level both increases migration speed and induces polarization in cells which exhibited random movement prior to the ROCK-inhibition [59]. In order to test if this discrepancy in outcomes is due to stochastic, microscopic effects influencing the dynamics of the macroscopic system, as has been reported in other theoretical studies [24], [14], [65], we implemented a stochastic spatiotemporal model in a 2D domain representing the cell. The effects of stochasticity at low molecular copy numbers have been previously investigated in a wave-pinning model, where it was found that, at very low copy numbers, symmetry breaking through constitutively imposing local elevations in activation rates fails to propagate along the domain (i.e. the wave-pinning mechanism fails) [64]. Here, we investigated if, at high copy numbers, stochastically-induced local activation would be able to propagate outwards to produce either transient or long-lived polarization in the absence of symmetry breaking activity gradients. As with [57], this work was done theoretically by studying the relationship between Rac, Rho and paxillin while varying the phosphorylation rate of paxillin. In the absence of activity gradients, stochastic realizations of the model revealed that cells still possessed two steady states in the form of a hysteresis, consisting of the induced and uninduced states. This phenomenon was demonstrated by showing that increasing the maximum paxillin phosphorylation rate caused a right-shifted jump to the induced state when starting from the uninduced state whereas decreasing the maximum phosphorylation rate caused a left-shifted or unapparent jump to the uninduced state when starting from the induced state.
Although a hysteresis, a critical component of the Rac/Rho-driven wave-pinning mechanism that drives cell polarity models [29], was observed both in the presence and absence of chemical cues (such as gradients in the activation rates of Rac and Rho), polarity was only detected in the former. In the absence of polarity, we only observed a global increase in active protein concentrations of the three species investigated. Consistent with previous theoretical investigations, imposing a gradient in the activation of Rac and Rho, which would be more realistically observed in cells, active Rac and Rho produced cellular polarity [64]. The hysteresis observed in both sets of simulations is consistent with the bistable nature of the model used (see Eqs. (2), (3), (4), (5), (6), (7) and (8), (9), (10)) and is consistent with the experimental results obtained in [57] which showed that the distribution of assembly and disassembly rates of adhesions in CHO-K1 cells is bimodal and that the recovery of these cells when treated with an inhibitor of paxillin dephosphorylation rate (called okadaic acid) is partial (i.e. it exhibits a hysteresis). Indeed, a similar type of hysteresis was observed when a PAK inhibitor (called IPA-3) was used, suggesting that bistability is an intrinsic property of Rac/Rho signalling [4], as well as when adhesion dynamics were analyzed at the protein-cluster level [71]. Together with previous deterministic results, the stochastic simulations presented here help to highlight the importance of activation gradients in generating polarity through Rac/Rho signalling pathways by demonstrating that, in a parameter regime estimated from CHO-K1 cells, activation gradients are required to produce polarization.
It is important to point out that, in the stochastic simulations presented in this paper, the jump between the two steady states (Fig. 3B) is less dramatic than that seen in the deterministic system [57]. This difference is due to the fact that, in the deterministic case, the system is either in the induced or uninduced state (but not both), producing a very pronounced jump when crossing the threshold (or fold) of the bistable switch as the value of is increased [57]. In the stochastic case, however, noise causes some lattice squares to be in the induced state while others to be in the uninduced state, blurring the system’s transitions between the two states.
To validate the theoretical results obtained, we further examined polarization in CHO-K1 cells experimentally. We increased RacGTP concentrations in CHO-K1 cells by two means: increasing Rac activation (by overexpressing βPIX, a Rac-GEF) or inhibiting Rac deactivation (inhibiting ROCK signalling). Once the induction of RacGTP was promoted, the cells experienced faster migration speeds, consistent with observations using other cell types [63], [59]. The distance travelled by these cells was also greater, an effect correspondingly seen in previous work on ROCK-inhibition in fibroblasts [59]. Although the fibroblasts studied by Totsukawa et al. [59] exhibited increased directionality in their overall travel, the CHO-K1 cells did not, suggesting that, although some polarity was established, external cues may be necessary to generate the internal protein gradients necessary for persistent directionality in this cell line, as is suggested by the model. The distribution of adhesion-related proteins in cells indicated that decreasing Rho signalling does not alter the amount of βPIX localized to adhesions, when Rac activation is promoted or deactivation is inhibited. These findings suggest that the faster migration rates, characteristic of cells with an amplified level of RacGTP, are not caused by increasing the concentration of the Rac-GEF βPIX but may be due to an increase in the activity of the Rac-GEF and potentially increased binding between active βPIX and paxillin. Future experiments with βPIX biosensors will need to be conducted to verify if βPIX activity is increased. Consistent with other published work and with increased Rac activity, we found that ROCK-inhibition decreased the average size of the adhesions [59], [60].
Although our model shown in Fig. 1 assumed active Rac and Rho inhibit each other’s GEFs, causing mutual inhibition, Byrne et al. [4] created a model in which Rac inhibits RhoGEF but Rho deactivates Rac by increasing the activity of Rac-GAP. Experimentally, this group inhibited PAK, a RhoGAP activated by Rac, activity using IPA-3 [4]. Interestingly, bistability and a hysteresis were also seen in Rac activation and Rho activation with the altered RhoGAP concentration. Both our model and the Bynre et al. [4] model emphasize that the starting condition of a cell determines how it responds to changes in the environment as there are two possible stable steady states that can be attained for a given cellular condition. Interestingly, our numerical simulations have shown that replacing Rac-GEF inhibition through Rho by Rac-GAP activation in our model, as was the case in Byrne et al. [4], produced bistability with a very small hysteresis range despite performing extensive parameter exploration using Latin Hypercube Sampling [33] (results not shown). This finding suggests that Rac-GEF inhibition through Rho could be the dominant pathway for Rac-inhibition and is more likely to be the process used in the cell to robustly produce bistable Rho/Rac signalling.
Previous studies have reported that Rac inactivation in biological systems can depend on a signalling pathway involving the activation of Rac-GAPs [52], [36]. ARHGAP22 is a Rac-specific GAP that has been shown to be a downstream effector of ROCK signalling, indicating another means of cross-talk and antagonism between Rho/Rac signalling [52]. Although ARHGAP22 has been shown to be localized at endosomes, is involved in regulating actin dynamics and can influence cell motility and morphology, its role in paxillin and adhesion signalling is not well-characterized [52], [36]. The mechanism by which an increased RhoGTP concentration leads to a decreased RacGTP concentration, whether it be through inhibition of Rac-GEFs, activation of Rac-GAPs or both, is not entirely known, but it is evident that it is a complex relationship with many factors to consider. ARHGAP22 is an interesting avenue to consider for further testing, since, unlike ROCK, it acts to decrease RacGTP levels in the cell without known involvement with RacGEF pathways. Continued experimental and mathematical modelling studies will be required to continue to unravel and understand the interplay between these processes.
These simulation and experimental results taken together indicate the importance of Rac gradients in generating cellular polarity and subsequent motility. Without protein activation gradients in the simulations, whole-cell protein levels could be varied by changes in parameters, but polarity was not observed. Similarly, increasing levels of RacGTP in the cell in a non-spatially constrained manner using ROCK-inhibition caused cells to migrate faster, but persistent polarity leading to increased directionality in the migration was not observed. Through mutual inhibition, Rho/Rac signalling aids in producing cell migration by creating spatially-segregated protrusive cell edges and retractive tails. The fact that a hysteresis and bistability are still observed without imposed gradients in these two proteins highlights the mutual inhibition between Rac and Rho that allows for two steady states. While it remains unclear how ROCK-inhibition might produce the increase in directionality observed by [59] in fibroblast cells, we have shown that neither ROCK-inhibition nor βPIX activation were capable of producing sustained polarity in CHO-K1 cells. Therefore, it is not surprising that we were not able to observe polarity through global changes in reaction rates because the model presented here was parameterized primarily from CHO-K1 cell data. Based on some preliminary results, the exploration of alternative parameter regimes (e.g., protein copy number) in which stochasticity may play a more significant role is a promising future avenue. Observation of cell migration on patterned substrates where cells have to turn slightly or fully turn around will also help us gain insight into the molecular mechanisms at play.
With the model and its parameter values, we designed a quantitative method for determining how biochemical perturbations to cells lead to localized Rac activation based on our previous experimental findings [57]. Furthermore, the experimental findings presented here quantified some of the downstream effects on cell directionality and velocity, as well as adhesion-related protein localization and adhesion size. It would be interesting to use this combination of modelling and experimentation to generate a biochemically-relevant, virtual cell and further investigate the intracellular processes and protein relationships through a top-down approach. Through this approach, measurements of cellular motility (e.g., protrusion rates, velocity) will inform how the molecular processes occurring at the subcellular level are regulating motility.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
This work was supported by the Fonds Nature et technologies—Gouvernement du Québec (http://www.frqnt.gouv.qc.ca/en/accueil) team grant to AK and CMB, and the Natural Sciences and Engineering Council of Canada (http://www.nserc-crsng.gc.ca/index_eng.asp) discovery grants to AK and CMB. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. Imaging and image analysis were conducted in the Advanced BioImaging Facility (ABIF).
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.csbj.2019.10.002.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
Transmitted light microscopy video of the migration of CHO-K1 cells expressing paxillin-EGFP before 10 µM Y-27632. Cells were imaged every 2 minutes for 3 h prior to the addition of the inhibitor. Scale bar is 50 µm.
Transmitted light microscopy video of the migration of CHO-K1 cells expressing paxillin-EGFP after treatment with 10 µM Y-27632. Cells were imaged every 2 min for 3 h after 1-h treatment with the inhibitor. Scale bar is 50 µm.
References
- 1.Bachman H., Nicosia J., Dysart M., Barker T.H. Utilizing fibronectin integrin-binding specificity to control cellular responses. Adv Wound Care. 2015;4(8):501–511. doi: 10.1089/wound.2014.0621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bement William M, Leda Marcin, Moe Alison M, Kita Angela M, Larson Matthew E, Golding Adriana E. Activator-inhibitor coupling between Rho signalling and actin assembly makes the cell cortex an excitable medium. Nat Cell Biol. 2015;17(11):1471–1483. doi: 10.1038/ncb3251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bokoch Gary M. Biology of the p21-activated kinases. Annu Rev Biochem. 2003;72:743–781. doi: 10.1146/annurev.biochem.72.121801.161742. [DOI] [PubMed] [Google Scholar]
- 4.Byrne K.M., Monsefi N., Dawson J.C., Degasperi A., Bukowski-Wills J.C., Volinsky N. Bistability in the Rac1, PAK, and RhoA signaling network drives actin cytoskeleton dynamics and cell motility switches. Cell Syst. 2016;2(1):38–48. doi: 10.1016/j.cels.2016.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chiu Chi-Li, Aguilar Jose S., Tsai Connie Y., GuiKai Wu., Gratton Enrico, Digman Michelle A. Nanoimaging of focal adhesion dynamics in 3D. PLoS ONE. 2014;9(6) doi: 10.1371/journal.pone.0099896. e99896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chung Chang K., Lee Susan, Briscoe Celia, Ellsworth Charlene, Firtel Richard A. Role of Rac in controlling the actin cytoskeleton and chemotaxis in motile cells. Proc Natl Acad Sci USA. 2000;97(10):5225–5230. doi: 10.1073/pnas.97.10.5225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cirit M., Krajcovic M., Choi C.K., Welf E.S., Horwitz A.F., Haugh J.M. Stochastic model of integrin-mediated signaling and adhesion dynamics at the leading edges of migrating cells. PLoS Comput Biol. 2010;6(2) doi: 10.1371/journal.pcbi.1000688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Das Sulagna, Yin Taofei, Yang Qingfen, Zhang Jingqiao, Wu Yi I., Ji Yu. Single-molecule tracking of small GTPase Rac1 uncovers spatial regulation of membrane translocation and mechanism for polarized signaling. Proc Natl Acad Sci USA. 2015;112(3):E267–E276. doi: 10.1073/pnas.1409667112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Deakin N.O., Turner C.E. Paxillin comes of age. J Cell Sci. 2008;121(Pt 15):2435–2444. doi: 10.1242/jcs.018044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Digman Michelle A., Brown Claire M., Horwitz Alan R., Mantulin William W., Gratton Enrico. Paxillin dynamics measured during adhesion assembly and disassembly by correlation spectroscopy. Biophys J. 2008;94(7):2819–2831. doi: 10.1529/biophysj.107.104984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Du X.P., Plow E.F., Frelinger A.L., 3rd, O'Toole T.E., Loftus J.C., Ginsberg M.H. Ligands “activate” integrin alpha IIb beta 3 (platelet GPIIb-IIIa) Cell. 1991;65(3):409–416. doi: 10.1016/0092-8674(91)90458-b. [DOI] [PubMed] [Google Scholar]
- 12.Edelstein-Keshet L., Holmes W.R., Zajac M., Dutot M. From simple to detailed models for cell polarization. Philos Trans R Soc London Ser B, Biol Sci. 2013;368(1629) doi: 10.1098/rstb.2013.0003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.El-Sibai M., Pertz O., Pang H., Yip S.C., Lorenz M., Symons M. RhoA/ROCK-mediated switching between Cdc42- and Rac1-dependent protrusion in MTLn3 carcinoma cells. Exp Cell Res. 2008;314(7):1540–1552. doi: 10.1016/j.yexcr.2008.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Erban, Radek, Jonathan Chapman, Philip Maini, 2007. A practical guide to stochastic simulations of reaction-diffusion processes.
- 15.Franz C.M., Jones G.E., Ridley A.J. Cell migration in development and disease. Dev Cell. 2002;2(2):153–158. doi: 10.1016/s1534-5807(02)00120-x. [DOI] [PubMed] [Google Scholar]
- 16.Gardel M.L., Schneider I.C., Aratyn-Schaus Y., Waterman C.M. Mechanical integration of actin and adhesion dynamics in cell migration. Annu Rev Cell Dev Biol. 2010;26:315–333. doi: 10.1146/annurev.cellbio.011209.122036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ghosh Atiyo, Leier Andre, Marquez-Lago Tatiana T. The spatial chemical langevin equation and reaction diffusion master equations: moments and qualitative solutions. Theor Biol Med Modell. 2015;12:(5). doi: 10.1186/s12976-015-0001-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gillespie Daniel T. A rigourous derivation of the chemical master equation. Phys A. 1992;188(1–3):404–425. [Google Scholar]
- 19.Gillespie Daniel T. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81(25):2340–2361. [Google Scholar]
- 20.Gorelik Roman, Gautreau Alexis. Quantitative and unbiased analysis of directional persistence in cell migration. Nat Protoc. 2014;9(8):1931–1943. doi: 10.1038/nprot.2014.131. [DOI] [PubMed] [Google Scholar]
- 21.Graessl Melanie, Koch Johannes, Calderon Abram, Kamps Dominic, Banerjee Soumya, Mazel Tomáš. An excitable Rho GTPase signaling network generates dynamic subcellular contraction patterns. J Cell Biol. 2017;216(12):4271–4285. doi: 10.1083/jcb.201706052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Guilluy Christophe, Garcia-Mata Rafael, Burridge Keith. Rho protein crosstalk: another social network? Trends Cell Biol. 2011;21(12):718–726. doi: 10.1016/j.tcb.2011.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hanna S., El-Sibai M. Signaling networks of Rho GTPases in cell motility. Cell Signal. 2013;25(10):1955–1961. doi: 10.1016/j.cellsig.2013.04.009. [DOI] [PubMed] [Google Scholar]
- 24.Hempel H., Schimansky-Geier Lutz, García-Ojalvo Jordi. Noise-sustained pulsating patterns and global oscillations in subexcitable media. Phys Rev Lett. 1999;82(18):3713–3716. [Google Scholar]
- 25.Holmes William R., Edelstein-Keshet Leah. Analysis of a minimal Rho-GTPase circuit regulating cell shape. Phys Biol. 2016;13:(4). doi: 10.1088/1478-3975/13/4/046001. [DOI] [PubMed] [Google Scholar]
- 26.Holmes William R., Park JinSeok, Levchenko Andre, Edelstein-Keshet Leah. A mathematical model coupling polarity signaling to cell adhesion explains diverse cell migration patterns. PLoS Comput Biol. 2017;13(5) doi: 10.1371/journal.pcbi.1005524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Holmes W.R., Lin B., Levchenko A., Edelstein-Keshet L. Modelling cell polarization driven by synthetic spatially graded Rac activation. PLoS Comput Biol. 2012;8(6) doi: 10.1371/journal.pcbi.1002366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Holmes W.R., Mata M.A., Edelstein-Keshet L. Local perturbation analysis: a computational tool for biophysical reaction-diffusion models. Biophys J. 2015;108(2):230–236. doi: 10.1016/j.bpj.2014.11.3457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jilkine A., Marée A.F., Edelstein-Keshet L. Mathematical model for spatial segregation of the Rho-family GTPases based on inhibitory crosstalk. Bull Math Biol. 2007;69(6):1943–1978. doi: 10.1007/s11538-007-9200-6. [DOI] [PubMed] [Google Scholar]
- 30.López-Colomé A.M., Lee-Rivera I., Benavides-Hidalgo R., López E. Paxillin: a crossroad in pathological cell migration. J Hematol Oncol. 2017;10(1):50. doi: 10.1186/s13045-017-0418-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Manser E., Loo T.H., Koh C.G., Zhao Z.S., Chen X.Q., Tan L., Tan I., Leung T., Lim L. PAK kinases are directly coupled to the PIX family of nucleotide exchange factors. Mol Cell. 1998;1(2):183–192. doi: 10.1016/s1097-2765(00)80019-2. [DOI] [PubMed] [Google Scholar]
- 32.Marée Athanasius F.M., Jilkine Alexandra, Dawes Adriana, Grieneisen Verônica A., Edelstein-Keshet Leah. Polarization and movement of keratocytes: a multiscale modelling approach. Bull Math Biol. 2006;68(5):1169–1211. doi: 10.1007/s11538-006-9131-7. [DOI] [PubMed] [Google Scholar]
- 33.Marino S., Hogue I.B., Ray C.J., Kirschner D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol. 2008;254(1):178–196. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Michaelson David, Silletti Joseph, Murphy Gretchen, D'Eustachio Peter, Rush Mark, Philips Mark R. Differential localization of Rho GtPases in live cells. J Cell Biol. 2001;152(1):111. doi: 10.1083/jcb.152.1.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Michaux Jonathan B, Robin François B, McFadden William M, Munro Edwin M. Excitable RhoA dynamics drive pulsed contractions in the early C. elegans embryo. J Cell Biol. 2018;217(12):4230–4252. doi: 10.1083/jcb.201806161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mori M., Saito K., Ohta Y. ARHGAP22 localizes at endosomes and regulates actin cytoskeleton. PLoS ONE. 2014;9:(6). doi: 10.1371/journal.pone.0100271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mori Y., Jilkine A., Edelstein-Keshet L. Asymptotic and bifurcation analysis of wave-pinning in a reaction-diffusion model for cell polarization. SIAM J Appl Math. 2011;71(4):1401–1427. doi: 10.1137/10079118X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mori Y., Jilkine A., Edelstein-Keshet L. Wave-pinning and cell polarity from a bistable reaction-diffusion system. Biophys J. 2008;94(9):3684–3697. doi: 10.1529/biophysj.107.120824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Morishita Yuji, Tsutsumi Koji, Ohta Yasutaka. Phosphorylation of serine 402 regulates RacGAP protein activity of FilGAP protein. J Biol Chem. 2015;290(43):26328–26338. doi: 10.1074/jbc.M115.666875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nayal A., Webb D.J., Brown C.M., Schaefer E.M., Vicente-Manzanares M., Horwitz A.R. Paxillin phosphorylation at Ser273 localizes a GIT1–PIX–PAK complex and regulates adhesion and protrusion dynamics. J Cell Biol. 2006;173(4):587–589. doi: 10.1083/jcb.200509075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nobes C.D., Hall A. Rho, Rac, and Cdc42 GTPases regulate the assembly of multimolecular focal complexes associated with actin stress fibers, lamellipodia, and filopodia. Cell. 1995;81(1):53–62. doi: 10.1016/0092-8674(95)90370-4. [DOI] [PubMed] [Google Scholar]
- 42.Obermeier A., Ahmed S., Manser E., Yen S.C., Hall C., Lim L. PAK promotes morphological changes by acting upstream of Rac. EMBO J. 1998;17(15):4328–4339. doi: 10.1093/emboj/17.15.4328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Park JinSeok, Holmes William R., Lee Sung Hoon, Kim Hong-Nam, Kim Deok-Ho, Kwak Moon Kyu. Mechanochemical feedback underlies coexistence of qualitatively distinct cell polarity patterns within diverse cell populations. Proc Natl Acad Sci USA. 2017;114(28):E5750–E5759. doi: 10.1073/pnas.1700054114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rajah Abira, Boudreau Colton G, Ilie Alina, Wee Tse-Luen, Tang Kaixi, Borisov Aleksandar Z. Paxillin S273 phosphorylation regulates adhesion dynamics and cell migration through a common protein complex with PAK1 and βPIX. Sci Rep. 2019;9(1):11430. doi: 10.1038/s41598-019-47722-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Reid Tim, Furuyashiki Tomoyuki, Ishizaki Toshimasa, Watanabe Go, Watanabe Naoki, Fujisawa Kazuko. Rhotekin, a new putative target for rho bearing homology to a serine/threonine kinase, PKN, and rhophilin in the rho-binding domain. J Biol Chem. 1996;271(23):13556–13560. doi: 10.1074/jbc.271.23.13556. [DOI] [PubMed] [Google Scholar]
- 46.Ren Xiang-Dong, Schwartz Martin Alexander. Determination of GTP loading on Rho. Methods Enzymol. 2000;325:264–272. doi: 10.1016/s0076-6879(00)25448-7. [DOI] [PubMed] [Google Scholar]
- 47.Ridley A.J., Schwartz M.A., Burridge K., Firtel R.A., Ginsberg M.H., Borisy G. Cell migration: integrating signals from front to back. Science. 2003;302(5651):1704–1709. doi: 10.1126/science.1092053. [DOI] [PubMed] [Google Scholar]
- 48.Ridley A.J. Rho GTPase signalling in cell migration. Curr Opin Cell Biol. 2015;36:103–112. doi: 10.1016/j.ceb.2015.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ridley Anne J. Rho GTPases and cell migration. J Cell Sci. 2001;114(15):2713–2722. doi: 10.1242/jcs.114.15.2713. [DOI] [PubMed] [Google Scholar]
- 50.Riento Kirsi, Ridley Anne J. ROCKs: multifunctional kinases in cell behaviour. Nat Rev Mol Cell Biol. 2003;4(6):446–456. doi: 10.1038/nrm1128. [DOI] [PubMed] [Google Scholar]
- 51.Sander Eva E., ten Klooster Jean P., van Delft Sanne, van der Kammen Rob A., Collarda John G. Rac downregulates rho activity: reciprocal balance between both GTPases determines cellular morphology and migratory behavior. J Cell Biol. 1999;147(5):1009–1022. doi: 10.1083/jcb.147.5.1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sanz-Moreno V., Gadea G., Ahn J., Paterson H., Marra P., Pinner S. Rac activation and inactivation control plasticity of tumor cell movement. Cell. 2008;135(3):510–523. doi: 10.1016/j.cell.2008.09.043. [DOI] [PubMed] [Google Scholar]
- 53.Schlenker Oliver, Rittinger Katrin. Structures of dimeric GIT1 and trimeric β-PIX and implications for GIT–PIX complex assembly. J Mol Biol. 2009;386(2):280–289. doi: 10.1016/j.jmb.2008.12.050. [DOI] [PubMed] [Google Scholar]
- 54.Schwanhäusser Björn, Busse Dorothea, Li Na., Dittmar Gunnar, Schuchhardt Johannes, Wolf Jana. Global quantification of mammalian gene expression control. Nature. 2011;473:337–342. doi: 10.1038/nature10098. [DOI] [PubMed] [Google Scholar]
- 55.Sells M.A., Knaus U.G., Bagrodia S., Ambrose D.M., Bokoch G.M., Chernoff J. Human p21-activated kinase (Pak1) regulates actin organization in mammalian cells. Curr Biol. 1997;7(3):202–210. doi: 10.1016/s0960-9822(97)70091-5. [DOI] [PubMed] [Google Scholar]
- 56.Slack Barbara E. Tyrosine phosphorylation of paxillin and focal adhesion kinase by activation of muscarinic m3 receptors is dependent on integrin engagement by the extracellular matrix. PNAS. 1998;95(13):7281–7286. doi: 10.1073/pnas.95.13.7281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Tang K., Boudreau C.G., Brown C.M., Khadra A. Paxillin phosphorylation at serine 273 and its effects on Rac, Rho and adhesion dynamics. PLoS Comput Biol. 2018;14:(7). doi: 10.1371/journal.pcbi.1006303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Thompson Gladstone, Owen Darerca, Chalk Peter A., Lowe Peter N. Delineation of the Cdc42/Rac-binding domain of p21-activated kinase. Biochemistry. 1998;37(21):7885–7891. doi: 10.1021/bi980140+. [DOI] [PubMed] [Google Scholar]
- 59.Totsukawa G., Wu Y., Sasaki Y., Hartshorne D.J., Yamakita Y., Yamashiro S. Distinct roles of MLCK and ROCK in the regulation of membrane protrusions and focal adhesion dynamics during cell migration of fibroblasts. J Cell Biol. 2004;164(3):427–439. doi: 10.1083/jcb.200306172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Tsuji T., Ishizaki T., Okamoto M., Higashida C., Kimura K., Furuyashiki T. ROCK and mDia1 antagonize in Rho-dependent Rac activation in Swiss 3T3 fibroblasts. J Cell Biol. 2002;157(5):819–830. doi: 10.1083/jcb.200112107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Turner Christopher E., John R., Jr., Glermey Keith Burridge. Paxillin: a new vinculin-binding protein present in focal adhesions. J Cell Biol. 1990;111(3):1059–1068. doi: 10.1083/jcb.111.3.1059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Vicente-Manzanares M., Webb D.J., Horwitz A.R. Cell migration at a glance. J Cell Sci. 2005;118(Pt 21):4917–4919. doi: 10.1242/jcs.02662. [DOI] [PubMed] [Google Scholar]
- 63.Walsh A.B., Bar-Sagi D. Differential activation of the Rac pathway by Ha-Ras and K-Ras. J Biol Chem. 2001;276(19):15609–15615. doi: 10.1074/jbc.M010573200. [DOI] [PubMed] [Google Scholar]
- 64.Walther Georg R, Marée Athanasius F.M, Edelstein-Keshet Leah, Grieneisen Verônica A. Deterministic versus stochastic cell polarisation through wave-pinning. Bull Math Biol. 2012;74(11):2570–2599. doi: 10.1007/s11538-012-9766-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Wang Hongli, Zhengping Fu, Xinhang Xu, Ouyang Qi. Pattern formation induced by internal microscopic fluctuations. J Phys Chem. 2007;111(7):1265–1270. doi: 10.1021/jp0674064. [DOI] [PubMed] [Google Scholar]
- 66.Warner H., Wilson B.J., Caswell P.T. Control of adhesion and protrusion in cell migration by Rho GTPases. Curr Opin Cell Biol. 2019;56:64–70. doi: 10.1016/j.ceb.2018.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Worthylake R.A., Lemoine S., Watson J.M., Burridge K. RhoA is required for monocyte tail retraction during transendothelial migration. J Cell Biol. 2001;154(1):147–160. doi: 10.1083/jcb.200103048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Yamao Masataka, Honda Naoki, Kunida Katsuyuki, Aoki Kazuhiro, Michiyuki Matsuda, Ishii Shin. Distinct predictive performance of Rac1 and Cdc42 in cell migration. Sci Rep. 2015;5:(1). doi: 10.1038/srep17527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Yang Hee W, Collins Sean, Meyer Tobias. Locally excitable Cdc42 signals steer cells during chemotaxis. Nat Cell Biol. 2016;18(2):191–201. doi: 10.1038/ncb3292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Zamir E., Geiger B. Molecular complexity and dynamics of cell-matrix adhesions. J Cell Sci. 2001;114(Pt 20):3583–3590. doi: 10.1242/jcs.114.20.3583. [DOI] [PubMed] [Google Scholar]
- 71.MacKay L, Khadra A. Dynamics of Mechanosensitive Nascent Adhesion Formation. Biophysical Journal. 2019;117(6):1057–1073. doi: 10.1016/j.bpj.2019.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Tan Z, L, Momi A, MacKay L, Khadra A. Data from: rac activation is key to cell motility and directionality: an experimental and modelling investigation. Anmar Khadra Repository. 2019 doi: 10.1016/j.csbj.2019.10.002. http://www.medicine.mcgill.ca/physio/khadralab/code_CSBJ1.html. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Transmitted light microscopy video of the migration of CHO-K1 cells expressing paxillin-EGFP before 10 µM Y-27632. Cells were imaged every 2 minutes for 3 h prior to the addition of the inhibitor. Scale bar is 50 µm.
Transmitted light microscopy video of the migration of CHO-K1 cells expressing paxillin-EGFP after treatment with 10 µM Y-27632. Cells were imaged every 2 min for 3 h after 1-h treatment with the inhibitor. Scale bar is 50 µm.