Coevolutive, evolutive and stochastic information in protein-protein interactions

Graphical abstract

Abstract

Here, we investigate the contributions of coevolutive, evolutive and stochastic information in determining protein-protein interactions (PPIs) based on primary sequences of two interacting protein families A and B. Specifically, under the assumption that coevolutive information is imprinted on the interacting amino acids of two proteins in contrast to other (evolutive and stochastic) sources spread over their sequences, we dissect those contributions in terms of compensatory mutations at physically-coupled and uncoupled amino acids of A and B. We find that physically-coupled amino-acids at short range distances store the largest per-contact mutual information content, with a significant fraction of that content resulting from coevolutive sources alone. The information stored in coupled amino acids is shown further to discriminate multi-sequence alignments (MSAs) with the largest expectation fraction of PPI matches – a conclusion that holds against various definitions of intermolecular contacts and binding modes. When compared to the informational content resulting from evolution at long-range interactions, the mutual information in physically-coupled amino-acids is the strongest signal to distinguish PPIs derived from cospeciation and likely, the unique indication in case of molecular coevolution in independent genomes as the evolutive information must vanish for uncorrelated proteins.

1. Introduction

While being selected to be thermodynamically stable and kinetically accessible in a particular fold [1], [2], interacting proteins A and B coevolve to maintain their bound free-energy stability against a vast repertoire of non-specific partners and interaction modes. Protein coevolution, in the form of a time-dependent molecular process, then translates itself into a series of primary-sequence variants of A and B encoding coordinated compensatory mutations [3] and, therefore, specific protein-protein interactions (PPIs) derived from this stability-driven process [4]. As a ubiquitous process in molecular biology, coevolution thus apply to protein interologs, either paralogous or orthologous, under cospeciation or in independent genomes.

Thanks to extensive investigations in the past following ingenious approaches based on the correlation of phylogenetic trees [5], [6], [7] and profiles [8], gene colocalization [9] and fusions [10], maximum coevolutionary interdependencies [11] and correlated mutations [12], [13], the problem of predicting PPIs based on multi-sequence alignments (MSAs) appears to date resolvable, at least for small sets of paralogous sequences – recent improvements [14], [15], [16], [17], [18] resulting from PPI prediction allied to modern coevolutionary approaches [19], [20], [21], [22], [23] to identify interacting amino acids across protein interfaces. In these previous studies, however, the information was taken into account as a whole, and it was not clarified, as discussed in recent reviews [4], [24], the isolated contributions of coevolutive, evolutive and stochastic information in resolving the problem. Differentiating functional coevolution from stochastic and phylogenetic sources remains looked for in the research field and may help introducing models capable of accurately detecting protein-protein interactions and interfaces, especially when the number of sequences or the amount of biological information are limited [25].

Here, by benefiting from much larger data sets made available in the sequence- and structure-rich era, we revisit the field by quantifying the amount of information that protein A stores about protein B stemming from each of these sources and, more importantly, their effective contributions in discriminating PPIs based on MSAs (Scheme 1). Specifically, under the assumption that the coevolutive information is imprinted on the interacting amino acids of protein interologs in contrast to other (evolutive and stochastic) sources spread over their sequences, we want the information to be dissected in terms of compensatory mutations at physically-coupled and uncoupled amino acids of A and B. Given a known set of protein three-dimensional amino-acid contacts and their underlying primary sequences we seek therefore differentiating functional coevolution from stochastic and phylogenetic signals for subsequent evaluation of their contributions in PPI recognition from primary sequences. It is worth emphasizing our study is not aimed at providing a method for prediction of protein-protein interactions nor protein-protein interfaces, hence it differs from previous studies in which sequence covariance is used to predict three-dimensional amino-acid contacts across interfaces and assemble models of protein complexes [26] or protein docking [27]. Anticipating our findings, we show that physically-coupled amino-acids store the largest per-contact mutual information (MI) content to discriminate concatenated MSAs with the largest expectation fraction of PPI matches – a conclusion that holds against various definitions of intermolecular protein contacts and binding modes, including native and non-native decoy structures. A significant fraction of that information results from coevolutive sources alone. Although, our analysis involved protein interologs under cospeciation that is, proteins evolving in the same genome, the derived conclusions are likely general to cases of non-cospeciating interologs given that the underlying thermodynamical principles must be the same for all cases.

Scheme 1.

Structural contacts mapped into M-long multi-sequence alignment (MSA) of protein interologs A and B. A set of pairwise protein-protein interactions is defined by associating each sequence l in MSA B to a sequence k in MSA A in one unique arrangement, {l(k)|z}_M, determined by the coevolution process z to which these protein families were subjected. Shown is a “scrambled” concatenated MSA of A and B associated to a given process z (red dashes). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2. Theory and methods

2.1. Decomposition of mutual information

In detail, consider two proteins A and B that interact via formation of i = 1,…,N amino-acid contacts at the molecular level. Proteins A and B are assumed to coevolve throughout M! distinct processes z described by the stochastic variable Z with an uniform probability mass function ρ(z), ∀z ∈ {1,…,M!}. Given any specific process z, their interacting amino-acid sequences are respectively described by two N-length blocks of discrete stochastic variables X^N ≡ (X₁,…,X_N) and Y^N ≡ (Y₁,…,Y_N) with probability mass functions {ρ(x^N),ρ(y^N),ρ(x^N,y^N|z)} such that,

$$\left\{\begin{array}{c}\rho \left(x^N\right)=\sum _{y^N}\rho \left(x^N,y^N|z\right)\hfill \\ \rho \left(y^N\right)=\sum _{x^N}\rho \left(x^N,y^N|z\right)\hfill \end{array}\right)$$ (1)

and

$$\sum _{x^N,y^N}\rho \left(x^N,y^N|z\right)=1$$ (2)

for every joint sequence ${\left\{x^N,y^N\right\}}_{{\left|x\right|}^{2N}}$ defined in the alphabet χ of size |χ|. Under these considerations, the amount of information that protein A stores about protein B is given by the mutual information I(X^N; Y^N|z) between X^N and Y^N conditional to process z [28]. As made explicit in Eq. (1), we are particularly interested in quantifying I(X^N; Y^N|z) for the situation in which marginals of the N-block variables {ρ(x^N), ρ(y^N)} are assumed to be independent of process z meaning that, for a fixed sequence composition of proteins A and B only their joint distribution depends on the process. Furthermore, by assuming N-independent contacts, we want that information to be quantified for the least-constrained model ρ*(x^N, y^N|z) that maximizes the conditional joint entropy between A and B – that condition ensures the mutual information to be written exactly, in terms of the individual contributions of contacts i.

For the least-constrained distribution {ρ*(x^N, y^N|z)}, the conditional mutual information

$$I\left(X^N;Y^N|z\right)=H\left(X^N\right)+H\left(Y^N\right)-H\left(X^N,Y^N|z\right)$$ (3)

writes in terms of the Shannon’s information entropies

$$\left\{\begin{array}{c}H\left(X^N\right)=\sum _{x^N}{\rho }^{\ast }\left(x^N\right)1n{\rho }^{\ast }\left(x^N\right)\hfill \\ H\left(Y^N\right)=-\sum _{y^N}{\rho }^{\ast }\left(y^N\right)1n{\rho }^{\ast }\left(y^N\right)\hfill \\ H\left(X^N,Y^N|z\right)=-\sum _{x^N,y^N}{\rho }^{\ast }\left(x^N,y^N|z\right)1n{\rho }^{\ast }\left(x^N,y^N|z\right)\end{array}\right)$$ (4)

associated with the conditional joint distribution {ρ*(x^N, y^N|z)} and the derived marginals {ρ*(x^N), ρ*(y^N)} of the N-block variables. From its entropy-maximization property, the critical distribution {ρ*(x^N, y^N|z)} factorizes into the conditional two-site marginal of every contact i

$${\rho }^{\ast }\left(x^N,y^N|z\right)=\prod _{i=1}^N{\rho }^{\ast }\left(x_i,y_i|z\right)$$ (5)

then allowing Eq. (4) to be written extensively, in terms of the individual entropic contributions

$$\left\{\begin{array}{c}H\left(X^N\right)=\sum _{i}H\left(X_i|z\right)\hfill \\ H\left(Y^N\right)=\sum _{i}H\left(Y_i|z\right)\hfill \\ H\left(X^N,Y^N|z\right)=\sum _{i}H\left(X_i,Y_i|z\right)\end{array}\right)$$ (6)

such that,

$$I\left(X^N;Y^N|z\right)=\sum _{i=1}^{N}I\left(X_i;Y_i|z\right)$$ (7)

(cf. SI for details). In Eq. (7), the conditional mutual information achieves its lower bound of zero if X^N and Y^N are conditionally independent given z i.e., ρ*(x^N, y^N |z) = ρ*(x^N) × ρ*(y^N). For the case of perfectly correlated variables ρ*(x^N, y^N |z) = ρ*(x^N) = ρ*(y^N), the conditional mutual information is bound to a maximum which cannot exceed the entropy of either block variables H(X^N) and H(Y^N).

Given a known set of protein amino-acid contacts and their underlying primary sequence distributions defining the stochastic variables X^N and Y^N, Eq. (7) thus establishes the formal dependence of their mutual information with any given process z. Because “contacts” can be defined for a variety of cutoff distances r_c, Eq. (7) is particularly useful to dissect mutual information in terms of physically-coupled and uncoupled protein amino acids. In the following, we explore Eq. (7) in that purpose by obtaining the two-site probabilities in Eq. (5)

$${\rho }^{\ast }\left(x_i,y_i|z\right)=\sum _{x_1^{\text{'}},...,x_N^{\text{'}},y_1^{\text{'}},...,y_N^{\text{'}}}{\delta }_{x_i^{\text{'}}{y}_i^{\text{'}}{x}_i{y}_i}{\rho }^{\ast }\left(x_1^{\text{'}},...,x_N^{\text{'}},y_1^{\text{'}},...,y_N^{\text{'}}|z\right)\equiv f_{x_i{y}_i|z}$$ (8)

from the observed frequencies $\mathbf{f}=\left\{{\text{f}}_{x_i,y_i|z}\right\}$ in the multiple-sequence alignment

$${\left\{x_k^N,y_l^N|z\right\}}_M$$

where the N-length amino-acid block l of protein B is joint to block k of protein A in one unique arrangement {l(k)|z}_M for 1 ≤ k ≤ M (cf. Scheme 1 and Computational Methods).

2.2. Computational methods

Table 1 details the interacting protein systems considered in the study. For each system under investigation, amino-acid contacts defining the discrete stochastic variables X^N and Y^N including physically coupled amino acids at short-range cut-off distances (r_c ≤ 8.0 Å) and physically uncoupled amino-acids at long-range cut-off distances (r_c > 8.0 Å) were identified from the x-ray crystal structure of the bound state of proteins A and B. The reference (native) multi-sequence alignment {x^N_k, y^N_l|z*}_M of the joint amino-acid blocks associated to X^N and Y^N was reconstructed from annotated primary-sequence alignments published by Baker and coworkers [22], containing M paired sequences with known protein-protein interactions and defined in the alphabet of 20 amino acids plus the gap symbol (|χ|=21). “Scrambled” MSA models were generated by randomizing the pattern {l(k)|z*}_M in which block l is joint to block k in the reference alignment.

Table 1.

Protein system A and B considered in the study.

	Complex description	PDB ID	Protein A	Protein B	M	MSA length
Obligate Dimers	Carbamoyl Phosphate Synthetase	1BXR	Chain A: Carbamoyl-Phosphate Synthetase large subunit	Chain B: Carbamoyl-Phosphate Synthetase small subunit	1004	1452
	Lactococcus Lactis Dihydroorotate Dehydrogenase B.	1EP3	Chain A: Dihydroorotate Dehydrogenase B (PYRD Subunit)	Chain B: Dihydroorotate Dehydrogenase B (pyrk Subunit)	552	572
	Polysulfide reductase native structure	2VPZ	Chain A: Thiosulfate Reductase	Chain B: NRFC Protein	676	927
	heterohexameric TusBCD proteins	2D1P	Chain B: Hypothetical UPF0116 protein yheM	Chain C: Hypothetical protein yheL	216	214
	3-oxoadipate coA-transferase	3RRL	Chain A: Succinyl-CoA:3-ketoacid-coenzyme A transferase subunit A	Chain B: Succinyl-CoA:3-ketoacid-coenzyme A transferase subunit B	1330	437
	Bovine heart cytochrome c oxidase	2Y69	Chain A: Cytochrome C Oxidase Subunit 1	Chain B: Cytochrome C Oxidase Subunit 2	1484	740
Non-Obligate Dimer	Toxin-antitoxin complex RelBE2 from Mycobacterium tuberculosis	3G5O	ChainA: Protein Rv2865	ChainB: Protein Rv2866	904	173

For any given MSA model, two-site probabilities ${\rho }^{\ast }\left(x_i,y_i|z\right)\equiv f_{x_i,y_i|z}$ were defined from the observable frequencies $f_{x_i,y_i|z}$ regularized by a pseudocount effective fraction λ* in case of insufficient data availability as devised by Morcos and coauthors [19]. More specifically, two-site frequencies were calculated according to

$$f_{x_i{y}_i|z}=\frac{{\lambda }^{\ast }}{{\left|\chi \right|}^2}+\left(1-{\lambda }^{\ast }\right)\frac{1}{M_z^{\mathit{eff}}}\sum _{m=1}^M\frac{1}{n_z^m}{\delta }_{x_i^m{y}_i^m\left|z,x_i{y}_i\right|z}$$ (9)

where, n^m_z = |{m′|1 ≤ m′ ≤ M, Hamming Disatnce(m,m′) ≥ δh}| is the number of similar sequences m′ within a certain Hamming distance δh of sequence m and $M_z^{\mathit{eff}}={\sum }_{m=1}^M{\left(n_z^m\right)}^{-1}$ is the effective number of distinguishable primary sequences at that distance threshold – the Kronecker delta ${\mathrm{\delta }}_{x_i^m{y}_i^m\left|z,x_i{y}_i\right|z}$ ensures counting of (x_i,y_i) occurrences only. In Eq. (9), two-site frequencies converge to raw occurrences in the sequence alignment for λ* = 0 or approach the uniform distribution $\frac{1}{{\left|x\right|}^2}$ for λ* = 1; Eq. (9) is identical to the equation devised by Morcos and coauthors [19] by rewriting λ* = λ/(λ + M^eff_z). Here, two-site probabilities ${\rho }^{\ast }\left(x_i,y_i|z\right)\equiv f_{x_i,y_i|z}$ were computed from Eq. (9) after unbiasing the reference MSA by weighting down primary sequences with amino-acid identity equal to 100%. An effective number of primary sequences M^eff_z = M (cf. Table S1) was retained for analysis and a pseudocount fraction of λ* = 0.001 was used to regularize data without largely impacting observable frequencies. Single-site probabilities {ρ(x^N), ρ(y^N)} were derived from ρ*(x_i, y_i|z) by marginalization via Eq. (1).

The conditional mutual information in Eq. (7) was computed from single- and joint-entropies according to Eq. (3). Given the fact that the maximum value of I(X_i; Y_i|z) is bound to the conditional joint entropy, Eq. (7) was computed in practice as a per-contact entropy-weighted conditional mutual information [29], H(X_i; Y_i|z)⁻¹ I(X_i; Y_i|z), to avoid that contributions of H(X_i, Y_i|z) contacts between highly variable sites are overestimated. Because $H(X_i,Y_i\mid z)$ and I(X_i, Y_i|z) have units of nats, Eq. (7) is dimensionless in the present form.

3. Results and discussion

Details of all protein systems under investigation are presented in Table 1. Each system involves two families of protein interologs A and B with known PPIs derived from cospeciation in the same genome [26]. We denote by {x^N_k, y^N_l|z*}_M their reference concatenated MSA associated to the native process z*. For convenience, in the following, we present and discuss results obtained for a representative system A and B – the protein complex TusBCD (chains B and C of 2DIP) which is crucial for tRNA modification in Escherichia coli. Similar results and conclusions hold for all other systems in Table 1 as presented in supplementary Figs. S1 through S4 (cf. SI).

3.1. Decomposition of mutual information

Fig. 1A shows the three-dimensional representation of stochastic variables embodying every possible amino-acid pairs along proteins A and B and their decomposition in terms of physically coupled amino acids at short-range cutoff distances (r_c ≤ 8.0 Å) and physically uncoupled amino-acids at long-range cutoff distances (r_c > 8.0 Å). In Fig. 1B, the total mutual information (coupled + uncoupled) across every possible amino-acid pairs of A and B amounts to 987.88 in the reference (native) MSA. As estimated from a generated ensemble of “scrambled” MSA models, expectation values for the mutual information <I(X^N; Y^N|z)>_M−n decreases significantly as decorrelation or the number of mismatched proteins in the reference MSA increases. The result also holds at the level of individual protein contacts i as the mutual information I(X_i; Y_i|z*) for the reference alignment is systematically larger than the mutual information expectation value for “scrambled” MSA models full of sequence mismatches that is, with a total number M of mismatched sequences (Fig. S1).

Fig. 1.

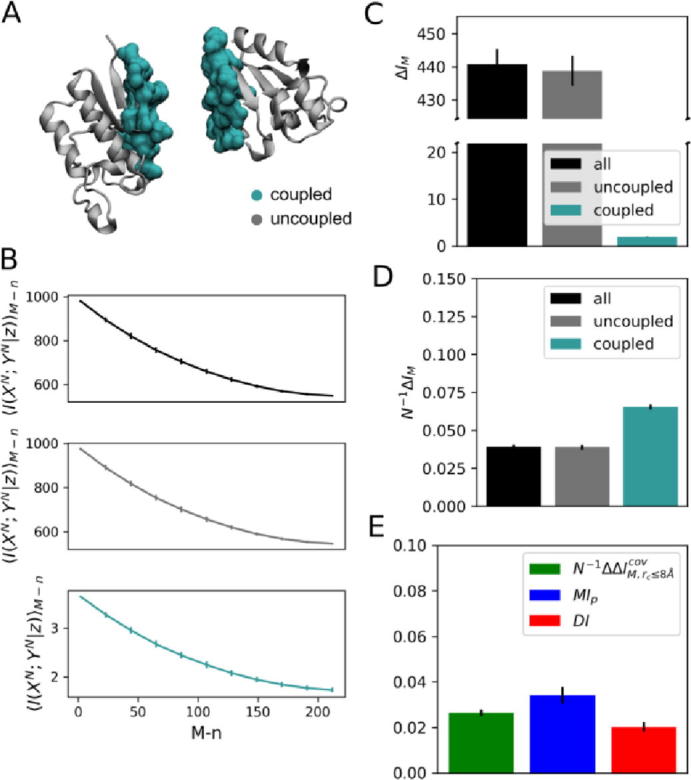
Informational analysis of protein complex TusBCD, chains B and C. (A) Three-dimensional representation of stochastic variables X^N and Y^N as defined from physically coupled amino acids at short-range cutoff distances r_c ≤ 8.0 Å (turquoise) and physically uncoupled amino-acids at long-range cutoff distances r_c > 8.0 Å (gray). Calculation of r_c involved C^β-C^β atomic separation distances. (B) Conditional mutual information <I(X^N; Y^N|z)>_M−n as a function of the number M − n of randomly paired proteins in the reference (native) MSA, for 0 ≤ n ≤ M. < I(X^N; Y^N|z)>_M−n are expectation values estimated from a generated ensemble of 500 MSA models. Mutual information of fully “scrambled” models featuring M unpaired sequences is similar to that calculated from randomized sequence alignments generated by aleatory swapping of lines within columns. (C) Mutual information gap ΔI_M between reference and 100 fully “scrambled” models featuring M unpaired sequences. (D) Per-contact mutual information gap N⁻¹ΔI_M,rc. (E) Mutual information decomposition $\left(N^{-1}\mathrm{\Delta }\mathrm{\Delta }{I}_{M,r_c\le 8\text{Å}}^{\mathit{Cov}}\right)$ according to Eq. (11) and comparison with functional mutual information (MI_p,rc≤8Å) and direct information (DI_rc≤8Å). In B, C, D and E error bars correspond to standard deviations.

As a measure of correlation, it is not surprising that mutual information in the reference MSA is larger than that of scrambled alignments. Not expected however, is the fact that correlation does not vanish at “scrambled” models meaning that part of the calculated mutual information results at random. Supporting that notion, the mutual information of fully “scrambled” models is found here to be very similar to the same estimate from randomized sequence alignments featuring aleatory swapping of lines within columns. Subtraction of that stochastic source from the native mutual information, as computed in the form of an information gap

$$\mathrm{\Delta }{I}_{M-n}\equiv \left|I\left(X^N;Y^N|z^{\ast }\right)-{〈I\left(X^N;Y^N|z\right)〉}_{M-n}\right|$$ (10)

between the reference MSA and “scrambled” models full of sequence mismatches, then reveals the isolated nonstochastic contributions to the total correlation between proteins A and B. Here, the information gap amounts to ~440 for every possible amino-acid pairs of A and B.

Fig. 1C shows the individual contributions of physically coupled and uncoupled amino acids to the total mutual information gap, ΔI_M = ΔI_M,rc≤8.0Å + ΔI_M,rc>8.0Å. As a direct consequence of the extensive property of Eq. (7), individual contributions to the total mutual information gap ($\mathrm{\Delta }{I}_{M,r_c}$) increase with cutoff distances defining amino-acid contacts (r_c) and consequently, with the block length (N) of the corresponding stochastic variables. As such, the information imprinted at physically uncoupled amino acids accounts for most of the total mutual information gap (438.8132 ± 4.5159). When normalized by the block length or the number of amino-acid contacts (Fig. 1D), the mutual-information contribution N⁻¹ΔI_M,rc reveals a distinct dependence being larger for physically coupled amino acids than uncoupled ones (0.0653 ± 0.0015 versus 0.039 ± 0.0004). The information-gap profile as a function of amino-acid pair distances shown in Fig. S2 makes sense of the result by showing few larger information-gap values at short distances in contrast to many smaller ones at long distances.

Under the assumption that the coevolutive information is imprinted on the interacting amino acids of interologs in contrast to other (evolutive and stochastic) sources spread over their primary sequences, the difference between short- and long-range contributions provides us with per-contact estimates for the information content resulting from coevolution alone that is,

$$N^{-1}\mathrm{\Delta }\mathrm{\Delta }{I}_{M,r_c\le 8\mathrm{\AA }}^{\mathit{Cov}}\stackrel{\mathit{def}}{\equiv }{N}^{-1}\mathrm{\Delta }{I}_{M,r_c\le 8\mathrm{\AA }}-N^{-1}\mathrm{\Delta }{I}_{M,r_c\le 8\mathrm{\AA }}$$ (11)

where, $N^{-\text{1}}{\mathrm{\Delta }}_{\mathit{IM},r_c>\text{8}\mathrm{\AA }}$ represents the per-contact mutual information resulting from evolution. As shown in Fig. 1E, the information content resulting from coevolution alone amounts to 0.0264 ± 0.0014 which compares well to independent measures of coevolutionary information i.e., functional mutual information ($M{I}_{p,r_c\le \text{8}\mathrm{\AA }}$) [29] and direct information ($D{I}_{r_{\mathit{c}}\mathit{\le }\text{8}\mathrm{\AA }}$) [19], 0.0340 ± 0.0037 and 0.0202 ± 0.0019. More specifically, MI_p is a metric formulated by Dunn and coworkers [29] in which mutual information is subtracted from structural or functional relationships whereas, DI is based on the direct coupling analysis that removes all kinds of indirect correlations by following a global statistical approach [19]. According to definition in Eq. (11), we then conclude that ~40% of the information content stored in physically coupled amino acids of the protein complex TusBCD results from coevolutive sources alone.

3.2. Degeneracy and error analysis of short and long-range correlations

The present analysis reveals quantitative differences between short- and long-range correlations of proteins A and B. Because the total mutual-information component $N^{-\text{1}}\mathrm{\Delta }{I}_{M,r_c}$ provides us with an unbiased (intensive) estimate for proper comparison of the information content between coupled and uncoupled amino acids, in the following, we focus our attention on $N^{-\text{1}}\mathrm{\Delta }{I}_{M,r_c}$ to dissect their effective contributions in determining PPIs based on sequence alignments. Accordingly, let us define the total number ω_S of native-like MSA models generated by scrambling of M − n sequence pairs in the reference alignment

$${\omega }_{S\left(r_c\right)}\equiv \sum _{n\in S\left(r_c\right)}{\omega }_{M,n}$$ (12)

in terms of rencontres numbers ω_M,n

$${\omega }_{M,n}=\frac{M!}{n!}\sum _{q=0}^{M-n}\frac{{\left(-1\right)}^q}{q!}$$ (13)

or permutations of the reference sequence set {l(k)|z*}_M with n fixed positions satisfying ∑^M_n=0 ω_M,n = M! (in combinatorics language). Here, S(r_c) denotes the set of fixed positions n

$$S\left(r_c\right)\equiv \left\{n|0\le n\le M,N^{-1}\mathrm{\Delta }{I}_{M-n,r_c}\le \delta I\right\}$$ (14)

for which the mutual information gap $N^{-1}\mathrm{\Delta }{I}_{M-n,r_c}$ is smaller than a certain resolution δI independently from the corresponding block length N or the number of amino-acid contacts. In simple terms, ω_S in Eq. (12) informs us on the degeneracy or the number of “scrambled” MSA models with a similar amount of mutual information of that in the reference (native) alignment.

As shown in Table S1, rencontres numbers ω_M,n is an astronomically increasing function of M − n, identical for any definition of the stochastic variables X^N and Y^N derived from the same number M of aligned sequences. For instance, there is 164548102752 alignments for the protein complex TusBCD with M − n = 5 scrambled sequence pairs. In contrast, the total number ω_S of native-like MSA models depends on the stochastic variables at various resolutions δI (Fig. 2A). That number is substantially smaller for definitions of X^N and Y^N embodying physically-coupled amino acids in consequence of the smaller number M − n of unpaired sequences required to perturb $N^{-1}\mathrm{\Delta }{I}_{M-n,r_c}$ of a fixed change δI such that ω_S accumulates less over MSA models satisfying the condition $N^{-\text{1}}\mathrm{\Delta }{I}_{M-n,r_c}\le \delta I$ in Eq. (14) (Fig. 2B).

Fig. 2.

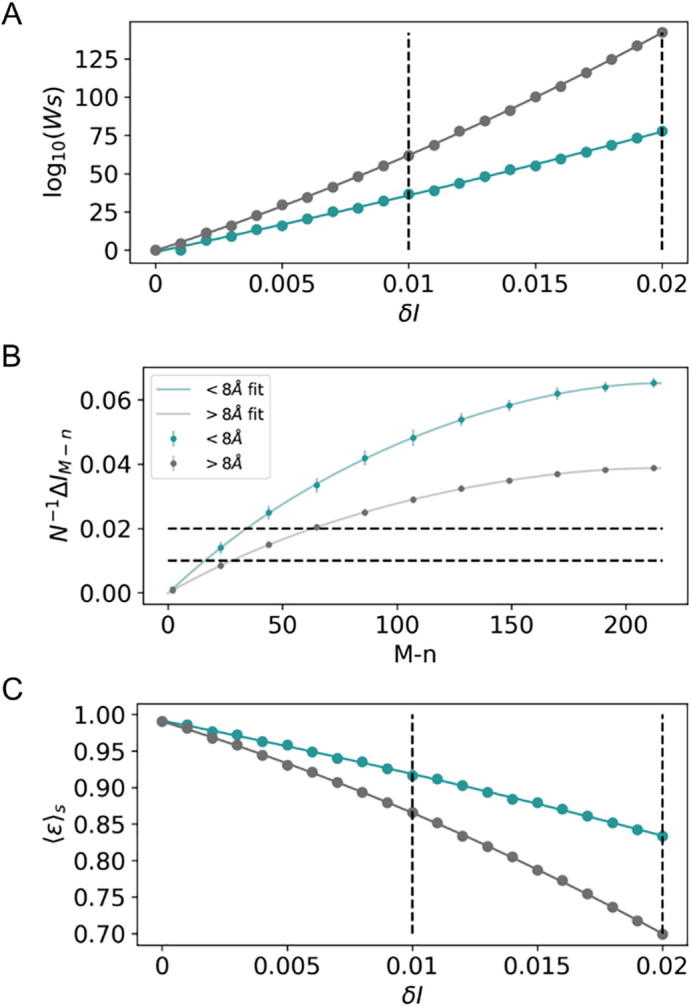
Degeneracy and error analysis for stochastic variables X^N and Y^N involving interacting amino acids at short-range distances r_c ≤ 8.0 Å (turquoise) and long-range distances r_c > 8.0 Å (gray). (A) Total number ω_S of native-like MSA models at various mutual-information resolutions δI. (B) Per-contact gaps of mutual information N⁻¹ΔI_M−n,rc as a function of the number M − n of “scrambled” sequence pairs in the reference native alignment. (C) Expectation values <ε>_S (Eq. (15)) for the fraction of sequence matches across native-like MSA models at various mutual-information resolutions δI. Dashed lines highlight differences at δI values of 0.01 and 0.02.

The degeneracy of native-like MSA models at a given resolution depends on the cutoff distance defining stochastic variables (Fig. 2A). That condition imposes distinct boundaries for the amount of PPIs amenable of resolution across definitions of the stochastic variables in terms of coupled and uncoupled amino acids. Indeed, the expectation value

$${〈\epsilon 〉}_S=\sum _{n\in S}{\left(M\sum _{n\in S}{\omega }_{M,n}\right)}^{-1}n{\omega }_{M,n}$$ (15)

for the fraction M⁻¹n of primary sequence matches among native-like MSA models decreases substantially with the degeneracy of such models meaning that <ε>_S is systematically larger for physically-coupled amino-acids at various mutual-information resolutions δI (Fig. 2C). For instance, the fraction of matches at δI = 0.02 is ~20% larger for coupled amino-acids than the same estimate for amino acids at long-range distances (0.8333 versus 0.6991). Linear extrapolation in Fig. 2C along increased values of mutual-information resolutions suggests even larger differences in the expectation fraction of PPI matches between short and long-range correlations of A and B.

3.3. Dependence with contact definition and docking decoys

So far, “contact” is actually any given pair of residues “i” in protein A and “j” in protein B within a given distance r_c* which can be redefined for a variety of cutoff distances. Specifically, our results were determined by defining physically coupled amino acids at short-range cutoff distances (r_c ≤ r_c*) and physically uncoupled amino-acids at long-range cutoff distances (r_c > r_c*) for a typical “contact” geometrical definition involving C^β-C^β atomic separation distances of 8.0 Å (that is, $r_c^{\ast }\stackrel{\mathit{def}}{\equiv }8.0$ Å). In the following, amino-acid “contacts” are loosely redefined for a variety of cutoff distances to study the dependence of the information encoded in short and long-range protein interactions with r_c*. Further analysis shows a clear dependence of the per-contact mutual information gap (N⁻¹ΔI_M,rc) of coupled amino acids with r_c* – which is not the case for uncoupled ones. As shown in Fig. 3A, that distinction is due the coevolutive information stored at short-range distances which reaches a maximum at r_c* ≈ 8.0 Å in contrast to evolutive sources uniformly spread over an entire range of r_c* values. Particularly interesting, the result strongly support the assumption that coevolutive information is imprinted preferentially on physically-coupled amino acids of interologs in contrast to other (evolutive and stochastic) sources spread over their primary sequences – a conclusion further supported by calculations of the mutual information subtracted from structural-functional relationships (MI_P) as a function of r_c*.

Fig. 3.

Dependence with contact definition r_c* and docking decoys. (A) Per-contact mutual information gap N⁻¹ΔI_M,rc and mutual information subtracted from structural-functional relationships MI_p,rc at various r_c*. (B) Per-contact mutual information gap N⁻¹ΔI_M,rc (turquoise), information content resulting from coevolution alone N⁻¹ΔΔI^Cov_M,rc (green) and mutual information subtracted from structural or functional relationships MI_p,rc (blue) at alternative interfaces generated by docking – only physically coupled amino acids as defined for r_c ≤ 8.0 Å were included in the calculations. Black bars represent the root-mean-square deviation (RMSD in Ȧ units) between the native bound structure and docking decoys as generated by GRAMM-X [30]. Docking solutions were selected following a stability binding-energy criterium according to the scoring function of GRAMM – all docking decoys considered in the study are low-energy configurations despite large RMSD values relative to the native structure. (C) Illustration of four docking decoys of chain B in the protein complex TusBCD (chain C is shown in gray). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Still, the information encoded in short and long-range amino-acid interactions was analyzed across the native binding interface between proteins as revealed by x-ray crystallography experiments. The dependence of the per-contact mutual information gap with non-native binding modes or docking decoys of proteins A and B was then analyzed further, at the typical definition of amino-acid contacts ($r_c^{\ast }\stackrel{\mathit{def}}{\equiv }8.0$ Å). Shown in Fig. 3B, there is a clear dependence of the information gap with binding modes – the per-contact mutual information gap reaches a maximum at the experimentally-determined native bound configuration of A and B (RMSD = 0.0 Å), meaning that N⁻¹ΔI_M,rc embodies coevolutive pressures in the native amino acids contacts beyond their accessibility at the molecular surface of proteins. The conclusion is further supported in Fig. 3B by noticing that the isolated coevolutive content for the bound configuration of A and B or the associated mutual information subtracted from structural-functional relationships are larger than the very same estimates for any docking decoys.

4. Concluding remarks

Overall, molecular coevolution as the maintenance of the binding free-energy of interacting proteins leads their physically coupled amino-acids to store the largest per-contact mutual information at r_c* ≈ 8.0 Å, with a significant fraction of the information resulting from coevolutive sources alone. In the present formulation, coupled amino acids are related to the smallest degeneracy of native-like MSA models and, therefore, to the largest expectation fraction of PPI matches across such models. These findings hold against any other definition of protein contacts, either across a variety of limitrophe distances discriminating coupled and uncoupled amino acids or alternative binding interfaces in docking decoys. Although presented for the protein complex TusBCD, results and discussion also extent to other protein systems, including obligate and non-obligate dimers, as shown in supplementary Figs. S1 through S4 (cf. SI).

Advances in PPI prediction [14], [15], [16], [17], [18] are highly welcome in the contexts of paralog matching, host-pathogen PPI network prediction and interacting protein families prediction. Recent studies suggest strategies like maximizing the interfamily coevolutionary signal [14], iterative paralog matching based on sequence “energies” [15] and expectation–maximization [18], which have been capable of accurately matching paralogs for some study cases. Despite these advances, the problem of PPI prediction remains unsolved for sequence ensembles in general, especially for proteins that coevolve in independent genomes though likely resulting from the same free-energy constraints – examples are phage proteins and bacterial receptors, pathogen and host-cell protein, neurotoxins and ion channels, to mention a few. Accordingly, to add efforts in the field, we have addressed the following questions in our study: knowing three-dimensional amino-acid contacts from x-ray crystal structures, what would be the information encoded by them in terms of stochastic, evolutive and coevolutive sources, and what would be the utility of such pieces of information in resolving PPIs from “scrambled” multi-sequence alignments. Since the Direct Information derived from modern coevolutionary approaches [19], [22] already filters out most of the information sources, the decomposition as proposed here does only make sense by considering the Mutual Information embodying unfiltered information. In this regard, it is worth emphasizing that our goals are neither the resolution of pair of residues highly-correlated via direct physical coupling [19], [22] nor to provide with a method for prediction of protein-protein interactions and interfaces [26], [27].

Although our study is not aimed at providing an approach for PPI prediction, the largest amount of non-stochastic information available in primary sequences helpful to differentiate MSA models with the largest expectation fraction of sequence matches as found here, might be of practical relevance in search of more effective heuristics to resolve protein-protein interactions from “scrambled” multi-sequence alignments. When compared to evolutive sources, that information is the strongest signal to characterize protein interactions derived from cospeciation and likely, the unique indication in case of coevolution without cospeciation as the non-stochastic information of uncoupled amino acids must vanish in independent proteins – indeed, low information between amino acid positions of multiple sequence alignments is typically indicative of independently evolved proteins. Developments of more effective heuristics based on that signal would be applied for resolution of the more general problem of PPIs under coevolution in independent genomes, providing us with a highly welcome advance in the field.

We believe the results are of broad interest as the stability principles of protein systems under coevolution must be universal, either under cospeciation or in independent genomes. We therefore anticipate that decomposition of evolutive and coevolutive information imprinted in physically-coupled and uncoupled amino acids and evaluation of their potential utility in resolving MSA models in terms of degeneracy and fraction of PPI matches should guide new developments in the field, aiming at characterizing protein interactions in general.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: