Dynamic Properties of the Lipid-Water Interface of Model Membranes As Revealed by Lifetime-Resolved Fluorescence Emission Spectra

Abstract

We examined the dynamic properties of the lipid-water interface region of model membranes, on the nanosecond time scale, by using the fluorescent probe 2-p-toluidinylnaphthalene-6-sulfonic acid (TNS). In particular, we examined the steady-state emission spectra of TNS as its average lifetime was decreased by oxygen quenching. Under these quenching conditions the centers of gravity (v_cg) of the emission spectra shift to shorter wavelengths. The lifetime dependence of these shifts reveals the time dependence of membrane relaxation around the excited-state dipole moment of TNS. The lipids investigated include dioleoyl-, dimyristoyl-, and dipalmitoyl-l-α-phosphatidylcholines, bilayers containing cholesterol, and an ether analogue of dipalmitoyl-L-a-phosphatidylcholine. For these lipids, the spectral relaxation times and the temperature dependence of the relaxations are similar in magnitude. Most relaxation times fall in the range of 0.6–6 ns, and except for the ether analogue, the activation energies for spectral relaxation are 10 ± 2 kcal/mol. The average energy loss during spectral relaxation was 1000 cm⁻¹. However, for the saturated phosphatidylcholines at temperatures below their transition temperatures, smaller relaxation losses were observed (~600 cm⁻¹), We attribute these smaller losses to ordering of the polar head groups around the ground-state dipole moment of TNS. Overall, these results indicate that the dynamic properties of the lipid-water interface region are similar among the phosphatidylcholines and depend only slightly on the chemical composition and phase state of the acyl side chains.

The functional properties of cell membranes appear to be dependent upon the dynamic behavior of the phospholipid molecules (Chapman, 1976; Melchior & Steim, 1976; Singer & Nicolson, 1972). For example, the permeabilities of model membrane to ions and nonelectrolytes and the activities of membrane-bound enzymes are dependent upon the chemical composition, temperature, and phase state of the lipid bilayers. Recently, much attention has been directed toward elucidating the dynamic properties of the acyl side chain region of lipid bilayers as revealed by their apparent microviscosities (Shinitzky et al., 1971; Cogen et al., 1973; Lentz et al., 1976; Lakowicz et al., 1979a,b). In the current investigation we characterize further the dynamic properties of model membranes but now with emphasis on the lipid-water interfacial region. In particular, we investigated the ability of this region to undergo relaxation around the excited-state dipole moment of 2-p-toluidinylnaphthalene-6-sulfonic acid (TNS).¹ This probe and other similarly charged fluorophores are known to bind to the polar head-group region of membranes (Jendrasiak & Estep, 1977; Lesslauer et al., 1971, 1972; Radda, 1971). The dipolar relaxation rate of the membrane is revealed by the rate at which the fluorescence emission of TNS shifts to longer wavelengths following excitation.

Generally, the time evolution of excited states is determined by fluorescence emission spectra obtained at nanosecond intervals following pulsed excitation, as has been described for fluorophores in solvents (Ware et al., 1968; Mazurenko, 1973) and in proteins and membranes (Brand & Gohlke, 1971; DeToma et al., 1976; Gafni et al., 1977). These time-dependent spectral shifts result from reorientation of the molecules surrounding the fluorophore around the changed (generally increased) dipole moment of the excited state. Under conditions where the solvent relaxation time is comparable to the fluorescence lifetime, the fluoroescence emission contains contributions from both relaxed and unrelaxed fluorophores (Bakhshiev & Piterskaya, 1966; Ware et al., 1968). Observation at the long-wavelength region of the emission generally reveals the longer lived fluorophores which have undergone relaxation prior to emission, whereas observation at short wavelengths selects for those shorter lived fluorophores which have emitted prior to relaxation.

In the current studies we used an alternative method to study the relaxation of membranes around excited-state dipoles. The lifetime of membrane-bound TNS is decreased by oxygen quenching. Except for the decreased lifetime the quenching has no other detectable effects on the membranes. Quenching by oxygen is a random collisional process, and the probability that any given excited fluorophore encounters an oxygen molecule is proportional to the time it spends in the excited state. As a result, the longer lived low-energy portion of the spectrum is quenched to a greater extent than the shorter lived high-energy region. Steady-state emission spectra collected under these conditions are shifted to shorter wavelengths as the lifetime of the fluorophore is decreased. We used the lifetime dependence of the spectral shifts to estimate both the rate of relaxation, and the total energy loss which results from the reorientation processes. Our results indicate that the dynamic properties of the lipid-water interface region of bilayers are similar, irrespective of the chemical composition and phase state of the acyl side chains. The marked differences observed for the nonpolar regions of bilayers do not appear to greatly affect the dynamic properties of the surfaces of these membranes.

Theory

The theory of solvent relaxation around excited-state dipoles has been presented by others (Bakshiev, 1964; Mazurenko, 1971), and we present here a simplified description of their results. The center of gravity of the fluorescence emission spectrum on the frequency scale (v_cg, in cm⁻¹) is given by

$${\nu }_{\text{cg}}=\frac{{\int }_{\nu }\nu I(\nu )\text{\hspace{0.17em}d}\nu }{{\int }_{\nu }I(\nu )\text{\hspace{0.17em}d}\nu }$$ (1)

where I(v) is the relative photon flux per frequency interval dv. Assume that v_cg decreases exponentially from the Franck-Condon state (v₀) to the completely relaxed state (v_∞) and that the time constant for this relaxation is τ_R. The basis for this assumption is the known exponential (or multiexponential) approach to equilibrium of dipoles when subject to an electric field (Frölich, 1958). Under these conditions v_cg at any time t following pulsed excitation is given by

$$v_{\text{cg}}(t)={\nu }_{\infty }+\Delta \nu e^{-t/{\tau }_{\text{R}}}$$ (2)

where Δv = v₀ − v_∞. Under steady-state conditions the observed center of gravity is averaged by the decay of fluorescence. Hence

$${\nu }_{\text{cg}}(\tau )=\frac{{\int }_0^{\infty }{\nu }_{\text{cg}}(t)e^{-t/\tau }\text{\hspace{0.17em}d}t}{{\int }_0^{\infty }{e}^{-t/\tau }\text{\hspace{0.17em}d}t}$$ (3)

where τ is the fluorescence lifetime. Application of eq 3 to 2 yields

$${\nu }_{\text{cg}}(\tau )={\nu }_{\infty }+\Delta \nu \frac{{\tau }_{\text{R}}}{{\tau }_{\text{R}}+\tau }$$ (4)

It is important to note that v_cg is a function of τ since we shall use this dependence on lifetime to obtain values for Δv and τ_R. From eq 4 one readily sees that in fluid solvents where τ_R << τ relaxation is complete prior to emission and v_cg = v_∞. In vitrified solvents where τ_R >> τ emission occurs prior to significant relaxation and v_cg = v₀.

For membrane-bound fluorophores τ_R. and τ are frequently comparable in magnitude. As a result the observed emission spectra are sensitive to both Δv and τ. We used oxygen quenching of fluorescence to vary τ and hence the time over which v_cg is averaged (eq 3). In particular, the fluorescence lifetime is given by

$$\tau =\frac{{\tau }_0}{1+K_{\text{D}}{P}_{{\text{O}}_2}}$$ (5)

where τ₀ is the lifetime in the absence of quenching and K_D is the dynamic portion of the observed quenching. Under quenching conditions which decrease τ, v_cg shifts to higher frequencies, the extent of the shift being dependent upon Δv, τ, and τ_R. Under our experimental conditions we could decrease the lifetime of membrane-bound TNS ~ 10-fold. We fit these lifetime-resolved v_cg, values to eq 4, the variables being v₀, v_∞, and τ_R.

It is important to realize that the meaning of τ can be ambiguous in the presence of spectral relaxation. In particular, τ is dependent upon the wavelength of observation. Increasing wavelengths select for those longer lived molecules which have relaxed prior to emission. In contrast, the apparent lifetime of the short-wavelength side of the emission is shortened by relaxation away from the wavelength of observation. We attempted to compensate for this potential difficulty by observing the entire emission during measurement of the fluorescence lifetimes.

We note that our mode of data analysis is only approximate and that both the spectral relaxation and the fluorescence emission may be multiexponential or nonexponential processes (Easter et al., 1978). Indeed, even simple solvents such as normal alcohols may display as many as three relaxation times (Mazurenko, 1971; Gard & Smyth, 1965). However, this single-exponential model provided an adequate description of our data.

Materials and Methods

Centers of gravity (in cm⁻¹) were calculated from the spectra obtained in the wavelength domain by using

$$v_{\text{cg}}=\frac{\sum _{i}I\left({\lambda }_i\right){\lambda }_i^{-3}}{\sum _{i}I\left({\lambda }_i\right){\lambda }_i^{-2}}$$ (6)

where the wavelength i ranges from 340 to 580 nm. This expression may be obtained from eq 1 by recalling that v = λ⁻¹, dv = −λ⁻² dλ, and the spectral data are evenly spaced in λ. For ease of interpretation we will sometimes refer to the inverse of v_cg (v_cg⁻¹, in nanometers). However, we note that v_cg⁻¹ is not equal to the average wavelength of emission calculated in the wavelength domain. Since the emission spectra used in the v_cg calculations were uncorrected for instrumental response and since vesicle preparations and instrumentation may vary between laboratories, we report the following v_cg values for TNS in solvents at 23°C: octanol, 23460 cm⁻¹; dioxane 23913 cm⁻¹. The spectral sensitivity of our instrument decreases smoothly by less than a factor of 2 as the observation wavelength is increased from 400 to 500 nm (G. Mitchell, personal communication). In addition, the largest shift (in v_cg⁻¹) that we observed was 13 nm. Thus, even though the use of uncorrected spectra may result in errors in the absolute values of v_cg, the relative errors in comparing the shifted but similarly shaped TNS spectra will be small.

In the presence of quencher, in our case dissolved oxygen, the fluorescence intensity is described by

$$F_0/F=\left(1+K_{\text{D}}\left[{\text{O}}_2\right]\right)\left(1+K_{\text{S}}\left[{\text{O}}_2\right]\right)$$ (7)

where K_D and K_S are the dynamic and static components of the observed quenching, [O₂] is the concentration of dissolved oxygen, and F₀ and F are the fluorescence intensities in the absence and presence of oxygen, respectively (Lakowicz et al., 1979b). To minimize the effects of quenching-induced spectral shifts on the observed intensities, we used the area under the emission spectrum from 340 to 580 nm to calculate these intensities. Since the spectral shifts are small and widths of the emission spectrum are not altered dramatically by quenching, the use of uncorrected emission spectra will not result in significant errors in the relative intensities.

All spectral intensities and distributions were corrected for contributions due to impurities in the lipids and for scattered light by subtraction of the signals obtained from unlabeled vesicles using identical instrumental conditions. Prior to subtraction these blank intensities were corrected for the filtering effect in the labeled samples which was due to light absorption by the fluorophore. K_D and K_S were separately determined by plots of K_app vs. [O₂] (Lakowicz et al., 1979b) where

$$K_{\text{app}}=\frac{\left(F_0/F\right)-1}{\left[{\text{O}}_2\right]}=K_{\text{S}}+K_{\text{D}}+K_{\text{S}}{K}_{\text{D}}\left[{\text{O}}_2\right]$$ (8)

All quenching constants are reported in units of psi⁻¹ since these values are known absolutely, whereas the effective concentration of oxygen near the lipid-water interface is not known. Fluorescence spectral data at increased oxygen pressures were obtained as described previously (Lakowicz & Weber, 1973; Lakowicz et al., 1979b).

Fluorescence emission spectra and lifetimes were obtained on equipment from SLM Instruments, Inc. For emission spectra the instrumental conditions were as follows: excitation wavelength, band-pass, and filter, 300 nm, 8 nm, and Corning 7–54, respectively: emission band-pass, 1 nm. Lifetimes were obtained by using the same excitation conditions, but the emission was observed through a Corning 0–51 filter, and polarizers were used in the excitation and emission paths to eliminate the effects of Brownian rotation on the observed lifetimes (Spencer & Weber, 1970). The Corning filter transmits virtually the entire TNS emission spectrum, while effectively removing all scattered light at the excitation wavelength. Lifetimes were obtained by the phase method (Spencer & Weber, 1969) at modulation frequencies of 10 and 30 MHz. The values reported are an average of these two measurements. The differences averaged 0.8 ns and are thus indicative of a decay which is nonexponential but which is dominated by a single exponential. This is not surprising since we are observing the complete emission, and such conditions may be expected to minimize the nonexponential character of the TNS decay which is apparent when discrete wavelengths are examined (DeToma et al., 1976: Easter et al., 1978).

Sources and purities of lipids were described previously (Lakowicz et al., 1979a). Vesicles were prepared by sonication of lipid suspensions in 0.01 Tris and 0.05 M KC1, pH 7.5, at a lipid concentration of 1 mg/mL. Subsequently, 1 mL of a freshly prepared TNS stock solution in buffer (1.3 × 10⁴ M, ∊ = 7700 M⁻¹) was added to each 9-mL volume of lipid suspension. The lipid to probe ratio was 100 to 1, which is substantially below the binding capacities of these membranes for TNS (Huang & Charlton, 1972) and other similar probes (Haynes & Staerk, 1974). The vesicles were incubated for 2 h at 45°C to ensure equilibration of TNS with both sides of the bilayer (Tsong, 1975) and to remove structural defects (Lawaczeck et al., 1976). Following incubation they were centrifuged at 54000g for 1 h. Vesicles containing N-methylniwtinamide (NMN) were prepared in a similar fashion except that the buffer was 0.025 M Tris and contained [KCl] plus [NMN] equal to 0.2 M, pH 7.5.

The fluorescence lifetime of unbound TNS is substantially shorter than membrane-bound TNS. Since the extent of quenching is proportional to the fluorescence lifetime, quenching could selectively remove the long-lived membrane-bound fluorophores from observation and thereby enhance the contribution due to unbound TNS. Control experiments showed that TNS at equivalent concentrations in the absence of lipid did not contribute significant fluorescence. Moreover, for DPPC, equivalent spectral shifts were observed at a 10-fold higher lipid concentration and these conditions which would further decrease the contributions of unbound TNS.

Results

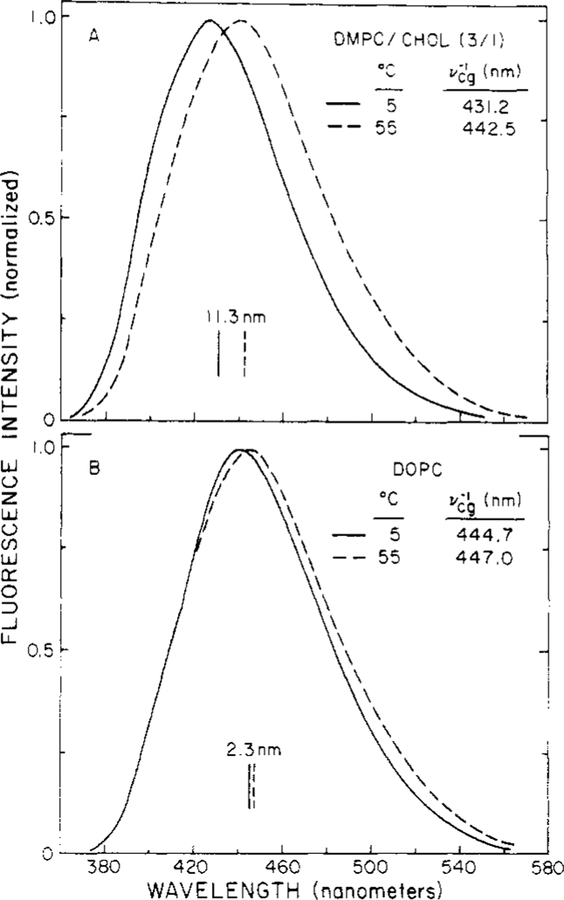
The fluorescence spectral distributions resulting from TNS bound to lipid vesicles are dependent upon the composition of the lipid and the temperature. For example, the spectra of TNS-labeled DMPC/Chol (3:1) vesicles appear to be the most temperature sensitive, whereas the spectra from DOPC shift only slightly as the temperature is varied from 5 to 55°C (Figure 1). The centers of gravity (v_cg⁻¹) of these emission spectra shift ~11 nm for DMPC/Chol (3:1) and −2.5 nm for both D O E and DPPC (Table II). This result is surprising since DPPC vesicles undergo a phase transition in this temperature region, whereas DOPC vesicles do not (Lentz et al., 1976; Lakowicz et al., 1979a). We used lifetime-resolved emission spectra to investigate the rates of membrane relaxation around the excited-state dipole of TNS and how these rates effect the observed steady-state emission spectra of TNS.

FIGURE 1:

Effects of temperature on fluorescence emission spectra of TNS-labeled vesicles. The vertical solid and dashed lines indicate v_cg⁻¹, in nanometers, at 5 and 55°C, respectively.

Table II:

Relaxation Times, Activation Energies, and v₀, v_∞, and Δv Values for TNS-Labeled Vesicles

lipid	temp (°C)	v0 (cm−1)	v∞ (cm−1)	Δv (cm−1)	τR (ns)	Ea (kcal/mol)
DOPC	5	22950	21985	965	2.37
	15	22950	21985	965	1.61
	25	22950	21985	965	0.94	7.5
	35	22950	21985	965	0.65
	45	22950	21985	965	0.45
DM PC	5	22955	22285	670	5.60
	15	23150	22365	785	2.41
	25	23200	22260	940	2.25	10.3
	35	23200	22210	990	1.15
	45	23200	22220	980	0.49
DMPC/Chol (6:1)	5	23160	22155	1005	6.80
	15	23058	22345	713	3.76
	27	23250	22250	1000	2.45	12.3
	37	23250	22250	1000	0.78
	45	23250	22250	1000	0.45
DMPC/Chol (3:1)	5	23360	23346	1014	8.60
	15	23360	23346	1014	4.50
	25	23360	23346	1014	2.45	10.6
	35	23360	23210	1150	1.52
	45	23360	22200	1160	0.75
DPPC	5	22760	22200	500	6.83
	17	22800	22300	500	3.28
	27	22950	22235	715	2.65
	37	23050	22230	820	1.75	9.4
	45	23050	22230	820	0.93
	50	23050	22230	820	0.60
	60	23050	22230	820	0.30
DPPC-E	25	22450	22400	350	6.90
	37	22650	22060	590	3.50
	45	23000	22200	800	0.71	22.3
	55	23000	22200	800	0.24
	61	23000	22200	800	0.16

Upon equilibration with increased pressures of oxygen the fluorescence yields of membrane-bound TNS decrease, as is illustrated by the Stern-Volmer plot for DMPC/Chol vesicles (Figure 2). We note that the intensities were obtained from the integral of the emission spectra from 340 to 580 nm and are thus insensitive to the spectral shifts which occur upon quenching (see below). Careful insepction of Figure 2 will reveal a small degree of upward curvature in the Stern-Volmer plots. We attribute these small positive deviations to an apparent static quenching constant, but we note that the nonzero K_s values do not indicate that TNS and oxygen form ground-state complexes (Lakowicz & Weber, 1973). The dynamic and static quenching constants were separately determined by plots of K_app vs. Po₂ (Lakowicz et al., 1979b) and are summarized in Table I. On the average the magnitudes of the static components are ~5% of the dynamic components. However, even though this percentage is small, it is necessary to correct for the static component. This is illustrated by comparing the τ values calculated for TNS bound to DMPC/Chol (3:1) at 25°C with and without correction for K_s. From K_D (eq 5) we obtain τ = 0.53 ns at 1538 psi In comparison, τ calculated from τ = τ₀(F/F₀) is 0.35 ns. Such differences in the quenched lifetimes can alter the derived membrane relaxation times. To illustrate further the need for correcting the apparent static quenching, we included on Figure 2 (dashed line) the τ₀/τ values expected at 25°C due to only dynamic quenching.

FIGURE 2:

Stern-Volmer plot for oxygen quenching of TNS-labeled DMPC/Chol (3: 1) vesicles. The fluorescence intensities were calculated from the integrals of the emission spectra from 340 to 580 nm. The dashed line illustrates the τ₀/τ values expected at 25°C for the dynamic component of the quenching (K_D, Table I).

Table I:

Fluorescence Lifetimes and Oxygen Quenching Constants for TNS-Labeled Lipid Vesicles

lipid	temp (°C)	τ0 (ns)a	KD × 103 (psi−1)	KS × 103 (psi−1)b
DOPC	5	7.1	4.02	0.28
	15	5.9	4.28	0.31
	25	4.7	5.10	0.13
	35	3.9	4.73	0.35
	45	3.1	4.56	0.18
DMPC	5	7.8	3.69	0.29
	15	7.6	4.97	0.28
	25	6.6	7.74	0.22
	35	4.9	7.75	0.20
	45	3.9	7.88	0.11
DMPC/Chol (6:1)	5	9.0	2.51	0.54
	15	8.6	6.14	0.29
	25	7.4	7.08	0.18
	35	4.9	8.11	0.09
	45	3.9	8.74	0.13
DMPC/Chol (3:1)	5	9.2	2.64	0.70
	15	8.1	4.22	0.47
	25	6.7	7.60	0.34
	35	5.5	6.96	0.46
	45	4.0	5.87	0.72
DPPC	5	7.5	2.54	0.23
	17	7.1	3.34	0.36
	27	6.5	2.65	0.47
	37	5.5	4.34	0.65
	45	4.6	6.36	0.19
	50	4.0	6.19	0.33
	60	3.1	6.19	0.07
DPPC-E	25	5.2	3.43	0.24
	37	4.8	4.43	0.23
	45	3.8	7.62	0.05
	55	2.6	8.25	0.00
	61	1.9	9.41	−0.29

^aThe average of the 10- and 30-MHz phase lifetimes is indicated.

^bThese apparent K_S values do not prove the existence of a ground-state complex between the fluorophore and quencher (Lakowicz &Weber, 1973).

Quenching of TNS fluorescence by oxygen shifts the emission to the blue, as is illustrated for DMPC/Chol (3:1) in Figure 3. For these vesicles and for the other vesicles investigated these spectral shifts were completely reversible. Upon release of oxygen pressure, both the original intensity and v_cg value were obtained. Moreover, equivalent pressures of nitrogen or argon did not result in significant changes in intensity or v_cg. Hence, the observed shifts are a result of the variation in fluorescence lifetime which occurs upon quenching and are not a result of dissolved gases or pressure-induced changes in the bilayers.

FIGURE 3:

Effects of oxygen quenching on fluorescence emission spectra of TNS-labeled DMPC/Chol(3:1) vesicles. The vertical solid and dotted lines illustrate v_cg⁻¹, in nanometers, in the absence and presence of oxygen, respectively. The fluorescence lifetimes at each oxygen pressure are shown on the figure.

The magnitude of these quenching-induced shifts is dependent upon the chemical composition of the bilayers. At 25°C the largest shifts were observed for DMPC/Chol (3:1) (Figure 3), where v_cg⁻¹ is blue shifted by 13 nm upon quenching. SimiIar shifts (Figure 4) were observed for DOPC (11 nm), but quenching of DPPC resulted in a smaller shift (4.0 nm). The smaller magnitude of the quenching-induced shifts in DPPC is partially a result of the longer quenched lifetimes. However, as is described in more detail below, we attribute these smaller shifts to ordering of the lipids around the TNS molecules in the ground state.

FIGURE 4:

Fluorescence emission spectra of TNS-labeled vesicles in the absence and presence of oxygen quenching. The vertical solid and dashed lines illustrate the unquenched and quenched value, respectively, of v_cg⁻¹, in nanometers.

We used the lifetime-resolved v_cg values to estimate the relaxation times (τ_R) of the membranes around the excited-state dipole moment of TNS and the total energy loss which occurs during relaxation (Δv). For each lipid at each temperature, we typically obtained spectra and v_cg values at five lifetimes or pressures, as is shown for DOPC and DPPC-E in Figure 5. For the unsaturated lipid DOPC, the v_cg values at temperatures from 5 to 45°C can be fit by single v₀ and v_∞ values, with τ_R beiig dependent upon temperature. In contrast, for the DPPC-E, a single v₀ value was not adequate to describe the time dependence of the spectral relaxation (Figure 5). In particular, at temperatures less than Tc, the apparent v₀ values are ~400 cm⁻¹ smaller than those above T_c. Moreover, the total energy losses during relaxation (Δv) are smaller at 25 and 37°C (470 cm⁻¹) than at 45, 55, and 61°C (800 cm⁻¹) (Table II). Smaller v₀ values at T < T_c were consistently observed for the other lipids, as is shown for DMPC and DPPC in Figure 6 and for DMPC/Chol (6:l) in Figure 7. For DMPC/Chol (3:1), which does not undergo a sharp phase transition over the temperature range investigated (Lakowicz et al., 1979a), the lifetime-resolved v_cg values can be fit to single v₀ and v_∞ values at all temperatures.

FIGURE 5:

Lifetime-resolved centers of gravity for TNS-labeled DOPC and DPPC-E vesicles. The solid and dashed lines are both used to represent the theoretical curves, fit through the data points shown, for the v₀, v_∞, and τ_R values listed in Table II. The dashed lines are used selectively to illustrate those data which could not be fit to the v₀ and v_∞, observed at temperatures above the transition temperature of the vesicles.

FIGURE 6:

Lifetime-resolved centers of gravity for TNS-labeled DMPC and DPPC vesicles.

FIGURE 7:

Lifetime-resolved centers of gravity for TNS-labeled DMPC/cholesterol vesicles at 3:1 and 6:1 molar ratios.

The values of v₀, v_∞, and Δv are summarized in Table II. From these data we note that Δv ranges from 800 to 1100 cm⁻¹ for the vesicles without clear transition temperatures and that Δv is near 500 cm⁻¹ for lipids at T < T_c. We attribute the smaller amount of relaxation at T < T_c to allignment of the lipid molecules around the ground-state dipole moment of TNS and suggest that at T < T_c thermal energy is inadequate to disrupt the orientations. At T < T_c these orientations appear to be randomized. The energy losses from these orientations are about twice kT, which is ~200 cm⁻¹ at 25°C, and are much less than the typical energy of a hydrogen bond which is near 1400 cm⁻¹ (5 kcal/mol).

We questioned whether the smaller v₀ values in the saturated lipids at T < T_c could be a result of movement of the TNS molecule into the polar head-group region of the bilayer. If such a temperature-dependent displacement occurred it could be revealed by an increased accessibility of the TNS molecules to water soluble quenchers. We investigated the temperature dependence of the quenching of DPPC-bound TNS by N-methylnicotinamide. These data and quenching constants are summarized in Figure 8. The bimolecular quenching constants are proportional to the collisional frequency of TNS with quencher and are seen to increase monotonically with temperature. A deeper penetration of the probe into the bilayers at T > T_c could result in a decrease in the apparent bimolecular quenching constant. Although these data do not eliminate the possibility that the TNS localization in the membrane is temperature dependent, such changes are too small to be revealed by this quenching method.

FIGURE 8:

Quenching of DPPC-bound TNS by N-methylnicotinamide. The bimolecular quenching constants (k_q) were obtained from τ₀/τ = 1 + k_qτ₀ [quencher]. 10-MHz phase lifetimes were used. The excitation wavelength was 335 nm, and the emission filters were Corning 7–51 and 0–51.

In addition to investigating the total energy losses from relaxation of the membranes, we also used our lifetime-resolved v_cg values to determine the characteristic times for the relaxation process. Overall, these relaxation times fall in a relatively narrow range from 0.16 to 8.6 ns, with most values being between 0.6 and 6 ns (Table II). The τ_R values for the unsaturated DOPC vesicles are smaller than those for DMPC and DPPC at all temperatures, and the τ_R values for DPPC are greater than those of DMPC. However, in contrast to the 40-fold differences in microviscosity of the acyl side chain region of these bilayers (Lentz et al., 1976), the differences in τ_R between the unsaturated and saturated lipids are only a factor of 2. These data imply that the dynamic properties of the lipid-water interfacial region of the bilayers are similar, irrespective of the acyl side chains. This conclusion is further supported by the small effects of cholesterol on the relaxation times of DMPC vesicles. At DMPC to cholesterol molar ratios of 6 to 1 and 3 to 1 the relaxation times are only 50% larger than those observed for DMPC alone (Figures 6 and 7 and Table II).

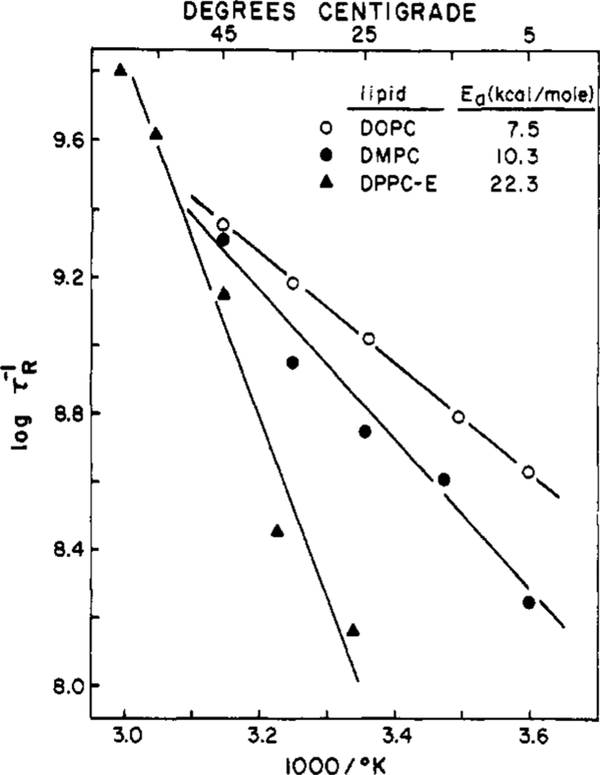
It is interesting to compare the temperature dependence of the τ_R values in these vesicles. For the lipids investigated the Arrhenius plots are linear to within our experimental limits, as is illustrated for DOPC, DMPC, and DPPC-E in Figure 9. Except for DPPC-E the activation energies are near 10 kcal/mol, which is equivalent to the breaking of two to three hydrogen bonds. A much higher activation energy was observed for the DPPC-E (22 kcal/mol), which probably indicates an increased importance of the packing of the side chains on the dynamic properties of the head groups when the carbonyl groups are absent. However, it is clear that the lipid-water interface region of these vesicles displays dynamically similar properties and that the marked changes observed for the acyl side chain regions at T = T_c do not occur at the interface.

FIGURE 9:

Arrhenius plots for membrane relaxation times of TNS-labeled DOPC, DMPC, and DPPC-E vesicles.

Discussion

We questioned whether the quenching-induced shifts could be a result of a heterogeneous probe population rather than spectral relaxation. In particular, if a red-shifted subpopulation had a longer lifetime than a blue-shifted subpopulation, then quenching could selectively remove the former, resulting in quenching-induced blue shifts. Although some heterogeneity may exist, we have recently demonstrated that relaxation is the dominant source of the observed shifts (Lakowicz et al., 1980). Using exciting light which was modulated sinusoidally at 30 MHz, we measured the phase angle (θ) and demodulation (M) on the long-wavelength edge of the emission. A ratio of M/cos ϕ in excess of unity at any given wavelength proves that the emission at this wavelength results from an excited-state reaction, such as relaxation, and not from direct excitation, as would occur for a heterogeneous population. The ratio was found to range from 1.1 to 1.4 in DMPC/CHOL, DMPC, and DOPC at 540 nm (Lakowicz et al., 1980; J. R. Lakowicz and H. Cherek, unpublished observations). A heterogeneous probe population can only result in values for M/cos ϕ < 1. Such ratios were observed on the short-wave-length side of the emission of TNS-labeled vesicles (Lakowicz et al., 1980; J. R. Lakowicz and H. Cherek, unpublished observations). At present, interpretation of these ratios in terms of the actual relaxation times is complicated by spectral overlap of the relaxed and the unrelaxed states. However, these observations prove that the emission spectrum of the TNS is decaying to longer wavelengths on a time scale comparable to that of the fluorescence lifetimes and support our interpretation of the quenching-induced shifts in terms of spectral relaxation rather than spectral heterogeneity.

We also questioned whether the observed spectral shifts could be the result of excitation-induced movement of the probe, rather than reorientation of the lipid molecules. If probe motion is the dominant cause of the spectral shifts, then our results indicate that these diffusive motions also occur on the nanosecond time scale and that these motions are not highly dependent on the phase state of the bilayer. We then arrive at similar conclusions about the dynamic properties of the lipid-water interface regions of these membranes.

Although our experimental data were well described by the single exponential model, that is, a single relaxation time, we realize that a more complete analysis is likely to reveal a more complex decay law for v_cg The relaxation times we can observe are limited by the lifetimes which can be obtained by using quenching (0.4–8 ns). Our results demonstrate the Occurrence of relaxation on this time scale, but our results do not disprove the existence of other faster or slower relaxation processes. For example, a relaxation which occurred in 0.2 ns would be complete even at the shortest quenched lifetime and hence unobservable. The presence of such a rapid relaxation would be revealed by apparent v₀ values smaller than those expected for the unrelaxed state. On the other hand, the observation of slower relaxations is limited by the lifetimes of the unquenched excited states. Hence, the relaxation times reported in Table II should be regarded as an estimate of what is probably a complex relaxation process.

Our results obtained in the lifetime domain are comparable to those obtained by using time-resolved methods. For TNS-labeled vesicles Brand and co-workers (Easter et al., 1978) observed Av values of 1100 and 1200 cm⁻¹ for egg phosphatidylcholine (PC) and egg PC/Chol(3: l), respectively. These values are in good agreement with our observed values of 965,990, and 1150 cm⁻¹ observed for DOPC, DMPC, and DMPC/Chol (3:1), respectively. Moreover, the relaxation times observed by these alternative methods are also in agreement (Table III). Easter et al. (1978) obtained τ_R values for TNS-labeled egg PC which ranged from 5.8 to 1.7 ns at 7 and 32°C, respectively, and observed that cholesterol had little effect on these relaxation times. We also found cholesterol to have little effect on the relaxation times of DMPC vesicles (Table II), and our τ_R values for DOPC and DMPC are comparable to those observed by Easter et al. (1978). We conclude that similar quantitative and qualitative conclusions are obtained by using either time-resolved or lifetime resolved studies of spectral relaxation.

Table III:

Comparison of Relaxation Times (τ_R) Obtained by Using Time-Resolved and Lifetime-Resolved Methods

	τR (ns)
temp (°C)	egg PCa	DOPCb	DMPCb
−1	8.6	3.5	7.8
7	5.8	2.2	4.5
20	3.5	1.1	2.1
32	1.7	0.7	1.0

^aFrom Easter et al. (1978, Figure 4) egg phosphatidylcholine.

^bInterpolated from data shown in Figure 9.

It is of interest to understand the roles of the membrane and of water in the observed spectral relaxations. The spectral relaxation time τ_R is approximately related to the dielectric relaxation time τ_D by

$${\tau }_{\text{R}}\simeq \frac{n^2+2}{ϵ+2}{\tau }_{\text{D}}$$ (9)

where n is the refractive index and ∊ is the static dielectric constant (Bakhshiev et al., 1969; Mazurenko & Bakhshiev, 1970). For polar solvents like water and ethanol τ_R is about 20- and 7-fold less than τ_D, respectively. For hydroxyl groups at 25°C the dielectric relaxation time is no greater than 0.10 ns (Gard & Smyth, 1965), and hence relaxation in water is likely to be complete in 0.01 ns. Thus, it is clear the phospholipids must play a dominant role in the observed nanosecond relaxation times, either directly or indirectly by strongly immobilizing the water at the lipid-water interface.

It is also of interest to understand the magnitudes of the structural rearrangements which could account for spectral losses of ~1000 cm⁻¹. The energy of a dipole in dielectric medium is given by

$$\hslash c{v}_{\text{cg}}=\hslash c{\left({\nu }_{\text{cg}}\right)}_v-\left(\mu *-\mu \right)R_{\text{or}}*+\text{ higher order terms}$$ (10)

where (v_cg)_v is the frequency in a vapor, μ* and μ are the excited- and ground-state dipole moments, respectively, ħ is Planck’s constant, c the speed of light, and R_or* is the orientation field around the dipole (Lippert, 1957; Birks, 1970). We are here concerned with the slowly occurring spectral shifts (nanosecond time scale) and have ignored other terms describing the more rapid electronic rearrangements. The orientation field is given by

$$R_{\text{or}}*=\frac{2\mu *\Delta f}{r^3}$$ (11)

where r is the Onsager radius and Δf is the orientation polarizability and is given by

$$\Delta f=\frac{ϵ-1}{2ϵ+1}=\frac{n^2-1}{2n^2-1}$$ (12)

The origin of the time-dependent spectral shifts resides in the time dependence of R_or*, which in turn may reflect time-dependent changes in r or Δf For TNS the excited-state dipole moment may be as large as 44 D (Seliskar & Brand, 1971). However, the smaller values observed for 2-anilinonaphthalene (15 D) and the sulfonamide derivative of TNS [15 D, Green (1975)] suggest that the observed value of 44 D may be a result of specific interactions with protic solvents (Green, 1975; McRae, 1957). Moreover, the similar total spectral losses (Δv) for TNS [Table II and Easter et al. (1968)l and 2-anilinonaphthalene (Badea et al., 1978) also indicate that the value of 44 D may be excessive. For our purposes of calculating the changes in Δf or r necessary for an energy loss of 1000 cm⁻¹, we will assume an intermediate value of μ* – μ = 20 D. Since μ* > μ, we can approximate Δv by

$$\Delta v=\frac{2\left(\mu *-\mu \right)\nu *\Delta f}{\hslash c{r}^3}\simeq \frac{2{\left(\mu *\right)}^{2}f}{\hslash c{r}^3}$$ (13)

Using eq 13 and an Onsager radius of 5 Å (Seliskar & Brand, 197 l), one can calculate that the orientation polarizability needs to change only slightly (0.032) to account for the observed energy losses of 1000 cm⁻¹. For comparative purposes we note that Δf values for water, methanol, ethanol, and ether are 0.32, 0.31,0.30, and 0.25, respectively. Alternatively one may assume that Δf remains constant and the observed spectral shifts are a result of changes in the Onsager radius. Then one may calculate that an energy loss of 1000 cm⁻¹ is attained by a decrease in r from 5 to 4.96 Å.

Hence, it is apparent that only minor changes in the environment surrounding the fluorophore are required to explain the time-dependent spectral relaxation around the TNS molecules. However, attributing these processes to any specific molecular event is difficult at this time since only minor changes in the environment are necessary and this environment appears to be highly dynamic.