Contribution of Nascent Cohesive Fiber-Fiber Interactions to the Non-Linear Elasticity of Fibrin Networks under Tensile Load

Abstract

Fibrin is a viscoelastic proteinaceous polymer that determines the deformability and integrity of blood clots and fibrin-based biomaterials in response to biomechanical forces. Here, a previously unnoticed structural mechanism of fibrin clots’ mechanical response to external tensile loads is tested using high-resolution confocal microscopy and recently developed three-dimensional computational model. This mechanism, underlying local strain-stiffening of individual fibers as well as global stiffening of the entire network, is based on previously neglected nascent cohesive pairwise interactions between individual fibers (crisscrossing) in fibrin networks formed under tensile load. Existence of fiber-fiber crisscrossings of reoriented fibers was confirmed using 3D imaging of experimentally obtained stretched fibrin clots. The computational model enabled us to study structural details and quantify mechanical effects of the fiber-fiber cohesive crisscrossing during stretching of fibrin gels at various spatial scales. The contribution of the fiber-fiber cohesive contacts to the elasticity of stretched fibrin networks was characterized by changes in individual fiber stiffness, the length, width, and alignment of fibers, as well as connectivity and density of the entire network. The results show that the nascent cohesive crisscrossing of fibers in stretched fibrin networks comprise an underappreciated important structural mechanism underlying the mechanical response of fibrin to (patho)physiological stresses that determine the course and outcomes of thrombotic and hemostatic disorders, such as heart attack and ischemic stroke.

1. Introduction

1.1. Biological Relevance and Importance of Fibrin Mechanics

Fibrin is an end product of blood clotting and a proteinaceous polymeric component of intra- or extravascular blood clots that form at the sites of injury. Fibrin provides jelly-like blood clots with elasticity that is important for their biological functions. As a major component of extracellular matrix, it also participates in various cellular processes, including adhesion, migration, proliferation and differentiation, wound healing, angiogenesis, inflammation, and others. Formation of the fibrin gel in blood vessels in vivo is one of the key events halting bleeding (hemostasis) and impairing blood flow by obstructive pathological blood clots (thrombosis)[1]. The mechanical response of fibrin to stresses generated by blood flow, deformations of the pulsating vessel wall, during platelet-driven clot contraction, diaphragmatic excursions, and gut motility determine the course and outcomes of thrombotic and hemostatic disorders, such as heart attack and ischemic stroke. In addition, fibrin is also employed in biomedicine as a versatile biomaterial of unique mechanical properties utilized in a variety of clinical and laboratory applications, including hemostatic fibrin sealants and scaffolds for tissue engineering[2]. Despite the vital clinical implications of the biomechanics of fibrin, both as the skeleton of blood clots and thrombi and as a widely used biomaterial, the structural mechanisms underlying the mechanical properties of fibrin remain largely unknown.

1.2. Multiscale Fibrin Mechanical Properties and their Structural Basis

Fibrin is a hydrogel built of a biopolymer that self-assembles to form porous 3D filamentous networks with mechanical properties substantially different from synthetic polymers[3,4]. The mechanical responses of fibrin gels to shear, tensile, and compressive loads are known to exhibit a highly nonlinear response known as strain-stiffening[5–8]. This bulk nonlinear behavior has a number of structural mechanisms at various spatial levels spanning six orders of magnitude, including molecular unfolding, interactions within and between individual fibers, spatial rearrangement of the filamentous network, and other mechanisms that are not fully understood[9].

3D fibrin networks consist of branched fibrin fibers resulting from self-assembly of fibrin monomers and oligomers further stabilized via intermolecular covalent isopeptide bonds. Formation of these bonds (fibrin crosslinking) is catalyzed by an active transglutaminase that circulates in the blood as an inactive proenzyme named clotting factor XIII; the active form of factor XIII is designated factor XIIIa. Following elongation of fibrin oligomers, they undergo lateral aggregation mediated, in part, by long unstructured polypeptide “arms” named αC-regions. The αC-regions comprise ~400-residue-long C-terminal portions of the α-chains extending from fibrin molecules and connecting fibrin oligomers (protofibrils) within a fiber. Multiple highly flexible αC-regions stretched between protofibrils can interact with each other to form αC-polymers followed by covalent crosslinking by factor XIIIa, making the αC-polymers stable and contributing to the elastic properties of fibrin. The entire cross-linked fibrin clots or individual fibers are known to show extremely large extensibility, quadrupling their length before breaking[5,7]. Mechanical properties of individual fibrin fibers were probed experimentally by atomic force microscopy (AFM)[7,10] and optical trapping[11], revealing the elastic moduli to be 1.7 and 14.5 MPa for uncross-linked and factor XIIIa cross-linked fibers, respectively. Studies of tensile properties of whole fibrin clots and individual fibers at large deformation revealed the molecular unfolding of fibrin molecules, suggesting the molecular mechanism of fibrin extreme extensibility[5,7,12,13].

The forced molecular unfolding in fibrin(ogen) has been demonstrated and analyzed both experimentally and computationally[5,14–18]. Forced elongations of several regions of the fibrin molecule have been shown to be a potential source of fibrin’s extensibility, namely unfolding of the γ chain nodules[16], extension of the α-helical coiled-coil connectors[14–18], and unraveling of the unstructured αC-polymers within a fiber[19–22]. Micromechanical properties of individual fibrin fibers were shown to determine the macroscopic characteristics of the fibrin network. In particular, the high strain of single fibers was shown to affect the overall strength of the network[10,12,20]. Even though aspects of the tension behavior of fibrin networks has been studied in detail, it is still not clear how microscopic structural characteristics, such as fiber connectivity, alignment, and fiber-fiber cohesion impact the mechanical response of the entire network, and how stress propagation within the network is affected by changes in its structural organization.

1.3. Overview of Modeling Studies of Fibrin Mechanics

Several theoretical and computational frameworks have been recently developed for modeling fibrin structural mechanics at different spatial scales ranging from molecular to macroscale[20,23–35]. At the molecular scale, fibrin mechanics is defined by the properties of monomeric fibrin, an elementary structural unit that shares structural and mechanical similarity with fibrinogen, a blood plasma protein, converted enzymatically to monomeric fibrin[36]. To model the dynamics of human fibrin(ogen) undergoing forced elongation, molecular dynamics (MD) simulations were used to characterize the α-to-β transition in α-helical coiled-coil connectors of the fibrin molecule, revealing distinct elastic, plastic, and non-linear regimes in force-extension profiles[17]. Zhmurov et al[37] used a model to elucidate structural mechanisms of forced elongation of fibrin molecules based on stepwise unfolding of γ nodules concomitant with partial stretching and contraction of α-helical connectors.

In order to explain the strain-stiffening behavior of stretched fibrin networks, two conceptually different types of models of cross-linked filamentous networks were previously developed and applied [38]. The first type assumed the existence of semiflexible filaments that undergo thermal fluctuations [34,39]. One entropic approach used the Worm-Like-Chain (WLC) to model the force- strain profiles of fibrin fibers under stretching, with fitting parameters obtained in atomic force microscopy experiments[12,40]. The second type modeled filaments as elastic rods that can bend and stretch but do not exhibit thermal fluctuations [41–43]. Both types of models were capable of capturing the strain-stiffening behavior of fibrin networks, but gave different predictions for the degree and onset of stiffening, suggesting that further studies are required to develop these entropic and athermal models to the mechanical properties of fibrin hydrogels [38].

At the macroscale fibrin network level, discrete and continuous modeling approaches have been used to account for elastic responses of fibrin networks to external tensile and shear deformations inducing stiffening[38,44,45] as well as to suggest mechanisms of softening-stiffening behavior of compressed fibrin networks[32,46–48]. Several continuous models of fibrin networks, including a three-chain model[49], an eight-chain model[50], and an isotropic network model[34], were used to predict the force-strain response of stretched fibrin clots[5]. All these models were shown to correctly reproduce fibrin network behavior under tension in the linear regime. However, at large strains, the results significantly deviated from experimental data[5]. All three models simulated isotropic networks and assumed affine network deformations. Meanwhile, biological networks such as those formed by fibrin are frequently anisotropic and their deformation is non-affine[51].

More recently, a phase transition method has been used to predict the shear viscoelastic response of compressed networks, which revealed a remarkable softening-stiffening behavior due to bent fibers and network densification[32]. Several discrete models have been developed to consider the formation of connections between individual fibers. One of such models, based on a bead-spring representation of individual fibers, was used to determine fibrin network elastic modulus for different network structures[45]. A similar model was developed to study how network connectivity affects the mechanical properties and structural integrity of tissue[52]. This model was simplified to construct a minimal 2D lattice model that was used to show that fiber-fiber interactions could influence clot stiffness in compressed fibrin networks[53]. However, the extent to which such interactions contribute to overall clot stiffness has not been quantified.

Another model, based on the beam theory approach and network geometries obtained using a random walk algorithm, was recently developed to study the behavior of layered biomaterials such as electrospun polymeric scaffolds with a particular focus on studying orientation and bending properties of the fibers as well as their initial intersections within one layer and the immediately adjacent layers[43,54,55]. Additionally, continuous models have also been developed to efficiently simulate deformation of 2D layered materials at a mesoscale[56,57]. Both types of models were used to investigate how the structure of electrospun single 2D scaffolds affect their macroscopic mechanical properties. Authors successfully simulated multiple layers and found limited difference between monolayered and multilayered biomaterials under in-plane load[43]. While both approaches are important for studying layered materials, these types of models are not designed to capture the impact of fiber cohesion on the dynamical changes of the 3D structure of fibrin networks under stretching[32,45].

To summarize, most existing models do not consider bending of individual fibers or physical contacts between them, which can significantly alter the mechanical response of the entire fibrin network. These components are included in the recently developed Cohesive Fibrin-Fibrin Crisscrossing Model (CFFCM) described in this paper and used to study and quantify the contribution of fiber cohesion to local and global strain stiffening.

1.4. Synopsis

Oblique cohesive pairwise interactions (crisscrossing) forming between fibers were found to play a role in the viscoelastic response of compressed fibrin networks[8,45]. We hypothesized that increasing fiber-fiber cohesion can also contribute to the mechanical response of fibrin gels under tensile load. In this paper, this hypothesis is tested and proven by using a combination of experiments and model simulations obtained with a recently developed and calibrated three-dimensional (3D) computational nonlinear model of a fibrin network.

Using 3D confocal microscopy of stretched fibrin gels, we have visualized directly the fiber-fiber crisscrossing at relatively low strains, which provided a basis for including these structural features in a model for the mechanical response of fibrin to stretching deformations. The main feature of the model introduced here for the first time is that it considers cohesive pairwise interactions between fibrin fibers, physically calibrated mechanical bending and stretching properties of individual fibers, as well as describes structural properties of the entire fibrin network, including fiber connectivity, fiber and node density, and fiber alignment. The model is used to quantify the mechanical effects of fiber-fiber cohesion on the stress-strain response of the fibrin network, as well as spatial redistribution of the internal stress and network structural changes after the external tensile load is imposed on the network. Model-based simulations of fiber alignment and densification, as well as computed stress-strain relations for stretched fibrin clots, are shown to be in good agreement with experimental data. Altogether, the results obtained demonstrate that increasing fiber-fiber cohesion provides an important structural mechanism of fibrin clot stiffening in response to tensile load as it increases the fibrin network connectivity and enhances the distribution of stresses through the network.

2. Methods

2.1. Confocal Microscopy and 3D Reconstruction of Stretched Fibrin Networks

2.1.1. Formation and Stretching of Fibrin Clots

Fibrin clots were prepared from pooled human citrated platelet-poor-plasma (PPP) by mixing with CaCl₂ (26 mM final concentration) and thrombin (0.3 U/mL final concentration, Sigma-Aldrich, USA). To visualize fibrin in a fluorescence microscope, Alexa-Fluor 488-labeled human fibrinogen (Molecular Probes, Grand Island, NY) was added to plasma samples (0.08 mg/mL final concentration). Plasma clots were formed for 2 hours at 37°C in 4×60mm cylindrical plastic tube with its internal surface pre-coated with 4% (v/v) Triton X-100 in phosphate-buffered saline (PBS) to prevent adhesion of fibrin fibers to the walls. The clots were slipped out of the tubes into 1x PBS and cut by a surgical knife into 30 mm-long pieces that were held in the grips of a home-built stretching device and extended in uniaxial tension to different extents. The clots in the stretched state were fixed by immersing them for 20 minutes into 2% glutaraldehyde dissolved in PBS, rinsing them three times with PBS, and cutting them into 4mm × 4mm pieces used for imaging.

2.1.2. Confocal Microscopy and 3D Reconstruction Methods

Samples of fixed fluorescently labeled fibrin clots (non-deformed or stretched) were applied to a coverslip and imaged in the middle, away from the clamped ends of the clot using a Zeiss LSM880 laser confocal microscope with Plan Apo 40x (NA1.2) water immersion objective lens to acquire a series of high-resolution 212.5 μm × 212.5 μm × 20 μm z-stack images using the Airyscan mode. The distance between z-stack planes was 0.2 μm. An Argonne laser with a 488-nm wavelength was used for fluorescent imaging. 3D structures of fibrin clots were reconstructed from confocal microscopy z-stack images and analyzed using Imaris software.

2.2. Model Description

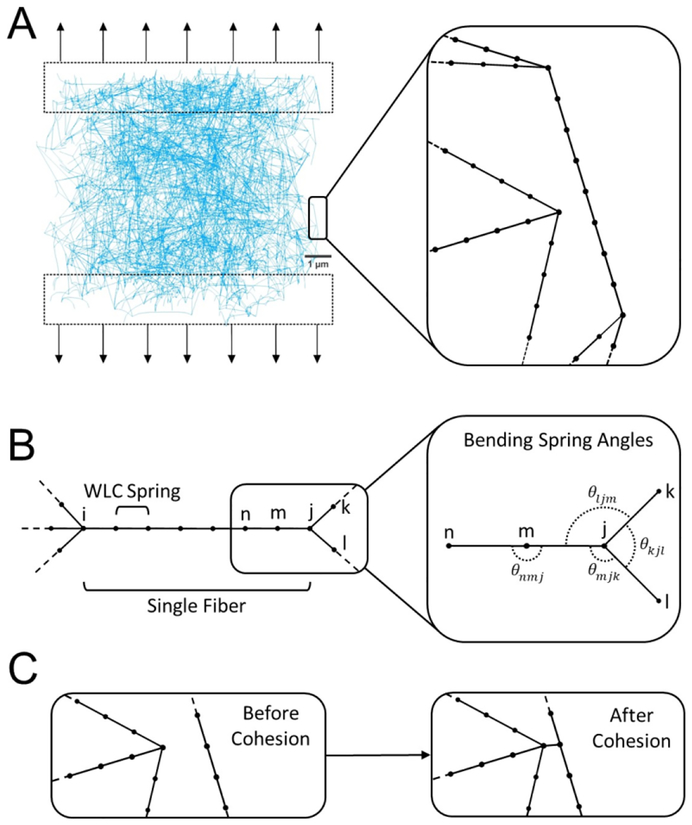
We use in this paper general bead and spring modeling approach to simulate single fibrin fibers, a method commonly used to model a single polymer or a system of polymers[25,29,58]. Specifically, we extend our previously developed model[45] by introducing interactions between individual fibers to represent fiber-fiber cohesion and potential fiber bending to study their biomechanical impacts on the fibrin network under stretching (Figure 1A). Though fibrin is a viscoelastic polymer, the elastic component is generally about an order of magnitude higher than the viscous component, although the viscous component increases at higher rates of deformation. In our simulations and with parametrization of fibrin mechanics at quasi-static rates, we did not address viscous properties or plasticity of fibrin networks. Each fiber in a network is represented as an elastic segment between two nodes (branch points) containing a series of sub-nodes connected by springs. We refer to network branch points as main nodes while using the term sub-nodes to indicate the nodes dividing the interior of a fiber (Figure 1B). We further assume that the mass of the individual fibrin fiber is lumped together at the main and sub-nodes in the model.

Figure 1.

Schematics of in silico fibrin clot stretching experiment and description of the individual fibrin fiber model. (A) Representative image of a three-dimensional fibrin network used in simulations. Black arrows show the direction of applied force. Zoomed section shows the detailed fibers. (B) Spatial discretization of a single fiber using 6 interior sub-nodes connected by WLC springs. i and j are the main nodes of the fiber. Zoomed section illustrates bending springs in a fiber using angular springs between nodes (including non-rotating both main and sub-nodes). (C) Representation of two fibers and a cohesive interaction between them.

The sub-nodes along a single fiber are placed equidistant to each other in order to represent a uniform distribution of mass and physical properties of the fiber. Moreover, a fixed spacing of sub-nodes serves to equally distribute possible fiber-fiber cohesion sites and points of fiber bending (see Figure 1B). Deformation is slowly applied to the network in order to keep the network at a quasi-equilibrium state. This state is achieved when the maximal normalized node speed is less than the width of a single fibrin fiber. A more detailed description of the quasi-equilibrium state is described in Supplementary Materials 1.2.4.

The dynamics of the fibrin network is formulated in terms of Langevin equations for each i-th node of the network as follows

$$m_i{\ddot{\mathit{x}}}_i={\mathit{F}}_i-\eta {\dot{\mathit{x}}}_i+{\mathit{F}}_i^B$$ (1)

where F_i is the deterministic force, $\eta {\dot{\mathit{x}}}_i$ is the viscous dampening force, and ${\mathit{F}}_i^B$ is the Brownian force satisfying the Fluctuation-Dissipation Theorem[59]. The inertial term is neglected and the system (1) is discretized using a Forward Euler scheme

$${\mathit{x}}_i^{n+1}={\mathit{x}}_i^n+\frac{dt}{\eta }\left({\mathit{F}}_i^n+{\mathit{F}}_i^{n,B}\right)$$ (2)

where the superscripts n and n+1 refer to the vector quantitates for the i-th node at subsequent time points n and n+1 and dt is the time step. η represents the drag coefficient. A detailed description of the model forces, coefficients, and calibration is continued in section 1.1–1.3 of the Supplementary Materials.

2.3. Statistical Analysis

Statistical analysis of experimental data was performed using GraphPad 7 software. Statistical significance between groups of samples was determined using Mann-Whitney U-test with a 95% confidence level. Results are presented as mean±standard deviation, unless otherwise indicated. 90 nodes of three independent donors were analyzed for network connectivity quantification.

In model simulations, statistical analysis was done by performing 5–10 simulations on independently generated fibrin networks. For model validation, section 3.2, 10 simulations were performed while 5 simulations were used for model prediction statistics in the remainder of the paper. We used 3-degree polynomial curves to fit the stress-strain data in Figures 3A, 4A, and 6A by performing a non-linear least squares optimization from the Python library SciPy[60]. The shaded error bars are calculated using the standard deviations in each polynomial coefficient given by ${\sigma }_i=\sqrt{co{v}_{ii}}$ where cov_iiis the diagonal element of the estimate covariance matrix of the optimized values of the estimated coefficients. In Figures 5 and S3, for each independent simulation, we calculated averages of node types for different levels of network strain. At each point of network strain, we calculated the mean and standard deviation from the resulting 5 average values. The error bars represent a single standard deviation from the mean.

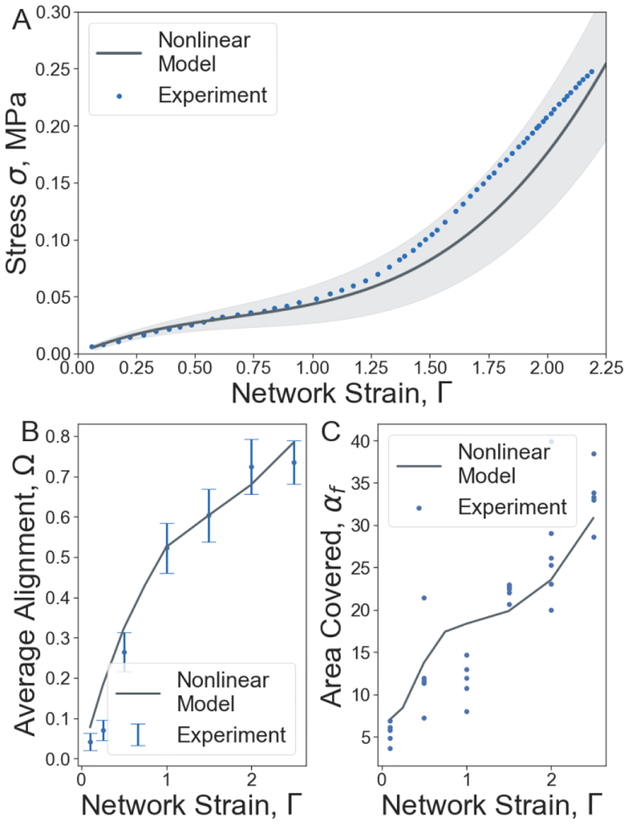
Figure 3.

Mechanical and structural changes of fibrin networks under uniaxial stretching. (A) Characterization of the mechanical and structural changes in the fibrin network in terms of the unidirectional tensile stress-strain response (M±SD, n=10). (B) Average fiber alignment in the central 50% region of the network. (C) Percent of the stretched fibrin clot cross-section area covered by fibers. The solid line shows the nonlinear model simulation results, circles are experimental data[5].

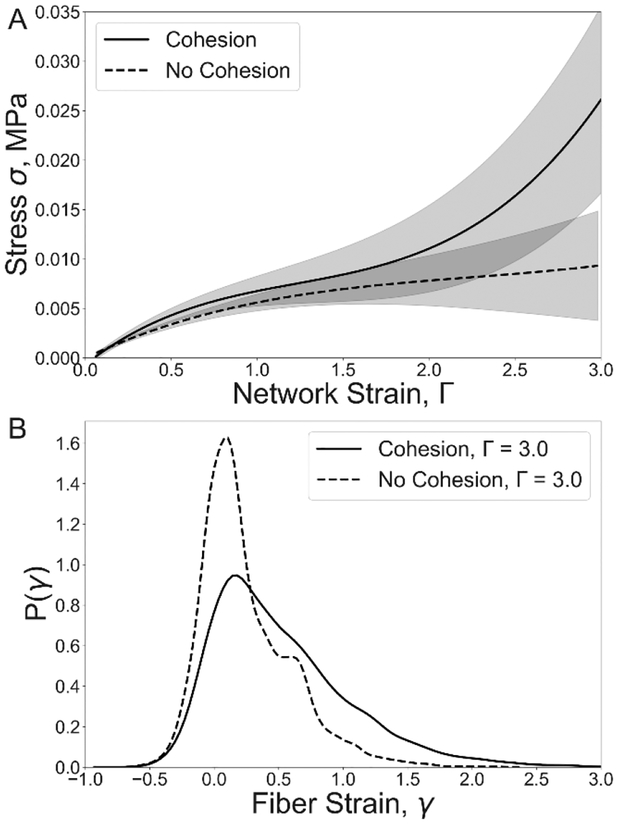
Figure 4.

Impact of fiber-fiber cohesion on the tensile stress-strain response and fiber strain distribution in stretched fibrin clots. (A) Tensile stress-strain responses (M±SD, n=5) for fibrin networks of cohesive and non-cohesive fibers of density 5 fiber/μm^3. (B) Corresponding strain distributions of individual fibers at the fibrin network strain.

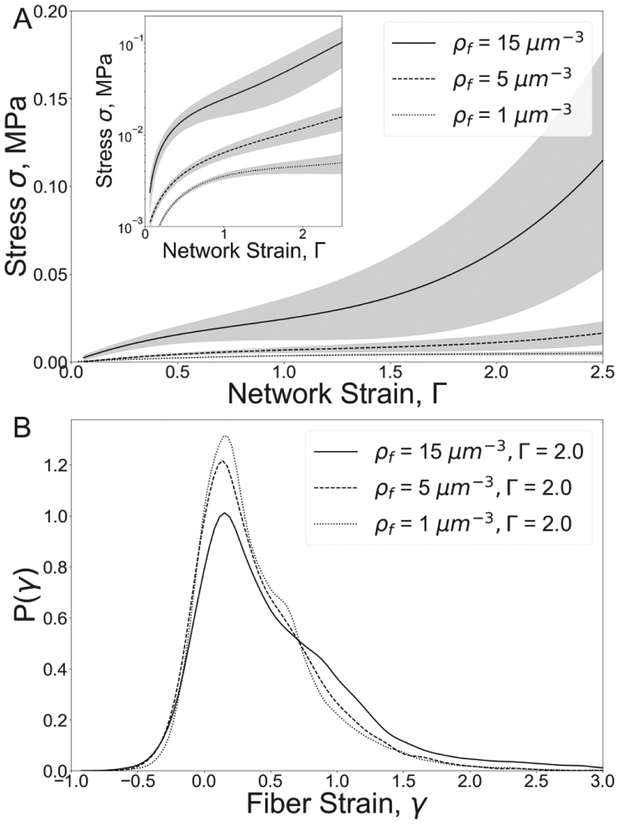
Figure 6.

Fibrin clot mechanical response and fiber strain probability distributions for different fiber densities. (A) Tensile stress-strain responses (M±SD, n=5) for fibrin networks of different fiber densities, ρ_f. The inset image shows the stress on a logarithmic scale. (B) Individual fiber strain distributions for the network strain Γ = 2.

Figure 5.

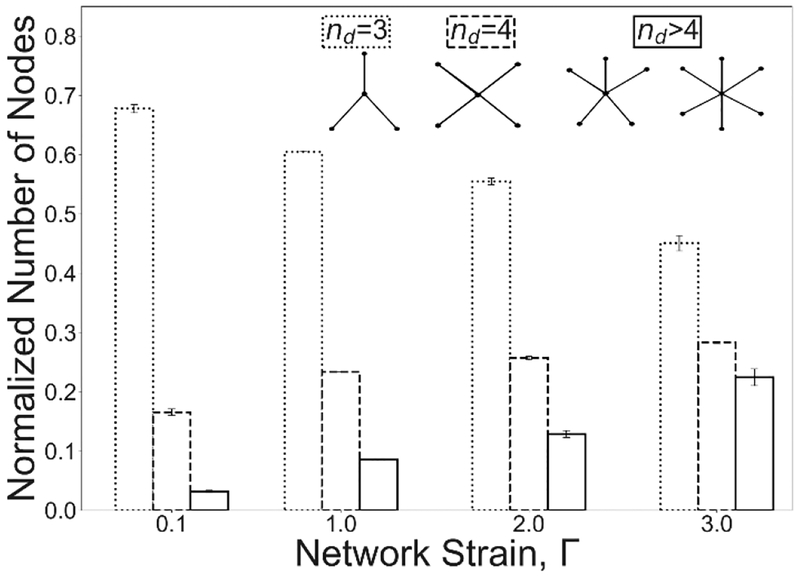
Strain-dependence of the node connectivity for fibrin networks with cohesive fibers. The fiber density ρ_f = 5 fibers/μm³. Dotted, dashed and solid lines in the columns correspond to the network connectivity degrees of 3, 4, and >4, respectively.

3. Results

3.1. Fiber Cohesion and Bending in Stretched Fibrin Network

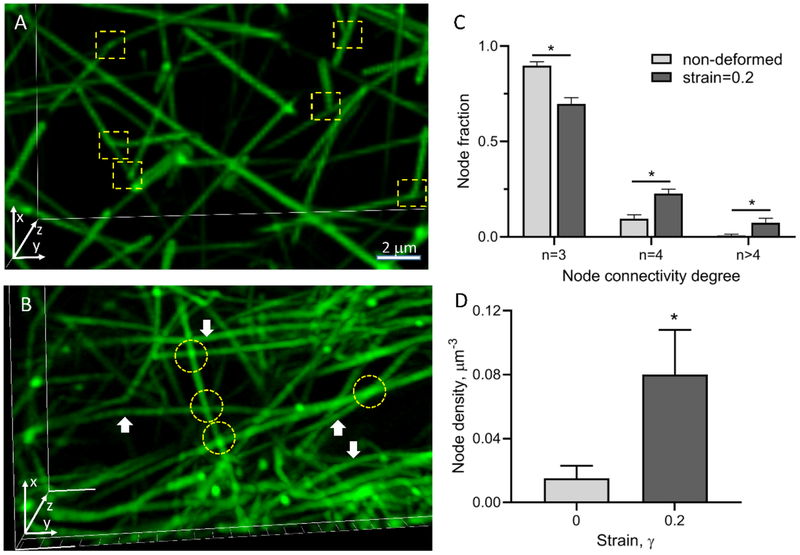
A 3D reconstruction of a hydrated fibrin network obtained using confocal microscopy revealed that non-deformed fibrin is an isotropic network of branched fibers, typically with three fibers joined at each branch point (Figure 2A), as observed in previous studies[45,61]. To observe structural alterations of fibrin networks upon application of a unidirectional tensile load, we stretched a cylindrical fibrin clot prepared as described in Methods to 20% strain and imaged the altered fibrin network structure using high-resolution fluorescence confocal microscopy. Subsequent 3D reconstruction of the stretched fibrin network structure revealed several specific structural changes (Figure 2B). First, most fibers were oriented in the direction of network stretching, which is consistent with earlier observations[5,6,38,62]. Second, some individual fibrin fibers were crisscrossed and formed cohesive contacts that were revealed by areas of increased fluorescence intensity (Figure 2B, yellow circles). The spots with increased fluorescence intensity confirmed that these fibers formed physical contacts between each other and not projected in separate planes.

Figure 2.

Visualization and quantitative structural analysis of non-deformed and stretched fibrin clots. (A) Reconstructed confocal microscopy-based 3D image of a fluorescently labeled non-deformed isotropic fibrin network. (B) Fibrin network stretched to a 20% strain in the y-direction. Fiber branch points are shown by yellow squares in (A) and fiber-fiber cohesion points are indicated by yellow circles in (B). Bent fibers are indicated by white arrows. (C,D) Quantification shows a node connectivity degree (C) and node density (D) in non-deformed fibrin clots and in the same clots stretched to a 20% strain (90 nodes analyzed in each fibrin clot prepared from 3 independent donors). The results in (C) and (D) are presented as M±SEM. A two-tailed Mann-Whitney U test, *P<0.05.

There were usually four fibers radiating from each of the crisscrossing points, indicating that formation of the cohesive contacts results in an increase of the number of 4-degree nodes in the network. The angles of crisscrossing were variable but most of them deviated from 90°; therefore, these inter-fiber contacts were mostly oblique. Further quantification of the reconstructed non-deformed and stretched three-dimensional fibrin networks revealed that stretching by 20% increased significantly the fraction of crisscrossing points (4-degree nodes) and nodes with connectivity degrees higher than 4 by a factor of 2.3 and 10 respectively, while the fraction of regular branching points (3-degree nodes) decreased by a factor of 1.3 (Figure 2C). Decrease of the fraction of regular branching points with strain can be both due to increase of crisscrossing points as well as due to interaction of 3-degree nodes with individual fibers or network nodes leading to increase of the fraction of nodes with connectivity degree higher than 4. It was also found that the density of fibers increased ~5-fold upon stretching at 20% strain (Figure 2D), implying that the pores between fibers were smaller and fibers became closer to each other. Finally, in the stretched clots (unlike what is observed in the non-stretched networks) a fraction of bent fibers (indicated by white arrows in Figure 2B) existed, suggesting the possibility of non-affine deformations of the fibrin network upon stretching[51,63]. The latter points out the fact that application of theoretical modeling approaches assuming an affine origin of network deformations might not be valid.

To the best of our knowledge, this is the first time that fiber-fiber cohesion and bending were directly visualized in fibrin networks under unidirectional external tensile load. These observations provide an experimental basis for a hypothesis that fiber-fiber cohesive crisscrossing may contribute to the mechanical response of the network. To test this hypothesis, we have used a specially developed multi-scale fibrin network model to computationally test the impact of fibrin fiber’s cohesive crisscrossing on the mechanical behavior of stretched fibrin networks.

3.2. Model Validation

To validate the computational model, we have simulated mechanical and structural responses of a high density fibrin network (30 fibers/μm³) by slowly applying a unidirectional stretching load and compared the response with experimental results[5]. The model was calibrated by fitting spring parameters and network structural features to microscopic experimental data as shown in section 1.2 of the supplementary materials. In Figure 3, we present a comparison between model simulation results and macroscopic experimental data. Comparison between experiment and simulation shows that simulation results fall within or near the range of experimentally observed network behavior in several different data fields. Simulations were performed by applying a linearly increasing external force to the opposite ends of a three-dimensional cubic fibrin network with volume 1000 μm³. The mechanical model correctly reproduces the linear and nonlinear parts of the stress-strain response curve measured in the experiments and here shown as blue dots (Figure 3A). As the strain increases from zero to 100%, the stress increases linearly, which is followed by a non-linear 545% increase in stress up to 0.236±0.063 MPa at 220% strain (Figure 3A).

To quantify changes in fibrin fiber orientation, average fibrin fiber alignment was calculated as $<cos\left(\text{2}\theta \right)>=\left(\text{1}/N\right){\sum }_{i=1}^{N}cos\left(\text{2}{\theta }_i\right)$, where θ_i is the smallest angle between the i-th fiber and the axis to which the force is applied. An angle ofθ = 0 occurs when the fiber is parallel to the direction of applied force with a resulting value of cos (2θ) = 1. Similarly, an angle of θ = π/2 occurs when the fiber is perpendicular to the direction of applied force. The perpendicular alignment results in a value of cos (2θ) =‒ 1. For fibers with no preferred alignment, the value of cos (2θ) will take a value between 1 and −1 respectively. The average orientation over all fibers in a randomly generated network, < cos(2θ) >, will be near 0.0. As the network is stretched, the fibers re-orient and the average orientation increase, but remains less than 1.0. In figures, the average alignment is referred to as Ω. Model simulations reveal a monotonic increase of the average fiber alignment with the increase of strain providing very good agreement with the experimentally measured orientation of fibrin fibers in stretched clots [8] (Figure 3B). The average alignment calculated from simulations is shown by dark lines while the experimental data mean and standard deviations are shown by blue dots and blue intervals respectively.

To find the percentile of the area covered by individual fibers, the middle cross-section area, S_c, of the clot is considered, and the relative area of fibers’ cross section is calculated as S_f=n_f*s_f, where n_f is the total number of fibers in the cross-section, and s_f = πd_f² is the fiber cross-section area. The calculated experimental percentage of the area covered by fibers from five different experiments are shown by blue dots, while the simulation average is shown by black solid line (Figure 3C). The simulations correctly predict the increase of the relative area covered by fibers, α_f=S_f/S_c, revealing a 4-fold increment in α_f at 220% strain (Figure 3C).

3.3. Fiber-Fiber Cohesion as a Mechanism of Network Stiffening

To assess the effect of fiber-fiber interaction on fibrin network mechanics, the stress-strain response curve was calculated for 5 different networks stretched up to 300% strain in the presence and absence of fiber-fiber cohesion. In section 3.2, a high density (30 fibers/μm³) simulated fibrin network was used. However, experimental work has shown wide ranges for fibrin density[5,8]. We therefore utilized a different fibrin network density of 5 fiber/μm³ to evaluate the impact of fiber cohesion on the mechanical response of the network to stretching loads. The stress-strain relation, σ(Γ) consisted of a linear portion for 0413<1 and a non-linear stiffening regime for Г>1 (Figure 4A). In contrast, in the absence of fiber-fiber cohesion, the stress-strain curve did not reveal stiffening and the tension in the network was 5 times lower than in the network with cohesive fibrin fibers at a maximum strain of 300%.

To evaluate the effect of cohesion on the strain of individual fibers within the networks, the fiber strain distribution for the two types of networks were calculated (Figure 4B). The fiber strain distribution of non-cohesive fibers revealed a distinct peak at 0.1 strain, with the fiber strain ranging from −0.5 to 2, where negative strain value corresponds to fiber compression. In cohesive networks, the peak of fiber strain shifted to 0.17 strain, and the number of fibers with strain greater than 100% increased more than 4-fold. Thus, the cohesion of fibers resulted in dramatic changes in the fiber strain distribution, leading to an increase in the strain of individual fibers in the network.

The change in stress distribution is due to network remodeling at the microscale. To quantify the change in network structure, differences in node degree were calculated as the networks were stretched. 3, 4, and greater than 4-degree nodes were counted for different network strains. Figure 5 shows a decrease by ⅓ in 3-degree nodes and a corresponding 2-fold and a 7-fold increase in 4 and >4-degree nodes, respectively, which is shown to be in a good agreement with the experimental data presented in Figure 2C.

3.4. Impact of Fibrin Network Density on Stretched Fibrin Clot Mechanics

Tensile deformation of a fibrin clot has been shown to result in a strain-dependent increase of network compaction manifesting as rising fiber and node density (Figure 2D). Fiber-fiber cohesion is correlated with network density such that high density increases the chance of fiber-fiber cohesion while low density decreases the chance of fiber-fiber cohesion.

To quantify exactly how changes of the fibrin clot density impact clot mechanical response to unidirectional stretching, the stress-strain curves were calculated for simulations for different clot densities (1–15 fiber/μm³) for strains from 0 to 250% (Figure 6). Increase in fibrin network density from 1 to 15 fiber/μm³ results in a significant 25-fold increase in the network stress at the maximal network strain of 250%. Denser networks of 15 fiber/μm³ demonstrated a distinct transition from a linear to a nonlinear regime at a network strain of 1.5. In contrast, sparse networks of low densities (<5 fiber/μm³) did not reveal stiffening behavior.

Analysis of fiber strain distributions revealed that there were more fibers at high strain (γ>1.0) in the networks of higher density, i.e. the mechanism of fiber cohesion is coupled to fiber density. As the network density increased from 1 to 15 fiber/μm³, the percent of high strained fibers (γ>1.0) increased by 200%, while the percent of low-strained fibers (0<γ<0.8) dropped by 15%. Thus, an increase in fibrin network density results in stiffening of the fibrin clot under tensile load accompanied by an increase in local strains within the clot.

3.5. Fiber Cohesion Increases Fiber Alignment in Stretched Fibrin Clots

As fibrin networks are stretched, individual fibers begin to align along the axis of applied stress. When force is applied to fibers at the edge of the clot, they immediately align with other neighboring fibers over the clot volume. Because fiber-fiber cohesion increases the connectivity of the stretched network (Figure 5) it triggers quicker and more efficient propagation of fiber alignment than that observed in non-cohesive networks. To evaluate the effect of fiber cohesion on fiber alignment upon stretching of fibrin clots, we analyzed the spatial distribution of fiber orientation in cohesive and non-cohesive networks undergoing stretching deformations for low (1 fiber/μm³) and intermediate (5 fibers/μm³) fiber densities. First, we found that the average fiber alignment in the central 50% region of clots stretched to 300% strain in the presence of fiber cohesion increased by 22% and 43% when compared to non-cohesive networks with fiber densities of 1, and 5 fibers/μm³, respectively (Figure S4 A, B). Furthermore, in higher density networks of 15 fibers/μm³ the average alignment increased by 57% at 250% strain.

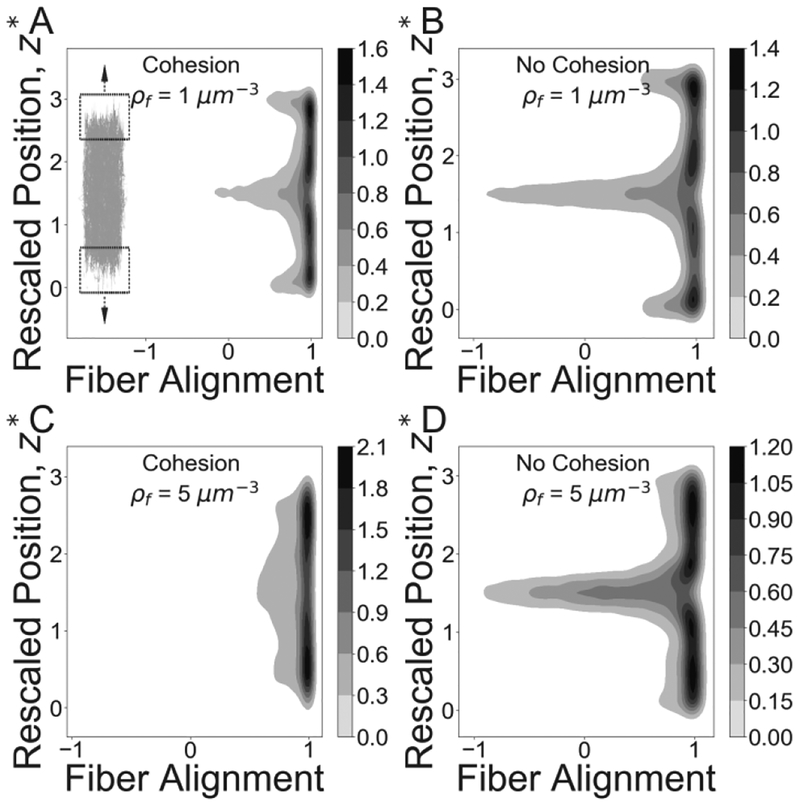
Next, we observed that cohesion induces a more uniform spatial alignment of fibers. In the presence of cohesion, fibers in the central portion of the clot (20% of the clot length) were found to be 45% more aligned in the direction of stretching than fibers in clots without cohesion at a concentration of 1 fiber/μm³ clot at 300% strain. Moreover, in the cohesive networks with higher fiber densities of 5 fibers/μm³, the same estimates yielded larger spatial increase in average fiber alignment of over 200% (Figure 7).

Figure 7.

Impact of cohesive fiber-fiber interactions on fiber network alignment. Joint distributions for network alignment and network strain are shown for cohesive and non-cohesive networks at 300% strain for fiber density 1/μm³ (A, B) and 5/μm³ (C, D). Simulated networks are shown alongside the joint density distribution to illustrate the corresponding location of aligned fibers. The Y-axis represents the scaled position along the length of the fiber network, z* =z/z₀. Z₀ is the original clot length and z ranges over the current network length from bottom (z = 0) top (z = 3 * z₀) Greyscale at each point corresponds to the relative number of fibers oriented along the direction of the strain.

Taken together, our simulation results suggest that cohesion of fibrin fibers enhances their alignment in clots undergoing stretching, which positively correlates with the increase of the initial clot density.

4. Discussion

Fibrin is a hydrogel with unique mechanical properties that determine behavior of blood clots and thrombi in the highly dynamic intra- and extravascular environment. In addition to the pathophysiological implications of fibrin clots, the rapidly developing field of bioengineering uses fibrin gels as a versatile biomaterial with tunable mechanical properties. Despite the great increase in our knowledge regarding the mechanics of fibrin, much about the structural mechanisms of fibrin’s viscoelasticity remains unknown. In this paper, we used a combined experimental and computational approach to further study the structural mechanics of fibrin networks. Our approach analyses experimental structural data extracted from fiber networks and uses it for calibration of a specially developed computational model based on basic physical principles that incorporates fiber-fiber cohesion during tensile deformation of fibrin networks.

Mechanical properties of fibrin have been studied across multiple spatial scales and under various types of deformation, including stretching, compression, and shear pressure[34,47,48]. One of the most general mechanical properties of fibrin is a non-linear mechanical response known as strain-stiffening behavior which has been explored extensively but still does not have a comprehensive structural explanation.

Although the structural basis for fibrin mechanics has been analyzed at various spatial scales, from the sub-molecular up to macroscopic levels, the mechanical behavior of the whole fibrin gel is governed largely by the properties of single fibers and their ensembles [9]. Stiffening of individual fibers plays a crucial role in the large scale elastic response of the entire network by equitably distributing the strain through the network [10,40]. Another important mechanism of strain-stiffening is the reorganization of the network architecture[40,64]. This architectural reformation includes fiber densification and bundling[5], but other structural alterations have been proposed, such as the natural inclination of fibers to adhere to one another[53,65].

In this paper, we successfully tested for the first time a stiffening mechanism based on fiber-fiber cohesion in stretched fibrin networks. First, we performed high-resolution optical microscopy that followed structural changes of stretched fibrin networks at the level of individual fibers. In addition to the well-known fiber alignments along the direction of strain, the observed structural alterations included the formation of fiber-fiber cohesive contacts named fiber crisscrossing and fiber densification (Figure 2). One consequence of the crisscrossing was shortening of fibrin fibers and their partial bending. Similar structural changes were revealed earlier in compressed fibrin networks. They were much more pronounced and their contribution to the non-linear mechanical response was straightforward[8]. However, such fiber-fiber cohesion has never been associated with tensile deformations of fibrin networks and the role of this structural mechanism has never been evaluated.

To establish mechanistic and quantitative relationships between the fiber-fiber cohesion and elasticity of individual fibers and bulk fibrin gel, we have developed a computational model that was calibrated based on comparing simulation results with the experimentally obtained stress-strain profile, alignment, and density data. (The structure of the developed biologically calibrated model and its distinction from previous modeling approaches for studying fibrin mechanics are summarized in section 2.2.)

Experimental data presented in this paper (Figure 2) suggests that fiber cohesion also correlates with clot stretching in addition to fiber alignment and densification. The computational model simulations were used to test the hypothesis that cohesion provides a previously unnoticed mechanism for fiber alignment and densification. To ensure that this behavior was due to fiber cohesion, the simulated network node connectivity was quantified and shown to vary as a function of network density and strain (Figure 5 and S3). Specifically, as network density increased from 1 to 15 fibers/μm³, a more rapid increase in nodes with connectivity degrees >4 (Figure S3C) was shown to be associated with a more rapid increase in average alignment (S4A–B) and densification (S4C–D).

Using the model, we have established the following structural and mechanical relationships that could not be explored experimentally at this time. (i) Fiber cohesion is shown to induce strain-stiffening in fibrin networks (3.3). This is supported by simulations in the absence of cohesive fiber-fiber interactions, which did not reveal stiffening of the networks and failed to predict the experimental data (Figure 4). (ii) Fiber cohesion is shown to alter the network structure (3.3). Since this has not yet been quantified in experiments, we predict and quantify network alterations in terms of node degree (Figure 5). (iii) Networks experience more alterations in the presence of high fiber density (3.4). This adds to more rapid network stiffening (Figure 6), which is associated with increased fiber alignment (Figure 7). (iv) We predict the change in fiber alignment due to a change in fiber density (3.5). We further validate this mechanism in Supplementary Materials by showing that fiber strain is distributed more equitably throughout the network (Figure S5).

Notice that our experiments and model have some objective limitations. It is not feasible at this time to experimentally study fibrin clots in which fiber-fiber crisscrossing is selectively prevented. Therefore, the impact of fiber cohesion has been confirmed by using a computational model. Although our simulations were done in the overdamped regime using one-way coupling with fluid, the model permits a two-way coupling extension for network-fluid interactions. Such two-way coupling may be important for modeling large compressive deformations of blood clots which are not considered here and are beyond the scope of the current study. The model can be also extended in the future to account for other types of network deformations including twisting behavior of fibers. These limitations do not affect the main conclusions of the paper and our results clearly show that forming cohesive fiber-fiber interactions make an important contribution to the mechanical response of fibrin networks under stretching deformation. Remarkably, model simulations incorporating fiber-fiber cohesion correctly describe the general behavior of real fibrin clots under unidirectional tension[8], including the stress-strain response as well as fiber orientation and fiber density changes. This suggests that fiber-fiber cohesive bond formation is an important mechanism contributing to fibrin clot stiffening and alignment.

Although the molecular mechanism of fiber-fiber cohesive bond formation is not known, various covalent and non-covalent bonds might form between fibers in contact. Covalent binding can be potentially mediated by isopeptide bonds formed by factor XIII as the fibers are brought in contact. However, a recent study[65] showed that blocking factor XIII by an inhibitor did not change the interaction force between fibrin fibers suggesting a non-covalent interaction between the fibers in contact, probably mediated by αC-regions, which allow for interactions between fibrin protofibrils and fibers. Vos et al.[53] estimated the force between two interacting fibers to be 760 pN, strong enough to maintain junction integrity, which supports the modeling assumption that fibers brought in contact form irreversible bonds perhaps originating from multiple non-covalent interactions.

5. Conclusions

The nascent cohesive crisscrossing of fibers in stretched fibrin networks described in this paper, comprise a previously unnoticed structural mechanism that, in combination with other structural rearrangements, underlies stiffening of fibrin gels upon tensile deformation. Notice that the described mechanism involves two spatial levels of fibrin mechanics, namely the non-linear elasticity of individual fibrin fibers as well as bulk strain-stiffening of the entire fibrin gel.

One of the most likely physiological conditions where fiber-fiber cohesion may play a role in determining fibrin elasticity is clot deformation under hydrodynamic blood flow. The analysis of the network orientation in clots formed in vitro under different flow conditions revealed that fibrin fibers orientations were not random. Instead, fibers were found to be aligned in the direction of the shear stress[62,66] and their alignment is associated with an increased number of fiber-fiber contacts and cohesive interactions. Such networks must be more resistant to stretching deformations in the direction of alignment as the initial degree of alignment increases, suggesting that the mechanical response and structural stability of a blood clot are greatly affected by the flow shear. In other words, clot breakage and formation of thrombotic emboli in the regions of the circulation system with high shear, can be mechanically regulated due to increased stiffness of the aligned fibrin clots. The developed model can be further applied to other types of network deformations such as shear and compression, emphasizing its universality and applicability to mechanics of natural biopolymers and for designing biomaterials and in tissue engineering.

We expect that findings described in this paper can be extended to other hydrogels with filamentous scaffolds such as collagen, fibronectin, actin, and others that may undergo interfilamentous interaction upon deformations.

Statement of Significance.

Fibrin is a viscoelastic proteinaceous polymer that determines the deformability and integrity of blood clots and fibrin-based biomaterials in response to biomechanical forces. In this paper, a novel structural mechanism of fibrin clots’ mechanical response to external tensile loads is tested using high-resolution confocal microscopy and newly developed computational model. This mechanism, underlying local strain-stiffening of individual fibers as well as global stiffening of the entire network, is based on previously neglected nascent cohesive pairwise interactions between individual fibers (crisscrossing) in fibrin networks formed under tensile load. Cohesive crisscrossing is an important structural mechanism that influences the mechanical response of blood clots and which can determine the outcomes of blood coagulation disorders, such as heart attacks and strokes.