Abstract
The behavior systems framework suggests that motivated behavior—e.g., seeking food and mates, avoiding predators—consists of sequences of actions organized within nested behavioral states. This framework has bridged behavioral ecology and experimental psychology, providing key insights into critical behavioral processes. In particular, the behavior systems framework entails a particular organization of behavior over time. The present paper examines whether such organization emerges from a generic Markov process, where the current behavioral state determines the probability distribution of subsequent behavioral states. This proposition is developed as a systematic examination of increasingly complex Markov models, seeking a computational formulation that balances adherence to the behavior systems approach, parsimony, and conformity to data. As a result of this exercise, a nonstationary partially hidden Markov model is selected as a computational formulation of the predatory subsystem. It is noted that the temporal distribution of discrete responses may further unveil the structure and parameters of the model but, without proper mathematical modeling, these discrete responses may be misleading. Opportunities for further elaboration of the proposed computational formulation are identified, including developments in its architecture, extensions to defensive and reproductive subsystems, and methodological refinements.
Keywords: algorithm, behavior system, bout, Markov model, reinforcement, temporal organization
1. Introduction
A key feature of the behavior systems approach to learning, motivation, and cognition is the organization of sequential actions into nested behavioral states (Bowers and Timberlake, 2018; Fanselow and Lester, 1988; Pelletier et al., 2017; Silva et al., 2019; Silva and Timberlake, 1998a; Timberlake, 2001a, 1994, 1993; Timberlake and Lucas, 1989; Timberlake and Silva, 1995). Early descriptions of the reproductive behavior of stickleback fish (Tinbergen, 1942, cited by Bowers, 2018) and digger wasps (Baerends, 1941) suggested such organization: A sexually ready animal typically seeks mates first, then select among them, then mates with a selected conspecific, and then engages in postcopulatory behavior. Each link in this behavioral chain may be expressed in various specific actions, such as postcopulatory nest-digging in female wasps. Despite the longevity of this idea in classical ethology, only more recent laboratory research has capitalized on the hierarchical structure of sequential actions to develop an ecological account of psychological processes in a broad range of species (Bowers, 2018).
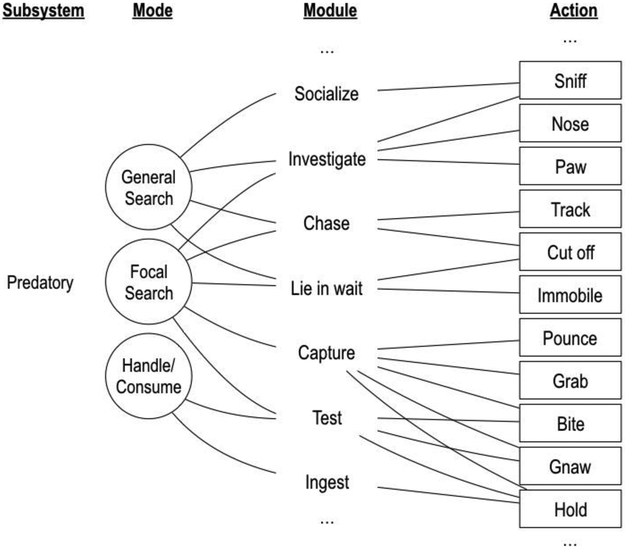
To illustrate the kind of behavioral organization postulated by the behavior systems framework, Figure 1 shows a hypothetical subset of actions and states that constitute the predatory behavior of a rat. Actions and states are organized according to the temporal proximity of a biologically relevant stimulus—general search occurs when preys are not readily available, consumption occurs when a prey is secured. One action in this subset, “sniffing,” may be an expression of either of two higher-order behavioral states—modules, in behavior-systems parlance: “socialize” or “investigate.” These modules, in turn, are nested within higher-order states—modes: “general search” and “focal search.” These modes are nested within a higher-order “predatory” subsystem, which is related to feeding functions, which is one of several functions that constitute a behavior system (Timberlake and Silva, 1995). A similar hierarchical organization of actions, arranged according to the temporal proximity of threats and conspecifics, is observed in defensive (Fanselow and Lester, 1988; Perusini and Fanselow, 2015) and reproductive (Akins and Cusato, 2015; Domjan, 1994; Domjan and Gutiérrez, 2019) subsystems. Implied by this organization of behavior is the notion that, within each level, the organism can only dwell in one state (or emit one action) at a time. In the predatory subsystem, for instance, if the rat is in focal search, it is not in general search, or if it is sniffing it is not pawing.1
Figure 1.
Hierarchical representation of a portion of the predatory subsystem of the rat, adapted from Timberlake (2001).
According to the behavior systems framework, actions, such as sniffing and pawing, are points of contact between organism and environment. At each of these points of contact, the relation between the organism and its proximal environment may change. For instance, by sniffing, the rat may enter in contact with proximal aerosolized particles that were previously undetected. This change in the relation between organism and environment may transition the organism to a new mode, module, or subsystem. The sniffed particles, for instance, may indicate the presence of a prey, which may transition the rat from investigating to chasing, which may be expressed in a new action, such as tracking; alternatively, an odor may indicate the presence of a predator, transitioning the rat from predation to defense. From an adaptive perspective, the dynamics of behavioral contact and state transition are shaped, either through natural selection or learning, to satisfy the function of the subsystem within which this process is embedded. In the example, the modes and modules that comprise the predatory subsystem of a rat support a cascade of actions that typically leads to the consumption of a prey.
2. Conditioned Responding: What and When
The behavioral systems framework has provided key guidance for empirical research and data interpretation over a broad range of phenomena, from unconditioned behavioral sequences (Baerends, 1976; Timberlake and Lucas, 1989), to fundamental learning functions (Krause and Domjan, 2017; Timberlake, 2004, 1994, 1993), to complex cognitive processes (Bowers, 2018; Bowers and Timberlake, 2018, 2017). Consider two examples:
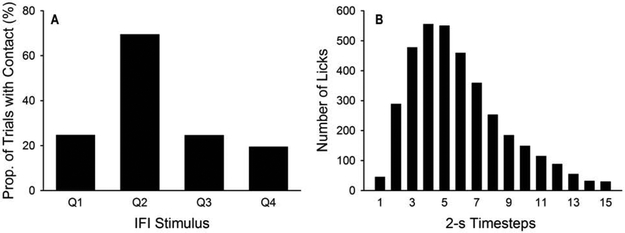
The first example is Silva and Timberlake’s (1998b) study on the response of hungry rats to stimuli presented at different times during an inter-food interval (IFI). In their Experiment 1, distinct visual stimuli signaled each of four 12-s quarters in a 48-s IFI. After sufficient training with these stimuli, presenting a rolling ball bearing (a prey-like stimulus) in the second quarter of the IFI (24-36 s before food) elicited more contact responses with the ball bearing than presenting it at other times (Figure 2A). These results support a key insight into associative learning: The behavioral expression of the association between two stimuli—e.g., visual stimulus and food—depends on the interval separating them. If the interval between conditioned stimulus and food is relatively long, the conditioned stimulus primes actions related to general search, such as tracking a moving object (Figure 1). In contrast, if the interval is relatively short, the conditioned stimulus primes actions related to focal search, such as grabbing an idle object. These actions are observed only if the appropriate stimuli are present to afford them, such as a rolling ball bearing for actions related to general search, and a metal lever for actions related to focal search (in sign-tracking experiments; see Anselme, 2016).
Figure 2.
(A) Proportion of trials in which rats contacted a ball bearing during each quarter of a 48-s inter-food interval (IFI). Adapted from Silva and Timberlake (1998b; Figure 3, group BB). (B) Number of licks rats made in each 2-s timestep across a 30-s IFI. Adapted from López-Crespo et al. (2004; Figure 2, Group FT 30).
The second example is Lucas, Timberlake and Gawley’s (1988) observational study of rat behavior across various IFIs (16-512 s). Drinking was among the behaviors recorded; its typical distribution over the IFI replicated a large number of studies showing excessive drinking early in the IFI (e.g., López-Crespo et al., 2004; Figure 2B), a pattern known as schedule-induced polydipsia. This behavior is generally treated as an anomaly, even as a model of compulsive behavior (Moreno and Flores, 2012). Lucas et al., however, suggest an alternative interpretation: drinking in rats is an action manifested in the early stages of the food-seeking behavior chain, particularly when pre-prandial behavior does not obscure it.
For learning scientists, a particularly important aspect of the behavior systems framework is that it is a theory of conditioned responding, whether Pavlovian (illustrated by the ball bearing study), elicited by a periodic stimuli (illustrated by schedule-induced polydipsia), or instrumental (Timberlake, 1993). This framework accounts for the form of the conditioned response (what the animal does; e.g., tracking vs. grabbing) and for its timing (when the animal does it; e.g., tracking typically happens earlier in the IFI than grabbing). It is important to highlight, however, that both accounts are typically formulated in qualitative form, relying primarily on verbal descriptions of response form and timing.
In most scientific domains, comprehensive accounts rely on explanations that are formulated qualitatively as theories (e.g., evolution by natural selection) and quantitatively as mathematical or computational models (e.g., population dynamics, artificial life). The latter explanations are neither substitutes of nor alternatives to the former. Instead, models complement theories by instantiating theoretical intuitions in algorithmic form and examining their implications. Complementing the qualitative formulation of the behavior systems framework with a quantitative formulation may thus aid in building a more comprehensive account of conditioned responding, enriching its account of behavior, broadening the range of its experimental predictions, and further solidifying its falsifiability.
The purpose of this paper is to identify those features of the behavior systems framework that may be more readily complemented with a quantitative account, and to articulate the foundation for such account. In particular, the paper focuses on the implications of the sequential organization of actions (illustrated in Figure 1) on the temporal organization of behavior. It examines the utility of representing such organization as a Markov model, with states representing various actions. On the basis of empirical data, various modifications are then introduced to this preliminary model: actions are replaced with discrete responses, which are then represented as the output of unobserved states, and the probability of states and outputs are made dynamic.
3. Modeling the Temporal Organization of Behavior
Although the behavior systems framework accounts for the form and timing of conditioned responding, only the latter seems—at least initially—amenable to a quantitative formulation. Whereas most quantitative theories of learning and motivation are agnostic about response form (Tsibulsky and Norman, 2007), they can be readily instantiated as mathematical state-based models that output the distribution of behavior over time (e.g., Daniels and Sanabria, 2017a; de Carvalho et al., 2016; Gershman et al., 2014). Therefore, as a first step to formulate the behavior systems framework quantitatively, it seems reasonable to focus on its account of the temporal organization of behavior.
Consider again Silva and Timberlake’s (1998b) ball-bearing contact study and Lucas et al.’s (1988) polydipsia study. The conventional qualitative formulation of the behavior systems framework explains performance in these studies in terms of the sequence of behavioral modes within the rat’s predatory subsystem, in which tracking a prey and drinking is the expression of a mode located early in the interval between feedings. The distribution of latencies to contacts and drinking bouts, or the precise distribution of the durations of those contacts and drinking bouts are beyond the scope of a qualitative formulation. These quantitative characteristics are nonetheless important, because they constrain the range of candidate mechanisms that may govern the transition between behavior modes, the duration of these modes, and the expression of actions within each mode. To account for the quantitative properties of the temporal organization of motivated behavior, and thus broaden the scope of the behavior systems framework, computational models of the processes that generate behavior may be devised and evaluated.
Computational models specify the interactions between components of a system, such that target features of the system may be simulated (Melnik, 2015; Pitt et al., 2002). The feature of behavior systems that this paper targets is the temporal organization of behavior that they imply. Simulating such organization requires precise rules that govern the relation among components of the system—in this case, among behavioral states and actions. The exercise of identifying these rules facilitates the identification of features of the system that are imprecisely defined in its qualitative description. For instance, when simulating the behavior of a rat engaged in food-seeking behavior, the behavior systems framework indicates that behavior should transition across behavioral modes, whose expression depends on available stimuli. Nonetheless, programming such simulation requires specifying the rules that govern those transitions—is the probability of a transition constant over time or variable? If variable, how does it vary? Is it independent on when prior transitions occurred, or on the duration of prior behavioral modes or actions (i.e., is it memoryless)? Specifying rules like these facilitates the distinction between structural aspects of the model—which define it—and parameters of that structure—which may vary between instantiations of the model (Lillacci and Khammash, 2010). It also promotes the formulation of more precise predictions and provides the analytic tools for testing those predictions. The importance of computational models to investigate complex systems, particularly in relation to behavior and cognition, has been widely discussed (Farrell and Lewandowsky, 2018; Kriegeskorte and Douglas, 2018; Tron and Margaliot, 2004).
Some preliminary steps are necessary to formulate a precise computational model of the temporal organization of behavior in any behavior subsystems (predatory, reproductive, defensive, etc.) Such steps involve focusing on a single subsystem, identifying key dependent measures, formulating the simplest model possible, and progressively building upon it to integrate relevant and available empirical data, thus seeking to balance three factors: adherence to the behavior systems approach, parsimony, and conformity to data. The preliminary formulation advanced here focuses on the predatory subsystem, particularly of the rat in laboratory conditions, mainly because informative data are more abundant for this motivational subsystem.
4. Behavior Systems as Markov Chains
From the perspective of the behavior systems framework, actions involved in seeking food, securing mates, or preventing predation are produced in a modal yet flexible order that facilitates contact with or avoidance of key stimuli. The simplest computational model that generates a stochastic sequence of actions is a Markov chain (Gagniuc, 2017). As applied to animal behavior, Markov chains involve the probabilistic transition between observable actions (states) in discrete timesteps,2 such that the probability distribution of actions in timestep t depends exclusively on the action realized in timestep t – 1.
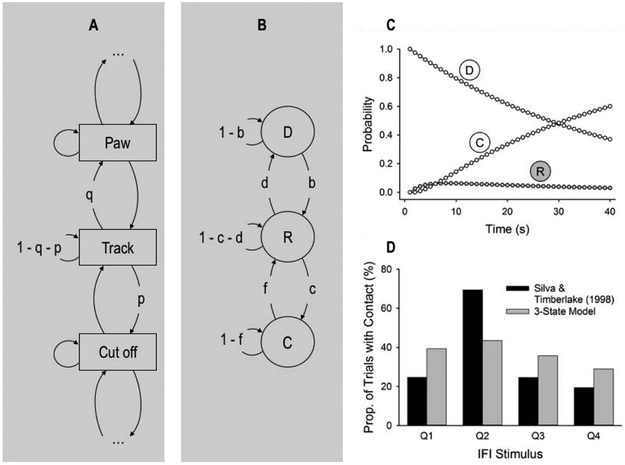
Markov chains have been widely used to model a broad range of behaviors in natural habitats (e.g., Meissner et al., 2015), including foraging patterns (e.g., van Gils et al., 2015). In relation to behavior systems, Figure 3 A shows a potential representation of a portion of the predatory subsystem of the rat as a Markov chain. In this example, a rat tracking a potential prey may transition to cutting off a escaping prey with probability p, or transition back to pawing its prey with probability q, or remain tracking with probability 1 − q − p; all transition probabilities from a state, including self-transitions, must add to unity.
Figure 3.
(A) Markov-chain model with actions represented as states. (B) Three-state model with disengagement, D, response, R, and consumption, C, states. (C) Probability of each state per time-step in a 40-s IFI according to the 3-state model, with b and c fit to Silva and Timberlake’s (1998b) data in Figure 2 (b = .0252, c = .3374; d = f = 0). The probability of state n in timestep t, pt(n), was pt(D) = (1 − b)pt-1(D), pt(R) = bpt-1(D) + (1 − c)pt-1(R), and pt(C) = cpt-1(R) + pt-1(C), with p1(D) = 1 and p1(R) = p1(C) = 0. (D) Proportion of trials with ball-bearing contact (state R) in each quarter of the IFI in the Markov-chain model simulation using the parameters of panel C, along with the data from Silva and Timberlake (1998b).
5. Actions as Markov States
Action sequences obtained from detailed and systematic behavioral observations, such as those provided by ethograms, may aid in further elaborating a model like Figure 3A. The wealth of behavioral information that these sequences contain is critical to study the adaptation of species-specific behavior to its ecological niche and its expression in natural and artificial environments (e.g., Pelletier et al., 2017). However, data drawn from ethograms confound multiple sources of variability, including those derived from mismatches among observations, behavioral categories, and functional actions, and those derived from the stochastic nature of transitions between actions. Methodological tactics such as interrater reliability address some but not all of these challenges. Also, the definition of each action may be refined on the basis of the correlation among its ostensive components, that is, among “sub-actions.” This latter solution, however, is rarely implemented in ethological studies, perhaps because it implies a potential infinite regression, having to define sub-actions in terms of sub-sub-actions, and so on. Slater (1973) discusses in detail the challenges of defining behavioral categories to characterize streams of behavior.
Methodological issues aside, an ethogram-based Markov chain is vulnerable to relying on incorrect assumptions. A key assumption of Markov chains is that they are memoryless: whether the organism remains in the same state or transitions to another state depends only on its current state and its transition probabilities to other states. If it is assumed that the predatory subsystem of a rat (Figure 3A) operates as a Markov chain, with individual actions constituting its states, then the probability of cutting off a prey’s escape after tracking it should not depend on what the rat was doing before tracking the prey. It is possible, however, that the tracking-cutting off sequence is the end portion of a longer pre-programmed “interception” sequence, such that cutting off after tracking is more likely if tracking is preceded by pawing. This would mean that a future state (in timestep t + 1) is selected on the basis of a prior state (in t − 1), a demonstration of memory that is incompatible with the representation of the system as a Markov chain. In fact, the categories that Staddon and Simmelhag (1971) used to describe the behavior of pigeons between periodic deliveries of food were analogous to the actions of Figure 3A, and show sequential dependencies that do not meet the memorylessness assumption of Markov chains (Staddon, 1972; for a similar finding in rats, see Staddon and Ayres, 1975). This problem may be addressed using higher-order Markov chains, in which the probability distribution of actions in timestep t depends on actions realized in timesteps t − 1, t − 2, etc. (Raftery, 1985). Such approach, however, entails a substantial increase in the complexity of the model.
Alternatively, instead of representing each action as a separate Markov state, these may be represented as components of higher-order functional units, more akin to modules or modes in Figure 1. These units may not only prove to meet the memorylessness assumption of Markov chains, but may also reflect the fractal organization of behavior (e.g., Magnusson et al., 2016; Seuront and Cribb, 2011). These module-like behavioral categories may be built on the basis of shared variance among its component actions (e.g., Espejo, 1997; Ivanov and Krupina, 2017). When such tactic is adopted, however, the memorylessness of behavioral categories is typically presumed; data supporting such presumption on any motivational subsystem has not been reported.
6. Discrete Responses as Markov States
There is yet another way of leveraging the notion that mode- or module-like behavioral categories, rather than specific actions, constitute memoryless Markov states. Instead of defining these categories in terms of intercorrelated actions, they are defined in terms of the occurrence of a discrete response, often measured automatically. These responses are thus treated as manifestations of an underlying behavioral category. Silva and Timberlake (1998b) adopted this assumption when interpreting discrete contacts with a rolling ball bearing as a manifestation of a general-search predatory state. Whether such contacts are memoryless or not (i.e., whether or not a Poisson process generates them) is an open empirical question. However, examples from other domains suggest that this is a fruitful approach. For instance, the locomotion of rats across predefined segments of a modified elevated plus-maze appears to show such memorylessness, and also appears to be associated with defensive actions (Tejada et al., 2010). As will be shown, the memorylessness that is characteristic of Markov processes is also evident in discrete, automatically-recorded food-reinforced responses, such as key pecking in pigeons and lever pressing in rats.
7. Modeling General Search Behavior Induced by Period Feeding
Discrete contact with moving objects, locomotion across discrete spaces, and discrete food-procurement responses are informationally leaner than ethogram-derived behavioral sequences. Nonetheless, discrete responses may provide a simpler and more reliable first step toward the validation and refinement of models such as the one shown in Figure 3A. To illustrate the advantage of this approach, a simple, generic, and preliminary Markov-chain representation of a behavior subsystem is proposed and applied to model general search behavior related to predation.
The Markov model in Figure 3B reformulates the model in Figure 3A in terms of only three states: A disengagement state (D), a target response state (R), and a consumption state (C). Each state is a generic representation of a category of actions: the actions in R are those that are expressed as the discrete target response (e.g., tracking and cutting off a moving prey-like object may be expressed as “contacting a rolling ball bearing”), whereas the actions in D and C are those that precede and follow, respectively, those in R (e.g., D may include postprandial behavior, Silva and Timberlake, 1998a; C may include biting and gnawing). The arrows indicate transition probabilities between states, each identified with a letter (b, c, d, f), and self-transitions (1 − b, 1 − f, etc.) For reference, Table 1 lists key components of this 3-state Markov model, along with more components introduced later in more elaborate models, and the role every component plays in each model.
Table 1.
Model components and their characteristics
| Component | 3- and 4-State* (Figs. 3-4) |
Visit-State (Fig. 7A) |
Hidden Markov (HMM; Fig. 7B) |
Partially Hidden Markov (PHMM; Fig. 9) |
Nonstationary PHMM (nPHMM) |
|---|---|---|---|---|---|
| States and Outputs | |||||
| D (disengagement)* | Observable State | Observable State | Hidden State | Hidden State | Hidden State |
| R (response) | Observable State | Observable State | Observable Output | Observable Output | Observable Output |
| V (visit) | --- | Observable State | Hidden State | Hidden State | Hidden State |
| C (consumption) | Observable State | Observable State | Hidden State | Hidden State | Hidden State |
| Transition and Output Probabilities | |||||
| b (D → R) | Fixed | --- | --- | --- | --- |
| b (D → V) | --- | Fixed | Fixed | Fixed | Dynamic |
| c (R → C) | Fixed | Fixed | --- | --- | --- |
| c (V → C) | --- | --- | Fixed | May depend on R | May depend on R |
| d (R → D) | Zero | --- | --- | --- | --- |
| d (V → O) | --- | Fixed | Fixed | Fixed | Dynamic |
| w (V → R) | --- | Fixed | Fixed | Fixed | Dynamic |
| q (D → R) | --- | --- | --- | Fixed | Dynamic |
In the 4-state model, D is split into two states, D1 and D2.
To test whether the 3-state model in Figure 3B can account for general search behavior, it was fit to the data in Figure 2, with the simplifying assumption that d = f = 0 (allowing d or f to take other values does not improve fit). This instantiation of the model thus assumes that, after each feeding, rats transition to D,3 from which, on each timestep, it may transition to R with probability b, and from R to C with probability c, where it dwells until the next feeding is completed; rats cannot return to a previous state. Figure 3C shows the fitted probability of each state at each of 40 timesteps in the IFI. Based on these probabilities, a fitted proportion of trials in which the (simulated) rat dwelt at least for one timestep in R (i.e., the proportion of trials with a ball-bearing contact) was computed for each quarter of the IFI. Figure 3D shows these proportions, along with the data from Silva and Timberlake (1998b).
It is readily evident from Figure 3D that the 3-state model, even when fit to data, cannot account for the high probability of observing contacts in the second quarter of the IFI; the model accounts for just 33% of the variance in the data. Nonetheless, a slightly more elaborate 4-state model (Figure 4A; transition probabilities of zero are removed) performs substantially better (Figures 4B and 4C). The new state (D1) may represent a post-prandial state, or some other pre-tracking interim state that more detailed observation may reveal (Staddon and Ayres, 1975). The improvement obtained from adding a second state before R is observed in a 10.6% increase, relative to the 3-state model (Figure 3D), in trials with a contact in the second quarter, and a reduction of similar magnitude in trials with a contact in the fourth quarter; this 4-state model accounts for 70% of the variance in the data. In fact, a 5-state model with three states prior to R (not shown) performs even better, accounting for 84% of the variance in the data.
Figure 4.
(A) Four-state Markov model with two disengagement states (D1 and D2). (B) Probability of each state per time-step in a 40-s IFI according to the 4-state model, with a, b, and c fit to Silva and Timberlake’s (1998b) data in Figure 2A (a = b = .1103, c = .5122). The probability of state n in timestep t, pt(n), was pt(D1) = (1 − a)pt-1(D1), pt(D2) = apt-1(D1) + (1 − b)pt-1(D2), pt(R) = bpt-1(D2) + (1 − c)pt-1(R), and pt(C) = cpt-1(R) + pt-1(C), with p1(D1) = 1 and p1(D2) = p1(R) = p1(C) = 0. (D) Proportion of trials with ball-bearing contact (state R) in each quarter of the IFI in the Markov-chain model simulation using the parameters of panel C, along with the data from Silva and Timberlake (1998b).
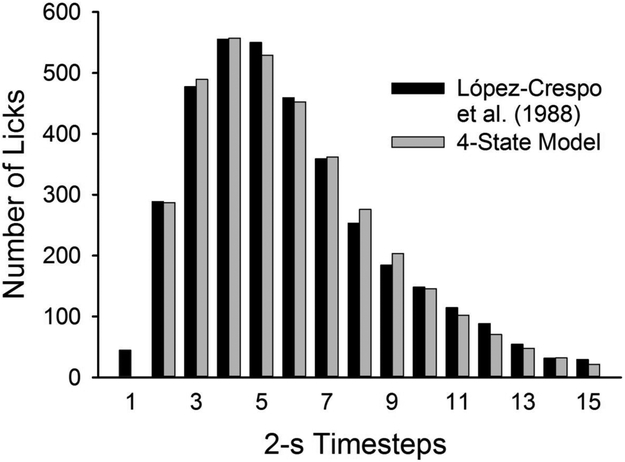
To further evaluate the 4-state model, its parameters were adjusted to account for the drinking data from López-Crespo et al. (2004; Figure 2B). Figure 5 shows that, when multiplied by a scaling factor and fitted to the data, the expected changes in the probability of R over the IFI closely resembles the pattern of drinking that periodic feeding elicits.
Figure 5.
Number of licks as a function of time in a 30-s IFI according to the 4-state model, with a, b, c, and a scaling factor k fit to López-Crespo et al.’s (2004) data in Figure 2B (a = b = .4014, c = .4932, k = 1783 licks). The number of licks in timestep t was k[bpt-1(D2) + (1 − c)pt-1(R)]; the probability of each state was calculated as in Figure 4. The data from López-Crespo et al.’s (2004) is shown again in black columns.
Figures 3 through 5 show that, when general search behavior is expressed and measured as discrete target responses (contacts, licks), inferences may be drawn about the computational processes that govern their temporal organization. The behavior systems framework suggests that such processes may be generically represented as relatively simple Markov-chain models. In the particular case of periodic feeding, Silva and Timberlake’s (1998b) data suggests that rats transition through at least 5 behavioral states in 48-s periods; 4 states are sufficient to explain López-Crespo et al.’s (2004) data. These states may thus constitute the “internal clock” of interval timing models, which are behaviorally expressed as distinct responses (cf. Fetterman et al., 1998).
8. Modeling Instrumental Focal-Search Behavior
Perhaps the validity of the Markov model proposed in Figure 4A derives from the simplicity of the data that validates it. In particular, the low-resolution nature of the data in Figure 2 may obscure key limitations of a simple Markov-chain model of the processes underlying those data. For instance, a Markov-chain model like Figure 4A with n states preceding R (i.e., D1, D2, D3, … Dn, R, etc.) with equal transition probabilities predicts that intervals between trial onset and first response (contact with a ball bearing in Silva and Timberlake’s, 1998b; lick in López-Crespo et al., 2004) would follow a negative binomial distribution. Such distribution is not visible when responses are just counted, particularly if those counts are binned within broad segments of the IFI.
Whereas data on the precise temporal organization of unconditioned and Pavlovian responses are scarce (a noticeable exception is Killeen et al., 2009), comparable data on instrumental behavior are abundant. These data have been collected to test different accounts of the distribution of instrumental behavior over time under various schedules of reinforcement, including periodic reinforcement (e.g., de Carvalho et al., 2016; Machado, 1997) and reinforcement with constant probability (e.g., Brackney et al., 2011; Daniels and Sanabria, 2017b; Shull et al., 2001). Markov models of predatory behavior may thus be also tested against data on the temporal distribution of instrumental behavior.
When applying the model in Figure 3B to represent instrumental lever pressing in the rat, the generic states D, R, and C and their corresponding transition probabilities (Table 1) adopt new meanings and values. Instead of including general search behavior, state R now includes all food-seeking actions related to the imminence of food consumption (e.g., grabbing, gnawing), which may be expressed as a lever press; as before, D and C include all actions that precede and follow, respectively, those in R. According to this model, a rat may initiate a bout of lever presses with probability b. After each lever press, one of three events may occur: it may be reinforced (with probability c), it may end the bout (with probability d), or the rat may continue the bout with another lever press (with probability 1 − c − d). Transition probability c thus defines the schedule of reinforcement (e.g., a constant c represents a random ratio schedule). Because completion of reinforcement transitions the rat from C back to D (see footnote 3), it may be assumed that f = 0.
The Markov-chain model of instrumental behavior predicts that this behavior is organized in response bouts of geometrically-distributed length [mean = 1 / (1 − c − d) timesteps], separated by pauses also of geometrically-distributed length [mean = 1 / (1 − b) timesteps]. These predictions are consistent with the typical performance in simple variable-interval (VI) schedules of reinforcement, where rats produce response bouts and pauses of exponentially-distributed length (Brackney et al., 2011; Brackney and Sanabria, 2015; Jiménez et al., 2017; Shull et al., 2001).
9. The Visit-State Models
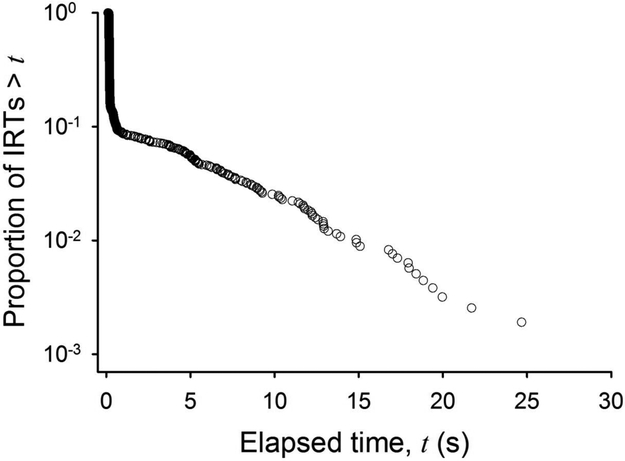
A closer examination of the distribution of instrumental inter-response times (IRTs) points at a limitation of the Markov-chain account of instrumental behavior, in interval schedules and otherwise. Regardless of schedule, the bout-and-pause pattern of instrumental behavior is typically expressed as a mixture of two IRT distributions (Blough and Blough, 1968; Brackney et al., 2011; Kirkpatrick and Church, 2003; Matsui et al., 2018; Reed, 2015; Reed et al., 2018; Shull et al., 2001; Tanno, 2016). One distribution, with a longer mean, corresponds to pauses between bouts of responding; the other distribution, with a shorter mean, corresponds to IRTs within those bouts. Under VI and variable-ratio (VR) schedules, where the probability of reinforcement is often constant over time and responses, respectively, both distributions are typically exponential (e.g., Matsui et al., 2018; but see Bowers et al., 2008; Tanno, 2016). The representation of this exponential-exponential mixture distribution in a semi-log survival plot shows a hockey-stick pattern normally observed in VI and VR data (Figure 6).
Figure 6.
Semi-log survival plot of inter-response times (IRTs) maintained by a tandem variable-interval (VI) 120-s fixed-ratio (FR) 5 schedule of reinforcement. The data are from a typical rat in Brackney et al. (2011).
Although, in the 3- and 4-state models (Figures 3B and 4A), between-bout IRTs may emerge from dwelling in D, within-bout IRTs cannot emerge from dwelling in R: the models do not allow for pauses between responses that are not disengagements. This may be solved by assuming that timesteps are separated by random pauses; under variable schedules, pauses would be exponentially distributed. Perhaps these pauses reflect the time it takes to produce the actions in R (Gharib et al., 2004). Regardless, the model would have to specify the parameters of that distribution and their provenance. In other words, addressing the limitations of the 3- and 4-state models necessarily entails added complexity.
Shull et al. (2001) suggested a parsimonious expansion of the 3-state model, one that fully accounts for the mixture distribution of IRTs. This visit-state model is shown in Figure 7A, with minor modifications with respect to Shull et al. (2001) for completeness and comparability. Killeen et al. (2002) first pointed out that the states of this model may be mapped to the modules and actions that constitute the behavior systems framework. Table 1 highlights the key differences between the 3-, 4-state models and the visit-state model.
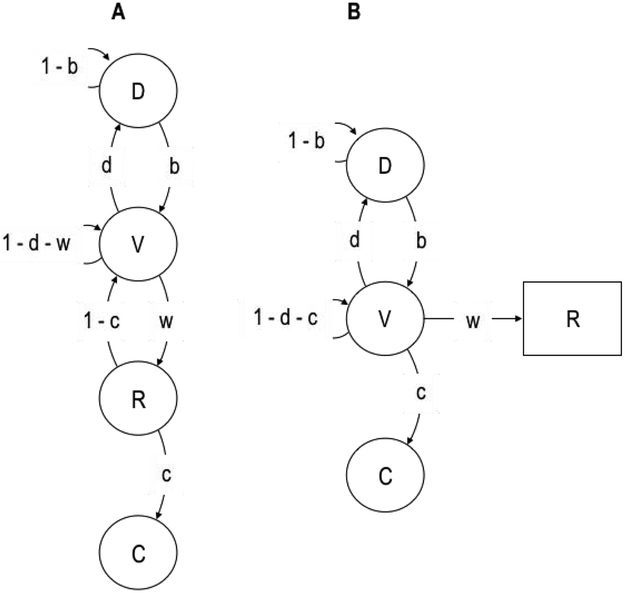
Figure 7.
(A) Visit-state model with four states, including a visit (V) state. (B) Hidden Markov model (HMM) with three unobservable states (circles) and one observable output (square).
By interpolating a visit (V) state between D and R in Figure 7A, the visit-state model can pause between responses without disengagement; those pauses are represented as self-transitions in V; there are no self-transitions in R. Nonetheless, if all the actions are already distributed among D, R, and C, what actions could V include? One possibility is that V corresponds not to any category of actions, but to the focal search mode, in which R-related actions may occur. Focal search may be expressed as R-related actions such as gnawing (through the activation of capture or test modules), but it may also be expressed as R-unrelated actions, such as tracking or pouncing (Figure 1), and other adjunctive behavior, such as drinking. The former would be expressed as lever presses; the latter would not. R-unrelated actions within the focal search mode may include responses directed at the lever that are, nonetheless, too weak to activate it. In any case, these actions may be represented each as an individual state connected to V. For simplicity, however, R-unrelated actions are represented as self-transitions in V. Thus, focal search—dwelling in V—sometimes results in lever presses (with probability w; Figure 7A) and sometimes not (with probability 1 − d − w). From this perspective, within-bout IRTs may not only reflect the time it takes to produce the actions in R, but it may also reflect the time it takes to produce R-unrelated actions while in focal search.
The analysis of discrete, measurable responses reveals key aspects of the temporal organization of behavior, including its fine structure—the short IRTs within response bouts. The mixture distribution of long and short IRTs, which justifies including V in the visit-state model, is not unique to instrumental behavior: it is also evident, although rarely reported, in Pavlovian, adjunctive, and even unconditioned behavior (Cabrera et al., 2013; Íbias et al., 2017, 2015; Killeen et al., 2009). For instance, rats and hamsters, when in a small enclosure furnished with a lever, will press the lever in bouts, generating IRT distributions similar to that in Figure 6, even though lever pressing has no programmed consequences (Cabrera et al., 2013). In this example, the emission of response bouts appears to reflect a rapid alternation between behavioral states V and R, which may correspond to the engagement of the defense-escape subsystem. Similarly, instrumental response bouts appear to reflect a similar alternation between states, which may correspond to a focal search for food.
10. Hidden States and Observable Outputs
The discrete responses that presumably unveil the underlying organization of behavior are only a small sample of the behavioral repertoire of an animal. The lever-pressing response is only one of many food-seeking behaviors expressed in the Skinner box (Timberlake, 2001b). This approach implies that only some behavior is observable—the discrete, measured response— and every other behavior is not. This distinction is not reflected in the models depicted in Figures 3, 4, and 7A. To incorporate it, it is necessary to couch the visit-state model as a hidden Markov model (HMM; Zucchini et al., 2016, 2008).
An HMM is a Markov model in which states are unobservable but may have probabilistic observable outputs. In the visit-state model, only the response state is actually observable, so it may be represented instead as an output of a hidden visit state. Figure 7B shows a preliminary sketch of the resulting HMM, applied to a rat lever pressing for food. In this sketch, states D, V, and C are hidden, but the response output from V is observable.4 Table 1 summarizes the key characteristics of the HMM and contrasts them against the visit-state model.
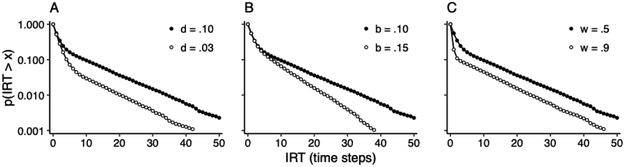
Figure 8 shows the result of simulating the HMM of Figure 7B with a baseline set of transition and output probabilities, and the effect of changing each probability separately.5 The results are shown as semi-log survival plots of IRTs expressed in timesteps. The hockey-stick pattern of these plots is consistent with the exponential mixture distribution of IRTs observed in rats responding on variable schedules of food reinforcement (cf. Figure 6). Moreover, the effects shown in Figure 8 are consistent with the effects of specific manipulations on VI performance. As d decreases, the “blade” (short) portion of the hockey-stick pattern of the IRT survival plot is extended (Figure 8A), reflecting longer dwellings in V. Schedule manipulations, such as appending a tandem ratio schedule to the VI schedule, have a similar effect on the IRT distribution of rats (Brackney and Sanabria, 2015; Shull, 2004; Shull et al., 2004, 2001; Shull and Grimes, 2003). As b increases, the slope of the “shaft” (long) portion of the survival plot becomes steeper (Figure 8B), reflecting shorter dwellings in D. Manipulations aimed at enhancing motivation, such as increasing the rate of reinforcement (Brackney et al., 2011; Reed, 2015, 2011; Reed et al., 2018; Shull, 2004; Shull et al., 2004, 2001; Shull and Grimes, 2003), the level of deprivation (Brackney et al., 2011; Johnson et al., 2009; Shull, 2004), and the magnitude of reinforcers (Shull et al., 2001), have a similar effect on rodent IRTs. Finally, as w increases, the slope of the blade portion of the plot becomes steeper (Figure 8C), reflecting the increased rate of responding within each visit. Motoric manipulations, such as changes in the manipulandum (Jiménez et al., 2017), have a similar effect on rat IRTs.
Figure 8.
Semi-log survival plots of simulated IRTs generated by the HMM of Figure 7B. A baseline simulation (closed circles) was generated using transition probabilities d = .10 and b = .10, and output probability w = .50. Each panel shows the effect of varying one of these probabilities (open circles): (A) The effect of reducing d to .03, (B) the effect of increasing b to .15, and (C) the effect of increasing w to .90.
Taken together, this pattern of empirical effects further validates the classification of motivated actions into three hidden states. When R corresponds to a focal-search action, the three states correspond to the three behavioral modes (post-food/general search, focal search, handle/consumption) that the behavior systems framework postulates. Moreover, empirical findings suggest that (a) the transition from post-food/general to focal search is governed not only by the proximity of the incentive (Silva and Timberlake, 1998a), but also by the motivational state of the organism and the quality of the incentive, and (b) the transition from focal search back to general search is governed by the completion of the learned actions required to retrieve the incentive.
So far, the HMM of Figure 7B appears to serve as a parsimonious computational hitch connecting theory (behavior systems) and data (e.g., distribution of IRTs in VI schedules). Nonetheless, further extensions of the model are required to strengthen that hitch. Some of these extensions are discussed next.
11. Instrumental Contingencies and “Disengaged” Responses
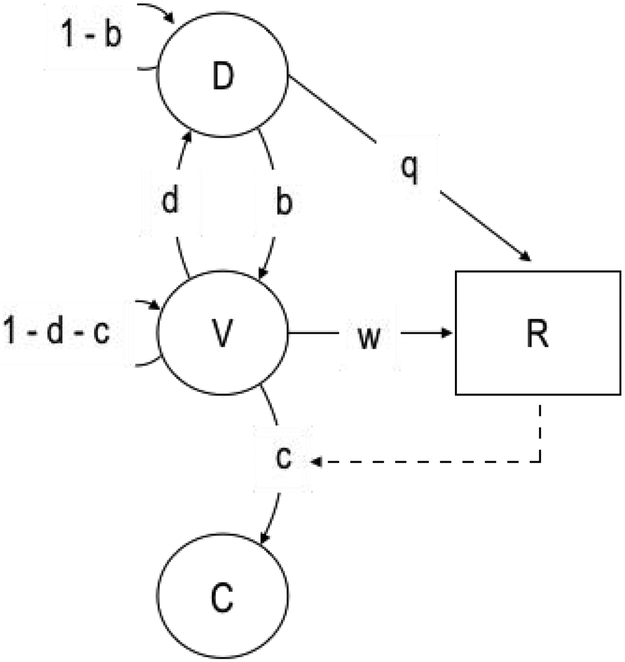
In the context of learning and motivation research, the contingencies that link actions to consequences are particularly important. These instrumental contingencies were represented in Figure 7A as c, the transition probability between R and C. However, in Figure 7B, R is no longer a state, and c is the transition probability between V and C; reinforcement cannot be contingent on V, because V is not observable. Incorporating an instrumental contingency into the HMM of Figure 7B would entail making the transition probability c a function of R; such function would represent a schedule of reinforcement. For instance, a random-ratio 1/c schedule would be implemented as c = 0 in the absence of R and c > 0 in the presence of R; in omission training (Sanabria et al., 2006), c = 0 in the presence of R and c > 0 in the absence of R for a period of time. Figure 9 represents a potential instrumental contingency as a dashed line connecting R and C. To the extent that the HMM includes a hidden state (C) that may be conditional on an observation (R), it constitutes a partially hidden Markov model (PHMM; Forchhammer and Rissanen, 1996). This distinct feature of the PHMM is highlighted in Table 1, indicating that c “may depend on R.”
Figure 9.
Representation of instrumental behavior as a partially hidden Markov model (PHMM). The PHMM adds to the HMM shown in Figure 6B the modulation of transition probability c by the observation of a lever press, and the output probability q (disengaged lever presses).
Another limitation of the models in Figure 7 is that they do not consider the possibility of responses that do not reflect the target behavioral mode. In fact, lever presses may occur as the expression of actions not related to the procurement of food, such as exploratory behavior (Cabrera et al., 2013). Inferences on the organization of behavior would be inaccurate if drawn from behavioral data that does not distinguish between responses that reflect the target behavioral mode and those disengaged responses that do not.
The visit-state model (Figure 7A) cannot represent disengaged responses adequately, because it does not allow for transitions from D to R without transitioning through V (D → V → R). Allowing a direct transition from D to R in that model would open a second route to initiate a visit (D → R → V). This second route seems at odds with the sequential organization of behavior implied in the behavior systems framework, and the mixture distribution of instrumental IRTs does not demand it. It would mean, for instance, that accidental lever presses during postprandial behavior would transition the rat into a food-seeking state. Moreover, one model that allows for this second route (Staddon and Simmelhag, 1971) fails to show the memorylessness that is characteristic of Markov models (Staddon, 1972; Staddon and Ayres, 1975).
The HMM (Figure 7B) cannot represent disengaged responses either, because it assumes that all responses are the output of V—i.e., that they all reflect the target behavioral model. To incorporate the disengaged responses, the PHMM of Figure 9 extends the HMM of Figure 7B by assuming that disengaged responses are the output of D with probability q; this additional parameter is listed as a component of the PHMM in Table 1. Unlike the visit-state model, disengaged responses in the PHMM do not entail the transition to a new state, so they do not create another route to V.
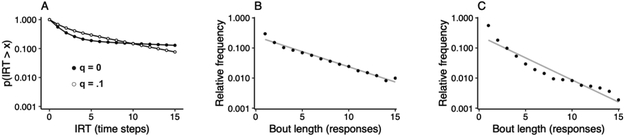
Disengaged responses may have a noticeable impact on the temporal organization of responses. When a rare disengaged response occurs, it (a) lowers the mean bout length by adding a one-response bout, and (b) increases the bout-initiation rate by turning an otherwise long between-bout IRT into two shorter IRTs. These effects are depicted in Figure 10A, showing that an increase in q (i.e., an increase in disengaged responses) produces a shorter blade and a steeper shaft of the IRT survival plot.
Figure 10.
Effect of disengaged lever presses (output probability q) on (A) the semi-log survival plot of IRTs, and on (B) the semi-log distribution of bout lengths. Data in panels (A) and (B) are from a simulation using three sets of parameters. In all sets, d = .10, and w = .50; in panel (A), b = .03 (both curves), q = 0 (closed circles), and q = .10 (open circles); in panel (B), b = .30 and q = .10. Panel (C) shows the mean estimated distribution of food-reinforced lever-press bouts, obtained from rats pressing 111-mm high levers in Jiménez et al. (2017). The lines in panels (B) and (C) are fits of geometric distribution functions.
Because IRT survival plots confound changes in q with simultaneous changes in d and b, evidence for the presence of disengaged responses must be sought elsewhere. One method to reveal these responses involves the estimation of the distribution of bout lengths (Brackney and Sanabria, 2015; Jiménez et al., 2017). According to the PHMM, bout lengths are sampled from a mixture of two geometric distributions, one generated from V and the other from D.6 If q is zero (no disengaged responses), then all bouts would be generated from V, and their lengths would thus be geometrically distributed; deviations from such distribution would therefore suggest the presence of disengaged responses. More precisely, a geometric distribution function fit to the distribution of bout lengths generated with q > 0 is expected to slightly underestimate the relative frequency of very short bouts (1-2 responses long) and slightly overestimate the relative frequency of bouts of intermediate length (Figure 10B).
A challenge to this approach is that bout lengths are not directly visible, so their distribution is not known. Nonetheless, the single-geometric-distribution hypothesis can be tested by calculating the probability that each IRT separates bouts or separates responses within a bout, assuming that all responses are V-generated. Based on these probabilities, an expected distribution of bout lengths may be obtained using Monte Carlo simulations, from which the likelihood of a single versus a mixture distribution can be established. Using food-reinforced IRTs obtained from rats pressing levers at various heights, Jiménez et al. (2017) showed that a mixture of two geometric distribution of bout lengths was substantially more likely than a single geometric distribution (Figure 10C). In all lever-height conditions, the estimated distribution of bout lengths deviated from a geometric distribution function as expected from the presence of disengaged responses.
In summary, the empirical data thus highlight the importance of disengaged responses that, if neglected, may bias the estimates of the parameters governing the temporal organization of behavior. Disengaged responses reflect a weakness of the discrete-response approach advocated here: responses aimed at tapping into one state may occasionally be emitted in another state. Including the possibility that D generates responses, as indicated in the PHMM of Figure 9, appears to address this vulnerability. Nonetheless, estimating the prevalence of disengaged responses is particularly challenging, because bouts are not defined in response streams. Monte Carlo simulations address this challenge.
12. Nonstationary Transition and Output Probabilities
The PHMM (Figure 9) predicts geometrically-distributed times in D and V, and geometrically-distributed times between responses within each state. Implemented in a continuous time scale, the PHMM entails two Poisson processes, one governing the initiation of bouts and another governing the production of responses within bouts. The PHMM cannot account for deviations from these restrictive predictions, even though those deviations are readily visible in data drawn from stable performance and from its acquisition. Allowing for dynamic transition and output probabilities addresses this limitation.
When applied to instrumental behavior, the restrictive predictions of the PHMM appear to account only for performance in simple VI and VR schedules of reinforcement. However, if a tandem FR schedule is appended to the VI schedule, for instance, the distribution of bout lengths, measured in number of responses, is not geometrical, but appears to peak around the FR requirement (Brackney and Sanabria, 2015). This distribution suggests a noisy counting process, absent in the PHMM, governing d. Also, when reinforcement is contingent on the interval between consecutive responses, a bimodal distribution of IRTs is typically observed, with one mode located close to zero and the other close to the interval requirement (e.g., Cho and Jeantet, 2010; Hill et al., 2012a). This distribution suggests a noisy timing process, also absent in the PHMM, governing w. What these examples indicate is that, to broaden the scope of the PHMM beyond variable-schedule performance, the model must be nonstationary (Sin and Kim, 1995). That is, the generality of the PHMM demands transition and output probabilities that can change rapidly. Table 1 highlights the dynamic nature of the transition and output probabilities of the nonstationary PHMM (nPHMM).
The nonstationarity of the PHMM was already suggested when, to account for instrumental behavior, c was made conditional on responding (Figure 9). In general, transition and output probabilities may vary over time as a function of the frequency of a significant event (response, reinforcer, or some stimulus) or the passage of time since some other event. The examples from tandem FR and IRT requirements illustrate this point. Also, the passage of time since the last reinforcer (i.e., in extinction, fixed-interval [FI] schedules) and the number of non-contingent reinforcers change distinct parameters of the distribution of instrumental IRTs and latencies to respond (Brackney et al., 2017; Cheung et al., 2012; Daniels et al., 2018; Daniels and Sanabria, 2017a). Transitions between general and focal search in the predatory behavior of rats are particularly attuned to the passage of time since the last feeding (Silva and Timberlake, 1998a), suggesting a close link between these transitions and time-sensitive IRT distribution parameters. Similarly selective changes in transition probabilities may occur when appetitive or aversive conditioned stimuli are introduced (e.g., Marshall et al., 2018). When reinforcers are delivered at a high rate, changes in the distribution of IRTs may occur due to satiation and habituation effects (e.g., Bizo et al., 1998).
Furthermore, it is not clear that IRTs under a simple VI schedule are always distributed according to a mixture of two exponential distributions, as would be predicted by the nPHMM operating on continuous time. Tanno (2016), for instance, has reported IRTs under a VI schedule that more likely follow a mixture of four log-normal distributions. Distributions of similar complexity have been suggested for the distribution of pigeon IRTs in simple VI schedules (Bowers et al., 2008; Davison, 2004; Smith et al., 2014). Also, rat and pigeon IRTs in simple VI schedules are not sequentially independent, but positively autocorrelated (Jiménez et al., 2017; Killeen et al., 2002), as would be expected from transition probabilities that fluctuate with hysteresis. These deviations from simple Poisson processes motivates further research on the temporal organization of behavior, which may inform the hierarchical structure of behavior that defines the behavior systems approach.
So far, the empirical examples that support a nPHMM come from stable performance: they involve changes in the distribution of IRTs that take place within each inter-reinforcer interval or session, but that are generally reset and repeated between reinforcers and sessions as long as conditions are kept constant. The scalloped pattern of FI-maintained cumulative records, for instance, implies an accelerated reduction in IRTs between reinforcers, but also a reset and repetition of that processes with every reinforcer (Daniels and Sanabria, 2017a). The PHMM predicts a distribution of IRTs with fixed mean and variance,7 and thus cannot account for rapid changes in IRT. To capture this feature of the data, a set of higher-order parameters must govern the dynamics of transition and output probabilities of the nPHMM. These higher-order parameters may vary with changes in sensorimotor capacity (due to maturation, exposure to neurotoxins, etc.) or with learning. It may be argued that, whereas molecular theories of stable instrumental performance inform how transition and output probabilities oscillate under constant conditions (e.g., Killeen and Sitomer, 2003), theories of learning inform the higher-order parameters that support such stability (e.g., Wagner and Brandon, 2001).
In summary, the nPHMM provides a unified computational framework for investigating the temporal organization of behavior at various levels of complexity, from drinking elicited by periodic food to complex schedule control and cognition (counting, timing, learning). The model is built upon simpler models, such as the 3-state model (Figure 3B), which are largely nested within the nPHMM. The strength of the model, however, is also the source of its main weakness: to be comprehensive, the model relies on dynamic transition and output probabilities, but says little about what governs those dynamic processes. Moreover, the nPHMM hints at the utility of a hierarchical architecture to account for higher-order processes but does not specify such architecture. The hierarchical structure of the behavior systems framework, along with theoretically-motivated empirical data, may guide these and other developments in the computational formulation proposed here.
13. Further Developments
The nPHMM is proposed as a computational implementation of the behavior systems approach. This model is a framework for the development of more precise, computational accounts of behavior and cognition. It formulates a bare-bones Markov structure, but it does not specify transition or outcome probabilities, or how those probabilities change as the system operates in an environment. The former are likely to vary between organisms, tasks, and developmental stages (e.g., Hill et al., 2012b); the latter are the substance of learning and performance theories.
Although the development of the nPHMM relied on empirical findings from food-seeking behavior, its applicability may extend beyond the predatory subsystem. To the extent that the behavior systems approach has been applied successfully to defensive (Fanselow and Lester, 1988; Perusini and Fanselow, 2015) and reproductive (Akins and Cusato, 2015; Domjan, 1994; Domjan and Gutiérrez, 2019) behavior, the nPHMM may also be useful in those contexts. Within the defensive motivational subsystem, for example, a constant probability of foot shock may reveal the parameters that govern the transition between pre- and post-encounter modes and the expression of the latter as freezing behavior. Within the reproductive subsystem, a constant probability of a mate may reveal analogous parameters related to social general and focal search, and the expression of the latter as precopulatory behavior. These examples suggest that a substantial amount of information is lost when dependent measures such as freezing and precopulatory behavior are aggregated into counts or total times (cf. Figure 2). Moreover, in trial-based Pavlovian learning, typical high-probability unconditioned stimuli likely obscure the structure of pauses and bouts by raising behavior close to a performance ceiling. Killeen et al. (2009) have shown that such ceiling may be avoided with low-probability unconditioned stimuli. Considering also that the events to which motivational subsystems are attuned (a predator, a prey, a mate) are significant but relatively rare and uncertain, it seems reasonable that laboratory assessments of these subsystems should be conducted with low-probability unconditioned stimuli.
The architecture of the model does not need to be limited to three hidden states. As shown in the analysis of predatory general search behavior (Figure 4A), D may be further divided into two Markov states corresponding to post-food focal search and general search modes. These states may be empirically disentangled, for example, based on observed head entries, which have a higher probability in post-food focal search than in general search. Also, the hierarchical structure of the behavior systems framework suggests a larger architecture, within which particular subsystems may be represented as nested nPHMMs. For instance, the detection of a predator during foraging may immediately transition the system from the predatory V state to its defensive analogue. Research on risky foraging under controlled conditions (e.g., Kim et al., 2016) may shed light on the nature of the transition between subsystems.
The nPHMM motivates new strategies to detect state transitions. For instance, a bout-like organization of instrumental lever pressing is typically inferred from tandem VI FR performance; such inference relies on the distribution of IRTs and on Monte Carlo simulations (Brackney and Sanabria, 2015). Daniels and Sanabria (2017b) have shown that key aspects of such bout-like organization may be readily visible when the components of the VI FR schedule are programmed in separate levers. Their data suggests that, whereas presses on the VI lever express transitions between D and V, presses on the FR lever are the observable output of V combined with disengaged responses. Instead of using Monte Carlo techniques to infer bout-length distribution, Daniels and Sanabria (2017b) were able to report on observed bouts, expressed as FR runs. Similar strategies may be developed to more precisely estimate transition and output probabilities, and to better visualize the effect of various experimental conditions on these parameters.
The key insights derived from the behavior systems framework emerge from establishing common ground between behavioral ecology and experimental psychology. By couching these insights as a Markov model, a large amount of statistical and computational work in fields as disparate as marketing (Netzer et al., 2017), keystroke biometrics (Monaco and Tappert, 2018), and population ecology (Bartolucci and Pennoni, 2007) are enlisted in the service of behavioral research. Such work includes established methods for the estimation of model structure and parameters (e.g., Zucchini et al., 2016). Moreover, the bout-like organization of behavior that emerges from the nPHMM has been linked to computational accounts of choice, such as reinforcement learning (Yamada and Kanemura, 2019). Therefore, the proposed Markov model is likely to bring to bear computational models in other domains to complement ecological explanations of behavior.
Finally, the nPHMM may also provide guidance to research on the neurobiology of behavior. The neural correlates of states and transitions may be identified and manipulated using neurophysiological techniques with fairly high spatial and temporal resolution during model-informed behavioral tasks. To the extent that the nPHMM explains relatively complex natural behavior, the identification of the neural correlates of the nPHMM would provide a comprehensive account of the neural substrate of that behavior.
14. Conclusions
Computational models have contributed substantially to our understanding of behavior and cognition, grounding and complementing qualitative accounts (e.g., Arantes et al., 2013). This paper aimed at examining whether such contribution could be extended to some aspects of the behavior systems framework. As a first step toward this aim, the analysis focused on the temporal organization of behavior that the behavior systems framework entails. This analysis sought to formulate the simplest model that adhered to the behavior systems approach and to relevant empirical data.
A key tactic in this process was the acknowledgement that measuring behavior involves attending only to a subset of the behavioral repertoire of an animal, such as contacting an object or licking. If appropriately selected, that subset may reflect primarily a target behavioral mode, but it may also be expressed in other behavioral modes. Temporal regularities of carefully selected discrete and overt behavior may aid in revealing the underlying structure of the behavioral modes that govern that behavior.
Relatively simple instantiations of the Markov model accounted for aggregated behavioral data obtained from periodic feeding. Past research has demonstrated that the disaggregation of those data reveals key processes that govern motivated behavior (Brackney et al., 2017, 2011; Brackney and Sanabria, 2015; Daniels and Sanabria, 2017b, 2017a; Yamada and Kanemura, 2019). Those processes and their behavioral expression are consistent with the behavior systems framework, but they cannot be characterized by the simplest Markov models. To account for detailed behavioral data, these models must incorporate (a) the distinction between observable measures and hidden processes, (b) the possibility that observable measures affect hidden processes, and (c) the notion that the parameters that govern those hidden processes may be dynamic. The result of incorporating these characteristics to address the limitations of simpler models is a nonstationary partially hidden Markov model, nPHMM, with only three hidden states: one for the target behavioral mode (V: post-food focal search, general search, pre-food focal search, etc.), one for the behavioral modes that precede it (D), and one for the behavioral modes that follow it (C).
The proposed nPHMM is an algorithmic embodiment of a few concepts that are central to the behavior systems framework: that adaptive actions are organized in nested sequences of behavioral states, that motivation involves transitioning between these states, and that learning involves adjustments to their organization. Such embodiment points at novel research questions about the larger structure of motivated behavior, the mechanisms that support transitioning between subsystems, the factors that govern the length of conditioned dwelling in a behavioral state, among many others. A well-developed stock of analytical techniques is available to support further empirical research that may answer these questions.
Highlights.
Motivated behavior comprises sequences of actions organized within nested states
This organization is represented as a nonstationary partially hidden Markov model
The model balances parsimony, fidelity to the behavior systems approach and to data
The Markov model formulates quantitative, verifiable behavioral predictions
Refinements in model architecture, applicability, and methodology are identified
Acknowledgments
Federico Sanabria and Tanya Gupta were supported by the National Institutes of Health (MH115245). Carter Daniels was supported by a Completion Fellowship from the Graduate College at Arizona State University. Cristina Santos by a Doctoral Fellowship (438355) from the Mexican National Council of Science and Technology (CONACyT).
Footnotes
If the action of a rat at a given moment is described as “simultaneously sniffing and pawing”, then either the actions “sniff’ and “paw” must be redefined so that they cannot occur simultaneously, or a new action, “sniffing-while-pawing” must be introduced into the representation of the behavior subsystem.
Discrete-time Markov processes may be generalized to continuous time. For simplicity, this paper considers only discrete-time processes.
The simplifying assumption that feeding is followed by D stems from the prevalence of post-reinforcement pauses (Felton & Lyon, 1966). Findings from Lucas, Timberlake & Gawley (1988) suggest that postprandial actions should be incorporated to the predatory subsystem of rats (cf. Figure 1; see also Harzem et al., 1978).
Breaks of an infrared beam positioned in the food port may serve as observable outputs of C.
For simplicity, these outputs are omitted.
The simulation was programmed in R for Mac OS X (R Core Team, 2017). The script is provided as supplementary material.
More specifically, a proportion of b/(b + d) bouts are V-generated and have a mean length of w/d responses (or 1/d timesteps). The remaining bouts are D-generated and have a mean length of q/b responses (or 1/b timesteps). The mixture weight of V-generated bouts is obtained from the stationary distribution of the PHMM.
There is, however, one situation in which this is not true. A large positive difference between c and d in the PHMM (Figure 9) implies prevalent dwelling in D early in the IFI and prevalent dwelling in V late in the IFI This means that the mean IRT is not constant over the IFI, but is 1/q (D-generated) early in the IFI and 1/w (V-generated) late in the IFI. Note also that Markov models in which c is sufficiently higher than d appear to account for behavior elicited by the periodic delivery of food (Figure 4; d is zero, so it is not shown). Alone, however, this progressive change in mean IRT cannot account for FI performance (Daniels and Sanabria, 2017a).
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akins CK, Cusato B, 2015. From biological constraints to flexible behavior systems : Extending our knowledge of sexual conditioning in Japanese quail. Int. J. Comp. Psychol 28. [Google Scholar]
- Anselme P, 2016. Motivational control of sign-tracking behaviour: A theoretical framework. Neurosci. Biobehav. Rev 65, 1–20. 10.1016/j.neubiorev.2016.03.014 [DOI] [PubMed] [Google Scholar]
- Arantes R, Tejada J, Bosco GG, Morato S, Roque AC, 2013. Mathematical methods to model rodent behavior in the elevated plus-maze. J. Neurosci. Methods 220, 141–148. 10.1016/j.jneumeth.2013.04.022 [DOI] [PubMed] [Google Scholar]
- Baerends GP, 1976. On drive, conflict and instinct, and the functional organization of behavior, in: Corner MA, Swaab DF (Eds.), Perspectives in Brain Research. Elsevier, Amsterdam, The Netherlands, pp. 427–447. [PubMed] [Google Scholar]
- Baerends GP, 1941. On the life-history of Ammophila campestris Jur. Proc. K. Ned. Akad. van Wet 44, 483–488. [Google Scholar]
- Bartolucci F, Pennoni F, 2007. A class of latent Markov models for capture-recapture data allowing for time, heterogeneity, and behavior effects. Biometrics. 63, 568–578. 10.1111/j.1541-0420.2006.00702.x [DOI] [PubMed] [Google Scholar]
- Bizo LA, Bogdanov SV, Killeen PR, 1998. Satiation causes within-session decreases in instrumental responding. J. Exp. Psychol. Anim. Behav. Process 24, 439–452. 10.1037/0097-7403.24.4.439 [DOI] [PubMed] [Google Scholar]
- Blough PM, Blough DS, 1968. The distribution of interresponse times in the pigeon during variable-interval reinforcement. J. Exp. Anal. Behav 11, 23–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowers MT, Hill J, Palya WL, 2008. Interresponse time structures in variable-ratio and variable-interval schedules. J. Exp. Anal. Behav 90, 345–362. 10.1901/jeab.2008.90-rence [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowers RI, 2018. A common heritage of behaviour systems. Behaviour 155, 415–442. 10.1163/1568539X-00003497 [DOI] [Google Scholar]
- Bowers RI, Timberlake W, 2018. Causal reasoning in rats’ behaviour systems. R. Soc. Open Sci 5, 171448 10.1098/rsos.171448 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowers RI, Timberlake W, 2017. Do rats learn conditional independence ? R. Soc. Open Sci 4, 160994 10.1098/rsos.160994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brackney RJ, Cheung THC, Neisewander JL, Sanabria F, 2011. The isolation of motivational, motoric, and schedule effects on operant performance: A modeling approach. J. Exp. Anal. Behav 96, 17–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brackney RJ, Cheung THC, Sanabria F, 2017. A bout analysis of operant response disruption. Behav. Processes 141 10.1016/j.beproc.2017.04.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brackney RJ, Sanabria F, 2015. The distribution of response bout lengths and its sensitivity to differential reinforcement. J. Exp. Anal. Behav 104, 167–185. 10.1002/jeab.168 [DOI] [PubMed] [Google Scholar]
- Cabrera F, Sanabria F, Jimenez ÁA, Covarrubias P, 2013. An affordance analysis of unconditioned lever pressing in rats and hamsters. Behav. Processes 92, 36–46. 10.1016/j.beproc.2012.10.003 [DOI] [PubMed] [Google Scholar]
- Cheung THC, Neisewander JL, Sanabria F, 2012. Extinction under a behavioral microscope: Isolating the sources of decline in operant response rate. Behav. Processes 90, 111–123. 10.1016/j.beproc.2012.02.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho YH, Jeantet Y, 2010. Differential involvement of prefrontal cortex, striatum, and hippocampus in DRL performance in mice. Neurobiol. Learn. Mem 93, 85–91. 10.1016/j.nlm.2009.08.007 [DOI] [PubMed] [Google Scholar]
- Daniels CW, Overby PF, Sanabria F, 2018. Between-session memory degradation accounts for within-session changes in fixed-interval performance. Behav. Processes 153 10.1016/j.beproc.2018.05.004 [DOI] [PubMed] [Google Scholar]
- Daniels CW, Sanabria F, 2017a. Interval timing under a behavioral microscope: Dissociating motivational and timing processes in fixed-interval performance. Learn. Behav 45, 29–48. 10.3758/s13420-016-0234-1 [DOI] [PubMed] [Google Scholar]
- Daniels CW, Sanabria F, 2017b. About bouts: A heterogeneous tandem schedule of reinforcement reveals dissociable components of operant behavior in fischer rats. J. Exp. Psychol. Anim. Learn. Cogn 43 10.1037/xan0000144 [DOI] [PubMed] [Google Scholar]
- Davison M, 2004. Interresponse times and the structure of choice. Behav. Processes 66, 173–187. 10.1016/j.beproc.2004.03.003 [DOI] [PubMed] [Google Scholar]
- de Carvalho MP, Machado A, Vasconcelos M, 2016. Animal timing: A synthetic approach. Anim. Cogn 19, 707–732. 10.1007/s10071-016-0977-2 [DOI] [PubMed] [Google Scholar]
- Domjan M, 1994. Formulation of a behavior system for sexual conditioning. Psychon. Bull. Rev 1, 421–428. [DOI] [PubMed] [Google Scholar]
- Domjan M, Gutiérrez G, 2019. The behavior system for sexual learning. Behav. Processes 162, 184–196. 10.1016/j.beproc.2019.01.013 [DOI] [PubMed] [Google Scholar]
- Espejo EF, 1997. Structure of the mouse behaviour on the elevated plus-maze test of anxiety. Behav. Brain Res 86, 105–112. [DOI] [PubMed] [Google Scholar]
- Fanselow MS, Lester LS, 1988. A functional behavioristic approach to aversively motivated behavior: Predatory imminence as a determinant of the topography of defensive behavior, in: Bolles RC, Beecher MD (Eds.), Evolution and Learning. Lawrence Erlbaum Associates, Hillsdale, NJ, pp. 185–212. [Google Scholar]
- Farrell S, Lewandowsky S, 2018. Computational modeling of cognition and behavior. Cambridge University Press, Cambridge, UK. [Google Scholar]
- Fetterman JG, Killeen PR, Hall S, 1998. Watching the clock. Behav. Processes 44, 211–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forchhammer S, Rissanen J, 1996. Partially Hidden Markov Models. IEEE Trans. Inf. Theory 42, 1253–1256. [Google Scholar]
- Gagniuc PA, 2017. Markov chains: From theory to implementation and experimentation. Wiley, Hoboken, NJ. [Google Scholar]
- Gershman SJ, Moustafa AA, Ludvig EA, 2014. Time representation in reinforcement learning models of the basal ganglia. Front. Comput. Neurosci 7, 1–8. 10.3389/fncom.2013.00194 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gharib A, Gade C, Roberts S, 2004. Control of variation by reward probability. J. Exp. Psychol. Anim. Behav. Process 30, 271–282. 10.1037/0097-7403.30.4.271 [DOI] [PubMed] [Google Scholar]
- Harzem P, Lowe CF, Priddle-higson PJ, 1978. Inhibiting function of reinforcement: Magnitude effects on variable-interval schedules. J. Exp. Anal. Behav 30, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill JC, Covarrubias P, Terry J, Sanabria F, 2012a. The effect of methylphenidate and rearing environment on behavioral inhibition in adult male rats. Psychopharmacology (Berl). 219, 353–362. 10.1007/s00213-011-2552-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill JC, Herbst K, Sanabria F, 2012b. Characterizing operant hyperactivity in the Spontaneously Hypertensive Rat. Behav. Brain Funct 8, 5 10.1186/1744-9081-8-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Íbias J, Daniels CW, Miguéns M, Pellón R, Sanabria F, 2017. The effect of methylphenidate on the microstructure of schedule-induced polydipsia in an animal model of ADHD. Behav. Brain Res 333, 211–217. 10.1016/j.bbr.2017.06.048 [DOI] [PubMed] [Google Scholar]
- Íbias J, Pellón R, Sanabria F, 2015. A microstructural analysis of schedule-induced polydipsia reveals incentive-induced hyperactivity in an animal model of ADHD. Behav. Brain Rresearch 278, 417–423. 10.1016/j.bbr.2014.10.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanov DG, Krupina NA, 2017. Changes in the ethogram in rats due to contagion behavior. Neurosci. Behav. Physiol 47, 987–993. 10.1007/s11055-017-0500-5 [DOI] [Google Scholar]
- Jiménez ÁA, Sanabria F, Cabrera F, 2017. The effect of lever height on the microstructure of operant behavior. Behav. Processes 140, 181–189. 10.1016/j.beproc.2017.05.002 [DOI] [PubMed] [Google Scholar]
- Johnson JE, Pesek EF, Christopher Newland M, 2009. High-rate operant behavior in two mouse strains: A response-bout analysis. Behav. Processes 81, 309–315. 10.1016/j.beproc.2009.02.013 [DOI] [PubMed] [Google Scholar]
- Killeen PR, Hall SS, Reilly MP, Kettle LC, 2002. Molecular analyses of the principal components of response strength. J. Exp. Anal. Behav 78, 127–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killeen PR, Sanabria F, Dolgov I, 2009. The dynamics of conditioning and extinction. J. Exp. Psychol. Anim. Behav. Process 35, 447–472. 10.1037/a0015626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killeen PR, Sitomer MT, 2003. MPR. Behav. Processes 62, 49–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim JJ, Choi J-S, Lee HJ, 2016. Foraging in the face of fear: Novel strategies for evaluating amygdala functions in rats, in: Amaral DG, Adolphs R (Eds.), Living without an Amygdala. Guilford Press, New York, NY, pp. 129–148. [Google Scholar]
- Kirkpatrick K, Church RM, 2003. Tracking of the expected time to reinforcement in temporal conditioning procedures. Learn. Behav 31, 3–21. [DOI] [PubMed] [Google Scholar]
- Krause MA, Domjan M, 2017. Ethological and evolutionary perspectives on Pavlovian conditioning, in: Call J (Ed.), APA Handbook of Comparative Psychology. Vol 2. Perception, Learning, and Cognition. APA, Washington, DC, pp. 247–266. 10.1037/0000012-012 [DOI] [Google Scholar]
- Kriegeskorte N, Douglas PK, 2018. Cognitive computational neuroscience. Nat. Neurosci 21, 1148–1160. 10.1038/s41593-018-0210-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lillacci G, Khammash M, 2010. Parameter estimation and model selection in computational biology. PLOS Comput. Biol 6, e1000696 10.1371/journal.pcbi.1000696 [DOI] [PMC free article] [PubMed] [Google Scholar]
- López-Crespo G, Rodríguez M, Pellón R, Flores P, 2004. Acquisition of schedule-induced polydipsia by rats in proximity to upcoming food delivery. Anim. Learn. Behav 32, 491–499. 10.3758/bf03196044 [DOI] [PubMed] [Google Scholar]
- Lucas GA, Timberlake W, Gawley DJ, 1988. Adjunctive behavior of the rat under periodic food delivery in a 24-hour environment. Anim. Learn. Behav 16, 19–30. 10.3758/BF03209039 [DOI] [Google Scholar]
- Machado A, 1997. Learning the Temporal Dynamics of Behavior. Psychol. Rev 104, 241–265. [DOI] [PubMed] [Google Scholar]
- Magnusson MS, Burgoon JK, Casarrubea M, 2016. Discovering hidden temporal patterns in behavior and interaction. Springer, New York, NY: [Google Scholar]
- Marshall AT, Halbout B, Liu AT, Ostlund SB, 2018. Contributions of Pavlovian incentive motivation to cue-potentiated feeding. Sci. Rep 8, 2766 10.1038/s41598-018-21046-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsui H, Yamada K, Sakagami T, Tanno T, 2018. Modeling bout–pause response patterns in variable-ratio and variable-interval schedules using hierarchical Bayesian methodology. Behav. Processes 157, 346–353. 10.1016/j.beproc.2018.07.014 [DOI] [PubMed] [Google Scholar]
- Meissner AM, Christiansen F, Martinez E, Pawley MDM, Orams MB, Stockin KA, 2015. Behavioural effects of tourism on oceanic common dolphins, Delphinus sp., in New Zealand: The effects of Markov analysis variations and current tour operator compliance with regulations. PLoS One 10, e0116962 10.1371/journal.pone.0116962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melnik R, 2015. Mathematical and computational modeling: With applications in natural and social sciences, engineering, and the arts. Wiley, Hoboken, NJ. [Google Scholar]
- Monaco JV, Tappert CC, 2018. The partially observable hidden Markov model and its application to keystroke dynamics. Pattern Recognit. 76, 449–462. 10.1016/j.patcog.2017.11.021 [DOI] [Google Scholar]
- Moreno M, Flores P, 2012. Schedule-induced polydipsia as a model of compulsive behavior: Neuropharmacological and neuroendocrine bases. Psychopharmacology (Berl). 219, 647–659. [DOI] [PubMed] [Google Scholar]
- Netzer O, Ebbes P, Bijmolt THA, 2017. Hidden Markov models in marketing, in: Leeflang P, Wieringa J, Bijmolt T, Pauwels K (Eds.), Advanced Methods for Modeling Markets. Springer, Cham, Switzerland, pp. 405–449. [Google Scholar]
- Pelletier AN, Kaufmann T, Mohak S, Milan R, Charmalie AD, Huffman MA, Gunst N, Rompis A, Wandia IN, Agung IG, Putra A, Pellis SM, Leca J-B, 2017. Behavior systems approach to object play : Stone handling repertoire as a measure of propensity for complex foraging and percussive tool use in the genus Macaca. Anim. Behav. Cogn 4, 455–473. [Google Scholar]
- Perusini JN, Fanselow MS, 2015. Neurobehavioral perspectives on the distinction between fear and anxiety. Learn. Mem 22, 417–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitt MA, Myung IJ, Zhang S, 2002. Toward a method of selecting among computational models of ognition. Psychol. Rev 109, 472–491. 10.1037//0033-295X.109.3.472 [DOI] [PubMed] [Google Scholar]
- R Core Team, 2017. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria: http://www.R-project.com [Google Scholar]
- Raftery AE, 1985. A model for high-order Markov chains. J. R. Stat. Soc. Ser. B 47, 528–539. [Google Scholar]
- Reed P, 2015. The structure of random ratio responding in humans. J. Exp. Psychol. Anim. Learn. Cogn 41, 419–431. [DOI] [PubMed] [Google Scholar]
- Reed P, 2011. An experimental analysis of steady-state response rate components on variable ratio and variable interval schedules of reinforcement. J. Exp. Psychol. Anim. Behav. Process 37, 1–9. 10.1037/a0019387 [DOI] [PubMed] [Google Scholar]
- Reed P, Smale D, Owens D, Freegard G, 2018. Human performance on random interval schedules. J. Exp. Psychol. Anim. Learn. Cogn 44, 309–321. [DOI] [PubMed] [Google Scholar]
- Sanabria F, Sitomer MT, Killeen PR, 2006. Negative automaintenance omission training is effective. J. Exp. Anal. Behav 86, 1–10. 10.1901/jeab.2006.36-05 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seuront L, Cribb N, 2011. Fractal analysis reveals pernicious stress levels related to boat presence and type in the IndoPacific bottlenose dolphin, Tursiops aduncus. Phys. A Stat. Mech. its Appl 390, 2333–2339. 10.1016/j.physa.2011.02.015 [DOI] [Google Scholar]
- Shull RL, 2004. Bouts of responding on variable-interval schedules: Effects of deprivation level. J. Exp. Anal. Behav 81, 155–167. 10.1901/jeab.2004.81-155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shull RL, Gaynor ST, Grimes JA, 2001. Response rate viewed as engagement bouts: Effects of relative reinforcement and schedule type. J. Exp. Anal. Behav 75, 247–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shull RL, Grimes JA, 2003. Bouts of responding from variable-interval reinforcement of lever pressing by rats. J. Exp. Anal. Behav 80, 159–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shull RL, Grimes JA, Bennett JA, 2004. Bouts of responding: the relation between bout rate and the rate of variable-interval reinforcement. J. Exp. Anal. Behav 81, 65–83. 10.1901/jeab.2004.81-65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva KM, Silva FJ, Machado A, 2019. The evolution of the behavior systems framework and its connection to interbehavioral psychology. Behav. Processes 158, 117–125. 10.1016/j.beproc.2018.11.001 [DOI] [PubMed] [Google Scholar]
- Silva KM, Timberlake W, 1998a. The organization and temporal properties of appetitive behavior in rats. Learn. Behav 26, 182–195. [Google Scholar]
- Silva KM, Timberlake W, 1998b. A behavior systems view of responding to probe stimuli during an interfood clock. Anim. Learn. Behav 26, 313–325. 10.3758/BF03199224 [DOI] [Google Scholar]
- Sin B, Kim JH, 1995. Nonstationary hidden Markov model. Signal Processing 46, 31–46. [Google Scholar]
- Slater PJB, 1973. Describing sequences of behavior, in: Bateson PPG, Klopfer PH (Eds.), Perspectives in Ethology. Springer US, Boston, MA, pp. 131–153. 10.1007/978-1-4615-7569-6_5 [DOI] [Google Scholar]
- Smith TT, McLean AP, Shull RL, Hughes CE, Pitts RC, 2014. Concurrent performance as bouts of behavior. J. Exp. Anal. Behav 102, 102–125. [DOI] [PubMed] [Google Scholar]
- Staddon JER, 1972. A note on the analysis of behavioural sequences in Columba livia. Anim. Behav 20 284–292. [Google Scholar]
- Staddon JER, Ayres SL, 1975. Sequential and temporal properties of behavior induced by a schedule of periodic food delivery. Behaviour 54, 26–49. [Google Scholar]
- Staddon JER, Simmelhag VL, 1971. The “superstition” experiment: A reexamination of its implications for the principles of adaptive behavior. Psychol. Rev 78, 3–43. [Google Scholar]
- Tanno T, 2016. Response-bout analysis of interresponse times in variable-ratio and variable-interval schedules. Behav. Processes 132, 12–21. [DOI] [PubMed] [Google Scholar]
- Tejada J, Bosco GG, Morato S, Roque AC, 2010. Characterization of the rat exploratory behavior in the elevated plus-maze with Markov chains. J. Neurosci. Methods 193, 288–295. 10.1016/j.jneumeth.2010.09.008 [DOI] [PubMed] [Google Scholar]
- Timberlake W, 2004. Trends in the study of Pavlovian conditioning. Int. J. Comp. Psychol 17, 119–130. [Google Scholar]
- Timberlake W, 2001a. Motivational modes in behavior systems, in: Mowrer RR, Klein SB (Eds.), Handbook of Contemporary Learning Theories. Lawrence Erlbaum Associates, Mahwah, NJ, pp. 155–209. [Google Scholar]
- Timberlake W, 2001b. Integrating niche-related and general process approaches in the study of learning. Behav. Processes 54, 79–94. [DOI] [PubMed] [Google Scholar]
- Timberlake W, 1994. Behavior systems, associationism, and Pavlovian conditioning. Psychon. Bull. Rev 1, 405–420. [DOI] [PubMed] [Google Scholar]
- Timberlake W, 1993. Behavior systems and reinforcement: An integrative approach. J. Exp. Anal. Behav 60, 105–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timberlake W, Lucas GA, 1989. Behavior systems and learning: From misbehavior to general principles, in: Klein SB, Mowrer RR (Eds.), Contemporary Learning Theories: Instrumental Conditioning Theory and the Impact of Biological Constraints on Learning. Lawrence Erlbaum Associates, Hillsdale, NJ, pp. 237–275. [Google Scholar]
- Timberlake W, Silva KM, 1995. Appetitive behavior in ethology, psychology, and behavior systems, in Thompson NS (Ed.), Perspectives in Ethology. Plenum Press, New York, NY, pp. 211–253. [Google Scholar]
- Tron E, Margaliot M, 2004. Mathematical modeling of observed natural behavior : A fuzzy logic approach. Fuzzy Sets Syst. 146, 437–450. 10.1016/j.fss.2003.09.005 [DOI] [Google Scholar]
- Tsibulsky VL, Norman AB, 2007. Mathematical models of behavior of individual animals. Curr. Pharm Des 13, 1571–95. [DOI] [PubMed] [Google Scholar]
- van Gils JA, van der Geest M, De Meulenaer B, Gillis H, Piersma T, Folmer EO, 2015. Moving on with foraging theory: Incorporating movement decisions into the functional response of a gregarious shorebird. J. Anim. Ecol 84, 554–564. 10.1111/1365-2656.12301 [DOI] [PubMed] [Google Scholar]
- Wagner AR, Brandon SE, 2001. A componential theory of Pavlovian conditioning, in: Mowrer RR, Klein SB (Eds.), Handbook of Contemporary Learning Theories. Lawrence Erlbaum Associates, Mahwah, NJ, pp. 23–64. [Google Scholar]
- Yamada K, Kanemura A, 2019. Simulating bout-and-pause patterns with reinforcement learning. bioRxiv 632745. 10.1101/632745 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zucchini W, MacDonald IL, Langrock R, 2016. Hidden Markov models for time series: An introduction using R, 2nd ed. CRC Press, Boca Raton, FL. [Google Scholar]
- Zucchini W, Raubenheimer D, Macdonald IL, 2008. Modeling time series of animal behavior by means of a latent-state model with feedback. Biometrics 64, 807–815. 10.1111/j.l541-0420.2007.00939.x [DOI] [PubMed] [Google Scholar]