A decade of test-retest reliability of functional connectivity: a systematic review and meta-analysis

Abstract

Background:

Once considered mere noise, fMRI-based functional connectivity has become a major neuroscience tool in part due to early studies demonstrating its reliability. These fundamental studies revealed only the tip of the iceberg; over the past decade, many test-retest reliability studies have continued to add nuance to our understanding of this complex topic. A summary of these diverse and at times contradictory perspectives is needed.

Objectives:

We aimed to summarize the existing knowledge regarding test-retest reliability of functional connectivity at the most basic unit of analysis: the individual edge level. This entailed (1) a meta-analytic estimate of reliability and (2) a review of factors influencing reliability.

Methods:

A search of Scopus was conducted to identify studies that estimated edge-level test-retest reliability. To facilitate comparisons across studies, eligibility was restricted to studies measuring reliability via the intraclass correlation coefficient (ICC). The meta-analysis included a random effects pooled estimate of mean edge-level ICC, with studies nested within datasets. The review included a narrative summary of factors influencing edge-level ICC.

Results:

From an initial pool of 212 studies, 44 studies were identified for the qualitative review and 25 studies for quantitative meta-analysis. On average, individual edges exhibited a “poor” ICC of 0.29 (95% CI=0.23 to 0.36). The most reliable measurements tended to involve: (1) stronger, within-network, cortical edges, (2) eyes open, awake, and active recordings, (3) more within-subject data, (4) shorter test-retest intervals, (5) no artifact correction (likely due in part to reliable artifact), and (6) full correlation-based connectivity with shrinkage.

Conclusion:

This study represents the first meta-analysis and systematic review investigating test-retest reliability of edge-level functional connectivity. Key findings suggest there is room for improvement, but care should be taken to avoid promoting reliability at the expense of validity. By pooling existing knowledge regarding this key facet of accuracy, this study supports broader efforts to improve inferences in the field.

1. Introduction

The brain has long been understood to be a network of interacting parts, but only in the past several decades have researchers been able to examine whole-brain networks in humans. Human brain networks are often estimated using functional magnetic resonance imaging (fMRI) to quantify similar activity across areas (Van Den Heuvel and Pol, 2010). While early detractors questioned whether this “functional connectivity” reflected more than a byproduct of fMRI noise, instrumental to its acceptance were early studies demonstrating that the same large-scale functional networks could be reliably detected across subjects, scans, and contexts (Damoiseaux et al., 2006; Fox et al., 2005; Fransson, 2005; van de Ven et al., 2004). Since reliability underlies the accuracy of a measure, those studies were important in removing a barrier to accurate inferences via functional connectivity. Following suit, others sought to characterize the reliability of individual connections within these large-scale networks, beginning with Shehzad et al. (2009). While some of the earliest reports suggested that many elements of functional connectivity were reliable (Blautzik et al., 2013; Chou et al., 2012; Faria et al., 2012; Guo et al., 2012; Li et al., 2012; Somandepalli et al., 2015; Song et al., 2012), diverging perspectives have emerged over the past decade.

Fundamentally, we have witnessed uncertainty in the estimated reliability of connectivity, with reports ranging from poor (Noble et al., 2017b; Pannunzi et al., 2017; Seibert et al., 2012) to robust (see above). The literature is further complicated (and enriched) by the diversity of research foci: the influence of acquisition and preprocessing strategies (e.g., Shirer et al., 2015), variability across brain networks (e.g., Pannunzi et al., 2016), differences between populations (e.g., Blautzik et al., 2013), and more. As a result, this body of literature now comprises many different answers to many different questions concerning the reliability of functional connectivity—even asking the same question often yields seemingly contradictory answers. It is no surprise that recommendations based on reliability have also been mixed. Adding to the uncertainty, individual studies are often limited by few subjects and/or repeated measurements, since there are many challenges involved in both scanning large numbers of subjects and getting them to come back multiple times for repeated scans.

The present work aims to begin to resolve this uncertainty by synthesizing the current understanding of the reliability of functional connectivity. A meta-analysis summarizing the magnitude of reliability in healthy individuals is presented, followed by a review summarizing consensus and/or disagreement regarding the following topics: spatial distribution of reliability, multivariate reliability, acquisition strategies, preprocessing strategies, and how reliability informs utility. Finally, we will provide some additional considerations and final thoughts gleaned from the literature.

1.1. fMRI-based functional connectivity

Functional connectivity analyses are used to explore the intrinsic organization of the brain in individuals typically at rest. To measure functional connectivity, similarities in the temporal fluctuations of blood oxygenation level dependent (BOLD) fMRI data are quantified (Biswal et al., 1995; Rogers et al., 2007). Brain regions that share similar temporal signatures are defined as functionally connected (Rubinov and Sporns, 2010). The regions used and estimation procedures for assessing temporal similarity vary between studies, but typically these are assessed in either a “seed”-based or “atlas”-based approach (Smith, 2012). Seed analyses may be designed to estimate the similarity between one or several regions and every voxel in the gray matter, whereas atlas analyses estimate the similarity between a set of pre-defined regions (or “nodes”) that can span the whole brain. Similarity between timeseries is most commonly estimated using a Pearson’s correlation, but a range of metrics may be used (e.g., partial correlation, mutual information, etc.; cf. Zhou et al., 2009). Calculating connections (or “edges”) between a seed region and all other areas results in a connectivity vector, whereas calculating edges between each pair of atlas nodes results in a connectivity matrix. This vector or matrix is then often used to characterize brain organization (Fox et al., 2005) or explore associations with behavior (Greene et al., 2018; Shen et al., 2017).

This review focuses on reliability of functional connectivity at the level of individual edges. This is the most basic element of functional connectivity and, therefore, the object of many studies. Notably, the test-retest reliability of other elements of functional connectivity is also a topic of active research. The similarity in the boundaries of regions and/or networks, often obtained via ICA, have been assessed using a number of strategies (e.g., Guo et al., 2012; Jovicich et al., 2016; Zuo et al., 2010b). Test-retest reliability has also been investigated for higher order graph theory metrics (e.g., clustering, network membership, etc.; Braun et al., 2012; Cao et al., 2014; Termenon et al., 2016; Wang et al., 2011) and dynamic measures (e.g., Choe et al., 2017; Zuo et al., 2010a). While valuable, these complex research topics deserve their own independent study; here, we restrict our focus to individual edge reliability.

1.2. Test-retest reliability via the intraclass correlation coefficient (ICC)

Reliability is complementary to validity in understanding the accuracy of a measure. Whereas validity broadly reflects correspondence of a test measure with a target measure of “ground truth,” reliability reflects stability of the test measure (Cronbach, 1988). Test-retest reliability is one type of reliability that assesses stability under repeated tests. It is a critical characteristic since it establishes the upper limit on one desirable form of validity—its correlation with a target measure (White et al., 2008; Nunnally Jr, 1970). This means that an ultimately valid measure that exhibits low reliability is likely to produce at most low correlations with the target. Intuitively, a method that corresponds with some ground truth has limited practical utility if individual measurements are extremely variable (Bennett and Miller, 2010; Nichols et al., 2017).

Numerous statistical measures have been used to assess test-retest reliability of functional connectivity, including but not limited to the Intraclass Correlation Coefficient (ICC), Pearson’s correlation, and the Kendall coefficient of concordance (Table 2 of Gisev et al., 2013, offers a primer in selecting measures of agreement). Each of these measures has its strengths. A few strengths of the ICC include: 1) the ability to assess absolute agreement in repeated measurements of an object (unlike, for example, Pearson’s correlation, wherein variables are scaled and centered separately), 2) the ability to explicitly model multiple known sources of variability, and 3) placing within-object variability in perspective by comparing to variability across the object of measurement. Due in part to these strengths, the ICC has been commonly used in the functional connectivity literature to assess reliability (e.g., Birn et al., 2013; Shah et al., 2016; Shehzad et al., 2009; Somandepalli et al., 2015). Therefore, we focus on ICC to facilitate comparisons across studies.

Table 2. Within-network reliability, ranked by consensus.

For each network, the studies that classify that network as most reliable (++), more reliable (+), less reliable (−), or least reliable (−−) are indicated. Networks are simply ranked by the net number of studies marked most/more reliable minus those marked less/least reliable. Studies are listed in chronological order.

Network	Evidence of reliability
1. Frontoparietal, Default Mode	++ Most reliable: Blautzik et al., 2013; Wisner et al., 2013; Zuo et al., 2014; Somandepalli et al., 2015; Marchitelli et al., 2017; Noble et al., 2017b; O’Connor et al., 2017; Mejia et al., 2018 −− Least reliable: Shirer et al., 2015; Pannunzi et al., 2016
2. Visual	++ Most reliable: Blautzik et al., 2013; Chen et al., 2015; Shirer et al., 2015
3. Sensorimotor	++ Most reliable: Blautzik et al., 2013 (sensorimotor, auditory), Shirer et al., 2015 (motor) + More reliable: Wisner et al., 2013 (motor, auditory, speech) − Less reliable: Chen et al., 2015 (motor)
4. Limbic	+ More reliable: Chen et al., 2015 − Less reliable: Noble et al., 2017b
5. Cerebellar	++ Most reliable: Pannunzi et al., 2016 −− Least reliable: Noble et al., 2017b; Mejia et al., 2018
6. Other (areas adjacent to non-grey matter)	−− Least reliable: Shah et al., 2016 (grey-white junction, near large sulci); Blautzik et al., 2017 (basal frontal sinus-adjacent areas)
7. Subcortical	−− Least reliable: Shah et al., 2016; Noble et al., 2017b; Mejia et al., 2018

The ICC essentially measures how much of the overall variability in a measure can be attributed to an object of measurement, typically subject (Shrout and Fleiss, 1979). Depending on whether and how sources of error (or “facets”; e.g., scanner) may be specified, one of three ICC forms may be used. In brief, usage is as follows: ICC(1,1) is used to estimate agreement in exact values when sources of error are unspecified; ICC(2,1) is often referred to as “absolute agreement” and is used to estimate agreement in exact values when sources of error are known (e.g., repeated runs) and modeled as random; and ICC(3,1) is often referred to as or “consistent agreement” and is used to estimate agreement in rankings when sources of error are known and modeled as fixed (resulting in a mixed effects ANOVA). The following show this ratio of variances for ICC(1,1) and ICC(2,1), where λ is the object, π is specified error source, and ε is unspecified error source:

$$ICC(1,1)=\frac{{\sigma }_{\lambda }^2}{{\sigma }_{\lambda }^2+{\sigma }_{\epsilon }^2}$$

$$ICC(2,1)=\frac{{\sigma }_{\lambda }^2}{{\sigma }_{\lambda }^2+{\sigma }_{\pi }^2+{\sigma }_{\epsilon }^2}$$

A theoretical derivation of these different forms has been described elsewhere (McGraw and Wong, 1996; Shrout and Fleiss, 1979; cf. Chen et al., 2018 for a recent eloquent discussion¹), but note that the object of measurement is modeled as random, and error sources like runs and sessions should be modeled as random unless a convincing argument can be made for expecting structured variability (e.g., habituation; Chen et al., 2018). Otherwise, misleading inferences could be made by exploiting the fact that typically ICC(1,1) < ICC(2,1) < ICC(3,1) (Shrout and Fleiss, 1979). Similarly, although each model can be generalized to assess reliability of average measures—ICC(1,k), ICC(2,k), ICC(3,k) with k>1—the default should be to use k=1 unless a convincing argument can be made otherwise (Cannon et al., 2018; Noble et al., 2017b). For example, absolute agreement of connectivity derived from a single session (k=1) is necessarily lower than that averaged over two sessions (k=2):

$$ICC(2,1)=\frac{{\sigma }_{person}^2}{{\sigma }_{person}^2+\frac{{\sigma }_{session}^2}{1}+\frac{{\sigma }_{\epsilon }^2}{1}}\hspace{1em}\hspace{1em}<\hspace{1em}\hspace{1em}ICC(2,2)=\frac{{\sigma }_{person}^2}{{\sigma }_{person}^2+\frac{{\sigma }_{session}^2}{2}+\frac{{\sigma }_{\epsilon }^2}{2}}$$

This may be used to estimate how much reliability improves when averaging over multiple measurements (e.g., repeated sessions), assuming they are interchangeable.

If multiple sources of error can be identified (e.g., runs, sessions, sites, scanners), Generalizability Theory provides a way to incorporate these error sources into the ICC (Webb and Shavelson, 2005; Webb et al., 2006)². The same method as described above (in this context, called a “Decision Study”) may be used to estimate the amount and type of data needed for desired levels of reliability (e.g., number of runs as well as number of sessions).

Another form of the ICC has been developed to account for covariates of no interest (e.g., age, sex, motion, etc.; Zuo et al, 2013). This can be useful in accounting for variability in scans that may be otherwise falsely attributed to person or error sources, thus artificially inflating or deflating reliability. Formally, this includes estimating variance components based on a multilevel design with different levels specified for between- and within-subject covariates.

Chen et al. (2018) have outlined additional valuable considerations regarding use of the ICC, including the use of Bayesian estimators to avoid negative estimates of the ICC. Negative ICCs may arise when one or more variance components are inadvertently estimated to be negative, often due to the use of a small number of samples relative to the variability in the dataset (Hocking, 1985). Since these are typically very close to zero, they are often simply set to zero (Braun et al., 2012; Noble et al., 2017b; Park et al., 2012). Negative estimates from ANOVA are small or zero using more robust estimation procedures (Chen et al., 2018), so this may be a close approximation; however, a principled approach is preferable whenever possible (Minke and Haynes, 2011; Müller and Büttner, 1994; Swallow and Monahan, 1984). Another promising approach is to apply shrinkage based on group-level estimates, designed to increase reliability of subject-specific estimates (Mejia et al., 2015; Shou et al., 2014).

The interpretation of the ICC can be complex. As a ratio of between- to within-subject variances, the ICC is akin to a measure of discriminability and is commonly categorized as follows: poor <0.4, fair 0.4–0.59, good 0.6–0.74, excellent ≥0.75 (Cicchetti and Sparrow, 1981). However, as with any statistical rule of thumb, these categories are not absolute and the context must be considered, e.g., good reliability in one context may not be good in another. It is also useful to consider how reliability relates to validity; as will be discussed below, these are complementary but not equivalent measures (see 3.7. How reliability relates to validity—or not). In summary, the formulation and interpretation of the ICC must be done with care to accurately reflect the strengths and limitations of the measure.

2. Methods

The Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines were followed in conducting this study (Moher et al., 2009). No protocol has been previously published for this review and meta-analysis. All analyses focused on the test-retest reliability of seed and atlas functional connections.

2.1. Objective

We aimed to summarize the current knowledge regarding test-retest reliability (as measured by the ICC) of human brain functional connectivity at the individual edge level. We included both quantitative and qualitative summaries: (1) a quantitative meta-analysis to estimate edge-level reliability, and (2) a qualitative review of factors influencing reliability. As discussed in the introduction, the individual edge level was chosen because it is the most basic element of functional connectivity, and the ICC was selected since it is commonly used to measure edge-level reliability, which facilitates comparability across studies.

2.2. Eligibility criteria

Original quantitative research studies were eligible for inclusion in the qualitative analysis if they reported (1) ICC of (2) individual-edge level functional connectivity obtained from (3) fMRI of the (4) human brain. From the pool of studies identified for qualitative analysis, studies were further eligible for inclusion in the quantitative meta-analysis if mean ICC values across all edges, as well as number of subjects and scans (used for estimating variance), could be readily determined from the text or from personal communication with the corresponding authors (for all studies where information was not readily determined from the text, two emails were sent before excluding any study except for three studies assessed during revision). For studies wherein multiple ICC results were presented, a typical value was sought for the quantitative analysis (i.e., 10–15 min duration, inter-session interval >1 day and <1 mo, median result from multiple pipelines).

2.3. Search procedure and studies identified

Literature was compiled by performing a search of Scopus on November 15, 2018 through titles, abstracts, and keywords. The search included all of the following words or their close synonyms: fMRI, functional connectivity, and ICC. Specifically, the following search string was used: TITLE-ABS-KEY(((fc*MRI OR rs*MRI or RSFC) OR ((“resting state”) and (*MRI or “magnetic resonance imaging” or neuroimaging))) OR ((f*MRI OR ((functional) and (*MRI or “magnetic resonance imaging” or neuroimaging))) AND (connectivity OR connectome OR “resting state”)) AND (“intraclass correlation” OR ICC OR “test retest reliability”)).

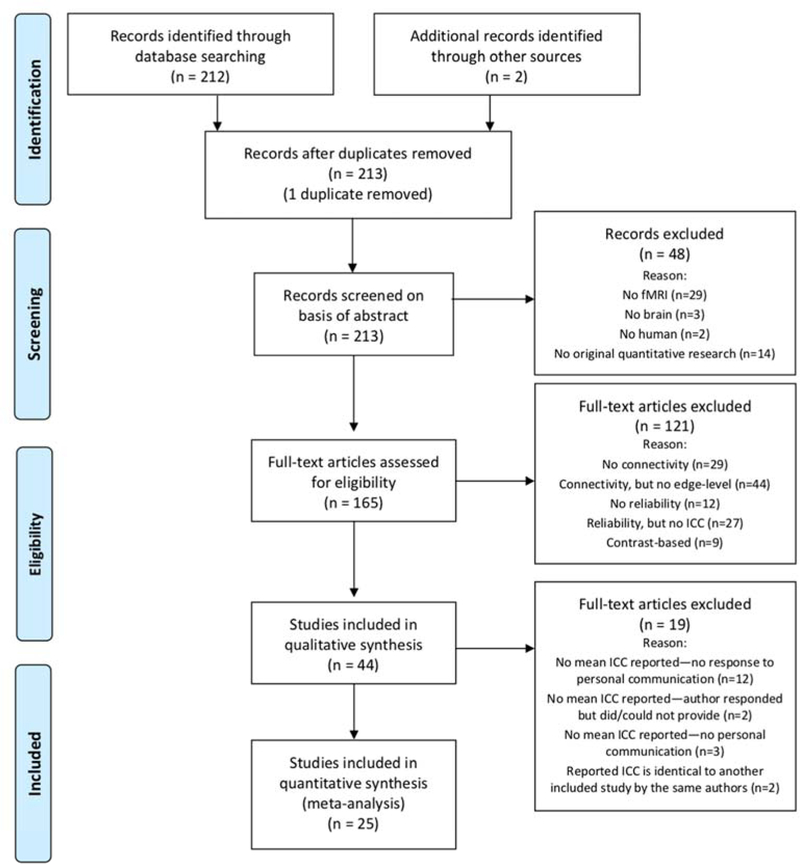
The results at each stage of the search strategy are shown in the PRISMA Consort Chart (Fig. 1). The initial search produced 212 results. 2 studies (Shah et al., 2016; Tomasi et al., 2016) were added by reviewing the references of this set, and 1 study was identified to be a duplicate. Screening and eligibility assessment according to the criteria in the above section were performed by one investigator (S.N.). 48 records were removed after screening abstracts for eligibility; only the following ineligible characteristics could be determined from the abstract alone: no fMRI, no brain, no human, or no original quantitative research. 121 records were removed after reviewing full articles for eligibility, which included scanning each article for inclusion of edge-level connectivity and reliability via the ICC. Although not part of the original criteria, 9 articles were excluded during this step for reporting reliability of a contrast (e.g., the difference between connectivity during a task and connectivity during rest) rather than reliability of a single measurement (e.g., connectivity during rest). 44 studies were then retained for the qualitative analysis.

Figure 1. PRISMA flow diagram summarizing publication selection for review and meta-analysis.

“Identification” refers to initial search; “screening” refers to removal of records based on title and abstract; “eligibility” refers to removal of records based on full-text; “included” refers to inclusion of studies for qualitative and quantitative analysis.

From: Moher D, Liberati A, Tetzlaff J, Altman DG, The PRISMA Group(2009). Preferred Reporting Items for Systematic Reviews and Meta-Analyses: The PRISMA Statement. Plos Med 6(7): e000097. Doi:10.137/journal.p.med1000097

From the pool of studies eligible for qualitative analysis, studies were also eligible for inclusion in the quantitative analysis if a mean ICC value was reported. 19 records were not eligible for the quantitative analysis for the following reasons: we were unable to identify or obtain an estimate of the mean ICC from 17 studies and found that the reported ICC was identical to other studies included in the meta-analysis in an additional 2 studies. As such, 25 studies were retained for the final quantitative meta-analysis (Table 1). Approximately half of the studies were excluded for not using fMRI (n=29), functional connectivity (n=29), or edge-level functional connectivity (n=44).

Table 1. Literature included in quantitative analysis.

For each study, the following categories are listed: the first author, year, dataset (NYU CSC TestRetest=New York University Child Study Center TestRetest; HCP=Human Connectome Project;

Authors	Year	Dataset	Subjects (#)	Duration (min)	Repetition (# sessions)	Intersession Interval	Node Resolution	Anatomical Scope	Anatomical Details	ICC Type	ICC Mean	ICC SD
Parkes et al.	2018	NYU CSC TestRetest	29	6	2	long (3 mo)	ROI-to-ROI	WB	Gordon atlas (n=333)	ICC(1,1)	0.24	0.19
Mejia et al.	2018	HCP	461	15	4	mixed (<1 d, 1 d)	Component-to-voxel	Mixed	WB components (n=94) to WB	ICC(1,1)	0.45	0.10
Conwell et al.	2018	original (University of Cologne)	30	6	3	medium (2 w)	Component-to-voxel	Mixed	DMN, SN, ECN components to WB	ICC(1,1)	0.45	0.23
Stirnberg et al.	2017	original (NA)	10	10	2	short (1 h)	Component-to-voxel	Mixed	DMN, Mot, Vis components to WB	ICC(2,1)	0.24	0.17
Noble et al.	2017	HCP	606	30	2	medium (1 d)	ROI-to-ROI	WB	Shen atlas (n=268)	ICC(2,1)	0.28	0.15
Pannunzi et al.	2017	original (Charité University Clinic)	5	5	42	medium (2 d)*	ROI-to-ROI	WB	Shen atlas (n=268)	ICC(1,1)	0.22	0.16
Zhang et al.	2017	HNU	30	10	10	long (>1 mo)	ROI-to-ROI	WB	Power atlas (n=264)	ICC(1,1)	0.42	0.14
Wang et al.	2017	original (Universityof Queensland)	20	28	2	long (3 mo)	ROI-to-ROI	WB	CC200 atlas (n=200)	ICC(1,1)	0.42	0.20
Noble et al.	2017	NAPLS2 Traveling Subjects	8	6	16	medium-mixed (1 d, 1.5 w)	ROI-to-ROI	WB	Shen atlas (n=268)	ICC(2,1)	0.15	0.12
Andoh et al.	2017	original (Montreal Neurological Institute)	14	6.3	3	medium (6 d, 9 d)	ROI-to-ROI	Aud	Left and Right Heshl’s gyri	ICC(2,1)	0.65	NA
Tomasi et al.	2016	HCP	40	14.4	4	mixed (20 min, 1.5 mo)	ROI-to-voxel	Mixed	OPJ, bi. dlPFC, bi. iPC, bi. thalamus, bi. caudal putamen seeds to WB	ICC(3,1)	0.33	0.32
Shah et al.	2016	HCP	476	15 (effectivel y 60)	4	mixed (<1 d, 1 d)	ROI-to-ROI	Mixed	Unspecified atlas (n=6923) to subset (n=264)	ICC(1,4)	0.47	0.28
Chen et al.	2015	HNU	30	10	10	long (>1 mo)	ROI-to-voxel	DMN	PCC seed to WB	ICC(2,1)	0.35	0.23
Zou et al.	2015	original (NA)	22	8	3	mixed (<1 d, 2 mo)	ROI-to-voxel	DMN	PCC seed to WB	ICC(2,1)	0.36	0.22
Lin et al.	2015	original (BNU)	57	6.8 (effectivel y 20.4)	3	mixed (20 min, 1.5 mo)	Voxel-to-voxel	Mixed	Grey matter voxels; positive connections only	ICC(1,3)	0.30	0.12
Kristo et al.	2014	original (University Medical Center Utrecht)	16	4.1	2	long (7 w)	ROI-to-voxel	Mot	Motor seed to WB	ICC(2,1)	0.24	NA
Yan et al.	2013	NYU CSC TestRetest	19	6.6	2	long (11 mo)	ROI-to-voxel	DMN	PCC seed to WB	ICC(3,1)	0.31	0.20
Wisner et al.	2013	original (NA)	33	6	2	long (9 mo)	Component-to-voxel	Mixed	WB components to WB	ICC(2,1)	0.20	0.23
Fiecas et al.	2013	NYU CSC TestRetest	25	6.6	3	mixed (45 min, 11 mo)	ROI-to-ROI	WB	AAL atlas (n=116)	ICC(2,1)	0.30	0.15
Yan et al.	2013	NYU CSC TestRetest	25	6.6	3	mixed (45 min, 5–16 mo)	ROI-to-voxel	DMN	PCC seed to WB	ICC(1,1)	0.25	NA
Song et al.	2012	ICBM	55	4.3	3	<not given>	ROI-to-ROI	Mixed	DMN, FP, cingulo-opercular, Sens/Mot	ICC(3,1)	0.32	0.14
Guo et al.	2012	original (University of California San Francisco)	24	8	2	long (13 m)	ROI-to-ROI	Sal	Functionally defined (n=68)	ICC (1,1)	0.26	NA
Faria et al.	2012	original (NA)	20	7.2	2	short (1 h)	ROI-to-ROI	WB	Enhanced Mori atlas (n=185)	ICC(3,1)	0.35	0.18
Wang et al.	2011	NYU CSC TestRetest	25	6.6	3	mixed (45 min, 5–16 mo)	ROI-to-ROI	WB	AAL atlas (n=90), HOA atlas (n=112), FDOS atlas (n=160)	ICC(1,1)	0.24	0.20
Shehzad et al.	2009	NYU CSC TestRetest	26	10	3	mixed (<1 h, 5 mo)	ROI-to-ROI	WB	Harvard-Oxford Structural Atlas (n=112)	ICC(1,1)	0.22	0.16

HNU=Hangzhou Normal University; NAPLS2=North American Prodromal Longitudinal Study 2; ICBM=International Consortium for Brain Mapping; unnamed datasets are listed as “original” alongside acquisition location), number of subjects, scan duration (effective duration given if used ICC(1,k) with k>1), number of repetitions, inter-session interval (m=minutes, d=days, mo=months, y=years; short: <1 day, medium: ≥1 day and <1 month, long: ≥1 month, mixed: multiple intervals), node resolution (specifies whether connectivity was measured between ROIs/region of interest, components, and/or voxels), anatomical scope and details (WB=whole brain; DMN=Default Mode Network, SN=Salience Network, FP=Frontoparietal Network, ECN=Executive Control Network, Mot=Motor Network, Sens=Sensory Network, Aud=Auditory Network, Vis=Visual Network; WB refers to whole brain volume unless specified as surface; bi.=bilateral), ICC type, ICC mean across edges, and ICC standard deviation across edges. Star (*) denotes values estimated from publication.

2.4. Statistical Methods

R was used for all statistical analyses (R Core Team, 2017). Excel data was extracted with the read.xls function in gdata (Warnes et al., 2017).

The metafor package was used to perform the meta-analysis analyze results (Viechtbauer, 2010). The rma.mv function was used to compute a meta-analytic estimate of the population ICC with studies nested by dataset; random effects were specified for dataset and the resulting model was fit using Restricted Maximum Likelihood Estimation. To our knowledge, no procedure has yet been documented for formal meta-analysis of ICC values; here we used the following two assumptions to conduct an ICC-based meta-analysis and have provided our justifications. First, meta-analysis was performed using the raw ICC values with the assumption that these were distributed normally. While not exact, this assumption is often made in the similar case of meta-analysis with Pearson’s correlation coefficient, and tends to be less skewed when values are far from one (Fisher, 1928, via Field, 2001) as is the case here. The alternative is typically to z-transform the Pearson’s correlation coefficient; here, however, the transformation of the meta-analytic estimate of the pooled z-coefficient back to an interpretable ICC estimate is not straightforward. Second, we assumed that the variance of the ICC for each study could be approximated as follows (Donner et al., 1986, via Shoukri et al., 2016):

$${\sigma }^2(\text{ICC}(1,1))=\frac{2\hspace{0.17em}\ast \hspace{0.17em}{(1-\text{ICC})}^2\hspace{0.17em}\ast \hspace{0.17em}{(1+(\text{n}-1)\hspace{0.17em}\ast \hspace{0.17em}\text{ICC})}^2}{\text{k}\ast \hspace{0.17em}\text{n}\hspace{0.17em}\ast \hspace{0.17em}(\text{n}-1)}$$

where n is the number of subjects measured (i.e., objects) and k is the number of repeated measurements per subject. Note that this estimate is specifically derived for ICC(1,1) but was also used here to estimate variance for ICC(2,1) and ICC(3,1). This is because studies rarely report the within-subject variance component required for estimating variance for ICC(2,1) and ICC(3,1) (Shoukri et al., 2016).

Effect size forest plots of all studies included in the meta-analysis were created with the forest function. A funnel plot showing the relationship between ICC coefficients and their estimated standard errors was created with the funnel function. Heterogeneity was assessed with Cochrane’s Q, and publication bias was assessed by estimating funnel plot asymmetry via the ranked regression test (ranktest function). An exploratory meta-analysis was conducted to estimate moderation by the following study characteristics reported in Table 1: dataset, number of subjects, year, scan duration, intersession interval, number of repeated sessions, node resolution, anatomical scope, ICC type. For this analysis, each moderator was included separately in the meta-analytic model described above. Another exploratory analysis was also performed to estimate whether studies could be separated into multiple distributions, without nesting of studies within dataset. A Gaussian finite mixture model was fit to the data using the normalmixEM function within the mixtools package, which uses expectation maximization to estimate groups (Benaglia et al., 2009). A Kolmogorov-Smirnov test, via the ks.test function, was used to estimate how well the multi-distribution model explained the data.

For comparison, a simpler arithmetic weighted mean was also calculated. This second estimate does not account for the nesting of studies within datasets and instead treated each study independently, weighted by the product of the number of subjects and number of repeated measurements (this product is proportional to the variance of the ICC; Pannunzi et al., 2016). To assess spatial variability in reliability, an arithmetic weighted mean of study standard deviations across edges was also calculated.

2.5. Data and Code Availability Statement

The R script used to conduct this meta-analysis is available at https://github.com/SNeuroble/fmri_scripts_other/tree/master/R/myscripts/TRT_review/trt_meta. R. Study data used for the meta-analysis is provided in Table 1.

3. Results

3.1. Meta-analysis: Estimated reliability of functional connectivity

In the following, we aim to provide an estimate of the reliability of functional connectivity across 25 studies identified for quantitative analysis. These studies spanned 16 unique datasets that ranged from 5 to 606 subjects, with subjects undergoing between 2 to 42 repeated measurements and laying in the scanner from 4.1 to 30 min (Table 1). The earliest known investigation was conducted by Shehzad and colleagues in 2009. Studies used short term (<1 day; n=2 studies), medium term (≥1 day and < 1 month; n=5 studies), long term (> 1 month; n=8 studies), or mixed (n=9 studies) intervals; one study did not specify the interval. 13 studies used unique datasets and 12 studies used overlapping publicly available datasets: 6 used the New York University Child Study Center Test-Retest dataset (NYU CSC TestRetest; Shehzad et al., 2009)⁴; 4 used the Human Connectome Project dataset (HCP; Van Essen et al., 2013)³; and 2 used the Hangzhou Normal University dataset (HNU)⁴; named datasets used once included the North American Prodromal Longitudinal Study 2 dataset (NAPLS2; Addington et al., 2007) and International Consortium for Brain Mapping dataset (ICBM; Evans et al., 2001)⁵.

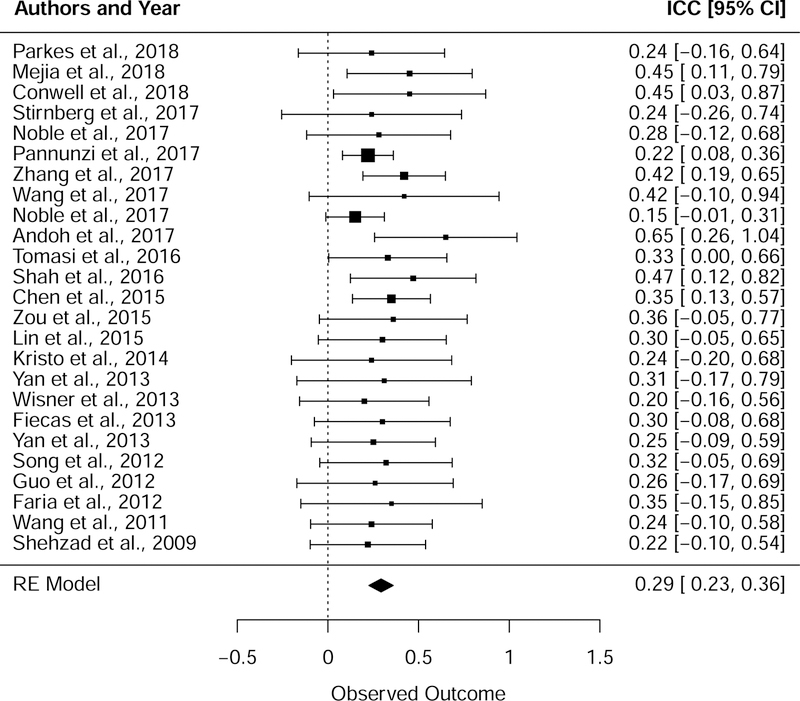
Combining studies, the estimated average reliability of edge-level functional connectivity was found to be poor (ICC µ = 0.29, 95% CI = 0.23 to 0.36, SE = 0.03; Fig. 2). The weighted arithmetic mean of ICC was somewhat larger than the meta-analytic estimate, on the threshold between poor and fair reliability (weighted mean of mean ICC = 0.38 +/− 0.09). The typical standard deviation across edges was about half as large (weighted mean of ICC standard deviation = 0.18 +/− 0.07), similar in magnitude to the estimated standard deviation of 0.2 +/− 0.038 by Pannunzi et al. (2017). We were neither able to detect heterogeneity in ICC estimates among the true effects (Test for Heterogeneity: Q = 12.30, p = 0.97) nor publication bias via the rank regression test for funnel plot asymmetry (Kendall’s tau = 0.13, p = 0.37). Exploratory inclusion of moderators of ICC (dataset, number of subjects, year, scan duration, number of repeated sessions, node resolution, anatomical scope, ICC type) did not suggest moderation by any characteristic in this sample (p>0.05 for all moderators; one moderator, anatomical scope, was associated with p<0.1 and may warrant further investigation; SI Table 2). Additionally, exploratory modeling of the distribution of ICCs as a random Gaussian mixture without nesting did not indicate support for a multimodal distribution in this sample (p=0.98 via Kolmogorov-Smirnov test; SI Fig. 1).

Figure 2. Summary of reliability across studies.

Forest plot depicting mean ICCs and 95% confidence intervals for the 25 studies included in the meta-analysis. The pooled estimate of the ICC was obtained using a random effects (RE) model with studies nested by dataset.

In summary, average reliability of functional connections was estimated from the literature to be poor. However, the literature suggests that greater reliability may be attained in a number of circumstances. In the following, we summarize results from the 44 studies identified for qualitative analysis and their implications for increasing reliability.

3.2. Spatial distribution of reliable edges

Although the networks investigated varied across studies, some consensus exists regarding the relative reliability of these networks (SI Table 2). The frontal and default mode networks were most often found to be the most reliable networks (Blautzik et al., 2013; Marchitelli et al., 2017; Mejia et al., 2018; Noble et al., 2017b; O’Connor et al., 2017; Somandepalli et al., 2015; Wisner et al., 2013; Zuo et al., 2014). Frontal networks identified across studies were spatially variable but included frontoparietal, control, attention, and executive networks. Visual networks were also amongst the most reliable (Blautzik et al., 2013; Chen et al., 2015; Shirer et al., 2015), although these were often spatially variable. Mixed results were found for sensorimotor networks, with three studies indicating greater reliability in sensorimotor, auditory, and speech cortices (Blautzik et al., 2013; Shirer et al., 2015; Wisner et al., 2013), versus one study indicating poorer reliability in motor cortex (Chen et al., 2015). Results were split for the limbic network (high for Chen et al., 2015; low for Noble et al., 2017b). Areas adjacent to non-grey matter (e.g., areas near the grey-white junction, large sulci, or frontal cavities) were sometimes listed as least reliable (Blautzik et al., 2017; Shah et al., 2016). The majority of studies did not list subcortical and cerebellar networks amongst the most reliable networks; in general, these have been found to be less reliable than cortical networks (Mejia et al., 2018; Noble et al., 2017b; Shah et al., 2016). One study demonstrated the opposite pattern (Pannunzi et al., 2017), with cerebellar regions showing greatest reliability and parietal and prefrontal regions showing the least reliability. This discrepancy is puzzling since similar overall ICC estimates are obtained using the same atlas in Noble et al. (2017b), but may be attributed to differences in acquisition duration, number of repeated measures, or processing strategies.

In summary, although there is some variability across studies, the literature generally agrees that frontal and default mode networks are most reliable whereas subcortical networks are least reliable. Higher reliability in cortical compared with subcortical areas may be attributed to several factors. First, stronger, positive edges generally exhibit greater reliability (Faria et al., 2012; Fiecas et al., 2013; Noble et al., 2017b; Shah et al., 2016; Shehzad et al., 2009; Stirnberg et al., 2017; Wang et al., 2011), although one study found the opposite (Wisner et al., 2013). Thus, differences in reliability may be partly explained by the observation that connectivity is generally estimated to be stronger in cortical compared with subcortical networks (Noble et al., 2017b; Shah et al., 2016). Second, connectivity in association areas, including frontoparietal and default mode networks, also tends to exhibit the most inter-subject variability (Mueller et al., 2013), which is directly proportion to ICC; interestingly, this was shown to be associated with evolutionary cortical expansion and sulcal depth. Third, subcortical areas may be particularly noisy. These areas share close proximity to non-neural sources (Brooks et al., 2013), are in central areas with lower SNR (Wiggins et al., 2009), and have smaller volumes (Shah et al., 2016)—although previous results suggest that small volume effects are only part of the story (Noble et al., 2017b). Reliability may be further improved with a more precise atlas of these fine structures (e.g., Garcia-Garcia et al., 2018). Fourth, subcortical areas may exhibit unique neural activity that is simply not shared with the rest of the brain.

While overall reliability is generally low, specific connections or connectivity with specific nodes may still show fair or greater reliability (Wisner et al., 2013; Noble et al., 2017b). For example, amongst generally low reliability subcortical areas, connectivity with the posterior lobe of the cerebellum typically shows greater reliability (Noble et al., 2017b; Shah et al., 2016). Indeed, the estimated variability across edges of studies included in the meta-analysis is about half the magnitude of the estimated mean ICC value. However, in many of these studies, the small number of measurements leads to large uncertainty of the estimators (Pannunzi et al., 2017), precluding current estimation at this level of granularity. Although it is challenging to repeatedly measure many subjects many times, future work with even larger samples may better illuminate reliability at the level of individual edges.

3.3. Influence of acquisition and processing strategies

Reliability can be altered by a multitude of acquisition and processing choices. The most comprehensive investigations of pipeline effects on edge-level reliability have been conducted by Shirer et al. (2015) and Parkes et al. (2018). These studies, coupled with the work of others, illustrate that the influence of acquisition and processing choices on reliability remains a complex issue. In the following and Table 3, we summarize the current knowledge about the strategies investigated in the literature.

Table 3. Summary of effects of acquisition and preprocessing strategies on reliability.

For each strategy in the left column, the right column summarizes whether the combined evidence across studies suggests that the given strategy increases (↑), decreases (↓), or has minimal/no effect on (=) reliability. Studies are grouped by strategy and listed in chronological order. For strategies for which evidence is mixed, studies are also grouped by whether they increase (↑), decrease (↓), or have minimal/no effect on (=) reliability. Acronyms are used for noise regression methods, including global signal (GS), white matter (WM), cerebrospinal fluid (CSF); see footnote 7 in the text for component regression acronyms.

ACQUISITION OR PROCESSING STRATEGY	EFFECT ON RELIABILITY
Multiple sites and/or scanners	= Minimal if harmonized Noble et al., 2017a (multiple sites); Noble et al., 2017b (multiple scanners); Andoh et al., 2017 (interleaved silent steady-state = conventional) (Tentative: Stirnberg et al., 2017, 3D-EPI > SMS-EPI)
Eyes open, awake, & engaged subjects	↑ Slightly increases Zuo et al., 2009 (eyes open>closed); Patriat et al., 2013 (eyes open>closed); Wang et al., 2017a (awake>sleep); Wang et al., 2017b (movie watching>rest)
Slice timing correction	= Minimal Shirer et al., 2015; Marchitelli et al., 2017
More data per subject	↑= Increases with diminishing returns Birn et al., 2013 (duration, sampling rate); Mueller et al., 2015 (duration); Shah et al., 2016 (duration, sampling rate>duration); Tomasi et al., 2016 (duration); Noble et al., 2017b (duration, longer>shorter interval averaging); Mejia et al., 2018 (duration); Shirer et al., 2015 (no high-frequency filter)
Short inter-scan interval	↑ Increases Shehzad et al., 2009; Birn et al., 2013; Fiecas et al., 2013; Pannunzi et al., 2016; Noble et al., 2017b; O’Connor et al., 2017
Noise regression	~↓ Generally decreases (may remove reliable artifact) ↑ : Braun et al., 2012 (GS); Marchitelli et al., 2016 (WM/CSF); Marchitelli et al., 2016 (FSL-FIX) (Guo et al., 2012, low>high motion subjects) ↓ : Shirer et al., 2015 (motion); Parkes et al., 2018 (motion); Guo et al., 2012 (GS); Song et al., 2012 (GS); Shirer et al., 2015 (GS); Parkes et al., 2018 (GS); Parkes et al., 2018 (WM/CSF); Birn et al., 2014 (WM/CSF/GS, RVTcor), Shirer et al., 2015 (CompCor), Zou et al., 2015 (PESTICA); Parkes et al., 2018 (ICA-AROMA, aCompCor) = : Shirer et al., 2015 (WM/CSF); Marchitelli et al., 2017 (WM/CSF)
Connectivity estimation via partial correlation	↓ Decreases Fiecas et al., 2013; Mejia et al., 2018
Connectivity estimation via shrinkage	↑ Increases Mejia et al., 2018

3.3.1. Multiple scanners and sites

For a number of reasons, a study may collect data across multiple sites or scanners. Although the use of multiple well-harmonized scanners has been shown to have minimal effects on reliability—even across sites and manufacturers (Noble et al., 2017a, Noble et al., 2017b)—uncontrolled differences across scanners and/or sites always offer the potential to introduce bias. For example, 3-dimensional echo planar imaging (3D-EPI) sequences may yield comparable or better reliability than simultaneous-multi-slice echo-planar imaging (SMS-EPI; Stirnberg et al., 2017), although 3D-EPI is accompanied by particularly challenging artifacts. On the other hand, another study showed that even when differences in connectivity are detected between sequences (interleaved silent steady-state, ISSS, versus conventional), differences in reliability may not be detected (Andoh et al., 2017).

The following studies did not meet criteria for the qualitative analysis—they estimated reliability for fMRI-based measures that were not edge-level functional connectivity. However, they further demonstrate the potential for site effects in fMRI. A couple studies have reported inter-site differences in edge-level connectivity (Jovicich et al., 2016; Biswal et al., 2010). Another study found differences in reliability of temporal signal-to-noise ratio (tSNR) across scanner manufacturers, although different head coils, sequences, and countries were also used across scanners (An et al., 2017). Global network measures may further amplify scanner effects, even with harmonized scanners (Noble et al., 2017a); scanner effects have also been shown for global measures under different scanning parameters (Yan et al., 2013b). Therefore, although multi-site/scanner can have minimal effects on reliability of edge-level functional connectivity, it is always important to be proactive in maximizing harmonization and measuring the effect of site and scanner since effects have been found in other fMRI-based measures.

3.3.2. Eyes open, awake, & engaged subjects

The greatest reliability was typically obtained when subjects laid awake with their eyes open and were engaged in a task. Slightly greater reliability was found when subjects were instructed to rest with eyes open compared with eyes closed (Patriat et al., 2013; Zou et al., 2009; though not part of the qualitative analysis, similar results have been found by Van Dijk et al., 2010). This may be due in part to participants becoming sleepy when allowed to rest with their eyes closed, since drowsiness has also been shown to reduce reliability (Wang et al., 2017a). Yet even more substantial is the effect of performing a naturalistic movie watching task. While the removal of sleep-relevant volumes results in a modest but significant increase in edge-wise reliability (∆ICC = 3.7%), reliability improves considerably when subjects are engaged in a naturalistic task (∆ICC = 31.5%; Wang et al., 2017b).

3.3.3. Slice timing correction

Evidence suggests that slice timing correction has minimal effects on reliability (Marchitelli et al., 2017; Shirer et al., 2015). This is consistent with work demonstrating that slice timing correction has minimal effects on functional connectivity (Wu et al., 2011).

3.3.4. Amount of data per subject

The influence of the amount of data per subject on reliability has been extensively explored. The acquisition of more frames of data is associated with greater reliability, whether through longer scan durations (Birn et al., 2013; Mejia et al., 2018; Mueller et al., 2015; Noble et al., 2017b; Shah et al., 2016; Tomasi et al., 2016), higher sampling rates (Birn et al., 2013), or multiple scans (Noble et al., 2017b). That said, different strategies for increasing data had different effects. For the same total number of frames, longer scan durations improved reliability more than higher sampling rates (Shah et al., 2016; although not part of the qualitative analysis, similar results were found by Horien et al., 2018a). For the same total scan time, averaging data across multiple sessions acquired farther apart in time (e.g., weeks) resulted in a more reliable measure than averaging across consecutive sessions (e.g., weeks instead of minutes). Relatedly, the use of a low-pass or narrow filter (i.e., discarding high frequency information) reduced both reliability and signal-noise separation (Shirer et al., 2015).

The greater reliability for longer scans compared with higher sampling rate may be because the majority of biologically relevant hemodynamic changes detectable by fMRI are thought to occur predominantly at lower frequencies (Birn et al., 2013). High frequency information may still be useful, however, in improving inferential power (Constable and Spencer, 2001) and enabling more accurate estimation of high frequency or short-lived artifacts (e.g., motion, cardiac). For example, cardiac pulsation occurs at a frequency of approximately 1 second or less; if samples are not acquired at twice this rate or more (the Nyquist rate), cardiac artifacts may be aliased into low frequency signals (Shmueli et al., 2007). Altogether, sufficient evidence is not currently available to recommend a specific scan duration for optimal reliability, especially since longer scans are associated with rapidly diminishing returns in reliability (Mueller et al., 2015; Tomasi et al., 2016; Van Dijk et al., 2010) and unwanted sleepiness. Additionally, there is an opportunity to identify whether averaging multiple sessions acquired farther apart in time may improve validity alongside reliability; we have previously hypothesized that the increase in reliability may be attributed to more completely capturing a portrait of a subject as they pass through multiple distinct states (Noble et al., 2017b).

3.3.5. Inter-scan interval

Whereas above we addressed the effect of averaging data across different inter-scan intervals, here we will address the effect of calculating reliability between scans acquired at different inter-scan intervals. Indeed, the inter-scan interval used for calculation of ICC is an important consideration. As is expected from the temporally correlated nature of the timeseries data, repeated measurements taken over shorter intervals are more reliable than those taken over longer intervals (Birn et al., 2013; Fiecas et al., 2013; Noble et al., 2017b; O’Connor et al., 2017; Pannunzi et al., 2017; Shehzad et al., 2009).

Decreasing reliability across longer timescales may be partly attributed to slow brain reorganization over time, or possibly increased variability due to accumulating sources of error. The same trend occurs for the whole-brain pattern of connectivity, with greater correlations between adjacent measurements than over longer timescales (e.g., weeks; Fig. 3). Since the ICC is dependent on the inter-scan interval, it should be selected so that interpretations are relevant to future research questions of interest. For example, it is intriguing that reliability calculated across different tasks within the same session is greater than the reliability calculated for the same task across sessions (O’Connor et al., 2017), yet it would be further illuminating to estimate the degree to which this effect can be attributed to closer similarity at shorter timescales. For example, another measure of brain organization, functional parcellation, shows greater similarity within- than between-tasks when accounting for session effects (Salehi et al., 2018). As discussed in the introduction, one solution that allows estimation of multiple sources of error (including timescales and task) is to estimate Generalizability Theory ICCs (e.g., Cannon et al., 2014; Forsyth et al., 2014; Friedman et al., 2008; Noble et al., 2017a; Noble et al., 2017b; Webb et al., 2006).

Figure 3. Similarity of adjacent sessions, separated by approximately one week.

Using the Yale Test-Retest dataset (Noble et al., 2017b), similarity was measured using the Pearson’s correlation between connectomes assessed about a week apart. A, Correlations between session pairs, averaged across subjects. B, Correlations between session pairs for each subject plotted as a function of inter-session interval. Lines indicate each subject, with colors indicating session pairs. The group level correlation is displayed in the bottom left.

3.3.6. Denoising strategies

Procedures designed to reduce the contribution of noise (e.g., motion, global signal, white matter, cerebrospinal fluid, and component regression; cf. Caballero-Gaudes and Reynolds, 2017) can have unexpected effects on reliability. Regression of head motion, a common and challenging confound (Power et al., 2012), was found to decrease reliability in two studies (Parkes et al., 2018; Shirer et al., 2015; with no detectable differences between volume- and slice-based corrections; Marchitelli et al., 2017). The use of head restraints is expected to show similar effects as motion regression. Amongst the intriguing discrepancies that warrant further investigation include the increase in reliability when removing high motion subjects (Guo et al., 2012) and during movie watching despite decreased motion (Wang et al., 2017b).

Large, shared signals across brain areas are often regressed as a proxy for unmeasured physiological noise. Commonly, researchers regress the global brain signal, which decreased reliability in four studies (Guo et al., 2012; Parkes et al., 2018; Shirer et al., 2015; Song et al., 2012) but increased reliability in one (Braun et al., 2012). Alternatively, researchers may regress non-gray matter tissue, which has been shown to increase reliability in one study (Marchitelli et al., 2016), decrease reliability in another (Parkes et al., 2018), and have minimal effects in others (Marchitelli et al., 2017; Shirer et al., 2015). Another common method is to regress components representing a broadly distributed signal using either a model-free (e.g., choosing the top component obtained by independent component analysis, ICA) or model-based (e.g., choosing components that match a model of physiological artifact) approach. Component regression predominantly decreased reliability: CompCor, PESTICA, RVTcor, and ICA-AROMA all decreased reliability (Birn et al., 2014; Parkes et al., 2018; Shirer et al., 2015; Zou et al., 2015) while FSL-FIX increased reliability (Marchitelli et al., 2016)⁶. Complicating the matter, many of these denoising strategies seem to overlap: tissue signals are highly correlated with each other and with the global signal (Vos de Wael et al., 2017), and global signal regression has been shown to reduce the effect of motion (Power et al., 2014).

As a whole, the evidence suggests that denoising procedures tend to (but don’t always) decrease reliability. Yet this does not necessarily diminish validity. In fact, a decrease in reliability is consistent with the successful removal of undesirable artifact, since high levels of reliability have been found for motion (Couvy-Duchesne et al., 2014; Yan et al., 2013a; Zuo et al., 2014) and cardiac pulsatility (Birn et al., 2014). Furthermore, two denoising techniques—global signal regression and CompCor—were found to improve signal-noise separation and group discriminability even while reducing reliability (Shirer et al., 2015). The situation is highly nuanced for global signal regression (cf. Murphy and Fox, 2017 for a comprehensive discussion), but it has improved brain-behavior findings in at least several cases (Boes et al., 2015; Hampson et al., 2010; Kruschwitz et al., 2015; Li et al., 2019). In these contexts, the present results provide indirect evidence that denoising may often reduce unwanted but reliable artifact.

3.3.7. Connectivity estimation

Estimating connectivity with full correlation generally resulted in higher reliability than partial correlation (Fiecas et al., 2013; Mejia et al., 2018), except in rare circumstances (e.g., for specific values of the penalty term; Mejia et al., 2018). Another strategy involves selecting or adjusting edges based on their estimated reliability. Recent work has suggested a shrinkage strategy wherein individual-level estimates are brought closer to group-level estimates based on their unreliability, which substantially increases reliability (Mejia et al., 2018).

Two additional studies that did not meet criteria for the qualitative analysis shed further light on this issue. One study added support for increased reliability of full compared with partial correlation in graph metrics (Telesford et al., 2010). Another study illustrated that a multivariate estimate of connectivity between regions that uses the voxelwise timeseries substantially improves reliability (from ICC=0.18 to ICC=0.43; Yoo et al., 2019).

4. Summary

In this study, we performed the first meta-analysis and systematic review exploring the reliability of functional connectivity, following PRISMA guidelines. Despite some studies suggesting that reliability of functional connectivity is high, the synthesis of nearly a decade of evidence confirms that individual edges show marked instability. This stands in contrast to the relatively high reliability of the pattern of whole-brain connectivity. The literature further suggests that studies with the highest reliability tend to have the following characteristics: (1) analyses restricted to stronger, within-network, cortical edges (with frontoparietal/default mode edges most reliable and non-grey matter adjacent and subcortical edges least reliable), (2) eyes open and awake recordings of subjects engaged in a task, (3) as much within-subject data as possible, with some sources of data contributing more than others, (4) test and retest measurements collected at shorter inter-scan intervals, (5) no artifact correction (e.g., global signal, motion), likely due to the higher reliability of artifacts like motion, and (6) connectivity estimated via full correlation with shrinkage rather than partial correlation.

4.1. Implications: how reliability relates to validity—or not

Reliability is a desirable quality that places an upper limit on the validity of a measure (i.e., its correspondence with some “ground truth” target, e.g., ability to predict clinical outcomes of depression; White et al., 2008; Nunnally Jr, 1970; Bennett and Miller, 2010; Nichols et al., 2017). Similarly, improving the reliability of a measure can potentially reduce the sample size required to detect an effect (Zuo and Milham, 2019). Recommendations are therefore often made for procedures that improve reliability. For example, eyes open acquisitions have been suggested on the basis of improved reliability (Van Dijk et al., 2010), and recent work by Mejia et al. (2018) has proposed the use of shrinkage-based approaches for stabilizing unreliable measurements. These strategies can potentially be used to increase the upper limit on the validity of a measure.

Accordingly, the pooled estimate of low reliability challenges our potential ability to make inferences at the individual edge level using standard methods. Although the implications for any particular study are case-specific and remain to be investigated, these findings motivate the need to improve existing methods. For the many existing studies that have used univariate or mass univariate inferential strategies, strictly exploratory re-analysis with more reliable strategies (e.g., multivariate inferential strategies) may be worth pursuing.

Yet while reliability is a desirable trait, the literature suggests that its desirability has limitations. In fact, some strategies that improve reliability may actually reduce validity (cf. Feldt, 1997). The present review highlights one particular issue for functional connectivity: the seemingly undesirable reduction in reliability after artifact removal. This is complicated by two pieces of evidence from the literature: 1) many artifacts are, themselves, highly reliable, and 2) artifact removal often improves measures of validity. We have previously demonstrated a dissociation between reliability and validity, wherein selecting for edges based on reliability did not influence prediction of fluid intelligence (Noble et al., 2017b). Two hypothetical examples further illustrate this dissociation: 1) an unreliable psychological measure expected to reflect a trait-level characteristic may actually reflect a useful state-level characteristic, and 2) a stopped clock may provide a perfectly reliable but perfectly useless measure of the time. Therefore, the characteristics associated with increased reliability listed above should not be seen as a set of recommendations but rather as a roadmap for further exploration.

Before recommending any particular strategy, there must be evidence that it improves validity. In practice, however, test-retest reliability is sometimes used as the sole basis for making recommendations since it can be challenging to identify a metric of validity. While this may be acceptable in cases where a strong argument can be made that validity will be maintained or improved, this is usually difficult to ascertain a priori and recommendations based on reliability alone should generally be avoided. Accordingly, Shirer et al. (2015) concluded that the optimal preprocessing pipeline should be selected based on desired outcome measures rather than reliability, wary of the fact that “common noise enhances reliability by providing a highly reliable, but non-neural, structure within the data.” We agree that validity should be prioritized over reliability (Noble et al., 2017b). In general, functional MRI designs that incorporate measures of both reliability and validity will have support from both cornerstones of scientific accuracy, and findings that improve both can be recommended with greater confidence.

4.2. Considerations regarding ICC as a measure of test-retest reliability

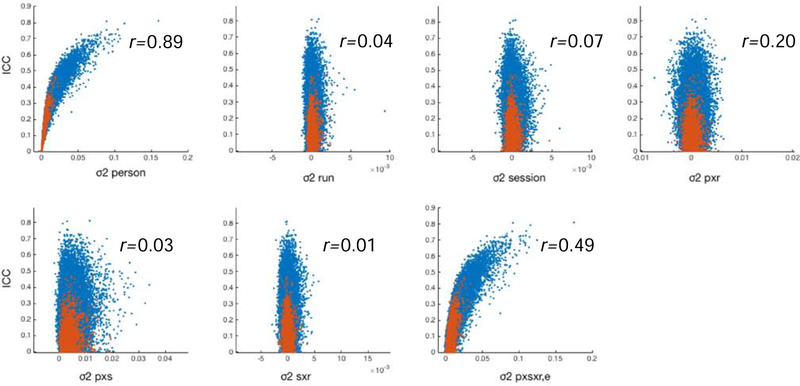
The ICC has several interesting properties, particularly in the context of functional connectivity. By definition, the ICC is influenced by two main factors: variability within subjects and variability between subjects. However, between-subject variability accounts for 80% of the variance in the ICC for functional connectivity analyses, compared to 24% by the next largest contributor, the residual (Fig 4). As such, reliability of functional connectivity is primarily driven by between-subject differences. This is somewhat counterintuitive; in comparing the reliability of two edges, one might desire the more reliable edge to reflect less within-subject variability rather than greater between-subject variability. As such, the ICC is akin to a measure of discriminability, and is complementary to a measure that reflects absolute scan-rescan deviations.

Figure 4. Correlation between variance components and ICC.

Variance components were calculated using the Yale Test-Retest dataset as described in Noble et al. (2017b). Each panel corresponds with a variance component and demonstrates the correlation between that variance component and ICC. Blue dots indicate “strong” edges (p<0.05), and red dots indicate “weak” edges (p>0.05). ICC is most correlated with variance between subjects, and second most correlated with overall variance (r=0.79; not shown).

The variance components that are estimated for the ICC naturally fill the role of an absolute scale measure. It is therefore worthwhile to report and/or analyze these estimates of variability on their own. Notably, the interpretation of within-subject variance components is the most interesting in this respect, yet also the most difficult to interpret. It is challenging to disentangle structured changes within an individual corresponding with an outcome of interest from completely random variability. Complicating matters, people undergo cyclical changes at very short (e.g., <1 day), very long (e.g., months), and developmental (>1 year) timescales. Modeling scans as random does not adequately capture this structured variability; in fact, an ANOVA may be suboptimal compared with explicit models of growth (e.g., Brandmaier et al., 2018).

Finally, unless driven by convincing reasons otherwise, it is advisable to design experiments and analyses to maximize generalizability to other studies. This often entails assessing reliability across the whole-brain, estimating reliability at a spatial resolution relevant to inference, modeling error sources as random rather than fixed (as appropriate), explicitly modeling multiple sources of error, and sharing data (Poldrack and Gorgolewski, 2014; Poline et al., 2012; see Acknowledgments). Note that the majority of studies do not perform inference at the level of average brain connectivity; therefore, assessing reliability of this average measure has limited practical relevance and estimating edge-level reliability is typically preferable. Summarizing results by reporting the maximum ICC is also not advisable; the frequently large variance in the ICC estimators (Pannunzi et al., 2017; Zuo et al., 2014) and the large number of edges raises the likelihood that very high (or low) ICCs may be obtained by chance. To promote accurate inferences, it is important to report the mean instead of the maximum reliability across edges, and smoothing results across the image may be used to similar effect (cf. Stirnberg et al., 2017). It is in all of our best interests to promote generalizable research (Munafò et al., 2017; Nosek et al., 2015).

4.3. Limitations

We made a decision to focus the scope of the meta-analysis and review to specific measures of connectivity and reliability. While not the focus of the present review, complementary measures have enriched our understanding of the test-retest reliability of functional connectivity. Although we measured ICC here, we have discussed complementary and sometimes preferable ways of measuring reliability in the above section and introduction (Gisev et al., 2013). We also restricted our measure of connectivity to univariate measures, but note that reliability is substantially improved with multivariate measures including multivariate connectivity (Yoo et al., 2019), global rather than local connectivity (Cao et al., 2014), and multivariate ICC (Shou et al., 2013; see also Noble et al., 2017b). Similarly, the pattern of whole-brain connectivity can be used to robustly distinguish individuals even at short scan durations (Anderson et al., 2011; Finn et al., 2015; Mueller et al., 2015; Noble et al., 2017b; Pannunzi et al., 2016) and even when scans are taken years apart (Horien et al., 2018b). High pattern-based discriminability despite lower multivariate reliability (Noble et al., 2017b) suggests that the whole-brain pattern of connectivity contains more unique information than the sum of its individual parts.

In addition, there are limitations to the generalizability of the meta-analysis. First, to our knowledge, resources for performing a meta-analysis using the ICC as an outcome measure are not available. We made several assumptions for the use of the ICC for estimating the group effect, but the robustness of these assumptions remain to be investigated. Another limitation concerns the heterogeneity in the study characteristics of the included studies. Although we did not detect heterogeneity or moderation by study characteristics, we are unable to rule these factors out. Differences in reliability may therefore be attributed to a number of study characteristics such as ICC type, various processing choices, etc. It is challenging to explicitly model these factors in the meta-analysis due to several reasons, including the differences in sample size across studies, but we hope that providing this summary of the data available today will support continued meta-analytic investigations in the future.

The generalizability of these results across populations may also be limited. Compared with typically developing subjects, some clinical populations (i.e., Alzheimer’s Disease, Attention Deficit Hyperactivity Disorder) exhibit lower reliability (Blautzik et al., 2013; Somandepalli et al., 2015). In addition, while the precise trajectory of reliability across the lifespan remains to be determined, evidence suggests that older adults exhibit lower reliability than younger adults (Conwell et al., 2018; Song et al., 2012). Differences in reliability may be linked to differences in other biological factors (e.g., phospho-tau; Conwell et al., 2018). In addition to these overall differences in reliability, there may be differences in the spatial distribution of reliability. Understanding the reliability of the population is important in planning population-specific studies wherein variability may play a central role—e.g., pre-/post-treatment study or studies evaluating short-term state-specific characteristics.

5. Closing comments

A spotlight has been cast on the reproducibility of biomedical science today. Attempts to replicate many studies have failed, leading a majority of scientists to endorse the existence of a “reproducibility crisis” (Baker, 2016). Addressing this topic has been particularly critical for the field of neuroimaging (cf. Poldrack et al., 2017, for a comprehensive discussion including best practices). With science agencies worldwide investing unprecedented funds into neuroscience research (Richardson, 2017), and functional connectivity leading the state-of-the-art in human research (Dworkin et al., 2018), it is increasingly important to understand the accuracy of functional connectivity—and improve it if we can.