Gain Modulation by Corticostriatal and Thalamostriatal Input Signals during Reward-Conditioned Behavior

SUMMARY

The cortex and thalamus send excitatory projections to the striatum, but little is known about how these inputs, either individually or collectively, regulate striatal dynamics during behavior. The lateral striatum receives overlapping input from the secondary motor cortex (M2), an area involved in licking, and the parafascicular thalamic nucleus (PF). Using neural recordings, together with optogenetic terminal inhibition, we examine the contribution of M2 and PF projections on medium spiny projection neuron (MSN) activity as mice performed an anticipatory licking task. Each input has a similar contribution to striatal activity. By comparing how suppressing single or multiple projections altered striatal activity, we find that cortical and thalamic input signals modulate MSN gain and that this effect is more pronounced in a temporally specific period of the task following the cue presentation. These results demonstrate that cortical and thalamic inputs synergistically regulate striatal output during reward-conditioned behavior.

In Brief

Lee et al. show that excitatory corticostriatal and thalamostriatal projections regulate striatal activity and gain in mice performing a Pavlovian reward conditioning task. They find that gain modulation by these projections is more evident in the period between cue and reward presentation.

Graphical Abstract

INTRODUCTION

An essential aspect of signal processing in the brain is the transformation of synaptic input to neuronal output. As a major input hub for the basal ganglia, the striatum receives convergent excitatory signals from the cortex and thalamus (Huerta-Ocampo et al., 2014; Hunnicutt et al., 2016), which are thought to drive neural activity patterns involved in sensory processing and movement control (Graybiel et al., 1994; Matsumoto et al., 2001; Ponvert and Jaramillo, 2019). Several disorders are thought to arise from aberrant corticostriatal and thalamostriatal signals and their effect on medium spiny projection neuron (MSN) output (Parker et al., 2016; Shepherd, 2013; Smith et al., 2014). Although synaptic input summation in the striatum has been studied in vitro (Carter et al., 2007; Goto and O’Donnell, 2002; Wolf et al., 2009), little is known about how individual or multiple corticostriatal and thalamostriatal inputs regulate striatal dynamics during behavior (Reig and Silberberg, 2014).

Here we trained mice to perform anticipatory licking in response to reward-associated cues and investigated how behaviorally evoked neural dynamics in the lateral striatum are shaped by a bilateral projection from the secondary motor cortex (M2), a cortical area involved in licking (Komiyama et al., 2010), and the parafascicular thalamic nucleus (PF), one of the primary sources of thalamostriatal input (Díaz-Hernández et al., 2018). This was carried out by monitoring changes in firing rate while transiently suppressing single or multiple projections using optogenetic terminal inhibition. This approach allowed us to elucidate the arithmetic rules of corticostriatal and thalamostriatal signal integration in vivo during behavior. The fractional change in firing rate observed when suppressing two or three inputs at the same time was a nonlinear sum of the change caused by suppressing individual inputs, and it closely fit a model of multiplication. In agreement with a multiplication-like rule, the gain of striatal output varied with the number of simultaneously suppressed inputs. Finally, we found evidence that even within the same behavioral task, the arithmetic rules of input summation can vary significantly across different periods.

RESULTS

Balanced Activity of D1 and D2 MSNs during Reward-Conditioned Licking

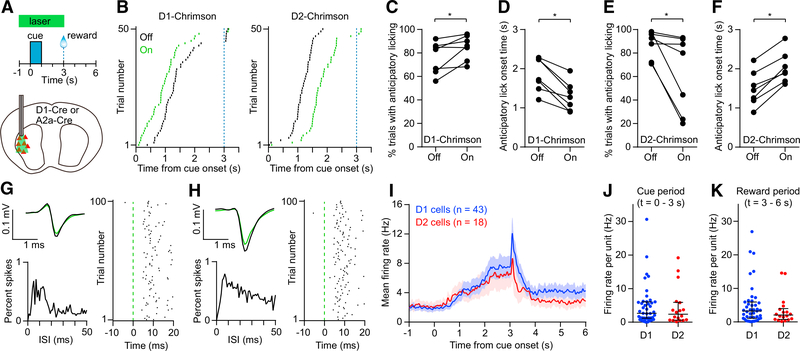
Head-restrained mice were trained on a Pavlovian conditioning task, in which an olfactory cue was associated with a sweetened milk reward. Animals learned to produce anticipatory licking movements preceding the time of reward delivery. To determine whether neural activity in the lateral striatum is sufficient to influence this behavior, in well-trained animals, we optogenetically activated D1 or D2 receptor-expressing MSNs on 50% of trials selected at random (Figures 1A and 1B). Stimulating D1 MSNs (n = 7 Chrimson⁺ D1-Cre mice) increased the proportion of trials with anticipatory licking (Figure 1C), and on those trials, the latency to licking was significantly reduced (median of differences = 0.64 s; Figure 1D). Stimulating D2 MSNs (n = 7 A2a-Cre mice) had the opposite effect on performance, reducing the proportion of trials with anticipatory licking (Figure 1E) and delaying the onset of licking on those trials (median of differences = 0.49 s; Figure 1F). Optical stimulation in control animals (n = 4 mCherry⁺ D1-Cre or A2a-Cre mice) had no significant effect on behavior (Figures S1A and S1B). These findings are in close agreement with the classical model of movement control by the direct and indirect basal ganglia pathway (Albin et al., 1989; Kravitz et al., 2010), and they confirm the role of the lateral striatum in mediating the anticipatory licking response (Sippy et al., 2015).

Figure 1. D1 and D2 MSNs Drive Opposing Behavioral Effects and Show Balanced Activity in a Reward-Conditioned Licking Task.

(A) Top: schematic of Pavlovian conditioning task in which an olfactory cue is paired with a reward. The green bar indicates the timing of the optical stimulus used to activate D1 or D2 MSNs in (B)–(F). Light was delivered on 50% of trials in random order. Bottom: optogenetic stimulation of D1 and D2 MSNs was carried out unilaterally in the lateral striatum.

(B) Lick rasters for a representative D1-Cre mouse (left) and A2a-Cre mouse (right). Green and black denote trials with laser on and off, respectively. Only the first lick in each trial is shown. The dashed blue line indicates the reward time.

(C) Activating D1 MSNs significantly increased the probability of anticipatory licking (n = 7, Wilcoxon signed rank test, p = 0.031).

(D) Activating D1 MSNs significantly reduced the anticipatory licking onset time (n = 7, Wilcoxon signed rank test, p = 0.016).

(E) Activating D2 MSNs significantly reduced the probability of anticipatory licking (n = 7, Wilcoxon signed rank test, p = 0.016).

(F) Activating D2 MSNs significantly increased the anticipatory licking onset time (n = 7, Wilcoxon signed rank test, p = 0.016).

(G) Optogenetically tagged D1 receptor-expressing cell. Top left: mean spike waveform on trials with laser on (green) and off (black). Bottom left: interspike interval (ISI) distribution. Right: spike raster aligned to laser onset.

(H) Same as (G) but for an optogenetically tagged D2 receptor-expressing cell.

(I) Mean firing rate versus time aligned to cue onset of 43 tagged D1 cells and 18 tagged D2 cells. Data represent mean ± SEM.

(J) Median firing rate of individual tagged D1 and D2 cells was not significantly different in the cue period (Mann-Whitney test, p = 0.62).

(K) Median firing rate of individual tagged D1 and D2 cells was not significantly different in the reward period (Mann-Whitney test, p = 0.37).

Lines and error bars in (J) and (K) represent median and interquartile range (IQR).

See also Figure S1.

Next, to compare the activity of these two populations during the behavioral task, we examined the firing properties of optogenetically tagged units (see STAR Methods). Measurements were carried out with an opto-microprobe, composed of a silicon-based multielectrode array attached to optical fibers (Lee et al., 2017). After recording striatal activity in well-trained animals performing the task, optogenetic tagging was carried out by applying pulses of light from the optical fibers. Units were positively identified if they responded to optical stimulation with short spike latency (<6 ms) and if the mean spike waveform during optical stimulation was highly correlated with the waveform preceding the optical stimulus (Pearson correlation coefficient > 0.95) (Figures 1G, 1H, and S1C). These criteria led to identification of 43 tagged D1 and 18 tagged D2 cells (from n = 10 mice per group). On average, both populations showed an increase in activity during the task (Figure 1I), consistent with work showing co-activation of the direct and indirect pathway during goal-directed movement (Jin et al., 2014; Shin et al., 2018; Sippy et al., 2015). Furthermore, the firing rate per cell was not significantly different between these populations (Figures 1J and 1K). To ensure these findings are insensitive to small variations in optogenetic tagging criteria, the identification of tagged units was performed again with a maximum spike latency of 4 and 8 ms. We further compared the activity only of tagged units that were also electrophysiologically identified as MSNs. None of these additional analyses yielded a significant difference between D1 and D2 activity (Figures S1D–S1F). The similar activity of D1 and D2 MSNs suggests a relatively balanced net level of excitatory drive to these populations during this behavior. We therefore treated all MSNs as a single group for the remainder of the study.

Deconstructing the Sources of Input Driving Striatal Activity

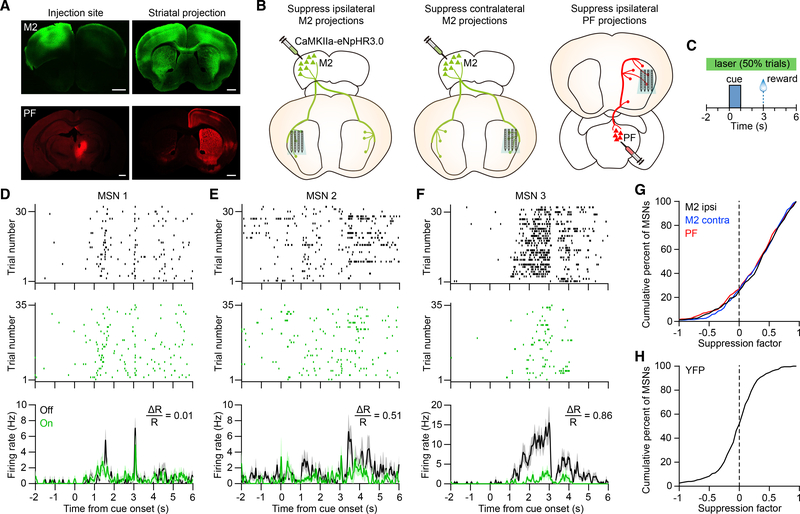
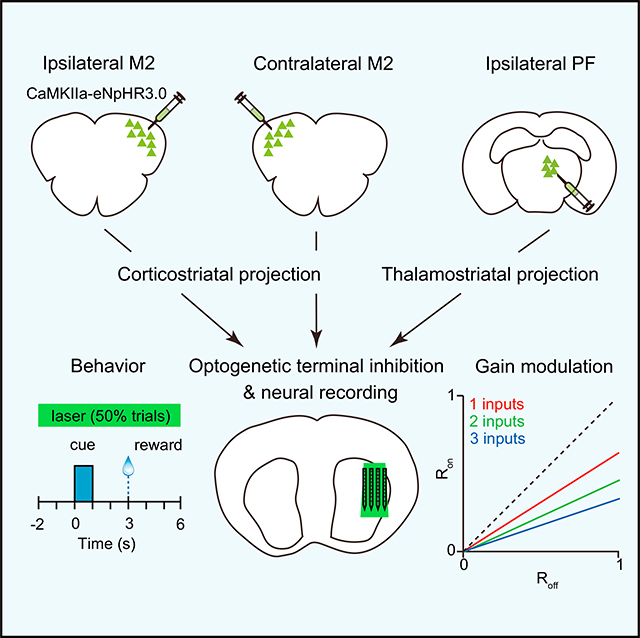
The M2 region of cortex is closely associated with tongue movements such as licking (Komiyama et al., 2010). Corticostriatal projections from this area overlap in the lateral region of the striatum with thalamostriatal projections from PF, a major source of thalamic input (Figures 2A and S2A) (Díaz-Hernández et al., 2018; Hunnicutt et al., 2016; Parker et al., 2016). We therefore tested the hypothesis that both M2 and PF projections contribute to activity in the lateral striatum during the behavioral task. Our approach involved measuring changes in striatal firing rate in response to transient optogenetic terminal inhibition of anatomically distinct projections. This was carried out by virally expressing eNpHR3.0 in the cell bodies of the input region and using an opto-microprobe to illuminate the anterograde projections in the lateral striatum while concurrently monitoring neural activity (Figures 2B and S2B). Experiments were carried out on three specific inputs corresponding to the ipsilateral M2, contralateral M2, and ipsilateral PF (n = 9 C57BL/6J mice per input group). Viral injections targeted the cortex and thalamus, and eNpHR3.0 expression was concentrated in the M2 or PF, as well as surrounding areas (Figure 2A, left). Optogenetic inhibition was carried out with a continuous 8 s optical stimulus overlapping the cue and reward periods and applied on 50% of trials selected at random (Figure 2C). Optical stimulation did not significantly alter the probability of anticipatory licking (Figures S2C–S2E). Suppressing the two cortical projections also had no effect on lick timing. Suppressing the PF projections produced a small but significant delay in licking (median of differences = 0.1 s; Figure S2E). Thus, compared with the effect of directly stimulating D1 or D2 MSNs, there was only a weak or insignificant behavioral effect of unilaterally suppressing the selected projections. Putative MSNs, fast spiking interneurons (FSIs), and tonically active neurons (TANs) were identified using established firing rate and spike waveform criteria (Figure S2F).

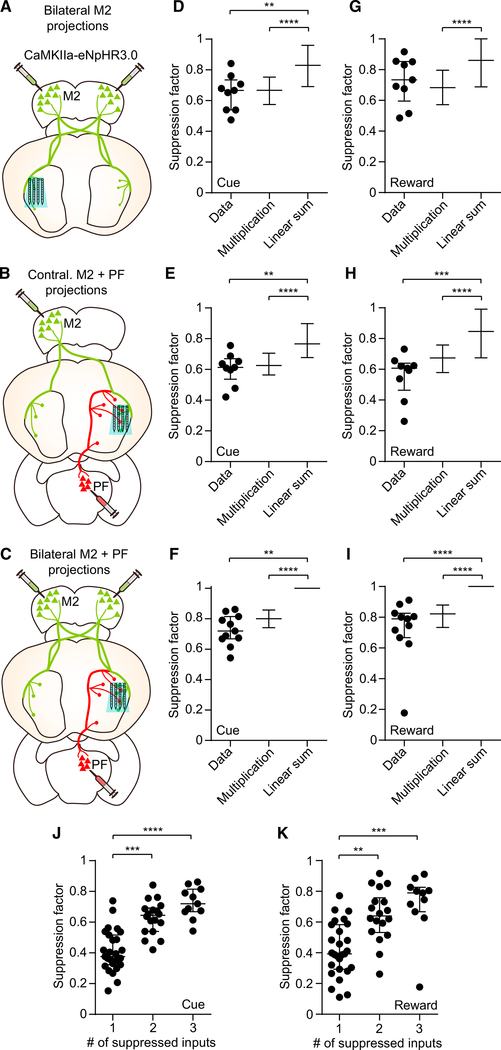
Figure 2. Deconstructing the Cortical and Thalamic Contributions to Striatal Dynamics.

(A) Anterograde projections from M2 (green) and PF (red) in the striatum. M2 and PF projections were obtained from different animals. Scale bars, 1 mm.

(B) Approach used to determine the contribution of three individual excitatory inputs (ipsilateral M2, contralateral M2, and ipsilateral PF) on behaviorally evoked activity in the striatum. The opto-microprobe for recording neural activity and delivering light to suppress terminals is inserted in the lateral striatum.

(C) Schematic of optical stimulation during the task. Light was delivered on 50% of trials in random order.

(D) Spike raster and mean firing rate of an MSN on anticipatory licking trials with laser on (green) and off (black). The unit’s suppression factor is 0.01.

(E) Same as (D) but for a different MSN with a suppression factor of 0.51.

(F) Same as (D) but for a different MSN with a suppression factor of 0.86. Data in (D)–(F) are from the ipsilateral M2 group, and firing rate plots represent mean ± SEM.

(G) Cumulative distribution of the MSN suppression factor for the ipsilateral M2 (black), contralateral M2 (blue), and PF (red) input groups. The median value was significantly higher than zero in each group (Wilcoxon signed rank test, p < 0.0001). The median suppression factor was 0.4 for ipsilateral M2 (n = 298 MSNs from 9 mice), 0.37 for contralateral M2 (n = 255 MSNs from 9 mice), and 0.36 for PF (n = 344 MSNs from 9 mice).

(H) Cumulative distribution of the MSN suppression factor for the YFP control group. The median value (equal to 0.04) was not significantly different from zero(n = 227 MSNs from 8 mice, Wilcoxon signed rank test, p = 0.2).

Suppression factors in (D)–(H) were calculated in the period from −2 to 6 s relative to cue onset.

See also Figure S2.

As a population, MSNs in the lateral striatum displayed a diverse range of firing patterns during the task (Figures 2D–2F, laser off trials). This heterogeneity is consistent with striatal encoding of multiple behaviorally relevant events such as anticipatory licking movements, sensory stimuli, and elapsed time (Bakhurin et al., 2017; Reig and Silberberg, 2014; Rueda-Orozco and Robbe, 2015; Sippy et al., 2015). Furthermore, the diversity of firing patterns is believed to reflect variations in the source and strength of synaptic input to MSNs, even between nearby cells (Kincaid et al., 1998). During laser stimulation, a large proportion of MSNs showed lower spiking activity (Figures 2D–2F), consistent with reduced excitatory signaling. To quantify these effects, we calculated the firing rate suppression factor per cell using the expression

$$\frac{\Delta R}{R}=\frac{R_{off}-R_{on}}{R_{off}},$$ (Equation 1)

where R_on and R_off represent the mean firing rate with illumination on and off, respectively. A suppression factor of positive one indicates complete silencing of the neuron, while negative values represent an increase in mean firing. The suppression factors across the population of MSNs exhibited a range of values (Figure 2G). This variability may result from differences in synaptic coupling strength between the individual MSNs and the suppressed input, as well as differences in the effectiveness of inhibiting distinct terminals with eNpHR3.0. The median suppression factor for each input type was significantly greater than zero, indicating a net reduction in striatal output. Optogenetic control measurements showed the median suppression factor had no significant deviation from zero (n = 8 YFP⁺ mice; Figure 2H). These results demonstrate that the selected corticostriatal and thalamostriatal projections each drive a portion of the total observed MSN activity. We also examined whether these projections affect the activity of other striatal cell types, presumably through direct connections or network interactions. Suppressing M2 and PF inputs produced a reduction in FSI firing (Figures S2G and S2H), consistent with a direct excitatory pathway to these cells (Bennett and Bolam, 1994). Concomitantly, we found a small increase in TAN firing (Figures S2I and S2J).

Similar Contributions of M2 and PF Projections on Striatal Activity

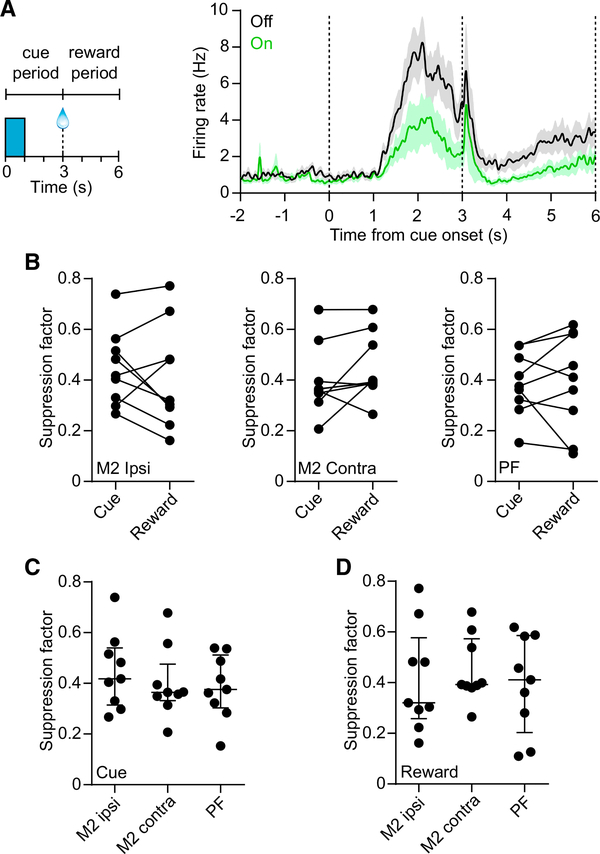
MSNs frequently showed different levels of activity in the periods preceding and following reward (Figures 2D and 2E) (Shin et al., 2018). We therefore examined whether M2 or PF inputs differentially regulate striatal dynamics during these periods. We separately calculated the suppression factor using data from the period defined as the cue (t = 0–3 s) and reward (t = 3–6 s) (Figure 3A). For each input, there was no significant difference in the suppression factors between the cue and the reward periods (Figure 3B). Furthermore, there was no significant difference in the suppression factors among the three sources of input in either period (Figures 3C and 3D). These results suggest a similar contribution from each input on MSN firing, corresponding to a median suppression factor of 0.38 (interquartile range [IQR] = 0.14) in the cue period, and 0.39 (IQR = 0.28) in the reward period (data represent n = 27 mice). There was also no significant difference in the FSI and TAN suppression factors among the three input groups (Figures S2K and S2L).

Figure 3. Similar Contributions from M2 and PF Projections on MSN Activity.

(A) Left: definition of the cue and reward periods used for analysis of firing rate suppression factor. Right: mean firing of 24 MSNs from one subject in the contralateral M2 input group. The dashed vertical lines demarcate the two periods. The median suppression factors for this subject are 0.56 and 0.61 in the cue and reward periods, respectively. Data represent mean ± SEM.

(B) There was no significant difference in suppression factors between the cue and the reward periods for the ipsilateral M2 group (n = 9, median of differences = −0.084, Wilcoxon signed rank test, p = 0.57), contralateral M2 group (n = 9, median of differences = 0.028, p = 0.13), or PF group (n = 9, median of differences = 0.044, p = 0.5).

(C) There was no significant difference in cue period suppression factors among the three input groups (n = 9 per group, Kruskal-Wallis test, H = 0.68, p = 0.71).

(D) Same as (C) but for the reward period (Kruskal-Wallis test, H = 0.45, p = 0.8).

Lines and error bars in (C) and (D) represent median and IQR.

See also Figure S2.

Differential Gain in the Cue and Reward Periods

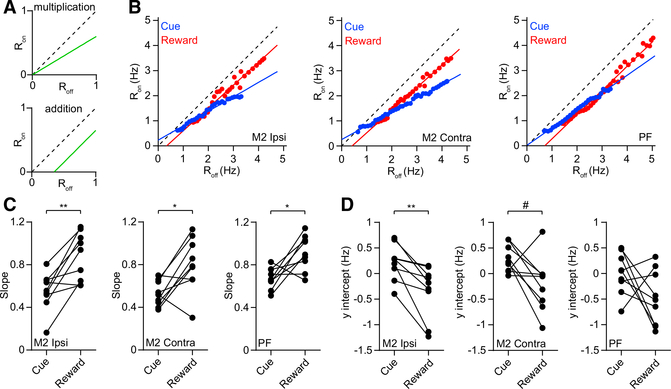
To establish the arithmetic rules underlying input summation in the striatum, we examined the relationship between neural firing rate during laser on and laser off trials (Atallah et al., 2012; Phillips and Hasenstaub, 2016). A generalized form of linear transformation from firing rate during laser off to firing rate during laser on can be represented as

$$R_{on}=g{R}_{off}+y.$$ (Equation 2)

For a purely multiplicative transformation (Figure 4A, top), y = 0 and the gain, g, equal to the line’s slope, is related to the suppression factor by the following expression:

$$g=\frac{R_{on}}{R_{off}}=1-\frac{\Delta R}{R}.$$ (Equation 3)

However, for a purely additive transformation (Figure 4A, bottom), g = 1 and the y intercept is related to the change in firing rate as follows:

$$y=\left(R_{on}-R_{off}\right)=-\Delta R.$$ (Equation 4)

To determine whether our data were consistent with either of these two regimes, we obtained the slope and y intercept from a linear fit of the mean population R_on versus R_off response during the cue and reward periods (see STAR Methods; Figure 4B). There was a statistically significant difference in the slope between contralateral M2 and PF input groups during the cue period (Figure S3A). There was no difference in the y intercepts among the three input groups (Figure S3B). For each of the three inputs, the change in MSN gain caused by optogenetic inhibition appeared to be more pronounced in the cue period compared with the reward period. In agreement with this observation, the slope was significantly lower in the cue period (Figure 4C). To rule out the possibility that the differential gain results from higher firing in one of these periods, we repeated the slope analysis, after excluding units with R_off values exceeding 4 Hz, and found the same relationship we had previously discovered (Figure S3C). In addition to differences in slope, two of the input groups showed lower y intercept values in the reward period (Figures 4D and S3D). Furthermore, data from each input corresponding to the cue period, but not the reward period, were consistent with the multiplicative transformation described by Equation 3 (Figures S3E–S3G). Conversely, data from each input corresponding to the reward period, but not the cue period, were consistent with the additive transformation described by Equation 4 (Figures S3H–S3J). Altogether, the results show that MSN gain is differentially regulated in these periods and suggest that the cue period corresponds more strongly to a multiplicative rather than an additive transformation. However, there appears to be some ambiguity about the type of transformation occurring in the reward period, because some results appear more consistent with multiplication (i.e., the slope is significantly less than one in Figure 4C, middle, and the y intercept is not significantly less than zero in Figure 4D, left and middle), while others are more consistent with addition (Figures S3E–S3J). This raises the possibility of a mixed multiplicative and additive transformation in the reward period.

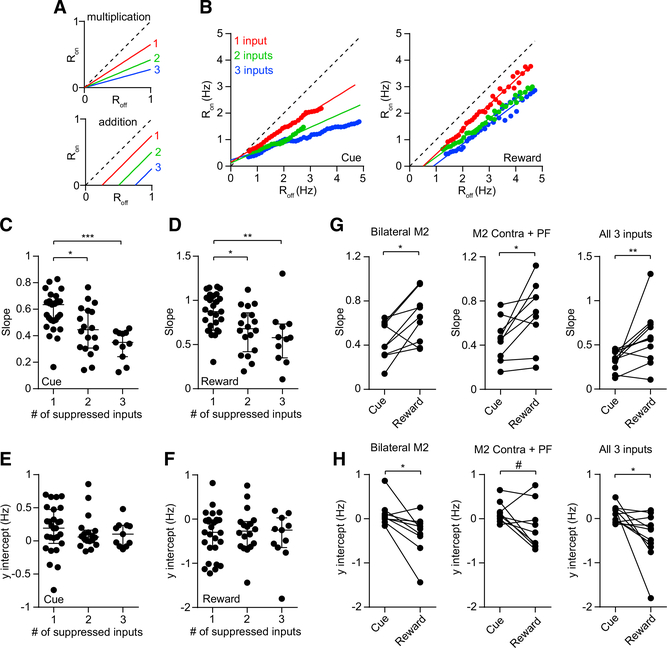
Figure 4. Differential Gain in the Cue and Reward Periods.

(A) Response of firing rate during laser on trials as a function of rate during laser off trials (R_on versus R_off) for hypothetical purely multiplicative (top) and additive (bottom) transformations. The gain is equivalent to the slope of the line. The dashed line indicates the diagonal with a slope of one.

(B) R_on versus R_off calculated from the pooled population of MSNs from the ipsilateral M2 group (left), contralateral M2 group (middle), and PF input group (right). Blue and red represent data from the cue and reward periods, respectively. The solid lines represent linear fits to the data.

(C) Slope of the line was significantly lower in the cue compared with the reward period for the ipsilateral M2 group (n = 9, Wilcoxon signed rank test, p = 0.008), contralateral M2 group (n = 9, p = 0.027), and PF group (n = 9, p = 0.02). For each input group, the cue period slope was significantly less than one (Wilcoxon signed rank test, p = 0.004). For the ipsilateral M2 and PF groups, the reward period slope was not significantly different from one (p = 0.25). For the contralateral M2 group, the reward period slope was significantly less than one (p = 0.039).

(D) The y intercept of the line was significantly lower in the reward period compared with the cue period for the ipsilateral M2 group (n = 9, Wilcoxon signed rank test, p = 0.004). The contralateral M2 group showed a trend toward significance (n = 9, p = 0.055). The PF group showed no significant difference (n = 9, p = 0.098). For the ipsilateral M2 and PF input groups, the cue period y intercept was not significantly different from zero (Wilcoxon signed rank test, p = 0.13 and p > 0.99, respectively). For the contralateral M2 group, the cue period y intercept was significantly greater than zero (p = 0.008). For the ipsilateral and contralateral M2 groups, the reward period y intercept was not significantly different from zero (p = 0.074 and p = 0.098, respectively). For the PF group, the reward period y intercept was significantly less than zero (p = 0.039).

See also Figure S3.

Although there may be various mechanisms for the differential gain effect, one possibility could be changes in inhibitory signaling between the cue and the reward periods, because inhibition can strongly modulate synaptic integration (Silver, 2010). To investigate the involvement of inhibition on striatal activity, we characterized the fraction of MSNs significantly excited or inhibited during the behavioral task, using laser off trials (Figure S3K). Notably, there was a significant reduction in the ratio of excited to inhibited cells after reward delivery (Figures S3L and S3M). These findings suggest a possible link between the MSN gain and the relative level of excitatory-to-inhibitory signaling in the cue and reward periods.

MSNs Combine Excitatory Input Signals via a Multiplication-like Rule

If individual inputs have a multiplicative effect on MSN firing, then a prediction is that multiple inputs may combine via a multiplication-like rule, most prominently in the cue period. To test this, we simultaneously suppressed inputs to the striatum from multiple areas, corresponding to bilateral M2 (two inputs, n = 9; Figure 5A), contralateral M2 plus ipsilateral PF projections (two inputs, n = 9; Figure 5B), or bilateral M2 plus ipsilateral PF projections (three inputs, n = 11; Figure 5C). Suppressing these projections again reduced MSN spiking activity (Figure S4) but did not significantly alter the probability or timing of anticipatory licking (Figures S5A–S5C). We compared the observed firing rate suppression factor to a model of multiplication or linear summation of individual inputs (see STAR Methods). In the model of N inputs combined via linear addition, the net suppression factor obeys the relationship

$${\left(\frac{\Delta R}{R}\right)}_N=\sum _{i=1}^N{\left(\frac{\Delta R}{R}\right)}_i,$$ (Equation 5)

where the subscript i refers to the ith single input. In the multiplication model, the net suppression factor corresponds to the following product:

$${\left(1-\frac{\Delta R}{R}\right)}_N=\prod _{i=1}^N{\left(1-\frac{\Delta R}{R}\right)}_i.$$ (Equation 6)

According to these expressions, if two hypothetical inputs each have a suppression factor of 0.4, inhibiting them together would produce a suppression factor of 0.8 under linear addition and 0.64 under multiplication. For all combinations of multiple inputs that were tested, the median suppression factor in the cue period was significantly different from the linear summation model but not different from the multiplication model (Figures 5D–5F). In the reward period, data from the bilateral M2 input suppression group were statistically similar to the model of addition and that of multiplication, i.e., they could not distinguish between these models (Figure 5G), whereas the other two groups were only similar to the model of multiplication (Figures 5H and 5I). Thus, the results are consistent with a multiplication-like rule for combining corticostriatal and thalamostriatal input signals. Furthermore, the multiplication model exclusively matches the experimental data in the cue period, but not the reward period, again suggesting that the reward period may coincide with mixed multiplicative and additive effects.

Figure 5. A Multiplication-like Rule for Combining Corticostriatal and Thalamostriatal Input Signals.

(A) Approach used to determine the combined contribution of two inputs corresponding to bilateral M2 on striatal activity.

(B) Approach used to determine the combined contribution of two inputs corresponding to contralateral M2 plus PF on striatal activity. (C) Approach used to determine the combined contribution of three inputs corresponding to bilateral M2 plus PF on striatal activity.

(D) Comparison of the cue period suppression factor observed from the bilateral M2 group (n = 9 in Data) to a model of individual input multiplication and linear summation (Kruskal-Wallis test, H = 40.29, p < 0.0001). Post hoc Dunn’s multiple comparison test showed that for data versus multiplication model, p > 0.99; data versus summation model, p = 0.008; and multiplication versus summation model, p < 0.0001.

(E) Same as (D) but from the contralateral M2 plus PF group (n = 9 in Data, Kruskal-Wallis test, H = 39.14, p < 0.0001). Post hoc Dunn’s multiple comparison test showed that for data versus multiplication model, p > 0.99; data versus summation model, p = 0.005; and multiplication versus summation model, p < 0.0001.

(F) Same as (D) but from the bilateral M2 plus PF group (n = 11 in Data, Kruskal-Wallis test, H = 1,074, p < 0.0001). Post hoc Dunn’s multiple comparison test showed that for data versus multiplication model, p = 0.6; data versus summation model, p < 0.0001; and multiplication versus summation model, p < 0.0001. The lack of apparent error bars in the linear summation models in (F) and (I) occurs because most suppression factor values were capped at one.

(G) Comparison of the reward period suppression factor observed from the bilateral M2 group to a model of input multiplication and linear summation (n = 9 in Data, Kruskal-Wallis test, H = 28.87, p < 0.0001). Post hoc Dunn’s multiple comparison test showed that for data versus multiplication model, p > 0.99; data versus summation model, p = 0.36; and multiplication versus summation model, p < 0.0001.

(H) Same as (G) but from the contralateral M2 plus PF group (n = 9 in Data, Kruskal-Wallis test, H = 37.58, p < 0.0001). Post hoc Dunn’s multiple comparison test showed that for data versus multiplication model, p = 0.29; data versus summation model, p = 0.0001; and multiplication versus summation model, p < 0.0001.

(I) Same as (G) but from the bilateral M2 plus PF group (n = 11 in Data, Kruskal-Wallis test, H = 854, p < 0.0001). Post hoc Dunn’s multiple comparison test showed that for data versus multiplication model, p = 0.6; data versus summation model, p < 0.0001; and multiplication versus summation model, p < 0.0001.

(J) Cue period suppression factor varied significantly as a function of the number of simultaneously suppressed inputs (n = 27 single, 18 double, and 11 triple inputs; Kruskal-Wallis test, H = 31.11, p < 0.0001). Post hoc Dunn’s multiple comparison test showed that for 1 versus 2 inputs, p = 0.002; 1 versus 3 inputs, p < 0.0001; and 2 versus 3 inputs, p = 0.35.

(K) Same as (J) but for the reward period (Kruskal-Wallis test, H = 21.55, p < 0.0001). Post hoc Dunn’s multiple comparison test showed that for 1 versus 2 inputs, p = 0.002; 1 versus 3 inputs, p = 0.0001; and 2 versus 3 inputs, p = 0.77).

Lines and error bars in (D)–(K) represent median and IQR.

See also Figures S4 and S5.

Next, we compared the firing rate suppression factor as a function of the number of simultaneously suppressed inputs (n = 27 single, 18 double, and 11 triple inputs). In both the cue and the reward periods, the suppression factor was significantly higher as more inputs were suppressed, but it scaled nonlinearly with number of inputs (Figures 5J and 5K), ruling out a linear summation process. The reward period suppression factor of the bilateral M2 group was significantly greater than the contralateral M2 plus ipsilateral PF group (Figure S5D), but the slope and y intercept associated with these groups was similar in both the cue and the reward periods (Figures S5E and S5F). Thus, overall there was no significant difference in the contributions of the two dual-projection groups in the cue period, and only a small difference was found in the reward period. We also examined the effect of multiple input suppression on the activity of other striatal cell types. Neither FSIs nor TANs showed a significant change in the median suppression factor as a function of the number of suppressed inputs (Figures S5G and S5H). These results suggest that in the striatum, only MSNs reliably show multiplication-like effects during input integration.

Cortical and Thalamic Inputs Jointly Modulate MSN Gain

A crucial prediction of multiplication-like effects is that, as more inputs are suppressed, the slope (i.e., gain) of the linear fit of R_on lowers as a function of R_off, whereas the y intercept should not change (Figure 6A, top). Conversely, purely additive effects are predicted to alter the y intercept, but not the slope (Figure 6A, bottom). To distinguish between these possible outcomes, we compared the slope and the y intercept per subject as a function of the number of simultaneously suppressed inputs (Figure 6B). For both periods, we observed a significant reduction in the slope as a function of the number of inputs (Figures 6C and 6D), but no change in the y intercept (Figures 6E and 6F).

Figure 6. Modulation of MSN Gain by Multiple Inputs.

(A) R_on versus R_off for hypothetical purely multiplicative (top) and additive (bottom) transformations. Red, green, and blue lines, respectively, denote suppression of 1, 2, and 3 inputs. In a multiplicative transformation, the gain changes with more suppressed inputs, whereas in an additive transformation, the y intercept changes with more suppressed inputs.

(B) R_on versus R_off calculated from the pooled population of MSNs from single-input (red), double-input (green), and triple-input (blue) group data. The solid lines represent linear fits to the data. Left and right plots represent data from the cue and reward periods, respectively.

(C) Cue period slope was significantly reduced as a function of number of suppressed inputs (n = 27 single, 18 double, and 11 triple inputs; Kruskal-Wallis test, H = 18.23, p = 0.0001). Post hoc Dunn’s multiple comparison test showed that for 1 versus 2 inputs, p = 0.026; 1 versus 3 inputs, p = 0.0001; and 2 versus 3 inputs, p = 0.26.

(D) Same as (C) but for the reward period (Kruskal-Wallis test, H = 12.12, p = 0.002). Post hoc Dunn’s multiple comparison test showed that for 1 versus 2 inputs, p = 0.042; 1 versus 3 inputs, p = 0.005; and 2 versus 3 inputs, p = 0.96.

(E) Cue period y intercept was not significantly altered as a function of number of suppressed inputs (Kruskal-Wallis test, H = 1.38, p = 0.5).

(F) Reward period y intercept was not significantly altered as a function of number of suppressed inputs (Kruskal-Wallis test, H = 0.07, p = 0.97). Lines and error bars in (C)–(F) represent median and IQR.

(G) Slope was significantly lower in the cue period compared with the reward period for the bilateral M2 group (left: n = 9, Wilcoxon signed rank test, p = 0.027), contralateral M2 plus PF group (middle: n = 9, p = 0.027), and bilateral M2 plus PF (i.e., all three inputs) group (right: n = 11, p = 0.005). Removing the outlier value in the rightmost plot preserves the significant difference (n = 10, p = 0.01). In both periods, the slope for the triple-input suppression group was significantly less than one (Wilcoxon signed rank test; cue, p = 0.0001; reward, p = 0.007). </p/> (H) The y intercept of the line was significantly lower in the reward period compared with the cue period for the bilateral M2 group (left: n = 9, Wilcoxon signed rank test, p = 0.02) and the triple-input suppression group (right: n = 11, Wilcoxon signed rank test, p = 0.014). There was also a trend toward significance for the contralateral M2 plus PF group (middle: n = 9, p = 0.055). Removing the outlier value in the rightmost plot preserves the significant difference (n = 10, p = 0.027). The y intercept for the triple-input suppression group was not significantly different from zero in the cue period (Wilcoxon signed rank test, p = 0.15), but it was significantly less than zero in the reward period (p = 0.019). </p/> See also Figures S5 and S6

For the groups corresponding to two or all three inputs being suppressed at the same time, the slope was significantly lower in the cue period (Figure 6G), while the y intercept was significantly lower in the reward period (Figure 6H). For the triple-input suppression group, the slope was significantly less than one in both periods. However, the y intercept was only significantly different from zero in the reward period. Thus, while gain modulation consistent with a multiplication-like summation rule was seen in both periods, the reward period appears to also exhibit additive effects.

There were only small or statistically insignificant changes in the slope corresponding to the FSI and TAN populations (Figures S5I and S5J). To account for possible errors in electrophysiological classification of different striatal cell types, we analyzed the slope using the firing rate of all recorded units, regardless of their classification (most of which are likely to be MSNs, because they are the most abundant cell type). We still found a significant gain modulation effect (Figure S5K), suggesting that errors in cell-type classification are unlikely to account for the finding of a multiplication-like summation rule in MSNs.

Next, we performed two analyses to address the potential concern that under additive transformations, firing rate floor effects may cause spurious changes in the slope (Figure 6A, bottom). First, we calculated the slope after removing the lower tercile of points from the linear fit of R_on as a function of R_off (Figures S6A and S6B). Although the effect was less pronounced, the slope showed a significant reduction as a function of the number of suppressed inputs (Figure S6C), and the y intercept did not significantly change (Figure S6D). Second, we calculated the slope after excluding all MSNs with a suppression factor greater than 0.75 (Figure S6E). Again, the slope, but not the y intercept, was significantly altered with more suppressed inputs (Figures S6F and S6G). Therefore, the data confirm that striatal gain is modulated, in agreement with the finding that corticostriatal and thalamostriatal input signals are combined via a multiplication-like rule.

Differential Gain Effects Persist during Widespread Input Suppression

Because the lateral striatum receives excitatory input from areas besides the three regions studied so far, we explored how more extensive suppression of cortical and thalamic inputs affects MSN firing. We performed eNpHR3.0 injections in ten locations (five per hemisphere) targeting the primary motor cortex (M1) and secondary motor cortex, as well as PF and ventroposterio-medial (VPM) thalamic nuclei. We then carried out recordings and light delivery in the striatum, which showed extensive expression of eNpHR3.0 (Figure 7A). Licking behavior did not significantly change during unilateral laser presentation (n = 7; Figure 7B). In parallel, MSN spiking activity was significantly reduced, but most cells were not completely silenced despite the widespread suppression of excitatory inputs (Figures 7C and 7D). There was a comparable reduction in FSI activity, whereas TANs tended to show a small increase in firing (Figure 7E). The MSN suppression factor was similar in the cue and reward periods (Figure 7F). We also found differences in gain during the cue and reward periods, which were consistent with our previous observations (Figures 7G and 7H). Thus, we confirmed that the differential MSN gain effects in the cue and reward periods can be generalized to a higher number of inputs.

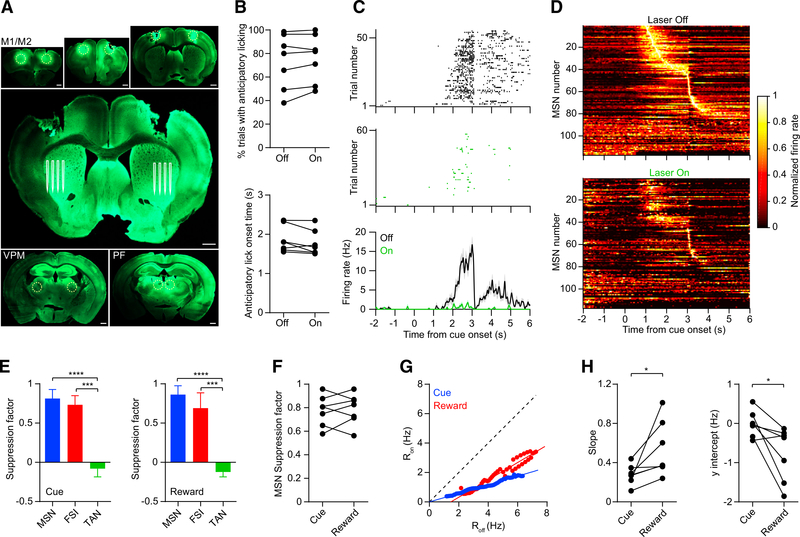
Figure 7. Striatal Activity during Widespread Cortical and Thalamic Input Suppression.

(A) Viral injection locations in M1, M2, VPM, and PF (dashed yellow circles in the small panels) and approximate region of the silicon microprobe electrodes in the striatum (white lines in the large panel). Because injections were bilateral, in some animals, we performed recordings on both striatal hemispheres (one hemisphere per session). Scale bars, 0.5 mm.

(B) Suppressing these inputs in the striatum did not significantly alter anticipatory licking probability (top: n = 7 recording sessions, maximum one session per hemisphere, Wilcoxon signed rank test, p = 0.22) or onset time (bottom: p = 0.11).

(C) Spike raster and mean firing rate of an MSN on anticipatory licking trials with laser on (green) and off (black). The neuron’s suppression factors are 0.93 and 0.98 in the cue and reward periods, respectively.

(D) Mean normalized firing rate as a function of time of 117 MSNs pooled from 7 recording sessions. Top and bottom plots show data from laser off and on trials, respectively. Each unit’s firing rate is normalized by the maximum rate during laser off trials. The units are ordered by their latency to peak firing.

(E) Median suppression factor of all 117 MSNs, 20 FSIs, and 32 TANs pooled from 7 recording sessions. Left: cue period (Kruskal-Wallis test, H = 72, p < 0.0001). Post hoc Dunn’s multiple comparison tests showed that for MSN versus FSI, p = 0.07; MSN versus TAN, p < 0.0001; and FSI versus TAN, p = 0.0002. Right: reward period (Kruskal-Wallis test, H = 67, p < 0.0001). Post hoc Dunn’s multiple comparison tests showed that for MSN versus FSI, p = 0.08; MSN versus TAN, p < 0.0001; and FSI versus TAN, p = 0.0004. Error bars represent IQR.

(F) Median MSN suppression factor per subject was not significantly different between the cue and the reward periods (n = 7, Wilcoxon signed rank test, p = 0.99).

(G) R_on versus R_off calculated from the pooled population of MSNs. Blue and red represent data from the cue and reward periods, respectively. The solid lines represent linear fits to the data.

(H) Left: the slope was significantly lower in the cue period compared with the reward period (n = 7, Wilcoxon signed rank test, p = 0.02). In both periods, the slope was significantly less than one (Wilcoxon signed rank test; cue, p = 0.02; reward, p = 0.03). Right: the y intercept of the line was significantly lower in the reward period compared with the cue period (Wilcoxon signed rank test, p = 0.03). The y intercept was not significantly different from zero in the cue period (Wilcoxon signed rank test, p = 0.69), but it was significantly less than zero in the reward period (p = 0.02).

DISCUSSION

To deconstruct the sources of input that drive striatal activity during behavior, we combined in vivo neural recordings with optogenetic terminal inhibition of corticostriatal and thalamostriatal projections. These results demonstrate that most MSN task-related activity can be eliminated by suppressing a large number of cortical and thalamic inputs. The incomplete elimination of MSN spikes suggests either that additional important input sources exist (e.g., dopaminergic) that were not virally targeted or that optogenetic terminal inhibition did not fully block neurotransmitter signaling.

Although our optogenetic terminal inhibition experiments precluded us from distinguishing between D1 and D2 MSNs, anatomical tracing studies suggest that M2 and PF connect to both populations with approximately equal likelihood (Huerta-Ocampo et al., 2014; Wall et al., 2013). Furthermore, using optogenetic tagging in a separate set of experiments, we found that D1 and D2 receptor-expressing cell populations display similar levels of activity in the anticipatory licking task. Altogether, the results suggest that during this behavior, there is no significant difference in how excitatory projections influence D1 and D2 MSN firing, although the extracellular recording technique used here may have a more limited ability to detect cell-type-specific effects than intracellular measurements (Sippy et al., 2015). Balanced activation of the D1 and D2 MSN populations may be important for coordinating appropriately timed actions (Tecuapetla et al., 2014, 2016).

This work directly compared the contributions of corticostriatal and thalamostriatal projections on neural activity in vivo. Previous work found differences in how these pathways innervate striatal microcircuits, as well as their potential function (Alloway et al., 2017; Ding et al., 2010; Doig et al., 2014; Smith et al., 2004, 2014). However, our results indicate a remarkable similarity in how M2 and PF inputs drive MSN activity, as measured by the suppression factor. Although there was a significant difference between corticostriatal and thalamostriatal gains, the effect was relatively small and only found between contralateral M2 and PF projections in the cue period. Thus, the data suggest a more overlapping role of certain corticostriatal and thalamostriatal pathways in shaping striatal output than was previously thought. In addition, because the corticostriatal pathway projects bilaterally via the intratelencephalic tract (Shepherd, 2013), we separately examined the contribution of ipsilateral and contralateral inputs. Before this work, little was known about the relative influence of these projections in controlling striatal activity in vivo. The results suggest a similar role of ipsilateral and contralateral inputs from M2 on MSN firing during this behavioral task. However, this study cannot rule out the possibility that greater differentiation of corticostriatal and thalamostriatal inputs occurs in the early stage of learning, when the strength of excitatory connections undergoes rapid changes (Koralek et al., 2013; Kupferschmidt et al., 2017).

Although suppressing individual and multiple inputs strongly reduced the average firing of MSNs, there was a notable lack of behavioral effects corresponding to these manipulations. This suggests a few possible interpretations. First, because the inputs were inhibited unilaterally, the intact striatal hemisphere may be sufficient to maintain behavior. In support of this interpretation, another study showed that bilaterally inhibiting the striatum using over-activation of FSIs reduces anticipatory licking (Lee et al., 2017). A second possibility is that the relative, not absolute, level of activity between D1 and D2 MSNs is the primary determinant of performance (Parker et al., 2016; Tecuapetla et al., 2014); thus, reducing the activity of each population by an equal amount may have a negligible effect on behavior. Third, the M2 and PF projections to the striatum may not be necessary for behavior, although this appears unlikely given that even more extensive suppression of excitatory inputs also did not alter behavior (Figure 7).

A further finding was that corticostriatal and thalamostriatal inputs have distinct effects on electrophysiologically identified striatal cell types. Notably, MSNs appeared to show stronger changes in firing rate and gain as more inputs were suppressed compared with FSIs and TANs. Furthermore, in contrast to the suppression of MSN and FSI activity during optogenetic terminal inhibition, TAN firing was only weakly altered and displayed a small increase. These results suggest either that M2 and PF may not be important sources of excitatory drive for cholinergic interneurons (Klug et al., 2018) or that glutamatergic signaling produces net inhibitory effects on these cells via GABAergic microcircuit interactions (Assous and Tepper, 2019).

An important finding of this work is that during a Pavlovian reward conditioning task, MSNs are capable of combining corticostriatal and thalamostriatal signals via a multiplication-like rule, with this type of interaction most pronounced in the cue period. Multiplication has long been theorized to be an important aspect of signal processing and computation in the brain (Blomfield, 1974). Several biophysical mechanisms have been proposed for how this arithmetic operation may emerge in single neurons, including nonlinearities in synaptic integration caused by shunting inhibition and NMDA receptors (Holt and Koch, 1997; Koch and Poggio, 1992; Silver, 2010). Although this study did not focus on resolving these mechanisms, a potential clue is the distinct gain and y intercept observed between the cue and the reward periods. The most parsimonious explanation for these differences is that both periods produce multiplication-like input summation effects but that the reward period also produces additive effects. It is intriguing that even within the same task, the arithmetic rules of input summation can vary markedly. The transition between the cue and the reward periods coincides with a significant reduction in the ratio of excited to inhibited MSNs. Thus, there may be a link between lower inhibition and stronger gain modulation in the cue period.

Previous studies in brain slices have often shown sublinear input summation effects in the striatum (Carter et al., 2007; Goto and O’Donnell, 2002; Wolf et al., 2009), whereas our data suggest the occurrence of a multiplication-like effect in vivo. The apparent discrepancy between in vitro and in vivo preparations may arise from differences in the spatiotemporal pattern of synaptic input delivered to the striatum (Carter et al., 2007). This suggests that there may be advantages to studying synaptic input integration effects in behaving animals as opposed to slice preparations. However, there are possible limitations of using optogenetic terminal inhibition (Wiegert et al., 2017). In this study, an assumption was that eNpHR3.0-mediated terminal inactivation was similar, on average, at all firing frequencies (i.e., that the effect of the laser on presynaptic glutamate release was linear and subtractive). A potential pitfall is that nonlinear effects of eNpHR3.0-mediated terminal inactivation on presynaptic terminals could account for some nonlinear postsynaptic responses. However, the differential gain modulation effect observed in the cue and reward periods suggests that this issue is not a strong confounding factor in our study. Gain modulation is thought to be critical for regulating motor output (e.g., vigor or timing) (Panigrahi et al., 2015; Yttri and Dudman, 2018), and it may significantly affect basal ganglia function in both health and disease.

STAR★METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for materials and resources used in this study should be directed to and will be fulfilled by the Lead Contact (smasmanidis@ucla.edu). This study did not generate new unique reagents.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All procedures were approved by the University of California, Los Angeles Chancellor’s Animal Research Committee. Experiments involving stimulation of D1 or D2 MSNs for behavioral testing or optogenetic tagging (Figures 1 and S1) used transgenic mice of both sexes (D1-Cre, Tg(Drd1-cre)EY262Gsat/Mmucd, MMRRC-017264-UCD; A2a-Cre, Tg(Adora2a-cre)KG139Gsat/Mmucd, MMRRC-031168-UCD) (Gong et al., 2007). The transgenic mice were maintained as hemizygous in a C57BL/6J background (The Jackson Laboratory 000664). For all other experiments male wild-type mice were used (C57BL/6J). Animals were 10–14 wks old at the time of the initial surgery. Animals were kept on a 12 hr light cycle, and group housed until the surgery.

METHOD DETAILS

Surgical procedures

Animals underwent surgical procedures under aseptic conditions and isoflurane anesthesia on a stereotaxic apparatus. Every surgical procedure involved attaching stainless steel head fixation bars on the skull, and injecting adeno-associated virus (AAV) in the targeted region or regions. AAV was obtained from the University of North Carolina Vector Core, and injected using pulled glass pipettes (Nanoject II, Drummond Scientific). For experiments involving optogenetic stimulation of D1 or D2 MSNs, AAV5/Syn-Flex-ChrimsonR-tdTomato (500 nL) or AAV5/EF1a-DIO-mCherry was unilaterally injected in the lateral striatum (coordinates relative to bregma: 1.0 mm anterior, 2.2 mm lateral, 3.2 mm ventral) in D1-Cre or A2a-Cre mice. For a subset of these experiments involving optogenetic activation of D1 or D2 MSNs during behavior, a ferrule-coupled optical fiber (0.2 mm diameter, 0.22 NA, Thor Labs) was also implanted during the surgery, terminating 0.2 mm above the viral injection site. Experiments involving optogenetic suppression of corticostriatal and/or thalamostriatal projections used male wild-type mice. In those experiments AAV5/CaMKIIa-eNpHR3.0-eYFP (300 nL) was injected unilaterally (or bilaterally for combined input suppression) in M2 (coordinates relative to bregma: 2.5 mm anterior, 1.5 mm lateral, 1.2 mm ventral). Alternatively (or additionally) AAV5/CaMKIIa-eNpHR3.0-mCherry (200 nL) was unilaterally injected in the PF thalamic nucleus (coordinates relative to bregma: 2.3 mm posterior, 0.6 mm lateral, 3.5 mm ventral). For the experiments involving widespread input suppression (Figure 7), AAV5/CaMKIIa-eNpHR3.0-eYFP (300 nL) was injected bilaterally in M2 as well as two other motor cortical regions (coordinates relative to bregma: 1.5 mm and 0.5 anterior, 1.5 mm lateral, 1.5 mm ventral). Additionally, AAV5/CaMKIIa-eNpHR3.0-eYFP (300 nL) was bilaterally injected in both PF and VPM thalamic nuclei (coordinates relative to bregma: 1.8 mm posterior, 1.65 mm lateral, 3.5 mm ventral). For the YFP control experiments shown in Figure 2H AAV5/CaMKIIa-eYFP (300 nL) was bilaterally injected in M2. All animals were individually housed after surgery, and recovered for at least 2 wks (5 wks for projection suppression experiments) before beginning habituation and behavioral conditioning (see Behavioral task). For experiments involving electrophysiological measurements with opto-microprobes (i.e., optogenetic tagging or input suppression), a second surgery under isoflurane anesthesia was completed 6–12 hr prior to recording to create a rectangular craniotomy above the lateral striatum. The dura was removed to facilitate device insertion. An additional craniotomy was made over the posterior cerebellum to accommodate a silver/silver-chloride electrical reference wire. After inserting the microprobe (see Opto-microprobe), mineral oil was placed in the craniotomy, and recording commenced after 40 minutes. Recordings were carried out with custom data acquisition hardware, and spike sorting was carried out with custom MATLAB scripts, as described in Shobe et al. (2015).

Immunohistochemistry

Mice were anaesthetized and transcardially perfused with 24°C phosphate-buffered saline (pH 7.3) and ice-cold paraformaldehyde. Brains were placed in paraformaldehyde overnight, and 100 μm coronal sections were prepared using a vibratome. Sections were blocked using normal serum, then incubated overnight at 4°C with chicken anti-GFP (Abcam, ab13970) or rabbit anti-DsRed (Takara, 632496) as primary antibodies (1:1000 dilution) (both primary antibodies were used when co-expressing virus in M2 and PF). After washing three times with PBS, the sections were incubated at 4°C with Alexa Fluor 488–conjugated donkey antibody to chicken IgG (Jackson ImmunoResearch, 703-545-155) or Alexa Fluor 647-conjugated donkey antibody to rabbit IgG (Jackson ImmunoResearch, 711-605-152) as secondary antibodies (1:200 dilution) for 4 hr (both secondary antibodies were used when co-expressing virus in M2 and PF). Sections were mounted using tissue mounting medium, and were imaged under confocal microscopy.

Behavioral task

Mice were food restricted to maintain their weight at around 90% of their baseline level, and given water ad libitum. Animals were initially habituated to the head fixation apparatus and to reliably consume uncued rewards (5 μL, 10% sweetened condensed milk), which were delivered via actuation of an audible solenoid valve. The reward delivery and lick meter port was located around 5 mm directly in front of the mouth, and animals had to extend their tongue out of the mouth to register as a lick. Subsequently, animals were trained on a Pavlovian reinforcement task using an olfactory cue, consisting of isoamyl acetate diluted 1:10 in mineral oil, and diluted another factor of 10 by mixing with clean air in an olfactometer (total air flow was 1.5 L/min). Behavioral trials consisted of a 1 s odor cue, followed by a reward 3 s after cue onset (100 trials per session, 25 ± 5 s intertrial interval). The behavioral task was controlled with a custom Labview program (National Instruments). Anticipatory licking was defined as a bout of licking that began between 0 to 3 s after cue onset. Animals were trained for 3 to 5 days before undergoing behavioral testing or electrophysiological recordings. To assess the effect of optogenetically stimulating D1 or D2 MSNs on behavior, a test session involved presentation of 90–150 behavioral trials, half of which were randomly paired with unilateral optical stimulation in the striatum (532 nm, 5 mW power at fiber output, 4 s continuous duration starting 1 s before cue onset).

Opto-microprobe for combined electrophysiology and optogenetics

The opto-microprobe is identical in design to the device described previously (Lee et al., 2017). Briefly, this device contains a total of 256 recording electrodes (gold-plated to an impedance of 100–300 kΩ) distributed evenly across four silicon prongs spaced apart by 0.2 mm. The electrodes on each prong span a depth of 1.05 mm. Optical illumination (532 nm laser) was delivered via a pair of optical fibers attached to the silicon prongs with epoxy (0.2 mm diameter, 0.22 NA), with their centers 0.4 mm apart, and terminating about 0.2 mm above the most dorsal electrodes. The power output was calibrated before each experiment. The device was inserted in the coronal plane, and the target coordinates of the most lateral prong in the lateral striatum were: 1.0 mm anterior, 2.5 mm lateral, 4.2 mm ventral to bregma. For the experiments involving widespread input suppression (Figure 7) we sometimes recorded in both hemispheres from the same animal, but at most once per hemisphere. Each recording session was treated as a separate sample during analysis.

Optogenetic tagging

After recording striatal activity for 100–160 behavioral trials, we presented optical stimuli for tagging (1 or 5 mW power output per fiber, 100 ms continuous duration, 50–100 trials, 5 s intertrial interval). The relatively long duration of the laser pulse was used in order to avoid potential problems in spike detection or sorting associated with photoelectric artifacts, which occur during the laser onset and offset time. For some subjects, to determine the false positive rate (Figure S1C) we repeated the optical stimulation and recording protocol on the contralateral striatal hemisphere, which had not received viral injection. For consistency the initial criteria for identifying optically tagged cells were selected to be similar or equivalent to those reported in the literature (Jin et al., 2014; Nonomura et al., 2018; Shin et al., 2018). The first criterion required that the latency to activation must not exceed 6 ms. Significantly activated cells were found by a paired t test between the number of spikes per second per trial in a 6 ms window after laser onset, and the number of spikes per trial in a 1 s baseline window before laser onset. The threshold for significance was defined as p < 0.01. The second criterion required a minimum Pearson correlation coefficient of 0.95 between the mean waveform of the last spike before laser onset in each trial, and the first spike after laser onset in each trial. The waveform duration used for calculating the correlation was 1.24 ms. These criteria resulted in 43 D1 (out of 711 total units from 10 mice, or 6%), 18 D2 cells (out of 864 total units from 10 mice, or 2.1%), and zero false positives (out of 534 total units from 7 control mice). To ensure that the comparison of D1 and D2 activity was insensitive to small variations in these criteria, we also performed analysis with the first criterion set to 4 and 8 ms. This changed the number of tagged D1 and D2 cells, but did not change the significance of the results. Furthermore, with a maximum latency of 8 ms, there were 2 false positive cells (equal to 0.4% of all recorded units from the control group), suggesting that the latency criterion should not exceed 6 ms. Finally, in Supplemental Information, we introduced a third criterion, that cells must also be electrophysiologically classified as MSNs (see Analysis of neural activity).

Corticostriatal and thalamostriatal input suppression

In total about 6 wks elapsed between the time of virus injection and recording, to allow time for anterograde halorhodopsin expression in the striatum. Recordings to suppress projections consisted of 70–260 behavioral trials, half of which were randomly paired with optical stimulation (10 mW power output per fiber, 8 s continuous duration starting 2 s before cue onset).

Analysis of neural activity

For electrophysiological classification of different cell types (Bakhurin et al., 2016), putative FSIs were defined by a narrow spike waveform (maximum width = 0.475 ms), and relatively high baseline firing (minimum rate = 0.25 Hz). MSNs and TANs were both defined by wider waveforms (minimum width = 0.55 ms, maximum width = 1.25 ms). TANs were separated from MSNs by the regularity of their baseline firing (maximum coefficient of variation = 1.5). The minimum baseline firing was defined as 0.02 Hz for MSNs and 2 Hz for TANs, and the maximum was defined as 10 Hz for both cell types. The majority of putative TANs showed a brief partial or complete pause in firing after reward delivery, consistent with previous reports (Figure S2I) (Aosaki et al., 1995).

All analysis of neural activity during behavior involved data from trials with anticipatory licking. The firing rate suppression factor per cell (Equation 1) was calculated from the number of spikes on trials with laser on or off. The time window for calculating this value was defined in the text or figure legend as either the full period of laser stimulation (−2 to 6 relative to cue onset), cue period (0 to 3 s), or reward period (3 to 6 s). The suppression factor per subject was defined as the median suppression factor of all simultaneously recorded units from a single animal. A small percentage of units (0.05% in the cue period and 1.73% in the reward period, out of 2140 total MSNs from all recordings in Figures 2, 3, 4, 5, and 6) had a suppression factor of negative infinity because the denominator in Equation 1 was equal to zero. These units were excluded from the calculation of median suppression factor, slope, and y intercept per subject in the cue or reward period.

To obtain the percentage of significantly excited and inhibited MSNs (Figures S3G and S3I), the firing rate of each cell was calculated in time bins of 0.5 s, using only data from laser off trials. In each time bin, a paired t test was performed between the number of spikes per second per trial, and the number of spikes per trial in a 1 s baseline window before cue onset. The criterion for significance was defined as p < 0.01.

To obtain each subject’s slope and y intercept of the R_on versus R_off response curve, we first calculated the mean absolute firing rate as a function of time (either in the cue or reward time period) of all simultaneously recorded units per subject, during laser on and off trials (e.g., Figure 3A, right). The firing rate was calculated in time steps of 5 ms, and a Gaussian convolution (standard deviation = 25 ms) was applied to smooth the data. This resulted in two time-varying rate vectors, R_on(t) and R_off(t). The time dependence was eliminated by plotting the mean R_on value at each time step as a function of the mean R_off value at the corresponding time step, in bins of 0.1 Hz. The straight line fit to this plot yielded the slope and y intercept per subject in the cue or reward period. In Figures 6B and S6B, the rate vectors were calculated from MSNs pooled across multiple subjects, but this was done only for visualization purposes.

Model of multiplication and addition

In Figure 5, data representing the observed suppression factor was compared to a model of multiplication or linear summation of experimentally measured individual input suppression factors. As shown in Figure 3, there were n = 9 suppression factor values associated with each individual input. To construct the models we entered all unique combinations of these values into the right hand side of Equations 5 and 6. There were 9² and 9³ unique combinations of double and triple input values, respectively. Sometimes, the sum of values in the linear summation model (Equation 5) exceeded one. In such cases we capped the value at one, since a suppression factor above one is not experimentally possible. The model that had a statistically insignificant difference to the observed data (p > 0.05) was interpreted as being more consistent with the results. With the exception of one result (Figure 5G) all observations were similar to the multiplication model but significantly different from the linear summation model. Data in Figure 5G could not differentiate between either model.

QUANTIFICATION AND STATISTICAL ANALYSIS

All statistical analyses were performed using standard MATLAB functions and GraphPad Prism software. Information about the sample size, statistical test used, and probability value, is provided in the figure legends. In the figures, ^# denotes p < 0.06, * p < 0.05, ** p < 0.01, *** p < 0.001, and **** p < 0.0001.

DATA AND CODE AVAILABILITY

Requests for data and custom MATLAB code for analysis with be fulfilled by the Lead Contact (smasmanidis@ucla.edu).

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Chicken polyclonal Anti-GFP	Abcam	Cat#13970; RRID: AB_300798
Rabbit Polyclonal Anti-DsRed	Takara	Cat# 632496; RRID: AB_10013483
Donkey Anti-Chicken Alexa Fluor 488	Jackson ImmunoResearch	Cat#703–545–155; RRID: AB_2340375
Donkey Anti-Rabbit Alexa Fluor 647	Jackson ImmunoResearch	Cat#711–605–152; RRID: AB_2340625
Chemicals, Peptides, and Recombinant Proteins
Isoamyl acetate	Sigma-Aldrich	Cat#W205508
Mineral oil	Sigma-Aldrich	Cat#M8410
Experimental Models: Organisms/Strains
Tg(Drd1-cre)EY262Gsat/Mmucd	Mutant Mouse Resource and Research Center	Cat#017264-UCD; RRID: MMRRC_017264-UCD
Tg(Adora2a-cre)KG139Gsat/Mmucd	Mutant Mouse Resource and Research Center	Cat#031168-UCD; RRID: MMRRC_031168-UCD
C57BL/6J	The Jackson Laboratory	Cat#000664; RRID: IMSR_JAX:000664
Recombinant DNA
AAV5/Syn-Flex-ChrimsonR-tdTomato	UNC Vector Core, MTA from Ed Boyden	N/A
AAV5/EF1a-DIO-mCherry	UNC Vector Core, MTA from Karl Deisseroth	N/A
AAV5/CaMKIIa-eNpHR3.0-eYFP	UNC Vector Core, MTA from Karl Deisseroth	N/A
AAV5/CaMKIIa-eNpHR3.0-mCherry	UNC Vector Core, MTA from Karl Deisseroth	N/A
AAV5/CaMKIIa-eYFP	UNC Vector Core, MTA from Karl Deisseroth	N/A
Software and Algorithms
MATLAB	Mathworks	Version R2017a
Prism	GraphPad Software	Version 6
Custom MATLAB scripts	This paper and, Shobe et al., 2015; Bakhurin et al., 2016; Lee et al., 2017	N/A
Labview	National Instruments	Version 2011
Other
Optical fiber	Thor Labs	Cat#UM22–200
Optical fiber ferrule	Thor Labs	Cat#CFLC270
Optical fiber ferrule sleeve	Thor Labs	Cat#ADAL1
50/50 fiber optic splitter	Thor Labs	Cat#FCMM625–50A-FC
532 nm laser	Opto Engine	Cat#MGL-III-532nm-100mW
Opto-microprobe	This paper and Lee et al., 2017	N/A

Highlights.

• Effect of suppressing excitatory inputs on striatal firing during behavior is analyzed

• Cortical and thalamic inputs modulate striatal activity and gain

• Suppressing multiple inputs suggests a multiplication-like integration rule

• Gain modulation is more pronounced in a temporally specific period of the task