A likelihood-based approach to transcriptome association analysis

Abstract

Elucidating the mechanistic underpinnings of genetic associations with complex traits requires formally characterizing and testing associated cell and tissue-specific expression profiles. New opportunities exist to bolster this investigation with the growing numbers of large publicly available -omics level data resources. Herein we describe a fully likelihood-based strategy to leveraging external resources in the setting that expression profiles are partially or fully unobserved in a genetic association study. A general framework is presented to accommodate multiple data types, and strategies for implementation using existing software packages are described. The method is applied to an investigation of the genetics of evoked inflammatory response in cardiovascular disease research. Simulation studies suggest appropriate type-1 error control and power gains compared to single regression imputation, the most commonly applied practice in this setting.

1 |. INTRODUCTION

Large-scale genome-wide association (GWA) studies have contributed substantially to knowledge on the genetic underpinnings of complex disease traits, including the identification of a vast array of single nucleotide polymorphisms (SNPs), protein-coding genes and regulatory elements, that associate with clinically relevant outcomes. The biological mechanisms underlying these genetic associations, particularly the relationships among susceptibility loci, expression profiles in disease relevant tissues, and complex traits, however, remains largely uncharacterized. Emerging cell and tissue-specific transcriptome-wide association (TWA) data will likely play a decisive role in elucidating these mechanisms. Moreover, the availability of large and comprehensive reference data panels, including sequencing data and genome-wide cell and tissue specific expression profiles, can serve as highly informative and tractable resources to enhance this investigation. Herein we propose a general approach to leveraging such reference multi-omic data in the context of genetic association studies for which transcriptome data are partially or fully unobserved.

The setting motivating this research is one in which two independent data resources are available: (1) GWA data, composed of complete genotype and trait information on each individual, in addition to the possible availability of expression profiles on a subset of cell types, and a subset of inidividuals; and (2) TWA data, composed of genotype and complete expression profiles, as measured by RNAseq, on multiple genes, several cell and tissue types and multiple isoforms, for an independent set of individuals. Analysis is based on all sNPs that are shared between the two data resources. Typically transcriptome data do not include a measured trait, although emerging resources for which trait data will be available, can additionally be incorporated into the proposed framework. The analytical goal is to leverage the transcriptome data in analysis of the GWA data to inform the mechanisms underlying gene-trait associations. For example, a GWA analysis may suggest that SNPs close to a particular gene are associated with a given trait. By leveraging transcriptome data, we can additionally unravel whether this association is mediated by expression of the same gene, or another gene or regulatory element.

The specific data example motivating this research is derived from the Genetics of Evoked Responses to Niacin and Endotoxemia (GENE) study, an NIH-sponsored investigation of the genomics of inflammatory and metabolic responses during low-grade endotoxemia ^1,2,3. In this study, n=294 individuals were genotyped at baseline and monitored during a 48 hour hospital visit after an endotoxin challenge. Multiple clinical variables and five plasma biomarkers – tumor necrosis factor alpha (TNFα), interleukin-6 (IL-6), interleukin-1 receptor agonist (IL-1RA), Serum Amyloid A (SAA) and high-sensitivity C-reactive protein (CRP) – were recorded repeatedly over time in increments of 1 to 12 hours. In a recent study, we investigated the genetic factors associated with IL-6 and CRP levels, and identified several genes and long non-coding RNAs that associate with the change in these biomarkers from baseline to peak, as well as the non-linear biomarker trajectories over time ⁴. The next crucial step of this investigation is to decipher the mechanistic relationships between these genomic classes and induced biomarker responses through targeted transcriptome analysis.

Expression data are generally unavailable or limited in GWA settings. For example, in the GENE study, whole-genome RNAseq data are available on a subset of individuals with extreme phenotypes and exclusively on one of many relevant blood cell types. Drawing inference in this setting is possible, however, through integration of reference transcriptome data. Several large reference panels that include genome-wide SNP data, as well as whole-genome RNAseq data on multiple cell and tissue types, are now publicly available offering new potential for integrated analysis platforms. Three well-described and comprehensive TWA resources are: (1) the Genotype Tissue Expression (GTEx) data V6p release, composed of RNAseq data on 53 tissues and whole-blood for a total of 449 donors ⁵; (2) the European Bioinformatics Institute Geuvadis data, composed of RNAseq data from lymphoblastoid cell lines of 465 individuals from the 1000 Genomes project ⁶; and (3) the Depression Genes and Networks study (DGN) sequencing data composed of whole-blood RNAseq for 922 individuals ⁷. In this manuscript we describe and evaluate a statistical strategy for integrating these available resources in the analysis of data arising from genetic association studies with limited to no observed transcriptome data to uncover mechanistic relationships.

A few notable publications describe methods for integrating reference transcriptome data for association studies ^8,9,10,11. For example, Gamazon et al. propose a two-stage strategy, termed PrediXcan, that first singly imputes cell-specific gene expression using genetic profiles and publicly available reference transriptome data resource, and second characterizes association between imputed expression and a measured trait ⁸. The first-stage prediction algorithm relates genotype to expression using the elastic net ¹², demonstrating similar performance to the least absolute shrinkage and selection operator (LASSO) ¹³. Predicted cell- specific genetically regulated expression (GReX) is then treated as known and used in a generalized linear model to evaluate association with a binary outcome. The approach of Gusev et al. similarly involves unit imputation while alternative predictive models are used ¹⁰, including a mixed effects model with random SNP-level effects and a Bayesian sparse linear mixed model (BSLMM) ¹⁴. Perhaps the most notable statistical shortcoming of these approaches, which can be viewed as special cases of regression imputation, is the lack of consideration of the uncertainty in the prediction of genetically regulated expression. Additionally, well-established statistical research indicates that two-stage imputation approaches are generally less powerful than fully likelihood-based approaches that integrate prediction of unobserved data and association analysis ^15,16.

As a robust alternative that addresses the limitations of current practice, we propose combining the two data resources, the GWA and TWA data, and framing the analysis in terms of a missing data problem. Specifically, we assume RNAseq data are only partially observed. We begin by presenting a unified strategy based on maximizing the observed data likelihood which is straightforward in the context of normalized expression data. The expectation-maximization (EM) algorithm is an established approach to estimation in the presence of missing data ¹⁷ in the case that solving for the observed data likelihood is not tenable, and in Section 2 we develop a simple EM-based strategy for this setting. We then discuss opportunities for practical and efficient implementation, and describe strategies for statistical inference. Our fully likelihood-based approach appropriately accounts for the error in prediction (not addressed in current methods) by integrating the prediction of unobserved data and association analysis. Simulation studies and application to the GENE study data are also described to fully characterize method performance and compare to the more common application of regression imputation for this setting (Sections 3 and 4). We conclude with a discussion in Section 5.

2 |. METHODS

2.1 |. A unified likelihood-based approach for normalized expression data

We first define a generalized linear model of association between expression and a univariate biomarker response, and second propose a similar modeling framework for the relationship between genotype and expression. Let y be an n×1 vector representing a univariate biomarker response on n individuals, and consider a generalized linear model of the form $g\left(E\left[\mathbf{y}\right]\right)=\mathbf{W}{\mathbf{\gamma }}_0+\mathbf{x}{\mathbf{\gamma }}_1$, where covariates are included in the design matrix W, cell-specific expression (for a single cell type) is represented by the n × 1 vector X and g(·) is a canonical link function. A general form of the conditional probability density function for y, given W and X, assuming an exponential family distribution, is given by ¹⁸:

$$f_{\mathbf{\Omega }}\left(\mathbf{y}|\mathbf{W},\mathbf{x}\right)=\prod _{i=1}^n\exp \left\{\left(y_i{\theta }_i-b\left({\theta }_i\right)\right)/a\left(\varphi \right)+c\left(y_i,\varphi \right)\right\},$$ (1)

where a(·), b(·) and c(·) are specified functions, Ω = (θ,ϕ), θ depends on the linear predictor and ϕ is a scale parameter. In our example of Section 4, the biomarker is a quantitative measure of immune modulation, and so we let g(·) be the identity link and assume the conditional probability density function is given by a multivariate normal distribution. In this case, ${\theta }_i={\mathbf{w}}_i^T{\mathit{\gamma }}_0+x_i^T{\gamma }_1$,$\varphi ={\sigma }^2,i=1,\hspace{0.17em}\dots \hspace{0.17em},n,$

$$a\left(\varphi \right)=\varphi ,b\left({\theta }_i\right)={\theta }_i^2/2\hspace{1em}\text{and}\hspace{1em}c\left(y_i,\varphi \right)=-\frac{1}{2}\left\{y_i^2/\varphi +\log \left(2\pi \varphi \right)\right\}.$$ (2)

Gene expression as measured by RNAseq are count data and can also be modeled with an exponential family distribution of the form of Equation 1. Let h_Θ(x Z) represent the product of probability distribution functions for expression counts conditional on genotype Z, where Z is defined explicitly. To begin we will apply LD pruning, as described in ¹⁹, in order to avoid high degrees of collinearity and an unidentifiable model. Alternative modeling strategies to account for moderate to large degrees of LD are described in Section 5. Untransformed RNAseq data are often assumed to follow a negative binomial distribution to account for over dispersion ^20,21, although normalized gene expression data, specifically Reads Per Kilobase of transcript, per Million mapped reads (RPKM), are typically modeled using a Gaussian model ⁸. In this manuscript, we begin by describing a likelihood based strategy based on a Gaussian model for expression data in Section 2.1. Secondly, we consider inference using the more general EM framework, which could be used with a wide variety of models; in Section 2.2 we develop an EM-type algorithm arising from a discrete exponential family distribution.

In our setting, the complete data are the combination of the primary data – composed of genotype and biomarker data – and the external data resource – composed of genotype and complete RNAseq data for an independent sample. Specifically we can think of the RNAseq data, represented by x, as unobserved in the primary data. In this case, the complete data are given by y and x, and the complete data likelihood is written:

$$L^c\left(\mathbf{\Phi }|\mathbf{y},\hspace{0.17em}\mathbf{W},\mathbf{Z},\mathbf{x}\right)=Pr\left(\mathbf{y},\mathbf{x}|\hspace{0.17em}\mathbf{W},\mathbf{Z},\mathbf{\Phi }\right)=f_{\mathbf{\Omega }}\left(\mathbf{y}|\hspace{0.17em}\mathbf{W},\mathbf{x}\right){\mathit{h}}_{\mathbf{\Theta }}\left(\mathbf{x}|\mathbf{Z}\right),$$ (3)

where Φ = (Ω, Θ) and f_Ω(y |W,x) and h_Θ(x|Z) are the conditional probability density functions of y and x, respectively. We further let the complete data log likelihood be denoted $l_{\mathbf{\Phi }}^c=\log L^c\left(\mathbf{\Phi }|\mathbf{y},\hspace{0.17em}\mathbf{W},\mathbf{Z},\mathbf{x}\right)$.

In order to estimate the elements of Φ we aim to maximize the observed data log likelihood, denoted $l_{\mathbf{\Phi }}^{\text{obs}}$, where the observed data in this setting are given by $\left\{{\left(y_i,{\mathbf{z}}_i,{\mathbf{w}}_i\right)}_{i=1}^n;{\left(x_j,{\mathbf{z}}_j\right)}_{j=1}^m\right\}$. The observed data likelihood is derived by integrating L^c (Φ| y, W, Z, x) over the missing information. In the special case that h_Θ(x Z) is given by a multivariate normal distribution and the model relating expression to the biomarker is linear with normally-distributed errors, it is straightforward to show that the observed data log likelihood is given by:

$$l_{\mathbf{\Phi }}^{\text{obs}}=\mathbf{\sum }_{i=1}^n\left[-\frac{1}{2}\log \hspace{0.17em}\left({\sigma }_{\delta }^2{\gamma }_1^2+{\sigma }_{ϵ}^2\right)-\frac{{\left(y_i-{\mathbf{w}}_i^T{\gamma }_0-{\mathbf{z}}_i^T\mathit{\beta }{\gamma }_1\right)}^2}{2\left({\sigma }_{\delta }^2{\gamma }_1^2+{\sigma }_{ϵ}^2\right)}\right]+\mathbf{\sum }_{j=1}^m\left[-\log \hspace{0.17em}{\sigma }_{\delta }-\frac{{\left(x_j-{\mathbf{z}}_j^T\mathbf{\beta }\right)}^2}{2{\sigma }_{\delta }^2}\right],$$ (4)

where $Y|\mathbf{w},x~\mathit{N}\left({\mathbf{w}}^T{\mathit{\gamma }}_0+x{\gamma }_1,{\sigma }_{ϵ}\right)$ and $X|\mathbf{z}~\mathit{N}\left({\mathbf{z}}^T\mathit{\beta },{\sigma }_{\delta }\right)$. As the corresponding estimating equations are difficult to solve, a numeric technique, such as the Newton-Raphson or Gauss-Legendre quadrature algorithm, can be applied to arrive at parameter estimates. Corresponding standard errors for the parameter estimates are obtained using the inverse of the observed fisher information matrix (see Appendix A).

2.2 |. An EM approach for expression data arising from a discrete exponential family distribution

The derivation of the observed data likelihood in Section 2.1 was facilitated by the use of normal models for the relationships between genotype and expression and expression and the trait. In general, deriving the observed data likelihood is not straight- forward. However, in the case of a discrete distribution function h_θ(x| Z), the conditional expectation of the complete data log likelihood is given by a weighted sum over possible gene expression patterns, where the weights correspond to posterior probabilities given the observed genotypes. Formally, we have:

$$\mathit{E}\left(l_{\mathbf{\Phi }}^c|\mathbf{y},\mathbf{W},\mathbf{Z}\right)=\mathbf{\sum }_{i=1}^n\mathbf{\sum }_{x_i\in {\chi }_i}{\pi }_i\left(\mathbf{\Phi };x_i\right)\hspace{0.17em}{l}_{\mathbf{\Phi },i}^c,$$ (5)

where $l_{\Phi ,i}^c$ is the contribution of the ith individual to the complete data log likelihood, and the weights are given by:

$${\pi }_i\left(\mathbf{\Phi };x_i\right)=\mathit{P}\mathit{r}\left(x_i|y_i,\hspace{0.17em}{\mathbf{w}}_i,{\mathbf{z}}_i\right)=\frac{f_{\mathbf{\Omega }}\left(y_i|{\mathbf{w}}_i,x_i\right)h_{\mathbf{\Theta }}\left(x_i|{\mathbf{z}}_i\right)}{{\mathbf{\sum }}_{x_i\in {\chi }_i}{f}_{\mathbf{\Omega }}\left(y_i|{\mathbf{w}}_i,x_i\right)h_{\mathbf{\Theta }}\left(x_i|{\mathbf{z}}_i\right)},$$ (6)

and χ_i is the set of all expression levels that are consistent with the observed genotypes for individual i.

For each iteration of the EM algorithm, in the E-step we substitute the current estimates of Φ into the calculation of the posterior expression probabilities, to arrive at the estimates ${\widehat{\pi }}_{\mathbf{x},i}^{\left(t\right)}={\pi }_i({\widehat{\mathbf{\Phi }}}^{\left(t\right)};x_i)$. Then in the M-step, we update the parameter estimates by maximizing the conditional expectation. Maximization at the (t + 1)th iteration proceeds by taking the partial derivative of the expected complete data log-likelihood given by Equation 5 with respect to each parameter, setting this equal to 0 and solving for the corresponding parameter. That is, at the (t + 1)th iteration we aim to find the roots of the partial derivatives with respect to each parameter in Φ = (ϕ₁, … , ϕ_K ). Formally, at the (t+1)th iteration of the M-step, we aim to find the roots of the following system of equations for k = 1, … , K:

$$\frac{\partial }{\partial {\mathit{\varphi }}_k}\mathit{E}\left(l_{\mathbf{\Phi }}^c|\mathbf{y},\mathbf{W},\mathbf{Z}\right)=\mathbf{\sum }_{i=1}^n\mathbf{\sum }_{x_i\in {\chi }_i}{\widehat{\pi }}_{x,i}^{\left(t\right)}\hspace{0.17em}{\mathbf{U}}_i\left({\varphi }_k;\mathbf{\Phi }\right),$$ (7)

where $U_i\left({\varphi }_k;\mathbf{\Phi }\right)=\partial l_{\mathbf{\Phi },i}^c/\partial {\varphi }_k$ is the ith individual’s contribution to the kth element of the score function for the complete data log likelihood (provided in Appendix B). Inference in this setting requires estimation of the covariance matrix, given by the inverse of the observed information matrix, which we approximate with the empirical observed information ^22,23. That is, we estimate the variance of the model parameters as I⁻¹ evaluated at the final iteration of the EM algorithm after a convergence criterion is met (see Appendix B), where:

$$\mathbf{I}=\mathbf{\sum }_{i=1}^n{E}_{\mathbf{\Phi }}\left(-{\partial }^2{l}_{\mathbf{\Phi },i}^c/\partial {\mathbf{\Phi }}^2|\mathbf{y},\mathbf{W},\mathbf{Z}\right)-\mathbf{\sum }_{i=1}^n{E}_{\mathbf{\Phi }}\left({\mathbf{U}}_i\left(\mathbf{\Phi }\right){\mathbf{U}}_i{\left(\mathbf{\Phi }\right)}^T|\mathbf{y},\mathbf{W},\mathbf{Z}\right)-\mathbf{\sum }_{i\ne j}{E}_{\mathbf{\Phi }}\left({\mathbf{U}}_i\left(\mathbf{\Phi }\right)|\mathbf{y},\mathbf{W},\mathbf{Z}\right)E_{\mathbf{\Phi }}{\left({\mathbf{U}}_j\left(\mathbf{\Phi }\right)|\mathbf{y},\mathbf{W},\mathbf{Z}\right)}^T.$$ (8)

The EM approach can be applied in general to exponential family distributions. For example, under the negative binomial model, letting Γ(n) = (n − 1)! be the usual Gamma function, ${\mu }_i=\exp \left({\mathbf{z}}_i^T\mathit{\beta }\right),\hspace{0.17em}{\theta }_i=\log \left[\left({\mu }_i/\alpha \right)/\left(1+{\mu }_i/\alpha \right)\right],\hspace{0.17em}\varphi =\alpha$,

$$a\left(\varphi \right)=1;b\left({\theta }_i\right)=-\alpha \log \left(1-\exp \left({\theta }_i\right)\right)\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}c\left(x_i,\varphi \right)=\log \left(\frac{\mathrm{\Gamma }\left(x_i+\varphi \right)}{\mathrm{\Gamma }\left(x_i+1\right)\mathrm{\Gamma }\left(\varphi \right)}\right).$$ (9)

where z_i is the vector of observed SNPs for individual i = 1, … , n and Θ = (α, β). In the context of RNAseq data and a univariate real-valued outcome, the model specifications of Equations 2 and 9 are generally appropriate. In this case, the ith contribution to the complete data log likelihood is given by:

$$\begin{gathered} l_{i,\mathbf{\Phi }}^c=\frac{1}{{\sigma }^2}\left\{y_i\left({\mathbf{w}}_i^T{\mathbf{\gamma }}_0+x_i{\gamma }_1\right)-{\left({\mathbf{w}}_i^T{\mathbf{\gamma }}_0+x_i{\gamma }_1\right)}^2/2\right\}-\frac{1}{2}\left\{y_i^2/{\sigma }^2+\log \left(2\pi {\sigma }^2\right)\right\}+\alpha \log \left(\alpha \right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+x_i\log \left({\mu }_i\right)-\left(\alpha +x_i\right)\log \left(\alpha +{\mu }_i\right)+\log \mathrm{\Gamma }\left(x_i+\alpha \right)-\log \mathrm{\Gamma }\left(x_i+1\right)-\log \mathrm{\Gamma }\left(\alpha \right). \end{gathered}$$

At the M-step, we find the roots of Equation 7, based on the corresponding elements of the score function.

Arriving at closed form solutions for γ₀, γ₁ and σ² at each iteration is straightforward. In fact, solving for γ₀ and γ₁ results in the familiar weighted least squares solutions, as detailed in Section 2.2. In general, closed form solutions may not exist, as is the case for β and α, so an alternative numeric technique, as described for the Gaussian setting, can be applied to identify roots to the corresponding weighted score functions. As it is not straightforward to maximize the expectation simultaneously with respect to the mean and scale parameters, we apply the expectation conditional maximization approach of ²⁴ in which we condition on current scale parameter estimates to update the mean parameter estimates, and then condition on mean parameters to update scale parameters. A bias adjustment is also made for σ at each iteration of the algorithm. In the next section we consider computationally efficient strategies for estimation in this setting, taking advantage of existing theory and functionalities.

Practical implementation of the EM strategy

In practice, at each iteration of the EM algorithm, we are maximizing a weighted likelihood function where the data for each individual are expanded to a dimension that equals the number of possible values of the unobserved data. To see this, first let $\tilde{y}=y_i{1}_{m_i}$ and ${\tilde{\mathbf{W}}}_i={\mathbf{w}}_i\otimes {\mathbf{1}}_{m_i}$, where ${\mathbf{1}}_{m_i}$ is a m_i × 1 vector of 1’s, m_i is the number of possible values of x_i for individual i and ⊗ represents kronecker product. Additionally define ${\tilde{x}}_i$ as an m_i ×1 vector with elements equal to the values of x_i that are consistent with the observed genotype data and let ${\widehat{\mathbf{p}}}_i^{\left(t\right)}$ be a vector of weights with elements equal to the set of posterior probabilities, ${\widehat{\pi }}_{\mathbf{x},i}^{\left(t\right)}$. Finally, the concatenated versions of ${\tilde{\mathbf{y}}}_i$, $\widetilde{{\mathbf{W}}_i}$ and ${\tilde{\mathbf{x}}}_i$ across all individuals are denoted $\tilde{\mathbf{y}}$, $\tilde{\mathbf{W}}$ and $\tilde{\mathbf{x}}$, respectively. Letting j index the combination of individual and possible values of unobserved data, j = 1, … , N where $N\hspace{0.17em}=\hspace{0.17em}{\mathbf{\sum }}_{i=1}^n{m}_i$, we can now write Equation 5 as:

$$E\left(l_{\mathbf{\Phi }}^c|\mathbf{y},\mathbf{W},\mathbf{Z}\right)=\mathbf{\sum }_{j=1}^N{\widehat{p}}_j^{\left(t\right)}\left[\log f_{\mathbf{\Omega }}\left({\tilde{\mathbf{y}}}_j|{\tilde{\mathbf{w}}}_j,{\tilde{x}}_j\right)+\log \hspace{0.17em}{h}_{\mathbf{\Theta }}\left({\tilde{x}}_j|{\tilde{\mathbf{z}}}_j\right)\right].$$ (10)

For example, in the case of γ₁, the primary parameter of interest, the EM algorithm involves calculating:

$$\frac{\partial }{\partial {\gamma }_1}E\left(l_{\mathbf{\Phi }}^c|\mathbf{y},\mathbf{W},\mathbf{Z}\right)=\mathbf{\sum }_{j=1}^N{\widehat{p}}_j^{\left(t\right)}\left[{\tilde{x}}_j\left({\tilde{y}}_j-{\tilde{\mathbf{w}}}_j^T{\gamma }_0-{\tilde{x}}_j{\gamma }_1\right)/{\sigma }^2\right],$$ (11)

and setting this equal equal to 0, yielding the familiar weighted least squares estimator:

$${\widehat{\gamma }}_1^{\left(t+1\right)}={\left({\tilde{\mathbf{x}}}^T{\widehat{\mathbf{P}}}^{\left(t\right)}\tilde{\mathbf{x}}\right)}^{-1}{\tilde{\mathbf{x}}}^T{\widehat{P}}^{\left(t\right)}\left(\tilde{y}-\tilde{\mathbf{W}}{\mathit{\gamma }}_0\right),$$ (12)

where ${\widehat{\mathbf{P}}}^{\left(t\right)}=diag\left({\widehat{p}}_j^{\left(t\right)}\right)$.

Based on this result, it is judicious to consider application of standard generalized linear model fitting procedures that employ weights in the maximization step of the algorithm described in Section 2.2. In order to assess the appropriateness of this strategy, we first note that the log likelihood for a generalized linear model with prior weights, as described in ²⁵, (Chapter 7, page 183) is given by:

$$\log f_{\mathbf{\Omega }}\left(y_i|{\mathbf{w}}_i,x_i\right)=A_i\left(y_i\theta -b\left(\theta \right)\right)/a\left(\varphi \right)+c\left(y_i,\varphi /A_i\right),$$ (13)

where A_i are known prior weights. Notably, this formulation differs from the weights introduced in ¹⁸ (Chapter 2, page 29) for the normal distribution, in which Equation 1 is modified by setting a(ϕ) equal to ϕ/A_i but weights are not introduced into c(y, ϕ). We focus on the model given by Equation 13 as it is the basis for the prior weight specification for the glm() function in R ²⁵.

In order to see the relationship of this to our setting, note that the score of γ₁, can be written:

$$\frac{\partial }{\partial {\gamma }_1}E\left(l_{i,\mathbf{\Phi }}^c|\mathbf{y},\mathbf{W},\mathbf{Z}\right)=\mathbf{\sum }_{j=1}^N{\widehat{p}}_{ij}^{\left(t\right)}\frac{\partial }{\partial {\gamma }_1}\left[A_i\left(y_i{\theta }_i-b\left({\theta }_i\right)\right)/a\left(\varphi \right)\right],$$ (14)

as log h_Θ(x | Z) and c(y, ϕ/A_i) do not depend on γ₁. Setting this equation equal to 0 and solving for γ₁ is equivalent to maximizing Equation 13 with respect to γ₁. This is similarly true for γ₀ and β. However, in terms of the scale parameter, ø, we need that:

$$\mathbf{\sum }_{j=1}^N{\widehat{p}}_j^{\left(t\right)}\frac{\partial }{\partial \mathit{\varphi }}c\left(y,\varphi \right)=\mathbf{\sum }_{j=1}^N\frac{\partial }{\partial \mathit{\varphi }}c(y,\varphi /{\widehat{p}}_j^{\left(t\right)}).$$ (15)

For the normal and negative binomial models this does not generally hold; however, it can be shown that a simple transformation, ${\widehat{\varphi }}^{\left(t+1\right)}={\widehat{\varphi }}_{\text{p}}^{\left(t+1\right)}\hspace{0.17em}\ast \hspace{0.17em}N/n$ where ${\widehat{\varphi }}_{\text{p}}^{\left(t+1\right)}$ is the estimated variance component based on specifying weights within the glm() function in R (see Appendix C). A simple transformation is not as straightforward for the negative binomial scale parameter (see Appendix C). Moreover, while the documentation for the glm.nb() function in R to fit a negative binomial regression similarly references the weighted regression approach of ²⁵ and applies an iterative procedure that uses the glm() function, the likelihood defined in the R code is of the form given in our setting (Equation 10).

3 |. SIMULATION STUDIES

Simulations are performed to evaluate type 1 error, power and convergence of the unified likelihood-based approach for normalized expression data (Section 3.1), and the EM strategy for count data (Section 3.2). Both approaches are compared to a standard application of two-stage regression imputation.

3.1 |. Unified approach to normalized expression data

To begin we investigate bias by simulating normalized data based on the modeling results from the example provided in Table 5 of Section 4. In this study, we sample with replacement from the observed genotypes across 20 SNPs within Capping Protein Regulator And Myosin 1 Linker 1 (CARMIL1, previously LRRC16A) that are present in both the GENE study and DGN data; these resampled observations serve as the independent data for the simulation. The minor allele frequencies of these SNPs range from 0.11 to 0.45 in the DGN data. LD pruning based on a threshold of 0.20 was applied to arrive at this subset of 20 independent signal SNPs. Parameter values for the simulations are γ₀ = −0.435, γ₁ = 4.650, σ_δ = 0.651, σ_ϵ = 1.195. The 20 SNP coefficients ranged from −0.915 to 0.675 and SNPs are assumed to influence gene expression according to an additive genetic model and an additive model of association.

TABLE 5.

Transcriptome-biomarker association analysis

		γ0	γ1	σϵ	β0	β1*(rs6938645)	σδ
Unified likelihood§:
LRRC16A	estimate:	4.650	0.157	1.195	−0.435	−0.915	0.651
	std err:	0.092	0.127	−	0.153	0.0431	−
	test stat:	50.653	1.238	−	−2.851	−21.212	−
	p-value:	< 0.001	0.216	−	0.004	< 0.001	−
Regression Imputation:
LRRC16A	estimate:	4.649	0.153	1.207	−0.431	−0.914	0.659
	std err:	0.092	0.126	−	0.155	0.0437	−
	test stat:	50.397	1.213	−	−2.789	−20.939	−
	p-value:	< 0.001	0.227	−	0.005	< 0.001	−

^§Coefficient estimates and standard errors are based on application of the unified likelihood strategy.

^*The coefficient estimate and corresponding standard error is reported for the strongest signal SNP within LRCC16A (rs6938645).

The distributions of bias across model parameters based on 1000 simulations for a range of sample sizes are illustrated in Figure 1. The center panel most closely reflects the observed sample sizes of our data example in Section 4. In all cases, bias is appropriately centered around zero and the variability is similar between the unified and regression imputation strategies. While decreasing the sample size of the GWA data set (left-hand panel) increases the variability in the parameter estimates, the impact of reducing the TWA sample size is larger (right-hand panel) with greater bias and variability for both the unified and single regression imputation approaches. Corresponding numerical summaries are provided in Table 1.

FIGURE 1. Simulation-based parameter distributions after convergence for normalized expression data.

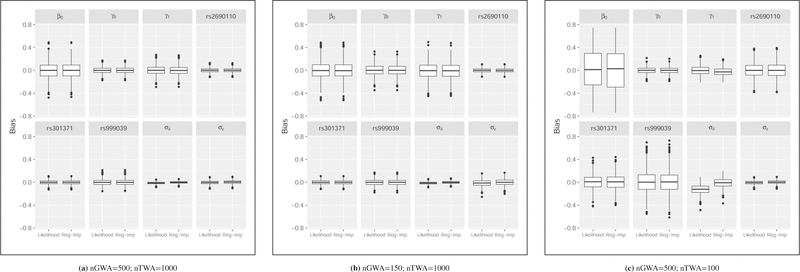
The distribution of parameter estimates minus their true values across 1000 simulations are illustrated. *A subset of the 20 SNPs analyzed are illustrated in this figure to reflect a range of effect sizes and minor allele frequencies: : rs2690110 has a minor allele frequency of 0.36 and an estimated parameter value (based on the observed data) of 0.25; rs301371 has a minor allele frequency of 0.42 and an estimated parameter value of 0.049; and rs999039 has a minor allele frequency of 0.17 and an estimated parameter value of 0.053. While decreasing the sample size of the GWA data set (left-hand and center panels) increases the variability in the parameter estimates, the impact of reducing the TWA sample size is more impactful (right-hand panel) with greater bias and variability for both the fully likelihood-based and single regression imputation approaches. Numerical summaries are provided in Table 1

TABLE 1.

Simulation-based estimates of bias and standard error under varying sample sizes for normalized expression data

		(a)§		(b)§		(c)§
Parameter	Method	bias*	se	bias*	se	bias*	se
β0	Likelihood-based	−0.0033	0.1421	0.0001	0.1493	0.0203	0.5069
	Reg-Imp	−0.0030	0.1422	0.0002	0.1493	0.0233	0.5271
β1 (rs2690110*)	Likelihood-based	0.0012	0.0374	−0.0010	0.0365	0.0020	0.1309
	Reg-Imp	0.0013	0.0376	−0.0010	0.0364	0.0013	0.1344
β2 (rs301371*)	Likelihood-based	0.0001	0.0364	−0.0004	0.0373	0.0035	0.1276
	Reg-Imp	0.0002	0.0365	−0.0004	0.0372	0.0031	0.1302
β3 (rs999039*)	Likelihood-based	−0.0000	0.0547	−0.0006	0.0545	0.0052	0.1924
	Reg-Imp	−0.0000	0.0549	−0.0007	0.0545	0.0055	0.1956
δ0	Likelihood-based	0.0006	0.0546	0.0049	0.0996	0.0016	0.0554
	Reg-Imp	0.0004	0.0546	0.0047	0.0996	−0.0002	0.0548
δ1	Likelihood-based	0.0004	0.0751	−0.0056	0.1388	−0.0012	0.0807
	Reg-Imp	−0.0021	0.0739	−0.0081	0.1364	−0.0241	0.0683
σδ	Likelihood-based	−0.0112	0.0212	−0.0122	0.0218	−0.1242	0.0818
	Reg-Imp	−0.0007	0.0212	−0.0016	0.0218	−0.0108	0.0808
σϵ	Likelihood-based	−0.0026	0.0312	−0.0122	0.0594	−0.0047	0.0315
	Reg-Imp	0.0040	0.0307	0.0011	0.0579	0.0027	0.0312

^*A subset of the 20 SNPs analyzed are included in this table to reflect a range of effect sizes and minor allele frequencies: rs2690110 has a minor allele frequency of 0.36 and an estimated parameter value (based on the observed data) of 0.25; rs301371 has a minor allele frequency of 0.42 and an estimated parameter value of 0.049; and rs999039 has a minor allele frequency of 0.17 and an estimated parameter value of 0.053.

Secondly we estimate type-1 error and power for a range of expression level effect sizes (γ/σ_ϵ). Here we generate 10,000 simulations per condition based on the sample sizes from our data example in Section 4 – nGWA=173 and nTWA=906 for the GENE and DGN data, respectively – after removing observations with missing genotypes. The observed data genotypes are used as input and again parameter values for the simulations are based on the results of our real data application (Table 5). The simulation results are illustrated in the left hand panel of Figure 2. Estimated type-1 error rates are 0.0539 and 0.0491 for the unified likelihood-based and regression imputation strategies, respectively. As expected power increases with increasing effect size and the unified approach is consistently slightly more powerful. Both approaches have approximately 80% power for a moderate effect size of 0.30.

FIGURE 2. Power of unified likelihood and regression imputation strategies for normalized expression data.

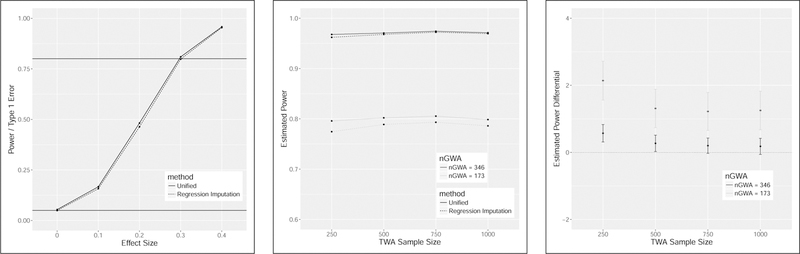
Power and type-1 error rates in the left-hand panel are estimated based 10,000 simulations per condition and a significance threshold of 0.05. The black horizontal lines have y-intercepts of 0.05 and 0.80. For the left hand panel, the observed data sample sizes of nGWA=173 and nTWA=906 are assumed and a range of effect sizes (μ/o_c ) are considered. For the center and right hand panel an expression effect size of 0.3 is assumed and the observed genotype data are used. Assumed parameter values are based on application to the CARMIL1, previously LRRC16A, gene (Table 5). A range of nTWA sample sizes are considered and the sample size of nGWA is assumed to be the observed sample size and then inflated by a factor of 2. Power remains relatively constant for nTWA sample sizes ranging from 250 to 1000. Power increases substantially with larger GWA sample size. Power of the likelihood-based approach is consistently higher than the regression imputation approach, though the difference is between 0 and 2% for the scenarios considered. This difference is statistically significant for the observed sample sizes.

We note that these simulations assume correct model specification and as the approach is likelihood-based, we expect it to be sensitive to model mis-specification. To evaluate this we first consider the case that y is incorrectly assumed to be normally distributed when in fact the errors arise from a log normal distribution. In this case, the type-1 error rates remained controlled at the nominal 0.05 level for both the unified and regression imputation approaches – for the unified approach, estimated errors based on 10,000 simulations are 0.0527, 0.0505 and 0.0494 for shift parameters (log mean) of 1, 2 and 3, respectively. On the other hand, if the expression data follow a log normal distribution and are incorrectly assumed to follow a normal distribution, then the type-1 error rate based on 10,000 simulations is estimated to reach 0.116 for a shift parameter of 3. This result is consistent with our expectation as correctly specifying the model is critical in likelihood-based strategies. We additionally note that the divergence from normality is readily apparent in these simulations by visual inspection of histograms and this level of extreme mis-specificaiton can be be avoided in practice.

Finally, we take a closer look at the the power differential between the unified and regression imputation strategies. Under the same simulation conditions just described and based on 10,000 simulations per condition, we estimated power for a range of TWA sample sizes. This is illustrated in the center panel of Figure 2 and suggests that the TWA sample size is not highly impactful. The unified strategy performs consistently slightly better with respect to power with a greater difference seen with a smaller TWA sample size. Interval estimates for the difference in proportions are illustrated in the right-hand panel of Figure 2 and in all cases the results of the simulation study provide statistically significant evidence that there is a non-zero difference in power for these methods, with an estimated difference of between 1.3 and 2.1%. We also considered inflating the GWA sample size by a factor of 2 in which case the power differential diminishes substantially, as shown by the darker lines in the center and right-hand panels of Figure 2.

3.2 |. EM approach for count data

In order to evaluate the EM approach, data are generated using parameter values for the negative binomial model given by γ₀ = 2.0, σ² = 1.0, β = (1.0, 0.4, 0.4) and ϕ = 1.2. In this case, each of two SNPs are assumed to influence gene expression based on an additive genetic model and an additive model of association. Both SNPs are generated with a minor allele frequency of 0.20. Sample sizes of 150 and 500 are considered for the GWA data (nGWA) and sample sizes of 1000 and 100 are considered for the TWA data (nTWA). 1000 simulations are conducted per condition to estimate type-1 error and evaluate convergence when γ = 0 and to estimate power under a range of effect sizes. The convergence criterion for the EM is defined as a maximum absolute difference of 1 × 10⁻⁶ in the parameters estimates between consecutive iterations of the EM.

The distributions of the resulting estimates are illustrated in Figure 3 and corresponding numerical values are given in Table 2. The samples sizes in Figure 3(a) are approximately equal to the sample sizes for the data example of Section 4. In this case, the number of iterations until convergence ranged from 16 to 479 with a median of 54 and in inter-quartile range of 42 to 71. As seen in this figure, the estimates after convergence are centered around the true parameter values in the cases in which nTWA=1000, with the exception of α, the scale parameter from the negative binomial model, which tends to be slightly over estimated. This bias is accentuated in the setting of a small TWA sample size as shown in Figure 3(c) where greater bias is also observed for α, η₁ and η₂. This result is expected as the maximum likelihood estimate of the scale parameter from a negative binomial model is known to be biased ²⁶.

FIGURE 3. Simulation-based distributions using EM-based and regression imputation strategies for expression as count data.

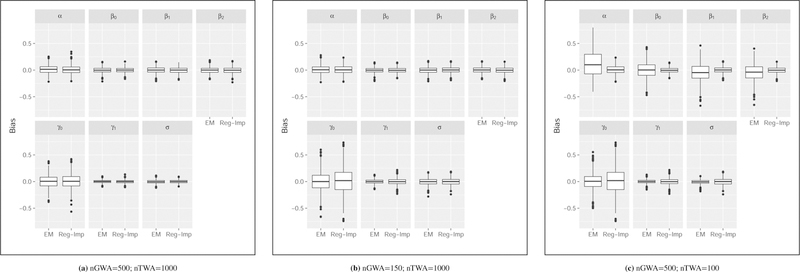
The distribution of bias for parameter estimates across 1000 simulations are illustrated. In all three scenarios, the upward bias observed for the scale parameter (α) is consistent with the known bias associated with the maximum likelihood estimator from a negative binomial model. This is accentuated with the EM approach in the small TWA sample size setting (right-hand panel). The results in the larger TWA settings (left-hand and middle panels) are generally consistent between the EM and regression imputation approaches. This is summarized numerically in Table 2.

TABLE 2.

Simulation-based estimates of bias and standard error under varying sample sizes for expression as count data

		(a)§		(b)§		(c)§
Parameter	Method	bias*	se	bias*	se	bias*	se
α	EM	0.0149	0.0786	0.0102	0.0794	0.1506	0.2944
	Reg-Imp	0.0078	0.0778	0.0087	0.0753	0.0087	0.0753
β0	EM	−0.0014	0.0489	−0.0032	0.0481	0.0007	0.1473
	Reg-Imp	0.0006	0.0484	−0.0025	0.0483	−0.0025	0.0483
Β1	EM	0.0005	0.0572	−0.0007	0.0571	−0.0503	0.1697
	Reg-Imp	−0.0027	0.0560	0.0019	0.0584	0.0019	0.0584
β2	EM	−0.0037	0.0565	0.0016	0.0565	−0.0478	0.1587
	Reg-Imp	−0.0023	0.0574	−0.0022	0.0576	−0.0022	0.0576
γ0	EM	−0.0006	0.1203	−0.0009	0.1810	−0.0005	0.1523
	Reg-Imp	0.0035	0.1329	0.0124	0.2454	0.0124	0.2454
γ1	EM	0.0005	0.0286	0.0002	0.0412	−0.0002	0.0383
	Reg-Imp	−0.0011	0.0317	−0.0024	0.0585	−0.0024	0.0585
σ	EM	−0.0045	0.0348	−0.0039	0.0636	−0.0083	0.0390
	Reg-Imp	−0.0010	0.0306	−0.0028	0.0596	−0.0028	0.0596

^§Sample sizes are as follows: (a) nGWA=500 and nTWA=1000; (b) nGWA=150 and nTWA=1000; and (c) nGWA=500 and nTWA=100.

^*Bias is defined as $(E({\widehat{\varphi }}_k)-{\varphi }_k)$ for k = 1, …, 7 where ϕ_k represents the kth parameter. Bias is estimated by replacing $E({\widehat{\varphi }}_k)$ with the mean of the corresponding parameter estimate across 1000 simulations.

Estimated type-1 error rates and power for a range of γ values and sample sizes are illustrated in Figure 4. For comparison, we again implement regression imputation similar to the strategies described in ⁸ for this setting with two notable differences: (1) a negative binomial model is assumed for the RNAseq data in place a Gaussian linear model; and (2) LD reduction is applied prior to model fitting to obviate the need for using penalized regression. These changes are made for consistency with the EM approach, and are not expected to change the relative performance of the two strategies. Based on these simulations, the EM strategy consistently performs better than regression imputation with respect to power while the estimated type 1 error rates are comparable and close to the nominal 0.05 level. A reduction in the GWA sample size (nGWA) from 500 to 100, holding the TWA sample size (nTWA) fixed at 1000, results in a substantial reduction in power; however, a change in nTWA from 1000 to 100, with nGWA fixed at 500, corresponds to only a modest reduction in power for both the EM and regression imputation approaches. In-line with the bias described above, type-1 error rate is slightly inflated at 0.084 for the EM approach in the small TWA sample size setting.

FIGURE 4. Power analysis for EM and regression imputation strategies.

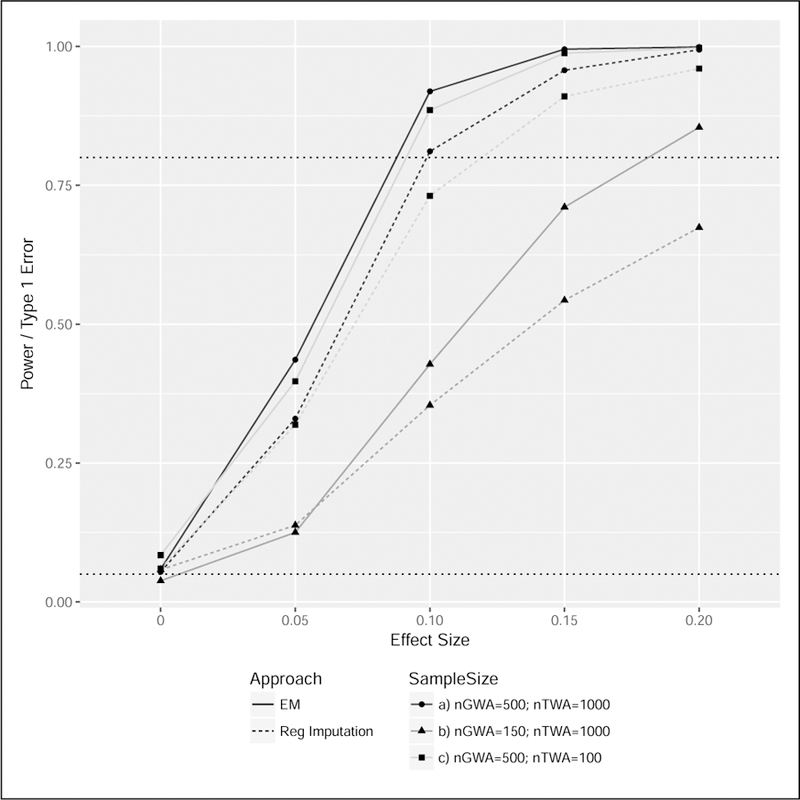
Power and type-1 error rates are estimated based 1000 simulations and a significance threshold of 0.05. The black horizontal dotted lines have y-intercepts of 0.05 and 0.80. Assumed parameter values are β = 2.0, σ² = 1.0, η = (1.0, 0.4, 0.4) and α = 1.2, where each of two SNPs are generated with a minor allele frequency of 0.20. Power of the EM approach is consistently higher than the regression imputation strategy. Similar to the unified likelihood approach described for normalized data, power increases substantially with increasing GWA sample size and is less impacted by TWA sample size.

4 |. APPLICATION TO THE GENE STUDY WITH THE DGN REFERENCE PANEL

In a recent investigation involving the GENE study data ⁴, we reported on three protein-coding genes whose genotypes associate (p < 5×10⁻⁶) with resting state or change from baseline to peak biomarker response after an endotoxin challenge, as indicated in Table 3. We now extend this analysis, interrogating these three genes further, by testing for association of gene-level expression in whole blood with biomarker response, using the DGN reference panel data. By testing for expression-trait association, we are investigating whether the corresponding gene expression is a potential mediator between the genotype and the biomarker. Due to differences in genotyping platforms between the GENE and DGN studies, only a subset of SNPs used in the original GENE study analysis are also available in the DGN data. The present analysis uses overlapping SNPs while alternative strategies for addressing inconsistencies across platforms are discussed in Section 5. LD pruning is applied based on this subset using a threshold of < 0 20¹⁹. The resulting numbers of SNPs are provided in the last three columns of Table 3.

TABLE 3.

Candidate loci interrogated in transcriptome association analysis

					# SNPs*
Gene§	Chr	Start	Stop	Biomarker○	(1)	(2)	(3)
COL5A2	1	189896640	190044605	CRP	7	2	1
PDIA5	6	122785855	122880953	CRP	38	12	6
LRRC16A	20	25279655	25620758	IL-6	341	63	20

^§Previously identified genes associated with biomarkers at the p < 5 × 10⁻⁶ level in the GENE study include: Collagen Type V Alpha 2 Chain (COL5A2), Protein Disulfide Isomerase Family A Member 5 (PDIA5) and Capping Protein Regulator And Myosin 1 Linker 1 (CARMIL1, previously LRRC16A).

^○Biomarker associations correspond to resting state (baseline) C-reactive protein (CRP) or change from baseline to peak after stimulus interleukin-6 (IL-6).

^*A subset of SNPs within each gene are used in the transciptome association analysis. Here (1) represents the number of SNPs in the original GENE study data; (2) represents the number of SNPs in both the GENE study and the DGN data; (3) represents the number of SNPs remaining after LD pruning using a threshold of 0.20.

Results of applying the EM strategy to the GENE study data (nGWA = 174), using DGN whole blood RNAseq as the reference panel (nTWA = 922), are provided in the top portion of Table 4. Here the top signal SNP is reported for each gene, corresponding to the column with heading η*, and for all three genes, a strong SNP-level association with the corresponding gene whole-blood RNAseq (p < 0.002) is observed. Whole-blood expression-level association with biomarker, on the other hand, is not statistically significant for any of the three genes under consideration. For completeness, the results of applying the alternative regression imputation approach described in Section 3 are also provided in this table. The EM algorithm is known to converge slowly and is expected to be computationally less efficient than the regression imputation approach. In this application, using a single 3.2 GHz Intel Xeon W processor, the EM approach takes 1 minute 16 seconds, 4 minutes 35 seconds, and 2 minutes and 5 seconds for the analysis of COL5A2, PDIA5 and LRRC16A, respectively.

TABLE 4.

Transcriptome-biomarker association analysis

		γ0	γ1	σ	β0	β1*	α
EM§:
COL5A2	estimate:	−0.377	−0.00914	1.118	3.126	−0.354	1.162
	std err:	0.179	0.00735	−	0.0346	0.0713	−
	test stat:	−2.113	−1.243	−	90.450	−4.970	−
	p-value:	0.0346	0.214	−	< 0.001	< 0.001	−
PDIA5	estimate:	−0.256	−0.00100	1.122	5.654	0.0904	4.003
	std err:	0.413	0.00128	−	0.0415	0.0285	−
	test stat:	−0.784	−0.619	−	136.104	3.176	−
	p-value:	0.536	0.433	−	< 0.001	0.002	−
LRRC16A	estimate:	4.362	0.00118	1.501	5.0286	−0.288	3.281
	std err:	0.346	0.00184	−	0.132	0.0370	−
	test stat:	12.609	0.656	−	38.049	−7.781	−
	p-value	< 0.001	0.523	−	< 0.001	< 0.001	−
Regression Imputation:
CoL5A2	estimate:	1.966	−0.119	1.075	3.123	−0.343	1.160
	std err:	0.638	0.0297	−	0.0346	0.0726	−
	test stat:	3.083	−4.015	−	90.917	−4.726	−
	p-value:	0.002	< 0.001	−	< 0.001	< 0.001	−
PDIA5	estimate:	0.529	−0.00348	1.120	5.651	0.0913	4.002
	std err:	0.920	0.00290	−	0.0415	0.0284	−
	test stat:	0.575	−1.203	−	158.692	2.937	−
	p-value:	0.566	0.231	−	< 0.001	0.002	−
LRRC16A	estimate:	4.166	0.00228	1.491	5.039	−0.288	3.280
	std err:	0.530	0.00292	−	0.131	0.0370	−
	test stat:	7.859	0.780	−	38.509	−7.789	−
	p-value	< 0.001	0.436	−	< 0.001	< 0.001	−

^§Coefficient estimates and standard errors are based on application of the EM strategy using a convergence criterion of < 1 × 10−6. Convergence is reached at 34 iterations for COL5A2, 71 iterations for PDIA5 and 34 iterations for LRCC16A.

^*The coefficient estimate and corresponding standard error is reported for the strongest signal SNP within each gene (rs9467471 for LRCC16A; rs836861 for PDIA5).

In this data example, the SNP-level associations with expression are generally consistent between the EM strategy and regression imputation. While inferences regarding the association between expression of PDIA5 and LRCC16A in whole blood and the biomarker are also consistent between the two approaches, regression imputation identifies a significant association (p < 0.001) between expression of COL5A2 in whole blood and baseline CRP that is not significant using the EM approach. The smaller estimated value of the negative binomial scale parameter $\left(\widehat{\alpha }=1.16\right)$ for this gene compared to corresponding parameter estimates for PDIA5 and LRCC16A ($\widehat{\alpha }=4.00$ and $\widehat{\alpha }=3.28$, respectively) suggests a greater rightward skew in the distribution of expression values. As reported in the simulation study based on $\widehat{\alpha }=1.2$, regression imputation, which is based on a mean value, performs less favorably with respect to type-1 error in this setting – 0.058 versus 0.032. In order to further investigate this result, we additionally evaluated bias for the parameter γ using regression imputation. For the purpose of comparison, we assume the same conditions as those indicated for the column labeled ‘(b)’ in Table 2, which are most similar to the real data example setting. Based on an additional 1000 simulations, the estimated bias is 0.0024 (se = 0.0585) which is ten-fold greater than what we observed for the EM setting (bias = 0.0002, se = 0.0412). Finally we apply the unified likelihood and regression imputation strategies using normalized whole blood expression of the LRRC16A gene. The resulting parameter estimates and inferences are similar between the unified and regression imputation strategies with slightly larger absolute test statistics for γ and α* in the unified approach (Table 5). This result is consistent with the slight increase in power observed in the simulation studies.

5 |. DISCUSSION

This manuscript describes a fully likelihood-based framework for transcriptome association analysis for normalized and count expression data. Similar to previously described regression imputation strategies, the likelihood-based approaches leverage both GWA data, which include genotype and trait information, and TWA data, which include genotype and cell or tissue specific expression profiles. The unified and EM approaches described in this work differ from regression imputation as they account for uncertainty in prediction of unobserved expression data, and additionally use available information on the trait to inform the missing data. Associated gains in power for expression-trait association analysis were observed in our simulation study (Section 3, Figures 4 and 2). Application of the two strategies to the GENE study and DGN data were generally consistent with the exception that regression imputation identified a significant association between COL5A2 expression and baseline CRP that was not identified using the EM – a result that may be attributable to a type-1 error. In general, the type-1 error rates are comparable between the likelihood-based and regression imputation approaches with both controlled at the 0.05 level, while more notable gains in power are observed using the likelihood-based strategies as compared to regression imputation.

In the data example provided, a normally distributed univariate trait and a single negative binomially distributed or normally distributed cell-specific gene expression was considered. The theory presented is based on a generalized linear model, and thus the framework is flexible for handling binary or repeatedly measured traits, as well as normally or Poisson distributed gene expressions. Additional extensions for survival outcomes can be achieved through inclusion of a Cox proportional hazards or fully parametric accelerated failure time model in place of Equations 1 and 2. Simultaneous consideration of multiple gene expressions, across cell or tissue types and/or across more than one gene or regulatory element, requires further extensions that account for the correlations among genes within a locus as well as expression profiles across compartments. In order to account for correlations among SNPs within a single gene, an LD pruning strategy was applied. Alternatively, a penalized regression approach, such as the elastic net, could be integrated into the likelihood-based framework; however, an alternative to cross-validation within each iteration of the EM to identify an appropriate tuning parameter may be needed to reduce the associated computational burden. For the data example, analysis was limited to SNPs present in both the GWA and TWA data resources. A common approach to address inconsistencies across platforms is SNP imputation based on the 1000 genomes or HapMap reference panels ^15,27. While existing regression imputation strategies, such as PrediXcan, simply treat these imputed SNPs as observed ⁸, the likelihood framework offers a natural structure for additionally and appropriately layering in these missing data components. The expected power gains from incorporating additional SNPs across platforms will depend on the extent to which the unobserved SNPs explain additional variability in expression. Finally, we focus in this manuscript on frequentist strategies; however, a well-established alternative strategy for missing data is a fully Bayesian MCMC approach, in which unobserved covariates, expression profiles in our setting, are treated as random variables. Our choice to use a frequentist approach stems from interest in classical hypothesis testing, although further research is needed to explore the relative advantages of a fully Bayesian approach in this setting, particularly with respect to extensibility and computational efficiency.

Abbreviations:

DGN

Depression Gene Network

EM

Expectation-Maximization

GENE

Genetics of Evoked Responses to Niacin and Endotoxemia

GWA

Genome-Wide Association

TWA

Transcriptome-Wide Association

APPENDIX A

Without loss of generality, we assume that $Y|w,x~N\left({\gamma }_0+x{\gamma }_1,{\sigma }_{ϵ}\right)$ and $X|\mathbf{z}~N\left({\mathbf{z}}^T\mathit{\beta },{\mathbf{\sigma }}_{\delta }\right)$, where w = 1, x is a scalar and z is a vector. The observed fisher information matrix is based on the following calculations.

The log likelihood function is:

$$l=\mathbf{\sum }_{i=1}^n\left[-\frac{1}{2}\log \left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)-\frac{{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathit{\beta }{\gamma }_1\right)}^2}{2\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}\right]+\mathbf{\sum }_{j=1}^m\left[-\frac{1}{2}\log {\sigma }_{\delta }^2-\frac{{\left(x_j-{\mathbf{z}}_i^T\mathit{\beta }\right)}^2}{2{\sigma }_{\delta }^2}\right]$$

The first order derivatives are:

$$\frac{\partial l}{\partial \mathbf{\beta }}=\mathbf{\sum }_{i=1}^n\frac{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathit{\beta }{\gamma }_1\right){\gamma }_1{\mathbf{z}}_i}{{\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2}+\mathbf{\sum }_{j=1}^m\frac{\left(x_j-{\mathbf{z}}_j^T\mathit{\beta }\right){\mathbf{z}}_j}{{\sigma }_{\delta }^2}$$

$$\frac{\partial l}{\partial {\gamma }_0}=\mathbf{\sum }_{i=1}^n\frac{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathit{\beta }{\gamma }_1\right)}{{\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2}$$

$$\frac{\partial l}{\partial {\gamma }_1}=\mathbf{\sum }_{i=1}^n\left[-\frac{{\sigma }_{\delta }^2{\gamma }_1}{{\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2}-\frac{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathit{\beta }{\gamma }_1\right)\left(-{\mathbf{z}}_i^T\mathit{\beta }\right)\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)-{\sigma }_{\delta }^2{\gamma }_1{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathit{\beta }{\gamma }_1\right)}^2}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}\right]$$

$$\frac{\partial l}{\partial {\sigma }_{\delta }^2}=\mathbf{\sum }_{i=1}^n\left[-\frac{1}{2}\frac{{\gamma }_1^2}{{\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2}-\frac{-2{\gamma }_1^2{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathit{\beta }{\gamma }_1\right)}^2}{4{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}\right]+\mathbf{\sum }_{j=1}^n\left[-\frac{1}{2}\frac{1}{{\sigma }_{\delta }^2}-\frac{-2{\left(x_j-{\mathbf{z}}_j^T\mathit{\beta }\right)}^2}{4{\sigma }_{\delta }^4}\right]$$

$$\frac{\partial l}{\partial {\sigma }_{ϵ}^2}=\mathbf{\sum }_{i=1}^n\left[-\frac{1}{2}\frac{1}{{\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2}-\frac{-2{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathit{\beta }{\gamma }_1\right)}^2}{4{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}\right]$$

The second order derivatives are:

$$\frac{{\partial }^{2}l}{\partial {\mathit{\beta }}^2}=\mathbf{\sum }_{i=1}^n\frac{-{\gamma }_1^2{\mathbf{z}}_i{\mathbf{z}}_i^T}{{\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2}+\mathbf{\sum }_{j=1}^m\frac{-{\mathbf{z}}_j{\mathbf{z}}_j^T}{{\sigma }_{\delta }^2}$$

$$\frac{{\partial }^{2}l}{\partial \mathit{\beta }\delta {\gamma }_0}=\mathbf{\sum }_{i=1}^n\frac{-{\gamma }_1{\mathbf{z}}_i}{{\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2}$$

$$\frac{{\partial }^{2}l}{\partial \mathit{\beta }\delta {\gamma }_1}=\mathbf{\sum }_{i=1}^n\left[\frac{\left[\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathit{\beta }{\gamma }_1\right){\mathbf{z}}_i-{\mathbf{z}}_i^T\mathit{\beta }{\gamma }_1{\mathbf{z}}_i\right]\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)-2{\sigma }_{\delta }^2{\gamma }_1^2\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathit{\beta }{\gamma }_1\right){\mathbf{z}}_i}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}\right]$$

$$\frac{{\partial }^{2}l}{\partial \mathbf{\beta }\partial {\sigma }_{\delta }^2}=\mathbf{\sum }_{i=1}^n\frac{-{\gamma }_1^3\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right){\mathbf{z}}_i}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}+\mathbf{\sum }_{j=1}^m\frac{-\left(x_j-{\mathbf{z}}_i^T\mathbf{\beta }\right){\mathbf{z}}_j}{{\sigma }_{\delta }^4}$$

$$\frac{{\partial }^{2}l}{\partial \mathbf{\beta }\partial {\sigma }_{ϵ}^2}=\mathbf{\sum }_{i=1}^n\frac{-\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right){\gamma }_1{\mathbf{z}}_i}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}$$

$$\frac{{\partial }^{2}l}{\partial {\gamma }_0^2}=\mathbf{\sum }_{i=1}^n\frac{-1}{{\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2}$$

$$\frac{{\partial }^{2}l}{\partial {\gamma }_0\partial {\gamma }_1}=\mathbf{\sum }_{i=1}^n=\frac{-{\mathbf{z}}_i^T\mathbf{\beta }\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)-2{\sigma }_{\delta }^2{\gamma }_1\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right)}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}$$

$$\frac{{\partial }^{2}l}{\partial {\gamma }_0\partial {\sigma }_{\delta }^2}=\mathbf{\sum }_{i=1}^n\frac{-{\gamma }_1^2\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right)}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}$$

$$\frac{{\partial }^{2}l}{\partial {\gamma }_0\partial {\sigma }_{\delta }^2}=\mathbf{\sum }_{i=1}^n\frac{-\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right)}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}$$

$$\begin{gathered} \frac{{\partial }^{2}l}{\partial {\gamma }_1^2}=\mathbf{\sum }_{i=1}^n-\frac{{\sigma }_{\delta }^2{\sigma }_{ϵ}^2-{\sigma }_{\delta }^4{\gamma }^2}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}-\frac{{\left({\mathbf{z}}_i^T\mathbf{\beta }\right)}^2\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)+2{\sigma }_{\delta }^2{\gamma }_1\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right)\left({\mathbf{z}}_i^T\mathbf{\beta }\right)}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2} \\ +\frac{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)\{{\sigma }_{\delta }^2{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right)}^2-2{\sigma }_{\delta }^2{\gamma }_1\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right)\left({\mathbf{z}}_i^T\mathbf{\beta }\right)\}-4{\sigma }_{\delta }^4{\gamma }_1^2\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right){\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right)}^2}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^4} \end{gathered}$$

$$\frac{{\partial }^{2}l}{\partial {\gamma }_1\partial {\sigma }_{ϵ}^2}=\mathbf{\sum }_{i=1}^n\left[\frac{{\sigma }_{\delta }^2{\gamma }_1}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}-\frac{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right)\left({\mathbf{z}}_i^T\mathbf{\beta }\right)}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}+\frac{2{\sigma }_{\delta }^2{\gamma }_1{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }\gamma \right)}^2}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^3}\right]$$

$$\frac{\partial l}{\partial {\left({\sigma }_{\delta }^2\right)}^2}=\mathbf{\sum }_{i=1}^n\left[\frac{{\gamma }_1^4}{2{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}-\frac{{\gamma }_1^2{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right)}^2}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^3}\right]+\mathbf{\sum }_{j=1}^m\left[\frac{1}{2{\sigma }_{\delta }^4}-\frac{{\left(x_j-{\mathbf{z}}_j\mathbf{\beta }\right)}^2}{{\sigma }_{\delta }^6}\right]$$

$$\frac{{\partial }^{2}l}{\partial {\sigma }_{\delta }^2\partial {\sigma }_{ϵ}^2}=\mathbf{\sum }_{i=1}^n\left[\frac{{\gamma }_1^2}{2{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}-\frac{{\gamma }_1{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right)}^2}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^3}\right]$$

$$\frac{{\partial }^{2}l}{\partial {\left({\partial }^2\right)}^2}=\mathbf{\sum }_{i=1}^n\left[\frac{1}{2{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^2}-\frac{{\left(y_i-{\gamma }_0-{\mathbf{z}}_i^T\mathbf{\beta }{\gamma }_1\right)}^2}{{\left({\sigma }_{ϵ}^2+{\sigma }_{\delta }^2{\gamma }_1^2\right)}^3}\right]$$

APPENDIX B

The elements of the score function are given by:

$${\mathbf{U}}_i\left({\gamma }_1;\mathbf{\Phi }\right)=x_i\left(y_i-{\mathbf{w}}_i^T{\mathbf{\gamma }}_0-x_i{\gamma }_1\right)/{\sigma }^2,$$

$${\mathbf{U}}_i\left({\mathbf{\gamma }}_0;\mathbf{\Phi }\right)={\mathbf{w}}_i^T\left(y_i-{\mathbf{w}}_i^T{\mathbf{\gamma }}_0-x_i{\gamma }_1\right)/{\sigma }^2,$$

$${\mathbf{U}}_i\left({\sigma }^2;\mathbf{\Phi }\right)=-\frac{n}{2{\sigma }^2}+\frac{{\left(y_i-{\mathbf{w}}_i^T{\mathbf{\gamma }}_0-x_i{\gamma }_1\right)}^T\left(y_i-{\mathbf{w}}_i^T{\mathbf{\gamma }}_0-x_i{\gamma }_1\right)}{2{\sigma }^4},$$

$${\mathbf{U}}_i\left(\mathit{\beta };\mathbf{\Phi }\right)={\mathbf{z}}_i^T\left(\frac{x_i-\exp \left({\mathbf{z}}_i^T\mathit{\beta }\right)}{1+\exp \left({\mathbf{z}}_i^T\mathit{\beta }\right)/\alpha }\right),$$

and

$${\mathbf{U}}_i\left(\alpha ;\mathbf{\Phi }\right)={\mathrm{\Psi }}_0\left(x_i+\alpha \right)-{\mathrm{\Psi }}_0\left(\alpha \right)-\frac{x_i+\alpha }{\exp \left({\mathbf{z}}_i^T\mathit{\beta }\right)+\alpha }-\log \left(\exp \left({\mathbf{z}}_i^T\mathit{\beta }\right)/\alpha +1\right)+1,$$

where ${\mathrm{\Psi }}_0\left(x\right)=d\left[\log \mathrm{\Gamma }\left(x\right)\right]/dx$ is the digamma function. Letting the expectation of the second derivative term in Equation 8 with respect to the parameters ϕ₁ and ϕ₂, be given by:

$${\mathcal{B}}_{\mathbf{\Phi },i}\left({\varphi }_1,{\varphi }_2\right)={\mathit{E}}_{\mathbf{\Phi }}\left(-{\partial }^2{l}_{\mathbf{\Phi },i}^c/\partial {\varphi }_1\partial {\varphi }_2|\mathbf{y},\mathbf{w},\mathbf{z}\right).$$

We have the following results:

$${\mathcal{B}}_{\mathbf{\Phi },i}\left({\gamma }_1,{\gamma }_1\right)=\mathbf{\sum }_{x_i\in {\chi }_i}{\widehat{\pi }}_{x,i}^{\left(t\right)}{x}_1^2/{\sigma }^2,$$

$${\mathcal{B}}_{\mathbf{\Phi },i}\left({\gamma }_1,{\mathbf{\gamma }}_0\right)={\mathcal{B}}_{\mathbf{\Phi },i}\left({\mathbf{\gamma }}_0,{\gamma }_1\right)=\mathbf{\sum }_{x_i\in {\chi }_i}{\widehat{\pi }}_{x,i}^{\left(t\right)}{x}_i{\mathbf{w}}_i/{\sigma }^2,$$

$${\mathcal{B}}_{\mathbf{\Phi },i}\left(\gamma ,{\sigma }^2\right)={\mathcal{B}}_{\mathbf{\Phi },i}\left({\sigma }^2,\gamma \right)=\mathbf{\sum }_{x_i\in {\chi }_i}{\widehat{\pi }}_{x,i}^{\left(t\right)}\frac{x_i\left(y_i-{\mathbf{w}}_i^T{\mathbf{\gamma }}_0-x_i{\gamma }_1\right)}{{\sigma }^4},$$

$${\mathcal{B}}_{\mathbf{\Phi },i}\left({\mathbf{\gamma }}_0,{\mathbf{\gamma }}_0\right)=\mathbf{\sum }_{x_i\in {\chi }_i}{\widehat{\pi }}_{x,i}^{\left(t\right)}{\mathbf{w}}_i{\mathbf{w}}_i^T/{\sigma }^2,$$

$${\mathcal{B}}_{\mathbf{\Phi },i}\left({\mathbf{\gamma }}_0,{\sigma }^2\right)={\mathcal{B}}_{\mathbf{\Phi },i}\left({\sigma }^2,{\mathbf{\gamma }}_0\right)=\mathbf{\sum }_{x_i\in {\chi }_i}{\widehat{\pi }}_{x,i}^{\left(t\right)}\frac{{\mathbf{w}}_i\left(y_i-{\mathbf{w}}_i^T{\mathbf{\gamma }}_0-{\mathbf{x}}_i{\gamma }_1\right)}{{\sigma }^4},$$

$${\mathcal{B}}_{\mathbf{\Phi },i}\left({\sigma }^2,{\sigma }^2\right)=\mathbf{\sum }_{x_i\in {\chi }_i}{\widehat{\pi }}_{x,i}^{\left(t\right)}\left[\frac{{\left(y_i-{\mathbf{w}}_i^T{\mathbf{\gamma }}_0-x_i{\gamma }_1\right)}^2}{{\sigma }^6}-\frac{1}{2{\sigma }^4}\right],$$

$${\mathcal{B}}_{\mathbf{\Phi },i}\left(\mathit{\beta },\mathit{\beta }\right)=\mathbf{\sum }_{x_i\in {\chi }_i}{\widehat{\pi }}_{x,i}^{\left(t\right)}{\mathbf{z}}_i{\mathbf{z}}_i^T\left[\frac{\alpha {\mu }_i\left(x_i+\alpha \right)}{{\left(\alpha +{\mu }_i\right)}^2}\right],$$

$${\mathcal{B}}_{\mathbf{\Phi },i}\left(\mathit{\beta },\alpha \right)={\mathcal{B}}_{\mathbf{\Phi },i}\left(\alpha ,\mathit{\beta }\right)=\mathbf{\sum }_{x_i\in {\chi }_i}{\widehat{\pi }}_{x,i}^{\left(t\right)}\hspace{0.17em}{\mathbf{z}}_i^T\left[\frac{{\mu }_i\left({\mu }_i-x_i\right)}{{\left(\alpha +{\mu }_i\right)}^2}\right],$$

$${\mathcal{B}}_{\mathbf{\Phi },i}\left(\alpha ,\alpha \right)=\mathbf{\sum }_{x_i\in {\chi }_i}{\widehat{\pi }}_{x,i}^{\left(t\right)}\left[-{\mathrm{\Psi }}_1\left(x_i+\alpha \right)+{\mathrm{\Psi }}_1\left(\alpha \right)-\frac{\left({\mu }_i^2+x_i\alpha \right)}{\alpha {\left({\mu }_i+\alpha \right)}^2}\right],$$

where x_i and µ_i = exp(z_iβ) are scalars. The remaining six second derivatives are equal to 0. The empirical observed information matrix of Equation 8 can be estimated using these results replacing each parameter with its estimate at the final iteration of the EM algorithm.

APPENDIX C

Under the Gaussian model, we have the partial derivative of the expectation of the complete data log likelihood with respect to ϕ given by:

$$\begin{gathered} \frac{\partial }{\partial \varphi }{L}_1=\hspace{0.17em}=\mathbf{\sum }_{j=1}^N{\widehat{p}}_j^{\left(t\right)}\frac{\partial }{\partial \mathbf{\varphi }}\left[\left({\tilde{y}}_j{\theta }_j-{\theta }_j^2/2\right)/\varphi -\frac{1}{2}\left({\tilde{y}}_j^2/\varphi +\log \left(2\pi \varphi \right)\right)\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\mathbf{\sum }_{j=1}^N-\frac{{\widehat{p}}_j^{\left(t\right)}({\tilde{y}}_j{\theta }_j-{\theta }_j^2/2)}{{\varphi }^2}+\frac{{\widehat{p}}_j^{\left(t\right)}{\tilde{y}}_j^2}{2{\varphi }^2}-\frac{{\widehat{p}}_j^{\left(t\right)}}{2\varphi } \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\mathbf{\sum }_{j=1}^N\left(\frac{{\widehat{p}}_j^{\left(t\right)}{({\tilde{y}}_j-{\theta }_j)}^2}{2{\varphi }^2}-\frac{{\widehat{p}}_j^{\left(t\right)}}{2\varphi }\right). \end{gathered}$$

Setting this equal to 0 yields the maximum likelihood estimate for ϕ:

$${\widehat{\varphi }}^{\left(t+1\right)}=\frac{{\mathbf{\sum }}_{j=1}^N{\widehat{p}}_j^{\left(t\right)}{\left({\tilde{y}}_j-{\theta }_j\right)}^2}{{\mathbf{\sum }}_{j=1}^N{\widehat{p}}_j^{\left(t\right)}}.$$

On the other hand, in specifying the weights option for glm() in R, the partial derivative of the log likelihood with respect to ϕ is given by:

$$\begin{gathered} \frac{\partial }{\partial \varphi }{L}_2=\hspace{0.17em}=\mathbf{\sum }_{j=1}^N\frac{\partial }{\partial \varphi }\left[{\widehat{p}}_j^{\left(t\right)}({\tilde{y}}_j{\theta }_j-{\theta }_j^2/2)/\varphi -\frac{1}{2}\left({\widehat{p}}_j^{\left(t\right)}{\tilde{y}}_j^2/\varphi +\log (2\pi \varphi /{\widehat{p}}_j^{\left(t\right)})\right)\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\mathbf{\sum }_{j=1}^N-\frac{{\widehat{p}}_j^{\left(t\right)}({\tilde{y}}_j{\theta }_j-{\theta }_j^2/2)}{{\varphi }^2}+\frac{{\widehat{p}}_j^{\left(t\right)}{\tilde{y}}_j^2}{2{\varphi }^2}-\frac{1}{2\varphi } \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\mathbf{\sum }_{j=1}^N\left(\frac{{\widehat{p}}_j^{\left(t\right)}{({\tilde{y}}_j-\theta j)}^2}{2{\varphi }^2}\right)-\frac{N}{2\varphi }. \end{gathered}$$

Setting this equal to 0 yields the weighted least squares estimator:

$${\widehat{\varphi }}_{\text{P}}^{\left(t+1\right)}=\frac{{\mathbf{\sum }}_{j=1}^N{\widehat{p}}_j^{\left(t\right)}{\left({\tilde{y}}_j-{\theta }_j\right)}^2}{N}.$$

Thus:

$${\widehat{\varphi }}_{\text{P}}^{\left(t+1\right)}\ast \frac{N}{n}={\widehat{\varphi }}^{(t+1)},$$

where $n={\Sigma }_{j=1}^N{\widehat{p}}_j^{\left(t\right)}$.

Under the negative binomial model, we have the left hand side of Equation 15 given by:

$$\begin{gathered} \mathbf{\sum }_{j=1}^N{\widehat{p}}_j^{\left(t\right)}\frac{\partial }{\partial \mathbf{\varphi }}c\left({\tilde{r}}_j,\varphi \right)=\mathbf{\sum }_{j=1}^N{\widehat{p}}_j^{\left(t\right)}\frac{\partial }{\partial \mathbf{\varphi }}\log \left(\frac{\mathrm{\Gamma }\left({\tilde{r}}_j+\varphi \right)}{\mathrm{\Gamma }\left({\tilde{r}}_j+1\right)\mathrm{\Gamma }\left(\varphi \right)}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\mathbf{\sum }_{j=1}^N{\widehat{p}}_j^{\left(t\right)}\left[{\mathrm{\Psi }}_0\left({\tilde{r}}_j+\varphi \right)-{\mathrm{\Psi }}_0\left(\varphi \right)\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\mathbf{\sum }_{j=1}^N{\widehat{p}}_j^{\left(t\right)}\mathbf{\sum }_{k=\varphi +1}^{r_j+\varphi -1}\frac{1}{k}. \end{gathered}$$

The right hand side of Equation 15 on the other hand is given by:

$$\begin{gathered} \mathbf{\sum }_{j=1}^N\frac{\partial }{\partial \mathbf{\varphi }}c({\tilde{r}}_j,\varphi /{\widehat{p}}_j^{\left(t\right)})=\mathbf{\sum }_{j=1}^N\frac{\partial }{\partial \mathbf{\varphi }}\log \left(\frac{\mathrm{\Gamma }({\tilde{r}}_j+{\varphi /\widehat{p}}_j^{\left(t\right)})}{\mathrm{\Gamma }\left({\tilde{r}}_j+1\right)\mathrm{\Gamma }({\varphi /\widehat{p}}_j^{\left(t\right)})}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}=\mathbf{\sum }_{j=1}^N\frac{{\mathrm{\Psi }}_0({\tilde{r}}_j+{\varphi /\widehat{p}}_j^{\left(t\right)})-{\mathrm{\Psi }}_0({\varphi /\widehat{p}}_j^{\left(t\right)})}{{\widehat{p}}_j^{\left(t\right)}} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}=\mathbf{\sum }_{j=1}^N\frac{1}{{\widehat{p}}_j^{\left(t\right)}}\mathbf{\sum }_{k=\varphi /{\widehat{p}}_j^{\left(t\right)}+1}^{r_j+\varphi /{\widehat{p}}_j^{\left(t\right)}-1}\frac{1}{k}. \end{gathered}$$

◻