Developing and Validating Risk Assessment Models of Clinical Outcomes in Modern Oncology

Abstract

The identification of prognostic factors and building of risk assessment prognostic models will continue to play a major role in 21st century medicine in patient management and decision making. Investigators often are interested in examining the relationship among host, tumor-related, and environmental variables in predicting clinical outcomes. We distinguish between static and dynamic prediction models. In static prediction modeling, variables collected at baseline typically are used in building models. On the other hand, dynamic predictive models leverage the longitudinal data of covariates collected during treatment or follow-up and hence provide accurate predictions of patients’ prognoses. To date, most risk assessment models in oncology have been based on static models. In this article, we cover topics related to the analysis of prognostic factors, centering on factors that are both relevant at the time of diagnosis or initial treatment and during treatment. We describe the types of risk prediction and then provide a brief description of the penalized regression methods. We then review the state-of-the art methods for dynamic prediction and compare the strengths and limitations of these methods. Although static models will continue to play an important role in oncology, developing and validating dynamic models of clinical outcomes need to take a higher priority. A framework for developing and validating dynamic tools in oncology seems to still be needed. One of the limitations in oncology that may constrain modelers is the lack of access to longitudinal biomarker data. It is highly recommended that the next generation of risk assessments consider longitudinal biomarker data and outcomes so that prediction can be continually updated.

INTRODUCTION

The identification of prognostic factors and building of risk assessment prognostic models will continue to play a major role in 21st century medicine in patient management and decision making.¹ Prognostic factors in oncology associate host and tumor variables with clinical outcomes independent of treatment.² Gospodarowicz et al³ classified factors as either tumor related, host, or environmental. Tumor-related factors are variables related to the tumor and reveal the tumor biology and pathology, such as size of tumor, lymph node involvement, presence of metastasis, and molecular markers (overexpression of PTEN gene, presence of androgen receptor variant AR-V7). Host factors are associated with patient characteristics, such as age and comorbidities. Finally, environmental factors are external to the patient, such as access to health care.³ Prognostic models are increasingly used in the design, conduct, and analysis of clinical trials. For example, in several trials of prostate cancer, randomization was stratified by the predicted survival probability determined by the prognostic model of overall survival.^4-7 In the TAILORx trial, Oncotype DX, a 21-gene score that predicts the likelihood of recurrence, is used to classify women with breast cancer by their risk group of recurrence.⁸ Prognostic factors also have been used for enriching the patient population in trials with targeted therapies. For example, in the ToGA trial, patients with human epidermal growth factor receptor 2–positive gastric cancer were randomly assigned to either trastuzumab plus chemotherapy or chemotherapy alone.⁹

In this article, we cover topics that are related to the analysis of prognostic factors, centering on factors that are relevant both at the time of diagnosis or initial treatment and during treatment or follow-up. We use the terms prognostic models, risk models, and risk assessments interchangeably. This article is organized in the following way. First, we describe the type of risk prediction and then provide a brief description of the penalized regression methods. Second, we review the state-of-the-art methods for dynamic prediction and compare the strengths and limitations of these methods. Third, we offer a concise discussion of validation and metrics for assessing models. Finally, we present recommendations for the next generation of risk assessment methods to be built in modern oncology.

CONTEXT SUMMARY

• Key Objective

• Building prognostic models will continue to play a role in 21st century medicine in patient management. We make a distinction between static and dynamic predictive models and provide a review of the state-of-the-art methods for dynamic predictive models to promote them for future use.

• Knowledge Generated

• To date, most risk assessment models in oncology have been based on static prognostic models. An understanding of the longitudinal relationship between host and tumor-related factors and their impact on clinical outcomes is critical. Regardless of whether static or dynamic modeling is the primary objective, we envision that this review will encourage investigators to take risk assessment as a discipline by itself.

• Relevance

• We expect to see an upsurge in dynamic risk assessments, and as such, it is highly recommended that the next generation of models consider the longitudinal data and outcomes so that predictions are updated.

TYPES OF RISK PREDICTIONS

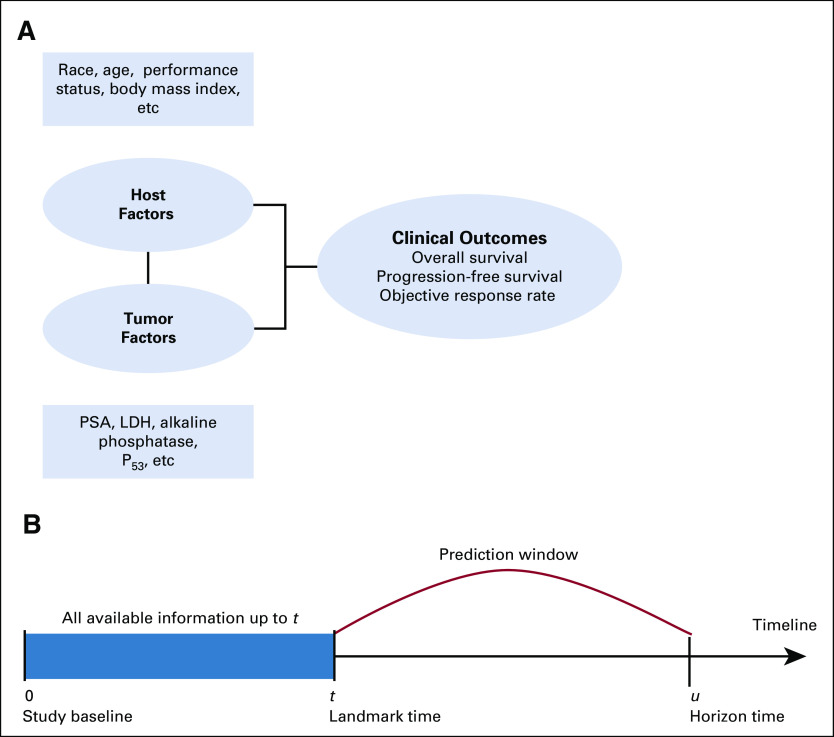
Investigators are interested in examining the relationship between host and tumor-related factors in predicting clinical outcomes (Fig 1A). We distinguish between static and dynamic prediction. In static prediction modeling, variables collected at baseline typically are used in building models. For example, prostate-specific antigen (PSA) measurements at baseline are used for prediction of recurrence. On the other hand, dynamic predictive models explicitly leverage the longitudinal data of covariates that are collected during treatment or follow-up. In patients with advanced cancer, the disease has substantially evolved and has a heterogeneous presentation within the patient.¹⁰ The inter- and intrapatient variability should be taken into account in statistical modeling.^11,12 Dynamic prediction incorporates time-dependent covariates so that risk prediction would be continually updated with new observations to reflect the patient’s prognosis.

FIG 1.

(A) Relationship between host and tumor-related factors and clinical outcomes. Modified from Halabi and Owzar.² (B) Dynamic risk prediction framework. LDH, lactate dehydrogenase; PSA, prostate-specific antigen.

We define terminology that is typically used in dynamic risk prediction. The term landmark time is defined as a current time point at which we have data (host, tumor-related variables, and outcomes). The term horizon time is defined as a future time point at which we want to predict a time-to-event outcome, such as overall survival. Dynamic predictive models essentially capture the historical information of the longitudinal measurements from the study baseline to the landmark time (t) such that the risk at horizon time (u) can be accurately predicted (Fig 1B).

IDENTIFICATION OF PROGNOSTIC FACTORS

Several popular strategies exist for identifying prognostic factors in static risk assessment. Standard variable selection approaches, such as forward selection, backward selection, and so forth, with logistic regression for binary end points,¹³ and proportional hazards regression for time-to-event end points,¹⁴ have been applied. Criticism for the stepwise variable selection has been well documented.^15,16 Of note, classification trees, such as recursive partitioning for both binary and time-to-event end points,^17-20 frequently have been used.^2,21-26

We concentrate on penalized methods that fit and shrink p predictors and in doing so, reduce the variance of the coefficient estimates.²⁷ Thus, these methods would improve the accuracy of the model.²⁸ The least absolute shrinkage and selection operator (LASSO) and adaptive LASSO (ALASSO) have been widely used to develop prognostic models of clinical outcomes.^29,30 We will briefly describe ridge regression and penalized methods. Ridge regression minimizes the residual sum of squares function, but a caveat is that it does not reduce all the coefficients exactly to 0.²⁸ Let y_i be the response, x_ij the jth covariate value (j = 1, 2, …, p) corresponding to the ith individual, β_j the regression coefficient jth covariate, and λ a tuning parameter. Similar to ridge regression, the first term in LASSO is the residual sum of squares, and LASSO minimizes this function subject to the l₁ penalty (Eq 1):

$${\displaystyle \sum }_{i=1}^n{\left(y_i-{\beta }_0-{\displaystyle \sum }_{j=1}^p{\beta }_j{x}_{ij}\right)}^2+\lambda {\displaystyle \sum }_{j=1}^p|{\beta }_j|.$$ (1)

A large tuning parameter causes the coefficient estimates to be equal to 0, thus the LASSO will have the sparsity property.²⁸ LASSO is an improvement over ridge regression, although it has the main limitation of tending to select too many unimportant variables, and it performs poorly in situations when p > n.^20,31-33 ALASSO has been proposed as an improvement over LASSO to overcome the limitation of LASSO.³⁴ ALASSO minimizes this function (Eq 2):

$${\displaystyle \sum }_{i=1}^n{\left(y_i-{\beta }_0-{\displaystyle \sum }_{j=1}^p{\beta }_j{x}_{ij}\right)}^2+\lambda {\displaystyle \sum }_{j=1}^p{w}_j|{\beta }_j|.$$ (2)

ALASSO uses a weighted penalty term in the l₁ penalty where w = (w₁, w₂, …, w_p) is the weight vector. If $\widehat{\beta }$ is a $\sqrt{n}$-consistent estimator [eg, $\widehat{\beta }$(OLS)] of β = (β₁, β₂, …, β_p), then an appropriate choice of the weight w is 1 / ǀ$\widehat{\beta }$ǀ. ALASSO is considered to be an improvement over LASSO because it has consistent variable selection as well as lower prediction error. Consequently, ALASSO tends to select fewer nonzero coefficients than the LASSO despite having a smaller prediction error. The ALASSO enjoys the oracle property.^30,34

Elastic net regression uses a combination of l₁ penalty and ridge l₂ penalty and is a compromise between LASSO and ridge regression. Furthermore, one of its main advantages when p > n is that it retains more than $n$ variables in the model.³⁵ Hastie et al²⁸ provided a thorough comparison of these shrinkage techniques.

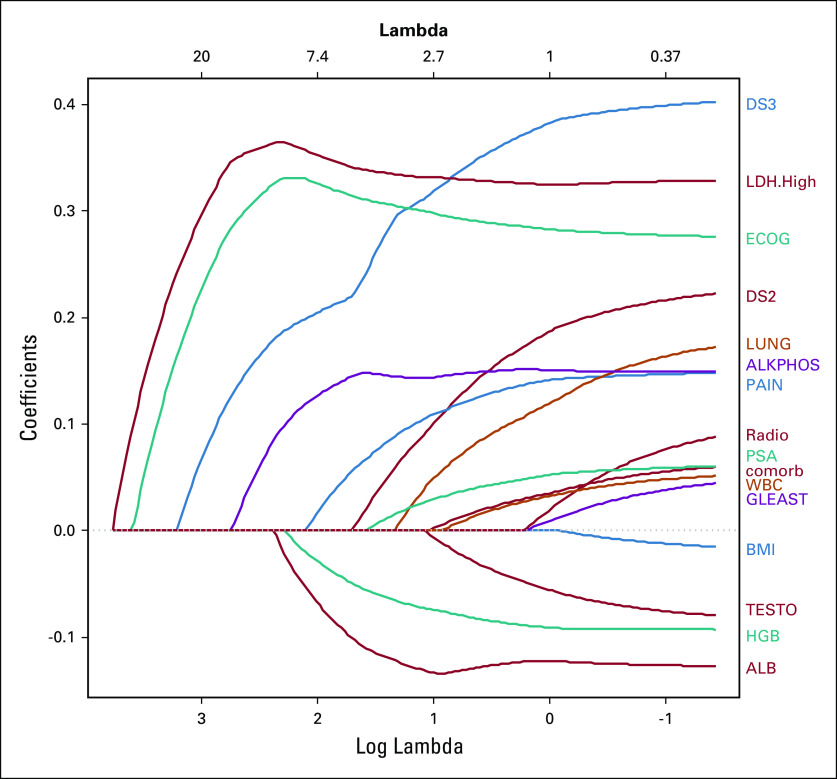
We applied LASSO and ALASSO from CALGB 90401, a phase III clinical trial in advanced prostate cancer, with the overall goal of building a model of overall survival.⁵ We had 22 variables that were common between CALGB 90401 and the Enthuse trial (external data set).³⁶ Because of missing data in the covariates, we used methods to impute them as described by White and Royston.³⁷ The regression’s estimates from the Cox proportional hazards model, LASSO, and ALASSO, are listed in Table 1. We considered LASSO and ALASSO and applied both the Akaike information criterion and the Bayesian information criterion to choose the optimal model of overall survival. LASSO and ALASSO selected eight and nine variables, respectively (Table 1). We determined the ALASSO model to be the final optimal model since it included the site of metastases for bone disease. Figure 2 shows the solution path for ALASSO, and we observe that lactate dehydrogenase (LDH) greater than the upper limit of normal and Eastern Cooperative Oncology Group (ECOG) performance status were selected early in the l₁ path compared with the other variables. This is followed by visceral disease, alkaline phosphatase, albumin, hemoglobin, pain, bone metastases, and then PSA (the Bayesian information criterion stopped at PSA). The final model selected the following prognostic factors: LDH greater than the upper limit of normal, ECOG performance status, metastatic site (presence of visceral disease, presence of bone metastases), PSA, alkaline phosphatase, albumin, hemoglobin, and analgesic opioid use.

TABLE 1.

Identified Prognostic Factors by LASSO and ALASSO in the Training Set

FIG 2.

Solution path for adaptive least absolute shrinkage and selection operator. ALB, albumin; ALKPHOS, alkaline phosphatase; BMI, body mass index; comorb, comorbidity; DS2, bone metastases; DS3, visceral metastases; ECOG, Eastern Cooperative Oncology Group performance status; GLEAST, Gleason score; HGB, hemoglobin; LDH.High, lactate dehydrogenase greater than or equal to the upper limit of normal; PAIN, opioid analgesic use; PSA, prostate-specific antigen; Radio, prior treatment with radiotherapy; TESTO, testosterone. Reproduced with permission.⁹⁶

We have focused on variable selection when the number of predictors is small relative to the sample size. There are two main challenges in identifying potential prognostic factors in high-dimensional space: computational intensity and a high false discovery rate.^38,39 Of note, several prescreening methods are useful in identifying prognostic features both in the large p, small n problem and in ultra-high-dimensional space.^31,32,39-41

The concept of variable selection is more challenging in building dynamic models because the main goal is to identify important factors that are related to the longitudinal process and the outcomes. In recent years, a few statistical studies extended the penalized method for the joint modeling of longitudinal data and survival outcomes.^42,43 The general idea is to postulate the joint likelihood linking the two submodels through latent random variables and to add shrinkage operators to select fixed and random effects. He et al⁴² proposed a variable selection method for joint modeling with a univariable longitudinal outcome, and Chen and Wang⁴³ extended the framework to incorporate multiple longitudinal outcomes. While these methods have not been implemented in oncology, the statistical development paves the way for dynamic risk prediction.

Heterogeneity of treatment effect (HTE) is another important area to consider when building prognostic models. HTE is the nonrandom, explainable variability in the direction and magnitude of treatment effects for individuals within a population.⁴⁴ There are different sources for HTE, and HTE may arise from an underlying causal mechanism, artifacts, measurements, or methods.^45,46 One main goal of HTE analyses is to predict whether a patient might benefit from a treatment. Traditionally, the Cox regression method has been used to identify subgroups of patients who may benefit from treatment.¹⁴ Recursive partitioning also has been used to identify a subgroup of patients.⁴⁷ While these classification tree methods have several advantages, they can create complicated structures and produce overfitting.^19,41,47 Other methods, such as permutation methods, SIDES (subgroup identification based on differential effect search), doubly robust augmented inverse probability–weighted estimator, and virtual twins, have been developed to take HTE into consideration.^45,48-52 The personalized prediction can be adequately addressed by the dynamic prediction framework, although it is an area for future research.

ESTIMATING PATIENT-SPECIFIC OUTCOME PREDICTION AND CONSTRUCTING RISK GROUPS

Once the final model is chosen, the next step is estimating patient-specific outcome prediction. The estimated survival function at time t is (Eq 3)

$$\widehat{S}\left(t\right)={[\widehat{S_0}\left(t\right)]}^{expR},$$ (3)

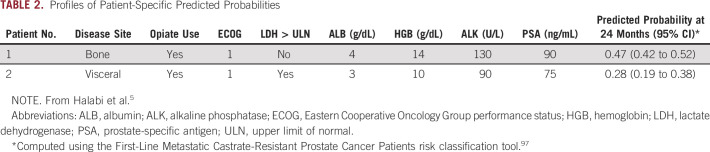
where R is the estimated linear predictor or risk score for the ith individual $(=\mathit{ }{\mathit{x}}_{\mathit{i}}{}^T\widehat{\mathit{\beta }}={\displaystyle \sum }_{j=1}^p{\widehat{\beta }}_j{x}_{ij})$, the baseline survival function is $\widehat{{\text{S}}_0}\left(t\right)=\exp \left(-{\widehat{\text{H}}}_0\left(t\right)\right)$, and the baseline cumulative hazard function is${\widehat{\text{H}}}_0\left(t\right)$. When we turned to our prognostic model of overall survival in prostate cancer, we computed a risk score from the estimated regression coefficients and the predicted survival at 24 months using the baseline cumulative hazard. We present the profiles of two patients with different baseline prognostic factors and their predicted overall survival at 24 months⁵ (Table 2). We observe that patient 2 had a worse predicted survival probability at 24 months than patient 1.

TABLE 2.

Profiles of Patient-Specific Predicted Probabilities

Another important task in static predictive modeling is to construct prognostic risk groups, which can be formed on the basis of their quantiles from the estimated linear predictor. In our overall survival model, we constructed two and three prognostic risk groups and determined the cut points from the training set on the basis of quantiles (33rd, 50th, and 67th percentiles).⁵ While demonstrating that the overall survival curves differ across the three risk groups is appropriate, this approach is not sufficient.⁵³ The optimal strategy would be to compute a measure of discriminative ability of the model.

METHODS FOR DYNAMIC MODELING

Let $T_i$ denote the true failure time and f_i(t) a set of longitudinal measurements at some time points up to landmark time t. We are interested in predicting the probability that a new patient i* is event free at least up to horizon time u > t given survival up to t. The conditional probability is defined as (Eq 4)

$${\pi }_{i^{\text{*}}}\left(u\text{|}t\right)=\mathrm{Pr}\left(T_{i^{\text{*}}}\ge u\text{|}{T}_{i^{\text{*}}}>t,{\mathrm{f}}_{i^{\text{*}}}\left(t\right),D_n\right)$$ (4)

where D_n denotes a sample from the target population and on which the prediction is based. This formulation enables a dynamic updating scheme. Indeed, if a new measurement for patient i* is observed at time t^′ > t, we can update the risk prediction by calculating π_i* (uǀt^′).

There are two general dynamic risk prediction frameworks: joint modeling and landmark analysis. Joint modeling comprises two linked submodels, one for the longitudinal process and one for the time-to-event data, and both depend on a common set of latent random variables.^54,55 In particular, the longitudinal data usually are modeled by a linear mixed-effects model. The time-to-event data are modeled by the proportional hazards model, with true longitudinal processes as time-varying covariates. The Cox regression coefficient quantifies the association between the latent longitudinal process and the hazard rate at time t. The longitudinal process and the event time process are assumed to be independent given the latent random effects, and the joint likelihood can be derived. The model can be estimated either using a frequentist approach that attains maximum likelihood through an expectation-maximization algorithm^54,56-58 or a Bayesian approach that uses Markov chain Monte Carlo to obtain posterior means.^59-61 While assuming that the parameters are readily estimated from the observed data, the conditional probability π_i* (uǀt) can be computed. A Monte Carlo estimate of π_i* (uǀt) can be obtained by sampling the random effects and the parameters from the corresponding distributions.⁶²

On the other hand, landmarking^63-66 consists of a series of related Cox regression models, where each one is defined at a distinct landmark time t.^63-66 For each pair of {u,t}, a separate model is fitted to the individuals who remain in the study and have not yet experienced the event of interest. The baseline hazard can be estimated using Breslow’s estimator.⁶⁷ Then π_i* (uǀt) is computed as the survival probability that treats the longitudinal observation at time t as a baseline covariate.

COMPARISON BETWEEN JOINT MODELING AND LANDMARKING

Joint modeling and landmarking approaches differ in three aspects: model assumptions, information used, and computational complexity. Joint modeling models the dual distribution of the longitudinal process and the failure times and hence satisfies the consistency conditions for dynamic prediction.⁶⁸ Moreover, it exploits the full information of collected data and takes into account the measurement error of the longitudinal data. This latter point is critical because it implies that joint modeling is more efficient than landmarking. However, joint modeling needs to specify a correct model for the longitudinal process and requires stronger assumptions than landmarking. Joint modeling also takes a considerable amount of effort to estimate the parameters, and the computational cost is high because it involves complicated joint distribution and numerical integration. In contrast, landmarking circumvents the aforementioned model assumptions and computational burden, but it is not a comprehensive probability model of the longitudinal process and failure times and, as such, does not satisfy the consistency conditions. Another major shortcoming is that landmarking only considers the patients at risk at the landmark time and does not fully explore the information.

Several articles have focused on the comparison of joint modeling and landmarking. Rizopoulos et al⁶⁹ compared the two prediction frameworks and proposed a compromise between joint modeling and landmarking. Suresh et al⁷⁰ contrasted joint modeling and landmarking for dynamic risk prediction in the context of a binary longitudinal marker and applied these approaches to a prostate cancer study. Ferrer et al⁷¹ compared the two approaches in the case of model misspecification, and they aimed for predicting competing risks of prostate cancer from PSA history.

Dynamic risk prediction (joint modeling) relies on model assumptions, and hence, its performance suffers from model misspecification. Functional data analysis, which is a nonparametric framework, has received considerable attention in medical studies because it is a flexible tool for modeling nonlinear longitudinal processes.^72-74 In particular, these methods have been incorporated with joint modeling⁷⁵ and are exploited to construct dynamic prediction models.^61,76-78

EXAMPLES

A few examples exist in cancer where longitudinal data were modeled with clinical outcomes. We have previously explored whether PSA decline at different landmark times is prognostic for overall survival in patients with advanced prostate cancer.⁷⁹ Fontein et al⁸⁰ developed a dynamic model for predicting overall survival in patients with breast cancer. The authors validated the overall survival model using a dynamic cross-validated C-index and reported C-indices of 0.72, 0.76, and 0.79 at 1, 2, and 3 years, respectively. Suresh et al⁷⁰ and Ferrer et al⁷¹ extended the landmarking approach and used prostate cancer studies as the testing bed. In addition, Proust-Lima and Taylor⁸¹ developed a dynamic prognostic tool that is based on joint modeling using PSA as a biomarker for prostate cancer recurrence. Other applications of dynamic models have been implemented to prostate cancer^82-85 and colorectal cancer.⁸⁶

We demonstrated the application of dynamic risk prediction using the DATATOP study,⁸⁷ a clinical trial that examined the benefits of deprenyl and α-tocopherol in slowing the progression of Parkinson disease (PD).⁸⁸ Multiple longitudinal biomarkers were collected in the DATATOP study, including Unified PD Rating Scale total score, modified Hoehn and Yahr scale, and Schwab and England activities of daily living. The biomarkers measured at baseline, 1 month, and every 3 months showed strong correlation between PD symptoms and the terminal event. We applied a joint modeling framework to account for the informative event times. We developed a Bayesian approach for parameter estimation and predicted patients’ future outcome trajectories (Fig 3A) and risk of functional disability (Fig 3B). Patient 169, who had more severe disease with earlier development of functional disability, and patient 718, who had less severe disease, were selected to illustrate the patient-specific predictions at clinically relevant future time points conditional on their available longitudinal measurements. The predicted Unified PD Rating Scale trajectories were biased, with wide uncertainty bands when only baseline measurements were used. Although dynamic prediction for longitudinal trajectories is an advantage of the joint modeling, our major interest was to predict the probability of functional disability after visits at time $t$ given the patients’ longitudinal profiles and event-free status up to time t. We found a similar pattern in that the risk predictions with higher accuracy were achieved on the basis of more longitudinal observations. For example, according to the longitudinal profiles of the first 12 months, the predicted probabilities in the next 3, 6, 9, and 12 months were 0.21, 0.46, 0.78, and 0.97, respectively, for patient 169 (Fig 3B, last plot, top row) and 0.02, 0.06, 0.13, and 0.30, respectively, for patient 718 (Fig 3B, last plot, bottom row). Therefore, patient 169, who had a higher risk of functional disability in the next few months, might need attentive medical intervention to control disease progression. Meanwhile, the Brier’s scores were 0.216 and 0.108, respectively, which implied a better prediction in terms of calibration given more follow-up data.

FIG 3.

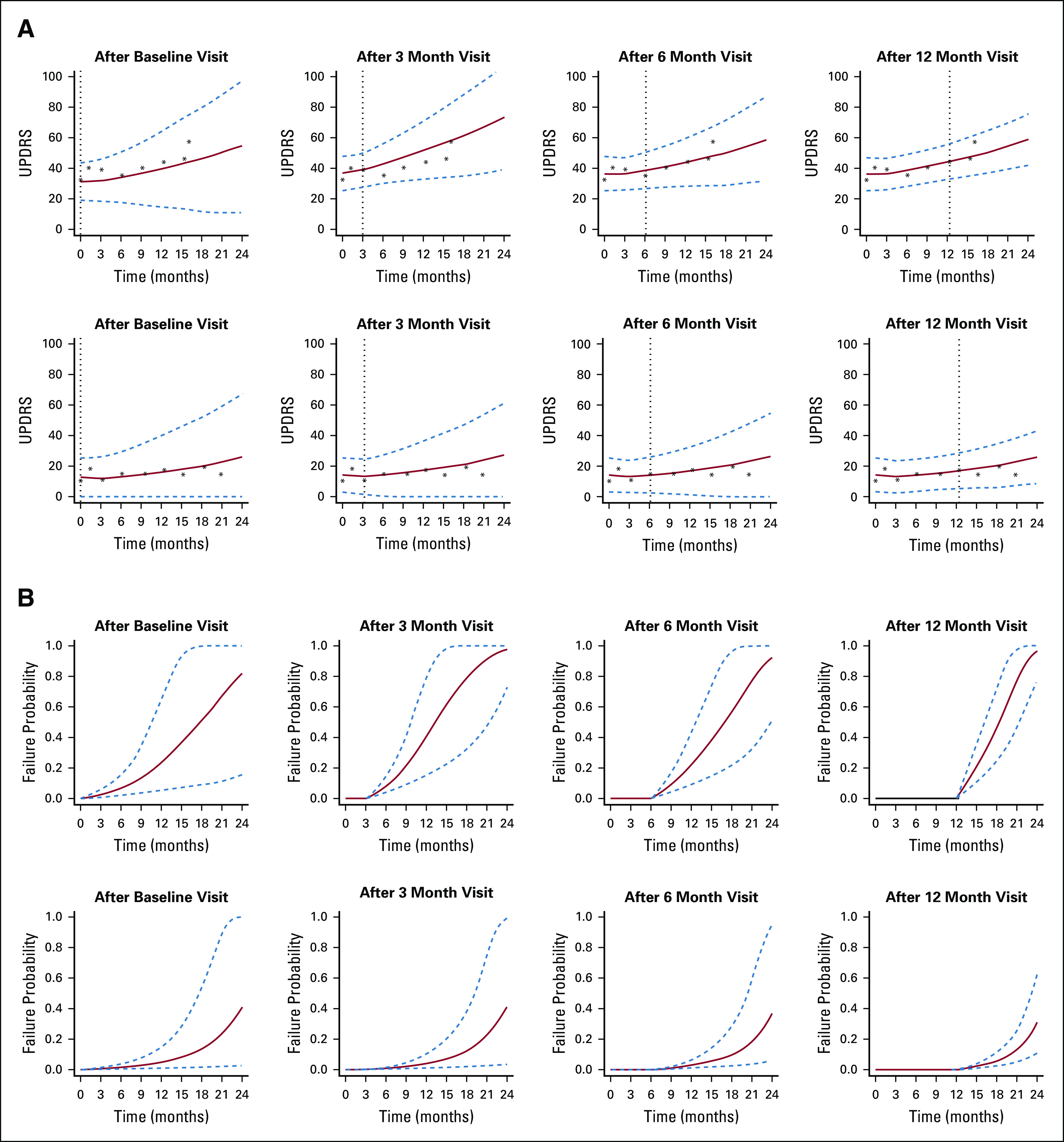
(A) Predicted Unified Parkinson Disease Rating Scale (UPDRS) trajectories and (B) predicted conditional failure probabilities for patient 169 (top rows) and patient 718 (bottom rows). Solid lines are the means of 2,000 Markov chain Monte Carlo samples. Dashed lines are the 2.5 and 97.5 percentiles of the 2,000 Markov chain Monte Carlo samples. The vertical lines represent the landmark time. Reproduced with permission.⁸⁷

VALIDATION AND ASSESSMENT OF PROGNOSTIC MODELS

The primary goal of a risk assessment is to provide accurate outcome prediction in new patients.^16,89 Overfitting remains one of the main challenges in model building. Overfitting occurs when a high predictive accuracy is estimated from a model that has been applied to the training set but has low accuracy when assessed in an independent data set.⁹⁰ A good example of overfitting is provided in Halabi and Owzar.²

The validation of a prognostic model is considered a critical step after a risk assessment model has been built. There are two types of validation: external and internal.^16,89,90 External validation, where the frozen model from the training data is applied to an independent data set, is the most rigorous approach. However, investigators often may not have access to the external data set. Of note, other types of resampling methods, such as cross-validation, bootstrapping, and bootstrapping using 0.632+, are considered appropriate approaches to model validation.^32,53,91,92

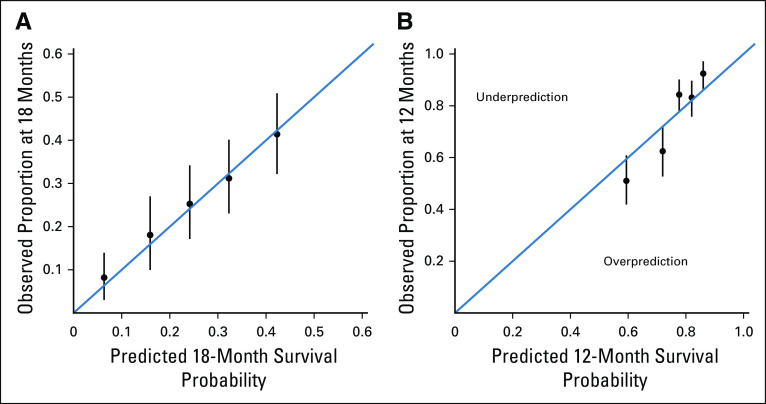
Assessment of the model’s performance usually is conducted by examining the calibration and discriminative ability of the model. Calibration signifies the extent of the match between the predicted and observed outcome.¹⁶ Often, investigators plot the predicted versus the observed outcome. The model would be calibrated if the data fall on a 45° line. Using data from two phase III clinical trials, we evaluated the overall survival model for calibration at different landmarks.^36,93 Figure 4A shows that the predicted survival probabilities at 18 months in the Enthuse 33 trial were close to the proportion of patients who survived 18 months. On the other hand, Figure 4B demonstrates that the model was not well gauged because the observed-predicted data points did not fall on the 45° line. The first two points (circles) show that the model overpredicted the proportion of patients who survived 12 months, whereas the third and fifth data points show that the model underpredicted the proportion of patients who survived 12 months.

FIG 4.

Calibration of the overall survival model for observed and predicted survival probability at (A) 18 months and (B) 12 months.

Discrimination describes the ability of a prognostic model to distinguish between patients with and without the outcome of interest.¹⁶ Several metrics are used to report the performance of a model. A widely used measure is concordance (C-index), which is the agreement between observed outcomes and prediction. Another widely used measure of predictive accuracy is the time-dependent area under the receiver operating characteristic curve (tAUROC),⁹⁴ which can be combined to form an integrated AUROC for the whole range of the study.⁹⁵ Circling back to our prognostic model in prostate cancer, we evaluated the performance of the model by implementing the integrated measure for the tAUROC by Uno et al,⁹⁵ which was 0.73 (95% CI, 0.70 to 0.73) and 0.76 (95% CI, 0.72 to 0.76) in the testing and validation sets, respectively.⁵

Dynamic models also need to be assessed for their discriminative ability and calibration. These measures can evaluate the performance of the model at various time points of the prediction. The tAUROC and Brier’s score are widely used for dynamic prediction validation.^69,70,82,87 In the DATATOP study,⁸⁷ we applied fivefold cross-validation to evaluate the predictive performance of our framework. Conditional on the longitudinal history up to month 3 and month 12, our model yielded tAUROCs of 0.744 and 0.766, respectively, for correctly assigning a higher risk of functional disability by month 15 to patients with more severe disease.

Criteria for evaluating risk assessments have been published by the Precision Medicine Core of the American Joint Commission on Cancer,⁵³ the Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis,⁹² and the Critical Appraisal and Data Extraction for Systematic Reviews of Prediction Modeling Studies.⁹¹ Investigators are encouraged to follow these guidelines as more rigorous tools of clinical outcomes would be developed in oncology. These models are anticipated to be implemented in both the design and the conduct of future trials.

Although static models will continue to play an important role in oncology, developing and validating dynamic models of clinical outcomes need to take a higher priority. A framework for developing and validating dynamic tools in oncology seems to be needed. One of the limitations is that modelers may be constrained by the lack of access to the longitudinal biomarker data; therefore, the next generation of risk assessments are highly recommended to take into consideration the longitudinal biomarker data and outcomes so that predictions are updated.

In summary, risk assessment will remain an important research task in precision oncology. We advocate for good clinical practice in risk assessment studies and recommend that investigators design these studies prospectively to obtain accurate individual outcome prediction and prognostic risk group classification. Prognostic studies should begin by asking fundamental questions that are pertinent to patient outcomes, define the primary end point a priori, justify the sample size, and describe the appropriate methods for variable selection and model assessment. Lastly, they should be validated using external data sets if available.

An understanding of the longitudinal relationship between host and tumor-related factors and their impact on clinical outcomes is critical. We expect to see an upsurge in dynamic risk assessments in oncology, and as such, the American Joint Committee on Cancer and the Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis guidelines should be extended to dynamic predictive modeling. Regardless of whether static or dynamic modeling is the primary objective, we envision that this review will bridge gaps in knowledge and motivate investigators to take risk assessment as a discipline by itself. Funding opportunities with the primary goal of building and validating high-quality prognostic models will be critical for personalized predictions.

AUTHOR CONTRIBUTIONS

Conception and design: All authors

Collection and assembly of data: All authors

Data analysis and interpretation: All authors

Manuscript writing: All authors

Final approval of manuscript: All authors

Accountable for all aspects of the work: All authors

AUTHORS' DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

The following represents disclosure information provided by authors of this manuscript. All relationships are considered compensated unless otherwise noted. Relationships are self-held unless noted. I = Immediate Family Member, Inst = My Institution. Relationships may not relate to the subject matter of this manuscript. For more information about ASCO's conflict of interest policy, please refer to www.asco.org/rwc or ascopubs.org/po/author-center.

Open Payments is a public database containing information reported by companies about payments made to US-licensed physicians (Open Payments).

Susan Halabi

Employment: ASCO TAPUR

Consulting or Advisory Role: Eisai, Ferring Pharmaceuticals, Bayer AG

No other potential conflicts of interest were reported.