Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Dec 2;19(12):8934–8940. doi: 10.1021/acs.nanolett.9b03853

Circular Dichroism Measurement of Single Metal Nanoparticles Using Photothermal Imaging

Patrick Spaeth †, Subhasis Adhikari †, Laurent Le †, Thomas Jollans †, Sergii Pud †, Wiebke Albrecht †,‡, Thomas Bauer §, Martín Caldarola §,⊥,*, L Kuipers §, Michel Orrit †,*
PMCID: PMC6909236  PMID: 31790264

Abstract

graphic file with name nl9b03853_0007.jpg

Circular dichroism (CD) spectroscopy is a powerful optical technique for the study of chiral materials and molecules. It gives access to an enantioselective signal based on the differential absorption of right and left circularly polarized light, usually obtained through polarization analysis of the light transmitted through a sample of interest. CD is routinely used to determine the secondary structure of proteins and their conformational state. However, CD signals are weak, limiting the use of this powerful technique to ensembles of many molecules. Here, we experimentally realize the concept of photothermal circular dichroism, a technique that combines the enantioselective signal from circular dichroism with the high sensitivity of photothermal microscopy, achieving a superior signal-to-noise ratio to detect chiral nano-objects. As a proof of principle, we studied the chiral response of single plasmonic nanostructures with CD in the visible range, demonstrating a signal-to-noise ratio better than 40 with only 30 ms integration time for these nanostructures. The high signal-to-noise ratio allows us to quantify the CD signal for individual nanoparticles. We show that we can distinguish relative absorption differences for right circularly and left circularly polarized light as small as gmin = 4 × 10–3 for a 30 ms integration time with our current experimental settings. The enhanced sensitivity of our technique extends CD studies to individual nano-objects and opens CD spectroscopy to numbers of molecules much lower than those in conventional experiments.

Keywords: Photothermal microscopy, chirality, circular dichroism, dissymmetry factor, linear dichroism, gold nanostructures

An object is chiral when its mirror image cannot be superimposed with the original object.1,2 The most prominent examples of chirality are found at all scales in life, from whole organisms to biomolecules such as DNA, most sugars, as well as amino acids, which often occur only in one handedness.3,4 Chirality at the molecular level arises from the relative spatial arrangement of the constituent atoms in a molecule; the two mirror-symmetric isomers of a chiral molecule are called enantiomers. Despite their identical chemical composition, enantiomers can have dramatically different biological activities, metabolism rates, and toxicities.5 Therefore, methods for detecting molecular chirality and separating enantiomers are highly relevant for drug development.

The standard optical technique to study chirality of biomolecules and biomacromolecules is circular dichroism (CD) spectroscopy,5−7 which gives access to the handedness of a molecule and also provides insight into the secondary structure and the conformational state of proteins.8,9 Circular dichroism measurements amount to detecting the differential absorption cross section of the object under study for left circularly polarized (LCP) and right circularly polarized (RCP) light

graphic file with name nl9b03853_m001.jpg 1

where σL and σR represent the absorption cross sections for LCP and RCP, respectively. The dissymmetry factor, g, defined as

graphic file with name nl9b03853_m002.jpg 2

gives a measure of the differential circular absorption cross section normalized by the average absorption cross section.

Equation 1 together with basic symmetry arguments shows that the mirror image of a chiral object presents the same absolute CD signal with the opposite sign. CD measurement as a function of light wavelength gives rise to a CD spectrum. Note that, even though the cross sections for right and left circularly polarized light may be large, the difference is generally very small for molecules, that is, typically g ≤ 10–3.5 Therefore, CD studies on molecules are carried out by measuring the signal from a large number of molecules in ensemble-averaged experiments.9 Because of the broad applicability of CD spectroscopy in biochemistry, it is highly desirable to improve its sensitivity, so as to analyze much smaller numbers of molecules, thereby reducing the amounts needed for chirality studies of newly synthesized compounds or for monitoring the conformational states of proteins.

To the chemist, chirality is a property of 3D objects which survives averaging over the random orientations of a macroscopic solution, as happens for chiral molecules. In microscopy or nanophotonics, however, we often deal with surfaces and nanostructures10,11 written on them by lithography. Although they may be chiral in 2D (i.e., such a structure does not coincide with its 2D image in a reflection with respect to a line in its plane), they are not necessarily chiral in 3D because, at least in a first approximation, they obviously present reflection symmetry in their own plane. In this case, dissymmetry in absorption of LCP and RCP light can arise from many different sources. The sample material itself can be chiral, either because of its structure or because of defects induced by the fabrication process. The 2D chiral shape of the structures, although not a source of 3D chirality by itself, can combine with front–back asymmetry to produce 3D chirality. As discussed by Arteaga et al.,12 mirror symmetry of a 2D chiral structure can be broken by the different refractive indices on either side of the interface, by inevitable surface roughness in sputtered or evaporated structures or by the illumination process itself, as incident light usually comes from only one side of the sample. Nonetheless, we use the term circular dichroism in this paper, irrespective of the origin of the observed dissymmetry.

Here, we present our experimental approach to image circular dichroism of single nanostructures, based on the differential detection of absorption by the photothermal effect rather than by the conventional extinction method, thus obtaining a photothermal circular dichroism (PT CD) image. Therefore, the plasmonic nanostructures in the present work are models of CD-active objects and are not used to enhance optical chirality signals, as proposed and realized by other groups.13,14 A similar approach, based on thermal lens spectroscopy, was used on solutions by Kitamori’s group15 and very recently has been proposed theoretically for the study of chiral nanoparticles.16 The photothermal version of circular dichroism achieves an improved sensitivity in the detection of individual chiral nanostructures, as shown below, while relaxing experimental requirements needed for polarization control on the experimental setup.

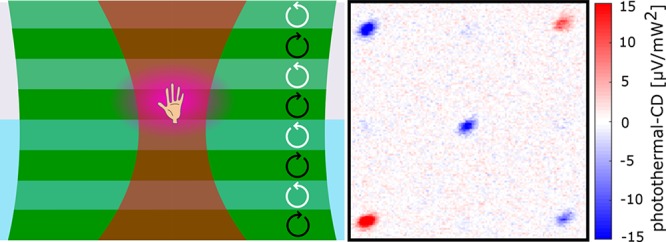
Figure 1 presents a conceptual scheme of the technique. For clarity, we show the scheme for normal photothermal microscopy on the left-hand side and for PT CD on the right-hand side. We illuminate the sample with a heating beam (represented in green/dark green in the figure) that is absorbed by the nano-object under study, for example, a (2D) chiral plasmonic nanostructure, here represented as a left hand. We periodically modulate the polarization state of this heating beam between LCP and RCP at a frequency fm (Figure 1b). As the chiral object presents different absorption cross sections for each handedness, the amount of absorbed energy differs for LCP and RCP light. The absorbed energy released as heat through nonradiative channels will thus increase the temperature of the nanostructure and create a nonuniform temperature distribution in the surrounding medium that will have slightly different amplitudes for LCP and RCP, as illustrated in Figure 1b,f. This local temperature increase creates a time- and space-dependent change in the refractive index Δn(r,t) through the thermorefractive coefficient ∂n/∂T17−19 of the surrounding medium, which is often called a thermal lens.20 (In the case of large metallic nanostructures, the temperature increase can modify the structure’s optical response, for example, by shifting its plasmon resonance; therefore, large structures themselves can significantly contribute to the photothermal signal.) A second beam, the probe (represented in red in Figure 1a,b), is used to detect the strength of the thermal lens through interference between the reflection at the substrate–medium interface and the light backscattered by the thermal lens.18 The small difference in backscattered light is detected by a lock-in amplifier at the polarization modulation frequency fm. As the only difference upon modulation is the circular polarization state, the amplified signal will be proportional to the difference between LCP and RCP absorption, which is exactly the circular dichroism signal we seek. Nonchiral particles, having no difference in circular absorption cross sections, will not give rise to any PT CD signal.

Figure 1.

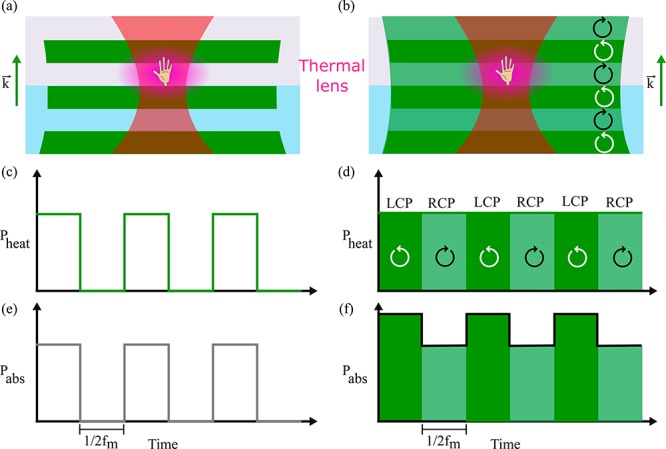
Figure 1

Open in a new tab

Photothermal and photothermal circular dichroism concept. (a) Scheme of the wide-field-heating photothermal detection of a chiral structure (illustrated as a hand) on a glass substrate. The heating beam is wide (green), and the probe beam (red) is focused to the diffraction limit. The heating beam intensity is modulated between on and off states at a frequency fm. Part of the absorbed power will be released as heat to the environment, creating a thermal lens (in purple) around the absorbing object. The wavevector direction (k) for both beams is shown. (b) Scheme for photothermal circular dichroism, where we modulate the polarization state of the heating beam between left and right circularly polarized light (dark and light green, respectively). The thermal lens is also created in this case (in purple). The wavevector direction (k) for both beams is shown on the right. (c) Time evolution of the heating power for the intensity-modulated photothermal microscopy, following the intensity modulation pattern at fm. (d) Time evolution of the heating power for the polarization-modulated photothermal microscopy. In this case, the heating power is constant and the only change is the polarization state. (e) Time evolution of the absorbed power by the nanostructure under study for the intensity-modulated photothermal case. Naturally, when the heating power is zero, the absorbed power is null. (f) Time evolution of the absorbed power by the nanostructure under study for the polarization-modulated photothermal case. As it is a chiral structure, the absorbed powers for LCP and RCP are different.

Photothermal circular dichroism builds on the well-established photothermal microscopy to detect absorbing nanoscale objects such as plasmonic nanoparticles,17,20−22 single conjugated polymer molecules,23 and even single small absorbing molecules at room temperature24 and combines it with the enantioselective signal provided by circular dichroism.

Experimental Setup

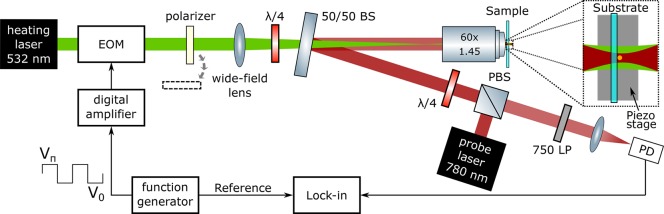
Sensing circular dichroism requires precise control of the polarization state. For that reason, great care must be taken with the illumination scheme and the choice of optical components. We implemented the concept of photothermal circular dichroism on a homemade optical microscope using a wide-field heating beam at a wavelength of 532 nm and a tightly focused probe beam at 780 nm. In this way, we still obtain diffraction-limited spatial resolution through the tightly focused probe beam, whereas the polarization of the heating beam is easily controlled thanks to its low numerical aperture (NA ∼ 0.025, corresponding to a spot diameter of 10 μm).

Figure 2 depicts a schematic representation of the microscope. The wide-field heating ensures a high-quality circular polarization state reaching the sample. This configuration is also less sensitive to possible lateral shifts in the heating beam due to mechanical drifts, thus improving stability. The heating and probe beams are combined via a nonpolarizing beamsplitter that is placed at a small angle (about 5°) with respect to the heating beam to minimize the incidence angle’s effect on the polarization state of the heating beam. We implemented a backward detection for photothermal imaging, where the backscattered probe beam is sent to a fast photodetector, and we suppressed noise efficiently with a lock-in amplifier. We used the “cat-eye reflector” configuration, consisting of a polarization beamsplitter and a quarter-wave plate to maximize the collection of photons scattered at the thermal lens.19 We want to emphasize here that, despite the wide-field illumination of the heating beam, this technique is still confocal as the probe beam is focused tightly on the sample. To obtain an image, we scan the sample with a translation stage while the overlap of the two beams remains constant.

Figure 2.

Figure 2

Open in a new tab

Photothermal circular dichroism setup. Implementation of the PT CD microscope using a 532 nm wide-field heating beam and a tightly focused probe beam at 780 nm. The polarization modulation is achieved using an electro-optical modulator (EOM), leading to an alternatingly vertical and horizontal linear polarization state (the EOM acts as a zero and half-wave plate at 45° with respect to the incoming polarization). A quarter-wave plate (λ/4) transforms these states into LCP and RCP light. The removable polarizer is added to achieve intensity modulation, i.e., conventional photothermal imaging. The wide-field lens focuses the heating beam in the back-focal plane of the objective to obtain wide-field illumination of the sample. The probe beam from a Ti:sapphire laser is combined with the heating beam using a 50/50 beamsplitter tilted by a small angle (5°). To efficiently detect the backscattered light at the probe wavelength, a “cat-eye reflector” configuration was implemented.19 The detector is a fast photodiode with variable amplification. A long-pass filter (750LP) prevents direct detection of the heating beam. The generated signal is filtered by the lock-in amplifier set to the modulation frequency fm created in the function generator and amplified to feed the EOM.

To implement photothermal circular dichroism, we need to modulate the heating beam’s polarization between RCP and LCP. To this end, we use an electro-optical modulator (EOM) to rotate the incoming linear horizontal polarization by 90° at frequencies of ∼100 kHz. We set the EOM principal axis at 45° with respect to the horizontal, and we apply a square modulation of the EOM voltage between the zero-wave plate (V0) and half-waveplate (Vπ) values. Thus, after the EOM, we have an alternating vertical (V)–horizontal (H) polarization state. Down the beam path, we use a quarter-wave plate with its axis at 45° to transform these two orthogonal linear states into LCP and RCP, respectively. Additionally, we can add a linear polarizer directly after the EOM to perform conventional, intensity-modulated photothermal imaging. More details about the experimental setup can be found in the Supporting Information.

Results and Discussion

As a model system for photothermal circular dichroism on single particles, we prepared a sample containing 2D nanostructures of either handedness, presenting circular dichroism resonances in the visible range. The sample consists of an array of 2D chiral gold nanostructures on a glass substrate in the form of gammadia, which present a strong chiral response in the visible range due to the presence of plasmonic resonances.25,26 These structures are convenient to test circular dichroism measurements because their four-fold symmetry (C4) implies that the linear dichroism ideally vanishes, provided the axis of rotational symmetry is oriented along the optical axis (as is the case presented here). Additionally, they can be easily fabricated in (2D) right- and left-handed versions. Note again that the design is based on the two-dimensional chiral character of the gammadia and that several effects can contribute to the circular dichroism signal, as discussed above.12,27 As an extra check, we also fabricated achiral structures with a similar shape.

We name our structures based on the geometrical properties: we call a gammadion “right-handed” if its arms point clockwise and “left-handed” if they point counterclockwise, when we look at them from the top, which is defined such that the structures sit on top of the glass substrate. In Figure 3, we show a scheme of the structures on the glass substrate, seen from the air side (above). This is a perspective view from the same side as used for the scanning electron microscopy (SEM) images (see Figure 4a,b), but note that in the optical measurements, we illuminate the structures from the bottom (from the glass substrate). For the wavelengths and structures used in this experiment, the left-handed enantiomer leads to a positive CD signal, as shown in Figure 1. (It is also important to note the convention used to define our polarization state. We follow the convention used by Jackson,28 where an observer facing the incoming plane wave with left circularly polarized state sees a counterclockwise rotation. This corresponds to the tip of the electric field vector tracing out a left-handed helix (positive helicity).)

Figure 3.

Figure 3

Open in a new tab

Handedness of gammadia. Definition of the L- and R-handed structures based on their geometrical shape. The structures are supported by a glass substrate. We also show the coordinate system used for clarity.

Figure 4.

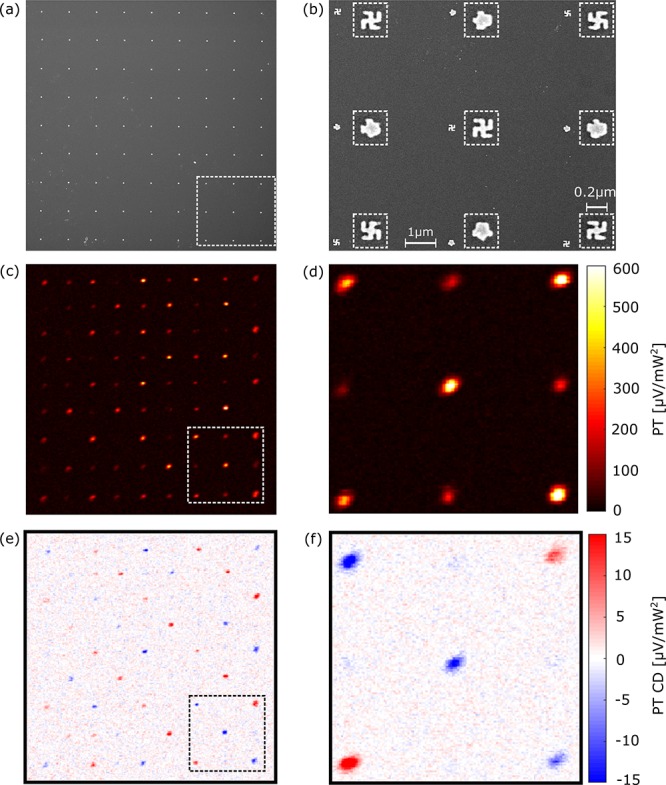
Figure 4

Open in a new tab

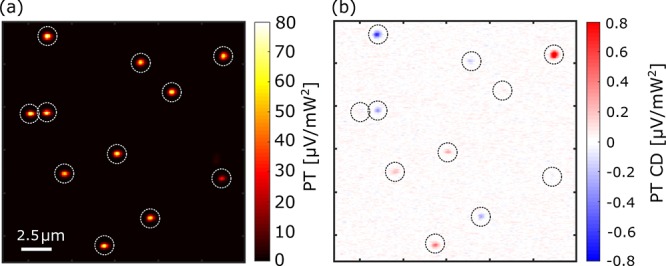
Chirality-sensitive photothermal imaging. (a) SEM image of a 9 × 9 nanogammadia array. From the 81 nanostructures, 20 are left-handed, 21 are right-handed, and 40 are achiral. The distance between the individual nanostructures is 4 μm in both directions. (b) Higher-resolution SEM image of the bottom right part of the array (the dashed rectangle in (a) shows the area for this image). Detailed images of the structures are shown in the dashed boxes, right of each structure. The scale bars are to show the average distance between two gammadia and the average size of the individual gammadia. (c) Photothermal image of the complete array, displaying the signal of each structure. We normalized the image with the heating power (Ph ∼ 9 mW) and the probe power (Pprobe ∼ 150 μW). (d) Higher-resolution photothermal image of the area shown in (b). (e,f) Photothermal circular dichroism images of the areas in (a) and (b), respectively. We also normalized the images using the heating and probe powers. These images show a clear change of sign in the signal, following the chirality of the nanostructures. As expected, the nominally achiral structures show nearly zero signal. Note that the optical and SEM images cannot be overlapped because they are observed from different sides of the interface.

We fabricated an array of alternating right-handed, achiral, and left-handed structures, as shown in the SEM images in Figure 4a,b. In the Supporting Information, we provide more details about the geometrical design of each type of structure and their locations in the array. With this array, we can measure the three types of structures in the same optical image and thus in the same experimental conditions. We embedded the structures in toluene to have a strong photothermal response (thanks to the high thermorefractive coefficient of toluene).

Figure 4c,d shows conventional photothermal images of the whole array of structures under intensity modulation of the heating beam (c) and a higher-resolution image of the bottom right part of the array (d). The signal in these images is normalized to both the heating and pump intensities, deduced from powers and beam areas (Ah ∼ 78 μm2 and Ap ∼ 0.196 μm2, respectively), to allow for comparison of images recorded under different conditions. Photothermal images taken with circularly polarized light show different intensities from different structures due to the two different absorption cross sections of the three type of structures, chiral (right- or left-handed) or achiral, at the heating wavelength of 532 nm.

Figure 4e,f depicts the photothermal circular dichroism images of the same areas as (c) and (d), where we clearly observe contrast for the right- and left-handed structures, with opposite signs, and hardly any signal from the achiral structures, demonstrating the desired enantioselectivity of the technique. We note that the signal-to-noise ratio (SNR) for the PT CD images is excellent, on the order of 40 with only 30 ms integration time in the lock-in amplifier and with moderate intensities used for imaging. For example, when we take the signal of the top left structure of Figure 4f and we average the pixels corresponding to the size of the point-spread function, we obtain a signal Sstru = −(1.53 ± 0.01) × 10–2 mV mW–2, whereas the standard deviation with the same number of pixels outside any structure gives N = (3.8 ± 0.1) × 10–4 mV mW–2, so the signal-to-noise ratio for this specific structure is Sstru/N = SNR ∼ 45. We note that the value for the noise mentioned above is similar to the value we measured when we turned off the heating laser and performed an image only with the probe laser. This is a significant improvement in sensitivity for detecting circular dichroism of individual chiral nanostructures with respect to the extinction-based detection schemes, in which a SNR ∼ 10 is typically obtained when using a 1 s integration time on the resonance of similar gold nanostructures.26

It is important to note that the imaging conditions for this sample are not optimized. First, the heating beam at 532 nm is not in resonance with the strongest CD resonance of the structure in the visible range, located at ∼700 nm according to our numerical simulations. Second, due to the non-negligible absorption at that wavelength, the probe laser intensity at 780 nm had to be kept low (Ip = 0.76 mW/μm2) to avoid boiling the surrounding liquid and reshaping of the structures at still higher powers. For the numerically calculated absorption spectra and g-factor, please refer to the Supporting Information.

The photothermal circular dichroism images in Figure 4e,f are proportional to the numerator of the dissymmetry factor g (defined in eq 2), whereas the photothermal images (c) and (d) are proportional to σL as we used an intensity-modulated heating beam with left circular polarization to take those photothermal images. Thus, we can use the signals from these images to calculate g for every structure fabricated. For this, we averaged the signal from 3 × 3 pixels centered at the maximum signal of each bright spot on Figure 4c,e. As we have correlated optical and geometrical information on our structures, we can distinguish structures with the same handedness, right-handed, left-handed, and achiral (the top right, top left, and top center structure in Figure 4b, respectively), and analyze their PT CD signals.

Figure 5a shows the results for the g factor of the 81 structures in the array correlated with their respective photothermal signals, using different colors and symbols for the three groups. We observe a clear separation of these groups according to their signals: we obtain positive values for left-handed structures (violet squares), negative values for the right-handed structures (green triangles), and values close to zero for most achiral structures (black dots). Every structure may have its particular fabrication imperfections which give rise to the observed distribution of g factors, in addition to, but without clear correlation with, the size and shape variations responsible for the dispersion in photothermal signals. The histograms for g factors are shown on Figure 5b. The mean values of these distributions correspond to gL = (3.9 ± 0.2) × 10–2, ga = (3 ± 3) × 10–3, and gR = −(3.3 ± 0.2) × 10–2 for left, right, and achiral structures, respectively. Despite the fabrication fluctuations, the obtained mean values for the distributions are as expected from the handedness of the structures. Moreover, they are in agreement within a factor of 2 with the values obtained using numerical simulations for the ideal gammadia, which give gL ∼ 0.061 at 532 nm for the left-handed structure. The Supporting Information provides the full spectra and more details on the numerical simulations. The difference between simulated and measured data may be attributed to fabrication imperfections of the structures.

Figure 5.

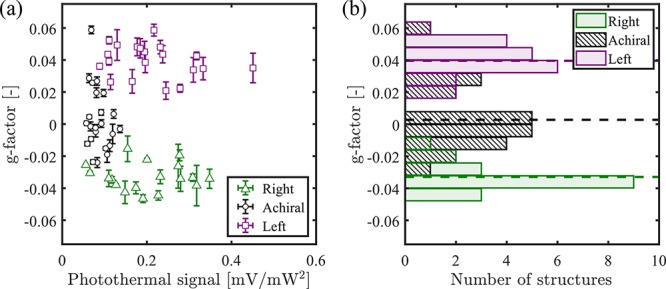
Figure 5

Open in a new tab

Chirality-sensitive signal analysis. (a) Dissymmetry factor g vs photothermal signal for the 81 nanostructures, separated by groups according to the handedness. The insets show the corresponding handedness for each group. We observe that the data for each group are clustered together and present some dispersion, presumably due to fabrication imperfections. (b) Histograms of g for the three types of structures. We can clearly see different distributions, showing our ability to distinguish chiral and nonchiral structures. The mean g factor for each group of nanostructures is shown in the figure as dashed horizontal lines. We assign the width of these distributions mainly to fabrication imperfections.

In addition to measuring circular dichroism, we can easily modify our experimental setup to measure linear dichroism (LD) in any desired frame of two orthogonal axes. It suffices to exchange the quarter-wave plate for a half-wave plate to rotate the vertical and horizontal polarization states after the electro-optical modulator to the desired axis. We call this photothermal linear dichroism (PT LD).

It is well-known that LD is usually much stronger than CD. We thus performed a set of LD measurements on the same gammadia shown in Figure 4b in two different directions: 0, 90° (modulation V–H, i.e., without any waveplate after the EOM) and 45, 135°. Although both signals should vanish for perfect gammadia, we observed nonzero LD. We attribute this LD to the imperfections in the nanofabrication. For the detailed experimental results, refer to the Supporting Information.

As a next step, we prepared a sample with nanospheres of 100 nm diameter dispersed on a glass substrate, and again we immersed this sample in toluene. Figure 6a shows a photothermal image, and Figure 6b shows the corresponding photothermal circular dichroism image. In this case, as the plasmonic resonance of the spheres is around 550 nm, the imaging conditions are close to optimal: we used a high intensity of the heating beam (heating power Ph = 16 mW) that is efficiently absorbed, and at the same time, we increased the probe intensity to Ip = 5000 kW/cm2. Because of the low absorption of the nanospheres at 780 nm, this larger probe intensity did not lead to significant heating. The calculated temperature increase at the probe power is 16 K. Therefore, we were more sensitive to chirality in these experimental conditions than in the experiments on gammadia.

Figure 6.

Figure 6

Open in a new tab

Circular dichroism of individual nanospheres. (a) Photothermal image showing several gold nanoparticles, diameter 100 nm, on glass. Note the high uniformity of the spots in shape and intensity. (b) Photothermal circular dichroism image of the area shown in (a). Although most particles show low chirality signals, two particles have high negative (top left corner) or positive (top right corner) chiral signals. The g values for them are −0.83 and 1.82%, respectively. Dashed circles are guides for the eye.

We observe that many particles show a dim signal, close to zero, as expected for achiral structures such as spheres. However, some particles show a strong signal, either positive or negative (see two examples in Figure 6b). We also performed high-angle annular dark-field scanning transmission electron microscopy imaging of gold nanospheres to obtain information about morphology and the crystalline structure of the particles. We found that some particles show defects in their crystalline structure and are nonspherical in shape (see Supporting Information for the images and more details). We therefore assign the chirality signals to the nonspherical shape and defects of nanospheres. We cannot assign the strong chirality signals to residual aggregates of nanospheres, as the photothermal signals of all particles are very uniform, indicating single nanospheres of very similar dimensions and ruling out dimers or higher aggregates. A correlation plot of photothermal signals and g factors and the histograms of photothermal signals and g factors for many single gold nanospheres are shown in the Supporting Information (Figure S8).

To further test the influence of linear dichroism in the sample on our PT CD signal, we measure both PT CD and PT LD on the sample of gold nanospheres. We observed a LD signal approximately 10 times bigger than the CD signal, with no clear correlation showing that the cross talk of LD into our signal is smaller than 10%. More details about this set of measurements can be found in the Supporting Information.

In summary, we presented an optical method, photothermal circular dichroism, that enables us to measure the chirality of absorbing nanostructures with unprecedented signal-to-noise ratio. We experimentally showed the enantioselective character of the signal by imaging right- and left-handed plasmonic structures with quantifying dissymmetry factors, g ∼ 0.04, measured with a signal-to-noise ratio of up to 40. From estimated errors in the factors measured, we believe we could measure dissymmetry factors as small as gmin = 0.004, which approaches the orders of magnitude needed to study biological molecules in small quantities.

Photothermal circular dichroism extends the capabilities of circular dichroism due to the increased sensitivity, extending the applications of the technique to smaller quantities of analytes or shorter experiment times. Our results demonstrate several advantages of photothermal circular dichroism. First, as our detection scheme relies on measuring the local temperature increase of the nanostructure under study due to the absorption of heating photons of a controlled polarization, the polarization state of the probe light scattered by the thermal lens is irrelevant. We only need to control the polarization state of the heating beam carefully. This is in contrast to the extinction26 or scattering-based29,30 detection of circular dichroism, where the polarization state of the complete beam path has to be carefully controlled. Second, as we are imaging with a photothermal-based technique, our signal can be optimized as reported earlier for photothermal signals.19 With available tunable laser sources for the heating beam, photothermal circular dichroism can also be extended to circular dichroism spectroscopy.

Acknowledgments

This work was supported by The Netherlands Organisation for Scientific Research (NWO/OCW), as part of the Frontiers of Nanoscience (NanoFront) program, and Open Technology Program (OTP, Project No. 16008). M.C. acknowledges the financial support of the Kavli Institute of Nanoscience Delft through the KIND fellowships program. T.B. and L.K. acknowledge the financial support of the European Research Council (ERC) through Project 340438-CONSTANS. W.A. acknowledges an Individual Fellowship from the Marie Sklodowska-Curie actions (MSCA) under the EU’s Horizon 2020 program (Grant 797153, SOPMEN). The authors acknowledge Dr. Benjamin P. Isaacoff for his help in the initial steps of this project. P.S. thanks Martin Baaske for helpful discussions. M.C. thanks Dr. Felipe Bernal Arango for help with the 3D image rendering.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.9b03853.

  • Details of the experimental setup, sample design and preparation, numerical simulations, measurement of linear dichroism on gammadia, characterization of nanospheres shape and size, linear dichroism influence on photothermal circular dichroism, more measurement of circular dichroism of gold nanospheres, line profiles of PT and PT CD signal of gold nanospheres, temperature increase due to absorption of the heating and probe beams (PDF)

  • Movie S1: Two intensity maps for the right-handed structure (AVI)

  • Movie S2: Time evolution of the difference ILCP(t) – IRCP(−t) (AVI)

  • Movie S3: Visualization of the tomography reconstruction for a characteristic particle as well as orthoslices through the reconstruction (MP4)

The authors declare no competing financial interest.

Supplementary Material

nl9b03853_si_001.pdf (1.2MB, pdf)
nl9b03853_si_002.avi (9.9MB, avi)
nl9b03853_si_003.avi (16.1MB, avi)
nl9b03853_si_004.mp4 (3.3MB, mp4)

References

  1. Kelvin W. T. B.Baltimore Lectures on Molecular Dynamics and the Wave Theory of Light; CJ Clay and Sons, 1904. [Google Scholar]
  2. Schäferling M.Chiral Nanophotonics; Springer, 2017; p 159. [Google Scholar]
  3. Alberts B.; Johnson A.; Lewis J.; Raff M.; Roberts K.; Walter P.. Molecular Biology of the Cell, 6th ed.; Garland Science: New York, 2010. [Google Scholar]
  4. Siegel J. S. Biochemistry: Single-handed cooperation. Nature 2001, 409, 777. 10.1038/35057421. [DOI] [PubMed] [Google Scholar]
  5. Fasman G. D.Circular Dichroism and the Conformational Analysis of Biomolecules; Springer Science & Business Media, 2013. [Google Scholar]
  6. Beychok S. Circular dichroism of biological macromolecules. Science 1966, 154, 1288–1299. 10.1126/science.154.3754.1288. [DOI] [PubMed] [Google Scholar]
  7. Berova N.; Nakanishi K.; Woody R. W.. Circular Dichroism: Principles and Applications; John Wiley & Sons, 2000. [Google Scholar]
  8. Johnson W. C. Jr Secondary structure of proteins through circular dichroism spectroscopy. Annu. Rev. Biophys. Biophys. Chem. 1988, 17, 145–166. 10.1146/annurev.bb.17.060188.001045. [DOI] [PubMed] [Google Scholar]
  9. Greenfield N. J. Using circular dichroism spectra to estimate protein secondary structure. Nat. Protoc. 2006, 1, 2876. 10.1038/nprot.2006.202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Schnoering G.; Poulikakos L. V.; Rosales-Cabara Y.; Canaguier-Durand A.; Norris D. J.; Genet C. Three-Dimensional Enantiomeric Recognition of Optically Trapped Single Chiral Nanoparticles. Phys. Rev. Lett. 2018, 121, 023902. 10.1103/PhysRevLett.121.023902. [DOI] [PubMed] [Google Scholar]
  11. Narushima T.; Okamoto H. Circular dichroism nano-imaging of two-dimensional chiral metal nanostructures. Phys. Chem. Chem. Phys. 2013, 15, 13805–13809. 10.1039/c3cp50854d. [DOI] [PubMed] [Google Scholar]
  12. Arteaga O.; Sancho-Parramon J.; Nichols S.; Maoz B. M.; Canillas A.; Bosch S.; Markovich G.; Kahr B. Relation between 2D/3D chirality and the appearance of chiroptical effects in real nanostructures. Opt. Express 2016, 24, 2242–2252. 10.1364/OE.24.002242. [DOI] [PubMed] [Google Scholar]
  13. García-Etxarri A.; Dionne J. A. Surface-enhanced circular dichroism spectroscopy mediated by nonchiral nanoantennas. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 235409. 10.1103/PhysRevB.87.235409. [DOI] [Google Scholar]
  14. Kramer C.; Schäferling M.; Weiss T.; Giessen H.; Brixner T. Analytic optimization of near-field optical chirality enhancement. ACS Photonics 2017, 4, 396–406. 10.1021/acsphotonics.6b00887. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Yamauchi M.; Mawatari K.; Hibara A.; Tokeshi M.; Kitamori T. Circular dichroism thermal lens microscope for sensitive chiral analysis on microchip. Anal. Chem. 2006, 78, 2646–2650. 10.1021/ac0519920. [DOI] [PubMed] [Google Scholar]
  16. Kong X.-T.; Khosravi Khorashad L.; Wang Z.; Govorov A. O. Photothermal Circular Dichroism Induced by Plasmon Resonances in Chiral Metamaterial Absorbers and Bolometers. Nano Lett. 2018, 2001–2008. 10.1021/acs.nanolett.7b05446. [DOI] [PubMed] [Google Scholar]
  17. Boyer D.; Tamarat P.; Maali A.; Lounis B.; Orrit M. Photothermal imaging of nanometer-sized metal particles among scatterers. Science 2002, 297, 1160–1163. 10.1126/science.1073765. [DOI] [PubMed] [Google Scholar]
  18. Berciaud S.; Lasne D.; Blab G. A.; Cognet L.; Lounis B. Photothermal heterodyne imaging of individual metallic nanoparticles: Theory versus experiment. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 045424. 10.1103/PhysRevB.73.045424. [DOI] [Google Scholar]
  19. Gaiduk A.; Ruijgrok P. V.; Yorulmaz M.; Orrit M. Detection limits in photothermal microscopy. Chemical Science 2010, 1, 343. 10.1039/c0sc00210k. [DOI] [PubMed] [Google Scholar]
  20. Selmke M.; Braun M.; Cichos F. Photothermal single-particle microscopy: detection of a nanolens. ACS Nano 2012, 6, 2741–2749. 10.1021/nn300181h. [DOI] [PubMed] [Google Scholar]
  21. Yorulmaz M.; Khatua S.; Zijlstra P.; Gaiduk A.; Orrit M. Luminescence quantum yield of single gold nanorods. Nano Lett. 2012, 12, 4385–4391. 10.1021/nl302196a. [DOI] [PubMed] [Google Scholar]
  22. Yorulmaz M.; Nizzero S.; Hoggard A.; Wang L.-Y.; Cai Y.-Y.; Su M.-N.; Chang W.-S.; Link S. Single-Particle Absorption Spectroscopy by Photothermal Contrast. Nano Lett. 2015, 15, 3041–3047. 10.1021/nl504992h. [DOI] [PubMed] [Google Scholar]
  23. Hou L.; Adhikari S.; Tian Y.; Scheblykin I. G.; Orrit M. Absorption and quantum yield of single conjugated polymer poly [2-methoxy-5-(2-ethylhexyloxy)-1, 4-phenylenevinylene](MEH-PPV) molecules. Nano Lett. 2017, 17, 1575–1581. 10.1021/acs.nanolett.6b04726. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Gaiduk A.; Yorulmaz M.; Ruijgrok P. V.; Orrit M. Room-Temperature Detection of a Single Molecule’s Absorption by Photothermal Contrast. Science 2010, 330, 353–356. 10.1126/science.1195475. [DOI] [PubMed] [Google Scholar]
  25. Kuwata-Gonokami M.; Saito N.; Ino Y.; Kauranen M.; Jefimovs K.; Vallius T.; Turunen J.; Svirko Y. Giant optical activity in quasi-two-dimensional planar nanostructures. Phys. Rev. Lett. 2005, 95, 227401. 10.1103/PhysRevLett.95.227401. [DOI] [PubMed] [Google Scholar]
  26. Vinegrad E.; Vestler D.; Ben-Moshe A.; Barnea A. R.; Markovich G.; Cheshnovsky O. Circular Dichroism of Single Particles. ACS Photonics 2018, 5, 2151–2159. 10.1021/acsphotonics.8b00016. [DOI] [Google Scholar]
  27. Nechayev S.; Barczyk R.; Mick U.; Banzer P. Substrate-Induced Chirality in an Individual Nanostructure. ACS Photonics 2019, 6, 1876–1881. 10.1021/acsphotonics.9b00748. [DOI] [Google Scholar]
  28. Jackson J. D.Classical Electrodynamics, 3rd ed.; John Wiley & Sons: New York, 1998. [Google Scholar]
  29. Karst J.; Cho N. H.; Kim H.; Lee H.-E.; Nam K. T.; Giessen H.; Hentschel M. Chiral Scatterometry on Chemically Synthesized Single Plasmonic Nanoparticles. ACS Nano 2019, 13, 8659–8668. 10.1021/acsnano.9b04046. [DOI] [PubMed] [Google Scholar]
  30. Wang L.-Y.; Smith K. W.; Dominguez-Medina S.; Moody N.; Olson J. M.; Zhang H.; Chang W.-S.; Kotov N.; Link S. Circular Differential Scattering of Single Chiral Self-Assembled Gold Nanorod Dimers. ACS Photonics 2015, 2, 1602–1610. 10.1021/acsphotonics.5b00395. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl9b03853_si_001.pdf (1.2MB, pdf)
nl9b03853_si_002.avi (9.9MB, avi)
nl9b03853_si_003.avi (16.1MB, avi)
nl9b03853_si_004.mp4 (3.3MB, mp4)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES