An Agent-Based Metapopulation Model Simulating Virus-Based Biocontrol of Heterodera Glycines

Abstract

With recently discovered soybean cyst nematode (SCN) viruses, biological control of the nematodes is a theoretical possibility. This study explores the question of what kinds of viruses would make useful biocontrol agents, taking into account evolutionary and population dynamics. An agent-based model, Soybean Cyst Nematode Simulation (SCNSim), was developed to simulate within-host virulence evolution in a virus-nematode-soybean ecosystem. SCNSim was used to predict nematode suppression under a range of viral mutation rates, initial virulences, and release strategies. The simulation model suggested that virus-based biocontrol worked best when the nematodes were inundated with the viruses. Under lower infection prevalence, the viral burden thinned out rapidly due to the limited mobility and high reproductive rate of the SCN. In accordance with the generally accepted trade-off theory, SCNSim predicted the optimal initial virulence for the maximum nematode suppression. Higher initial virulence resulted in shorter lifetime transmission, whereas viruses with lower initial virulence values evolved toward avirulence. SCNSim also indicated that a greater viral mutation rate reinforced the virulence pathotype, suggesting the presence of a virulence threshold necessary to achieve biocontrol against SCN.

Heterodera glycines, the soybean cyst nematode (SCN), is the most economically damaging pest of soybean (Glycine max) crops in the United States, causing yield losses estimated between $0.7 to $2 billion each year (Schmitt et al., 2004; Koenning and Wrather, 2010). Managing SCN involves an integrated pest management approach consisting of crop rotation, using resistant cultivars, and nematicide seed treatments (Kurle et al., 2011). One notable seed treatment commercially available under the brand name Clariva®, uses the SCN pathogen Pastueria nishizawae as a biocontrol agent. Long-term studies reveal SCNs are becoming resistant to the more widely used lineages of resistant cultivars, most notably PI88788 (Niblack et al., 2008). Hence, there is a need to develop alternative nematode control strategies to mitigate soybean losses.

The discovery of five RNA viral pathogens of the SCN (Bekal et al., 2011, 2014) creates the possibility of using such viruses as biocontrol agents. However, their transmission modes, virulence, and nematode pathogenicity are currently not well understood. Hypothetically, however, these viruses could become a useful tool in the management of SCN infestations in the field. The decade-long viability of SCN eggs in the soil (Schmitt et al., 2004) implies that developing and testing virus-based SCN biocontrol technologies will require at least a decade. Over this period, it is reasonable to expect that the virus and the nematode could both evolve in potentially unpredictable ways. Numerical simulations to model interactions between the virus, its SCN host, and the soybean plant would serve to provide insight into the long-term interactions within this ecosystem. This study documents the development of Soybean Cyst Nematode Simulation Framework (SCNSim), an agent-based simulation engine designed to explore the biocontrol outcomes of a range of hypothetical viruses interacting with the SCN.

The simulation recapitulates essential features of the SCN life-cycle as well as the potential pathogenicity due to a hypothetical virus. SCNSim uses published data on the SCN life cycle and takes into account an environmental (i.e., temperature) model as well as soybean planting and growth timelines (Schmitt et al., 2004; Niblack et al., 2006). The resulting simulation generates dynamical behavior that can be interpreted from the perspective of host–pathogen coevolution.

Modeling host–pathogen coevolution: theoretical and experimental investigations of biocontrol are generally motivated by the desire to contain infectious disease (Rock et al., 2014). In contrast, in this study, the desirable outcome is a viral pandemic in the nematodes and the resulting protection of the soybean plant. Such models capturing interspecies interactions at multiple trophic levels need to be complex enough to capture the adaptive arms race between the nematode host and the viral pathogen.

Similar to many microbial biocontrol agents, the basic system of equations modeling an epidemic-the Susceptible-Infected-Recovered (SIR) type models-must be sufficiently rich to provide insight into host-pathogen interaction (Brauer, 2008; Rock et al., 2014). Here S, I, and R represent compartmentalized portions of the total population and stand for susceptible, infected, and recovered host individuals, respectively. The dynamic system of equations is parameterized with terms for the rate of transmission b and the rate of recovery r of an infected individual. This type of SIR model has been used in modeling the impact of vaccination and reinfection behaviors within host populations (Rock et al., 2014).

Pathogens, including viruses, acquire an adaptive tradeoff between fecundity and host resistance, commonly known as the trade-off theory. Exploitation of the host improves the pathogens transmissibility, but at the cost of the survival of the host and therefore reduce the duration of transmission. This adaptive tradeoff phenomenon is driven by the costs of resistance (energetic or otherwise) and risk of pathogenic infection (Galvani, 2003; Demas et al., 2012; Raberg˚ and Stjernman, 2012). The virulence–transmissibility tradeoff has been demonstrated empirically in malaria models where transmission and virulence are positively correlated until the benefit of increased transmission no longer outweighs the concomitant increase in host mortality (Mackinnon and Read, 2004b; Alizon et al., 2009; Raberg˚ and Stjernman, 2012). Another example is the canonical study of the myxoma virus in invasive European rabbit (Oryctolagus cuniculus) populations in Australia (Fenner and Ratcliffe, 1965). Within 2 years, the myxoma virus fatality cases caused by the most prevalent strains dropped from 90% to 99% to between 70% and 95% over 30 years. (Fenner and Ratcliffe, 1965; Kerr et al., 2012).

Following the SIR paradigm, a definition of fitness emerged called the basic reproductive ratio of the pathogen, $R_0=\left(\left(bS\right)/\left(b+v+r\right)\right)$ where b is the transmission rate, S is the number of susceptible hosts, b is the baseline mortality rate of the host, r is the recovery rate at which the infected hosts are free of the pathogen, and V is the mortality rate of infected hosts (Anderson and May, 1982; Raberg˚ and Stjernman, 2012). R₀ is the rate of new infections emerging with respect to the rate of depletion of the existing infections through death or recovery of the host, or through the loss of a viable pathotype. The term R₀ provides a quantification of the fitness of the pathogen at the epidemic level to determine if the epidemic will go extinct (R₀ < 1) or will persist (R₀ > 1).

From a game-theoretic perspective, pathogens will evolve to maximize R₀, i.e., to maximize their disease spread and duration of infection (Alizon et al., 2009). The SIR model assumes that pathogen adaptive dynamics occur in much shorter time scales than their evolutionary dynamics, and host population densities are at or near maximum capacity. The SIR model is not sufficient to capture host–pathogen dynamics in cases where the pathogens have a relatively high mutation rate (Berngruber et al., 2013). The biggest drawback of the traditional SIR approach is that it assumes that the system evolves along a smooth continuum, which implies that traditional SIR models are only useful over a large sample space. However, the virus-SCN-soybean ecosystem is marked with a number of limitations for SIR, such as a narrow soybean planting season, a number of different SCN life stages and a relatively small, finite number of SCN interacting with the soybean plant. Therefore, the results of the SIR models are not easily interpreted in this system.

On the other hand, agent-based models are a class of numerical models that represent hosts and pathogens as individual agents, capable of movement and interaction with each other and their host environment. Typically, agents in the agent-based model can be modeled as complex units with discontinuous behavior. While such models are more complex to build and require greater computational resources, they are finding increasing value in the modeling of infectious disease dynamics (Siettos and Russo, 2013).

The objective of this study was to use an agent-based model to investigate combinations of viral transmission and virulence in order to identify viral properties that resulted in the highest suppression of nematode populations, and whether these characteristics and their dynamical evolution over time would follow behaviors posited by existing ecological theories. In particular, it is hypothesized that the epizootic behavior of these SCN viruses would follow the adaptive virulence trade-off hypothesis which suggests that virulence is an unavoidable consequence of transmissibility. A successful viral biocontrol agent would evolve toward an intermediate or optimum virulence that balances the epizootic and trade-off characteristics of the virus (Alizon et al., 2009).

Materials and methods

Construction of SCNSim: the SCNSim framework employed an object-oriented, discrete time simulation to model the evolution of nematodes and their viral pathogens as they interact with each other within a single soybean plant. The Nematode class was a state-based abstraction for the SCNs. Instances of the Nematode class (i.e., Nematode agents) recapitulated the SCN life cycle as they hatched, grew, mated and reproduced. Their survival and successful transition was predicated upon a Health parameter that was increased as they fed upon the plant and decreased as they progressed through their life cycle. Viral infections in the nematodes were instance properties parameterized by their intensity or viral load (L), transmissibility (b), durability (D), and virulence (v) as described in greater detail below. The Environment class implemented stochastic temperature variation which can be set to either ideal greenhouse conditions (practically constant temperatures), or to mimic regional data. In this study, Champaign County, IL average monthly temperatures were used (Illinois State Climatologist’s Office, 2014). The Soybean class modeled the soybean plant that grows within the typical soybean growing season (early April to late August). The Soybean model was characterized by Age, Health, and Size, the latter two of which were negatively impacted by SCN parasitism and positively affected by optimal temperatures (27° C). While SCNSim can model yearly planting or planting at alternate years to simulate crop rotations, this study assumed yearly planting.

An outbreak of RNA virus on SCN was characterized by combinations of several scale-free virulence properties as described in Table 1. These properties coevolved with the SCN population. Each property was randomly varied at model initiation to create a population of viruses described by a normal distribution of the properties. Viruses were transmitted according to dynamic transmission rates (b) which were probabilities that governed the disease transmission. This stochastic event was applied to both vertical transmission from females to eggs, and horizontal transmission from males to females during mating.

Table 1.

Numerical properties of the viruses in the Soybean Cyst Nematode Simulation Framework SCNSim.

			Definition
Property	Symbol	Range	in vivo	in silico
Viral Load	L	0 1	Amount of viral particles per host	Scalar multiplier to nematode health decrement
Virulence	V0, v	R > 0	Pathogen damage inflicted on host	Multiplier to Viral Load
Transmissibility	b0, b	0 1	Rate of infection of suscep-tible population	Proportion of viral load sexu-ally transmitted from infected male to a recipient female or from female to egg
Prevalence	i0, i	0 1	Disease prevalence in a population	Fraction of initial population infected
Durability	D	0 1	Longevity of virus parti-cles.	The complement is an ampli-fying constant on increasing viral load.
Mutation Rate	M	0 1	Proportion of progeny gen-eration with significant ge-netic variation	Probability of virus proper-ties undergoing mutation

SCNSim simulated the random nature of viral evolution as well as direct the population kinetics of the infected SCN. During the simulation, the diversity of viruses increased according to a mutation rate (m). The initial conditions of the simulation were modeled using initial prevalence (i₀) and the outbreak parameters described in Table 1. The viruses decreased nematode health at a rate strongly correlated with the viruses’ virulence parameter (v) and viral load (L). The longevity of the viral infection was described by a durability factor (D). In SCNSim, D increased viral load. The model assumed that the combined effects from the dynamic virus properties and environmental conditions would control the rate of growth the nematode population.

The Nematode Agent: within the SCNSim framework, the Nematode agents recapitulated the different stages in the SCN life cycle (Fig. 1). SCNSim considered the initial SCN population densities per soybean plant, with each cyst capable of producing a uniformly distributed number of eggs between 300 and 500. The model assumed that each transition between the nematode stages was determined by the environment and the health of the Nematode agent. The major environmental constraints that dictated the periods of nematode growth are detailed in Table 2.

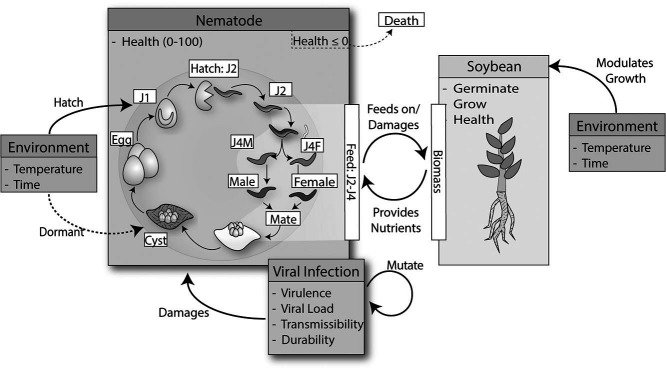
Figure 1:

The Soybean Cyst Nematode Simulation (SCNSim) framework. Environment, Nematode, Viral Infection and Soybean boxes represent classes in an object-oriented framework, with their respective properties listed within the boxes, and interactions between each other shown by solid arrows. The Nematode class is a simplified model of the life cycle of the nematode Heterodera glycines. SCNSim stochastically simulates a population of nematode agents governed by a dynamic environment, health of the host soybean crops, and the nature of the viral infec- tion. Nematode transition between life stages. Stages J2-J4 feed on the soybean plant diminishing the plant health. The environment modulates the growth of the soybean plant as well as the hatching and transition to the cyst stage in the nematode. The viral parameters are a property of the nematode objects that reduce their health. Viruses transmit horizontally and vertically. Nematodes are removed from simulation when their Health parameter drops below zero.

Table 2.

Environmental set points and nematode stages modeled in the Soybean Cyst Nematode Simulation Framework (SCNSim) based on figures in Schmitt et al. (2004).

Model compartment	Parameter description	Value
SCN life cycle laws	SCN eggs per cyst	300-500a
	Minimum hatching temperature	16° C
	Maximum hatching temperature	36° C
	Cyst dormancy initialize temperature	< 20° C
	Probability of hatching from egg sac	0.2b
	Probability of hatching from cyst	0.002b
SCN life stages	Egg state	1-5 d
	J1 state	1-2 d
	Unhatched J2	1-3000 d
	Hatched J2	1-4 d
	J3	3-4 d
	J4 male	5-6 d
	J4 female	3-4 d
	Adult male	1-21 d
	Adult female	2-60 d
	Range of mating	1-21 d
	Gestation period	3-5 d
	Egg Sac	1-3000 d
	Cyst	1-3000 d
Soybean growth	Minimum germinate temperature	13 ° C
	Soybean germinate date	115 days (about April 25)
	Soybean harvest date	240 days (about August 28)
	Optimal soybean growth temperature	27° C
SCN Parasitism	Minimum soybean age for parasitism	20 days post germinationc
	Maximum soybean age for parasitism	100 days post germinationc
	Feed rate	5%

^aAccording to Biology and Management of Soybean Cyst Nematode 2^nd ed., a female cyst growing in optimal conditions may produce up to 600 eggs. However, the averages found in fields has been reported to be much lower, ranging between 60 and 200, depending on the location (Koenning, 2004).

^bIf hatching is allowed by environment; ^cSoybeans typically take 20 d to produce root exudates that attract SCN. After 100 d, soy-beans are usually within reproductive maturity and root development slows while a woody epidermis prevents new SCN from penetrating.

Nematode Health was measured on a scale of 0 to 100, where 0 corresponds to a dead nematode, and 100 to a completely healthy nematode. Starvation during the hatched J2 stage and infection caused nematodes to lose their health at varying rates depending on the length of the starvation period and the severity of the viral infection. On the other hand, it was assumed that parasitizing soybeans replenishes nematode health at a fixed rate. The health parameter quantified the probability with which the Nematodes transitioned to their next life stage. Repeated failure to develop caused an irreversible decrease in Health that would eventually cause the Nematode to die.

Any viral infection the male carried was transmitted to the female according to the probability of transmission. The total resulting viral load was then divided equally among the eggs.

SCN females transitioned from egg sacs to dormant, egg-containing cysts between growing seasons or if temperatures dropped below 20° C (Schmitt et al., 2004). Eventually, the cysts would release SCN juveniles in the following Spring when favorable conditions returned. This dormant cyst phase slowly degraded over 3000 days, given that the cysts remain viable for about 9 years (Schmitt et al., 2004). It was assumed that the metabolism in the dormant phase occured at a negligible rate and viruses do not mutate or cause damage.

As multiple Nematode agents advanced through their simulated life cycle, the simulation engine generated data for the means and standard deviations of the nematode population distribution including distributions across the simulated nematode stages as well as means and standard deviations of the dynamic virulence properties and means of environmental variables. Data generated in each run were stored in a database separately, along with the variables corresponding to the initialization of the simulation.

Assumptions: at the time of this writing, relatively little is known about the epidemiology of the SCN viruses, including their pathogenesis, transmission rates, mutation rates, and etiologies. Thus, broader definitions were needed to describe their in silico counterparts and the following simplifying assumptions were made: (1) Viruses were only pathogenic to SCN, i.e., no mutualism, symbiosis, commensalism or competition between viruses was assumed; (2) viruses began inflicting damage immediately after infection; (3) differences in success rates between horizontal and vertical transmission were ignored; (4) contact transmission of viruses was ignored; (5) spatial dimension was ignored, i.e., metapopulation dynamics did not influence the epizootic; (6) soybean immune responses against nematode parasitism were ignored, except for biomass reduction; (7) soil moisture did not impact the model, and (8) nematodes replenished their Health at 5% per feeding event as they fed on the soybean plant. Based on data available, an initial population of 10 cysts increased to 5000 within one growing season (Schmitt et al., 2004). To replicate this nematode growth rate in the absence of viral infection in the simulation model, the feeding rate was calibrated to 5%.

Simulation data generation: Each unique combination of the varying initial conditions for virus properties were simulated 10 times over a 5-year period of continuous soybean monoculture. Simulation data were generated to correspond to a frequency of 4-day sampling interval (Table 3). In the data, each unique combination of virus properties is referred to as a pathotype. The replicates were averaged for each combination at each time point. Data points where there was no SCN activity (days 1–99, and 256–365) were removed. Where appropriate, medians of each non-normally distributed variables were determined for each within-treatment crop year for expedited qualitative analyses. The simulation code is available at https://github.com/kbhalerao/SCNSim and the entire database of simulated data can be made available upon request.

Table 3.

Simulation parameters used in producing data on the Soybean Cyst Nematode Simulation SCNSim framework.

Simulation configuration	Sampling frequency	4 days
	Iterations	10
	Simulation duration	5 years
Virus properties	Mutation rates (m)	0, 0.1, 0.2, 0.4, 0.6, 0.8
	Virulence (V0)	0.1, 0.5, 1, 1.5, 2, 2.5, 4
	Transmissibility (b0)	0.5
	Infection rate (i0)	0.2, 0.8
	Durability (D)	0.5
	Viral load (L)	0.5

Replication ratio: The basic reproduction ratio from the SIR models, $R_0=\left(\left(bS\right)/\left(b+V+r\right)\right)$, was adapted to the outputs from SCNSim which was called the viral replication ratio in this study, R_v, to distinguish it from R₀, and was computed as:

$$R_V=\frac{b\left(1i\right)}{b+d+\tilde{r}95}$$ (1)

where each of the terms are initially at their maximum capacity and birth rates are not taken into consideration. Therefore, with the exception of the mortality rate terms b and d, the total population is relatively unchanging compared to the nematode population in SCNSim. All the terms that make up R_v are normalized to the total nematode population. b is the dynamic transmissibility, i was the prevalence or infected portion of the nematode population, b is the baseline mortality rate sans any viral infection, d is the mortality rate attributed to viral infection, and r˜₉₅ is the avirulent proportion of i; the proportion of infected nematodes with high ( 95%) health. b was derived by averaging the 10 iterations of the fraction of dead nematodes to live nematodes in the control data while preserving the time-scale resolution.

To determine a recovery ratio r equivalent to the one used in R₀, an approximation, r˜₉₅ was used, representing the proportion of nematodes with an avirulent infection. This term was calculated by taking the median of the subset of i where SCN Health 95. This approximation could be refined in future improvements of SCNSim when knowledge about the possibility for a nematode to be cured from the virus becomes available.

R_v was plotted with respect to m in order to find the critical mutation rates, m_crit, at the error threshold. m_crit values were determined by interpolating themutation rate at R_v = 1 using the slope between the points crossing the threshold.

Statistical analysis: Data were subjected to the Shapiro–Wilk test (Shapiro and Wilk, 1965) to test for heteroscedasticity. Since heteroscedasticity was significant in most of the variables observed, non-parametric tests were used for further analysis of variance (Kruskal and Wallis, 1952; Daniel, 1990), and permutation tests were used for multi-factorial analysis of variance (ANOVA) (Wheeler, 2010). Results from the virus treatment simulations were compared to a control simulation which assumed null viral infection rates. Statistical analyses were performed using R® Statistical Software (R Core Team, Vienna, Austria) (R Core Team, 2013).

A total of 31 variables and over a million records were used in the analysis. All data were subjected to scaled principle component analysis using the prcomp function in R®. Variables analyzed included population distribution across multiple nematode stages (J1, J2, J3, J4, J4 males, J4 females, males, females, nematodes mating, fertilized females, females with egg sacs, cysts, and average number of eggs per cyst), population mean and standard deviations of virus properties (virulence, transmissibility, viral load, durability), and epidemiological measures (number of deaths in nematodes due to viral infections as well as due to other factors such as starvation), average health of the nematode, and the propensity of the virus to mutate.

Variables ‘Nematodes’ and ‘Cyst’ were chosen to represent the SCN population, ‘Virulence’ and ‘Transmissibility’ were used to describe the viral epizoology, and ‘Fraction Infected’ and ‘Death by virus’ were used to describe disease impacts on SCN. Nematode mortality rates attributed to viruses, d, was calculated as the percentage of deaths due to the virus in the Nematode population. Mortality rate here is distinct from the baseline mortality rate, b, as well as the enhanced mortality rate which is equivalent to the total mortality rate.

Results

To evaluate the extent of nematode suppression by SCN viruses, final mortality rates of SCN were compared across multiple factors. For all pathotypes of viruses where V₀ = 0.1, all median virus-related mortality rates were 0.0%. Thus, V₀ = 0.1 is omitted from further discussion where it is not different from the control treatment.

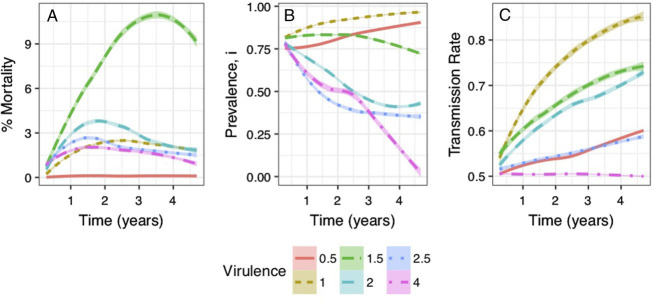
Simulation on Inundative release of viruses: based on data collected on SCNSim simulations across multiple virus properties listed in Table 3, nematode mortality rates were broken down by infection prevalence, mutation rate and initial starting virulence as shown in Figure 2. As expected, the greater the starting prevalence i₀ of the viral infection, the greater was the observed nematode suppression.

Figure 2:

Soybean cyst nematode mortality across viral pathotypes. Each panel describes the mortality in the nematode population as a function of the mutation rate for a given initial virulence V₀. Greater prevalence of the infection resulted in higher mortalities than the low release treatments.

Overall, the i₀ = 0.8 treatments had significantly higher (P < 0.001, Kruskal–Wallis) mortalities than the i₀ = 0.2 treatments with median mortalities at 1.17% and 0.12%, respectively (Figure 2). The i₀ = 0.2 treatments experienced suppressed mortality rates even as the prevalence (i) eventually increased above 80% in some treatments.

Moreover, the average mortality rates due to viruses for simulations with initial prevalence i₀ = 0.2 were not significantly different from the baseline control mortality rates during the final year (p = 0.295, two-sided Wilcoxon rank sum) (data not shown). This suggests at i₀ = 0.2, a rather low initial prevalence, viral infection rates on SCN remained negligible.

This result agrees with the stochastic modeling study by Shea and Possingham (2000) which identified the notion that a high release strategy results in greater biocontrol. However, treatments within each i₀ experienced steady declines in i over time. Within the i₀ = 0.2 treatments over a 5-year period, there was an 11% annual decrease in i; median i at the end of 5 years was 0.09. On the other hand, treatments with an initial prevalence of i₀ = 0.8 declined by 7.7% over the same period, with the median prevalence i = 0.49.

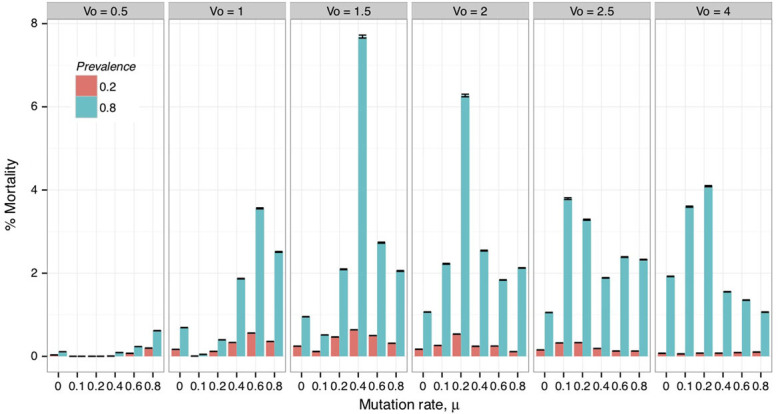
Nematode suppression across viral pathotypes: effects of viral virulence on SCN mortality when i₀ = 0.8 were highest when initial virulence and mutation rates were V₀ = 1.5 and m = 0.4 (Fig. 2). The i₀ = 0.2 treatment followed similar trends albeit with much more attenuated nematode suppression.

Dynamic evolution of SCN viral pathogenicity: Figure 3 shows the time course evolution of mortality, prevalence, and viral transmissibility for the viral mutation rate of m = 0.4. The maximum mortality rate is seen for the virus with initial virulence of V₀ = 1.5 in the fourth crop year. Divergent behavior in the prevalence of the SCN virus appeared between around V₀ = 1.5 (Fig. 3B). For viruses with V₀ < 1.5, the prevalence i of the virus steadily increased toward i = 1 over time. Increasing prevalence combined with reduced mortality suggests a situation where the viral infection is endemic within the population and is of no benefit as a biocontrol agent.

Figure 3:

SCN suppression over time at mutation rate of 0.4 across initial virulence V₀: (A) virus mortality rate changes over time; (B) virus prevalence changes over time; and (C) virus transmission rate changes over time for different virus initial virulence (V₀) rate.

At V₀ = 1.5, the prevalence remained relatively constant at i₀ decreasing slightly after the third crop season. For V₀ > 1.5, prevalence decreased over time. For V₀ = 2.0 and V₀ = 2.5, i appeared to initially crash rapidly before equilibrating at a lower i. At the highest virulence of V₀ = 4 prevalence decreases dramatically to i = 0. The viruses appear to stop transmitting entirely (Figure 3C, causing the virus to be diluted out at a ratecongruent with the nematode population growth rate.

The dynamic evolution of SCN viral pathogenicity modeled with SCNSim indicates that it is more important to select a virus strain with an intermediate starting virulence V₀ to be an effective biocontrol agent.

Replication ratio–disease fitness: the replication ratio was used to compare the disease fitness across combinations of virulence factors. According to the tradeoff hypothesis, epizootics with high fitness are expected to have high b and low v. One-factor analysis determined the factors V₀ and i₀ contributed significantly to the variation in R_v (p < 0.001) while their interaction effects with initial and final years were not significantly different.

For the i₀ = 0.2 treatment, mean R_v was 1.62 ( 6.4e −5), while that for the i₀ = 0.8 treatment was significantly lower at 0.82 ( 7.4e−5). This difference was expected: the i₀ = 0.2 viruses have many more susceptible hosts to infect and. On the other hand, i₀ = 0.8 treatments may be reinfecting each other frequently. The resulting accumulated viral load leads to higher mortality and negatively impacts the fitness of the epizootic. The evolutionary fitness of an infectious agent may not be conducive to its performance as a biocontrol agent.

Figure 4 shows that within the V₀ factor the relationship of R_v as a function of mutation rate. In some cases, the data follow an approximately sinusoidal pattern indicating optimal bounds on replication ratios. This pattern is especially clear in V₀ = 0.5 as the peak and trough are both present within the range of mutation rates. However, the 0.5 virulence treatment is the only group to cross the R_v = 1 line from above the threshold to below with increasing mutation rate. The change in shape of the curves between V₀ = 0.5 and V₀ = 1 indicates the existence of a virulence threshold between the two V₀s. Below this threshold, higher mutation rates lead to the disease dying out. Virus treatments with insufficient starting virulence and high mutation rates may generate a diverse population of harmless viruses; viruses can either persist and do little to no damage or be selected out of the SCN population. This notion is consistent with the idea that a parasite evolves to maximize its fitness in its environment (Mackinnon and Read, 2004a,2004b)

Figure 4:

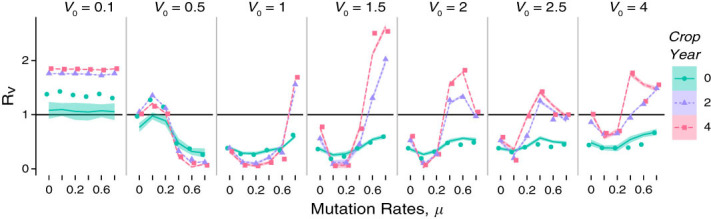
Replication ratio (R_v) with respect to mutation rate of viruses with respect to mutation rate at five different initial virulence rate (V₀) over 4 crop years. Median R_v values are accompanied by smoothing (loess) curves with 95% confidence bands.

On the other hand, above this virulence threshold, increasing mutation rates improves the fitness of the epizootic. At these higher V₀ values, increasing mutation rates could lead to diverse populations of viruses that are damaging, but less so with high R_v values. Meanwhile in each virulence treatment, the amplitudes generally increased with crop years indicating that over time, the effect of mutation rate on R_v is also amplified Figure 4. The effects on virus fitness appear to be cumulative; viruses with high or low fitness will only increase or decrease, respectively, with time.

Correlation between virulence and transmissibility. Figure 5 shows the parametric relationships between b and virulence for each V₀ m pathotype within i₀ = 0.8. Each individual panel within the grid reveals a linear locus along which the dynamic properties of transmissibility and virulence evolve. At the extreme values of ranges tested (i.e., low initial virulence and mutation rate, and high initial virulence and mutation rates), the virus did not appear to have the opportunity to mutate.

Figure 5:

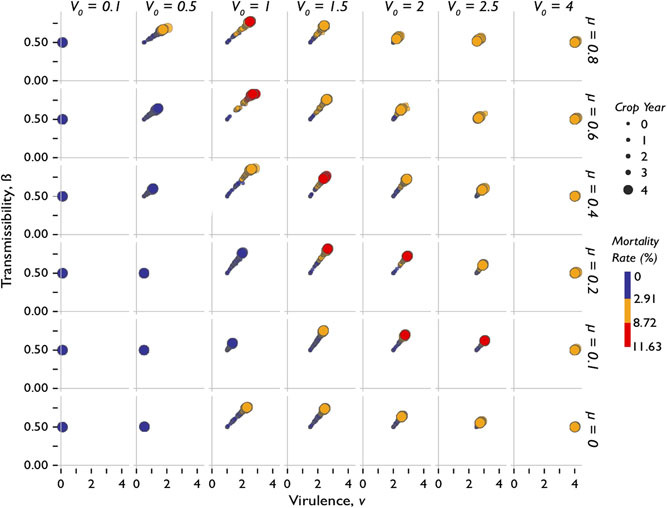
Four-dimensional scatter plot showing virus-caused nematode mortali- ties over time across treatments by mutation rates and virulences. Each panel in the grid layout denotes the evolution of transmissibility b and virulence v over time for a specific mutation rate and initial virulence.

Furthermore, this study suggested a positive relationship between transmissibility and virulence, as opposed to an inverse relationship posited by Raberg˚ and Stjernman (2012).

However, as indicated by the time component, in some simulations, the relationship between transmissibility and virulence does not evolve monotonically. Figure 6 highlights three distinct trends found in Figure 5. For instance in V₀ = 2.5, m = 0.4, by the final crop season, both b and v have dropped uniformly along the same rate they were rising at during the previous years. For these viruses, b and v are behaving as if they are approaching an optimum or simply decreasing after reaching a maximum. Furthermore it appears that despite varying levels of m, viruses with initial virulences V₀ = 4 and V₀ = 0.1 remain relatively unchanged.

Figure 6:

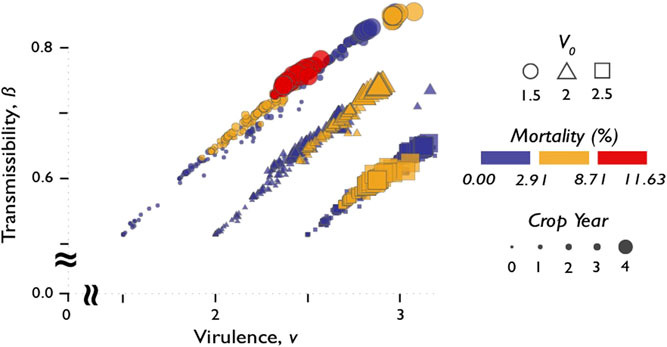
Relationship between transmissibility and virulence across three distinct initial virulence values (V₀ = 1.5, 2.0, and 2), with a single mutation rate, m = 0.4 over 4 years. Mortality rate of soybean cyst nematodes are shown in different colors.

Although Raberg˚ and Stjernman (2012) reported an inverse relationship between virus virulence and transmissibility, the data generated from SCNSim revealed that at intermediate virus V₀, viral transmissibility and virulence are linearly coupled, and this coupling appears independent of mutation rate m. Thus, for the purpose of developing effective biocontrol agents using SCN viruses, it is important to select virus strains with intermediate virulences.

Figure 5 also visibly supports the notion of optimal virulence: greatest nematode mortality is achieved by intermediate pathotypes, which lay on a diagonal of the grid. Within these intermediate pathotypes, b and v are largely increasing throughout the duration of the simulation. This is however, only partly in agreement with the tradeoff hypothesis: At low values of initial virulence, b and v appeared positively correlated as expected, and caused an increase in mortality (Mackinnon and Read, 2004b). However as suggested by Mackinnon and Read (2004b), increases in v increased did not lead to asymptotic values of transmissibility b. This difference may be due to the absence of modeling the nematode host immune response in SCNSim. Thus, the main selection pressure for the viruses is to adjust their b and v in order to keep up with the nematode population growth rate. If a nematode immune response was included in the model, one may expect the viruses to become more virulent in order to counteract the strengthened immune response (Raberg˚ and Stjernman, 2012).

Discussion

SCNSim represents the first attempt at capturing the evolutionary dynamics of host–pathogen interaction in the context of biocontrol of SCNs with viruses. A key advantage of SCNSim is that it is possible to model host morbidity through the stochastic events driven by the health parameter of the nematode and permits the modeling of diseases with small case fatalities (Mackinnon and Read, 2004b).

Because morbidity manifests at the individual nematode, this is a crucial advantage of agent-based models over the continuous, differential Susceptible-Infected-Recovered (SIR) models (Rock et al., 2014), where it is difficult to interpret model results where there are few discrete individuals. The SCNSim simulation supports the idea that the best biocontrol agents have intermediate values for initial virulence. It also illustrates that biocontrol agent performance also strongly depends upon the mutation rate, i.e., the adaptability or evolvability of the pathogen, which allows the pathogen to rapidly achieve an optimum under selection. Moreover, SCNSim highlights the fact that the virulence and transmissibility properties of a virus that maximize the reproductive fitness of a pathogen can be counterproductive to its use a biocontrol agent. Virulence levels below optimal will lead to avirulence, whereas higher virulences kill the nematode rapidly, reducing the opportunity for transmission. From a practical standpoint, the ideal virus-based biocontrol strategy for SCN would include (1) a design for optimally initial virulence, (2) adaptable viruses (3) delivery mechanisms to ensure sufficiently high disease prevalence to permit vertical transmission of the pathogen, and (4) multiple years of successive treatment, allowing the biocontrol agent to maximize nematode suppression over multiple years.