Methodological considerations when analysing and interpreting real-world data

Abstract

In the absence of relevant data from randomized trials, nonexperimental studies are needed to estimate treatment effects on clinically meaningful outcomes. State-of-the-art study design is imperative for minimizing the potential for bias when using large healthcare databases (e.g. claims data, electronic health records, and product/disease registries). Critical design elements include new-users (begin follow-up at treatment initiation) reflecting hypothetical interventions and clear timelines, active-comparators (comparing treatment alternatives for the same indication), and consideration of induction and latent periods. Propensity scores can be used to balance measured covariates between treatment regimens and thus control for measured confounding. Immortal-time bias can be avoided by defining initiation of therapy and follow-up consistently between treatment groups. The aim of this manuscript is to provide a non-technical overview of study design issues and solutions and to highlight the importance of study design to minimize bias in nonexperimental studies using real-world data.

Rheumatology key messages

• Nonexperimental studies based on real-world data can provide timely answers to urgent clinical questions.

• Rigorous study design features, including active comparators and new users, minimize the potential for bias.

• Propensity scores can help us to identify study populations with equipoise between treatments compared.

Introduction

According to the US Food & Drug Administration’s latest definition [1, 2], real-world data are ‘data relating to patient health status and/or the delivery of healthcare routinely collected from a variety of sources’. Primary data are collected for research purposes, following pre-specified study protocols, applying strong methods to monitor data quality and ensure comprehensive follow-up, e.g. the data from Norfolk Arthritis Register (NOAR) assessed patients on the association of early treatment and disease activity over 20 years [3]. In contrast, secondary health data are pre-existing data [4] that have been collected for non-research purposes, including administrative purposes, e.g. insurance claims data such as US Medicare [5] or originally for another research study. Such healthcare databases are often large and representative of populations [6].

The US Food & Drug Administration defined real-world evidence as ‘the clinical evidence about the usage and potential benefits or risks of a medical product derived from analysis of real-world data’ [1, 2]. Real-world evidence can provide valuable information on the effectiveness and safety of a medical product and inform patient care and therapeutic development [7]. However, without a valid methodologic approach, real-world evidence can lead to flawed conclusions [8]. Thus, in the following paper, we discuss important methodological considerations when analysing and interpreting real-world data.

Data sources and data quality

Secondary health data are an important source for real-world evidence as they often allow us to study less selected populations [1, 9], e.g. all patients actually treated [1, 6], than would be possible to recruit into a randomized trial or prospective cohort study. In claims data, enrolment data, demographic data, medical care and pharmacy claims data are linked by a common patient identification number, yielding a longitudinal record of healthcare encounter data. Overall, claims data are often ‘almost ideal for prescription drugs in the outpatient setting, i.e. for most of the drugs used’ [8]. Claims data are obviously not perfect because we lack information on over-the-counter drugs, sample use, and need to estimate the end date of a prescription from the days’ supply when patients stop taking a medication. Compared with exposure assessment, the disease data are less accurate [8] and usually require algorithms to identify important covariates and outcomes.

As medical practices increasingly become electronic, more electronic health record (EHR) data become available. Compared with claims databases, EHR databases tend to have better validity of diagnosis data [10], cover results of diagnostic tests, including laboratory data, and contain information on lifestyle (e.g. smoking and body mass index). However, EHR databases often do not capture all medical encounters and therefore lack longitudinal completeness (e.g. patient care received outside of a given health system is unobservable) [1].

Treatment registries such as drug/device registries, service/procedure registries, or disease registries have been used for studies of the effectiveness and safety of medical interventions. For example, the British Society for Rheumatology Biologics Register has provided valuable information on the safety and effectiveness of TNF inhibitors (TNFi) [11]. Treatment registries are often limited, however, by lack of data on alternative treatments.

With appropriate confidentiality safeguards [10], researchers are increasingly able to link healthcare databases, e.g. claims data with EHR data, which can provide a more integrated picture of the patient’s health and healthcare. The linked datasets have unique advantages for epidemiologic research on medical interventions because they can combine the defined population and longitudinal completeness of claims data with the cross-sectional richness of clinical or registry data [8].

The major limitation of secondary health data is that important data, e.g. disease activity scores, which would be collected in any primary data collection, are not systematically collected [10]. This limitation can, however, sometimes be addressed by data linkages and minimized by study design. Notably, the abundance of available data alone does not provide valid answers to important questions. It is the quality of the data combined with sound study design and statistical analysis that determines the validity of the results, and we posit that study design has a larger influence on validity of observational studies than analysis [8]. Finally, while state-of-the art study design and analysis will allow us to validly estimate treatment effects in certain settings, this does not imply that they can be implemented in all settings.

Study design

The three main epidemiologic designs for real-world evidence are the cohort study, the case-control study, and the self-controlled (e.g. case-crossover) study [12]. Cohort studies enrol participants based on treatments at a certain point in time and follow them over time to compare the incidence of outcomes. Case-control studies identify cases with the outcome of interest, select controls from the source population (in the risk set for the outcome), and then compare treatment histories between cases and controls. Self-controlled studies compare treatments and outcomes within individuals rather than across individuals by looking at different treatment periods within the same person, assuming intermittent treatments and transient effects on outcomes. We will focus on cohort studies in this paper.

Unlike randomized trials, where characteristics of participants are balanced in expectation, treated and untreated groups in a nonexperimental study usually have meaningful differences in their demographic and clinical characteristics that can affect outcomes. Thus, sound study design is needed to minimize such differences and statistical approaches are typically needed to adjust for remaining differences in measured characteristics to estimate treatment effects.

These designs are informed by a causal framework and can support a causal interpretation of the result given key assumptions. That is, while statistical associations often cannot be interpreted as causal effects, the causal framework tells us exactly when they can. Interpretation for causal effects requires a well-defined treatment as a hypothetical intervention [13] and the concept of potential outcomes (i.e. outcomes for the same person under all treatments, both factual and counterfactual) to compare the outcome, in fact, observed with counterfactual outcomes that could have been observed had the treatment taken on a different level that is actually not observed [14].

Potential biases

While the potential direction and magnitude of bias needs to be evaluated for each specific study, there are some common study design-related biases that will tend to harm the internal validity of real-world evidence, most of which are related to confounding/selection bias. Sometimes, it may be hard to differentiate between confounding and selection bias. Epidemiologists may use the term confounding (by indication) for the same thing statisticians/econometricians may use the term selection bias. For those interested in the distinction between these two as used by epidemiologists, we refer to Hernán et al. [15].

Confounding by indication

In observational studies, confounding by indication is a major concern as treatments are prescribed to patients by physicians based on their characteristics rather than being assigned randomly [16, 17]. For example, Raaschou et al. [18] compared TNFi initiators to biologic-naïve patients with respect to risk for cancer recurrence. The authors noted the potential for selection bias if patients were prescribed TNFi after clinical guidelines cautioned against TNFi use in patients with a history of cancer [19, 20]. In turn, the TNFi-treated patients may have a lower baseline risk of recurrence (more favourable tumour characteristics) than biologic-naïve users [18]. In such a scenario, it might be impossible to estimate the effects of TNFi on cancer recurrence.

Confounding by frailty

Confounding by frailty has been identified as another potential bias for real-world evidence using population-based data, particularly those among older adults [21–24]. Because frail persons (close to death) are less likely to be treated with a multitude of preventive treatments [21, 25], frailty would lead to confounding when comparing treated with untreated. This confounding would bias the association between treatments and outcomes associated with frailty (e.g. mortality). In this setting, the untreated cohort has a higher prevalence of frail persons and therefore mortality risk irrespective of the treatment effect on mortality. This will make the drug look (too) good (more protective or less harmful than it actually is). Here again the crux of the problem is that frailty is difficult to measure and therefore hard to control for [26].

Prevalent user related biases

Another common study design-related potential bias stems from allowing participants to enter the cohort at some time after treatment initiation [27]. In pharmacoepidemiology, such participants are called prevalent users because they are already on treatment when they are observed to enter the cohort and start of treatment is unknown or ignored. The problem lies in the fact that prevalent-user designs will miss early events. Prevalent users are survivors of the early period of treatment and thus excluding individuals who experience early events may lead to substantial bias [28–31]. Mixing incident and prevalent users can obscure early harm if the person-time is weighted toward the latter. Besides, if we try to control for confounding in prevalent users, confounders measured while on treatment may have already been affected by the treatment itself [31]. The new-user design avoids this conundrum. A good example for the differences between prevalent and new-user designs is the Nurses’ Health Study, which reported a decreased risk of major coronary heart disease in women who were prevalent users of oestrogen with progestin, compared with women who did not use postmenopausal hormones [32]. After the results from the Women’s Health Initiative randomized trial showed an increased risk of coronary heart disease among postmenopausal women in the oestrogen plus progestin arm compared with placebo [33], a re-analysis of Nurses’ Health Study cohort implementing a new-user design (restricting original cohort to hormone therapy nonusers during the prior ‘washout’ period, then establish hormone therapy ‘initiators’ or ‘non-initiators’ and start follow-up) demonstrated results compatible with the Women’s Health Initiative trial [34]. This example shows that implementing a new-user design plays a key role in reducing the potential for bias in observational studies.

Immortal-time bias

Immortal-time bias arises when treatment is defined based on some future event and the period of follow-up prior to treatment initiation is inappropriately classified as ‘treated’ [35]. The term ‘immortal’ is used with respect to the outcome of interest (e.g. mortality) and highlights the fact that the outcome of interest cannot occur during this period by logic, as exposure has yet to be defined. Thus, the addition of immortal person-time to a given treatment group leads to an underestimation of the true rate/risk in that group and spurious beneficial effects of treatments. Immortal-time bias often occurs when treatments are administered in a certain sequence (for example, starting biologic DMARDs only after synthetic DMARDs), or when the follow-up starts at a different time point in treated and untreated groups [36]. The bias is often strong, which can lead to its detection because results are ‘too good to be true’. In many situations, however, immortal-time bias cannot be distinguished from an expected treatment benefit and can mask actual harm. Several practices reduce the potential for immortal person-time, including implementation of the new-user study design whenever possible and avoiding the use of future information to define cohorts (analyse the data as they are collected, i.e. prospectively). For instance, in a cohort study addressing the effects of biologic DMARDs on mortality and following patients from the beginning of the date of the first diagnosis of rheumatoid arthritis, the biologic DMARDs patients will have immortal-time as these patients have to survive to receive a biologic DMARD. If patients had the outcome of interest prior to initiating a biologic DMARD, then their person-time and event would be attributed to the non-DMARD group, which results in immortal-time bias favouring biologic DMARDs [36]. Assigning person-time correctly, e.g. by comparing biologic DMARDs initiators to patients who have not (yet) initiated a biologic DMARD, follow-up will start from initiation date and there will be no immortal time.

ACNU design

Over the past two decades, there have been rapid advances in study design to minimize the potential for bias in real-world evidence. Arguably the most influential development was the new-user study design [28–31]. With a hypothetical intervention [13] (a well-defined treatment), a new-user study design identifies all patients in a defined population, i.e. patients who start a specific treatment after a certain length of time free of the treatment (washout period), and follows this patient cohort for endpoints from the time of treatment initiation (T₀) [27]. The new-user design aligns treatment initiation with start of follow-up, which is a prerequisite for dealing with time varying hazards and solves issues of comparability between prevalent users and non-users.

The second influential development was to apply the principles of the new-user design to all individuals in the cohort, not just those who received the treatment of interest. To do so, we identify initiators of the drug of interest and initiators of an alternative treatment for the same indication. By restricting both cohorts to patients with the same indication for treatment and without contraindications [28, 37], this so called active-comparator, new-user (ACNU) design can dramatically reduce the potential for confounding by indication and frailty in some settings [37, 38], a major argument previously used against the usefulness of non-randomized treatment comparisons [39]. Because the ACNU uses the same timeline for both cohorts, it also minimizes the potential for immortal time bias and obviously avoids prevalent user biases.

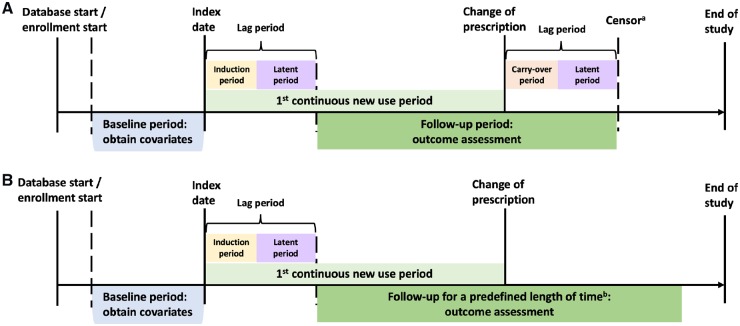
The implementation of the ACNU design depends on the presence of an appropriate active-comparator treatment used for the same (or at least: similar) indication as the treatment of interest. The ACNU design requires that patients are neither exposed to the drug of interest nor to the comparator drug during the washout period. Additional inclusion and exclusion criteria are applied as in any other cohort study or randomized controlled trial. Patients are then followed over time to ascertain the outcome of interest. A general algorithm for the ACNU design is shown in the study schematic in Fig. 1.

Fig. 1.

ACNU study design schematics

Panel A illustrates why the active-comparator design (top) is superior to traditional design (bottom) by controlling for unmeasured confounding by DAS (assuming for simplicity that DAS does not affect choice between etanercept and infliximab). The same logic would apply for unmeasured confounding by frailty. DAS could obviously be controlled for analytically if DAS data in proximity to the treatment decision were available. Panel B provides a detailed picture of how to identify periods of new use of drug A (the same process would apply to drug B) in a claims or other healthcare database. One individual can have multiple new use periods. The individual can also be a new user of drug A and later a new user of drug B (or vice versa). Often, analyses will be restricted to the first period of new use. The date of discontinuation (or switching or augmenting) may be used as a censoring date in as-treated analyses. ACNU: active-comparator, new-user.

Although it is not always necessary to study patients from the start of treatment [40, 41] or to use an active-comparator [42] (e.g. assessing the effects of a dose change following a laboratory test [41]), generally speaking, non-initiator or non-active comparator designs will be more prone to bias compared with the ACNU design. Non-initiator cohorts usually suffer from difficulties in establishing a clear and meaningful start of follow up (T₀), which may induce substantial bias.

New users do not necessarily need to be drug naïve: they are only required to be naïve for the treatments compared during the wash-out period (e.g. one year). The ACNU design will not work in settings where a treatment, e.g. TNFi, is generally used as a second line treatment after a first line treatment, e.g. methotrexate, or in settings where many patients are switched from a standard treatment to a newly marketed one. From a purely methodological point of view, a better design in this setting might be to compare two different TNFi added to methotrexate. Admittedly, ACNU designs often exclude many patients. The recently proposed prevalent new-user design [43] allows patients to be on the comparator treatment before initiating the treatment of interest and matches these switchers to patients not switching with a similar history of comparator drug use. In practice, the potential gains in sample size will depend on the specific treatment patterns and data availability and may be smaller than anticipated [44]. Any gain in sample size will need to be weighed against the difficulties in the interpretation of causal effects of the treatment (switching to a drug of interest from a comparator or not is not the same clinical question as initiating a drug of interest or the comparator), and increased potential for confounding bias when comparing patients switching or adding treatments with those staying on treatment [44]. Thus, the ACNU design is still considered the current standard in pharmacoepidemiologic research [45]. The concept of ACNU design has been applied by some of the biologics registers since 2001, e.g. BSRBR [11] and RABBIT [46].

Treatment changes after initiation

Once new-user cohorts have been identified, it is then necessary to make decisions about how to deal with treatment changes over time. Similar to a randomized trial, there are two general possibilities: use the actual treatment received (as-treated), i.e. account for treatment changes; or ignore treatment changes (initial-treatment) (Fig. 2). Note that both of these depend on using time since treatment initiation as the underlying timescale, as we would do in a randomized trial.

Fig. 2.

Risk period for as-treated and initial-treatment analysis

The timeline in the Panel A illustrates as-treated analysis. ^aPatients are censored the earliest of the following: lag period after change of initial Rx, end of enrolment, end of study (data), or death. If a treatment has an immediate effect on the incidence rate for the outcome (i.e. no induction period) and there is no delay for diagnosis (i.e. no latent period), follow-up could start at the date of the first prescription. Similarly, the lag period for stopping can be set to zero, i.e. the date of discontinuation (or switching or augmenting) may be used as a censoring date, if the biologic carry-over period is short and there is no latent period. The timeline in the Panel B shows initial-treatment analysis. ^bPatients will be followed for a fixed period of time, e.g. 2 years, and are censored at the earliest of the following events: predefined follow-up length of time after index date, end of enrolment, end of study (data), or death.

The as-treated analysis approach is similar to the per-protocol analysis in a randomized trial but not the same, as there is no pre-specified protocol. For the as-treated approach, the first challenge is to estimate the date when the patient discontinued use of the initial treatment. As this date is rarely known in secondary data, we typically use the days’ supply of the last prescription plus a grace period to allow for less than perfect adherence and assume that treatment stopped at the end of this interval. Other treatment changes include switching of treatment groups and augmenting (adding the comparator treatment to the initial treatment). The advantage of the as-treated approach is that it considers periods at actual risk due to the treatment. The disadvantage is that e.g. censoring patients stopping the initial treatment has the potential to introduce selection bias because changing treatments is usually due to a lack of effectiveness or side effects that are very likely to affect outcome risk. Over time, we therefore end up with a select group of patients who do well on the treatment and therefore are not representative of all patients who initially received the treatment anymore.

Inverse-probability of censoring weights can be used in as-treated analyses to address selection bias from informative censoring [15]. Censoring weights are not widely used in pharmacoepidemiologic studies using secondary databases as the prediction of adherence is often difficult due to missing data on e.g. lab data that drive treatment decisions, or subtle side effects [8]. In situations where we do have data that allow us to predict treatment changes over time (e.g. antiretroviral treatment in patients with HIV [47]), censoring weights and other methods to reduce selection bias should be used. These methods, including marginal structural models [48] and g-methods [49], are discussed below.

The initial-treatment approach is similar to the intent-to-treat analysis in a randomized trial [50] but not the same again, as we have no information on the physicians’ intent. Patients would only be censored for death and end of enrolment in the database. The advantage of the initial-treatment analysis is that it protects against selection bias introduced by conditioning on continuous treatment. It will, however, introduce bias due to increasing misclassification of exposure over time, which tends to move the effect estimate towards the null (but this is not guaranteed!). While this is seen as good (as it is more rigorous) when comparing treatments to no treatment (placebo), it will be worrisome for safety and for comparative effectiveness because it may fail to detect differences. To minimize exposure misclassification, researchers often restrict initial-treatment analyses to a predefined duration after drug initiation (e.g. 6 months, 1 year, 2 years).

Risk periods

An additional advantage of the new-user design is that it allows us to define various risk periods in relation to treatment initiation. These risk periods are often determined based on bio-mechanism and characteristics of the disease outcome of interest. With large data, also it may be possible to empirically derive risk periods. If a treatment has an immediate effect on the incidence rate for the outcome (i.e. no induction period [12]) and there is no delay for diagnosis (i.e. no latent period [12]), follow-up could start on the day of the first prescription. Otherwise, induction and latent periods should be carefully considered. After drug initiation, person-time and outcomes during the induction and latent period should be ignored. After treatment discontinuation, person-time and outcomes during a period equivalent to the biologic carry-over effect (usually: short) and the latent period combined should be added to allow for the diagnosis of the end point that was already present, albeit subclinical, before the stopping of the treatment (Fig. 2). Very often, the two periods at the start and the end of treatment are set to the same duration, which results in lagging all time at risk by e.g. 6 months. For instance, if the outcome of interest, rheumatoid arthritis, is diagnosed a week after initiation of a drug of interest, the rheumatoid arthritis would be very unlikely caused by the drug, as it would require time to develop and to be diagnosed. In this hypothetical setting, it would be reasonable to start follow-up only e.g. 6 months after drug initiation. That is, patients with rheumatoid arthritis diagnosis during the first 6 months would be excluded [51]. Similarly, a latent period allowing for the diagnosis of rheumatoid arthritis developed during treatment should be added after discontinuation of the treatment (Fig. 2).

Missing data

Missing data on comorbidities, disease activity (e.g. DAS28), co-medications (e.g. over-the counter aspirin use), body mass index, smoking/alcohol use, and lab values (e.g. C-reactive protein level) will bias effect estimates if they affect treatment choice and, independently, the outcome of interest due to residual confounding. Unless all risk factors for the outcome of interest are known and measured (well) so that we can use analytic techniques to control for any differences in these across patient groups compared, our best bet to reduce the potential for confounding bias is to compare treatments that are generally used for the same patients (by the same or different physicians), i.e. the ACNU design. For example, using data from two external validation studies, Stürmer et al. [52] could show that body mass index was well balanced between initiators of insulin glargine and human NPH insulin, two alternative second line diabetic therapies, and thus could not confound a comparison of outcomes for which body mass index would be a risk factor. More recently, Wang et al. [53] demonstrated that clinical measures available for a small proportion of Medicare fee-for-service beneficiaries such as Haemoglobin A1c, blood pressure, low-density lipoprotein cholesterol are also well balanced between initiators of incretin therapy and other similar treatments (e.g. dipeptidyl peptidase-4 inhibitor vs sulfonylurea).

When internal validation data are available, i.e. when we have additional information on a potential confounder for a subset of the patients, we can use this information to adjust for confounding in the main study by using methods for handling missing data. Multiple imputation is arguably the most widely used and easy-to-implement method [54, 55], and rheumatology researchers have used this technique to deal with missing data [56–59]. Using multiple imputation for confounding control does require data on the outcome in the validation study. The general idea is to fit a model predicting the missing covariate based on the measured covariates (the expected value), the exposure, and the outcome. Instead of using a single predicted value for the missing covariate, several values of the missing covariate are created in separate datasets by drawing parameters from the posterior distribution of the prediction model [55]. These datasets without missing values are then analysed separately using the same analytic techniques. Finally, the treatment effect is estimated by taking the mean estimate across the separate analyses using a simple formula for the variance. The minimal assumption needed for multiple imputation is missing at random, i.e. missingness is not related to the unobserved values of the variables with missing data [54, 55]. The validation study does not need to be a random sample of the main study. Absolute size of the validation study will be more important than relative size [60]. The above-mentioned study [53] also highlighted that multiple imputation cannot replace selection of a good active comparator: comparing glucagon-like peptide-1 receptor agonist initiators with insulin initiators (which is usually reserved for more severe diabetes [61]), the HbA1c categories were not well-balanced, which led to residual confounding even after multiple imputation [53].

Misclassification and measurement error

Although missing information on treatments, covariates and outcomes is common in real-world data, in claims databases, it is often assumed there are no missing data, as the presence of a code is used to define the presence of a condition and the absence of a code is used to define absence of the condition. In such a setting we would be concerned about misclassification. Misclassification of drug treatments can occur due to free samples [62], out-of-pocket payments (e.g. $4 generics in the US), and non-pharmacy dispensing (e.g. during hospitalizations, stays in nursing homes, etc.). The extent of exposure misclassification will depend on the specific setting and may often be small for drugs when studies are based on dispensed prescriptions [8]. Outcome misclassification will be common and should ideally be quantified based on a validation study [63]. Effects of outcome misclassification on treatment effect estimates will depend on the scale of association (relative vs absolute) and on whether misclassification is likely to be differential with respect to the exposure (classification error depends on the actual values of other variables [12]) or non-differential across treatment cohorts. When misclassification is nondifferential with respect to exposure, high specificity definitions or algorithms will be preferred for ratio measures, as perfect specificity will generate unbiased estimates, even with imperfect sensitivity [64]. Absolute measures, however, will suffer from both low sensitivity and low specificity. Misclassification of covariates will generally lead to residual confounding. Using all available information to define confounders, even if differential, will often improve confounding control [65].

Analysis methods

Propensity scores (and beyond)

Propensity scores (PSs) are increasingly used in epidemiologic and comparative effectiveness research as an alternative to multivariable outcome models to control for measured confounding [66]. PSs can help to identify study populations in ‘equipoise’ between treatments compared [67–69] and can be used as a diagnostic to evaluate covariate balance, i.e. a measure of their performance for confounding control. PSs estimate the probability (propensity) for treatment for every patient based on the patient’s own measured characteristics, which can be predicted using logistic regression, for example. In expectation, treated and untreated patients (or those treated with drug A vs B) with the same PS will have the same distribution of characteristics used to estimate the PS (are ‘exchangeable’) allowing us to directly compare outcomes between treated and untreated patients without confounding. These methods still assume no unmeasured confounding conditional on the balance of the measured covariates, which is generally more plausible with the above-mentioned ACNU design [68].

PS implementation

PSs can be implemented by matching, weighting, stratification and modelling [68–71]. Matching untreated individual patients to each treated patient based on the estimated PS can be conceptualized as counterfactuals, representing the experience of the treated people if they had been untreated. Being able to estimate this so-called treatment effect in the treated is useful when the treatment effect is not the same in all patient subgroups. While PS matching is intuitive and widely used, King and Nielsen [72] recently argued that it may increase covariate imbalance and degrade causal inference. A recent paper by Ripollone et al. [73] suggests that the issue raised by King and Nielsen can be reproduced but has little relevance for standard pharmacoepidemiologic settings. Weighting strategies can be used with PSs to create re-weighted pseudo-populations in which treatment is independent of the measured confounders [74]. Similar to matching, the standardized mortality/morbidity ratio weighting ‘standardizes’ the covariate distribution of the untreated patients to those of the treated patients. Both PS matching (assuming we can identify untreated matches for nearly all treated patients) and standardized mortality/morbidity ratio weighting [75] seek to estimate the average treatment effect in the treated, which answers the question ‘what would have happened if those actually initiating treatment, did, contrary to the fact, not initiate treatment’ [75]. Inverse-probability of treatment weighting estimates the treatment effect in a population whose distribution of covariates is equal to that found in the entire study population [48]. Inverse-probability of treatment weights allow us to estimate the average treatment effect in the entire population, which answers the question ‘what would have happened if everyone had initiated treatment vs what would have happened if no one had initiated treatment’ [48]. Other weighting methods include the average treatment effect in the untreated weights [75], matching weights [76], and overlap weights [77]. These different weighting methods will all result in the same treatment effect estimate if the treatment effect is uniform for all subgroups of patients (with slight differences in precision). Estimates will be different, however, if some patient subgroups have more benefit or harm [74].

PS trimming

Strong and implausible treatment effect heterogeneity over the PS has been observed in previous studies [78, 79]. These studies showed that those patients very likely to be treated (high PS) that were actually not treated and patients that were very unlikely to be treated (low PS) but were actually treated, i.e. the patients treated contrary to prediction, had a very high mortality. The most plausible explanation in the empirical examples is unmeasured confounding by frailty leading physicians to override the most likely treatment based on measured characteristics [8]. Based on this assumption, Stürmer et al. [24] demonstrated in a large-scale simulation study that trimming the tails of the PS distribution reduces the impact of unmeasured confounding by frailty and proposed a range of cut-points that allows the reporting and discussion of patterns (Fig. 3). Various cut-points for trimming PS tails (or, conversely, focusing on a population with better equipoise between treatments) have been proposed [24, 80, 81]. The concept has recently been extended to more than two treatments [82] and efforts are ongoing to provide guidance on which trimming method and cut-points to use [83].

Fig. 3.

Schematic of asymmetric propensity score trimming

In the untreated group (red line), a small portion of patients were very likely to be treated (high propensity score) but were actually not treated. Similarly, in the treated group (blue line), a small portion of patients were very unlikely to be treated (low propensity score) but were actually treated. Trimming both tails of the overlapping propensity score distribution will remove some of the patients treated contrary to prediction and thus tend to reduce unmeasured confounding by frailty.

PSs do not allow us to balance unmeasured covariates and confounders [84]. As with any other analytic strategy, they need to be combined with sound study design such as ACNU design [66] to limit the potential for unmeasured confounding.

Specific methods for time-varying treatments and confounders

For time-varying treatments and confounders that are affected by prior treatment, standard approaches for confounding adjustment can result in bias [85]. Intuitively, if an exposure can plausibly affect confounders in the future, then standard modelling approaches that put those confounders in the same model for the outcome as exposure will end up controlling for a causal intermediate, which has long been known to yield biased effect estimates [85, 86]. Marginal structural models allow us to adjust for time-varying confounders by inverse-probability of treatment weighting [48], which separates control for confounding from the model for the outcome, which consequently allows one to obtain valid estimates of treatment effects [47, 48]. Rheumatology researchers have used marginal structural model to handle time-varying confounders in well controlled data collection situations [86–90].

An alternative set of strategies are (semi-parametric) g-estimation and the (highly-) parametric g-formula. Both these methods and inverse-probability of treatment weights are rooted in using standardization, which avoids the issue of adjusting for factors that are caused by the exposure. G-estimation is an estimating equation-based method (similar to maximum likelihood) to estimate the parameters of structural nested models, which characterize the effects of brief ‘blips’ of treatment [49, 91]. The parametric g-formula is an analytic approach that relies on combining the causal framework with predictive models and simulations to allow us to contrast health outcomes in the same population under different treatment regimens [91]. To our knowledge, neither g-estimation nor the g-formula have been applied to analytic problems in rheumatology, but both have seen applications to problems of estimating effects of occupational exposures that are subject to time-varying confounding [91–96], estimating effects of multiple exposures on chronic conditions, estimating overall effects of HIV treatments that may vary over time or be subject to adverse events that lead to treatment modification [97, 98], and many more examples from complex longitudinal data. While a full explanation of both of these methods is better left to longer tutorial papers (e.g. Hernán et al. [98] and Keil et al. [91]), we note here that the statistical machinery of both g-methods can be based on standard regression approaches such as generalized linear models in conjunction with standard data processing and variable creation. Some software packages exist to routinize these methods for simple cases [99–102]. Briefly, inverse-probability of treatment weighting and g-estimation rely on models for exposures and the outcome, while the parametric g-formula relies on models for confounders and the outcome. We note that, of these three approaches, the g-formula is the most general and, in our experience, provides a valuable set of tools that can broaden our understanding of how health is affected by when, where, and how patients are treated. Crucially, this approach can open up the possible questions we can ask beyond what is possible from comparisons of means or regression coefficients. For example, we have used the g-formula previously to ask the question ‘what would be the effect on mortality of a hypothetical treatment that completely eliminated graft-vs-host-disease in bone-marrow transplant recipients’ [91]. Having such answers from observational studies can help target future research in areas where such treatments might be of greatest benefit. Compared with ACNU design, which limits unmeasured confounding by design, confounding bias may be more difficult to control using inverse-probability of treatment weights or g-estimation because we often have limited data on the drivers of treatment change (lack of effectiveness, side effects), which complicates modelling of the treatment process. So-called doubly-robust methods (such as augmented inverse-probability treatment weighting [103] or targeted minimum loss estimation [104]) also require models for treatment, and thus may also not improve inference in this context [105]. The parametric g-formula requires models for each time-varying-confounder as well as each outcome, and is potentially subject to stronger modelling assumptions, especially when there are several time-varying confounders. These modelling assumptions in the g-formula can potentially be relaxed using machine learning algorithms. Machine learning classification techniques or regression algorithms can be used to fit the g-formula under far fewer assumptions about model form relative to parsimonious parametric models. Crucially, previous use of machine learning with the g-formula has been hindered by the rich data needs of machine learning algorithms. Leveraging large healthcare databases (real-world data) could overcome this difficulty. Current work on machine learning in causal inference is focused on enhancing the validity of confidence intervals for causal estimands, which remains a challenge [106].

Conclusion

Real-world data is often population-based and unselected, already collected, and relatively easy to access, all of which provide advantages for research on the effects of medical interventions. Without randomization nor the possibility to collect data on patient characteristics needed to address confounding analytically, however, we need to rely on study design to address confounding, including confounding by indication and frailty, which can be achieved by the active-comparator, new-user study design in specific settings. A promising active-comparator is in treatment equipoise, i.e. there are no known strong predictors of either treatment leading to minor imbalances of measured covariates prior to adjustment. PSs can then be used to address remaining covariate imbalances between treatment groups. Both state-of-the-art study design and analysis methods are needed to generate high quality real-world evidence. Their impact on the potential for residual bias needs to be carefully evaluated for each study.

Funding: This study was funded by R01AG056479 from the National Institute on Aging, National Institutes of Health, Bethesda, MD, USA.

Disclosure statement: T.S. receives investigator-initiated research funding and support from the National Institute on Aging as a principal investigator (R01 AG056479) and from NIH as co-investigator (R01 CA174453, R01 HL118255, and R21-HD080214); receives salary support as co-Director of the Biostatistics, Epidemiology, and Research Design (BERD), North Carolina Translational and Clinical Sciences Institute (UL1TR002489) and from the Center for Pharmacoepidemiology (current members are GlaxoSmithKline, UCB BioSciences, Merck and Takeda); receives research support from pharmaceutical companies (Amgen, AstraZeneca and Novo Nordisk) to the Department of Epidemiology, UNC; and owns stock in Novartis, Roche, BASF, AstraZeneca and Novo Nordisk. T.S. does not accept personal compensation of any kind from any pharmaceutical company. The other authors have declared no conflicts of interest.