Abstract
In this paper, we introduce a method for estimating patient-specific reference bony shape models for planning of reconstructive surgery for patients with acquired craniomaxillofacial (CMF) trauma. We propose an automatic bony shape estimation framework using pre-traumatic portrait photographs and post-traumatic head computed tomography (CT) scans. A 3D facial surface is first reconstructed from the patient’s pre-traumatic photographs. An initial estimation of the patient’s normal bony shape is then obtained with the reconstructed facial surface via sparse representation using a dictionary of paired facial and bony surfaces of normal subjects. We further refine the bony shape model by deforming the initial bony shape model to the post-traumatic 3D CT bony model, regularized by a statistical shape model built from a database of normal subjects. Experimental results show that our method is capable of effectively recovering the patient’s normal facial bony shape in regions with defects, allowing CMF surgical planning to be performed precisely for a wider range of defects caused by trauma.
Keywords: Craniomaxillofacial (CMF), Trauma, Surgical planning, Simulation, Facial bone estimation, Three-dimensional facial reconstruction, Sparse representation, Adaptive-focus deformable shape model (AFDSM)
1. Introduction
In routine clinical practice of craniomaxillofacial (CMF) surgical planning using computer-aided surgical simulation (CASS), a three-dimensional (3D) bone model is reconstructed from a computed tomography (CT) or cone beam computed tomography (CBCT) scan of patient’s head. (Note: We will use CT to represent both CT and CBCT in the following text). After that, a surgeon simulates the surgery by virtually cutting the 3D model into multiple bony segments and moving them individually to their desired positions. This is mainly achieved based on 3D cephalometric analysis, in which the patient’s clinical examination and cephalometric values are compared to the normative values derived from normal subjects [1]. The cephalometric analysis is a group of anatomical landmark-based linear and angular measurements of the skeleton and face. While cephalometric analysis works reasonably well in correcting straightforward jaw deformities, it is inadequate in treating patients with complex CMF defects (e.g. trauma). Instead of relying on population-averaged measurements, patient-specific reference anatomy is needed for high-precision planning of complex reconstructive surgery. Ideally, the pre-traumatic CT scan of the patient can be used to construct a reference shape model for surgical planning. Unfortunately, such pre-traumatic CT scan usually does not exist. Therefore, the purpose of this article is to estimate a patient-specific reference bony shape model for planning the surgical correction of post-traumatic CMF defects.
There are several methods proposed in the past decade for CMF skeleton reconstruction. The most commonly used method is the mirror-imaging mapping [2], which is realized by mapping the normal facial skeleton side to the defected side. Since it is based on the hypothesis of absolute symmetric human facial structure, this method is very limited and cannot handle the cases losing normal structures on both sides (e.g. bilateral defects). Statistical shape model (SSM) is another common method applied for normal facial skeleton estimation [3]. In this method, a set of facial bone shapes from normal subjects are first acquired, and then the principal component analysis (PCA) is applied on these shapes to construct a SSM [4]. By fitting the established SSM onto the remaining normal parts of patient’s facial bone, the patient’s normal bone shape is estimated. A main limitation of the SSM-based method is its weak generalization capability, because the SSM is constructed on a small available dataset of normal subjects. Recently, the method of using geometric deformation was proposed to estimate the normal facial bone [5, 6]. The main idea of this method is to deform the patient’s defected facial bone with an estimated deformation field to obtain its normal version. The deformation field can be calculated using the surface interpolating techniques of thin plate spline (TPS) or Laplacian surface editing [7] based on the two sets of landmarks, which are the landmarks located on the patient’s bone and the corresponding normal bone landmarks estimated, respectively. The geometric deformation-based method is able to produce an accurate normal bone estimation relative to other conventional methods. However, it cannot be used for the patients with large defects, for which only a limited number of landmarks located on the remaining structures would cause the deformation field estimation to fail. Bottom line, all abovementioned methods only work on certain types of defects, they cannot be generalized to all types of CMF defects. Thus, there is an urgent need, from clinicians, to develop a generalized method of using reference shape model.
Our hypothesis is that the patient’s (casual) portrait photographs, taken prior to the trauma, can be utilized to restore the “normal” bony shape in the areas with traumatic defects. Our approach involves three steps. First, we reconstruct the patient’s 3D facial surface from pre-trauma two-dimensional (2D) portrait photographs. Second, we generate an initial estimate of the patient’s normal bony shape via sparse representation [8] based on a database of paired facial and bony shape models. Third, we refine the initial estimate of the bony shape by registering it to the post-traumatic bony shape (i.e., the post-traumatic 3D CT model). The deformable registration is regularized by a SSM constructed from the bony shape surfaces of normal subjects.
The contribution of this study is that we applied the 2D portrait photographs and 3D post-traumatic CT for patient-specific reference model estimation, with an initialization from a correction model and the refinement from a deformable shape model. Clinically, this approach makes a paradigm shift on the way that surgeon used to plan reconstructive surgeries. Instead of using linear and angular measurements and surgeon’s imagination, a patient-specific reference bony shape model can accurately guide surgeons to plan the reconstructive surgery in treating patients with post-traumatic CMF defects.
2. Method
The proposed method, summarized in Fig. 1, consists of three major steps: 1) reconstruction of pre-traumatic 3D facial surface, 2) estimation of initial reference bony shape model, and 3) refinement of the bony shape model.
Fig. 1.
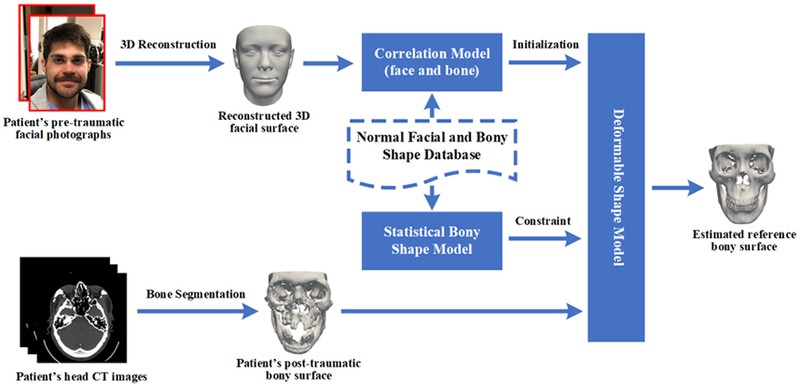
Overview of our proposed approach.
2.1. Reconstruction of Pre-Traumatic 3D Facial Surface
A 3D facial surface is estimated based on the patient’s pre-traumatic 2D portrait photographs. This is achieved by matching a set of 68 3D facial key-points, which are reconstructed from a photograph using a convolutional neural network (CNN) based method [9], with the corresponding key-points on the mean face of the Basel Face Model (BFM) [10]. For each photograph, the mean face is warped using a dense deformation field generated by TPS interpolation. Finally, all warped surfaces are merged into a single 3D facial surface using the method described in [11].
2.2. Estimation of Initial Reference Bony Shape Model
We construct a model that relates facial and bony surfaces, both of which are obtained with head CT scans of a group of normal subjects. An initial estimation of the patient’s normal bony structure is obtained by feeding the patient’s 3D facial surface to this model.
Normal Facial and Bony Shape Database.
3D facial and bony surfaces are generated using marching cubes for each normal subject after CT bone segmentation. The facial and bony surfaces of different subjects are rigidly aligned using the landmarks extracted using the method described in [12]. In order to establish correspondences for the extracted surfaces across the different subjects, we non-rigidly map a template surface onto each aligned surface using coherent point drift (CPD) algorithm. The template surface is defined as one of the aligned surfaces, and its shape is the closest to the averaged shape of the entire set of surfaces.
Correlation Model.
The initial bone shape model is estimated using sparse representation technique with paired face and bone dictionaries, DFace and DBone. Each column of a dictionary matrix corresponds to the 3D coordinates of all points of a surface. Given a vector containing the coordinates of surface points of a patient’s estimated normal facial surface, we solve for the sparse coefficient vector C:
| (1) |
where λ1 and λ2 are the two regularization parameters used to control the sparsity of the representation and are empirically set to 0.1 and 0.01, respectively. With the calculated sparse coefficient vector C*, the patient’s normal bony surface points are estimated by
| (2) |
Finally, the patient’s normal bony surface model can be derived from the bone template surface based on the estimated surface points.
Initial Normal Bony Shape Estimation.
We first map the patient’s normal facial surface onto the imaging space of the CT facial template using iterative closest point (ICP) algorithm. Then, the corresponding points on the mapped facial surface are extracted by non-rigid surface matching between the mapped facial surface and the normal facial template surface using the CPD algorithm. Finally, we achieve an initial normal bony shape estimation by inputting the corresponding points into the correlation model.
2.3. Refinement of the Initially-Estimated Reference Model
To refine the initially-estimated reference bony shape, we utilize the adaptive-focus deformable shape model (AFDSM) [13] to deform the initial estimation onto the patient’s post-traumatic bony surface. The AFDSM-based non-rigid surface matching is realized by first defining an attribute vector on each vertex. The neighboring vertexes of each vertex Vi are organized into different layers on the surface mesh, where each neighboring vertex in the kth layer is connected to Vi by k edges. After that, the attribute vector Fi of vertex Vi is defined as follows,
| (3) |
where fi,k denotes the determinant of a matrix that contains position information of vertex Vi and its three nearest neighboring vertexes within the kth layer, R denotes the number of neighboring layers for Vi (R = 6), and N is the total number of vertexes on the surface mesh. Based on the attribute vector Fi, the energy function is defined as follows,
| (4) |
where denotes the degree of attribute vector difference between the initial and deformed shapes for vertex Vi, and denotes the degree of attribute vector difference between the deformed and target shapes for vertex Vi. The initial and target shapes are defined as the initially-estimated bony surface and the patient’s post-traumatic bony surface, respectively. We applied a greedy deformation algorithm to minimize the energy function E in Eq. (4) based on affine transformation.
To guarantee the normality of the deformed shape after each optimization iteration, the deformation procedure is further regularized within a statistical normal shape. A SSM of the bony shape is constructed from the normal bony shape database (see Section 2.2) via PCA, as given below,
| (5) |
where denotes the reconstructed bony shape by applying the SSM on Si, and Si denotes the bony shape at the i-th iteration, denotes the mean bony shape from the normal bony shape database, Wi is a coefficients vector, and P is a matrix of principal components. The is used to constrain the optimization as follows,
| (6) |
where is the corresponding updated bony shape, and αi is a hyperparameter that determines the weight between and Si, and is gradually reduced so that the last deformed shape is closer to the target shape (αiϵ[0.60, 0.95]). At the end of each iteration, the deformed shape is updated and used as input for the next iteration.
3. Experiments and Results
3.1. Materials and Methods
A set of CT scans of 30 normal subjects were used to construct the normal facial and bony shape database. These de-identified CT data were collected in an unrelated project [14]. For each subject, the CT scans were segmented for generating 3D models. Following the clinical routine, 51 anatomic landmarks were digitized.
We first simulated synthetic patient data from CT images of normal subjects for evaluation. For each testing synthetic sample, synthetic 2D portrait photographs were first generated. The BFM mean facial surface was deformed onto the testing subject’s facial CT surface using the CPD algorithm. A statistical facial texture model [10] was then applied to assign a color value on each surface vertex of the deformed BFM surface. The deformed facial surface was then rendered in 3D space, and multiple screen shots of the 3D face were taken to mimic 2D portrait photographs. Afterward, synthetic post-traumatic bony shape was generated. An experienced CMF surgeon manually edited the normal CT bony surface, mimicking a unique type of common realistic CMF trauma on the testing subject.
To perform evaluation on synthetic patient data, each subject was used in turn as the testing sample, while the remaining 29 subjects were used to construct a normal facial and bony shape database. Each synthetic patient data was fed into our proposed framework to estimate the reference bony shape. Then, the quantitative evaluation was completed by measuring the distances between the corresponding landmarks on the estimated and original bony surfaces. The qualitative evaluation was completed by a different CMF surgeon, who ranked the similarity of the two surfaces using a 1-3 visual analog score (VAS, 1: the same, 2: similar but not the same, and 3: different).
Finally, our approach was tested on three real patients who suffered from severe facial trauma due to traffic accidents and gunshot wounds. Each patient had undergone multiple surgeries to reconstruct their facial defects. We used the patient’s pre-traumatic 2D portrait photographs and post-traumatic CT scans to estimate a reference model with our proposed approach. The predicted reference shape models were compared to their actual postoperative CT models after final reconstructive surgery.
3.2. Results
The quantitative results for synthetic data are summarized in Table 1. The averaged distance between the estimated and the actual surface was 3.7 mm, which is a high degree of accuracy for post-traumatic reconstructive planning. The qualitative results of synthetic data also showed: same (26/30), similar (4/30), and different (0/30). Fig. 2 shows the results of eight randomly selected synthetic testing subjects. In addition, the CMF surgeon was satisfied with all the results that he would use them clinically as a reference model to guide reconstructive surgery.
Table 1.
Facial bone estimation error (in mm) on synthetic data with our proposed approach.
| Mean | Standard Deviation | Median | Minimum | Maximum |
|---|---|---|---|---|
| 3.68 | 0.43 | 3.66 | 2.91 | 4.90 |
Fig. 2.
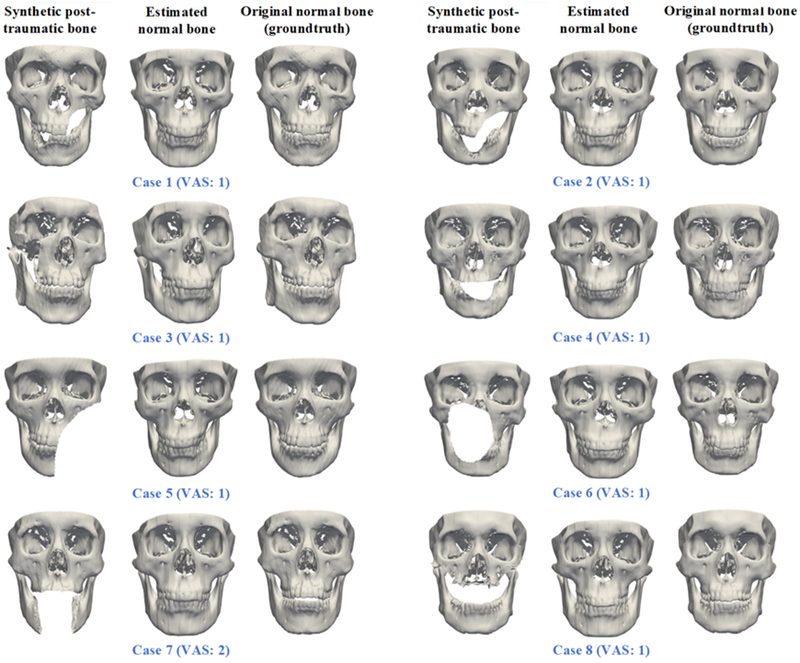
The qualitative evaluation results (shown on eight randomly selected synthetic patients).
We also successfully estimated the reference models for real patients. According to the CMF surgeon after visual inspection of the results, our estimated bony shape models for the real patients were clinically acceptable. Fig. 3 illustrates the comparison of the original trauma, the estimated reference bony shape model, and the postoperative outcome of a representative patient. Please note: His surgery was planned using conventional CASS method. Therefore, the postoperative outcome was not necessarily a ground truth.
Fig. 3.
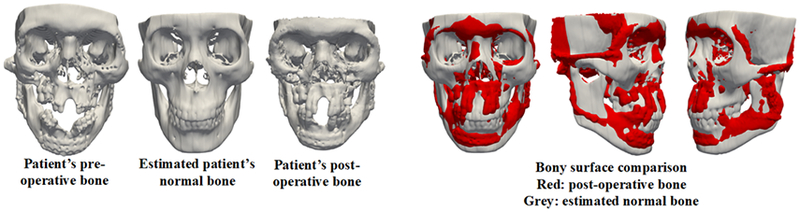
A comparison of the original trauma, the estimated reference bony shape model, and the postoperative outcome of a real patient.
4. Discussion and Conclusion
There is no definitive quantitative measures on the success of post-traumatic reconstruction due to its complexity. The current clinical standard for post-traumatic reconstruction is “surgeons do the best and patient accepts surgical outcomes”. Clinicians plan surgery and evaluate postoperative outcomes subjectively for overall facial harmony, with the limited help of linear and angular measurements of size, position, orientation and symmetry measurement of each facial unit. Therefore, without an estimated patient-specific reference model as we proposed in this study, we have to rely on surgeon’s subjective evaluation as they do clinically, and this is why the proposed approach is important in the field of CMF skeleton reconstruction.
To conclude, we propose an automatic approach to estimate a patient-specific reference shape model for guiding the surgical planning of CMF post-traumatic reconstruction. In this approach, a 3D facial model is reconstructed from the patient’s portrait photographs that were taken prior to the trauma. Then, a sparse representation is applied to construct a correlation model between face and bone. After that, the reconstructed 3D face is fed into the correlation model to achieve an initial estimation. Finally, the AFDSM algorithm is applied to refine the initial estimation based on the patient’s post-traumatic bone model and a statistical normal shape model. The results of evaluations have confirmed that our proposed approach is capable of estimating the normal bony shape of post-traumatic CMF patients.
Acknowledgment.
This work was supported in part by NIH grants (R01 DE022676 and R01 DE027251).
References
- 1.Xia J, et al. : Algorithm for planning a double-jaw orthognathic surgery using a computer-aided surgical simulation (CASS) protocol. Part 2: three-dimensional cephalometry. Int. J. Oral Maxillofac. Surg 44(12), 1441–1450 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gellrich NC, et al. : Computer assisted oral and maxillofacial reconstruction. J. Comput. Inform. Technol 14 (1):71–77 (2006) [Google Scholar]
- 3.Anton FM, et al. : Virtual reconstruction of bilateral midfacial defects by using statistical shape modeling. J. Oral Maxillofac. Surg 47(7), 1054–1059 (2019) [DOI] [PubMed] [Google Scholar]
- 4.Heimann T, Meinzer H: Statistical shape models for 3D medical image segmentation: A review. Med. Imag. Anal 13(4), 543–563 (2009) [DOI] [PubMed] [Google Scholar]
- 5.Wang L, et al. : Estimating patient-specific and anatomically correct reference model for craniomaxillofacial deformity via sparse representation. Med. Phys 42(10), 5809–5816 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Xie S, et al. : Laplacian deformation with symmetry constraints for reconstruction of defective skulls. In Proc. International Conference on Computer Analysis of Images and Patterns, pp. 24–35. (2017) [Google Scholar]
- 7.Sorkine O, et al. : Laplacian surface editing. In Proceedings of Eurographics/ACM SIGGRAPH symposium on Geometry processing, pp. 175–184. (2004) [Google Scholar]
- 8.Donoho DL: For most large underdetermined systems of linear equations the minimal ℓ1-norm solution is also the sparsest solution. Commun. Pure Appl. Math 59(6), 797–829 (2006) [Google Scholar]
- 9.Bulat A, Tzimiropoulos G: How far are we from solving the 2d & 3d face alignment problem?(and a dataset of 230,000 3d facial landmarks). In Proc. IEEE Int. Conf. Comp. Vis, vol. 1, p. 8 (2017) [Google Scholar]
- 10.Paysan P, et al. : September A 3D face model for pose and illumination invariant face recognition. In Proceedings of IEEE International Conference on Advanced Video and Signal Based Surveillance, pp. 296–301 (2009) [Google Scholar]
- 11.Piotraschke M, Blanz V: Automated 3d face reconstruction from multiple images using quality measures. In Proc. IEEE Conf. Comput. Vis. Pattern Recognit, pp. 3418–3427. (2016) [Google Scholar]
- 12.Zhang J, et al. : Automatic craniomaxillofacial landmark digitization via segmentation-guided partially-joint regression forest model and multiscale statistical features. IEEE Trans. Biomed. Eng 63(9), 1820–1829 (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shen D, Davatzikos C: An adaptive-focus deformable model using statistical and geometric information. IEEE Trans. Pattern Anal. Mach. Intell 22(8), 906–913 (2000) [Google Scholar]
- 14.Yan J, et al. : Three-dimensional CT measurement for the craniomaxillofacial structure of normal occlusion adults in Jiangsu, Zhejiang and Shanghai Area. China J. Oral Maxillofac. Surg 8, 2–9 (2010) [Google Scholar]


