Improved free-energy landscape reconstruction of bacteriorhodopsin highlights local variations in unfolding energy

Abstract

Precisely quantifying the energetics that drive the folding of membrane proteins into a lipid bilayer remains challenging. More than 15 years ago, atomic force microscopy (AFM) emerged as a powerful tool to mechanically extract individual membrane proteins from a lipid bilayer. Concurrently, fluctuation theorems, such as the Jarzynski equality, were applied to deduce equilibrium free energies (ΔG₀) from non-equilibrium single-molecule force spectroscopy records. The combination of these two advances in single-molecule studies deduced the free-energy of the model membrane protein bacteriorhodopsin in its native lipid bilayer. To elucidate this free-energy landscape at a higher resolution, we applied two recent developments. First, as an input to the reconstruction, we used force-extension curves acquired with a 100-fold higher time resolution and 10-fold higher force precision than traditional AFM studies of membrane proteins. Next, by using an inverse Weierstrass transform and the Jarzynski equality, we removed the free energy associated with the force probe and determined the molecular free-energy landscape of the molecule under study, bacteriorhodopsin. The resulting landscape yielded an average unfolding free energy per amino acid (aa) of 1.0 ± 0.1 kcal/mol, in agreement with past single-molecule studies. Moreover, on a smaller spatial scale, this high-resolution landscape also agreed with an equilibrium measurement of a particular three-aa transition in bacteriorhodopsin that yielded 2.7 kcal/mol/aa, an unexpectedly high value. Hence, while average unfolding ΔG₀ per aa is a useful metric, the derived high-resolution landscape details significant local variation from the mean. More generally, we demonstrated that, as anticipated, the inverse Weierstrass transform is an efficient means to reconstruct free-energy landscapes from AFM data.

I. INTRODUCTION

Membrane proteins perform critical biological functions, such as light harvesting, signaling, and transport. To carry out these and other diverse functions, they fold into equilibrium structures within a lipid bilayer.¹ Yet, predicting the structure and stability of membrane proteins significantly lags behind the success for globular proteins.¹ For instance, models still struggle to predict the tilt and overall packing of transmembrane (TM) α-helices. Hence, there is an ongoing need to better quantify the molecular forces that drive and stabilize the folding of membrane proteins. As with globular proteins,² the energy landscape provides the fundamental framework for understanding membrane-protein folding and structure stabilization.³

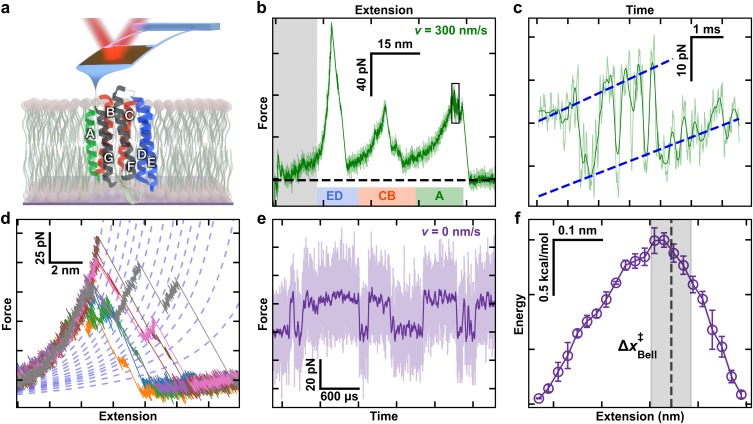
Single-molecule force spectroscopy (SMFS) has emerged as an important tool in determining the energetics underlying the folding and unfolding of individual proteins.^4–7 For membrane proteins, atomic force microscopy (AFM) is the modality of choice⁸ since individual proteins can be mechanically extracted from their native bilayer.⁹ In the canonical assay, the tip of a cantilever is pressed into bacteriorhodopsin (BR) embedded in its native lipid bilayer to promote nonspecific attachment.⁹ The tip is then retracted at a constant velocity, while force is deduced from the bending of the cantilever, revealing a series of unfolding peaks in the force-extension curve [Figs. 1(a) and 1(b)]. The dominant peaks correspond to pulling on the top of TM helix pairs or a terminal helix, notably the ED and CB helix pairs as well as the A helix. Importantly, these AFM-based studies provide insight into the energetics of membrane proteins in lipid bilayers, rather than in detergent. Moreover, AFM studies provide a reproducible reference state, the fully unfolded protein. In contrast, the “unfolded” protein in ensemble unfolding assays retains α-helical content and therefore provides a poor reference state.¹

FIG. 1.

High-resolution studies of bacteriorhodopsin (BR). (a) A cartoon illustrating BR being unfolded from its C-terminal end using a modified, ultrashort cantilever. Each helix is denoted by a letter. Color coding highlights the unfolding topology as helix pairs or the terminal A helix is extracted. (b) A canonical force-extension curve while stretching at v = 300 nm/s shows the major intermediates corresponding to pulling on the top of the E, C, and A helices. The initial portion of the force-extension curves was not analyzed due to the confounding effects of non-specific surface adhesion (grey box). The colored bars correspond to the colored helical regions from panel (a). (c) Force-vs-time record of the highlighted black box in panel (b) shows near-equilibrium unfolding and refolding at the top of helix A over a 13-amino-acid (aa) segment. (d) Multiple force-extension curves of BR show numerous detected unfolding intermediates. Curves were well modeled by a worm-like chain model within a particular state (dashed lines). (e) Force-vs-time record shows repeated unfolding and refolding of a 3-aa segment during an equilibrium assay (v = 0 nm/s) near the top of helix E. For clarity, 5-MHz data (light purple) were smoothed to 25 kHz (dark purple). (f) A reconstructed 1D free-energy landscape based on ∼100-ms records of equilibrium data with 1-μs resolution tilted to F_1/2, the force at which the two states are equally likely to be occupied. Reconstruction was based on p_fold.⁴⁰ Error bars represent the standard error of the mean. Dashed line represents the location of transition state determined from a Bell analysis of state lifetime, with the grey box denoting the standard deviation in that localization. The data for Figs. 1(b)–1(f) are from Ref. 18.

Complementing experimental advances that led to SMFS studies of individual proteins and nucleic-acid structures, theoretical advances enabled the determination of equilibrium free-energy values (ΔG₀) from analysis of non-equilibrium force-extension curves.¹⁰ Such analysis provides important information beyond the distances to transition states (Δx^$‡$) and the zero-force dissociation rate constant (k_off) determined using the Bell-Evans analysis of dynamic force spectroscopy data.^11,12 In particular, as demonstrated in pioneering studies of structured RNA using optical tweezers,^13,14 a 1D free-energy landscape can be obtained by extending the Jarzynski equality²⁴ via the weighted histogram method developed by Hummer and Szabo.¹⁰ Salient to this present work, Hummer and Szabo’s original paper applied the weighted histogram method to deduce the free-energy landscape for the ED helix pair bacteriorhodopsin, yielding an average of ΔG₀ of 1.1 per amino acid (aa) estimated from eight force-extension curves. Using significantly more traces (N ≈ 600), Preiner et al. extended this analysis over five helices (E–A) and reported an average ΔG₀ of 1.3 ± 0.2 kcal/mol/aa (mean ± SD).¹⁵

A higher-resolution description of the free-energy landscape enables a more quantitative comparison between the location and lifetimes of short-lived unfolding intermediates and the underlying energy landscape. Recent advances in applying modified ultrashort cantilevers optimized for 1-μs resolution SMFS^16,17 enabled the measurement of bacteriorhodopsin with a 100-fold higher time resolution and 10-fold higher force precision that, in turn, revealed rapid near-equilibrium folding [Fig. 1(c)] and a multitude of previously unresolved, transiently occupied intermediates [Fig. 1(d)].¹⁸ These cantilevers also enabled the first equilibrium study of membrane protein folding, where a particular three-amino-acid transition near the top of the E helix repeatedly unfolded and refolded [Fig. 1(e)]. Reconstruction of the free-energy landscape underlying this transition [Fig. 1(f)] revealed an unexpectedly large ΔG₀ per aa (2.7 kcal/mol) at F = 0 pN. Here, we merged these experimental advances in acquiring high-resolution force-extension curves with theoretical advances in reconstructing the landscape from non-equilibrium records. In particular, we used the inverse Weierstrass transform (IWT) applied in conjunction with the Jarzynski free-energy integral to avoid convolving the compliance of the AFM cantilever into the resulting free-energy landscape.¹⁹ Importantly, the IWT works best for studies using a stiffer force probe¹⁹—making it particularly suitable for AFM-based assays (k ≈ 6–100 pN/nm)—due to their higher probe stiffness relative to earlier application in an optical-trapping-based assay (k = 0.4 pN/nm).²⁰ The resulting landscape yielded an average unfolding free energy per amino acid (aa) of 1.0 ± 0.1 kcal/mol (mean ± SD), in close agreement with past single-molecule studies.^10,15,21 Moreover, on a smaller spatial scale, this landscape also agreed with the recent equilibrium measurement that showed an unexpectedly high ΔG₀ per aa near the top of the E helix. Hence, while average unfolding ΔG₀ per aa is a useful metric, the resulting high-resolution landscape confirmed significant local variations from the mean.

II. FREE-ENERGY LANDSCAPE RECONSTRUCTION

As background, the Jarzynski equality is remarkable because it relates the work done during many repetitions of a non-equilibrium process to the equilibrium free-energy difference as a function of an experimental parameter. For our work, the experimental parameter was the position of the cantilever base relative to the surface or “z.”²² More precisely, the Jarzynski equality is a thermodynamic relationship between the Helmholtz free energy of a system A(z) and the measured work W(z),

$$e^{-\beta A\left(z\right)}={⟨e^{-\beta W\left(z\right)}⟩}_N,$$ (1)

where z is the zero-force equilibrium position of the force probe, β is the inverse of the thermal energy k_BT, and the average is taken over N independent stretching trajectories, each starting and ending at the same choice of z.^10,23,24 The Jarzynski equality is exact only in the limit as N → ∞ but is approximately true for finite N. In practice, SMFS experiments apply the Jarzynski equality by repeatedly folding or unfolding a single molecule of interest using a force probe. In this case, the work is the integral of the force as a function of the cantilever position z. For example, in the constant velocity experiments used in our AFM assay, z(t) = vt + z_i, and the integral for each stretching experiment starts at the same well-defined z_i associated with the aligned curves (see below). Tip-sample separation, which is also the molecular extension (x) in an AFM assay, is not uniquely defined at all values of z. The molecule may be in different folding states and therefore different molecular extensions, referred to henceforth as q as is common in the landscape-reconstruction literature.¹⁹ The Jarzynski equality requires that all molecules included in the calculation start (z_i) and finish (z_f) in an equilibrium state.

Hummer and Szabo’s original extension of the Jarzynski equality for SMFS studies determines the landscape as a function of molecular extension (q), instead of SMFS probe position (z), and also removes the energetic contribution of the force probe via a weighted histogram method.¹⁰ In subsequent work, they applied an IWT to simplify this calculation and make more efficient use of a limited set of force-extension curves by assuming a stiff, harmonic pulling apparatus.^19,20 Put differently, the curvature (i.e., the second spatial derivative) of the true underlying energy landscape should not exceed the stiffness of the force probe. Indeed, the consequence of not fulfilling this assumption was theoretically anticipated¹⁹ and experimentally demonstrated for a RNA pseudo-knot studied using an optical trap.²⁰ In that case, the derived landscape was filtered by the soft probe leading to a lower barrier height (akin to applying a spatial filter that smooths out sharp features). Hence, energy landscape reconstruction by the IWT is well suited to AFM-based assays due to the higher stiffness of AFM cantilevers in comparison to optical traps.^19,20

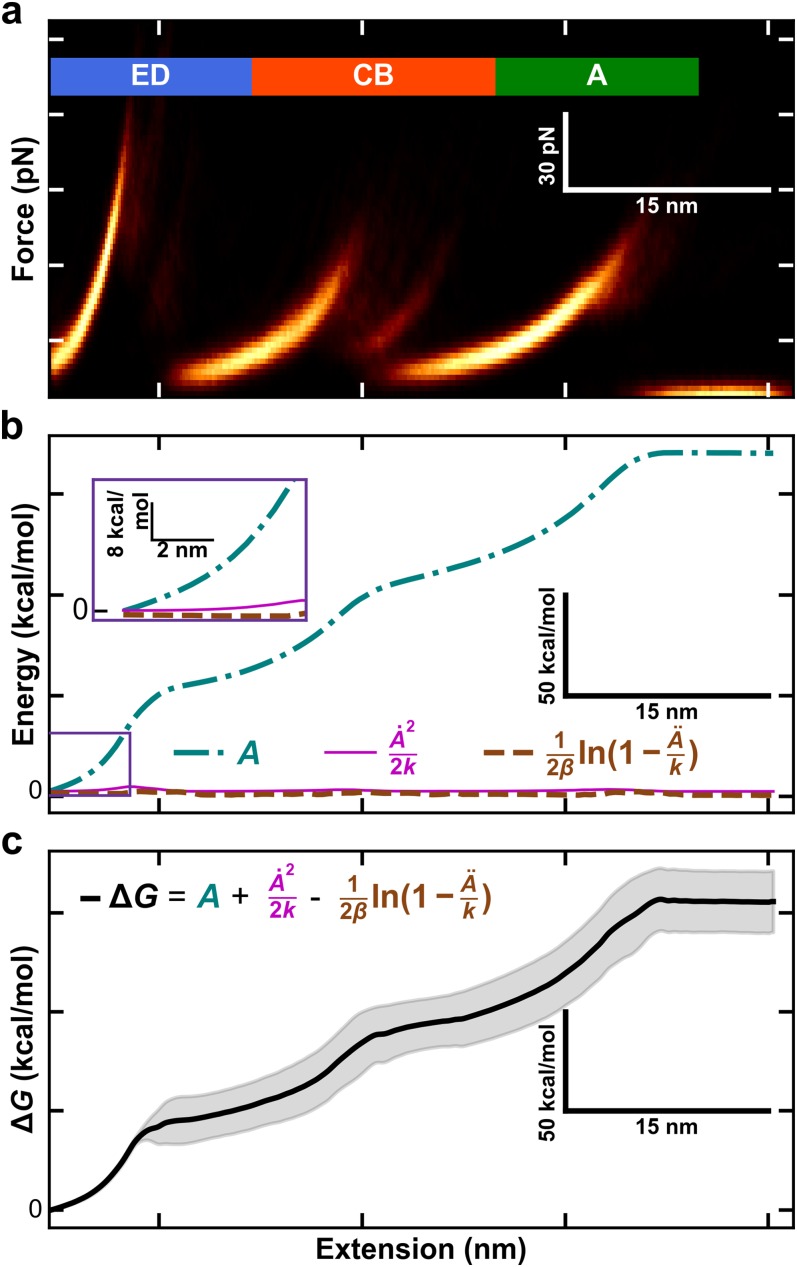
As an input for IWT reconstruction of BR, we used a set of 106 force-extension curves of BR extracted from its native lipid bilayer (purple membrane for BR) acquired using focused-ion-beam modified BioLever Fast cantilevers (AC10DS, Olympus). The details of this data acquisition and the force-extension curves have been previously published.¹⁸ Briefly, modified cantilevers (k ≈ 10–40 pN/nm) were pressed into the purple membrane at ∼1 nN for 1 s and retracted from the surface at a constant velocity (v) of 300 nm/s. Data were recorded at 5 MHz on a commercial AFM (Cypher ES, Asylum Research) and then smoothed with a second-order, 501-point Savitsky-Golay filter for all subsequent analyses. As is standard for SMFS-studies of BR,⁸ the curves were laterally aligned to superimpose the major obligate intermediate associated with pulling on the top of the E helix. These aligned traces [Fig. 2(a)] then served as an input to calculate the free-energy landscape via the IWT. The unfolding of the GF helix pair was not analyzed due to the confounding effects of non-specific tip-sample adhesion.

FIG. 2.

Process for free-energy landscape reconstruction of BR using an inverse Weierstrass transform (IWT). (a) A heat map of all force-extension curves used in this work. Data within ∼18 nm of the surface are excluded due to surface adhesion. (b) Different components for calculating the molecular free energy ΔG₀ as a function of the molecular extension when using the IWT. The three components used in computing ΔG₀ as defined in Eq. (5): A (aqua, dotted-dashed) and terms involving its first and second derivative (pink solid line and brown dashed line, respectively). To promote comparison to panels (a) and (c), the plotted lateral axis is q, molecule extension. (c) The ΔG₀ free energy as a function of molecular extension. Shaded region reports the standard deviation as deduced from a bootstrap analysis.

The IWT reconstructs the free-energy landscape, approximately removing the contribution of the force probe, by calculating statistics on an ensemble of N force-extension curves. For a particular curve n with measured force F_n(z), the work used by the IWT is defined as

$$W_n\left(z\right)={\int }_{z_i}^z{F}_n\left(z^{\prime }\right)d{z}^{\prime },$$ (2)

where z runs from z_i to z_f at a given velocity v for all N force-extension curves. The Jarzynski equality determines the Helmholtz free energy A(z), which includes energy from the probe. The IWT approximately removes the contribution of the probe by calculating the so-called work-weighted ensemble statistics. The work-weighted force and force squared, denoted with double brackets, are defined at each z as

$$⟨⟨F\left(z\right)⟩⟩=\frac{{⟨e^{-\beta W_n\left(z\right)}{F}_n\left(z\right)⟩}_N}{e^{-\beta A\left(z\right)}}$$

and

$$⟨⟨F^2\left(z\right)⟩⟩=\frac{{⟨e^{-\beta W_n\left(z\right)}{F_n}^2\left(z\right)⟩}_N}{e^{-\beta A\left(z\right)}},$$ (3)

where ${⟨X⟩}_N$ denotes an average of X over the ensemble of force-extension curves at a fixed z. These work-weighted values are related to the first and second spatial derivatives of the Helmholtz free energy as follows:

$$Ȧ\left(z\right)=⟨⟨F\left(z\right)⟩⟩$$

and

$$1-\frac{Ä\left(z\right)}{k}=\frac{\beta }{k}\left(⟨⟨F^2\left(z\right)⟩⟩-{⟨⟨F\left(z\right)⟩⟩}^2\right).$$ (4)

The IWT-based reconstruction uses the first and second derivatives to reconstruct the free-energy landscape as a function of molecular extension¹⁹

$$G\left(q=z-\frac{Ȧ\left(z\right)}{k}\right)\approx A\left(z\right)-\frac{Ȧ{\left(z\right)}^2}{2k}+\frac{1}{2\beta }\text{ln}\left(1-\frac{Ä\left(z\right)}{k}\right).$$ (5)

Importantly, G(q) is approximately the free energy of the molecule, instead of the free energy of the molecule and the probe. To avoid errors associated with numerical derivatives of noisy data, we calculated the energy derivatives, $Ȧ\left(z\right)$ and $Ä\left(z\right)$, directly from the primary work-weighted force and force squared (see Fig. S1 of the supplementary material) which, in turn, allowed G(q) to be determined. To avoid errors in combining data sets acquired using different cantilever stiffnesses (k), we chose z_i = 18 nm + (20 pN/k), which corresponded to approximately F = 20 pN at an extension of 18 nm when pulling on the top of the ED helix pair. Each set of data, containing a minimum of 20 force-extension curves, corresponded to one cantilever and was reconstructed separately. After the transform was completed, the resulting free-energy landscapes were functions of molecular extension q (instead of z) and were averaged based on the number of traces associated with each cantilever data set. As in previous work,¹⁵ we found that we needed a minimum of 20 traces per cantilever to limit reconstruction error to reasonable levels.

Uncertainties in the landscape and its first derivative were determined by a bootstrap analysis.²⁵ In brief, 250 synthetic data sets were generated from the original set of 106 curves using random resampling with replacement. Only synthetic data sets with $1-\frac{Ä\left(z\right)}{k}>0$, as required by the IWT, were counted towards the total of 250. From the resulting ensemble of 250 landscapes, the standard deviation in simulated mean values was calculated after smoothing with a third order, piecewise polynomial to 0.4 nm. This smoothing choice was chosen to approximately minimize the product of error in $Ġ\left(q\right)$ and in the least-squared fitting of G(q) across the bootstrapping rounds (see Fig. S2 of the supplementary material). Future work with more traces from individual cantilevers and from cantilevers with a narrower range in k will decrease the uncertainties in landscape reconstruction.

We illustrate the process of calculating the IWT for BR from Eq. (5) in Fig. 2. The starting data consist of 106 aligned force-extension curves. As shown in Fig. 2(a), the resulting heat map represents the ensemble of measurements needed to apply Jarzynski’s inequality and the inverse Weierstrass transform. To highlight the contributions of the three components in Eq. (5) in determining G(q), we color coded a plot of A(z) and the IWT corrections [Fig. 2(b)]. The corrections were obtained as described above, using work-weighted histogram statistics.^19,23 The resulting G(q) was deduced from the sum of these three components and represents the free energy of the ED, CB, and A helical pairs of bacteriorhodopsin [Fig. 2(c)]. Shaded regions represent the standard deviation deduced from the aforementioned bootstrap analysis.

III. RESULTS AND DISCUSSION

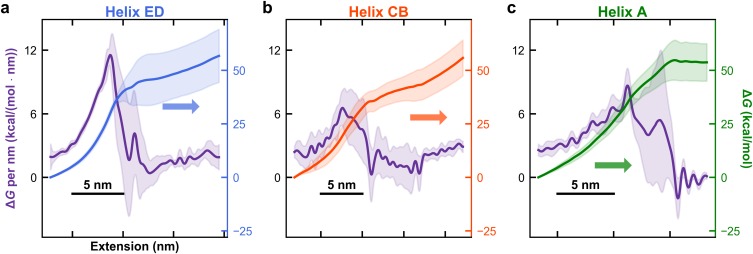
The local unfolding free energy of BR depended on the individual structural element being unfolded. Our resulting high-resolution free-energy landscape of BR’s final five helices showed significant variation in slope as a function of extension and therefore unfolding energy per amino acid [Fig. 2(c)]. To highlight this variation, we computed the free-energy landscape and ΔG₀ per nm as a function extension for the individual major structural components (ED, CB, and A helices) [Figs. 3(a)–3(c)]. The mean ΔG₀ per aa is 1.0 ± 0.1 kcal/mol (mean ± SD) when calculated from the unfolding of the ED, CB, and A helices [156 ± 15 kcal/mol (mean ± SD) over 160 amino acids of helices, traditionally taken as the top of the E-helix in AFM-based assays²⁶]. This average value is slightly larger than bulk denaturation studies that report ∼0.5 kcal/mol/aa²⁷ and similar to past single-molecule results of 1.1–1.3 kcal/mol per aa.^10,15,21

FIG. 3.

Local unfolding free energies as a function of extension vary broadly between and within BR’s major structural elements (the ED, CB, and A helices, respectively). (a) Local unfolding free energy per nm (left axis) and reconstructed energy landscape (right axis) for the ED helix pair. The local unfolding free-energy is the spatial first derivative of the reconstructed landscape. The standard deviations in the deduced values are the shaded region around the measured value as deduced by a bootstrap analysis. [(b) and (c)] Same analysis for the BC helix pair and the A helix, respectively.

For completeness, we note that most rigorous to-date experimental determination of the total ΔG₀ for the E–A helices is 227 ± 38 kcal/mol (mean ± SD) and is therefore significantly higher than our value of 156 ± 15 kcal/mol, a result not precisely reflected in the reported 1.3 kcal/mol per aa.¹⁵ The origin of this difference is that this prior work used 171 amino acids in their analysis, which includes an extra 11 amino acids associated with the loop between the top of E and F helices and the first turn of the F-helix. If we reanalyze this earlier result with the same number of amino acids as used in this present work, their value now becomes 1.4 ± 0.2 kcal/mol per aa. Our average unfolding energy per amino acid therefore lies below this prior experimental result. Possible origins of this difference could be the improved precision of our force-extension curves and/or some reduction in the total ΔG₀ values due to the IWT poorly resolving stiff portions of the landscapes compared to the weighted histogram method (see below).²⁰ Finally, a recent coarse-grained molecular dynamics simulation predicts a free energy of transfer from bulk water to lipid of −130 kcal/mol for the 160-aa sequence in our work or about 0.8 kcal/mol per aa for unfolding BR from its lipid bilayer (see Sec. S1 of the supplementary material).²⁸

Our work also documented that ΔG₀ per nm varied more than 15-fold, from 11 kcal/mol at the top of the ED helix pair to 0.6 kcal/mol at the bottom of the same helix pair. While it has long been known that hydrophobicity of the amino-acid sequence within the lipid bilayer and inter- and intra-helix interactions contribute to this variation,²⁹ recent work also shows variations in the strength of hydrogen bonds within TM helices.³⁰ To convert this local, single-molecule force spectroscopy derived metric to the more commonly reported ΔG₀ per aa, we note that there are ∼3 amino acid residues per nm of contour length for an unstructured peptide based on crystallography (0.36 nm/aa).³¹ Given the elevated forces experienced during unfolding portions of the records, we approximated extension with contour length and therefore approximated a local value for ΔG₀ per aa as 1/3 of ΔG₀ per nm after taking the spatial derivative of the reconstructed free-energy landscape [e.g., Fig. 2(c)]. As described in Sec. II, the landscapes and its derivatives were calculated for each set of data derived from a cantilever of fixed stiffness, after smoothing with a piecewise polynomial to 0.4 nm. At the top of the ED helix pair, we observed the highest local ΔG₀ per aa followed by the top of the CB and A helices.

One immediate trend from these data was a higher ΔG₀ per aa when BR was more fully folded. Thus, looking forward, an assay that probes the initial unfolding of a membrane protein where most, if not all of intra- and inter-helix bonds are still intact, offers the best opportunity to precisely quantify ΔG₀ per aa under native-like conditions. Unfortunately, while a few studies have quantified the initial unfolding of the GF helix,^26,32 precise quantification remains hindered by non-specific adhesion between the tip and the surface.^8,9,15 Another trend in our data was that ΔG₀ per aa for unwinding the first portion of a TM helix pair was higher than when unfolding the second helix. Put more simply, once the first helix in a TM helix pair was extracted, the second helix took significantly less energy to extract.

Interestingly, we also achieved agreement between the unfolding free energies obtained by equilibrium and dynamic assays. As discussed in the Introduction, we had previously deduced an unexpectedly high ΔG₀ per aa [2.7 ± 0.1 kcal/mol (mean ± SEM)] for a particular transition near the top of the ED helix pair after reconstruction of the free-energy landscape from equilibrium data [Fig. 1(f)].¹⁸ The present IWT analysis of dynamic data yielded an average ΔG₀ per aa near the top of the ED helix, 2.9 ± 0.5 kcal/mol (mean ± SD), in agreement with the previous equilibrium result for a specific three-amino-acid transition.¹⁸

We emphasize that the ΔG₀ per aa measured here does not correspond to breaking a particular hydrogen-bond or fully solvating an amino acid out of a lipid bilayer but results from a convolution of angstrom-scale motion of each amino acid along the stretching axis. We also note that the reported values include the contribution of the extended, unfolded protein. In other words, since the ED helix was folded at the start of the analysis, the entropic contribution to stretching unfolded polypeptides to high force is part of the resulting ΔG₀. Future experimental advances and/or applying more sophisticated analysis can minimize or theoretically separate out the energy associated with stretching these compliant unfolded peptides.³³ However, the situation for BR is distinctly different from standard optical-trapping assays which use much longer, 300–600-nm double-stranded nucleic acid handles to accommodate the geometry of optical-trapping studies.^34–36

Somewhat unexpectedly, we observed a local landscape stiffness—the second derivative of the reconstructed landscape—greater than any particular cantilever stiffness used. Yet, Hummer and Szabo’s implementation of the IWT assumed a stiff probe, which should limit the reconstructed landscape from having a stiffness that exceeds the force probe.¹⁹ More quantitatively, the greatest landscape curvature for BR was 8 kcal/(mol nm²) or 55 pN/nm, larger than the stiffest cantilever used (40 pN/nm). We attribute this small discrepancy to errors in polynomial fitting and numerical differentiation. On the scientific front, it is therefore likely that our reconstructed landscape represents a lower bound on the local value of ΔG₀ per nm, akin to early studies of RNA pseudoknots studied with optical traps.²⁰ Hence, as shown in that optical-trapping work,²⁰ the weighted histogram method is better for reconstructing landscapes containing such “stiff” features. For the vast majority of BR’s landscape, the stiff-spring approximation of the IWT was fulfilled and yielded a more accurate landscape reconstruction (Fig. S3 of the supplementary material). In addition, the almost-negligible correction to the landscape from the $Ä$ term outside of the ED helix [Fig. 2(b), brown] confirmed that higher-order corrections were unlikely to affect the landscape of the CB and A helices. In fact, the corrections of the IWT to the Jarzynski equality were small except near the top of the E helix, which interestingly is also the same location where equilibrium flickering was previously reported [Fig. 1(e)]. Looking forward, using a stiffer cantilever is the obvious means to fulfill the stiff probe assumption. Yet, stiffer ultrashort cantilevers are not overdamped (quality factor Q > 0.5),¹⁶ violating an assumption underlying traditional force spectroscopy theories.^11,37,38 Hence, there is also ongoing need to optimize modified ultrashort cantilevers for higher k but low Q.

IV. CONCLUSION

As anticipated,^19,20 the IWT provides an efficient and accessible means to reconstruct free-energy landscapes when using AFM, even for complicated landscapes such as BR. The energy landscape reconstruction presented here highlights significant variation along the unfolding free-energy landscape. The overall trend is similar to early work¹⁵ but with improvements associated with reconstruction of the landscape from much higher resolution force-extension curves^16,18 and using the IWT¹⁹ that efficiently removes the energy contribution associated with the bending of the cantilever. As a result, we achieved a more accurate and higher-resolution reconstruction. The resulting landscape yielded an average ΔG₀ per aa of 1.0 ± 0.1 kcal/mol, in much better agreement with past single-molecule studies than our one prior determination of ΔG₀ per aa (2.7 kcal/mol) derived from an equilibrium assay probing a particular three-aa transition near the top of the ED helix pair. Importantly, on a smaller spatial scale, this high-resolution landscape also agreed with that prior equilibrium measurement of the three-aa transition (ΔG₀ = 2.9 ± 0.5 kcal/mol/aa). Indeed, the highest-measured curvature of the free-energy landscape (∼55 pN/nm) was limited by cantilever stiffness (∼10–40 pN/nm) and hence represents a lower bound of local determination of ΔG₀ per aa due to the underlying assumption of a stiff probe in applying the IWT.^19,20 Future developments that enable efficient unfolding and refolding over reversible transitions would enable comparing energy landscapes deduced from state-based models³⁹ with those used here, providing another method for investigating and verifying local free-energy landscape reconstruction of membrane proteins.

SUPPLEMENTARY MATERIAL

See supplementary material for three graphs that show the curvature of the BR landscape as a function of molecular extension and details of data analysis.