Molecular transport through membranes: Accurate permeability coefficients from multidimensional potentials of mean force and local diffusion constants

Abstract

Estimating the permeability coefficient of small molecules through lipid bilayer membranes plays an important role in the development of effective drug candidates. In silico simulations can produce acceptable relative permeability coefficients for a series of small molecules; however, the absolute permeability coefficients from simulations are usually off by orders of magnitude. In addition to differences between the lipid bilayers used in vitro and in silico, the poor convergence of permeation free energy profiles and over-simplified diffusion models have contributed to these discrepancies. In this paper, we present a multidimensional inhomogeneous solubility-diffusion model to study the permeability of a small molecule drug (trimethoprim) passing through a POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) lipid bilayer. Our approach improves the permeation model in three ways: First, the free energy profile (potential of mean force, PMF) is two-dimensional in two key coordinates rather than simply one-dimensional along the direction normal to the bilayer. Second, the 2-D PMF calculation has improved convergence due to application of the recently developed transition-tempered metadynamics with randomly initialized replicas, while third, the local diffusivity coefficient was calculated along the direction of the minimum free energy path on the two-dimensional PMF. The permeability is then calculated as a line integral along the minimum free energy path of the PMF. With this approach, we report a considerably more accurate permeability coefficient (only 2–5 times larger than the experimental value). We also compare our approach with the common practice of computing permeability coefficients based only on the translation of the center of mass of the drug molecule. Our paper concludes with a discussion of approaches for minimizing the computational cost for the purpose of more rapidly screening a large number of drug candidate molecules.

I. INTRODUCTION

Small molecules (<900 Da, generated by chemical synthesis), biomolecules (>10 000 Da, generated by bioengineering), and peptides (∼300-10 000 Da, generated by chemical synthesis and bioengineering) are usually selected as compounds for pharmaceutical drugs.¹ Small molecules are most commonly used for various reasons, including high chemical stability² and well-studied physicochemical properties.³ These advantages enable them to be taken orally, whereas peptides and biomolecules generally require parenteral administration (e.g., by injection) due to their degradation in the human digestion system. However, oral administration requires small molecules with high rates of absorption, especially for those absorbed through the intestines. As a result, pharmaceutical companies typically screen the absorption potential early in the discovery and development phase, when the investment in a compound is low, to remove poor performers and to identify candidates that need to be modified.⁴ Lipid bilayer membranes, in various forms, are the main physical barrier for the absorption of drug molecules, whether they are traversed in the transcellular pathway (moving through cells) or in the less common paracellular pathway (passing in between cells).⁵ Passive permeation,⁶ facilitated permeation,⁷ and vesicular transport⁸ are three main mechanisms for the transcellular process, among which passive permeation is dominant, especially for small molecules.⁹

Due to its importance, great effort has been devoted to understanding passive permeation of small molecules through bilayers for over 100 years.^9,10 In the first lipid bilayer permeation model proposed by Overton,¹¹ the permeability coefficient of a solute is solely correlated to its oil/water partition coefficient such that the lipid bilayer is represented by a homogeneous oil slab. Later, planar lipid bilayers were employed as one of the main experimental models to investigate the permeability coefficient of small molecules, in which two chambers with different concentrations of permeant are separated by planar lipid bilayers formed on small holes (∼1 mm²) in a polyethylene or Teflon platform.^12,13 In recent years, scientists have developed various lipid assays in vitro that are closely related to the observed physiological drug absorption data. Caco-2 is a cell-based assay that mimics the passage of drugs through the intestinal mucosa, where a monolayer of human colorectal carcinoma cells (characterized by morphological and functional similarities to the small intestinal epithelium cells) is grown on a filter separating two stacked microwell plates.^14,15 Madin–Darby Canine Kidney (MDCK) is another cell-based assay that is widely used with a similar experimental apparatus.¹⁶ Besides the cell-based assay, Parallel Artificial Membrane Permeation Assay (PAMPA) has been developed to utilize a filter coated with a solution of lipid material in inert organic solvent acting as the artificial membrane.^17,18 Since their introduction, the aforementioned in vitro methods have been greatly adapted by both academia and pharmaceutical industries in drug development, as tools of measuring permeability coefficients. However, despite their success, there are some shortcomings.

For example, the preparation of stable monolayers for the cell-based assay experiments (Caco-2 and MDCK) requires up to three weeks in a contamination-free environment, and the assay needs to be examined for tight-junction formation prior to use (to eliminate any potential paracellular pathways).¹⁹ The cell-based assay also contains endogenous transporter and efflux systems, which usually work against the passive permeation process, therefore complicating the data interpretation and reducing the reproducibility of the experiments.²⁰ The PAMPA methods focus on simplicity and flexibility, eliminating the slow growth period and possible contributions from transporters, while enabling the use of different lipids to construct the bilayer.²¹ Although the results from the two methods are generally similar, the PAMPA sometimes shows worse linear correlation with oral absorption than the cell-based assays do, which could be arguably allotted to the unknown phase formed by lipids in the PAMPA membranes.^22–24 Regardless of the experimental method chosen, the relative permeability coefficients of a series of small molecules are typically better reproduced than the absolute permeability coefficients of individual small molecules due to difficulties in measurement calibration and experimental perturbations.^9,25

In addition to the value of the permeability coefficient itself, it is important to understand the passive permeation process at an atomistic resolution, which is generally not possible with in vitro experiments alone, in order to provide a fundamental insight that can facilitate drug development both specifically and broadly. In this light, molecular dynamics (MD) simulations, which have revealed atomistic information for numerous physical and chemical processes in biological systems, offer a promising tool. Developed from the homogeneous model,²⁶ the inhomogeneous solubility-diffusion model is a more accurate in silico model that takes account the inhomogeneity of the interface between the bulk water and the lipid bilayer.^27,28 In this model, the resistivity coefficient (R), which is the inverse of the permeability coefficient (P_m), is computed as

$$R=\frac{1}{P_m}={\int }_{r_2}^{r_1}\frac{\text{exp}\left[\beta W(r)\right]}{D(r)}dr.$$ (1)

In this equation, r is a collective variable (CV) describing the permeation process, e.g., often the z component distance (z is perpendicular to the membrane) between the center of mass of the permeating drug and the center of mass of the lipid bilayer. W(r) is the free energy profile (potential of mean force or PMF) of the permeation with respect to r and D(r) is the local diffusivity of the permeating drug along the direction of r. Lee et al.²⁹ have recently computed the permeability coefficient of urea, benzoic acid, and codeine using MD simulations with different enhanced sampling techniques and concluded that their permeability coefficients agree within 1.5 log units (∼30-fold difference) of the experimental values. In a similar study in 2017, Bennion et al.³⁰ employed umbrella sampling³¹ MD simulations to comprehensively assess the passive permeability profile of a range of compounds through a lipid bilayer. Even though their in silico results differ from the in vitro results by about five log units, the relative permeability coefficients of a series of custom synthesized and closely related compounds are qualitatively predicted. Therefore, it remains very challenging for computational simulations to estimate a permeability coefficient that is within an order of magnitude of the experimental result.

There are several sources that contribute to the disagreement between in vitro and in silico permeability coefficients. The first one is the differences between the membrane used in the experiments and the simplified lipid bilayers used in the simulations. This difference is more significant in the cell-based assay experiment, where the cell membrane is made of various kinds of lipids, cholesterol, and transporters; however, even for the PAMPA experiment, a direct comparison between simulation and experiment is difficult to make (i.e., egg yolk was widely used to make the artificial membrane¹⁷) unless the artificial membrane is specifically made of a couple kinds of synthetic phospholipids.²¹ Simulating a physiologically relevant and multicomponent lipid bilayer that is consistent with the experiment remains mostly infeasible given the limited computation resources.³²

Besides the difference in the lipid bilayer, the accuracy of the in silico permeability coefficient depends largely upon the accuracy of the PMF, W(r) [because of the exponential factor in Eq. (1)], and the local diffusivity coefficient, D(r). Permeation is usually a rare event corresponding to high free energy barrier; thus, enhanced sampling methods are usually employed to assist the calculation of the PMF. Lee et al.²⁹ have computed the permeation PMF using umbrella sampling,³¹ replica exchange umbrella sampling,³³ adaptive biasing force,³⁴ and multiple-walker adaptive biasing force³⁵ and reported no definitive advantage for any of these methods in their ability to predict the drug permeability coefficient. However, none of the above enhance sampling methods utilized metadynamics (MetaD)³⁶ that is able to converge the estimate of PMF with proper tempering.^37,38 The recent development of transition tempered MetaD³⁹ (TTMetaD) has been proven to provide a reliable estimate of the PMF at the early stage of the simulation, especially for systems in which a rough knowledge of the PMF landscape is available prior to the simulation (i.e., an estimate of the positions of the minima and barrier between them on the PMF).⁴⁰ This behavior of the free energy sampling is essential for drug candidates considered by pharmaceutical companies since the number of drugs needing to be screened is usually large. The good performance of an enhanced sampling method with limited sampling is thus highly desirable to reduce the overall computational cost and hence time to solution. This has motivated us to utilize TTMetaD to achieve a more accurate permeation PMF and to do so more efficiently.⁴⁰ Moreover, TTMetaD has proven to be so accurate and rapidly convergent that it becomes possible to calculate a two-dimensional PMF for the drug permeation process, i.e., a PMF involving the coordinate of the permeating molecule normal to the membrane (usually the z-coordinate) plus a second key coordinate such as an orientation of the molecule relative to the lipid bilayer plane. These 2-D PMFs reveal a great deal more about the molecular conformations and orientations that are the most pertinent to the permeation process, and they can in principle provide valuable information to the drug designer to enhance the permeation.

A third challenge is the diffusion model that utilizes D(r) in Eq. (1), which is generally chosen as simply the diffusion along the z component (perpendicular to the lipid bilayer) of the distance between the center of mass of the permeating drug and the center of mass of the lipid bilayer.^29,30 Though the center of mass translation of a small molecule through a lipid bilayer is the most important component of a permeation process, there are other important degrees of freedom such as orientation of the drug with respect to the membrane, especially for drug candidate molecules that have both hydrophobic region(s) and hydrophilic region(s). Besides being an over simplified model to represent local diffusion, if this orientational degree of freedom is slow enough, using only the center of mass translation CV also slows down the convergence of the enhanced sampling calculation, sometimes leading to hysteresis in the PMF estimates.

As an example, the permeation of trimethoprim through a POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) lipid bilayer has clearly shown its preference in the orientation of the permeant: the difference in lipophilicity of the trimethoxybenzyl and pyrimidine group leads to tilted metastable configurations of trimethoprim interacting with the membrane (see Fig. 1).⁴⁰ As a result, the minimum free energy path (MFEP), which represents the average pathway over a large ensemble of the permeation processes, is zigzag instead of a straight diagonal line. An ideal representation of r should contain the information of the position of trimethoprim (which can be realized in the traditional usage of the center of mass distance) as well as the orientation of trimethoprim, and the local diffusivity coefficient, D(r), should represent the local diffusion along the direction of the MFEP. To our knowledge, there has not been such a permeability coefficient calculation that utilizes the MFEP from a multidimensional PMF, taking into account slow degrees of freedom other than the simple center of mass translation.

FIG. 1.

Left panel: Definition of the collective variables (CVs) used in the TTMetaD simulation. Right panel: 2D PMF (in kcal/mol) of trimethoprim permeation through a POPC lipid bilayer after 2.5 μs of simulation (0.5 μs on 5 replicas).

The purpose of this paper is therefore to demonstrate, through the example of the permeation of trimethoprim through POPC bilayer, that a combination of TTMetaD to improve the quality of W(r) and to increase its dimensionality, along with a computation of D(r) along the MFEP and a calculation of the permeability along that path from Eq. (1), can provide a systematic estimate of the permeability coefficient that is within one order of magnitude of the experimental result. As a comparison, we have also followed the conventional protocol of permeability coefficient calculation with only one CV (the center of mass translation). This paper concludes with discussions of the computational cost of our method and presents a test case that uses significantly less simulations but provides a reasonably accurate result. We anticipate this method can become a new standard of in silico permeability coefficient calculation. Future work will also focus on utilizing this approach to screen the relative permeability coefficient of a series of small molecule drugs.

II. METHODS

A. Transition-tempered metadynamics

In MetaD simulations, the process of interest (permeation in this case) is sampled by introducing a bias force on a small number of preselected CVs, s, that are expected to transition the system across the free energy barriers and to delineate the reactant and product minima. A history dependent bias potential (V_G), which usually has the form of a summation of Gaussian functions centered on previously visited points in CV space, is systematically added to the Hamiltonian.³⁶ As a result, the system is discouraged from revisiting configurations that have already been sampled and is encouraged to explore the high-energy regions of CV space. After a long simulation, the bias potential offsets the resistance from the system and makes the sampling in CV space ergodic and diffusive; therefore, the negative of the MetaD bias potential can be used to estimate the underlying PMF.^38,41

In its original implementation, the MetaD bias potential (V_G) took the form³⁶

$$V_G\left(s(R),t\right)={\int }_0^{t}d{t}^{\prime }\mathit{\text{w\hspace{0.17em}exp}}\left[-\sum _{i=1}^d\frac{{\left(s_i\left(R\right)-s_i\left(R(t^{\prime })\right)\right)}^2}{2{\sigma }_i^2}\right],$$ (2)

where w is the bias energy addition rate, computed as the height of individual Gaussian functions added, w₀, divided by a deposition stride τ. The index i represents the ith CV, which is a function of the system coordinates, R, and s_i(R(t′)) is the value of the CV calculated at time t′. σ is the width of the Gaussian function. Since the bias energy addition rate (w) is constant along the simulation, this approach is usually referred to as non-tempered MetaD. It is obvious that non-tempered MetaD yields a bias potential that does not converge asymptotically,³⁸ in contrast to the fact that the PMF is a time independent property. A suggested solution to this problem is to calculate the time average of the bias potential after the motion of the system on the CV space becomes diffusive.⁴¹ Practically, however, we have found this approach can show false convergence or instability in the late stages of simulations, likely due to too much bias energy being added.^40,42

Well-Tempered Metadynamics (WTMetaD)³⁷ was developed to address this convergence issue by tempering the height of the Gaussian functions exponentially with respect to the local bias potential, V_G(s,t). A time-dependent bias energy addition rate, w(t), replaces the time-independent energy addition rate, w, in Eq. (2),

$$\mathit{\text{w}}(t)={\mathit{\text{w}}}_0\text{\hspace{0.17em}exp}\left[-\frac{V_G(s\left(R\right),t)}{k_B\mathrm{\Delta }T}\right],$$ (3)

where ΔT is a parameter that tunes the tempering of the Gaussian height and needs to be chosen prior to the simulation. In spite of the success of WTMetaD in many simulations, it bears an obvious trade-off between exploration of CV space in the early stages of a simulation and the asymptotic convergence rate.^39,40,42 On one hand, a large value of ΔT builds up a fast-growing but noisy bias potential that hinders the convergence; on the other hand, a small value of ΔT generates a smooth but slow-growing bias potential that might decrease the efficiency of escaping a minimum. The original WTMetaD paper suggests that ΔT should be chosen according to the free energy barrier to make (ΔT + T) the same order of magnitude as the barrier height.³⁷ However, barrier heights are typically the quantity that is sought, not known a priori, which complicates the implementation of WTMetaD and leads to many trial simulations that either remain stuck in minima or place too much bias force into the system, forcing it into clearly unphysical regions of phase space.

Inspired by WTMetaD, transition-tempered MetaD (TTMetaD)³⁹ was designed to converge rapidly and asymptotically without sacrificing the exploration in the early stages of simulations.^40,42 TTMetaD tempers the Gaussian height with a similar exponential rule as WTMetaD, but the amount of tempering is determined according to the overall progress of the MetaD sampling. The time-independent energy addition rate w in Eq. (2) is replaced by

$$\mathit{\text{w}}(t)={\mathit{\text{w}}}_0\text{\hspace{0.17em}exp}\left[-\frac{V^{*}(s\left(\lambda \right),t)}{k_B\mathrm{\Delta }T}\right],$$ (4)

in which V^* is the minimal bias on the maximally biased path among all the continuous paths s(λ) that connect all of the preselected basin points in the CV space. One needs to roughly define positions of the basins on the PMF prior to the simulation, and TTMetaD tracks the region that the bias energy has expanded to. The tempering does not kick in until all the basins are fully covered, and it tempers according to the least biased point. Therefore, TTMetaD is able to explore the CV space with full Gaussians and use more aggressively tempered Gaussians to converge the simulation once the basins have been filled.

Metadynamics with a tempering rule (e.g., TTMetaD) has been proven to converge the bias energy asymptotically to a linearly scaled inverse of the underlying PMF.³⁸ Therefore, the PMFs of the permeation of trimethoprim were estimated as the inverse of the bias energy throughout the simulation.

B. Diffusion along the minimum free energy path (MFEP)

According to Eq. (1), the permeability coefficient computed from the solubility-diffusion model depends on the local diffusivity, D(r), where r is the permeation collective variable. Herein, we employed restrained MD simulations (umbrella sampling) to calculate the local diffusivity coefficient of trimethoprim at different positions along the MFEP. A harmonic potential restrained the trimethoprim to oscillate at specified points along the permeation pathway while the surrounding water and lipid molecules effectively served as the frictional bath for the solute. This method assumes that the harmonic potential overwhelms the underlying PMF that governs the interaction between the small molecule drug and its surrounding. Lee et al.²⁹ discussed the magnitude of the harmonic potential and concluded that any value above the conventional umbrella sampling spring [10.0 kcal/(mol/Ų)] constant are appropriate.

The umbrella sampling simulations provided a time series of motion along r, which was used to calculate the local diffusivity. One way to do this is to use a numerical Laplace transform of the velocity autocorrelation functions for several values of the transform parameter τ and extrapolate it to the limit of τ = 0.⁴³ Improving upon this, Hummer⁴⁴ derived a method wherein the local diffusion coefficients could be estimated directly from the autocorrelation function of r in a harmonically restrained simulation,

$$D(r)=\frac{{\left[var(r)\right]}^2}{{\int }_0^{\infty }{C}_r\left(t\right)dt}.$$ (5)

In the above equation, var(r) is the variance of r and C_r(t) is the autocorrelation function of r at time t, computed as

$$C_r\left(t\right)=\frac{\mathrm{\Delta }t}{t_s-t}\sum _{i=0}^{\left(t_s-t\right)/\mathrm{\Delta }t}(r\left(i\right)-\overline{r})(r\left(i+t\right)-\overline{r}),$$ (6)

in which r(i) is the time series of r from the restrained simulations of length t_s, with Δt as the MD integration time step, and $\overline{r}$ is the average value of r.

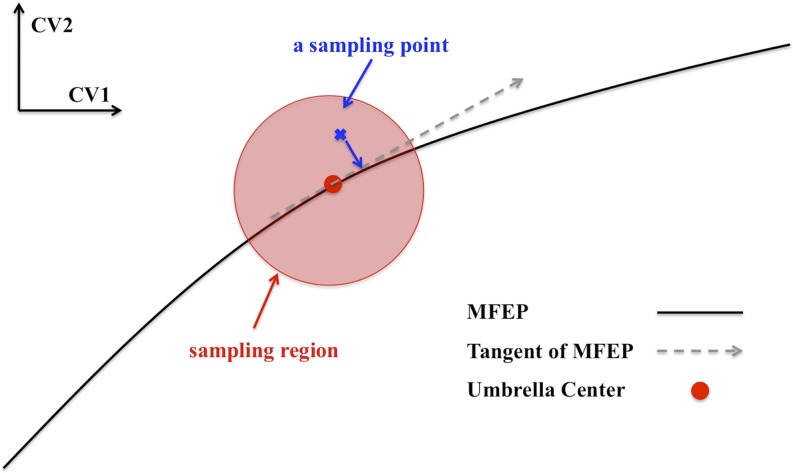
As discussed in the Introduction, the z component of the distance between the center of mass of the permeating drug and the center of mass of the lipid bilayer has typically been used as r to study permeation processes.^29,30 As a result, the local diffusivity coefficient represents the diffusion of the center of mass of the small molecule drug perpendicular to the lipid bilayer regardless of its orientation or any other relevant slow degree of freedom. However, the multidimensional PMF of trimethoprim permeation clearly shows that the orientation of the molecule is significant (Fig. 1) and, thus, that the diffusion should be evaluated along the MFEP. Therefore, we employed two-dimensional umbrella sampling simulations to restrain both CVs of the trimethoprim molecule along the MFEP, and the time series of the sampled points from the simulations were projected onto the tangent of the MFEP. A restraining force constant of 47.8 kcal/(mol/Ų) [20 000 kJ/(mol/nm²)] was chosen to make the sampled region of each umbrella window so small that the tangent of the MFEP is a good approximation of the MFEP in the sampling vicinity. Those projected points correspond to a time series of the reaction coordinate, r, with which we are able to calculate the local diffusivity coefficient using Eq. (5). This process is illustrated in Fig. 2. There are 41 umbrella windows covering the reaction coordinate from 0 to 0.5, corresponding to the black curve from (−4 nm, −4 nm) to (0 nm, 0 nm) on the 2D PMF (Fig. 3). Each window was equilibrated for 50 ns and then underwent another 50 ns simulation as the production run.

FIG. 2.

A diagram showing the method of generating a time series of diffusion of r (reaction coordinate) along the MFEP.

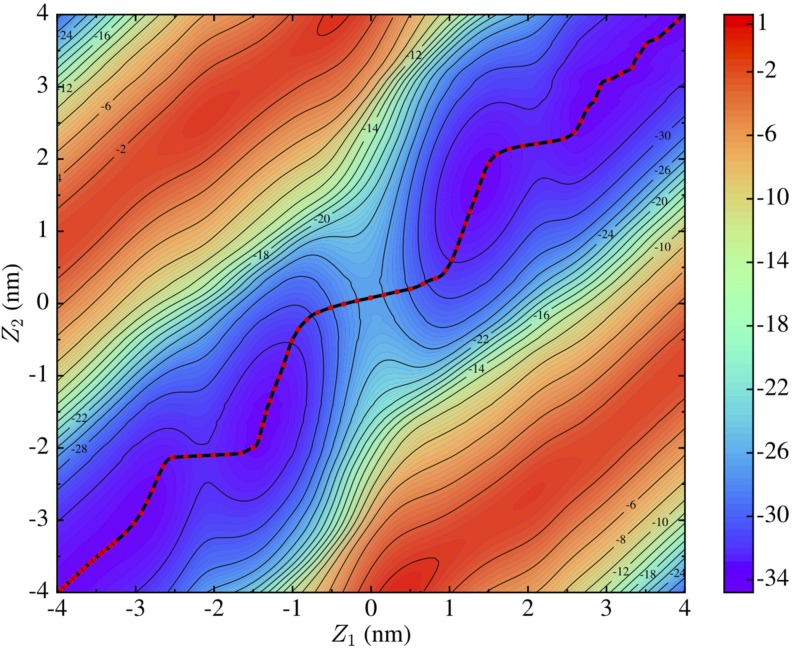
FIG. 3.

2D potential of mean force for trimethoprim permeation through the POPC lipid bilayer using longer sampling times than in our previous work (Ref. 40) and without symmetrization. The black curve traces the MFEP. The energy units are kcal/mol.

The convergence of a MetaD free energy profile requires filling the underlying minima in the free energy landscape. Thus, it is generally believed that it takes a longer simulation time to reach convergence when sampling more CVs, corresponding to more CV space. However, the underlying physics of the systems are important, and this intuitive conjecture is not necessarily true. In cases where this is a coupled, orthogonal slow CV, which corresponds to a non-negligible barrier in the free energy surface, overlooking that CV introduces hysteresis in the bias energy and, in some cases, even prevents the simulation from converging. Specifically, in the case of trimethoprim, there is an orientational preference when the drug interacts with the lipid head groups corresponding to a free energy difference that is larger than the thermal fluctuations. Therefore, it is important to include explicitly sampling of the orientation CV in the MetaD simulations; in fact, the MetaD simulations with both CVs (center of mass distance and orientation) converge substantially faster than that with only one CV (center of mass distance).

C. Calculation of a 1D PMF from a 2D PMF

W(r) in Eq. (1) corresponds to the free energy of a system with respect to r. The variable r is often the z component distance (z is perpendicular to the membrane) between the center of mass of the permeating drug and the center of mass of the lipid bilayer. All the TTMetaD calculations performed herein involved two collective variables; therefore, the permeation PMF was two-dimensional. In order to use Eq. (1), we must first calculate W(r) from the 2D PMF. This problem can be generalized as the following: Consider a 2D free energy sampling using collective variables x and y that yields a PMF given by F(x,y). The MFEP on this 2D PMF can be described by a normalized coordinate, ξ(x,y), that is a function of x and y. For any point on the MFEP, ξ₀, the tangent vector along the MFEP, $\overrightarrow{{\xi }_0}$, and the normal vector, $\overrightarrow{{\eta }_0}$, can form a local 2D coordinate system, which can be understood as a result of a transformation from the previous coordinates x and y. Applying this transformation to all the points on the MFEP, ξ(x,y), leads to a collection of the local $\overrightarrow{\eta }$ axis orthogonal to $\overrightarrow{\xi }$. As a result, the points, F(x,y), on the original PMF of coordinates x and y can be transformed to on a new set of coordinates F(ξ,η).

As a result of the above argument, the free energy profile of the MFEP, F(ξ₀), can be formulated in the new coordinate system as

$$F\left({\xi }_0\right)=-\frac{1}{\beta }\text{ln}\int \text{exp}\left(-\beta F(x,y)\right)\cdot \delta (\xi \left(x,y\right)-{\xi }_0)dxdy.$$ (7)

Changing the integration variables from dxdy to dξdη gives

$$\begin{array}{ccc}\hfill F\left({\xi }_0\right)& =\hfill & -\frac{1}{\beta }\text{ln}\int \text{exp}(-\beta F(x,y))\cdot \delta (\xi \left(x,y\right)-{\xi }_0)\hfill \\ \hfill & \hfill & \times \left|\frac{\partial (x,y)}{\partial (\xi ,\eta )}\right|d\xi d\eta ,\hfill \end{array}$$ (8)

where |∂(x,y)/∂(ξ,η)| is the Jacobian. As discussed above, the free energy, F(x,y), can be expressed in the coordinates ξ and η as

$$\begin{array}{ccc}\hfill F\left({\xi }_0\right)& =\hfill & -\frac{1}{\beta }\text{ln}\int \text{exp}(-\beta F(\xi (x,y),\eta (x,y)))\cdot \delta (\xi \left(x,y\right)-{\xi }_0)\hfill \\ \hfill & \hfill & \times \left|\frac{\partial (x,y)}{\partial (\xi ,\eta )}\right|d\xi d\eta .\hfill \end{array}$$ (9)

Integrating over ξ then yields

$$F\left({\xi }_0\right)=-\frac{1}{\beta }\text{ln}\int \text{exp}(-\beta F({\xi }_0,\eta ))\cdot {\left|\frac{\partial (x,y)}{\partial (\xi ,\eta )}\right|}_{{\xi }_0}d\eta .$$ (10)

Note that by definition, the local coordinate system (ξ,η) is just a rotation of the original coordinate system (x,y). The Jacobian for any rotational transformation equals unity, i.e.,

$${\left|\frac{\partial (x,y)}{\partial (\xi ,\eta )}\right|}_{{\xi }_0}\equiv 1.$$ (11)

The equation that we then adopt in this work to construct the free energy profile along the MFEP is given by

$$F\left({\xi }_0\right)=-\frac{1}{\beta }\text{ln}\int \text{exp}(-\beta F({\xi }_0,\eta ))d\eta .$$ (12)

We note that (x,y) and (ξ,η) in the above derivation can be dummy variables and can be any combination of collective variables in a PMF. As we will show later, this expression will also be used to compute the permeation free energy with respect to the center of mass distance (r) between the drug molecule and the lipid bilayers from two-dimensional (r and an angle CV) TTMetaD calculations.

D. Calculation of W(r′) on the minimum free energy path

The MFEP of a multidimensional free energy landscape is, within the limits of the sampled degrees of freedom and those faster than them, the physically relevant pathway for, e.g., lipid bilayer permeation. For example, and as discussed in the Introduction, a line integral of Eq. (1) along the MFEP from a multidimensional PMF can better account for the hydrophilic-hydrophobic interactions during drug permeation. We denote the reaction coordinate along the MFEP to be r′ to distinguish it from the commonly used center of mass distance between the drug and lipid bilayer, r.

Therefore, the free energy value along the MFEP is taken as W(r′) in Eq. (1) and is computed by integrating the 2D PMF over the direction orthogonal to the MFEP. The detailed procedure of computing W(r′) is explained as follows: Suppose r_i′(z₁, z₂) is a random point on the MFEP (e.g., Fig. 3). A line crossing r_i′ that is orthogonal to the tangent of the MFEP at r_i′ can be sketched, which we define as l_i. The coordinates of the points on this line l_i are denoted as $(z_1^{l_i},z_2^{l_i})$. Since the free energy of the 2D landscape has already been computed (see Fig. 3), F(z_1, z₂) is known for all the values of z₁ and z₂ and, consequentially, the free energy of every point on the line l_i, i.e., $F(z_1^{l_i},z_2^{l_i})$ is known. For every l_i that is orthogonal to the tangent of MFEP at r_i′, the points $(z_1^{l_i},z_2^{l_i})$ sitting on this line can be projected to r_i′; and based on their relative position on the line l_i, we map those points to another degree of freedom, l, that is orthogonal to the MFEP. Through this approach, we obtain a free energy F(r′, l) from F(z_1, z₂); then, Eq. (12) was applied to integrate over l to get the one-dimensional permeation free energy profile with respect to r′, W(r′) for Eq. (1).

From a more intuitive perspective, we summarize the procedure for calculating the free energy profile of the permeation as follows: After the 2D PMF with respect to the two pre-defined collective variables is sampled (Sec. II A), we then extract the free energy profile along the minimum free energy path (MFEP) along the 2D PMF. This was done in two separate steps, as described above and again here. First, at each point on the MFEP, we construct a local orthogonal coordinate system with one axis along the tangent vector at this point and the other axis aligning with the normal vector. Based on this new coordinate frame, the previous 2D PMF is transformed to a 2D PMF with respect to the two new collective variables in which the first represents the MFEP coordinate and the second denotes the orthogonal degrees of freedom. Then, the free energy profile along the MFEP is obtained by integrating over the orthogonal collective variable with Eq. (12) in the above discussion.

E. Molecular dynamics simulations

There were 16 × 2 POPC molecules in the lipid bilayers spanning a 3.2 nm × 3.2 nm region (approximately), a size that has been proven to be appropriate for the permeation of a small molecule.⁴⁵ The bilayer was solvated with a hydration ratio of 65 and with periodic boundary conditions enforced along all the directions of Cartesian space. CHARMM36,⁴⁶ CHARMM general force fields (CGenFF),⁴⁷ and TIP3P⁴⁸ were used to model the POPC lipid, trimethoprim, and water, respectively. The lipid and the water plus small molecules were individually coupled to two 323 K heat baths using velocity rescaling with a stochastic term.⁴⁹ This temperature is higher than the physiological temperature (310 K) and was chosen to be consistent with our previous study on the permeation of trimethoprim.⁴⁰ Pressure control was also applied by a Berendsen barostat⁵⁰ in which the box was rescaled every 5 ps. The cutoff distance for the short-range neighbor list was 12 Å and the neighbor list was updated every 40 steps. Fast smooth Particle-Mesh Ewald (SPME)⁵¹ was used to compute the long-range electrostatic interactions. All hydrogen bonds were constrained by linear constraint solver (LINCS)⁵² and the MD integration time step was 2 fs. The MD simulations were consistent with the simulations of trimethoprim in our previous paper⁴⁰ and were carried out using GROMACS-5.1.4⁵³ patched with PLUMED2⁵⁴ modified by the Voth research group to perform TTMetaD.^39,55 The total simulation time analyzed in this paper is about 30 μs, of which 7.5 μs was from our previous work.⁴⁰

III. RESULTS

A. Potential of the mean force

The central advantage of TTMetaD is a reliable estimate of the PMF early in the simulations without prior knowledge of the free energy barrier height. Therefore, our previous simulations of trimethoprim permeation⁴⁰ were intentionally stopped after 500 ns when they showed aggressive tempering and ample sampling of CV space. To test the robustness of TTMetaD to the choice of CV(s), the previous simulations were carried out with three different sets of CVs (2 CVs in each set). Although, as demonstrated,⁴⁰ these CV choices produced similar final 1D PMFs, the third set was not effective at capturing the orientational dependence of permeation, which was best captured by the second CV set. Thus, the second CV set, composed of (1) the z component distance between the center of mass of the trimethoxybenzyl group and the membrane, z₁ and (2) the z component distance between the center of mass of the pyrimidine group and the membrane, z₂ (see the left panel of Fig. 1), was selected for the 2D permeability coefficient calculation presented herein.

Given that tempered MetaD simulations are only guaranteed to reach asymptotic convergence with infinite sampling,³⁸ achieving diffusive motion in CV space and agreement between replicas are commonly accepted criteria convergence in practice.^40,42,56,57 In this work, we extended our previous simulations to refine the estimate of PMF of the permeation of trimethoprim through a POPC lipid bilayer. This is an effort to show that with a lengthy TTMetaD calculation, one is able to get an almost exact PMF that benefits the calculation of the permeability coefficient. We simulated 16 replicas with randomized velocities to avoid false convergence and decreased the required wall and central processing unit (CPU) times.^40,42 After 500 ns of additional sampling for each replica, the final 2D PMF was estimated (see Fig. 3), which was then symmetrized with respect to the center of the membrane (figure not shown) to generate as much sampling as possible to calculate the 1D PMF. The string method at zero temperature⁵⁸ was employed to search for the MFEP on the symmetrized 2D PMF, and the 1D free energy profile of the permeation (red curve in Fig. 4) is computed from Eq. (12) to integrate over the direction orthogonal to the MFEP. To evaluate the change in the free energy profile due to the extended sampling conducted herein, we compared the new MFEP with the MFEP from the previous simulations;⁴⁰ the difference is ∼0.76 kcal/mol. The total TTMetaD simulation time for calculating this 2D permeation free energy profile was 10.5 μs.

FIG. 4.

The permeation energy profile from MFEP (2D) and the center of mass translation (1D) calculated from TTMetaD. The reaction coordinate represents the permeation process from one side of the lipid bilayer to the other: 0 and 1 correspond to (−4 nm, −4 nm) and (4 nm, 4 nm) in the 2D case. The same values correspond to (−4 nm) and (4 nm) in the 1D case.

The advantage of the aforementioned method of computing a permeability coefficient can be seen from its comparison to the commonly used 1D permeability coefficient model, where only the distance (r) between center of masses of the drug molecule and membrane is used. For clarity, we name our model (MFEP from a 2D PMF) the 2D model and the model that uses only center of mass distance the 1D model. The free energy profile for the permeation in the 1D model, W(r) in Eq. (1), was computed as follows: To avoid unnecessary computation, we reused two sets of TTMetaD simulations from our previous work⁴⁰ in which the CVs were the center of mass distance and an angle (the details of the CV definitions can be found in Fig. 2 of Ref. 40). As noted earlier, these two sets of simulations were originally designed to test the robustness of TTMetaD to the choice of CVs. Using Eq. (12), we integrated over the angle CV in each 2D PMF to obtain the 1D free energy profile for the permeation, W(r). Again, for a more accurate estimate of the permeation PMF, each of the five replicas in these two sets of simulations was extended to 1100 ns from our previous simulations,⁴⁰ making the total simulation time (11 μs) for the 1D model comparable to that for the 2D model (10.5 μs). The permeation energy profile for the 1D model is depicted as the blue curve in Fig. 4.

The approach described above is quite different from a conventional 1D free energy calculation, e.g., a TTMetaD simulation with the center of mass distance as the only CV. Our permeation free energy profile for the 1D model was mapped from two TTMetaD PMFs, each with two collective variables. In addition to avoiding unnecessary new simulations, we consider our approach to be superior to a conventional 1D free energy calculation because biasing the extra CV enhanced the sampling of the center of mass distance and eliminated the hysteresis from the orientation of the drug molecule (see Sec. II). The permeation energy profiles from 1D and 2D models agree reasonably well, bearing ∼0.2 kcal/mol differences near the center and head group of the lipid bilayer. The evidence for the convergence of these calculations has been well-discussed in our previous work.⁴⁰ This energy profile (blue curve in Fig. 4) was then used to compute the permeability coefficient with the local diffusion coefficient computed from 1D umbrella sampling (restraining only z), as described below.

B. Local diffusivity coefficient

For the 2D model, 2D umbrella sampling was employed to restrain both CVs of the system to collect a time series of the reaction coordinate (i.e., the motion of trimethoprim) along the MFEP. The autocorrelation function of the reaction coordinate is depicted in Fig. 5 for trimethoprim in the bulk water (top panel), at the water-bilayer interface (middle panel), and inside the lipid bilayer (bottom panel).

FIG. 5.

The autocorrelation function of the diffusion of trimethoprim along the MFEP in Fig. 3. The blue and red curves represent the data from 2D umbrella simulations and the fitted result from Eq. (13), respectively.

The autocorrelation function of the reaction coordinate, C_r(t) in Eq. (5), needs to decay to zero in order to make the integral converge asymptotically to a finite value (so that the local diffusion coefficient is a non-zero value). This is not particularly a problem when the trimethoprim is solvated in bulk water—the autocorrelation function (blue curve in Fig. 5) decays to zero (the gray line in Fig. 5) and oscillates around it. It has been shown that such oscillations in the autocorrelation function can happen even at long times with extensive sampling.⁴⁴ However, a heterogeneous environment can delay the convergence of the autocorrelation function, which is exactly the case when the trimethoprim molecule is near the interface and inside the lipid bilayer (middle and bottom panels of Fig. 5). This behavior is consistent with the findings of Lee et al.,²⁹ where the autocorrelation function of the urea restrained at 10 Å and 0 Å away from the center of the membrane only decayed to 8% and 13% of its initial values in 5 ps, respectively. Other work⁵⁹ has shown that the convergence of an autocorrelation function for a molecule restrained in lipid bilayers can require microsecond to millisecond of simulations. Through biased and unbiased simulations, Chipot and Comer⁶⁰ showed that one-dimensional translocation of methanol across a pure lipid membrane is sub-diffusive instead of a typical diffusive motion. In a follow-up paper,⁶¹ Chipot and Comer used the fractional version of the solubility-diffusion model to take into account the sub-diffusion motion. Their study of the permeation of short-chain alcohols shows that the relative permeability coefficients are highly correlated with existing experimental results, albeit their values are off by three to four orders of magnitude, worse than their previous work with the common solubility-diffusion model.²⁹ All of the aforementioned research suggests that the slow diffusion of the lipid tails and the inhomogeneity of the bilayer interface slow down the convergence of autocorrelation calculations and therefore present a very challenging problem in computing the local diffusivity coefficient. However, since the benefit from the sub-diffusion model in permeability coefficient calculation is not obvious,⁶¹ we decided to follow the common solubility-diffusion model in this research.

There have also been methods proposed to improve the autocorrelation convergence in heterogeneous environments. For example, using a cut off distance for the integral, which is usually chosen as a value when the autocorrelation function drops below a threshold value of 5% of the variance, has been suggested to limit the contribution of noise.⁶² On the other hand, the goal of this work is not to understand the sub-diffusive nature of small molecules inside the lipid bilayer nor to compute the most accurate local diffusivity; instead, we are interested in computing the local diffusivity with reasonable accuracy and a computational cost so that it can be applied to small molecule drug screening. Therefore, we have chosen to fit the autocorrelation function to a function converging asymptotically. To increase the quality of the fitting, the autocorrelation function calculation was gathered from a 100 ns restrained simulation (50 ns equilibration and 50 ns production) and was evaluated to 100 ps, much longer than the common practice of 20 ns of sampling and 5 ps correlation time.²⁹ Many functional forms have been tested to minimize the root mean square deviation (RMSD) between the fitted function and the autocorrelation data. The summation of two Gaussian functions [Eq. (13)] gives the best overall fitting for trimethoprim at different positions along the MFEP,

$$C_r\left(t\right)=a_1\text{exp}\left[-\left(t^2/b_1\right)\right]+a_2\text{exp}\left[-\left(t^2/b_2\right)\right],$$ (13)

where a₁, a₂, b₁, and b₂ are the fit parameters. Good agreement between the fitted curve (red) and the autocorrelation data is demonstrated in Fig. 5. The local diffusivity coefficient along the MFEP is shown in the red curve in Fig. 6. We have also computed the local diffusivity coefficients of the center of mass translation along the z direction for the 1D case with the same approach and the data are also shown in the blue curve in Fig. 6.

FIG. 6.

The local diffusivity coefficient of the diffusion of trimethoprim from 2D umbrella simulations (along the MFEP in Fig. 3) and 1D umbrella simulations (along the blue curve in Fig. 4). The reaction coordinate represents the whole permeation process from one side of the membrane to the other: 0 and 1 correspond to (−4 nm, −4 nm) and (4 nm, 4 nm) in the 2D case. The same values correspond to −4 nm and 4 nm in the 1D case. 0.5 is the center of the membrane. Only half of the permeation system is shown in this figure. The inset highlights the local diffusivity when trimethoprim is in the tail region of the lipid. Dots denote the essential points used in the permeability calculation below.

The local diffusivity coefficients of trimethoprim from the 2D and the 1D umbrella sampling show a very similar trend: the drug diffuses an order of magnitude slower in the lipid tail region than it does in the bulk water. This result qualitatively agrees well with the diffusivity coefficient calculation of different drugs reported by Lee et al.²⁹ The inset in Fig. 6 illustrates the local diffusivity when trimethoprim is in the tail region of the lipid, demonstrating trimethoprim diffuses on average ∼40% slower along the MFEP (i.e., the molecule is held at a certain configuration while diffusing) than it does in the z direction (center of mass translation diffusion). This difference plays a role in the permeability coefficient calculation because the configurations of trimethoprim inside the lipid correspond to high free energy [Eq. (1)].

C. Comparison with experimental permeability coefficient

The permeability coefficient from 2D PMF was computed from Eq. (1) by integrating from one side of the membrane [r = 0, corresponding to (−4 nm, −4 nm) on Fig. 3] to the other side [r = 1, corresponding to (4 nm, 4 nm) on Fig. 3]. The trapezoidal rule was used for the integration with Δr = 0.0125. The permeability coefficient from the center of mass translation (1D) was also computed from Eq. (1) by integrating it from r = 0 (z = −4 nm) to r = 1 (z = 4 nm). The results of the permeability coefficient from those calculations are summarized in Table I.

TABLE I.

The permeability coefficient (P_m) from different methods.

Method	Lipid bilayer/membrane	Pm (nm/s)
In vitro	MDCKa,b	374
In vitro	PAMPA (egg lecithin)c,d	72
In vitro	PAMPA (skin)e,d	170
In silico (1D)f	POPC	1732
In silico (2D)g	POPC	1885
In silico (2D)h	POPC	587.5

^aExperimental data are from Ref. 63.

^bThe permeability is scaled from 310 K to 323 K according to Ref. 64.

^cExperimental data are from Ref. 65.

^dThe permeability is scaled from 310 K to 323 K according to Ref. 66.

^eExperimental data are from Ref. 67.

^fTotal TTMetaD simulation time is 11 μs: 10 replicas with 1.1 μs/replica.

^gTotal TTMetaD simulation time is 2.5 μs: 5 replicas with 0.5 μs/replica.

^hExtended from g (16 replicas with 0.5 μs/replica), total TTMetaD simulation time is 10.5 μs.

It is of interest to compare the permeability coefficient from simulations with those from experiments. Some degree of disagreement is expected due to the differences between the simulation conducted with homogeneous lipid bilayers and the experimental lipid bilayers made up of different kinds of lipids and sometimes proteins (e.g., the MDCK assay). Another difference between our simulations and experiments are the temperatures. To take advantage of the extensive simulation data from our previous work, the permeation of trimethoprim was simulated at 323 K, i.e., higher than the physiological temperature at which the drug permeability experiments are usually conducted. However, various efforts have focused on determining the temperature dependence of permeability coefficients measured by experiment. Sinkó and co-workers⁶⁶ measured the effective permeability (log P_e) of seven drugs representing diverse structures and different acid–base properties on three different PAMPA models (GIT, BBB, and Skin) with the temperature range of 288 K–328 K. Their result shows that the slope of the log P_e = aT + b regression equation is a good measure of the temperature effect on permeability and suggests the values of parameters a and b for small molecule drugs. Kulkarni et al.⁶⁴ studied the influence of the experimental temperature on the permeability coefficients with cell-based assays. Their research concludes that the permeability coefficient and temperature are related by an exponential relationship that conformed to the Arrhenius equation, similar to the PAMPA experiments.⁶⁶ As a result, we are able to estimate the permeability coefficient of trimethoprim at 323 K from the cell-based assay (MDCK) experiment⁶³ and the artificial membrane assay (PAMPA) experiment^65,67 conducted at 310 K. The results of the permeability coefficient from those experiments are summarized in Table I. As discussed before, even though there are some disagreements between the experimental permeability coefficients due to differences in the measurements and perturbations, all the experiments yield a permeability coefficient value between ∼75 and ∼400 nm/s.

IV. DISCUSSION

A. Permeation along the MFEP

The results in Table I demonstrate improved accuracy when permeation is modeled along the MFEP compared to those using the z-direction center of mass translation. The permeability coefficient predicted from the 2D permeation PMF (last row in Table I) is only ∼2–5 times larger than the experiment. This is a small difference compared to recent work reporting errors of one to two orders of magnitude.²⁹ This result also supports our expectation that small molecules with groups of different hydrophobicity (e.g., trimethoprim) have a more complicated permeation pathway that optimizes hydrophilic-hydrophobic interactions. For these cases, the local diffusivity is best represented by the diffusive motion along the MFEP, as opposed to the oversimplified, and most commonly used model (i.e., diffusion of the center of mass along the direction perpendicular to the lipid bilayers).

It is important to appreciate, however, that the quality of the permeation free energy profile, W(r) in Eq. (1), governs the accuracy of the permeability coefficient more significantly than the local diffusivity coefficient, D(r). This partially explains why the in silico permeability coefficients reported in the early 2000’s were usually off by a few orders of magnitude, when the sampling capacity, and thus accuracy of W(r), was more limited.^68–70 Herein, the 1D permeation free energy from TTMetaD, even applied with the common practice of local diffusivity (the z-direction-only; see the third to last row in Table I), is able to predict a permeability coefficient within one order of magnitude of the experimental value, highlighting the ability to calculate a reliable PMF within reasonable simulation times.

B. Computational cost of screening drug candidates

As reviewed earlier in this paper, computational simulation of small molecule drug permeation provides mechanistic information at atomistic resolution that can be quite valuable in the pharmaceutical industry. Predicting the permeability coefficients of small molecule drugs before synthesis is environmentally friendly and has the potential to decrease cost during pharmaceutical design and development. To accomplish this goal, the simulation methodology must provide reliable permeability estimates with low to moderate computational effort and within a reasonable time frame.

Moreover, instead of the absolute permeability coefficient of each molecule, the relative permeability coefficients of a series of molecular candidates are often sought for screening purposes. We have shown herein that calculating the diffusion along the MFEP of an extensively sampled 2D PMF is more accurate than simply using the z-direction. But how does this method work when sampling times are limited? To answer this, we revisited our previous simulations⁴⁰ and used the 5 TTMetaD replicas (500 ns each) to compute an average PMF (Fig. 1). The MFEP is computed on this PMF to estimate W(r) following Eq. (12). The local diffusivity coefficient was approximated as the same D(z) from the converged PMF (Fig. 6). The resulting permeability coefficient is shown in the second to last row in Table I. Even though the total simulation time used to calculate this 2D PMF is only a quarter of the simulation time used to obtain the 1D simulation, the results are comparable. More importantly, the permeability coefficient computed from this very limited sampling is within one order of magnitude of the experimental result. Comparing this result with the fully converged 2D TTMetaD calculation (last row in Table I), it is fair to conclude that the accuracy of the permeation free energy profile is less with less sampling, but a significant amount of computational time is saved (2.5 μs vs. 10.5 μs) and the result is still reasonable.²⁹

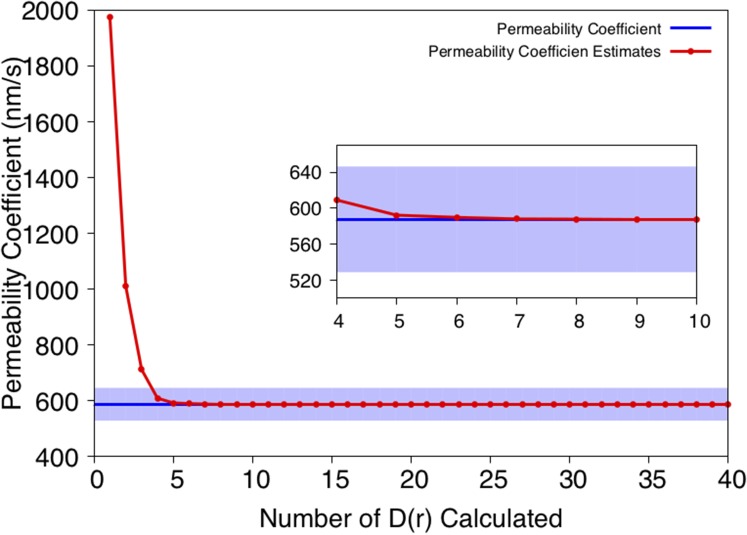
The permeability coefficient is dominated by the permeation free energy [Eq. (1)] because of the exponential dependence. Accordingly, the local diffusion along the highest free energy regions of the PMF will play the most significant role in the integration of Eq. (1). Therefore, we also explored the minimum number of local diffusivity coefficients that are needed for a reasonable estimate of the permeability coefficient. For this purpose, the integral [Eq. (1)] was evaluated from the center of the lipid bilayer [r = 0.5, corresponding to (0 nm, 0 nm) in Fig. 3] to the outside of the lipid bilayer. The predicted permeability coefficient vs. the number of restrained calculations (i.e., 100 ns of 2D umbrella samplings per calculation) is shown in Fig. 7. We conclude that only four of the points on the MFEP corresponding to the highest free energy are needed to estimate the permeability coefficient within 10% of the error of the converged (most accurate) value. These four points correspond to the trimethoprim in the center of the membrane and are highlighted with red dots in Fig. 6.

FIG. 7.

The estimate of permeability coefficient vs. number of local diffusivities calculated from 2D umbrella sampling.

From the above tests, we conclude that 2.9 μs of simulation are needed for the present method to predict a permeability coefficient that agrees to within one order of magnitude of the experimental result (500 ns of TTMetaD with 5 replicas and 100 ns of 2D umbrella sampling on 4 points). These simulations produced ∼250 ns/day on a graphics processing unit (GPU) node with four NVIDIA GeForce GTX TITAN X cores; therefore, the method took less than 60 h of wall time to screen a small molecule drug candidate with five such GPU nodes. With these and continued improved efficiencies, simulation-based permeability coefficients may be an increasingly attractive option in the pharmaceutical industry and academia.

It should be emphasized that assessing the permeability of small molecule drugs through a lipid bilayer remains very challenging both in vitro and in silico. For example, the inhomogeneous solubility-diffusion [Eq. (1)] requires a very accurate free energy profile of the permeation; a difference of k_BT in W(r) introduces approximately 2.72-fold difference in the permeability coefficient. Given this level of sensitivity to W(r), combined with the errors from the force field parameters and the limitations in the complexity of the lipid bilayer models, we do not anticipate this level of agreement (within one order of magnitude) between in vitro and in silico studies to be universally obtained—especially considering the diversity of drug molecules and lipid bilayers. Nevertheless, our model improves the physical accuracy of permeation coefficient calculation and contributes to the collective progress toward accurate in silico studies of drug permeation. Currently, we are applying this methodology to a series of drugs to verify its advantages in predicting relative permeability coefficients. We believe its advantages will be further demonstrated in the comparison of relative permeability where the errors from the force field and lipids may cancel out.

As a final note, the enhanced sampling method described in this paper, TTMetaD, is available in the most recent version of PLUMED (v.2.4). TTMetaD is easy to understand and apply, and, compared to a conventional non-tempered MetaD or WTMetaD simulation, the extra input parameters that TTMetaD requires are straightforward to incorporate. A detailed user manual for this method is also available upon request, and the new features require no specialized or separate mathematical library.