Enspara: Modeling molecular ensembles with scalable data structures and parallel computing

Abstract

Markov state models (MSMs) are quantitative models of protein dynamics that are useful for uncovering the structural fluctuations that proteins undergo, as well as the mechanisms of these conformational changes. Given the enormity of conformational space, there has been ongoing interest in identifying a small number of states that capture the essential features of a protein. Generally, this is achieved by making assumptions about the properties of relevant features—for example, that the most important features are those that change slowly. An alternative strategy is to keep as many degrees of freedom as possible and subsequently learn from the model which of the features are most important. In these larger models, however, traditional approaches quickly become computationally intractable. In this paper, we present enspara, a library for working with MSMs that provides several novel algorithms and specialized data structures that dramatically improve the scalability of traditional MSM methods. This includes ragged arrays for minimizing memory requirements, message passing interface-parallelized implementations of compute-intensive operations, and a flexible framework for model construction and analysis.

I. INTRODUCTION

Markov state models (MSMs)^1–4 are a powerful tool for representing the complexity of dynamics in protein conformational space. They have proven useful both as quantitative models of protein behavior^5–8 and for producing insights about the mechanism of protein conformational transitions.^9–12 And, with the rise of special-purpose supercomputers,^13,14 distributed computing platforms,¹⁵ and the dramatic increases in the power of consumer-grade processors [especially graphical processing units (GPUs)] the size of molecular dynamics (MD) data sets that MSMs are built on have grown in size commensurately.

With the increasing size of MD datasets, there is ongoing and substantial interest in making more tractable models by distilling protein landscapes into a small number of essential states. Typically this is achieved by making assumptions about the relevant features. In particular, existing MSM libraries PyEMMA2¹⁶ and MSMBuilder3^17–19 offer state-of-the-art, modular components for the newest theoretical developments from the MSM community. These libraries emphasize early conversion to coarse-grained models, particularly through the use of time-lagged independent components analysis (tICA),^20–22 but also through deep learning^23,24 or explicit state-merging.^25–28 All these approaches merge states that are kinetically close to one another to build a more interpretable model.

Kinetic coarse-graining is effective when the most interesting process is also the slowest, for example, when studying folding. However, physiologically relevant conformational changes can also occur quickly. For example, the opening of druggable cryptic allosteric sites can occur many orders of magnitude faster than the global unfolding process.^29,30 Thus, for biological questions where the underlying physical chemistry is irreducibly high-dimensional or the features in which it is low-dimensional are not known, building models with a large number of states is an effective strategy for ensuring that important states are not overlooked. An alternative approach to extracting insight from large MD datasets is to retain the size and high dimensionality, and to manually learn which features are relevant to the biological question. For example, one approach to understanding sequence-function relationships is to compare simulations of different sequences to form hypotheses about which features are important, which can then be used to propose experiments. This approach has been successfully leveraged to, for example, understand the determinants of protein stability,⁸ enzyme catalysis,⁷ and biochemical properties.²⁹ The downside of this approach is that it is substantially more computationally demanding, due to the much larger size of both the input features and the resulting model.

In this paper, we present enspara, which implements methods that improve the scalability of the MSM methods. We implement a “ragged array” data structure that enables memory-efficient in-memory handling of data with heterogeneous lengths, and develop tools which use sparse matrices, vastly reducing memory usage of the models themselves while speeding up certain calculations on them. We further introduce clustering methods that can be parallelized across multiple nodes in a supercomputing cluster using Message Passing Interface (MPI), a user-friendly command-line interface (CLI) for large clustering tasks, thread-parallelized routines for information-theoretic calculations, and a new framework for rapid experimentation with methods for estimating MSMs.

II. RESULTS AND DISCUSSION

A. Ragged arrays

The most computation-intensive step in any molecular dynamics-based approach is actually generating the simulation data. One approach to mustering the computation necessary to solve this problem is to harness the power of distributed computing to generate many parallel simulations on many computers. Indeed, one of the points where MSMs excel is in unifying such parallel simulations into a single model. An example of this is the distributed computing project Folding@home.¹⁵ However, in these scenarios, individual trajectories often substantially differ in their lengths. In Folding@home, the trajectory length distribution shows strong positive skew, with a few trajectories one or more orders of magnitude longer than the median trajectory. Historically, atomic coordinates, as well as features computed on trajectories, have been represented as “square” arrays of n_trajectories × n_timepoints × n_features (or n_atoms × 3), which assumes uniform trajectory length.^16,31

To represent non-uniform trajectory lengths, a number of approaches exist. One approach, found in MSMBuilder2,¹⁸ is to use a two-dimensional square array with the “overhanging” timepoints filled with a null value. This is also the solution provided by numpy,³² with its masked array object. While this approach maintains the in-memory arrangement that makes array slicing and indexing fast, it can dramatically inflate the memory footprint of datasets with highly non-uniform length distributions. The other approach, used by the latest version of MSMBuilder,¹⁹ sacrifices speed for memory by building a python list of numpy arrays. While this is more memory-efficient, it cannot easily be sliced, cannot easily take advantage of numpy’s vectorized array computations, and can be very slow to read and write from disk via python’s general-purpose pickle library.

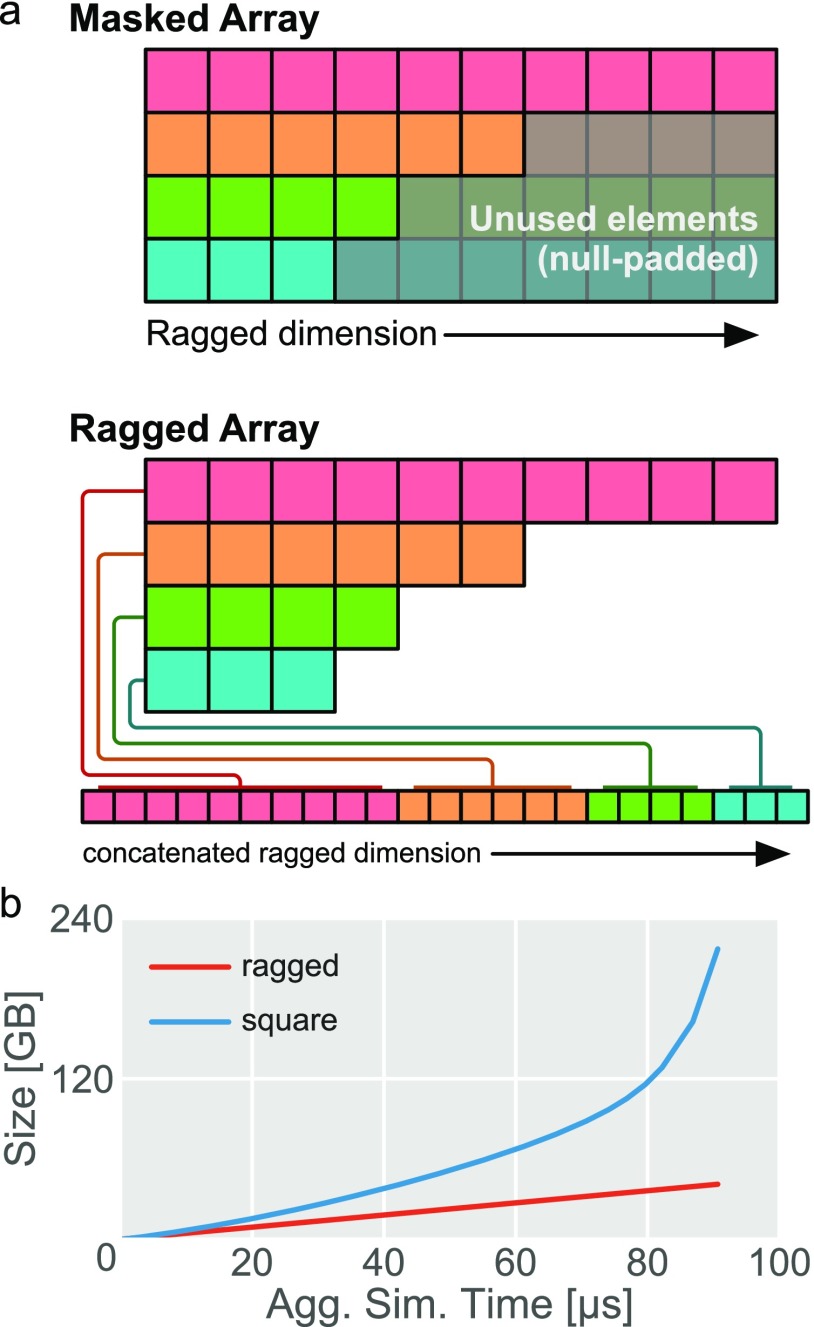
In enspara, we introduce an implementation of the ragged array, a data structure that relaxes the constraint that the rows in a two-dimensional array be the same length [Fig. 1(a)]. The ragged array maintains an end-to-end concatenated array of rows in memory. When the user requests access to particular elements using a slice or array indices, the object translates these array slices or element coordinates appropriately to the concatenated array, uses these translated coordinates to index into the concatenated array, and then reshapes the data appropriately and returns it to the user. On trajectory the length distributions described, the ragged array scales much better than the padded square array [Fig. 1(b)], such as the square array used in MSMBuilder2 while retaining the useful properties of an array which are lost in a list-of-arrays representation.

FIG. 1.

Ragged arrays compactly store non-uniform length data in memory. (a) A schematic comparison between the memory footprint of a masked, uniform array and our implementation of the ragged array interface. In the masked array, rows of length lower than the longest row are padded with additional, null-valued elements to preserve the uniformity of the array. In the ragged array, however, rows are stored concatenated and memory is not expended. (b) A plot of memory used by traditional and ragged arrays as a function of aggregate simulation time as trajectories of increasing length are added from a previously published Folding@home dataset.¹¹

B. SIMD clustering using MPI

Among the more expensive and worst-scaling steps in the Markov state model construction processes is clustering, and substantial effort has been spent on improving the speed of these calculations.^33–35 The most popular clustering algorithms for use in the MSM community are k-means³⁶ (generally composed of k-means++³⁷ initialization and Lloyd’s algorithm³⁸ for refinement) for featurized data, and k-hybrid¹⁸ (composed of k-centers³⁹ initialization and k-medoids⁴⁰ refinement) for raw atomic coordinates. Both of these algorithms scale roughly with O(nkdi), where n is the number of observations, d is the number of features per observation, k is the number of desired cluster centers, and i is the number of iterations required to converge. Unfortunately, with the possible exception of i, these numbers are all generally very large. As discussed in Sec. II D, the number of clusters k must be large for some problems, proteins are intrinsically high-dimensional objects (i.e., high d), and the increasing speed of simulation calculations⁴¹ has increased the number of timepoints that must be clustered, n, into the millions.

To address the poor scaling of clustering, the MSM community has developed a number of approaches to managing this problem. One approach is to reduce the number of observations by subsampling data³¹ so that only every nth frame is used. Another approach is to reduce the number of features by including only certain atoms (as in Refs. 42, 43, and 8), using a dimensionality reduction algorithm like principal components analysis (PCA),^44,45 or creating a hand-tuned set of order parameters (e.g., specific, relevant pairwise atomic distances). Yet a third approach is to use tICA^20,21 as a dimensionality reduction, which has the benefit of reducing both the number of features and the number of clusters needed to satisfy the Markov assumption, but has the disadvantage that it may obscure important fast motions and can be sensitive to parameter choices (in particular the lag time).²⁰

An alternative or complimentary approach to preprocessing data to reduce input size is to parallelize the clustering algorithms themselves so that many hundreds, rather than many tens, of cores can be simultaneously utilized. Message Passing Interface (MPI)⁴⁶ is a parallel computing framework that enables communication between computers that are connected by low-latency, high-reliability computer networks, like those commonly encountered in academic cluster computing environments. This approach to interprocess communication has enabled numerous successful parallel applications including molecular dynamics codes like GROMACS^47,48 (among many others). This approach to interprocess communication allows information to be shared easily across a network between an arbitrary number of distinct computers. Thus, for a successfully MPI-parallelized program, the amount of main memory and number of cores available is increased from what can be fit into one computer to what can be fit into one supercomputing cluster—a difference of one or two dozens of processors to hundreds of processors. However, because interprocess communication is potentially many orders of magnitude slower than, for example, in thread-parallelization, single-core algorithms must generally be adjusted to scale well under these constraints.

In this work, we present low-communication, same-instruction-multiple-data (SIMD) variants of clustering algorithms that are popular in the MSM community, k-centers, k-medoids, and k-hybrid.¹⁸ Specifically, data—atomic coordinates/features and distances between coordinates and medoids—are distributed between parallel processes which can reside on separate computers, allowing more data to be held in main memory, and allowing more processors in toto to be brought to bear on the data.

The k-centers initialization algorithm³⁹ repeatedly computes the distance of all points to a particular point and then identifies the maximum distance amongst all distances computed this way. This introduces the need for communication to (1) distribute the point to which distances will be computed and (2) collectively identify which distance is largest. (1) is solved trivially by the MPI scatter directive and (2) is solved by computing local maxima and then distributing these maxima with MPI allgather. Implementation details of k-medoids are somewhat more complex but follow a similar pattern. The full code is available on our GitHub repository. In brief, during each iteration, (1) all nodes must collaborate to choose a new random centroid for each existing center—achieved by choosing a random number on the highest-ranked node and MPI scattering it to all other nodes—before (2) recomputing the assignment of each frame that could possibly have changed its state assignments. This step is potentially embarrassingly parallel in the number of frames assigned to the cluster. Finally, (3) the costs (usually mean-squared distances from each point to its cluster center) are computed and compared between the new and old assignments, and the cheaper assignment is accepted.

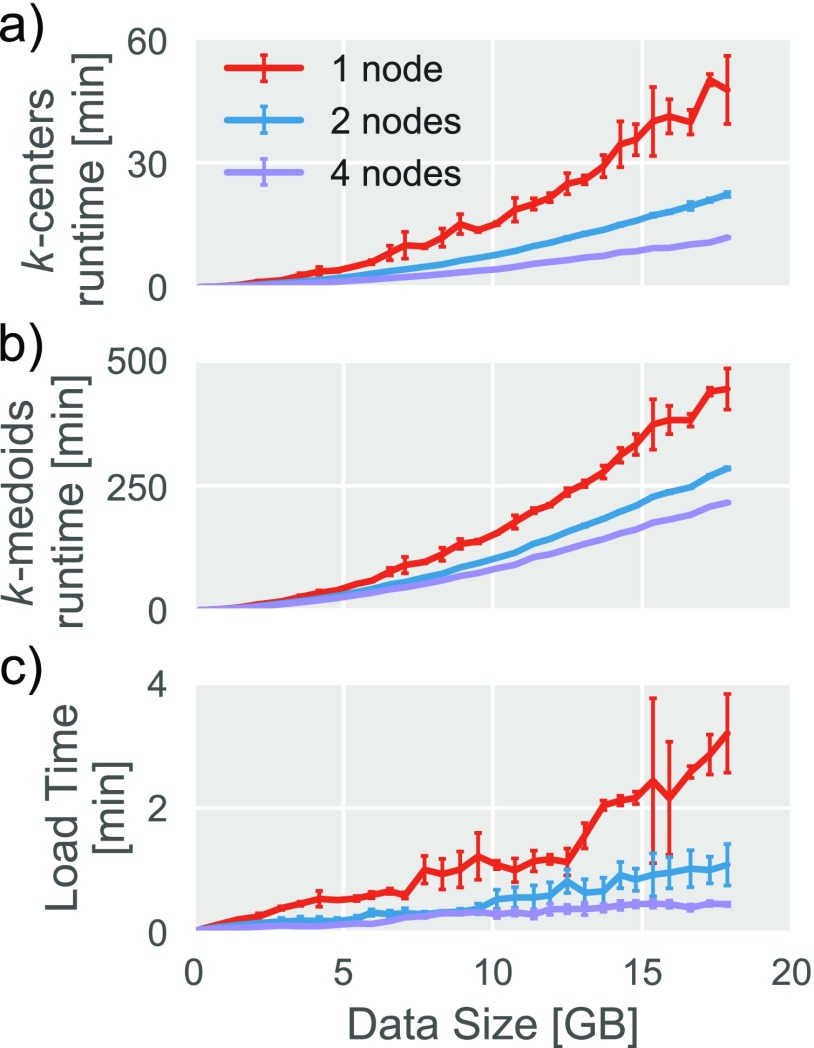
The performance characteristics of this implementation as a function of data input size is plotted in Figs. 2(a) and 2(b), which show marked decreases in runtime as additional computers are added to the computation. In both the k-centers and the k-medoid case, growth of runtime as a function of data input size is roughly quadratic. While this is expected for k-medoids, it may be surprising that k-centers also grow quadratically (see, for example, Ref. 34). This is because we have chosen a fixed cluster radius for k-centers (rather than a fixed number of cluster centers). As new data (molecular dynamics trajectories with different initial velocities) are added, both the number of cluster centers and the number of data points to which each center must be compared increases, apparently roughly proportionally, leading to roughly quadratic scaling.

FIG. 2.

SIMD reformulation of clustering algorithms allows greater scaling. (a) The runtime of the parallelized k-centers code as a function of data input size. (b) The runtime of the parallelized k-medoids code as a function of data input size. (c) The load time of the parallel code as a function of input data size. Points represent the average and error bars the standard deviation across three trials.

A further advantage of a parallelized algorithm is that, if configured correctly, it can also decrease load times. In the traditional high-performance computing (HPC) environment used in many academic settings, data typically reside on a single central, “head” node and are distributed to “worker” nodes via a network file system (NFS). The NFS can transfer data to any particular worker node only as quickly as the network allows, which is generally orders of magnitude slower than the rate at which it can be loaded from disk into memory. However, if network topology allows nodes to independently communicate with the head node (and hence filesystem), the network bottleneck is reduced or removed and load times can be substantially decreased, as shown in Fig. 2(c). While load times do not dominate the overall runtime of the algorithms we discuss here, low load times are desirable since many forms of misconfiguration can only be detected after data have been loaded.

C. Flexible, well-scaling clustering CLI

In this section, we illustrate how enspara can be used to analyze an MD dataset using our clustering command-line interface (CLI), and use the flexibility enspara offers to compare the usefulness of different ways of clustering the same MD trajectories.

Clustering, or assigning frames of the trajectory to discrete states, is the first step in analyzing most MD datasets using MSM technology. In enspara, we focus on offering mechanisms for clustering large datasets into many states, since other libraries already offer excellent mechanisms for reducing data size using various preprocessing strategies like tICA. For this purpose, enspara provides a command-line application, in addition to a clustering application programming interface (API), which handles some common tasks [Figs. 3(a)–3(c)]. This clustering application can take trajectories in formats accepted by MDTraj [Fig. 3(a)] or numpy arrays of numerical features [Fig. 3(c)], supports several different distance metrics, provides easy support for clustering different topologies into shared state spaces [Fig. 3(b)], and supports execution under MPI.

FIG. 3.

enspara offers a flexible, well-scaling, and multipurpose clustering CLI. (a) A CLI invocation clustering trajectories with a shared topology with the k-hybrid algorithm using backbone RMSD, stopping k-centers at 3 Å, and with 20 rounds of k-medoids refinement. (b) A CLI invocation clustering trajectories with differing topologies by a small subset of shared atoms using the k-centers algorithm to discover 1000 states. (c) A CLI invocation clustering euclidean distances between feature vectors representing frames stored in a group of numpy NPY-format files using k-hybrid. (d) An MSM’s ability to predict the results of an experimental measurement of solvent exposure as a function of number of clusters. Dashed lines are models constructed using euclidean distance between vectors of residue sidechain solvent accessible surface area, whereas solid lines use backbone RMSD. Blue traces used k-centers, and red traces used k-hybrid. The experimental measurement is a previously published²⁹ biochemical labeling assay that classifies a residue as exposed, buried, or transiently exposing. Residues exposure class was predicted as “buried” if no state exists where the residue was exposed, “exposed” if the residue is never buried, and “transient” if the residue populates both exposed and buried states in the MSM. The y-axis represents the fraction of these residues that were classified correctly. Error bars represent the standard deviation of three trials (k-centers are deterministic and have no error bars).

In enspara, we have implemented many of these options because different choices for cluster size/number, clustering algorithm, and cluster distance metric can dramatically impact MSM’s predictive power. As an example, in Fig. 3(d), we investigate the effect of clustering algorithm (k-centers vs. k-hybrid) and cluster number on the ability of an MSM to retrodict a previously described biochemical thiol labeling assay.^29,30 In this case, the MSM’s ability to sufficiently represent the protein’s state space is positively related to the number of clusters used to represent the state space. Interestingly, k-centers appear to perform better than k-hybrid in this case. This may be related to the fact that these exposed states are high energy and hence rare, giving rise to a tendency in k-medoids to lump these rare states in with more populous adjacent states.

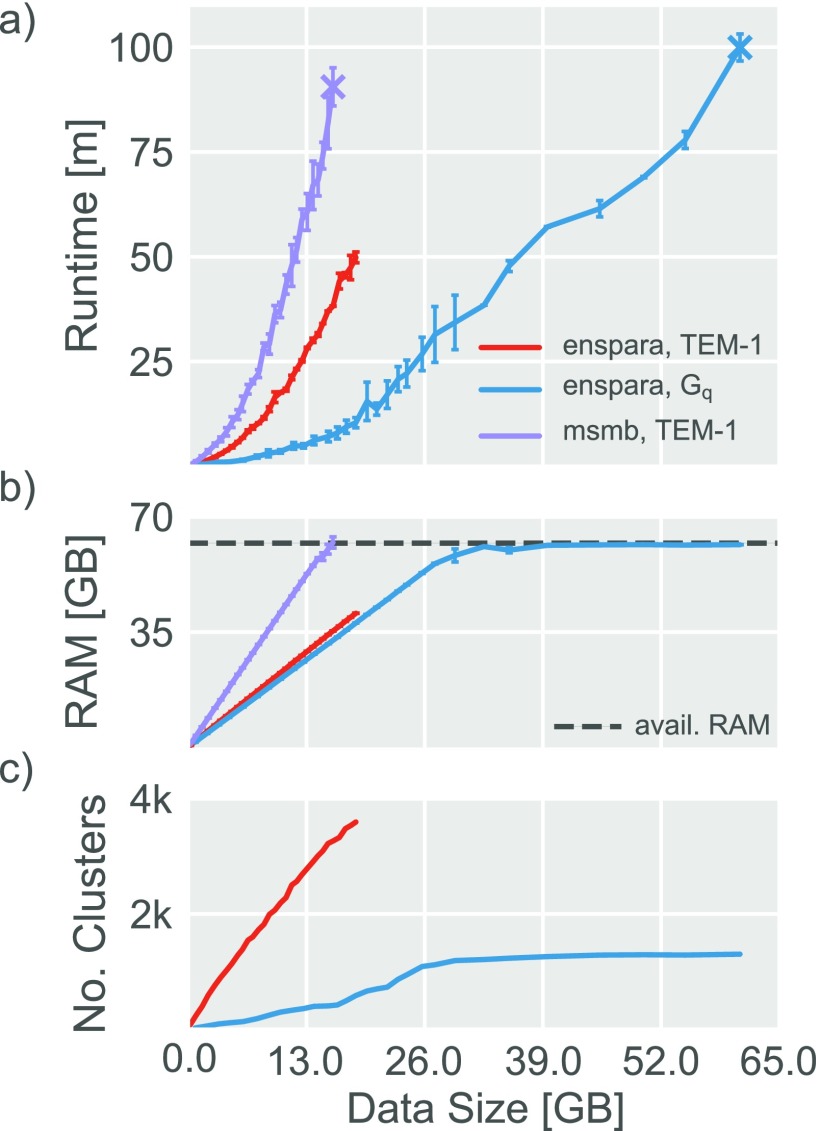
Because of this potential need for very large state spaces, it is often necessary to handle a large amount of data. In part, this challenge is a computer scientific one, which can be addressed by new parallel algorithms, such as that described in Sec. II. In addition to efficient algorithms, however, there are also software engineering concerns like effective memory management. Our CLI places an emphasis on these large clustering tasks and large state spaces, and hence scales better than existing codes that place an emphasis on smaller state spaces (Fig. 4). For purposes of reference, clustering of the TEM-1 dataset used all 2026 protein heavy atoms across 90.5 μs total simulation time saved every 100 ps and the G_q dataset used all 2655 protein heavy atoms across 20.5 μs saved every 10 ps. All these values trade off against one another, however, meaning that if every 10th frame were used to cluster the G_q dataset, 205 μs of data could be clustered on a single node (and up to 1.03 ms on 5 nodes using MPI).

FIG. 4.

The CLI provided by enspara has favorable memory and performance characteristics. (a) Runtime as a function of data input size for the enspara cluster CLI on the TEM-1 and G_q datasets, and the MSMBuilder CLI on the TEM-1 dataset. For TEM-1/MSMBuilder and G_q/enspara, the final point represents the largest data size that can be run without exceeding available memory. (b) Process-allocated memory usage as a function of data input size for the enspara cluster CLI on the TEM-1 and G_q datasets, and the MSMBuilder CLI on the TEM-1 dataset. Apparent memory use by enspara appears to stop growing after 32 GB because, on the computer system tested (see Sec. IV), the operating system allocates double the necessary RAM to enspara. Where MSMBuilder runs out of RAM loading ∼16 GB, enspara is capable of using almost all of the available 64 GB RAM. (c) Number of clusters as a function of data input size for TEM-1 and G_q datasets. The change in runtime growth of the G_q dataset around 26 GB of data loaded is a consequence of the slowdown in state discovery as new data are added. For (a) and (b), error bars represent the standard deviation of three trials.

D. Sparse matrix integration

Building a Markov state model with tens of thousands of states presents some methodological challenges. One of these is the representation of the transition counts and transition probability matrices. Most straightforwardly, this is achieved using dense arrays, such as the array or matrix classes available in numpy, and this is the strategy employed by extant MSM softwares, MSMBuilder3^18,19,31 and PyEMMA.¹⁶ The problem with this representation is that the memory usage of these matrices grows with the square of the number of states in the model. To make matters worse, the computational cost of the eigendecomposition that is typically required to calculate a model’s stationary distribution (equilibrium probabilities) and principal relaxation modes grows with the cube of the number of elements in the matrix.⁴⁹

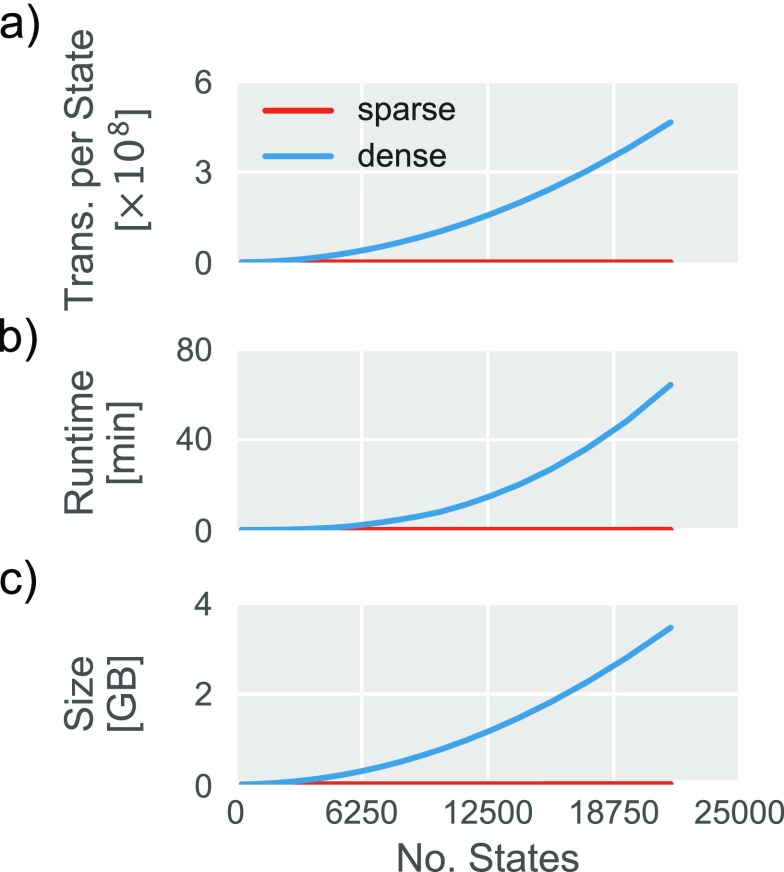
To address the computational challenges posed by traditional arrays, enspara has been engineered to support sparse arrays wherever possible. Sparse arrays have been supported by MSMBuilder in the past, but were dropped with version 3. PyEMMA also makes heavy use of dense arrays, although there is some support for sparse arrays. Sparse arrays, rather than growing strictly with the square of the number of states, grow linearly in the number of non-zero elements in the array. In the worst case where every element of the transition counts matrix is non-zero (i.e., every possible transition between pairs of states is observed) this becomes the dense case. However, this is very unusual: the number of observed transitions is generally several orders of magnitude smaller than the number of possible transitions [Fig. 5(a)]. By implementing routines that support scipy’s sparse matrices, it becomes possible to keep much larger Markov state models in memory [Fig. 5(b)] and analyze those models much more quickly [Fig. 5(c)].

FIG. 5.

The performance characteristics of sparse and dense matrices representing the same MSM. (a) The mean number of transitions per state in a transition counts matrix as a function of the number of states in the model. Any pair of states with an observed transition between them has a nonzero entry in the transition counts matrix and consumes memory in both sparse and dense cases. In contrast, a sparse matrix does not require memory for zero elements of the transition counts matrix. (b) The runtime of an eigendecomposition as a function of the number of states in a model. (c) The memory footprint of the transition probability matrix as a function of the number of states in a model.

E. Fast and MSM-ready information theory routines

Recent studies^50–52 have demonstrated the usefulness of information theory, and mutual information (MI) in particular, for identifying and understanding the salient features of conformational ensembles. MI is a nonlinear measurement of the statistical non-independence of two random variables. MI is given by

$$MI\left(X,Y\right)=\sum _{y\in Y}\sum _{x\in X}P\left(x,y\right)\log \frac{P\left(x,y\right)}{P\left(x\right)P\left(y\right)},$$ (1)

where P(x) is the probability that random variable X takes on value x, P(y) is the probability that random variable Y takes on value y, and P(x, y) is the joint probability that random variable X takes on value x and that random variable Y takes on value y.

Historically, the joint distribution P(x, y) is estimated by counting the number of times that combination of features appeared in each frame.^50,51 This computation can become a bottleneck when it must be computed over hundreds or thousands of different features and for datasets with hundreds of thousands or millions of observations. This is because it is highly iterative (which is notoriously slow in many higher-level programming languages, including python) and because the number of joint distributions that must be calculated grows with the square of the number of features to be tracked. Consequently, in the worst case, this involves examining every frame of a trajectory n² times, where n is the number of random variables of interest.

In enspara, we take two overlapping approaches to address the problem of the poor scalability of pairwise MI calculations. The first approach is to use the joint distribution implied by the equilibrium probabilities of a Markov state model, rather than by counting co-occurrences from full trajectories. Specifically, the joint probability P(x, y) is estimated by ∑_s∈Sπ(s), where π(s) is the equilibrium probability of state s from the MSM and S is the set of states where x = X and y = Y. This works by reducing the number of individual observations, usually by orders of magnitude. Existing codes^51,53 either do not provide the option to compute MI with weighted observations or require a specific object-based framework to do so.⁵⁴

Our second approach is to implement a fast joint counts calculation routine. This routine is both thread-parallelized and much faster than the equivalent numpy routine even on a single core. This approach is needed because, in some cases (e.g., Ref. 51), information from a Markov state model cannot be trivially substituted for frame-by-frame calculations. To address this case, we also implement a function using cython⁵⁵ and OpenMP⁵⁶ that takes a trajectory of n features and returns a four-dimensional joint counts array with dimension n × n × s_n × s_n, where s_n is the number of values each feature n can take on. The value of returning this four-dimensional joint counts matrix is that it renders the problem embarrassingly parallel in the number of trajectories: this function can be run on each trajectory totally independently, and the resulting joint counts matrices can be summed before being normalized to compute joint probabilities. We recommend combining this with a pipelining software like Jug.⁵⁷

Additionally, in this package, we include a reference implementation of Correlation of All Rotameric and Dynamical States (CARDS) framework.⁵¹ In brief, this method takes a series of molecular dynamics trajectories and computes the mutual information (MI) between all pairs of dihedral angle rotameric states, and between all pairs of dihedral angle order/disorder states. A dihedral angle is considered disordered if it frequently hops between rotameric states. This implementation parallelizes across cores on a single machine using the thread-parallelization described in Sec. II E.

F. Flexible and interoperable model fitting and analysis

With enspara, a major goal is maximal flexibility. This means loosely coupled, function-based components and the use of widely accepted datatypes for input and output of these functions. This helps us maximize interoperability with existing MSM softwares, other python libraries, and prototypes of novel analysis strategies in the future.

One important way we achieve flexibility in enspara is by constructing an API that accepts widely used datatypes, rather than datatypes that are unique to enspara. This is most important for our analysis functions, which accept parameters of MSMs rather than MSM objects themselves. For example, mutual information calculations (see Sec. II E) that use equilibrium probabilities from an MSM accept a vector of probabilities rather than an MSM object. (Note also that any function that accepts a RaggedArray will also accept a numpy array.³²) A crucial consequence of this API pattern is that enspara’s MSM analysis routines are interoperable with both PyEMMA’s and MSMBuilder’s MSM objects. It also allows integration with simple, hand-crafted models, as it was used to do in Zimmerman et al.⁵⁸

Another way we achieve flexibility is to preference function-based semantics over object-based semantics. A successful and prominent API pattern for machine learning tasks was promulgated by scikit-learn,⁵³ which represents various machine learning tasks (clustering, featurization, etc.) as objects. While this nicely contains the logic and complexities of each algorithm inside a fairly uniform API, it also makes the behavior of these algorithms difficult to modify with novel approaches, since new ideas must either be integrated into the existing object completely or the object must be entirely duplicated. An object can also obscure state from the user, hindering comprehension, modification, or reuse of code. To address this in enspara, wherever object interfaces exist, they are thin wrappers for chains of function calls. Consequently, an interested user can then easily intercept control flow to inject new behavior.

A noteworthy example of this in enspara is our semantic for estimating transition probability matrices. Estimating a transition probability matrix from observed state transitions is a crucial step in building an MSM, yet there is not a uniform procedure for accomplishing this that works in all cases. Many different estimators exist, and more are in active development.^31,58–66 Perhaps the simplest procedure to estimate the transition probability matrix, T, is to row-normalize the transition count matrix, C,

$$T_{ij}^{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{z}\mathrm{e}}=\frac{C_{ij}}{{\sum }_k{C}_{ik}},$$ (2)

where T_ij is the probability of observing a transition from state i to j and C_ij is the number of times such a transition was observed. While this method is simple, it can and often does generate a non-ergodic state space. In an effort to address this difficulty and to condition the MSM to be well-behaved, one can include an additional pseudocount ĉ before estimation

$$T_{ij}^{\mathrm{p}\mathrm{s}\mathrm{e}\mathrm{u}\mathrm{d}\mathrm{o}}=\frac{C_{ij}+ĉ}{{\sum }_k\left(C_{ik}+ĉ\right)},$$ (3)

which ensures ergodicity.⁵⁸ A more dramatic conditioning comes when forcing the counts matrix to obey detailed balance by averaging forward and reverse transitions

$$C_{ij}^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}}=\frac{C_{ij}+C_{ji}}{2},$$ (4)

$$T_{ij}^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}}=\frac{C_{ij}^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}}}{{\sum }_k{C}_{ik}^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}}}.$$ (5)

Yet a third proposed way of estimating an MSM is to find the maximum likelihood estimate for T subject to the constraint that it satisfies detailed balance.^2,31 Framed as a Bayesian inference, the transition probabilities are solved as the most likely given a transition counts matrix, such that

$$T_{ij}^{\mathrm{M}\mathrm{L}\mathrm{E}}=\text{argmax\hspace{0.17em}}P\left(T_{ij}^{*}|C\right).$$ (6)

Additionally, there exist more sophisticated schemes of estimation, such as those that draw on inspiration from observable operator models,⁶² and projected MSMs.⁶⁷ While it is beyond the scope of this article to review this area of study in exhaustive detail, we hope these few examples demonstrate the variety and importance of estimators. This poses a major challenge to writing a framework that can readily estimate a transition probability matrix; estimators are an active area of research, and a flexible framework that allows users to quickly modify an existing estimator or try a new one would be of great utility.

To address this difficulty, we treat fitting methods as simple functions, which we call builders, that take a transition counts matrix and return transition and equilibrium probabilities. These built-in functions, along with our MSM object can be used to quickly fit an MSM using commonly used approaches [Fig. 6(a)]. Alternatively, for users who wish to slightly modify existing MSM estimation methods, the function-level interface provides fine-grained control over the steps in fitting an MSM [Fig. 6(b)]. Finally, for users who wish to prototype entirely new MSM estimation methods, any function or callable object is accepted as a builder, as long as it accepts a transition counts matrix C as input and returns a 2-tuple of transition probabilities and equilibrium probabilities.

FIG. 6.

(a) An example usage of the high-level, object-based API to fit a Markov state model. (b) An example usage of enspara’s low-level, function-based API to fit a Markov state model. (c) A custom method that fits a Markov state model and is interoperable with enspara’s existing API.

III. CONCLUSION

In this work, we have presented enspara, a library for building Markov state models at scale. We introduced an implementation of the ragged array, which dramatically improved the memory footprint of MSM-associated data. We developed a low-communication, parallelized version of the classic k-centers and k-medoids clustering algorithms, which simultaneously reduce runtime and load time while vastly increasing the ceiling on memory use for those algorithms by allowing execution on multiple computers simultaneously. In addition, enspara has turn-key sparse matrix usage. Finally, we implement a function-based API for MSM estimators which greatly increases the flexibility of MSM estimation to enable rapid experimentation with different methods of fitting. Taken together, these features make enspara the ideal choice of MSM library for many-state, large-data MSM construction and analysis.

IV. METHODS

A. Source code and documentation

The source code to enspara is available on GitHub at https://github.com/bowman-lab/enspara, where installation instructions can also be found. In brief, it can be downloaded from GitHub and installed using setup.py.

Documentation takes two forms, docstrings and a documentation website. Individual functions and objects are documented as docstrings, which indicate parameters and return values, and briefly describe each functions role. The library as a whole is documented at https://enspara.readthedocs.io, which gives a high-level description of the library’s functionality, as well as providing worked-through examples of enspara’s use.

Finally, at https://enspara.readthedocs.io/tutorial, we give an in-depth tutorial example analyzing data from a public dataset.

B. Libraries and hardware

Eigenvector/eigenvalue decomposition experiments were performed on a Ubuntu 16.04.5 (xenial) workstation with an Intel i7-5820K CPU (central processing unit) @ 3.30 GHz (12 cores) with 32 GB of RAM using SciPy version 1.1.0 and numpy 1.13.3. Probabilities were represented as 8-byte floating point numbers.

Thread parallelization experiments were performed on the same hardware using OpenMP 4.0 (2013.07) with gcc 5.4.0 (2016.06.09) and cython 0.26 in Python 3.6.0, distributed by Continuum Analytics in conda 4.5.11.

Clustering scaling experiments were performed on identical computers running CentOS Linux release 7.3.1611 (Core) with Intel Xeon E5-2697 v2 CPUs @ 2.70 GHz and 64 GB of RAM linked to a head node with two Intel 10-Gigabit X540-AT2 ethernet adapters and nfs-utils 1.3.0. We used the mpi4py^68–70 and Python 3.6.0 with Open MPI 2.0.2. Clustering used as a distance metric the root-mean square deviation (RMSD) function provided in the MDTraj 1.9.1.³⁵

C. Simulation data

For example simulation data, we used a previously published 90.5 μs TEM-1 β-lactamase dataset¹¹ and a 122.6 μs G_q dataset.⁷¹ As described previously, simulations were run at 300 K with the GROMACS software package^47,48 using the Amber03 force field⁷² and TIP3P⁷³ explicit solvent. Data were generated using the Folding@home distributed computing platform.¹⁵

D. Residue labeling analysis

Residue labeling behavior for residues A150, L190, S203, A232, A249, I260, and L286 was measured in Bowman et al.²⁹ and for S243 in Porter et al.³⁰ “Exposed” residues label almost immediately, “pocket” or “transiently-labeling” residues label on the order of 10⁻³ or 10⁻⁴ s⁻¹, and buried residues label on the order over days.

Residue labeling behavior was predicted according to the procedure described in Ref. 30. In brief, sidechain atoms’ solvent exposure to a 2.8 Å probe was calculated (using the Shrake-Rupley⁷⁴ algorithm implemented by MDTraj³⁵) for the representative structure for each MSM state, and the residue was called as exposed if its exposed area exceeded 2 Ų.