Internal force corrections with machine learning for quantum mechanics/molecular mechanics simulations

Abstract

Ab initio quantum mechanics/molecular mechanics (QM/MM) molecular dynamics simulation is a useful tool to calculate thermodynamic properties such as potential of mean force for chemical reactions but intensely time consuming. In this paper, we developed a new method using the internal force correction for low-level semiempirical QM/MM molecular dynamics samplings with a predefined reaction coordinate. As a correction term, the internal force was predicted with a machine learning scheme, which provides a sophisticated force field, and added to the atomic forces on the reaction coordinate related atoms at each integration step. We applied this method to two reactions in aqueous solution and reproduced potentials of mean force at the ab initio QM/MM level. The saving in computational cost is about 2 orders of magnitude. The present work reveals great potentials for machine learning in QM/MM simulations to study complex chemical processes.

INTRODUCTION

The free energy change along the reaction coordinate (RC), or the potential of mean force (PMF), is a central quantity for describing the pathways and barriers of a chemical reaction.^1–5 Based on chemical intuition, one or a set of collective variables of the molecular structure is often defined as RC to capture the major geometric change in a chemical process. The PMF can be calculated from molecular dynamics (MD) simulations. In order to cross high-energy barriers efficiently, some RC-guided enhanced sampling techniques such as umbrella sampling^6,7 are necessary. However, MD simulations with the ab initio quantum mechanical or QM/MM method are still limited to relatively small molecules because of a large computational cost on electronic structure calculations.^8–12 A reparameterization or correction of a semiempirical QM (SQM) model to ab initio QM is an attractive way to achieve a higher accuracy with an affordable computational cost. One example is the force matching method, in which some specific parameters in the low-level model were modified with a fitness function to match the high-level calculations on the selected configurations along the reaction path.^13–15 Ruiz-Pernía et al. developed another dual-level QM/MM method in which the difference between SQM/MM and ab initio QM/MM potential energies was approximated as a spline interpolation function of RC.^16,17 These methods are as efficient as SQM/MM since only a few configurations are required for ab initio QM/MM calculations. The applications to complex reactions in the condensed phase and biochemical environment revealed their success, but there are still some nontrivial concerns in practice. First, an explicit fitness function has to be designed to map the correction term for each system, which restricts the accuracy and availability for these approaches. Second, the selection on the configurations for ab initio calculations is limited to the reaction path along RC. It may be largely affected by the fluctuation of MM environment, which is not easy to capture because of the complexity of a QM/MM energy landscape.

Machine learning (ML) is being increasingly used in the past decades to save the computational cost and overcome the limitation on conventional MD simulations. Botu and Ramprasad proposed an adaptive scheme combined with “big-data” techniques to predict atomic forces and accelerate materials simulations.¹⁸ Li et al. developed a machine learning approach to perform QM-accurate MD simulations with a growing database.¹⁹ Stecher et al. applied the Gaussian process regression to construct free energy surfaces after umbrella sampling simulations.²⁰ Recently, we developed a QM/MM neural network method to predict the SQM/MM and ab initio QM/MM potential energy differences based on the low-level MD simulations, and then the high-level PMF was produced using a reweighting scheme,²¹ achieving a significant reduction of computational effort in free energy prediction compared with direct ab initio QM/MM calculations. However, a direct QM/MM MD algorithm guided with machine learning is still absent. In this paper, we present a machine learning method to predict the ab initio QM/MM forces with the information on RC. First, internal forces are introduced to correct the difference of atomic forces between SQM/MM and ab initio QM/MM models along RC directions. Their values are predicted using the k-nearest neighbor (kNN) algorithm²² for any configuration during QM/MM MD. Second, MD simulations are performed using SQM/MM forces with the correction term, both of which can be obtained at a much lower computational cost than ab initio calculations. Finally, a highly accurate PMF is achieved based on MD samplings with ML corrections.

The rest of this paper is organized as follows. We first describe the construction on the ML database. The central question is how to calculate the internal force from SQM/MM and ab initio QM/MM atomic forces. Then we will use the machine learning scheme to predict the high-level atomic forces for any configuration during SQM/MM MD and correct the low-level MD evolution, followed by computational validation, discussion, and conclusion.

THEORETICAL FOUNDATION

The key point of our method is that the dimensionality of machine learning can be reduced with some prior knowledge of reaction coordinate. Here we focus our discussions on the systems where a combination of bond lengths on the QM subsystem is defined as RC. Only the forces acting on the QM atoms involved in RC are corrected using ML, and the correction terms on the internal forces are added only along the direction of the corresponding bond length in RC. The deviation of SQM/MM forces from ab initio QM/MM forces should be reduced significantly with ML corrections. Consider RC as the distance between atoms i and j. Its value at time t, $r_{ij}\left(t\right)$, can be written as

$$r_{ij}\left(t\right){\widehat{\mathbf{r}}}_{ij}\left(t\right)={\mathbf{r}}_j\left(t\right)-{\mathbf{r}}_i\left(t\right),$$ (1)

where ${\mathbf{r}}_i\left(t\right)$ and ${\mathbf{r}}_j\left(t\right)$ are the Cartesian coordinates of atoms i and j at time t, respectively, and ${\widehat{\mathbf{r}}}_{ij}$ is the unit vector along the direction from i to j. The Cartesian coordinate and velocity of atom i at the next MD step can be expressed based on the common used velocity Verlet integration schemes²³ as follows:

$${\mathbf{r}}_i\left(t+\mathrm{\Delta }t\right)={\mathbf{r}}_i\left(t\right)+{\mathbf{v}}_i\left(t\right)\mathrm{\Delta }t+\frac{{\mathbf{F}}_i\left(t\right)}{2m_i}\mathrm{\Delta }{t}^2$$ (2)

and

$${\mathbf{v}}_i\left(t+\mathrm{\Delta }t\right)={\mathbf{v}}_i\left(t\right)+\frac{{\mathbf{F}}_i\left(t\right)+{\mathbf{F}}_i\left(t+\mathrm{\Delta }t\right)}{2m_i}\mathrm{\Delta }t,$$ (3)

where Δt is the integration time step, m_i is the mass of atom i, and ${\mathbf{v}}_i\left(t\right)$ and ${\mathbf{F}}_i\left(t\right)$ are the velocity and force of atom i at time t, respectively. Given the same coordinates and velocities at time t, the deviation of ${\mathbf{r}}_i\left(t+\mathrm{\Delta }t\right)$ between different potential energies (e.g., SQM/MM and ab initio QM/MM) only originates from the difference of ${\mathbf{F}}_i\left(t\right)$, leading to

$$\begin{array}{c}\left[{\mathbf{r}}_j^H\left(t+\mathrm{\Delta }t\right)-{\mathbf{r}}_j^{LC}\left(t+\mathrm{\Delta }t\right)\right]-\left[{\mathbf{r}}_i^H\left(t+\mathrm{\Delta }t\right)-{\mathbf{r}}_i^{LC}\left(t+\mathrm{\Delta }t\right)\right]\hfill \\ =\frac{\mathrm{\Delta }{t}^2}{2m_j}\left[{\mathbf{F}}_j^H\left(t\right)-{\mathbf{F}}_j^L\left(t\right)-{\mathbf{F}}_j^{corr}\left(t\right)\right]\hfill \\ -\frac{\mathrm{\Delta }{t}^2}{2m_i}\left[{\mathbf{F}}_i^H\left(t\right)-{\mathbf{F}}_i^L\left(t\right)-{\mathbf{F}}_i^{corr}\left(t\right)\right].\hfill \end{array}$$ (4)

Here ${\mathbf{r}}_i^H\left(t+\mathrm{\Delta }t\right)$ and ${\mathbf{r}}_i^{LC}\left(t+\mathrm{\Delta }t\right)$ are the Cartesian coordinates of atom i at time t + Δt. The former one is calculated from ${\mathbf{F}}^H\left(t\right)$, and the latter one is calculated from ${\mathbf{F}}^L\left(t\right)+{\mathbf{F}}^{corr}\left(t\right)$. ${\mathbf{F}}_i^H\left(t\right)$ and ${\mathbf{F}}_i^L\left(t\right)$ are the high-level and low-level forces on atom i at time t, respectively, and ${\mathbf{F}}_i^{corr}\left(t\right)$ is the internal force correction on atom i at time t. The variables with the subscript j denote the corresponding coordinates or forces of atom j. ${\mathbf{F}}_i^{corr}\left(t\right)$ and ${\mathbf{F}}_j^{corr}\left(t\right)$ are added along the direction of ${\widehat{\mathbf{r}}}_{ij}$ with the magnitudes as $F_i^{corr}\left(t\right)$ and $F_j^{corr}\left(t\right)$, respectively. They should be constrained by the condition

$$F_i^{corr}\left(t\right)+F_j^{corr}\left(t\right)=0,$$ (5)

which ensures that the total correction force of the whole system is zero at any time. Note that we cannot obtain any prior knowledge about ${\widehat{\mathbf{r}}}_{ij}\left(t+\mathrm{\Delta }t\right)$ at time t, which means that we have to introduce an approximation as ${\widehat{\mathbf{r}}}_{ij}\left(t+\mathrm{\Delta }t\right)\approx {\widehat{\mathbf{r}}}_{ij}\left(t\right)$. Both sides of Eq. (4) are projected onto ${\widehat{\mathbf{r}}}_{ij}$ under this approximation, leading to

$$\begin{array}{c}\frac{2}{\mathrm{\Delta }{t}^2}\left[{\mathit{r}}_{ij}^H\left(t+\mathrm{\Delta }t\right)-{\mathit{r}}_{ij}^{LC}\left(t+\mathrm{\Delta }t\right)\right]\hfill \\ \approx \frac{\left[{\mathbf{F}}_j^H\left(t\right)-{\mathbf{F}}_j^L\left(t\right)\right]\cdot {\widehat{\mathbf{r}}}_{ij}\left(t\right)-F_j^{corr}\left(t\right)}{m_j}\hfill \\ -\frac{\left[{\mathbf{F}}_i^H\left(t\right)-{\mathbf{F}}_i^L\left(t\right)\right]\cdot {\widehat{\mathbf{r}}}_{ij}\left(t\right)-F_i^{corr}\left(t\right)}{m_i},\hfill \end{array}$$ (6)

where $r_{ij}^H\left(t+\mathrm{\Delta }t\right)$ and $r_{ij}^{LC}\left(t+\mathrm{\Delta }t\right)$ are the distances between atoms i and j at time t + Δt. The former is calculated from ${\mathbf{F}}^H\left(t\right)$, and the latter is calculated from ${\mathbf{F}}^L\left(t\right)+{\mathbf{F}}^{corr}\left(t\right)$. In order to get the same values of $r_{ij}^H\left(t+\mathrm{\Delta }t\right)$ and $r_{ij}^{LC}\left(t+\mathrm{\Delta }t\right)$, we have the relationship between the internal force corrections and the atomic forces calculated at two levels as

$$\begin{array}{c}\frac{\left[{\mathbf{F}}_j^H\left(t\right)-{\mathbf{F}}_j^L\left(t\right)\right]\cdot {\widehat{\mathbf{r}}}_{ij}\left(t\right)-F_j^{corr}\left(t\right)}{m_j}\hfill \\ -\frac{\left[{\mathbf{F}}_i^H\left(t\right)-{\mathbf{F}}_i^L\left(t\right)\right]\cdot {\widehat{\mathbf{r}}}_{ij}\left(t\right)-F_i^{corr}\left(t\right)}{m_i}=0.\hfill \end{array}$$ (7)

Herein the values of the correction forces can be solved using the low-level and high-level atomic forces through Eqs. (5) and (7). Similarly, the internal force corrections at time t + Δt can be derived from Eq. (3) in order to get the same values of $v_{ij}^H\left(t+\mathrm{\Delta }t\right)$ and $v_{ij}^{LC}\left(t+\mathrm{\Delta }t\right)$, leading to the same expressions as Eqs. (5) and (7). The projections of r^H and r^LC (and v^H and v^LC) onto the direction of RC are expected to keep identical at sequential MD steps, so the internal force corrections at any time can be obtained recursively in the same way. The above derivation can be extended directly to any linear combination of bond lengths involving more than two atoms.

One motivation of machine learning is to reduce the expensive computational cost on the high-level forces in Eq. (7). Next we propose an ML scheme to predict the internal force corrections without ab initio calculations. For example, QM atom i is included in RC as a RC-related atom. First, its chemical environment is represented by the neighboring QM atoms within a cut-off distance r_cut. In other words, the position of atom i can be constructed with the positions of its neighbors, and the construction weight $w_j^{\left(i\right)}$ summarizes the contribution from atom j. Similar to the scheme used in the locally linear embedding algorithm,²⁴ the construction error ε_i is measured as

$${\epsilon }_i=\mid {\mathbf{r}}_i-\sum _{j\ne i}{w}_j^{\left(i\right)}{\mathbf{r}}_j{\mid }^2,$$ (8)

which is minimized with the constraint of $\sum _j{w}_j^{\left(i\right)}=1$ to obtain the optimal weights as the input features. The weights are further scaled to reduce the contribution from distant atoms with a cutoff function as

$$f_{cut}\left(r_{ij}\right)=\left\{\begin{array}{cc}1-2{\left[e^{-r_{cut}\left(r_{ij}-r_{cut}\right)}+1\right]}^{-1}& r_{ij}\le r_{cut}\hfill \\ 0& r_{ij}>r_{cut}\hfill \end{array}\right..$$ (9)

Second, the Mulliken atomic charges of the RC-related atoms, which have been calculated with the low-level electrostatic-embedding QM/MM model, are employed as another input feature to include the contributions from MM environment. As discussed in our previous work,²¹ Mulliken atomic charges reflect external potentials of the MM environment with reduced degrees of freedom as small as the number of QM atoms. This feature also captures the polarization of the QM subsystem in response to MM electrostatic potentials. The input vector for atom i is thus expressed as

$${\mathbf{v}}^{\left(i\right)}=\left(w_1^{\left(i\right)}{f}_{cut}\left(r_{i1}\right),\dots ,w_M^{\left(i\right)}{f}_{cut}\left(r_{iM}\right),q_i\right),$$ (10)

where q_i is the Mulliken charge of atom i, and M is the number of the neighbors of atom i that depends on the cutoff distance.

The k-nearest neighbor algorithm is utilized in this work. The predictions on the correction forces acting on different atoms are independent. For example, the correction term ${\mathbf{F}}_i^{corr}$ is only dependent on ${\mathbf{v}}^{\left(i\right)}$, where atom i is included in RC. The Euclidean distance between two configurations m and n is calculated as

$$d_{mn}^{\left(i\right)}=\parallel {\mathbf{v}}_m^{\left(i\right)}-{\mathbf{v}}_n^{\left(i\right)}\parallel ,$$ (11)

where ${\mathbf{v}}_m^{\left(i\right)}$ and ${\mathbf{v}}_n^{\left(i\right)}$ are the input vectors of configurations m and n for atom i, respectively, which have been defined in Eq. (10). For a new configuration x, the k nearest samples in the database are selected based on the Euclidean distances, and the correction force on atom i of configuration x can be predicted in terms of a weighted average as

$$F_{i\left(x\right)}^{corr}=\frac{\sum _p^k{\left[d_{xp}^{\left(i\right)}\right]}^{-1}{F}_{i\left(p\right)}^{corr}}{\sum _p^k{\left[d_{xp}^{\left(i\right)}\right]}^{-1}},$$ (12)

where p is one of the k nearest samples, and $F_{i\left(p\right)}^{corr}$ and $F_{i\left(x\right)}^{corr}$ are the correction forces on atom i of configuration p and x, respectively. The correction forces on other RC-related atoms of configuration x can be predicted in the same way.

The procedure of QM/MM MD simulation combined with our internal force machine learning correction is outlined as follows: (1) Define a set of geometric parameters that are involved in the reaction coordinate z and perform low-level SQM/MM MD simulations along z (e.g., umbrella sampling). (2) Choose a few configurations from MD trajectories in the whole range of z as data points in the ML database and calculate their input vectors for RC-related atoms using Eq. (10) and the ab initio QM/MM forces F^H. (3) Apply F^L obtained in step 1 and F^H obtained in step 2 to Eq. (7) to calculate F^corr for all samples in the ML database using Eqs. (5) and (7) or the variant formulation (e.g., see the Appendix). (4) Perform SQM/MM MD simulations with the correction forces. At each MD step, the input vectors for RC-related atoms are calculated using Eq. (10). The ML correction forces are predicted using Eqs. (11) and (12) and added to the SQM/MM atomic forces to update atomic coordinates and velocities for the next integration step. (5) Calculate the free energy change along z based on the MD samplings obtained in step 4.

COMPUTATIONAL VALIDATION

To demonstrate the capability of this method, we calculated the PMFs for two aqueous systems, the Menshutkin reaction between methyl chloride and ammonia and the aliphatic Claisen rearrangement reaction of allyl vinyl ether (AVE), at different QM/MM levels. For both reactions, the solute was defined as the QM subsystem and solvated in a cubic water box with a $16\AA$ extended distance. The MM subsystem for the Menshutkin and Claisen rearrangement reaction contains 1686 and 1745 water molecules, respectively. The TIP3P water model was employed under periodic boundary condition.²⁵ The cutoff distance for nonbonded interactions was set as 14 Å. The QM/MM van der Waals (vdW) interactions were described with the Amber-ff14SB force field.²⁶ The Hartree-Fock (HF) method with the 6-31G(d) basis set and the self-consistent charge density functional tight binding (SCC-DFTB) method with the second-order formulation^27,28 were used, respectively, as the high-level and low-level QM models. Note that the two levels were selected based on the difference of the QM/MM MD simulation results, while their comparisons with experiments are not important for our purpose presently. The MD simulations for free energy calculations were carried out after geometry optimization on the solute in the gas phase and solvent equilibration. The integration time step was set as 1 fs, and the system temperature was maintained at 300 K using a Berendsen thermostat²⁹ with a time constant of 1.0 ps during all simulations. All the calculations were implemented in the modified Amber 14 program package³⁰ combined with the GAUSSIAN 03 program³¹ for Hartree-Fock calculations.

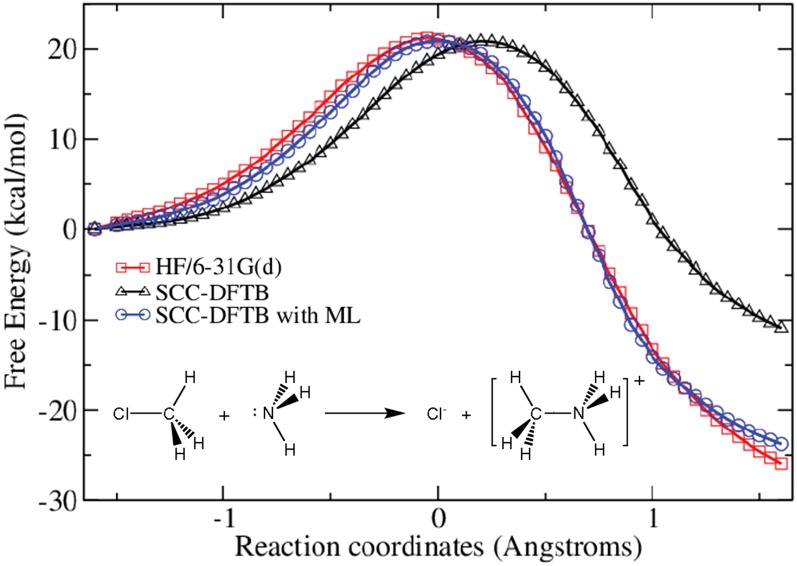
The reaction coordinate for the Menshutkin reaction of methyl chloride and ammonia transfer was chosen as z = r_C–Cl − r_C–N. Umbrella samplings with 64 windows centering from z = −1.6 to 1.6 Å were applied. The SCC-DFTB/MM MD simulations were performed for 1 ns for each window, and the snapshots were saved every 5 ps from each window to build the ML database. Then 1 ns SCC-DFTB/MM MD simulations with ML corrections were performed for each window. In addition, the HF/6-31G(d)/MM MD simulations were performed for 20 ps for each window to obtain the high-level free energy change as our reference. The cutoff distance r_cut to construct the input vectors for ML was set as 3.8 Å, and the hyperparameter k in kNN was set as 5. The weighted histogram analysis method (WHAM)^32,33 was applied to calculate PMFs based on MD samplings. The PMFs obtained at different levels were shown in Fig. 1. The reaction free energies at the SCC-DFTB/MM and HF/6-31G(d)/MM levels are −10.9 and −25.9 kcal/mol, respectively. The values of free energy barriers at two levels are similar (20.8 and 21.2 kcal/mol), but the locations of transition state along RC are different. The low-level MD simulations with ML corrections reproduce the free energy profile in good agreement with the results obtained at the high-level, that is, −23.8 and 20.8 kcal/mol for the reaction free energy and barrier, respectively. A corrected position along RC for the transition state is also obtained. We also checked the convergence of the size of ML database using 50 snapshots from each window, getting similar reaction free energy and barrier with less than 2 kcal/mol difference from the previous results. It suggests that 200 snapshots per window, that is, 200 times of ab initio QM/MM calculations, have been sufficient to construct a database for ML training. On the other hand, a typical ab initio QM/MM MD needs at least tens of thousands times for ab initio calculations. The saving in the computational cost is about 2 orders of magnitude.

FIG. 1.

Potential of mean force for the Menshutkin reaction. Different colors and shapes represent MD simulations with different methods (black triangle: SCC-DFTB/MM; red square: HF/6-31G(d)/MM; blue circle: SCC-DFTB/MM with ML corrections).

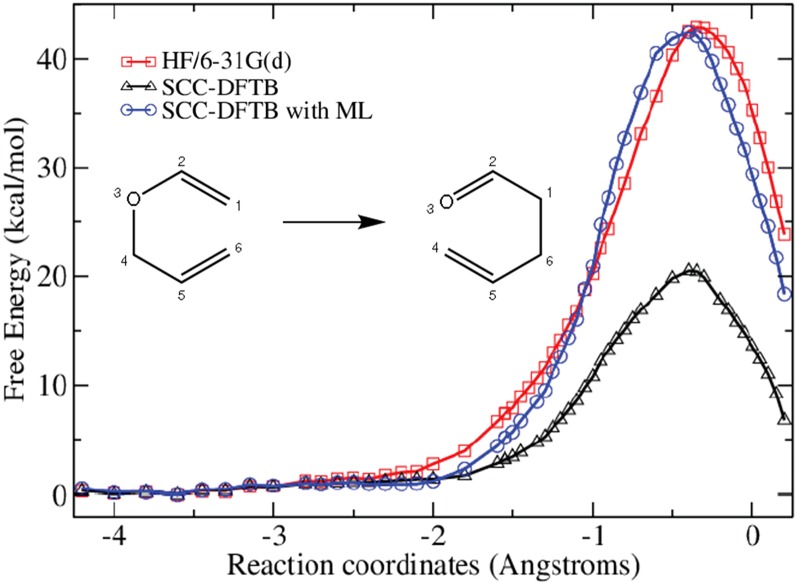
The reaction coordinate for the Claisen rearrangement of AVE was chosen as z = r_O3–C4 − r_C1–C6. Umbrella samplings with 53 windows centering from z = −4.2 to $0.2\AA$ were applied. The simulation time at different levels, the size of the database for training, the hyperparameters in ML, and the method for free energy calculations were set as the same as those in the first system. As shown in Fig. 2, the free energy barriers at the SCC-DFTB/MM and HF/6-31G(d)/MM levels are 20.7 and 42.9 kcal/mol, respectively. The simulation with ML corrections achieves 42.4 kcal/mol, but the position of the transition state has a slight deviation. On account of the complication of the Claisen rearrangement of AVE such as the transition from extended to compact forms in the reactant region and the stereochemistry of transition states,^34,35 the identification of an accurate RC is challenging. It may cause some errors in our case because only the forces on RC-related atoms are corrected with ML. A preceding optimization on the transition path^36–39 or a further force correction along some additional selected degrees of freedom beyond RC may be useful to remedy this problem and overcome the RC-dependence as the main disadvantage of this method. The combination with RC-free enhanced sampling techniques^40,41 may be even beneficial to some more complex systems without obvious RCs.

FIG. 2.

Potential of mean force for the Claisen rearrangement reaction of AVE. Different colors and shapes represent MD simulations with different methods (black triangle: SCC-DFTB/MM; red square: HF/6-31G(d)/MM; blue circle: SCC-DFTB/MM with ML corrections).

Several improvements can be made to address the limitations observed in this method. One extension is the optimal choice of ML algorithms for force predictions. In order to measure the quality of kNN used in this paper, we constructed two testing sets for each system. The first one (set 1) consists of several configurations (200 snapshots from each window) that were sampled during original SCC-DFTB/MM simulations but excluded from the database of kNN. The second one (set 2) includes some other configurations (100 snapshots from each window) that were sampled during SCC-DFTB/MM simulations with ML corrections. The comparisons of predicted and reference correction forces were shown in Figs. S1 and S2 in the supplementary material. Compared with the reference values obtained from Eqs. (5) and (7), the mean absolute errors (MAEs) on the predicted atomic forces for set 1 and set 2 were 0.29 and 0.35 eV/Å for the system of the Menshutkin reaction, respectively. The larger error for set 2 reflects the deviation originated from the insufficient overlap between sampling spaces at two levels, which can be remedied with an adaptive ML database. For the system of the Claisen rearrangement reaction, the MAEs for set 1 and set 2 were 0.25 and 0.28 eV/Å, respectively. Although the errors on the calculated reaction free energies and free energy barriers for the two systems are as small as 1-2 kcal/mol, the intrinsic error of kNN on force predictions cannot be ignored. More recent ML algorithms based on nonlinear kernel, such as Gaussian process regression, have been reported to achieve higher accuracy within 0.1 eV/Å for the bulk silicon¹⁹ and would be introduced in our future work. We further checked the energy conservation under the present ML-based model. The dynamic energy estimation scheme reported recently⁴² was employed. The energy evolution of one representative trajectory during NVE simulations can be seen in Fig. S3 in the supplementary material. An energy drift of $1.8\times 10^{-4}$ kcal/mol per atom per picosecond was observed during a 10 ps evolution, showing that the energy conservation cannot be implied strictly because of the force-based predictions with ML.¹⁹ Another extension is the optimal choice of MD algorithms for sampling, such as the thermostat applied to QM/MM systems. Here we compared two sets of simulation results on the Claisen rearrangement of AVE, that is, using the Berendsen thermostat with a time constant of 1.0 ps²⁹ and using Langevin dynamics with a friction coefficient of 1.0 ps⁻¹.⁴³ On the one hand, the free energy barriers using Langevin dynamics were calculated as 21.3 and 43.4 kcal/mol with original SCC-DFTB/MM and our ML-based model, respectively, indicating a small difference from the corresponding results using the Berendsen thermostat (within 1 kcal/mol, see above). On the other hand, the fluctuation of kinetic energy was reproduced with Langevin dynamics as the same as the analytical value but underestimated by 20% with the Berendsen thermostat, which means that the latter cannot give a canonical ensemble. On account of the significant role of sampling not only on free energy calculations but also on ML database constructions, special care should be taken in the MD simulation techniques.

CONCLUSION

Compared with some recently reported ML methods combined with QM/MM calculations, in which the QM/MM reaction free-energy profiles or excitation energies were predicted satisfyingly,^21,44 this method has three additional outstanding features. The first one is its dimensionality reduction. As the same as our previous work,²¹ thousands of MM degrees of freedom are reduced to the number of QM atoms using Mulliken charges. In this method, furthermore, only the input vectors for the atoms included in RC (2-4 atoms in general) are necessary, and the dimensionality of an input vector is determined by a cutoff distance. Therefore, the computational cost on ML would grow more slowly with the increase on QM degrees of freedom. The second feature is “truly force based,”⁴² that is, atomic forces rather than a potential energy surface are predicted directly, avoiding the difficulty to calculate the gradients of some artificial input variables. Finally, compared with the neural network based models, the ML problem is moved from an input-feature space into a data-point space by kNN in our method, making it much easier to extend to a “learn-on-the-fly” scheme.⁴⁵

In summary, we develop a machine learning internal force correction, which is guided by the information on a predefined reaction coordinate. It provides a pathway to improve the semiempirical QM/MM free energy calculations and achieves the accuracy of an ab initio QM/MM model. On the one hand, the use of RC can describe the dominant physical or chemical change in the reaction and capture the principal components contributing to a large portion of the free energy change. On the other hand, the use of ML can overcome the limitation of physical approximations or function forms in conventional RC-guided methods and decrease the computational cost on electronic structure calculations by about 2 orders of magnitude. The application to two systems reveals its reliability and efficiency. The limitations and some possible extensions are also discussed. This method makes a bridge between two active research topics, reaction coordinate guided sampling and machine learning based force field, and provides great potential for a broad range of interesting applications in molecular simulations.

SUPPLEMENTARY MATERIAL

See supplementary material for Figs. S1 and S2 for the comparisons of predicted and reference correction forces for two systems. Figure S3 for the energy evolution of one representative trajectory during NVE simulations using SCC-DFTB/MM with ML corrections.

APPENDIX: INTERNAL FORCES ON TESTING SYSTEMS

In order to construct the ML database, we need to calculate the internal force corrections based on SQM/MM and ab initio QM/MM atomic forces. The derivation in the main text can be extended to any linear combination of bond lengths involving more than two atoms. The RC for our second testing system is defined as z = r_O3–C4 − r_C1–C6 with four atoms. The force corrections on O3 and C4 are decoupled from that on C1 and C6, and Eqs. (5) and (7) can be applied without any change.

The RC for our first testing system is defined as z = r_C–Cl − r_C–N. Note that one carbon atom is involved with two bond lengths, making it a little complicated. On the one hand, the correction force acting on C should be added along two directions, that is,

$${\mathbf{F}}_{\mathrm{C}}^{corr}={\mathbf{F}}_{\mathrm{C}\left(\text{Cl}\right)}^{corr}+{\mathbf{F}}_{\mathrm{C}\left(\text{N}\right)}^{corr},$$ (A1)

where ${\mathbf{F}}_{\mathrm{C}\left(\text{Cl}\right)}^{corr}$ and ${\mathbf{F}}_{\mathrm{C}\left(\text{N}\right)}^{corr}$ are, respectively, along the direction of ${\widehat{\mathbf{r}}}_{Cl\text{–}\mathrm{C}}$ and ${\widehat{\mathbf{r}}}_{\mathrm{N}\text{–}\mathrm{C}}$. On the other hand, the correction forces on Cl and N are only added along ${\widehat{\mathbf{r}}}_{Cl\text{–}\mathrm{C}}$ and ${\widehat{\mathbf{r}}}_{\mathrm{N}\text{–}\mathrm{C}}$, respectively. Similar to Eq. (5), their components should satisfy

$${\mathbf{F}}_{Cl}^{corr}\left(t\right)+{\mathbf{F}}_{\mathrm{C}\left(\text{Cl}\right)}^{corr}\left(t\right)=0$$ (A2)

and

$${\mathbf{F}}_{\mathrm{N}}^{corr}\left(t\right)+{\mathbf{F}}_{\mathrm{C}\left(\text{N}\right)}^{corr}\left(t\right)=0,$$ (A3)

at any time t. Applying these correction terms to Eq. (4), we have

$$\begin{array}{c}\left[{\mathbf{r}}_{\mathrm{C}}^H\left(t+\mathrm{\Delta }t\right)-{\mathbf{r}}_{\mathrm{C}}^{LC}\left(t+\mathrm{\Delta }t\right)\right]-\left[{\mathbf{r}}_{Cl}^H\left(t+\mathrm{\Delta }t\right)-{\mathbf{r}}_{Cl}^{LC}\left(t+\mathrm{\Delta }t\right)\right]\hfill \\ =\frac{\mathrm{\Delta }{t}^2}{2m_{\mathrm{C}}}\left[{\mathbf{F}}_{\mathrm{C}}^H\left(t\right)-{\mathbf{F}}_{\mathrm{C}}^L\left(t\right)-{\mathbf{F}}_{\mathrm{C}}^{corr}\left(t\right)\right]\hfill \\ -\frac{\mathrm{\Delta }{t}^2}{2m_{Cl}}\left[{\mathbf{F}}_{Cl}^H\left(t\right)-{\mathbf{F}}_{Cl}^L\left(t\right)-{\mathbf{F}}_{Cl}^{corr}\left(t\right)\right]\hfill \end{array}$$ (A4)

and

$$\begin{array}{c}\left[{\mathbf{r}}_{\mathrm{C}}^H\left(t+\mathrm{\Delta }t\right)-{\mathbf{r}}_{\mathrm{C}}^{LC}\left(t+\mathrm{\Delta }t\right)\right]-\left[{\mathbf{r}}_{\mathrm{N}}^H\left(t+\mathrm{\Delta }t\right)-{\mathbf{r}}_{\mathrm{N}}^{LC}\left(t+\mathrm{\Delta }t\right)\right]\hfill \\ =\frac{\mathrm{\Delta }{t}^2}{2m_{\mathrm{C}}}\left[{\mathbf{F}}_{\mathrm{C}}^H\left(t\right)-{\mathbf{F}}_{\mathrm{C}}^L\left(t\right)-{\mathbf{F}}_{\mathrm{C}}^{corr}\left(t\right)\right]\hfill \\ -\frac{\mathrm{\Delta }{t}^2}{2m_{\mathrm{N}}}\left[{\mathbf{F}}_{\mathrm{N}}^H\left(t\right)-{\mathbf{F}}_{\mathrm{N}}^L\left(t\right)-{\mathbf{F}}_{\mathrm{N}}^{corr}\left(t\right)\right],\hfill \end{array}$$ (A5)

which leads to

$$\frac{\left[{\mathbf{F}}_{\mathrm{C}}^H\left(t\right)-{\mathbf{F}}_{\mathrm{C}}^L\left(t\right)\right]\cdot {\widehat{\mathbf{r}}}_{Cl\text{–}\mathrm{C}}\left(t\right)-F_{\mathrm{C}\left(\text{Cl}\right)}^{corr}\left(t\right)-F_{\mathrm{C}\left(\text{N}\right)}^{corr}\left(t\right)\left[{\widehat{\mathbf{r}}}_{\mathrm{N}\text{–}\mathrm{C}}\left(t\right)\cdot {\widehat{\mathbf{r}}}_{Cl\text{–}\mathrm{C}}\left(t\right)\right]}{m_{\mathrm{C}}}-\frac{\left[{\mathbf{F}}_{Cl}^H\left(t\right)-{\mathbf{F}}_{Cl}^L\left(t\right)\right]\cdot {\widehat{\mathbf{r}}}_{Cl\text{–}\mathrm{C}}\left(t\right)-F_{Cl}^{corr}\left(t\right)}{m_{Cl}}=0$$ (A6)

and

$$\frac{\left[{\mathbf{F}}_{\mathrm{C}}^H\left(t\right)-{\mathbf{F}}_{\mathrm{C}}^L\left(t\right)\right]\cdot {\widehat{\mathbf{r}}}_{\mathrm{N}\text{–}\mathrm{C}}\left(t\right)-F_{\mathrm{C}\left(\text{N}\right)}^{corr}\left(t\right)-F_{\mathrm{C}\left(\text{Cl}\right)}^{corr}\left(t\right)\left[{\widehat{\mathbf{r}}}_{\mathrm{N}\text{–}\mathrm{C}}\left(t\right)\cdot {\widehat{\mathbf{r}}}_{Cl\text{–}\mathrm{C}}\left(t\right)\right]}{m_{\mathrm{C}}}-\frac{\left[{\mathbf{F}}_{\mathrm{N}}^H\left(t\right)-{\mathbf{F}}_{\mathrm{N}}^L\left(t\right)\right]\cdot {\widehat{\mathbf{r}}}_{\mathrm{N}\text{–}\mathrm{C}}\left(t\right)-F_{\mathrm{N}}^{corr}\left(t\right)}{m_{\mathrm{N}}}=0.$$ (A7)

Combined with Eqs. (A2), (A3), (A6), and (A7), the internal force corrections on C, Cl, and N are solved using the low-level and high-level forces acting on the three atoms. The correction values at the following MD steps can be obtained in the same way based on the velocity Verlet integration schemes of Cartesian coordinates and velocities.