Learning High-dimensional Generalized Linear Autoregressive Models

Abstract

Vector autoregressive models characterize a variety of time series in which linear combinations of current and past observations can be used to accurately predict future observations. For instance, each element of an observation vector could correspond to a different node in a network, and the parameters of an autoregressive model would correspond to the impact of the network structure on the time series evolution. Often these models are used successfully in practice to learn the structure of social, epidemiological, financial, or biological neural networks. However, little is known about statistical guarantees on estimates of such models in non-Gaussian settings. This paper addresses the inference of the autoregressive parameters and associated network structure within a generalized linear model framework that includes Poisson and Bernoulli autoregressive processes. At the heart of this analysis is a sparsity-regularized maximum likelihood estimator. While sparsity-regularization is well-studied in the statistics and machine learning communities, those analysis methods cannot be applied to autoregressive generalized linear models because of the correlations and potential heteroscedasticity inherent in the observations. Sample complexity bounds are derived using a combination of martingale concentration inequalities and modern empirical process techniques for dependent random variables. These bounds, which are supported by several simulation studies, characterize the impact of various network parameters on estimator performance.

I. Autoregressive Processes in High Dimensions

Imagine recording the times at which each neuron in a biological neural network fires or “spikes”. Neu-ron spikes can trigger or inhibit spikes in neighboring neurons, and understanding excitation and inhibition among neurons provides key insight into the structure and operation of the underlying neural network [1], [2], [3], [4], [5], [6], [7]. A central question in the design of this experiment is “for how long must I collect data before I can be confident that my inference of the network is accurate ?” Clearly the answer to this question will depend not only on the number of neurons being recorded, but also on what we may assume a priori about the network. Unfortunately, existing statistical and machine learning theory give little insight into this problem.

Neural spike recordings are just one example of a non-Gaussian, high-dimensional autoregressive process, where the autoregressive parameters correspond to the structure of the underlying network. This paper examines a broad class of such processes, in which each observation vector is modeled using an exponential family distribution. In general, autoregressive models are a widely-used mechanism for studying time series in which each observation depends on the past sequence of observations. Inferring these dependencies is a key challenge in many settings, including finance, neuroscience, epidemiology, and sociology. A precise understanding of these dependencies facilitates more accurate predictions and interpretable models of the forces that determine the distribution of each new observation.

Much of the autoregressive modeling literature focuses on linear auto-regressive models, especially with independent Gaussian noise innovations (see e.g. [8], [9], [10], [11]). However, in many settings linear Gaussian models with signal-independent noise are restrictive and fail to capture the data at hand. This challenge arises, for instance, when observations correspond to count data -e.g., when we collect data by counting individual events such as neurons spiking. Another example arises in epidemiology, where a common model involves infection traveling stochastically from one node in a network to another based on the underlying network structure in a process known as an “epidemic cascade” [12], [13], [14], [15]. These models are used to infer network structure based on the observations of infection time, which is closely related to the Bernoulli autoregressive model studied in this paper. Further examples arise in a variety of applications, including vehicular traffic analysis [16], [17], finance [18], [19], [20], [21], social network analysis [22], [23], [24], [25], [26], biological neural networks [1], [2], [3], [4], [5], [6], [7], power systems analysis [27], and seismology [28], [29].

Because of their prevalence across application domains, time series count data (cf [30], [31], [32], [33], [34]) and other non-Gaussian autoregressive processes (cf. [35], [36], [37]) have been studied for decades. Although a substantial fraction of the this literature is focused on univariate time series, this paper focuses on multivariate settings, particularly where the vector observed at each time is high-dimensional relative to the duration of the time series. In the above examples, the dimension of the each observation vector would be the number of neurons in a neural network, the number of people in a social network, or the number of interacting financial instruments.

This paper focuses on estimating the parameters of a particular family of time series that we call the vector generalized linear autoregressive (GLAR) model which incorporates both non-linear dynamics and signal-dependent noise innovations. We adopt a regularized likelihood estimation approach that extends and generalizes our previous work on Poisson inverse problems (cf [38], [39], [40], [41]). While similar algorithms have been proposed in the above-mentioned literature, little is known about their sample complexity or how inference accuracy scales with the key parameters such as the size of the network or number of entities observed, the time spent collecting observations, and the density of edges within the network or dependencies among entities.

In this paper, we conduct a detailed investigation of the GLAR model. In addition, we examine our results for two members of this family: the Bernoulli autoregressive and the log-linear Poisson autoregressive (PAR) model. The PAR model has been explicitly studied in [42], [43], [44] and is closely related to the continuous-time Hawkes point process model [45], [46], [47], [48], [49] and the discrete-time INGARCH model [50], [51], [52], [53]. However, that literature does not contain the sample complexity results presented here. The INGARCH literature is focused on low-dimensional settings, typically univariate, whereas we are focused on the high-dimensional setting where the number of nodes or channels is high relative to the number of observations. Additionally, existing sample complexity bounds for Hawkes processes [48] focus on a linear (as opposed to log-linear) model with samples collected after reaching the stationary distribution. The log-linear model is largely used in practice both for numerical reasons and modeling efficacy for real world data. We note that linear models can predict inadmissible negative event rates, whereas the log-linear model enforces the feasibility of the predicted model. The log-linear and linear models exhibit very different behaviors in their properties and stationary distributions, making this work a significant step forward from the analysis of linear models. The extension of these prior investigations to the high-dimensional, non-stationary setting is non-trivial and requires the development of new theory and methods.

In this paper, we develop performance guarantees for the vector GLAR model that provide sample complexity guarantees in the high-dimensional setting under low­dimensional structural assumptions such as sparsity of the underlying autoregressive parameters. In particular, our main contributions are the following:

• Formulation of a maximum penalized likelihood estimator for vector GLAR models in high­dimensional settings with sparse structure.

• Mean-squared-error (MSE) bounds on the proposed estimator as a function of the problem dimension, sparsity, and the number of observations in time for general GLAR models. These mean-squared error bounds are identical to the bounds in the linear Gaussian setting (see e.g. [8], [54]) up to log and constant factors.

• Application of our general result to obtain sample complexity bounds for Bernoulli and Poisson GLAR models.

• Analysis techniques for generalized linear models that adapt to signal-dependent noise that simultaneously leverage martingale concentration inequalities, empirical risk minimization analysis, and covering arguments for high-dimensional regression.

A. Comparison to Gaussian Analysis

There has been a large body of work providing theoretical results for certain high-dimensional models under low-dimensional structural constraints (see e.g. [55], [41], [56], [57], [58], [59], [60], [61], [49]). The majority of prior work has focused on the setting where samples are independent and/or follow a Gaussian distribution. In the GLAR setting, however, non-Gaussianity and temporal dependence among observations can make such analyses particularly challenging and beyond the scope of much current research in high-dimensional statistical inference (see [62] for an overview).

This problem is substantially harder than the Gaussian case from a technical perspective because we can not exploit linearity and spectral properties of linear Gaussian time-series. In our case we have signal-dependent noise, and we can not exploit the same linear spectral properties. One of the important steps is to prove a restricted eigenvalue/restricted strong convexity condition for high-dimensional models (see e.g. [8], [63], [10]). In the Gaussian linear auto-regressive setting, the restricted eigenvalue/strong convexity convexity condition reduces studying the covariance structure of Gaussian design matrices. The greatest technical challenge associated with non-linear time series models with signal-dependent noise is proving a restricted eigenvalue/strong convexity condition. Much of the technical work in this manuscript focuses on proving strong convexity of the objective function over the domain of X_t for all t.

To further expand on this point, consider momentarily a LASSO estimator of the autoregressive parameters. In the classical LASSO setting, the accuracy of the estimate depends on characteristics of the Gram matrix associated with the design or sensing matrix. This matrix may be stochastic, but it is usually considered independent of the observations and performance guarantees for the estimator depend on the assumption that the matrix obeys certain properties (e.g., the restricted eigenvalue condition [8], [63], [10]). In our setting, however, the “design” matrix is a function of the observed data, which in turn depends on the true underlying network or autoregressive model parameters. Thus a key challenge in the analysis of a LASSO-like estimator in the GLAR setting involves showing that the data- and network-dependent Gram matrix exhibits properties that ensure reliable estimates.

Perhaps the most closely related prior work in the high-dimensional setting is [8]. In [8], several performance guarantees are provided for different linear Gaussian problems with dependent samples including the Gaussian autoregressive model. Since [8] deals exclusively with linear Gaussian models, they exploit many properties of linear systems and Gaussian random variables that cannot be applied to non-Gaussian and nonlinear autoregressive models. In particular, compared to standard autoregressive processes with Gaussian noise, in the GLAR setting the conditional variance of each observation is dependent on previous data instead of being a constant equal to the noise variance. Works such as [41], [55], [64] provide results for non-Gaussian models but still rely on independent observations. Weighted LASSO estimators for Hawkes processes address some of these challenges in a continuous-time setting [48]. As we show after stating the main results, we achieve the same mean-squared error bounds for non-linear time series up to log and constant factors whilst avoiding the restrictive linear Gaussian assumptions.

The remainder of the paper is structured as follows: Section II introduces the generalized linear autoregressive model and Section III presents the novel risk bounds associated with the regularized maximum likelihood estimator of the process. We then use our theory to examine two special cases (the Poisson and Bernoulli models) in Sections III–A and III–B, respectively. The main proofs are provided in Section IV, while supplementary lemmas are deferred to the appendix. Finally, Section V contains a discussion of our results, their implications in different settings, and potential avenues for future work.

II. Problem Formulation

In this paper we consider the generalized linear autoregressive model:

$$X_{t+1,m}|X_t~p\left({\nu }_m+a_m^{*\top }{X}_t\right),$$ (1)

where X_t+1, _m is the m^th variate of X_t+1 where 1 ≤ m ≤ M, ${\left(X_t\right)}_{t=0}^{\infty }$ are M-variate vectors and a* ∈ [α_min, α_max]^M is an unknown parameter vector, ν ∈ [ν_min, ν_max]^M is a known, constant offset parameter, and p is an exponential family probability distribution. Specifically, X ~ p(θ) means that the distribution of the scalar X is associated with the density p(x|θ) = h(x) exp[ϕ(x)θ − Z(θ)], where Z(θ) is the so-called log partition function, ϕ(x) is the sufficient statistic of the data, and h(x) is the base measure of the distribution. Distributions that fit such assumptions include the Poisson, Bernoulli, binomial, negative binomial and exponential. According to this model, conditioned on the previous data, the elements of X_t are independent of one another and each have a scalar natural parameter. The input of the function p in (1) is the natural parameter for the distribution, i.e., ${\nu }_m+a_m^{*\top }{X}_t$ is the natural parameter of the conditional distribution at time t + 1 for observation m. A similar, but low-dimensional, model appears in [44], but that work focuses on maximum likelihood and weighted least squares estimators in univariate settings that are known to perform poorly in high-dimensional settings (as is our focus). For these distributions it is straightforward to show when they have strongly convex log-partition functions, which will be crucial to our analysis. Note that this distribution has $\mathbb{E}\left[\varphi \left(X_{t+1,m}\right)|X_t\right]=Z^{\prime }\left(\nu +a_m^{*\top }{X}_t\right)$ and $Var\left(\varphi \left(X_{t+1,m}\right)|X_t\right)=Z^{″}\left(\nu +a_m^{*\top }{X}_t\right)$, the first and second derivatives of the log-partition function, respectively. Compared to standard autoregressive processes with Gaussian noise, the conditional variance is now dependent on previous data instead of being a constant equal to the noise variance.

We can state the conditional distribution explicitly as:

$$\mathbb{P}\left(X_{t+1}|X_t\right)=\prod _{m=1}^{M}h\left(X_{t+1,m}\right)\text{exp}\left(\varphi \left(X_{t+1,m}\right)\left({\nu }_m+a_m^{*\top }{X}_t\right)-Z\left({\nu }_m+a_m^{*\top }{X}_t\right)\right),$$

where h is the base-measure of the distribution p. Using this equation and observations, we can find an estimate for the network A* which is constructed row-wise by $a_m^{*}$ (i.e. $a_m^{*\top }$ is the m^th row of A*).

In general, we observe T + 1 samples ${\left(X_t\right)}_{t=0}^T$ and our goal is to infer the matrix A*. In the setting where M is large, we need to impose structural assumptions on A* in order to have strong performance guarantees. Let

$$\mathcal{S}:=\left\{(\mathcal{l},m)\in {\{1,\dots ,M\}}^2:A_{\mathcal{l},m}^{*}\ne 0\right\}.$$

In this paper we assume that the matrix A* is s-sparse, meaning that A* belongs to the following class:

$${\mathcal{A}}_s=\left\{A\in {\left[a_{\text{min}},a_{\text{max}}\right]}^{M\times M}|\Vert A{\Vert }_0\le s\right\}.$$

where $\Vert A{\Vert }_0:={\Sigma }_{\mathcal{l}=1}^M{\Sigma }_{m=1}^{M}1\left(\left|A_{\mathcal{l},m}\right|\ne 0\right)$ and 1(·) is the indicator function. That is, we assume $\left|\mathcal{S}\right|\le s$. Furthermore, we define

$${\rho }_m\triangleq {\Vert a_m^{*}\Vert }_0\text{\hspace{1em} and \hspace{1em}}\rho \triangleq \underset{m}{\text{max}}{\rho }_m,$$

so ρ is the maximum number of non-zero elements in a row of A*.

We might like to estimate A* via a constrained maximum likelihood estimator by solving the following optimization problem:

$$\underset{A\in {\mathcal{A}}_s}{\text{arg min}}\frac{1}{T}\sum _{t=0}^{T-1}\sum _{m=1}^M\left(Z\left({\nu }_m+a_m^{\top }{X}_t\right)-a_m^{\top }{X}_t\varphi \left(X_{t+1,m}\right)\right)$$ (2)

or its Lagrangian form

$$\underset{A\in {\left[a_{\text{min}},a_{\text{max}}\right)}^{M\times M}}{\text{arg min}}\frac{1}{T}\sum _{t=0}^{T-1}\sum _{m=1}^M(Z\left({\nu }_m+a_m^{\top }{X}_t\right)-a_m^{\top }{X}_t\varphi \left(X_{t+1,m}\right)+\lambda \Vert A{\Vert }_0.$$ (3)

However, these are difficult optimization problems due to the non-convexity of the ℓ₀ norm. Therefore, we instead find an estimator using the element-wise ℓ₁ regularizer, the convex relaxation of the ℓ₀ function, along with the negative log-likelihood to create the following estimator:

$$\widehat{A}=\underset{A\in {\left[a_{\text{min}},a_{\text{max}}\right]}^{M\times M}}{\text{arg min}}\frac{1}{T}\sum _{t=0}^{T-1}\sum _{m=1}^M(Z\left({\nu }_m+a_m^{\top }{X}_t\right)-a_m^{\top }{X}_t\varphi \left(X_{t+1,m}\right))+\lambda \Vert A{\Vert }_{1,1},$$ (4)

where ∥·∥₁ is the ℓ₁ norm and $\Vert A{\Vert }_{1,1}={\Sigma }_{m=1}^M\Vert a_m{\Vert }_1$. The above is the regularized maximum likelihood estimator (RMLE) for the problem, which attempts to find an estimate of A* which both fits the empirical distribution of the data while also having many zero­valued elements. Notice that we assume the elements of A* are bounded and we use these bounds in the estimator definition. One reason for this is that bounds on the elements of A* can enforce stability. If the elements of A* are allowed to be arbitrarily large, the system may become unstable and therefore impossible to make proper estimates. Knowing loose bounds facilitates our analysis but in practice does not appear to be necessary. In the experiment section we discuss choosing these bounds in the estimation process.

We note that while we assume that ν is a known constant vector, if we assume there is some unknown constant offset that we would like to estimate, we can fold it into the estimation of A. For instance, consider appending ν as an extra column of the matrix A*, and appending a 1 to the end of each observation X_t. Then for indices 1, …, M the observation model becomes $X_{t+1,m}|X_t~p\left(a_m^{*\top }{X}_t\right)$ where $a_m^{*}$ and X_t are the appended versions. We can then find the RMLE of this distribution to find both $\widehat{A}$ and $\widehat{\nu }$, but for clarity of exposition we assume a known ν.

Estimating the network parameters in the autoregressive setting with Gaussian observations can be formulated as a sparse inverse problem with connections to the well-known LASSO estimator. Consider the problem of estimating the $a_m^{*}$. Define

$$y_m=\left[\begin{array}{c}{X}_{2,m}\\ X_{3,m}\\ ⋮\\ X_{T,m}\end{array}\right]$$

and

$$X=\left[\begin{array}{cccc}{X}_{1,1}& X_{1,2}& \cdots & X_{1,M}\\ X_{2,1}& X_{2,2}& \cdots & X_{2,M}\\ ⋮& ⋮& \ddots ⋮& \\ X_{T-1,1}& X_{T-1,2}& \cdots & X_{T-1,M}\end{array}\right],$$

where y_m is the time series of observed counts associated with the m^th node and X is a matrix of the observed counts associated with all nodes. Then $y_m=X{a}_m^{*}+{ϵ}_m$, where ${ϵ}_m:=y_m-X{a}_m^{*}$ is noise, and we could consider the LASSO estimator for each m:

$${\widehat{a}}_m=\underset{a}{\text{arg min}}{\Vert y_m-\text{Xa}\Vert }_2^2+\lambda \Vert a{\Vert }_1.$$

However, there are two key challenges associated with the LASSO estimator in this context: (a) the squared residual term does not account for the non-Gaussian statistics of the observations and (b) the “design matrix” is data-dependent and hence a function of the unknown underlying network. In classical LASSO analyses, performance bounds depend on the design matrix satisfying the restricted eigenvalue condition or restricted isome-try property or some related condition; it is relatively straightforward to ensure such a condition is satisfied when the design matrix is independent of the data, but much more challenging in the current context. As a result, despite the fact that we face a sparse inverse problem, the existing LASSO literature does not address the subject of this proposal.

III. Main results

In this section, we turn our attention to deriving bounds for $\Vert \widehat{A}-A^{*}{\Vert }_F^2$, the difference in Frobenius norm between the regularized maximum likelihood estimator, $\widehat{A}$, and the true generating network, A*, under the assumption that the true network is sparse. We assume that $A^{*}\in {\mathcal{A}}_s$. Recall $\rho \triangleq \underset{m}{\text{max}}\Vert a_m^{*}{\Vert }_0$ is the maximum number of non-zero elements in a row of A*. First we define a family of autoregressive processes, $\mathcal{G}$ generated by Equation 1 that will permit low approximation errors in the sparse regime. The definition of this class involves several sufficient conditions that concern stability and convexity of the autoregressive process that allow the underlying network to be estimated successfully. Without stability of the process it would be impossible to learn about the underlying model, this is similar to the assumption that the maximum eigenvalue of a Gaussian Autoregressive process being bounded by 1. The convexity conditions similarly are sufficient for learning the underlying network and in generally more easily satisfied in the Gaussian case due to the form of the distribution function. For general exponential family distributions it requires proving which distributions would fit into this family. After the definition of this class of autoregressive processes and statement of the main theorem, we show significant results proving that both the Bernoulli and Poisson distributions fit in this family.

Definition III.1.

We define a class of autoregressive processes $\mathcal{G}$ as any process generated by Equation 1 such that for any realization there exists a subset of observations ${\left\{X_{{\mathcal{T}}_t}\right\}}_{t=1}^{\left|\mathcal{T}\right|}$ for $\mathcal{T}\subseteq \left\{0,1,\dots ,T-1\right\}$ that satisfies the conditions:

1. There exists a constant U such that $U\ge {\text{max}}_{t\in \mathcal{T}}\Vert X_t{\Vert }_{\infty }$ where U is independent of T.

2. Z(·) is σ-strongly convex on a domain determined by U:

   $$Z(x)\ge Z(y)+Z^{\prime }(y)(x-y)+\frac{\sigma }{2}\Vert x-y{\Vert }_2^2$$

   for all $x,y\in [-\tilde{\nu }-9\rho \tilde{a}U,\tilde{\nu }+9\rho \tilde{a}U]$ where $\tilde{\nu }\triangleq \text{max}\left(\left|{\nu }_{\text{min}}\right|,\left|{\nu }_{\text{max}}\right|\right)$, and $\tilde{a}\triangleq \text{max}\left(\left|a_{\text{min}}\right|,\left|a_{\text{max}}\right|\right)$, where σ is independent of T.

3. The smallest eigenvalue of ${\mathrm{\Gamma }}_t\triangleq \mathbb{E}\left[X_{{\mathcal{T}}_t}{X}_{{\mathcal{T}}_t}^{\top }|X_{t-1}\right]$ is lower bounded by ω > 0, which is independent of T.

We define the constant ξ as a constant such that $\xi \triangleq \left|\mathcal{T}\right|/T$, which will be determined in part by the constant U, and can be set such that ξ is very close to 1.

For ξ ≈ 1, membership in $\mathcal{G}$ means most of the observed data is bounded independent of T. The condition allows us to analyze time series in which the maximum of a series of iid random variables can grow with T, but any percentile is bounded by a constant. Our analysis will then be conducted on the bounded series ${\left\{X_{{\mathcal{T}}_t}\right\}}_{t=1}^{\left|\mathcal{T}\right|}$. We prove to these conditions to be true with high probability for the Bernoulli and Poisson cases in Sections III–A and III–B, respectively, and the corresponding values of U, σ, ξ, and ω are computed explicitly. Other exponential family distributions and their associated autoregressive processes likely belong to $\mathcal{G}$ as well, but proving the conditions and parameters of their inclusion remains an open problem beyond the scope of this paper

Theorem 1.

Assume λ ≥ $\underset{1\le m\le M}{\text{max}}\frac{2}{T}{\Vert \sum _{t=0}^{T-1}\left(\varphi \left(X_{t+1,m}\right)-\mathbb{E}\left[\varphi \left(X_{t+1,m}\right)|X_t\right]\right)X_t\Vert }_{\infty }$ and let $\widehat{A}$ be the RMLE for a process which belongs to $\mathcal{G}$ as defined in Definition III.1. For any row of the estimator and for any δ ∈ (0,1), with probability at least 1 — δ,

$${\Vert {\widehat{a}}_m-a_m^{*}\Vert }_2^2\le \frac{144}{{\xi }^2{\sigma }^2{\omega }^2}{\rho }_m{\lambda }^2$$

for $T\ge \frac{c{\rho }_m^2}{{\omega }^2}\left(\frac{{\rho }_m\text{log}(2M)}{{\omega }^2}+\text{log}(1/\delta )\right)$ where c is independent of M, T, ρ and s. Furthermore,

$${\Vert \widehat{A}-A^{*}\Vert }_F^2\le \frac{144}{{\xi }^2{\sigma }^2{\omega }^2}s{\lambda }^2$$

with probability greater than 1 – δ for $T\ge \frac{c{\rho }^2}{{\omega }^2}\left(\left(\frac{\rho }{{\omega }^2}+1\right)\text{log}(2M)+\text{log}(1/\delta )\right)$.

To apply Theorem 1 to specific GLAR models, we need to provide bounds on λ, as well as σ, ω, U and ξ for inclusion in $\mathcal{G}$. We do this in the next section for Bernoulli and Poisson GLAR models.

We can compare the results of Theorem 1 to the related results of [8]. In that work they arrive at rates for the Gaussian autoregressive process that are equivalent with respect to the sparsity parameter, number of observations and regularization parameter. However, we incur slightly different dependencies on ξ, σ and ω. These are due mainly to the fact that our bounds hold for a wide family of distributions and not just the Gaussian case, which has nice properties related to restricted strong convexity and specialized concentration inequalities. Additionally, the way λ is defined is very similar, but bounding λ for a non-Gaussian distribution will result in extra log factors. It is an open question whether this bound is rate optimal in the general setting.

A. Result 1: Bernoulli Distribution

For the Bernoulli distribution we have the following autoregressive model:

$$X_{t+1,m}|X_t~\text{Bernoulli }\left(\frac{1}{1+\text{exp}\left(-\nu -a_m^{*\top }{X}_t\right)}\right).$$ (5)

The first observation about this model is that the sufficient statistic ϕ(x) = x and the log-partition function Z(θ) = log(l + exp(θ)), which is strongly convex when the absolute value of θ is bounded. One advantage of this model is that the observations are inherently bounded due to the nature of the Bernoulli distribution, so $\mathcal{T}=[0,1,\dots ,T-1]$ and ξ = l. Using this observation we derive the strong convexity parameter of Z on the bounded range, thus $\sigma ={(3+\text{exp}(\tilde{\nu }+9\rho \tilde{a}))}^{-1}$.

To derive rates from Theorem 1, we must prove that this process belongs to $\mathcal{G}$ as defined in Definition III.1; this is shown with high-probability by Theorem 2.

Theorem 2.

For a sequence X_t generated from the Bernoulli autoregressive process with the matrix A* and the vector ν, we have the following properties:

1. The smallest eigenvalue of the matrix ${\mathrm{\Gamma }}_t=\mathbb{E}\left[X_t{X}_t^{\top }|X_{t-1}\right]$ is lower bounded by $\omega ={(3+\text{exp}(\tilde{\nu }+\rho \tilde{a}))}^{-1}$.

2. Assuming 1 ≤ t ≤ T and that T ≥ 2 and log(MT) ≥ 1, then

   $$\underset{1\le i,j\le M}{\text{max}}\frac{1}{T}\left|\sum _{t=0}^{T-1}{X}_{t-1,i}\left(X_{t,j}-\mathbb{E}\left[X_{t,j}|X_{t-1}\right]\right)\right|\le \frac{3\text{\hspace{0.17em}log}(MT)}{\sqrt{T}}$$

   with probability at least at least $1-\frac{1}{MT}$.

Using these results we get the final sample error bounds for the Bernoulli autoregressive process.

Corollary 1.

The RMLE for the Bernoulli autoregressive process defined by Equation 5, and setting $\lambda =\frac{6\text{log}(MT)}{\sqrt{T}}$ has error bounded by

$${\Vert A^{*}-\widehat{A}\Vert }_F^2\le C{\left(3+e^{\tilde{\nu }+9\tilde{a}}\right)}^4\frac{slo{g}^2(MT)}{{\xi }^{2}T}$$

with probability at least 1 − δ for $T\ge \text{max}\left(\frac{2}{\delta M},\frac{c{\rho }^2}{{\omega }^2}\left(\left(1+\frac{\rho }{{\omega }^2}\right)\text{log}(2M)+\text{log}(2/\delta )\right)\right)$ for constants C, c > 0 which are independent of M, T, s and ρ.

The lower bound on the number of observations T comes from needing to satisfy the conditions of both parts of Theorems 1 and 2. In order to get this statement we use a union bound over the high probability statements of Theorem 1 described in (9) and Theorem 2 which holds with probability greater than $1-\frac{1}{MT}$.

B. Result 2: Poisson Distribution

In this section, we derive the relevant values to get error bounds for the vector autoregressive Poisson distribution. Under this model we have

$$X_{t+1,m}|X_t~Poiss\left(\text{exp}\left(\nu +a_m^{*\top }{X}_t\right)\right).$$

We assume that α_max = 0 for stability purposes, thus we are only modeling inhibitory relationships in the network. Deriving the sufficient statistic and log-partition function yields ϕ(x) = x and Z(θ) = exp(θ). The next important values are the bounds on the magnitude of the observations, which will both ensure the strong convexity of Z and the stability of the process.

Lemma 1.

For the Poisson autoregressive process generated with A* ∈ [α_min, 0]^M×M and constant vector ν ∈ [ν_min, ν_max]:

1. If log MT ≥ 1, there exists constants C and c which depend on the value ν_max, but are independent of T,M,s and ρ such that 0 ≤ X_t, _m ≤ C log(MT) with probability at least 1 – e^−clog(MT) for all 1 ≤ t ≤ T and 1 ≤ m ≤ M.

2. For any α ∈ (0, 1) such that αMT is an integer, there exist constants U and c which depend on the values of ν_max and α, but independent of T, M, s and ρ, such that with probability at least 1−e^−cMT, 0 ≤ X_t, _m ≤ U for at least αMT of the indices. We define $\mathcal{T}$ to be these αMT indices.

As a consequence of Lemma 1, we have ∥|X_t∥_∞ ≤ U for at least ξT values of t ∈ {1, 2, …, T} where ξ = 1 − (1 – α)M. We additionally assume that U is large enough such that $\alpha >\frac{M-1}{M}$ and therefore ξ ∈ (0,1).

Using this Lemma, we prove that this process belongs to $\mathcal{G}$ with high-probability, by deriving the strong convexity parameter of Z and a lower bound on the smallest eigenvalue of Γ_t. In the Poisson case, Z(·) = exp(·) and therefore the strong convexity parameter, $\sigma =\text{exp}\left(-\tilde{\nu }+9\rho a_{\text{min}}U\right)$.

Theorem 3.

For a sequence X_t generated from the Poisson autoregressive process with the matrix A*, with all non-positive elements, and the vector ν, we have the following properties

1. The smallest eigenvalue of the matrix ${\mathrm{\Gamma }}_t=\mathbb{E}\left[X_{{\mathcal{T}}_t}{X}_{{\mathcal{T}}_t}^{\top }|X_{{\mathcal{T}}_{t-1}}\right]$, for consecutive indices ${\mathcal{T}}_t$ and ${\mathcal{T}}_{t-1}$ in $\mathcal{T}$ as defined in the definition of $\mathcal{G}$, is lower bounded by $\frac{4\xi }{5}\text{exp}\left({\nu }_{\text{min}}+\rho a_{\text{min}}U\right)$.

2. Assuming X_t, _m ≤ C log(MT) for all 1 ≤ m ≤ M and 1 ≤ t ≤ T and that T ≥ 2 and log (MT) ≥ 1, then

   $$\underset{1\le i,j\le M}{\text{max}}\frac{1}{T}\left|\sum _{t=0}^{T-1}{X}_{t-1,i}\left(X_{t,j}-\mathbb{E}\left[X_{t,j}|X_{t-1}\right]\right)\right|\le 4C^2{e}^{{\nu }_{\text{max}}}\frac{{\text{log}}^3(MT)}{\sqrt{T}}$$

   with probability at least at least 1−exp(−clog (MT)) for some c > 0 independent of ρ, s,M and T.

Using Theorem 3, we can find the error bounds for the PAR process by using the result of Theorem 1.

Corollary 2.

Using the results of Theorem 1 and using the Poisson autoregressive model with A* with all non­positive values, the RMLE admits the overall error rate of

$${\Vert \widehat{A}-A^{*}\Vert }_F^2\le C\text{exp}\left(20\left|a_{\text{min}}\right|U\rho \right)\frac{s{\text{log}}^6(MT)}{{\xi }^{3}T}$$

with probability at least 1 − δ for $T\ge \text{max}\left({\left(\frac{4}{\delta M}\right)}^c,\frac{c{\rho }^2}{{\omega }^2}\left(\left(\frac{\rho }{{\omega }^2}+1\right)\text{log}(2M)+\text{log}(4/\delta )\right)\right)$ for constants C, c > 0 which are independent of M, T, s and ρ

Again, the lower bound on the number of observations comes from combining the high probability statements of each of the constituent parts of the corollary in the same way as was done in the Bernoulli case. In this case all of Theorem 1, both parts of Lemma 1 and Theorem 3 need to hold.

Remark:

It is worthwhile comparing the theoretical results in the Bernoulli and Poisson processes compared to results for Gaussian processes in [8], [10]. The mean-squared error bounds in the Gaussian case is $\frac{s\text{log}M}{T}$ [8], [10] whilst our bound for Bernoulli, Poisson, and Gaussian random variables are the same up to log and constant factors. The additional log factors arise because our analysis is more general and does not exploit specific properties of the linear Gaussian process. Hence our analysis is not optimal in the linear Gaussian setting since additional log factors are incurred to ensures the process satisfies Definition III.1 using our more general analysis that applies to non-linear models with signal-dependent noise.

C. Experimental Results

We validate our theoretical results with experimental results performed on synthetically generated data using the Poisson autoregressive process. We generate many trials of synthetic data with known underlying parameters and then compare the estimated values. For all trials the constant offset vector ν is set identically at 0, and the 20×20 matrices A* are set such that s randomly assigned values are in the range [−1,0] and with constant ρ = 5. Data is then generated according the process described in Equation 1 with the Poisson distribution. X₀ is chosen as a 20 dimensional vector drawn randomly from Poisson(1), then T observations are used to perform the estimation. The parameters s and T are then varied over a wide range of values. For each (s, T) pair 100 trials are performed, the regularized maximum likelihood estimate $\widehat{A}$ is calculated with $\lambda =0.1/\sqrt{T}$ and the MSE is recorded. The MSE curves are shown in Figure 1. Notice that the true values of A* are bounded by −1 and 0, but in our implementation we do not enforce these bounds (we set α_min = −∞ and α_max = to in Equation 4). While α_min = −∞ would cause the theoretical bounds to be poor, the theory can be applied with the smallest and largest elements of the matrix estimated from the unconstrained optimization. In other words, the theory depends on having an upper and lower bound on the rates, but mostly as a theoretical convenience, while the estimator can be computed in an unconstrained way.

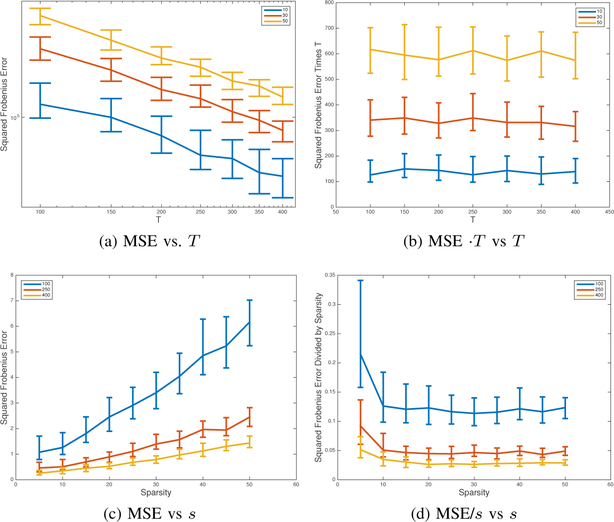
Fig. 1:

A series of plots to show the behavior of the MSE of the RMLE for the Poisson Autoregressive process to show how error scales with time horizon, T, and sparsity, s. Our theoretical analysis states that error should decay as $\frac{1}{T}$ and should grow like s both up to constants and log factors. The top row of plots shows the MSE behavior over a range of T values, from 100 to 400 all less than or equal to M² = 400, where (a) is the MSE and (b) is the MSE multiplied by T to show that the MSE scales as $\frac{1}{T}$. The bottom row shows the MSE behavior over a range of s values, where (c) shows MSE and (d) shows MSE divided by s to show that the MSE is linear is s. Plots (b) and (d) are included to show the values which are expected to scale as constants, which is confirmed. In all plots the median value of 100 trials is shown, with error bars denoting the middle 50 percentile.

We show a series of plots which compare the MSE versus increasing behavior of T and s, as well as comparing the behavior of MSE·T and of MSE/s. Plotted in each figure is the median of 100 trials for each (s, T) pair, with error bars denoting the middle 50 percentile. These plots show that setting λ proportional to T⁻¹ gives us the desired T⁻¹ error decay rate. Additionally, we see that the error increases approximately linearly in the sparsity level s, as predicted by the theory. Finally, Figure 2 shows one specific example process and the estimates produced. The first image is the ground truth matrix, generated to be block diagonal, in order to more easily visualize support structure whereas in the first experiment the support is chosen at random. One set of data is generated using this matrix, and then estimates are constructed using the first T = 100, 316 and 1000 data points. The figure shows how with more data, the estimates become closer to the original, where much of the error comes from including elements off the support of the true matrix.

Fig. 2:

These images show the ground truth A* matrix (a) and 3 different estimates of the matrix created using increasing amounts of data. We observe that even for a relatively low amount of data we have picked out most of the support but with several spurious artifacts. As the amount of data increases, fewer of the erroneous elements are estimated. All images are scaled from 0 (dark) to −1 (bright).

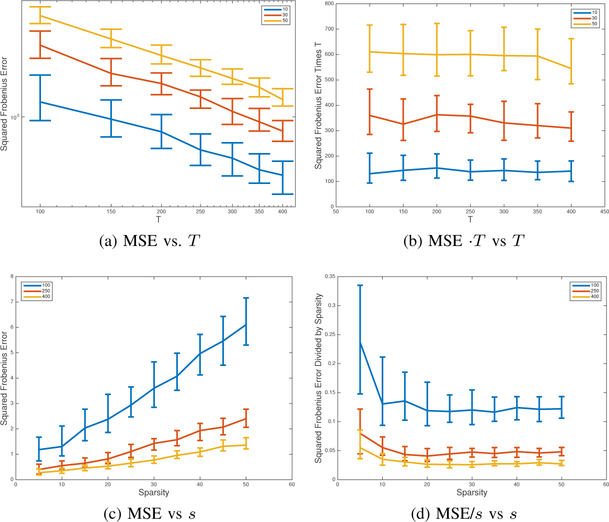
One important characteristic of the our results is that it does not depend on any assumptions about the stationarity or the mixing time of the process. To show that this is truly a property of the system and not just our proof technique, we repeat the experimental process described above, but for each set of observations of length T, we first generate 10,000 observations to allow the process to mix. In other words, for every matrix A we generate T+10,000 observations, but only use the last T to find the RMLE. The plots in figure 3 show the results of this experiment. The important observation is that the results both scale the same way, and have approximately the same magnitude as the experiment when no mixing was done.

Fig. 3:

Repeat of experimental set up from Figure 1, but now allowing for mixing. The top row of plots shows the MSE behavior over a widely varying range of T values, from 100 to 400, where (a) is the MSE and (b) is the MSE multiplied by T to show that the MSE is behaving as 1/T. The bottom row shows the MSE behavior over a range of s values, where (c) shows MSE and (d) shows MSE divided by s to show that the MSE is linear is s. Plots (b) and (d) are included to show the values which are expected to scale as constants, independent of mixing time, which is confirmed. In all plots the median value of 100 trials is shown, with error bars denoting the middle 50 percentile. Most importantly, the behavior and magnitude of errors in this plot matches the results with no mixing.

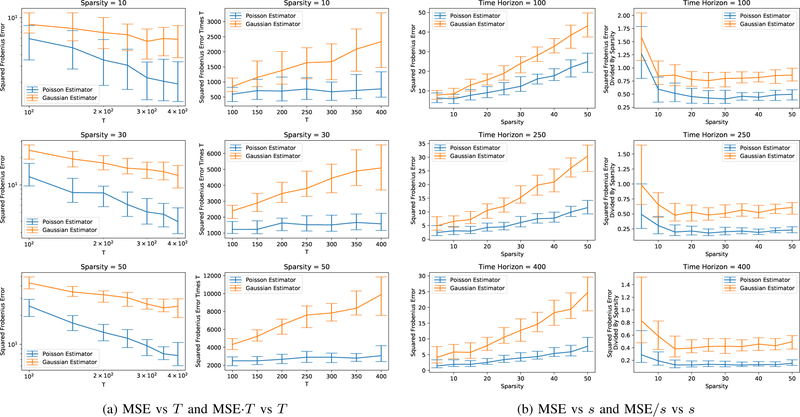
Up to this point we have shown the results of estimating the underlying network when the data was generated using a Poisson Autoregressive Process and using the RMLE associated with it. We have shown these results in order to demonstrate that the rates predicted by our theoretical error bounds match the rates seen empirically. A natural question is how well would estimating the underlying network perform when the data generation process was Poisson Autoregressive? Gaussian estimators have many nice properties and their error rates have been studied extensively, so being able to use this as an estimator would seem like a logical choice if the approximation error with the non-Gaussian data was relatively small. To test this hypothesis data was generated in much the same way as the previous experimental set-ups, except values in the A* matrix were allowed to vary from 0 to −2.5, meaning even more inhibition was possible. We then made estimates of the underlying network using both the Poisson AR loss function as well as the more traditional Gaussian, using the same regularization parameter for each. The results of these experiments are shown in Figure 4. These plots show a few key characteristics, the most important being that the Poisson based objective function soundly outperforms the Gaussian. We also see that as the time horizon gets larger, meaning more observations are available, and as sparsity decreases the gap between the two increases. Both of these make intuitive sense because as more observations are revealed the Poisson objective function can more closely narrow in on the underlying network whereas the Gaussian objective function is still stuck with some amount of approximation error that will not decrease with increasing data. Additionally as more elements of the matrix A* are non-zero, the Gaussian estimate will get worse comparatively because it will be wrong in more locations. With a very sparse true matrix the Gaussian estimate could set lots of elements to zero and be “accidentally” correct, which will not happen with a less sparse true matrix. For all of these reasons, we find it convincing that using the objective function which matches the generative process to be extremely important for accurate estimation in the autoregressive regime.

Fig. 4:

Repeat of the experimental set up from Figure 1, but with the true A* matrix allowed to have elements ranging from 0 to 2.5. This time both the Poisson Autoregressive RMLE is estimated as well as an estimator based on the Gaussian approximation to the Poisson distribution. We see that the Poisson based estimator consistently and significantly outperforms the Gaussian estimator and that the gap increases with increasing T and decreasing sparsity. In all plots the median value of 100 trials is shown, with error bars denoting the middle 50 percentile.

IV. Proofs

A. Proof of Theorem 1

Proof: We start the proof by making an important observation about the estimator defined in Equation 4: this loss function can be completely decoupled by a sum of functions on rows. Therefore we can bound the error of a single row of the RMLE and add the errors to get the final bound. For each row we use a standard method in empirical risk minimization and the definition of the minimizer of the regularized likelihood for each row:

$$\frac{1}{T}\sum _{t=0}^{T-1}Z\left({\nu }_m+{\widehat{a}}_m^{\top }{X}_t\right)-{\widehat{a}}_m^{\top }{X}_t\varphi \left(X_{t+1,m}\right)+\lambda {\Vert {\widehat{a}}_m\Vert }_1$$

$$\le \frac{1}{T}\sum _{t=0}^{T-1}Z\left({\nu }_m+a_m^{*\top }{X}_t\right)+a_m^{*\top }{X}_t\varphi \left(X_{t+1,m}\right)+\lambda {\Vert a_m^{*}\Vert }_1.$$

We define ${ϵ}_{t,m}\triangleq \varphi \left(X_{t+1,m}\right)-\mathbb{E}\left[\varphi \left(X_{t+1,m}\right)|X_t\right]$, which is conditionally zero mean random variable. By using a moment generating function argument, we know that $\mathbb{E}\left[\varphi \left(X_{t+1,m}\right)|X_t\right]=Z^{\prime }\left({\nu }_m+a_m^{*\top }{X}_t\right)$, and therefore $\varphi \left(X_{t+1,m}\right)=Z^{\prime }\left({\nu }_m+a_m^{*\top }{X}_t\right)+{ϵ}_{t,m}$. Hence

$$\frac{1}{T}\sum _{t=0}^{T-1}Z\left({\nu }_m+{\widehat{a}}_m^{\top }{X}_t\right)-{\widehat{a}}_m^{\top }{X}_t\left(Z^{\prime }\left({\nu }_m+a_m^{*\top }{X}_t\right)+{ϵ}_{t,m}\right)+\lambda {\Vert {\widehat{a}}_m\Vert }_1\le \frac{1}{T}\sum _{t=0}^{T-1}Z\left({\nu }_m+a_m^{*\top }{X}_t\right)-a_m^{*\top }{X}_t\left(Z^{\prime }\left({\nu }_m+a_m^{*\top }{X}_t\right)+{ϵ}_{t,m}\right)+\lambda {\Vert a_m^{*}\Vert }_1.$$

Now we use the definition of a Bregman divergence to lower bound the left hand side. An important property of Bregman divergences is that if they are induced by a strongly convex function, then the Bregman can be lower bounded by a scaled ℓ₂ difference of its arguments. This is where our squared error term will come.

$$\frac{1}{T}\sum _{t=0}^{T-1}Z\left({\nu }_m+{\widehat{a}}_m^{\top }{X}_t\right)-Z\left({\nu }_m+a_m^{*\top }{X}_t\right)-Z^{\prime }\left({\nu }_m+a_m^{*\top }{X}_t\right)\left({\widehat{a}}_m^{\top }{X}_t-a_m^{*\top }{X}_t\right)\le \left|\frac{1}{T}\sum _{t=0}^{T-1}{ϵ}_{t,m}{\mathrm{\Delta }}_m^{\top }{X}_t\right|+\lambda \left({\Vert a_m^{*}\Vert }_1-{\Vert {\widehat{a}}_m\Vert }_1\right),$$

where ${\mathrm{\Delta }}_m={\widehat{a}}_m-a_m^{*}.\text{ Let }{B}_Z(\cdot \Vert \cdot )$ denote the Bregman divergence induced by Z. Hence

$$\frac{1}{T}\sum _{t=0}^{T-1}{B}_Z\left({\nu }_m+{\widehat{a}}_m^{\top }{X}_t\Vert {\nu }_m+a_m^{*\top }{X}_t\right)\le \left|\frac{1}{T}\sum _{t=0}^{T-1}{ϵ}_{t,m}{\mathrm{\Delta }}_m^{\top }{X}_t\right|+\lambda \left({\Vert a_m^{*}\Vert }_1-{\Vert {\widehat{a}}_m\Vert }_1\right).$$

First we upper bound the right-hand side of the inequality as follows:

$$\begin{gathered} \frac{1}{T}\sum _{t=0}^{T-1}{B}_Z\left({\nu }_m+{\widehat{a}}_m^{\top }{X}_t\Vert {\nu }_m+a_m^{*\top }{X}_t\right) \\ \le \left|\frac{1}{T}\sum _{t=0}^{T-1}{ϵ}_{t,m}{\mathrm{\Delta }}_m^{\top }{X}_t\right|+\lambda \left({\Vert a_m^{*}\Vert }_1-{\Vert {\widehat{a}}_m\Vert }_1\right) \\ =\left|\frac{1}{T}\sum _{t=0}^{T-1}{ϵ}_{t,m}{\mathrm{\Delta }}_m^{\top }{X}_t\right|+\lambda ({\Vert a_{m,\mathcal{S}}^{*}\Vert }_1-{\Vert {\widehat{a}}_{m,\mathcal{S}}\Vert }_1-{\Vert {\widehat{a}}_{m,{\mathcal{S}}^c}\Vert }_1) \\ \le \left|\frac{1}{T}\sum _{t=0}^{T-1}{ϵ}_{t,m}{\mathrm{\Delta }}_m^{\top }{X}_t\right|+\lambda {\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1-\lambda {\Vert {\mathrm{\Delta }}_{m,{\mathcal{S}}^c}\Vert }_1 \\ \le {\Vert {\mathrm{\Delta }}_m\Vert }_1{\Vert \frac{1}{T}\sum _{t=0}^{T-1}{X}_t{ϵ}_{t,m}\Vert }_{\infty }+\lambda {\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1-\lambda {\Vert {\mathrm{\Delta }}_{m,{\mathcal{S}}^c}\Vert }_1 \end{gathered}$$

In the above, we use the defintion of $\mathcal{S}$ as the true support of A* and have used the decomposability of ∥·∥₁. The decomposability of the norm means that we have the property $\Vert x{\Vert }_1=\Vert x_{\mathcal{S}}{\Vert }_1+\Vert x_{\mathcal{S}}C{\Vert }_1$.

Note that ${\Vert \frac{1}{T}\sum _{t=0}^{T-1}{X}_t{ϵ}_{t,m}\Vert }_{\infty }\le {\text{max}}_{1\le m\le M}{\Vert \frac{1}{T}{\sum }_{t=0}^{T-1}{X}_t{ϵ}_{t,m}\Vert }_{\infty }$. Under the assumption that $\underset{1\le m\le M}{\text{max}}{\Vert \frac{1}{T}\sum _{t=0}^{T-1}{X}_t{ϵ}_{t,m}\Vert }_{\infty }\le \lambda /2$ and by the non-negativity of the Bregman divergence on the left hand side of the inequality, we have that

$$0\le \frac{\lambda }{2}{\Vert {\mathrm{\Delta }}_m\Vert }_1+\lambda {\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1-\lambda {\Vert {\mathrm{\Delta }}_{m,{\mathcal{S}}^c}\Vert }_1.$$

Using the decomposability of the ℓ₁ norm, this inequality implies that for all rows 1 ≤ m ≤ M, we have that ${\Vert {\mathrm{\Delta }}_{m,{\mathcal{S}}^c}\Vert }_1\le 3{\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1$. Since ${\Vert {\mathrm{\Delta }}_{m,{\mathcal{S}}^c}\Vert }_1\le 3{\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1$, $\Vert {\mathrm{\Delta }}_m{\Vert }_1\le 4\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}{\Vert }_1$ and consequently

$${\Vert {\mathrm{\Delta }}_m\Vert }_1\le 4\sum _{j\in \mathcal{S}}\left|{\mathrm{\Delta }}_{m,j}\right|\le 8{\rho }_m\tilde{a}$$

where the final inequality follows since $\left|{\mathrm{\Delta }}_{m,j}\right|\le 2\tilde{a}$ for all j. Using this inequality and the fact that ${\Vert a_m^{*}\Vert }_1\le {\rho }_m\tilde{a}$ implies that ${\Vert {\widehat{a}}_m\Vert }_1\le 9{\rho }_m\tilde{a}$, and therefore for all $t\in \mathcal{T}$ the range of both ${\nu }_m+a_m^{*\top }{X}_t$ and ${\nu }_m+{\widehat{a}}_m^{\top }{X}_t$ are in [$-\tilde{\nu }-9\rho \tilde{a},\tilde{\nu }+9\rho \tilde{a}$].

Now to lower bound the Bregman divergence in terms of the Frobenius norm, we use the first condition of membership in $\mathcal{G}$. Inherently, the RMLE will admit estimates which should converge to the true matrix A* under a Bregman divergence induced by the log-partition function, but we are interested in convergence of the Frobenius norm. Therefore, to convert from one to the other, we require the log-partition function to be strongly convex. This issue is side-stepped in the Gaussian noise case, due to the fact that the Bregman in question would identically be the Frobenius norm. By Definition III.1, Z is σ-strongly convex, and therefore on $T$ it is true that $B_Z\left({\nu }_m+{\widehat{a}}_m^{\top }{X}_t\Vert {\nu }_m+a_m^{*\top }{X}_t\right)\ge \frac{\sigma }{2}{\left({\mathrm{\Delta }}_m^{\top }{X}_t\right)}^2$ and $B_Z\left({\nu }_m+{\widehat{a}}_m^{\top }{X}_t\Vert {\nu }_m+a_m^{*\top }{X}_t\right)\ge 0$ on the rest of the time indices.

Therefore

$$\frac{1}{T}\sum _{t=0}^{T-1}{B}_Z\left({\nu }_m+{\widehat{a}}_m^{\top }{X}_t\Vert {\nu }_m+a_m^{*\top }{X}_t\right)\le \frac{\lambda }{2}{\Vert {\mathrm{\Delta }}_m\Vert }_1+\lambda {\Vert {\mathrm{\Delta }}_{m,S}\Vert }_1-\lambda {\Vert {\mathrm{\Delta }}_{m,{\mathcal{S}}^c}\Vert }_1,$$

Implies

$$\frac{\sigma }{2T}\sum _{t\in \mathcal{T}}{\left({\mathrm{\Delta }}_m^{\top }{X}_t\right)}^2\le \frac{\lambda }{2}{\Vert {\mathrm{\Delta }}_m\Vert }_1+\lambda {\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1-\lambda {\Vert {\mathrm{\Delta }}_{m,{\mathcal{S}}^c}\Vert }_1.$$

Define ${\Vert {\mathrm{\Delta }}_m\Vert }_T^2=\frac{1}{T}{{\sum }_{t\in \mathcal{T}}\left({\mathrm{\Delta }}_m^{\top }{X}_t\right)}^2$ for any $\mathrm{\Delta }\in {ℝ}^{M\times M}$, then we have the bound:

$$\frac{\sigma }{2}{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\le \frac{\lambda }{2}{\Vert {\mathrm{\Delta }}_m\Vert }_1+\lambda {\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1-\lambda {\Vert {\mathrm{\Delta }}_{m,{\mathcal{S}}^c}\Vert }_1\le \frac{3\lambda }{2}{\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1.$$

Therefore we can define the cone on which the vector Δ_m must be defined:

$${\mathcal{B}}_{m,\mathcal{S}}:=\{\mathrm{\Delta }\in {\left[a_{\text{min}}-a_{\text{max}},a_{\text{max}}-a_{\text{min}}\right]}^M|{\Vert {\mathrm{\Delta }}_{m,{\mathcal{S}}^c}\Vert }_1\le 3{\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1\},$$

and restrict ourselves to studying properties of vectors in that set. Since ${\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1\le \sqrt{{\rho }_m}{\Vert {\mathrm{\Delta }}_m\Vert }_2$ where ρ_m is the number of non-zeros of $a_m^{*}$, we have that

$${\Vert {\mathrm{\Delta }}_m\Vert }_T^2\le \frac{3}{\sigma }\lambda \sqrt{{\rho }_m}{\Vert {\mathrm{\Delta }}_m\Vert }_2={\delta }_m{\Vert {\mathrm{\Delta }}_m\Vert }_2,$$ (6)

where ${\delta }_m\triangleq \frac{3}{\sigma }\lambda \sqrt{{\rho }_m}$ Now we consider three cases: if ∥Δ_m∥_T ≥ ∥Δ_m∥₂, then max(∥Δ_m∥_T, ∥Δ_m∥₂) ≤ δ_m. On the other hand if ∥Δ_m∥_T ≤ ∥Δ_m∥₂ and ∥Δ_m∥₂ ≤ δ_m, then max(∥Δ_m∥_T, ∥Δ_m∥₂) ≤ δ_m.

Hence the final case we need to consider is ∥Δ_m∥_T ≤ ∥Δ_m∥₂ and ∥Δ_m∥₂ ≥ δ_m. Now we follow a similar proof technique to that used in Raskutti et al. [60] adapted to dependent sequences, to understand this final scenario. Let us define the following set:

$${\mathcal{B}}_m\left({\delta }_m\right):=\left\{{\mathrm{\Delta }}_m\in {\mathcal{B}}_{m,\mathcal{S}}|{\Vert {\mathrm{\Delta }}_m\Vert }_2\ge {\delta }_m\right\}.$$ (7)

Further, let us define the alternative set:

$${\mathcal{B}}_m^{\prime }\left({\delta }_m\right):=\left\{{\mathrm{\Delta }}_m\in {\mathcal{B}}_{m,\mathcal{S}}|{\Vert {\mathrm{\Delta }}_m\Vert }_2={\delta }_m\right\}.$$ (8)

We wish to show that for ${\mathrm{\Delta }}_m\in {\mathcal{B}}_m\left({\delta }_m\right)$, we have ${\Vert {\mathrm{\Delta }}_m\Vert }_T^2\ge \kappa {\Vert {\mathrm{\Delta }}_m\Vert }_2^2$ for some κ ∈ (0, 1) with high probability, and therefore Equation 6 would imply that max(∥Δ_m∥_T, ∥Δ_m∥₂) ≤ δ_m/κ. We claim that it suffices to show that ${\Vert {\mathrm{\Delta }}_m\Vert }_T^2\ge \kappa {\Vert {\mathrm{\Delta }}_m\Vert }_2^2$ is true on ${\mathcal{B}}_m^{\prime }\left({\delta }_m\right)$ (δ_m) with high probability. In particular, given an arbitrary non-zero ${\mathrm{\Delta }}_m\in {\mathcal{B}}_m\left({\delta }_m\right)$, consider the re-scaled vector ${\tilde{\mathrm{\Delta }}}_m=\frac{{\delta }_m}{{\Vert {\mathrm{\Delta }}_m\Vert }_2}{\mathrm{\Delta }}_m$. Since ${\mathrm{\Delta }}_m\in {\mathcal{B}}_m\left({\delta }_m\right)$, We have ${\tilde{\mathrm{\Delta }}}_m\in {\mathcal{B}}_m\left({\delta }_m\right)$ and ${\Vert {\tilde{\mathrm{\Delta }}}_m\Vert }_2={\delta }_m$ by construction. Together, these facts imply ${\tilde{\mathrm{\Delta }}}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)$. Furthermore, if ${\Vert {\tilde{\mathrm{\Delta }}}_m\Vert }_T^2\ge \kappa {\Vert {\tilde{\mathrm{\Delta }}}_m\Vert }_2^2$ is true, then ${\Vert {\mathrm{\Delta }}_m\Vert }_T^2\ge \kappa {\Vert {\mathrm{\Delta }}_m\Vert }_2^2$ is also true. Alternatively if we define the random variable ${\mathcal{Z}}_T\left({\mathcal{B}}_m^{\prime }\right)={\text{sup}}_{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}\left\{{\delta }_m^2-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}$, then it suffices to show that ${\mathcal{Z}}_T\left({\mathcal{B}}_m^{\prime }\right)\le (1-\kappa ){\delta }_m^2$.

For this step we use some recent concentration bounds [65] and empirical process techniques [66] for martingale random variables. Recall that the empirical norm is ${\Vert {\mathrm{\Delta }}_m\Vert }_T^2=\frac{1}{T}\sum _{t\in \mathcal{T}}{\left({\mathrm{\Delta }}_m^T{X}_t\right)}^2$. Further let ${\left(t_i\right)}_{i=1}^{|\mathcal{T}|}$ denote the indices in $\mathcal{T}$. Next we define the conditional expectation

$$Y_T:=\frac{1}{T}\sum _{i=1}^{\left|\mathcal{T}\right|}\mathbb{E}\left[{\left({\mathrm{\Delta }}_m^T{X}_{t_i}\right)}^2|X_{t_1},X_{t_2},\dots ,X_{t_i-1}\right].$$

Then we have

$${\mathcal{Z}}_T\left({\mathcal{B}}_m^{\prime }\right)=\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{{\delta }_m^2-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\le \underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{{\delta }_m^2-Y_T\right\}+\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}.$$

To bound the first quantity, ${\text{sup}}_{{}_{{\mathrm{\Delta }}_m\in {{\mathcal{B}}^{\prime }}_m\left({\delta }_m\right)}}\left\{{\delta }_m^2-Y_T\right\}$, we first note that

$$\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{{\delta }_m^2-Y_T\right\}\le {\delta }_m^2-{\delta }_m^2\omega =(1-\omega ){\delta }_m^2$$

by the definition of $\mathcal{G}$ and the fact that $\Vert {\mathrm{\Delta }}_m{\Vert }_2^2={\delta }_m^2$ since ${\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)$. Thus

$${\mathcal{Z}}_T\left({\mathcal{B}}_m^{\prime }\right)\le (1-\omega ){\delta }_m^2+\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}.$$

Now we focus on bounding sup ${\text{sup}}_{{}_{{\mathrm{\Delta }}_m\in {{\mathcal{B}}^{\prime }}_m\left({\delta }_m\right)}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}$. First, we use a martingale version of the bounded difference inequality using Theorem 2.6 in [65] (see Appendix VII–D):

$$\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\le \mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\right]+\frac{\omega {\delta }_m^2}{4},$$

with high probability. Recall that on $\mathcal{T}$, we have $0\le {\left({\mathrm{\Delta }}_m^{\top }{X}_t\right)}^2\le {\Vert {\mathrm{\Delta }}_m\Vert }_1^2{\Vert X_t\Vert }_{\infty }^2\le U^2{\Vert {\mathrm{\Delta }}_m\Vert }_1^2$ Because ${\mathrm{\Delta }}_m\in {{\mathcal{B}}^{\prime }}_m\left({\delta }_T\right)$, it is true that $\Vert {\mathrm{\Delta }}_m{\Vert }_1\le 4\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}{\Vert }_1$. We then use the the relationship between the ℓ₁ and ℓ₂ norms to say ${\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1\le \sqrt{{\rho }_m}{\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_2\le \sqrt{{\rho }_m}{\Vert {\mathrm{\Delta }}_m\Vert }_2$ where ρ_m is the number of non-zeros in the m^th row of the true matrix A*. Putting these together means ${\left({\mathrm{\Delta }}_m^{\top }{X}_t\right)}^2\le 16U^2{\rho }_m{\delta }_m^2$. In particular, we apply Theorem 4 in Appendix VII–D with $Z_T={\text{sup}}_{{}_{{\mathrm{\Delta }}_m\in {{\mathcal{B}}^{\prime }}_m\left({\delta }_m\right)}}\left\{Y_T-\Vert {\mathrm{\Delta }}_m{\Vert }_T^2\}\right\}$, $a=\frac{\omega {\delta }_m^2}{4}$, $L_t=-\frac{16U^2{\rho }_m{\delta }_m^2}{T}$ and $U_t=\frac{16U^2{\rho }_m{\delta }_m^2}{T}$, and therefore $C_T^2=\frac{{32}^4{U}^4{\rho }_m^2{\delta }_m^4}{T}$. Therefore, applying Theorem 4

$$\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\le \mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\right]+\frac{\omega {\delta }_m^2}{4},$$

with probability at least $1-\text{exp}\left(-\frac{2T}{{32}^4{U}^4{\rho }_m^2}\right)$. Since $T\ge {32}^4{U}^4{\rho }_m^2\text{log}(M)$, the above statement holds with probability at least $1-\frac{1}{M^2}$. Hence

$${\mathcal{Z}}_T\left({\mathcal{B}}_m^{\prime }\right)\le (1-\omega ){\delta }_m^2+\frac{\omega {\delta }_m^2}{4}+\mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\right].$$

Now we bound $\mathbb{E}\left[{\text{sup}}_{{}_{{\mathrm{\Delta }}_m\in {{\mathcal{B}}^{\prime }}_m\left({\delta }_m\right)}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\right]$. Here we use a recent symmetrization technique adapted for martingales in [66]. To do this, we introduce the so-called sequential Rademacher complexity defined in [66]. Let ${\left({ϵ}_t\right)}_{t=1}^T$ be independent Rademacher random variables, that is $\mathbb{P}\left({ϵ}_t=+1\right)=\mathbb{P}\left({ϵ}_t=-1\right)=\frac{1}{2}$. For a function class $\mathcal{F}$, the sequential Rademacher complexity ${\mathcal{R}}_T(\mathcal{F})$ is:

$${\mathcal{R}}_T(\mathcal{F}):=\underset{X_1,X_2,\dots ,X_T}{\text{sup}}\mathbb{E}\left[\underset{f\in \mathcal{F}}{\text{sup}}\frac{1}{T}\sum _{t=1}^T{ϵ}_{t}f\left(X_t\left({ϵ}_1,{ϵ}_2,\dots ,{ϵ}_{t-1}\right)\right)\right].$$

Note here that X_t is a function of the previous independent random variables (ϵ₁, ϵ₂, …, ϵ_t−1). Using Theorem 2 in [66] (also stated Appendix VII–D) with $f\left(X_t\right)={\left({\mathrm{\Delta }}_m^T{X}_t\right)}^2$ and noting that even though we use the index set $\mathcal{T}$, ${\left(X_t\right)}_{t\in \mathcal{T}}$ is still a martingale, it follows that:

$$\mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\right]\le 2\underset{X_{t_1},X_{t_2},\dots ,X_{\left|\mathcal{T}\right|}}{\text{sup}}\mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\frac{1}{T}\sum _{i=1}^{\left|\mathcal{T}\right|}{ϵ}_{t_i}{\left({\mathrm{\Delta }}_m^T{X}_{t_i}\right)}^2\right].$$

Additionally since $\left|{\mathrm{\Delta }}_m^{\top }{X}_t\right|\le 4U\sqrt{{\rho }_m}{\delta }_m$ by the argument above and using the symmetry of Rademacher random variables

$$\begin{gathered} \mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\right] \\ \le 2\underset{X_1,X_2,\dots ,X_{\left|\mathcal{T}\right|}}{\text{sup}}\mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\left({\delta }_m\right)}}{\text{sup}}\frac{1}{T}\sum _{i=1}^{\left|\mathcal{T}\right|}{ϵ}_{t_i}{\mathrm{\Delta }}_m^T{X}_{t_i}\left|{\mathrm{\Delta }}_m^T{X}_{t_i}\right|\right] \\ \le 8U\sqrt{{\rho }_m}{\delta }_m\underset{X_1,X_2,\dots ,X_{\left|T\right|}}{\text{sup}}\mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\frac{1}{T}\sum _{i=1}^{\left|\mathcal{T}\right|}{ϵ}_{t_i}{\mathrm{\Delta }}_m^T{X}_{t_i}\right] \end{gathered}$$

The final step is to upper bound the sequential Rademacher complexity ${\mathcal{R}}_T=\mathbb{E}\left[{\text{sup}}_{{}_{{\mathrm{\Delta }}_m\in {{\mathcal{B}}^{\prime }}_m\left({\delta }_m\right)}}\frac{1}{T}{\sum }_{i=1}^{|\mathcal{T}|}{ϵ}_t{\mathrm{\Delta }}_m^{\top }{X}_{t_i}\right]$ where X_ti is a function of (ϵ₁, ϵ₂, …, ϵ_ti−1). Clearly:

$$\frac{1}{T}\sum _{i=1}^{\left|\mathcal{T}\right|}{ϵ}_t{\mathrm{\Delta }}_m^{\top }{X}_{t_i}\le {\Vert \frac{1}{T}\sum _{i=1}^{\left|\mathcal{T}\right|}{ϵ}_t{X}_{t_i}\Vert }_{\infty }{\Vert {\mathrm{\Delta }}_m\Vert }_1.$$

Because ${\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)$ we have ${\Vert {\mathrm{\Delta }}_m\Vert }_1={\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1+{\Vert {\mathrm{\Delta }}_{m,{\mathcal{S}}^c}\Vert }_1\le 4{\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1$ and ${\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_1\le \sqrt{{\rho }_m}{\Vert {\mathrm{\Delta }}_{m,\mathcal{S}}\Vert }_2\le \sqrt{{\rho }_m}{\Vert {\mathrm{\Delta }}_m\Vert }_2=\sqrt{{\rho }_m}{\delta }_m$.

$$\begin{gathered} \mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\right] \\ \le 8U\sqrt{{\rho }_m}{\delta }_m\underset{X_1,X_2,\dots ,X_{\left|\mathcal{T}\right|}}{\text{sup}}\mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\frac{1}{T}\sum _{i=1}^{\left|\mathcal{T}\right|}{ϵ}_{t_i}{\mathrm{\Delta }}_m^T{X}_{t_i}\right] \\ \le 8U\sqrt{{\rho }_m}{\delta }_m\left(\underset{X_1,X_2,\dots ,X_{\left|T\right|}}{\text{sup}}{\Vert \frac{1}{T}\sum _{i=1}^{\left|\mathcal{T}\right|}{ϵ}_{t_i}{X}_{t_i}\left({ϵ}_1,\dots ,{ϵ}_{t_i-1}\right)\Vert }_{\infty }\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}{\Vert {\mathrm{\Delta }}_m\Vert }_1\right) \\ \le 32U^2{\rho }_m{\delta }_m^2\underset{X_1,X_2,\dots ,X_{\left|T\right|}}{\text{sup}}{\Vert \frac{1}{T}\sum _{i=1}^{\left|\mathcal{T}\right|}{ϵ}_{t_i}{X}_{t_i}\left({ϵ}_1,\dots ,{ϵ}_{t_i-1}\right)\Vert }_{\infty }. \end{gathered}$$

Finally, we use Lemma 6 applied to the index set $\mathcal{T}$ :

$$\begin{gathered} \mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\prime }\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\right] \\ \le 32U^2{\rho }_m{\delta }_m^2\underset{X_1,\dots ,X_{\left|T\right|}}{\text{sup}}{\Vert \frac{1}{T}\sum _{i=1}^{\left|\mathcal{T}\right|}{ϵ}_{t_i}{X}_{t_i}\left({ϵ}_1,\dots ,{ϵ}_{t_i-1}\right)\Vert }_{\infty } \\ \le 128U^4{\rho }_m{\delta }_m^2\frac{\text{log}(MT)}{\sqrt{T}}, \end{gathered}$$

with probability at least $1-\frac{1}{{(MT)}^2}$. Now if we set $T=\frac{{256}^2{U}^8{\rho }_m^2{\text{log}}^2(MT)}{{\omega }^2}$,

$$\mathbb{E}\left[\underset{{\mathrm{\Delta }}_m\in {\mathcal{B}}_m^{\text{'}}\left({\delta }_m\right)}{\text{sup}}\left\{Y_T-{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right\}\right]\le \frac{\omega {\delta }_m^2}{4}$$

with probability 1 – (MT)⁻².

Overall this tells us that on the set ${\mathcal{B}}_m^{\prime }\left({\delta }_m\right)$ we have that ${\Vert {\mathrm{\Delta }}_m\Vert }_T^2\ge \frac{3\omega }{4}{\Vert {\mathrm{\Delta }}_m\Vert }_2^2$ with high probability. Now we return to the main proof. After considering all three cases that can follow from 6, we have

$$\text{max}\left({\Vert {\mathrm{\Delta }}_m\Vert }_2^2,{\Vert {\mathrm{\Delta }}_m\Vert }_T^2\right)\le \frac{144}{{\sigma }^2{\omega }^2{\xi }^2}{\rho }_m{\lambda }^2$$

with probability at least $1-\text{exp}\left(\frac{c^{\prime }{\rho }_m}{{\omega }^2}\text{log}(2M)-\frac{c{\omega }^{2}T}{{\rho }_m^2}\right)$, which bounds the error accrued on any single row, as a function of the sparsity of the true row. Combining, to get an overall error yields,

$${\Vert \widehat{A}-A^{*}\Vert }_F^2\le \frac{144}{{\sigma }^2{\omega }^2{\xi }^2}{\lambda }^2\sum _{m=1}^M{\rho }_m=\frac{144}{{\sigma }^2{\omega }^2{\xi }^2}{\lambda }^{2}s$$

with probability at least

$$1-\text{exp}\left(\text{log}(M)+\frac{c^{\prime }\rho }{{\omega }^2}\text{log}(2M)-\frac{c{\omega }^{2}T}{{\rho }^2}\right).$$ (9)

B. Proof of Theorem 2

1). Part 1:

Proof: The matrix Γ_t can be expanded as

$$\mathbb{E}\left[X_t{X}_t^{\top }|X_{t-1}\right]=\mathbb{E}\left[X_t|X_{t-1}\right]\mathbb{E}{\left[X_t|X_{t-1}\right]}^{\top }+\text{Diag}\left(\text{Var}\left(X_t|X_{t-1}\right)\right)$$

Thus Γ_t has two parts, one is the outer product of a vector with itself, and the second is a diagonal matrix. Therefore, the smallest eigenvalue will be lower bounded by the smallest element of the diagonal matrix, because the outer product matrix will always be positive semi-definite with smallest eigenvalue equal to 0. Using properties of the Bernoulli distribution, the conditional variance is explicitly given as (2 + exp(ν + A*X_t−1) + exp(−ν−A*X_t−1))⁻¹ and therefore the smallest eigenvalue of Γ_t is lower bounded by ${(3+\text{exp}(\tilde{\nu }+\rho \tilde{a}))}^{-1}$. ■

2). Part 2:

Proof: In order to prove this part of the Theorem, we use of Markov’s inequality and Lemma 5 in the case of the Bernoulli autoregressive process. Define the sequence $\left(Y_n,n\in \mathbb{N}\right)$ as

$$Y_n\triangleq \frac{1}{T}\sum _{t=0}^{n-1}{X}_{t,m}\left(X_{t+1,\mathcal{l}}-\mathbb{E}\left[X_{t+1,\mathcal{l}}|X_t\right]\right).$$

Notice the following values:

$$Y_n-Y_{n-1}=\frac{X_{n-1,m}}{T}\left(X_{n,\mathcal{l}}-\mathbb{E}\left[X_{n,\mathcal{l}}|X_{n-1}\right]\right)M_n^k=\sum _{i=1}^n\mathbb{E}\left[{\left(\frac{X_{i-1,m}}{T}\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)\right)}^k|X_1,\dots ,X_{i-1}\right].$$

The first value shows that $\mathbb{E}\left[Y_n-Y_{n-1}|X_1,\dots ,X_{n-1}\right]=0$ and therefore Y_n (and the negative of the sequence, −Y_n) is a martingale. Additionally, we know $\left|Y_n-Y_{n-1}\right|\le \frac{1}{T}\triangleq B$ and

$$\begin{gathered} M_n^2=\sum _{i=1}^n\mathbb{E}\left[{\left(\frac{X_{i-1,m}}{T}\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)\right)}^2|X_1,\dots ,X_{i-1}\right] \\ =\frac{1}{T^2}\sum _{i=1}^n{X}_{\mathfrak{k}-1,m}^2\mathbb{E}\left[{\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)}^2|X_{i-1}\right] \\ \le \frac{n}{4T^2}\triangleq {\widehat{M}}_n^2 \end{gathered}$$

where the last step follows because Bernoulli random variables are bounded by one, and the variance is bounded by ¼. We also need to bound $M_n^k$ as follows:

$$\begin{gathered} M_n^k=\sum _{i=1}^n\mathbb{E}\left[{\left(\frac{X_{i-1,m}}{T^2}\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)\right)}^k|X_1,\dots ,X_{i-1}\right] \\ =\sum _{i=1}^n\mathbb{E}\left[{\left(\frac{X_{i-1,m}}{T^2}\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)\right)}^2{\left(\frac{X_{i-1,m}}{T^2}\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)\right)}^{k-2}|X_{i-1}\right] \\ \le B^{k-2}{M}_n^2 \end{gathered}$$

We use these values to get a bound on the summation term used in Lemma 5.

$$\begin{gathered} D_n\triangleq \sum _{k\ge 2}\frac{{\eta }^k}{k!}{M}_n^k\le \sum _{k\ge 2}\frac{{\eta }^k{B}^{k-2}{M}_n^2}{k!} \\ \le \frac{{\widehat{M}}_n^2}{B^2}\sum _{k\ge 2}\frac{{(\eta B)}^k}{k!}\triangleq {\widehat{D}}_n \\ {\tilde{D}}_n\triangleq \sum _{k\ge 2}\frac{{\eta }^k}{k!}{\left(-1\right)}^k{M}_n^k\le {\widehat{D}}_n. \end{gathered}$$

In the above ${\tilde{D}}_n$ corresponds to the sum corresponding to the negative sequence −Y₀, −Y₁, … which we also need to obtain the desired bound. Now we use a variant of Markov’s inequality to get a bound on the desired quantity.

$$\begin{gathered} \mathbb{P}(\left|Y_n\right|\ge y) \\ =\mathbb{P}\left(Y_n\ge y\right)+\mathbb{P}\left(-Y_n\ge y\right) \\ \le \mathbb{E}\left[e^{\eta Y_n}\right]e^{-\eta y}+\mathbb{E}\left[e^{\eta \left(-Y_n\right)}\right]e^{-\eta y} \\ =\mathbb{E}\left[e^{\eta Y_n-D_n+D_n}\right]e^{-\eta y}+\mathbb{E}\left[e^{\eta \left(-Y_n\right)-{\tilde{D}}_n+{\tilde{D}}_n}\right]e^{-\eta y} \\ \le \mathbb{E}\left[e^{\eta Y_n-D_n}\right]e^{{\widehat{D}}_n-\eta y}+\mathbb{E}\left[e^{\eta \left(-Y_n\right)-{\tilde{D}}_n}\right]e^{{\widehat{D}}_n-\eta y} \\ \le 2e^{{\widehat{D}}_n-\eta y}. \end{gathered}$$

The final inequality comes from the use of Lemma 5, which states that the given terms are supermartingales with initial term equal to 1, so the entire expectation is less than or equal to 1. The final step of the proof is to find the optimal value of η to minimize this upper bound.

$$\begin{gathered} \mathbb{P}\left(\left|Y_n\right|\ge y\right)\le 2\text{exp}\left({\widehat{D}}_n-\eta y\right) \\ =2\text{exp}\left(\frac{{\widehat{M}}_n^2}{B^2}\left(e^{\eta B}-1-\eta B\right)-\eta y\right) \end{gathered}$$

Setting $\eta =\frac{1}{B}\text{log}\left(\frac{yB}{{\widehat{M}}_n^2}+1\right)$ yields the lowest such bound, giving

$$\begin{gathered} \mathbb{P}(\left|Y_n\right|\ge y) \\ \le 2\text{exp}\left(\frac{{\widehat{M}}_n^2}{B^2}\left(\frac{yB}{{\widehat{M}}_n^2}-\text{log}\left(\frac{yB}{{\widehat{M}}_n^2}+1\right)\right)-\frac{y}{B}\text{log}\left(\frac{yB}{{\widehat{M}}_n^2}+1\right)\right) \\ =2\text{exp}\left(-\frac{{\widehat{M}}_n^2}{B^2}H\left(\frac{yB}{{\widehat{M}}_n^2}\right)\right) \end{gathered}$$

where H(x) = (1 + x) log(1 + x) − x. We use the fact that $H(x)\ge \frac{3x^2}{2(x+3)}\text{ for }x\ge 0$ to further simplify the bound.

$$\begin{gathered} \mathbb{P}\left(\left|Y_n\right|\ge y\right)\le 2\text{exp}\left(\frac{-3y^2}{2yB+6{\widehat{M}}_n^2}\right) \\ =2\text{exp}\left(-\frac{6y^2{T}^2}{4yT+3n}\right) \end{gathered}$$

To complete the proof, we set n = T and take a union bound over all indices because Y_T considered specific indices m and ℓ, which gives the bound

$$\begin{gathered} \mathbb{P}\left(\underset{1\le i,j\le M}{\text{max}}\frac{1}{T}\left|\sum _{t=0}^{T-1}{X}_{t-1,i}\left(X_{t,j}-\mathbb{E}\left[X_{t,j}|X_{t-1}\right]\right)\right|\ge 3\frac{\text{log}(MT)}{\sqrt{T}}\right) \\ \le \text{exp}\left(\text{log}\left(2M^2\right)-\frac{54\text{log}(MT)}{12/\sqrt{T}+3}\right) \\ \le \frac{1}{MT}. \end{gathered}$$

Here we have additionally assumed that T ≥ 2 and that log(MT) ≥ 1. ■

C. Proof of Theorem 3

1). Part 1:

Proof: We start with the following observation:

$$\begin{gathered} \mathbb{E}\left[X_{{\mathcal{T}}_t}{X}_{{\mathcal{T}}_t}^{\top }|X_{t-1}\right] \\ =\mathbb{E}\left[X_{{\mathcal{T}}_t}|X{\mathcal{T}}_{t-1}\right]\mathbb{E}{\left[X_{{\mathcal{T}}_t}|X_{{\mathcal{T}}_{t-1}}\right]}^{\top }+Diag\left(Var\left(X_{{\mathcal{T}}_t}|X_{{\mathcal{T}}_{t-1}}\right)\right) \end{gathered}$$

Thus Γ_t has two parts, one is the outer product of a vector with itself, and the second is a diagonal matrix. Therefore, the smallest eigenvalue will be lower bounded by the smallest element of the diagonal matrix. In order to lower bound this variance, we must consider the two cases, one where ${\mathcal{T}}_{t-1}={\mathcal{T}}_{t-1}$ where the previous term in the sequence $\mathcal{T}$ is the previous term in the overall sequence, and the other case where ${\mathcal{T}}_{t-1}={\mathcal{T}}_{t-1}$ where the previous term is not in the sequence $\mathcal{T}$. The variance of $X_{\mathcal{T}}$ can be characterized based on these two possible situations:

$$\begin{gathered} Var\left(X_{{\mathcal{T}}_{t,i}}|X_{{\mathcal{T}}_{t-1}}\right) \\ =pVar\left(X_{\mathcal{T},t}|X_{t-1},{\mathcal{T}}_{t-1}={\mathcal{T}}_t-1\right) \\ +(1-p)Var\left(X_{{\mathcal{T}}_{t,i}}|X_{{\mathcal{T}}_{t-1}},{\mathcal{T}}_{t-1}<{\mathcal{T}}_t-1\right) \end{gathered}$$

where p is the probability that ${\mathcal{T}}_{t-1}={\mathcal{T}}_{t-1}$. Because variances are lower bounded by 0, we can lower bound this entire term by the first part of the sum, where ${\mathcal{T}}_{t-1}={\mathcal{T}}_{t-1}$. For this term, we know that $X_{\mathcal{T}t}$ is drawn from a Poisson distribution, with the added information that each element is bounded above by U because it is an element of the sequence $X{\mathcal{T}}_1,X{\mathcal{T}}_2$, …. Thus using Lemma 3 we know that the variance of each value is lower bounded by $\frac{4}{5}\text{exp}\left({\nu }_i+a_i^{*\top }{X}_{t-1}\right)$ which can in turn be lower bounded by exp(ν_min + ρα_minU). Finally, since there are at least ξT elements of 1, 2, …, T which are in the bounded set of observations, then the worst case distribution of the observations with elements greater than U is that they are never consecutive. This maximizes the number of times there is a break in the sequence ${\mathcal{T}}_1,{\mathcal{T}}_2$, …, which means there would be a total of T − ξT times when there was a break. Thus the probability that consecutive elements are in the set is at least ξ, meaning that the minimum eigenvalue of $\mathbb{E}\left[X_{{\mathcal{T}}_t}{X}_{{\mathcal{T}}_t}^{\top }|X_{{\mathcal{T}}_{t-1}}\right]$ is lower bounded by $\frac{4\xi }{5}\text{exp}\left({\nu }_{\text{min}}+\rho a_{\text{min}}\text{U}\right)$.

2). Part 2:

Proof: To prove this part of the Theorem, we use of Markov’s inequality and Lemma 5 as they pertain specifically to our problem. Define the sequence $\left(Y_n,n\in \mathbb{N}\right)$ as

$$Y_n\triangleq \frac{1}{T}\sum _{t=0}^{n-1}{X}_{t,m}\left(X_{t+1,\mathcal{l}}-\mathbb{E}\left[X_{t+1,\mathcal{l}}|X_t\right]\right).$$

Notice the following values:

$$\begin{gathered} Y_n-Y_{n-1}=\frac{X_{n-1,m}}{T}\left(X_{n,\mathcal{l}}-\mathbb{E}\left[X_{n,\mathcal{l}}|X_{n-1}\right]\right) \\ {M}_n^k=\sum _{i=1}^n\mathbb{E}\left[{\left(\frac{X_{i-1,m}}{T}\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)\right)}^k|X_1,\dots ,X_{i-1}\right]. \end{gathered}$$

The first value shows that $\mathbb{E}\left[Y_n-Y_{n-1}|X_1,\dots ,X_{n-1}\right]=0$ and therefore Y_n (and the negative of the sequence, −Y_n) is a martingale. Additionally, we have assumed that $\left|X_{m,i}\right|\le C$ log MT for 1 ≤ m ≤ M and 1 ≤ i ≤ T, so it is true that $\left|Y_n-Y_{n-1}\right|\le \frac{C^2{\text{log}}^2(MT)}{T}\triangleq B$. Additionally:

$$\begin{gathered} M_n^2=\frac{1}{T^2}\sum _{i=1}^n{X}_{i-1,m}^2\mathbb{E}\left[{\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)}^2|X_{i-1}\right] \\ =\frac{1}{T^2}\sum _{i=1}^n{X}_{i-1,m}^2\text{exp}\left({\nu }_{\mathcal{l}}+a_{\mathcal{l}}^{*\top }{X}_{i-1}\right) \\ \le \frac{n{C}^2{\text{log}}^2(MT)e^{{\nu }_{\text{max}}}}{T^2}\triangleq {\widehat{M}}_n^2 \end{gathered}$$

where the last step follows because $X_{\mathcal{l},i}|X_{i-1}$ ~ Poisson ($\text{exp}\left({\nu }_{\mathcal{l}}+a_{\mathcal{l}}^{*\top }{X}_{i-1}\right)$) and the mean and variance of a Poisson random variable are equal. The final line uses the fact that X_t is bounded. We will also need to bound $M_n^k$ as follows:

$$\begin{gathered} M_n^k=\sum _{i=1}^n\mathbb{E}\left[{\left(\frac{X_{i-1,m}}{T^2}\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)\right)}^k|X_1,\dots ,X_{i-1}\right] \\ =\sum _{i=1}^n\mathbb{E}\left[{\left(\frac{X_{i-1,m}}{T^2}\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)\right)}^2{\left(\frac{X_{i-1,m}}{T^2}\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)\right)}^{k-2}|X_{i-1}\right] \\ \le B^{k-2}{M}_n^2 \end{gathered}$$

We need to use these values to get a bound on the summation term used in Lemma 5.

$$\begin{gathered} D_n\triangleq \sum _{k\ge 2}\frac{{\eta }^k}{k!}{M}_n^k\le \sum _{k\ge 2}\frac{{\eta }^k{B}^{k-2}{M}_n^2}{k!} \\ \le \frac{{\widehat{M}}_n^2}{B^2}\sum _{k\ge 2}\frac{{(\eta B)}^k}{k!}\triangleq {\widehat{D}}_n \\ {\tilde{D}}_n\triangleq \sum _{k\ge 2}\frac{{\eta }^k}{k!}{\left(-1\right)}^k{M}_n^k\le {\widehat{D}}_n \end{gathered}$$

In the above ${\tilde{D}}_n$ corresponds to the sum corresponding to the negative sequence −Y₀, −Y₁, … which we will also need to obtain the desired bound. Now we are able to use a variant of Markov’s inequality to get a bound on the desired quantity.

$$\begin{gathered} \mathbb{P}(\left|Y_n\right|\ge y) \\ =\mathbb{P}\left(Y_n\ge y\right)+\mathbb{P}\left(-Y_n\ge y\right) \\ \le \mathbb{E}\left[e^{\eta Y_n}\right]e^{-\eta y}+\mathbb{E}\left[e^{\eta \left(-Y_n\right)}\right]e^{-\eta y} \\ =\mathbb{E}\left[e^{\eta Y_n-D_n+D_n}\right]e^{-\eta y}+\mathbb{E}\left[e^{\eta \left(-Y_n\right)-{\tilde{D}}_n+{\tilde{D}}_n}\right]e^{-\eta y} \\ \le \mathbb{E}\left[e^{\eta Y_n-D_n}\right]e^{{\widehat{D}}_n-\eta y}+\mathbb{E}\left[e^{\eta \left(-Y_n\right)-{\tilde{D}}_n}\right]e^{{\widehat{D}}_n-\eta y} \\ \le 2e^{{\widehat{D}}_n-\eta y} \end{gathered}$$

The final inequality comes from the use of Lemma 5, which states that the given terms are supermartingales with initial term equal to 1, so the entire expectation is less than or equal to 1. The final step of the proof is to find the optimal value of η to minimize this upper bound.

$$\begin{gathered} \mathbb{P}\left(\left|Y_n\right|\ge y\right) \\ \le 2\text{exp}\left({\widehat{D}}_n-\eta y\right) \\ =2\text{exp}\left(\frac{{\widehat{M}}_n^2}{B^2}\left(e^{\eta B}-1-\eta B\right)-\eta y\right) \end{gathered}$$

Setting $\eta =\frac{1}{B}\text{log}\left(\frac{yB}{{\widehat{M}}_n^2}+1\right)$ yields the lowest such bound, giving

$$\begin{gathered} \mathbb{P}\left(\left|Y_n\right|\ge y\right) \\ \le 2\text{exp}(\frac{{\widehat{M}}_n^2}{B^2}\left(\frac{yB}{{\widehat{M}}_n^2}-\text{log}\left(\frac{yB}{{\widehat{M}}_n^2}+1\right)\right)-\frac{y}{B}\text{log}\left(\frac{yB}{{\widehat{M}}_n^2}+1\right)) \\ =2\text{exp}\left(-\frac{{\widehat{M}}_n^2}{B^2}H\left(\frac{yB}{{\widehat{M}}_n^2}\right)\right) \end{gathered}$$

where H(x) = (1 + x) log(1 + x) − x. We can use the fact that $H(x)\ge \frac{3x^2}{2(x+3)}$ for x ≥ 0 to further simplify the bound.

$$\begin{gathered} \mathbb{P}\left(\left|Y_n\right|\ge y\right) \\ \le 2\text{exp}\left(\frac{-3y^2}{2yB+6{\widehat{M}}_n^2}\right) \\ =2\text{exp}\left(-\frac{3y^2{T}^2}{2C^2\left(Ty+3n{e}^{{\nu }_{\text{max}}}\right){\text{log}}^2(MT)}\right) \end{gathered}$$

To prove the proof, we set n = T and take a union bound over all indices because Y_T considered specific indices m and ℓ, which gives the bound

$$\begin{gathered} \mathbb{P}({\text{max}}_{i,j}\frac{1}{T}\left|\sum _{t=0}^{T-1}{X}_{t-1,i}\left(X_{t,j}-\mathbb{E}\left[X_{t,j}|X_{t-1}\right]\right)\right|\ge 4C^2{e}^{{\nu }_{\text{max}}}\frac{{\text{log}}^3(MT)}{\sqrt{T}}) \\ \le \text{exp}(\text{log}\left(2M^2\right)-\frac{48C^4{\text{exp}}^{2{\nu }_{\text{max}}}{\text{log}}^4(MT)}{8C^4{e}^{{\nu }_{\text{max}}}{\text{log}}^3(MT)/\sqrt{T}+6C_1^2{e}_{{}_{\text{max}}}^{\nu }}) \\ \le \text{exp}\left(2\text{log}(MT)-\frac{24C^2{e}_{{}_{\text{max}}}^{\nu }\text{log}(MT)}{4C^2/\sqrt{T}+3}\right) \\ \le \text{exp}(-c\text{log}(MT)) \end{gathered}$$

where $c=\frac{24C^2{e}^{{\nu }_{\text{max}}}-8C^2-6}{4C^2+3}$ which is positive for sufficiently large C. Here we have additionally assumed that T ≥ 2 and that log(MT) ≥ 1.

V. Discussion

Corollaries 1 and 2 provide several important facts about the inference process. Primarily, if ρ is fixed as a constant for increasing M (suggesting that the maximum degree of a node does not increase with the number of nodes in a network), then the error scales inversely with T, linearly with the sparsity level s and only logarithmically with the dimension M in order to estimate M² parameters. These parameters will dictate how much data needs to be collected to achieve a desired accuracy level. This rate illustrates the idea that doing inference in sparse settings can greatly reduce the needed amount of sensing time, especially when s ≪ M². Another quantity to notice is that we require T ≥ ω⁻⁴ρ³ log(M). If ρ is fixed as a constant for increasing M, this tells us that T needs to be on the order of log(M), which is significantly less than the total M² parameters which are being estimated, and therefore including the sparsity assumption has lead to a significant gain. One final observation from the risk bound is that it provides guidance in the setting of the regularization parameter. We see that we would like to set λ generally as small as possible, since the error scales approximately like λ², but we also require λ at least as large as $\tilde{O}\left(T^{-1/2}\right)$ for the bounds to hold. The balance between setting λ small enough to have low error, while maintaining that it’s large enough is an equivalent argument to needing to set λ large enough for it to take effect, but not too large to cause over smoothing.

A. Dense rows of A*

The exponential scaling in Corollaries 1 and 2 with the maximum number of non-zeros in a row, ρ, at first seems unsatisfying. However, we can imagine a worst-case scenario where a large ρ relative to s and M would actually lead to very poor estimation. Consider the case of a large star-shaped network, where every node in the network influences and is influenced by a single node, and there are no other edges in the network. This would correspond to a matrix with a single, dense row and corresponding column. Therefore, we would have ρ = M and s = 2M − 1. In the Poisson setting, this network would have M − 1 independently and identically distributed Poisson random variables at every time with mean ν, but the central node of the network would be constantly inhibited, almost completely. In a large network, it would be very difficult to know if this inhibition was coming from a few strong connections or from the cumulative effect of all the inhibitions. Additionally, since the central node would almost never have a positive count, it would also be difficult to learn about the influence that node has on the rest of the network. Because of networks like this, it is important that not only is the overall network sparse, but each row also needs to be sparse. This requirement might seem restrictive, but it has been shown in many real world networks that the degree of a node in the network follows a power-law which is independent of the overall size of the network [67], and ρ would grow slowly with growing M.

B. Bounded observations and higher-order autoregressive processes

Recall that the definition of $\mathcal{G}$ ensures that most observations are bounded. Bounded observations are important to our analysis because we use martingale concentration inequalities [68] which depend on bounded conditional means and conditional variances, the latter condition being equivalent to Z being strongly convex. Since the conditional means and variances are data-dependent, bounded data (at least with high probability) is a sufficient condition for bounded conditional means and conditional variances. In some settings (e.g., Bernoulli), bounded observations are natural and ξ = 1. In other settings (e.g., Poisson) there is no constant U independent of T that is an upper bound for all observations with high probability. Furthermore, if we allow U to increase with T in violation of $\mathcal{G}$ in Definition III.1, we derive a bound on $\Vert \widehat{A}-A^{*}{\Vert }_F^2$ that increases polynomially with T. To avoid this and get the far better bound in Theorem 1, our proof focuses on characterizing the error on the set $\mathcal{T}$ defined in the definition of $\mathcal{G}$.

Thus far we have focused on the case where $X_{t+1,m}|X_t~p\left({\nu }_m+a_m^{*\top }{X}_t\right)$, a first order autoregressive process. However, we could imagine a simple, higher-order version where $X_{t+1,m}|X_{t-q+1},\dots ,X_t~p\left({\nu }_m+a_m^{*\top }{\sum }_{i=0}^{q-1}{\alpha }_i{X}_{t-i}\right)$ for some known sequence α_i. This process could be reformulated as a process $X_{t+1,m}|X_{t-q+1},\dots ,X_t~p\left({\nu }_m+a_m^{*\top }{\tilde{X}}_t\right)$ where ${\tilde{X}}_t\triangleq {\sum }_{i=0}^{q-1}{\alpha }_i{X}_{t-1}$, and much of the same proof techniques would still hold, especially in the case of the Bernoulli autoregressive process, where $\mathcal{T}$ is easily defined. However, in the more general GLAR case finding the right analogy to $\mathcal{T}$ in the higher space is not an obvious extension. A true order-q autoregressive process where ${\tilde{X}}_{t+1,m}|X_{t-q+1},\dots ,X_t~p\left(\nu +{\sum }_{i=0}^{q-1}{a}_m^{*\top }{X}_{t-i}{X}_{t-i}\right)$ could also be formulated as an order-1 process by properly stacking vectors and matrices, however, in this case proving the key lemmas and showing that the process belongs to $\mathcal{G}$ is also an open question.

C. Stationarity

As stated in the problem formulation, we restrict our attention to bounded matrices A* ∈ [α_min, α_max]^M×M; in the specific context of the log-linear Poisson autoregressive model, we use α_max = 0, corresponding to a model that only accounts for inhibitory interactions. One might ask whether these constraints could be relaxed and whether the Poisson model could also account for stimulatory interactions.

These boundedness constraints are sufficient to ensure that the observed process has a stationary distribution. The stationarity of processes is heavily studied; once a process has reached its stationary distribution, then data can be approximated as independent samples from this distribution and temporal dependencies can be can be ignored. While stationarity does not play an explicit role in our analysis, we can identify several sufficient conditions to ensure the vector GLAR processes of interest are stationary. In particular we assume that A* = A^*⊤ which ensures reversibility of the Markov chain described by the process defined by $X_{t+1,m}|X_t~p\left({\nu }_m+a_m^{*\top }{X}_t\right)$. We derive the stationary distribution π(x), and then establish bounds on the mixing time. Note that this is a Markov chain with transition kernel:

$$P(x,y)=\mathbb{P}\left(X_{t+1}=y|X_t=x\right)=\text{exp}\left({\nu }^{\top }y+y^{\top }{A}^{*}x-\sum _{i=m}^{M}Z\left({\nu }_m+a_m^{*\top }X\right)\right)\prod _{m=1}^{M}h\left(y_m\right).$$

If we further assume that the entries of Xt take on values on a countable domain to ensure a countable Markov chain, we can derive bounds on the mixing time.

Lemma 2.

Assume A* = A^*⊤, then the Markov chain $X_{t+1,m}~p\left({\nu }_m+a_m^{*\top }{X}_t\right)$ is a reversible Markov chain with stationary distribution:

$$\pi (x)=C_{\nu ,A*}\text{exp}\left({\nu }^{\top }x+\sum _{m=1}^{M}Z\left({\nu }_m+a_m^{*\top }x\right)\right)\prod _{m=1}^{M}h\left(x_m\right)$$

$$C_{\nu ,A^{*}}={\int }_{x_1}{\int }_{x_2}\dots {\int }_{x_M}(\text{exp}\left({\nu }^{\top }x+\sum _{m=1}^{M}Z\left({\nu }_m+a_m^{*\top }x\right)\right)\prod _{m=1}^{M}h\left(x_m\right)d{x}_M)\dots d{x}_{2}d{x}_1.$$

Further, if $X_t\in {\mathbb{Z}}_{+}^M$, α_max = 0 and Z(·) is an increasing function, then for any $y\in {\mathbb{Z}}_{+}^M$, if ν_m ≤ ν_max < ∞ for all 1 ≤ m ≤ M and α_min ≤ 0 we have that

$${\Vert P^t(y,.)-\pi (.)\Vert }_{TV}\le {\left(1-h{(0)}^{-2M}{e}^{-2MZ\left({\nu }_{\text{max}}\right)}\right)}^t.$$

Notice that for large M, the chain will mix very slowly, and additionally this bound has no dependence on the sparsity of the true matrix A*. Conversely, our results require T to be greater than a value that scales roughly like ρ³ log(M), which has a much milder dependence on M, and varies based on the sparsity of A*. What we can conclude from these observations is that while the RMLE needs a certain amount of observations to yield good results, we do not necessarily need enough data to reach the stationary distribution. Additionally, under conditions where mixing time guarantees are not given (i.e. non-symmetric A*, uncountable domain), we still have guarantees on the performance of the RMLE.

VI. Conclusions

Instances of the generalized linear autoregressive process have been used successfully in many settings to learn network structure. However, this model is often used without rigorous non-asymptotic guarantees of accuracy. In this paper we have shown important properties of the Regularized Maximum Likelihood Estimator of the GLAR process under a sparsity assumption. We have proven bounds on the error of the estimator as a function of sparsity, maximum degree of a node, ambient dimension and time, and shown how these bounds look for the specific examples of the Bernoulli and Poisson autoregressive proceses. In order to prove this risk bound, we have incorporated many recently developed tools of statistical learning, including concentration bounds for dependent random variables. Our results show that by incorporating sparsity the amount of data needed is on the order of ρ³ log(M) for bounded degree networks, which is a significant gain compared to the M² parameters being estimated.

While this paper has focused on generalized linear models, we believe that the extension of these ideas to other models is possible. Specifically, for modeling firing rates of neurons in the brain, we are interested in settings in which we observe

$$X_{t+1,m}|X_t~Poisson\left(g\left(a_m^{*\top }{X}_t+\nu \right)\right)$$

and exploring possible functions g beyond the exponential function considered here. Such analysis would allow our results to apply to stimulatory effects in addition to inhibitory effects, but key challenges include ensuring that the process is stable and, with high probability, bounded. Another direction would be settings where the counts are drawn from more complicated higher-order or autoregressive moving average (ARMA) models which would better model real-world point processes.

VII. Appendix

A. Supplementary Lemmas

First we present supplementary Lemmas which we use throughout the proofs of the main Theorems.

Lemma 3.

Let X be a Poisson random variable, with the following probability density function:

$$p(X=k|\lambda )=\frac{{\lambda }^k{e}^{-k}}{k!}$$

and let X′ be a random variable defined by the following pdf:

$$q(k|\lambda )=\{{}_{0otherwise}^{\frac{c}{k!}{\lambda }^k{e}^{-\lambda }ifk\le U}$$

Where $c=\frac{1}{1-\mathbb{P}(X>U)}>1$. Roughly speaking, X′ is generated by taking a Poisson pdf, and removing the tail probability, and scaling the remaining density so that it is a valid pdf. For this random variable, assuming U ≥ max(6, 1.5eλ, λ + 5) then

$$Var\left(X^{\prime }\right)\ge \frac{4}{5}Var(X)=\frac{4\lambda }{5}$$

Proof: Define the error terms ${ϵ}_1\triangleq \mathbb{E}{[X]}^2-\mathbb{E}{\left[X^{\prime }\right]}^2$ and ${ϵ}_1\triangleq \mathbb{E}{[X]}^2-\mathbb{E}{\left[X^{\prime }\right]}^2$. We know

$$\begin{gathered} Var\left(X^{\prime }\right)=\mathbb{E}\left[X^{\prime 2}\right]-\mathbb{E}{\left[X^{\prime }\right]}^2 \\ =\left(\mathbb{E}\left[X^2\right]-{ϵ}_2\right)-\left(\mathbb{E}{[X]}^2-{ϵ}_1\right) \\ \ge \underset{Var(X)}{\underbrace{\left(\mathbb{E}\left[X^2\right]-\mathbb{E}{[X]}^2\right)}}-\left(\left|{ϵ}_1\right|+\left|{ϵ}_2\right|\right) \\ =\lambda -\left(\left|{ϵ}_1\right|+\left|{ϵ}_2\right|\right) \end{gathered}$$ (10)

Our strategy will be to show ϵ₁, ϵ₂ are small relative to λ, which will tell us Var(X’) ≈ Var(X) = λ. Intuitively, the error terms should be small relative to λ because X’ differs from X only by cutting off the extreme edge of the pdf, given the assumptions on the size of U relative to λ.

First, we bound ϵ₁. We have

$${ϵ}_1=\mathbb{E}{[X]}^2-\mathbb{E}{\left[X^{\prime }\right]}^2=\left(\mathbb{E}[X]+\mathbb{E}\left[X^{\prime }\right]\right)\left(\mathbb{E}[X]-\mathbb{E}\left[X^{\prime }\right]\right)$$

Since $\mathbb{E}\left[X^{\prime }\right]\le \mathbb{E}[X]$, the first term is bounded by $2\mathbb{E}[X]=2\lambda$. To bound the second term, we note that the pdf for X’ is given explicitly as

$$q\left(k|\lambda \right)=\{{}_{0\text{\hspace{0.17em}\hspace{0.17em}otherwise}}^{\frac{c}{k!}{\lambda }^k{e}^{-\lambda }\text{\hspace{0.17em}if\hspace{0.17em}}k\le U}$$

where $c=\frac{1}{1-\mathbb{P}(X>U)}>1$. And therefore

$$\mathbb{E}\left[X^{\prime }\right]=c\sum _{k=1}^U\frac{{\lambda }^k{e}^{-\lambda }}{(k-1)!}\ge \sum _{k=1}^U\frac{{\lambda }^k{e}^{-\lambda }}{(k-1)!}$$

Using this fact to bound $\mathbb{E}[X]-\mathbb{E}\left[X^{\prime }\right]$ gives us

$$\begin{gathered} \mathbb{E}[X]-\mathbb{E}\left[X^{\prime }\right]\le \mathbb{E}[X]-\sum _{k=1}^U\frac{{\lambda }^k{e}^{-\lambda }}{(k-1)!} \\ =\sum _{k=U+1}^{\infty }\frac{{\lambda }^k{e}^{-\lambda }}{(k-1)!} \\ =\frac{\lambda }{e^{\lambda }}\sum _{k=U}^{\infty }\frac{{\lambda }^k}{k!} \end{gathered}$$

Note ${\sum }_{k=U}^{\infty }\frac{{\lambda }^k}{k!}$ is the remainder term of the degree U − 1 Taylor Polynomial for e^λ. We can bound this using Taylor’s Remainder theorem:

$$\sum _{k=U}^{\infty }\frac{{\lambda }^k}{k!}\le \frac{e^{\lambda }{\lambda }^U}{U!}$$

and so

$$\mathbb{E}[X]-\mathbb{E}\left[X^{\prime }\right]\le \lambda \frac{{\lambda }^U}{U!}\le \frac{\lambda }{{1.5}^U}\frac{{\left(\frac{U}{e}\right)}^U}{U!}$$

where the second inequality comes from the assumption that U ≥ 1.5eλ. Here, the second fraction is small by Sterling’s approximation formula. Formally, Sterling tells us

$$\frac{{\left(\frac{U}{e}\right)}^U}{U!}\le \frac{1}{\sqrt{2\pi U}}$$

and therefore

$$\mathbb{E}[X]-\mathbb{E}\left[X^{\prime }\right]\le \frac{\lambda }{{1.5}^U\sqrt{2\pi U}}.$$

Combining the two terms tells us

$$\left|{ϵ}_1\right|\le 2\lambda \frac{\lambda }{{1.5}^U\sqrt{2\pi U}}\le \frac{\lambda }{10}$$

since U ≥ 6.

$${ϵ}_2=\mathbb{E}\left[X^2\right]-\mathbb{E}\left[{X^{\prime }}^2\right]$$

$$\mathbb{E}\left[X^{\prime 2}\right]=c\sum _{k=1}^U\frac{k{\lambda }^k{e}^{-\lambda }}{(k-1)!}\ge \sum _{k=1}^U\frac{k{\lambda }^k{e}^{-\lambda }}{(k-1)!}$$

and therefore

$${ϵ}_2\le \mathbb{E}\left[X^2\right]-\sum _{k=1}^U\frac{k{\lambda }^k{e}^{-\lambda }}{(k-1)!}=\sum _{k=U+1}^{\infty }\frac{k{\lambda }^k{e}^{-\lambda }}{(k-1)!}\le \frac{(U+1){\lambda }^2}{U{e}^{\lambda }}\sum _{k=U-1}^{\infty }\frac{{\lambda }^k}{k!}$$

where the last inequality is due to the fact that $\frac{k}{k-1}\le \frac{U+1}{U}$ for all k ≥ U +1. Here ${\sum }_{k=U-1}^{\infty }\frac{{\lambda }^k}{k!}$ is the remainder term for the degree U − 2 Taylor Polynomial approximation to e^λ. By the Taylor’s remainder formula, we can bound this by

$$\frac{e^{\lambda }{\lambda }^{U-1}}{(U-1)!}$$

and so

$$\left|{ϵ}_1\right|\le \lambda (U+1)\frac{{\lambda }^U}{U!}$$

and since $\lambda \le \frac{U}{1.5e}$, it follows from Sterling’s approximation that

$$\left|{ϵ}_1\right|\le \lambda \frac{U+1}{{1.5}^U\sqrt{2\pi U}}\le \frac{\lambda }{10}$$

since U ≥ 6.

Putting the bounds for ϵ₁ and ϵ₂ back into Equation 10 to get the final form of the Lemma

$$Var\left(X^{\prime }\right)\ge \frac{4}{5}Var(X)=\frac{4}{5}\lambda$$

We next present a one-sided concentration bound for Poisson random variables due to Bobkov and Ledoux [69]: random variables.

Lemma 4

(Proposition 10 in [69]). If X ~ Poisson(λ):

$$\mathbb{P}(X-\lambda >t)\le \text{exp}\left(-\frac{t}{4}\text{log}\left(1+\frac{t}{2\lambda }\right)\right).$$

Lemma 5

(Lemma 3.3 in [68]). Let $\left(Y_n,n\in \mathbb{N}\right)$ be a martingale. For all k ≥ 2, let

$$\mathbb{P}(X-\lambda >t)\le \text{exp}\left(-\frac{t}{4}\text{log}\left(1+\frac{t}{2\lambda }\right)\right).$$

Then for all integers n ≥ 1 and for all η such that for all i ≤ n, $\mathbb{E}\left[\text{exp}\left(\left|\eta \left(Y_i-Y_{i-1}\right)\right|\right)\right]\le \infty$,

$${\epsilon }_n\triangleq \text{exp}\left(\eta Y_n-\sum _{k\ge 2}\frac{{\eta }^k}{k!}{M}_n^k\right)$$

is a super-martingale. Additionally, if Y₀ = 0, then $\mathbb{E}\left[{\epsilon }_n\right]\le 1$.

Lemma 6.

Let ${\left({ϵ}_t\right)}_{t=0}^T$ be i.i.d. Rademacher random variables(i.e $\mathbb{P}\left({ϵ}_t=+1\right)=\mathbb{P}\left({ϵ}_t=-1\right)=\frac{1}{2}$ and ${\left\{X_t\right\}}_{t=0}^T$ are a sequence of random variables, where X_t ∈ [0, U]^M, X_t(ϵ₁, ϵ₂, …, ϵ_t−1) is a function of (ϵ₁, ϵ₂, …, ϵ_t−1). Then

$$\underset{X_1,\dots ,X_T}{\text{sup}}{\Vert \frac{1}{T}\sum _{t=1}^T{X}_t\left({ϵ}_1,{ϵ}_2,\dots ,{ϵ}_{t-1}\right){ϵ}_t\Vert }_{\infty }\le 2U\frac{\text{log}(MT)}{\sqrt{T}},$$

with probability at least $1-\frac{1}{{(MT)}^2}$

Proof:To prove this Lemma, we once again use Markov’s inequality and Lemma 5. For a fixed m ∈ {1, …, M}, define the sequence ($Y_n,n\in \mathbb{N}$) as

$$Y_n\triangleq \frac{1}{T}\sum _{t=1}^n{X}_{t,m}{ϵ}_t.$$

Notice the following values:

$$Y_n-Y_{n-1}=\frac{1}{T}{ϵ}_n{X}_{n,m}{M}_n^k=\sum _{t=1}^n\mathbb{E}\left[{\left(\frac{1}{T}{X}_{t,m}{ϵ}_t\right)}^k|{ϵ}_1,\dots ,{ϵ}_{t-1}\right]\text{ .}$$

The first value shows that $\mathbb{E}\left[Y_n-Y_{n-1}|{ϵ}_1,\dots ,{ϵ}_{n-1}\right]=0$ and therefore Y_n (and the negative of the sequence, −Y_n) is a martingale. Additionally, we have assumed that 0 ≤ X_{m, i} ≤ U for 1 ≤ m ≤ M and 1 ≤ i ≤ T, so it is true that $\left|Y_n-Y_{n-1}\right|\le \frac{2U}{T}\triangleq B$. Additionally:

$$M_n^2=\sum _{t=1}^n\mathbb{E}\left[{\left(\frac{1}{T}{X}_{t,m}{ϵ}_t\right)}^2|{ϵ}_1,\dots ,{ϵ}_{t-1}\right]=\frac{1}{T^2}\sum _{t=1}^n{ϵ}_t^2\mathbb{E}\left[X_{t,m}^2|{ϵ}_1,\dots ,{ϵ}_{t-1}\right]\le \frac{4n{U}^2}{T^2}\triangleq {\widehat{M}}_n^2$$

We will also need to bound $M_n^k$ as follows:

$$\begin{gathered} M_n^k=\sum _{i=1}^n\mathbb{E}\left[\left(\frac{X_{i-1,m}}{T^2}{\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)}^k|X_1,\dots ,X_{i-1}\right)\right] \\ =\sum _{i=1}^n\mathbb{E}\left[{\left(\frac{X_{i-1,m}}{T^2}\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)\right)}^2{\left(\frac{X_{i-1,m}}{T^2}\left(X_{i,\mathcal{l}}-\mathbb{E}\left[X_{i,\mathcal{l}}|X_{i-1}\right]\right)\right)}^{k-2}|X_{i-1}\right]\le B^{k-2}{M}_n^2 \end{gathered}$$

We need to use these values to get a bound on the summation term used in Lemma 5.

$$\begin{gathered} D_n\triangleq \sum _{k\ge 2}\frac{{\eta }^k}{k!}{M}_n^k\le \sum _{k\ge 2}\frac{{\eta }^k{B}^{k-2}{M}_n^2}{k!} \\ \le \frac{{\widehat{M}}_n^2}{B^2}\sum _{k\ge 2}\frac{{(\eta B)}^k}{k!}\triangleq {\widehat{D}}_n \\ {\tilde{D}}_n\triangleq \sum _{k\ge 2}\frac{{\eta }^k}{k!}{\left(-1\right)}^k{M}_n^k\le {\widehat{D}}_n \end{gathered}$$

In the above ${\tilde{D}}_n$ corresponds to the sum corresponding to the negative sequence −Y₀, −Y₁, … which we will also need to obtain the desired bound. Now we are able to use a variant of Markov’s inequality to get a bound on the desired quantity.

$$\begin{gathered} \mathbb{P}(\left|Y_n\right|\ge y) \\ =\mathbb{P}\left(Y_n\ge y\right)+\mathbb{P}\left(-Y_n\ge y\right) \\ \le \mathbb{E}\left[e^{\eta Y_n}\right]e^{-\eta y}+\mathbb{E}\left[e^{\eta \left(-Y_n\right)}\right]e^{-\eta y} \\ =\mathbb{E}\left[e^{\eta Y_n-D_n+D_n}\right]e^{-\eta y}+\mathbb{E}\left[e^{\eta \left(-Y_n\right)-{\tilde{D}}_n+{\tilde{D}}_n}\right]e^{-\eta y} \\ \le \mathbb{E}\left[e^{\eta Y_n-D_n}\right]e^{{\widehat{D}}_n-\eta y}+\mathbb{E}\left[e^{\eta \left(-Y_n\right)-{\tilde{D}}_n}\right]e^{{\widehat{D}}_n-\eta y} \\ \le 2e^{{\widehat{D}}_n-\eta y} \end{gathered}$$

The final inequality comes from the use of Lemma 5, which states that the given terms are supermartingales with initial term equal to 1, so the entire expectation is less than or equal to 1. The final step of the proof is to find the optimal value of η to minimize this upper bound.

$$\mathbb{P}\left(\left|Y_n\right|\ge y\right)\le 2\text{exp}\left({\widehat{D}}_n-\eta y\right)=2\text{exp}\left(\frac{{\widehat{M}}_n^2}{B^2}\left(e^{\eta B}-1-\eta B\right)-\eta y\right)$$

Setting $\eta =\frac{1}{B}\text{log}\left(\frac{yB}{{\widehat{M}}_n^2}+1\right)$ yields the lowest such bound, giving

$$\mathbb{P}\left(\left|Y_n\right|\ge y\right)\le 2\text{exp}(\frac{{\widehat{M}}_n^2}{B^2}\left(\frac{yB}{{\widehat{M}}_n^2}-\text{log}\left(\frac{yB}{{\widehat{M}}_n^2}+1\right)\right)-\frac{y}{B}\text{log}\left(\frac{yB}{{\widehat{M}}_n^2}+1\right))=2\text{exp}\left(-\frac{{\widehat{M}}_n^2}{B^2}H\left(\frac{yB}{{\widehat{M}}_n^2}\right)\right)$$

where H(x) = (1 + x) log(1 + x) − x. We can use the fact that $H(x)\ge \frac{3x^2}{2(x+3)}\text{ for }x\ge 0$ to further simplify the bound.

$$\begin{gathered} \mathbb{P}\left(\left|Y_n\right|\ge y\right) \\ \le 2\text{exp}\left(\frac{-3y^2}{2yB+6{\widehat{M}}_n^2}\right) \\ =2\text{exp}\left(-\frac{3y^2{T}^2}{2C^2\left(Ty+3n{e}^{{\nu }_{\text{max}}}\right){\text{log}}^2(MT)}\right) \end{gathered}$$

To complete the proof, we set n = T and take a union bound over all indices because Y_T considered specific indices m, which gives the bound

$$\begin{gathered} \mathbb{P}\left(\underset{m}{\text{max}}\frac{1}{T}\left|\sum _{t=1}^T{X}_{t,m}{ϵ}_t\right|\ge |2U\frac{\text{log}(MT)}{\sqrt{T}}\right) \\ \le \text{exp}\left(\text{log}(M)-\frac{12U^{2}T{\text{log}}^2(MT)}{4U^2(\sqrt{T}\text{log}(MT)+3T)}\right) \\ \le \text{exp}\left(\text{log}(MT)-\frac{3\text{log}(MT)}{1/\sqrt{T}+3/\text{log}(MT)}\right) \\ \le \text{exp}(-2\text{log}(MT)). \end{gathered}$$

B. Proof of Lemma 1

1). Part 1:

Proof:For all 1 ≤ t ≤ T and 1 ≤ m ≤ M, X_t, _m|X_t−1 is drawn from a Poisson distribution with mean $e^{{\nu }_m}+a_m^{*\top }{X}_{t-1}$ for some $a_m^{*}\in {\left[a_{\text{min}},0\right]}^M$. Because of the range of values $a_m^{*}$ can take, we know that $e^{{\nu }_m+a_m^{*1}{X}_{t-1}}\le e^{{\nu }_{\text{max}}}$ where ν_m ≤ ν_max for some ν_max < ∞ for all m. Therefore, we know that

$$\mathbb{P}\left(X_{t,m}\ge \eta +e^{{\nu }_{\text{max}}}|X_{t-1}\right)\le \mathbb{P}\left(Y\ge \eta +e^{{\nu }_{\text{max}}}\right)$$

where Y is a Poisson random variable with mean e^νmax. To bound this quantity we use the result of Lemma 4,

$$\mathbb{P}\left(Y>\eta +e^{{\nu }_{\text{max}}}\right)\le \text{exp}\left(-\frac{\eta }{4}\text{log}\left(1+\frac{\eta }{2e^{{\nu }_{\text{max}}}}\right)\right).$$

Setting $\eta =C\text{log}MT-e^{{\nu }_{\text{max}}}$,

$$\begin{gathered} \mathbb{P}(Y>C\text{\hspace{0.17em}log}MT) \\ \le \text{exp}(-\frac{C\text{\hspace{0.17em}log}MT-e^{{\nu }_{\text{max}}}}{4}\text{log}\left(1+\frac{C\text{\hspace{0.17em}log}MT-e^{{\nu }_{\text{max}}}}{2e^{{\nu }_{\text{max}}}}\right)) \\ \le \text{exp}\left(-\frac{C\text{\hspace{0.17em}log}MT-e^{{\nu }_{\text{max}}}}{4}\right). \end{gathered}$$

Here, we have assumed that C ≥ e^νmax (2e − 1) and log MT ≥ 1. This upper bound is not dependent on the value of X_t−1, so this quantity is also an upper bound for the unconditional probability of X_t,_m ≥ C log MT. Using this for a single index t, m of our data X, and taking a union bound over all possible indices 1 ≤ m ≤ M, 1 < t ≤ T gives

$$\begin{gathered} \mathbb{P}\left(\underset{1\le m\le M,1\le t\le T}{\text{max}}{X}_{t,m}>C\text{\hspace{0.17em}log\hspace{0.17em}}MT\right) \\ \le \text{exp}\left(\text{log\hspace{0.17em}}MT-\frac{C\text{\hspace{0.17em}log}MT-e^{{\nu }_{\text{max}}}}{4}\right) \\ \le \text{exp}(-c\text{\hspace{0.17em}log\hspace{0.17em}}MT) \end{gathered}$$

for $c\le \frac{C-e^{{\nu }_{\text{max}}}}{4}-1$. Thus if C > max(e^νmax (2e − 1), 4 + e^νmax), then c > 0, and the bound is valid. ■

2). Part 2:

Proof:We are interested in bounding the number of observations X_t,_m for 1 ≤ m ≤ M and 1 ≤ t ≤ T that are above the value U. Saying at least $j\triangleq \alpha MT$ observations are less than a certain value, is equivalent to saying that the j^th smallest observation is less than that value. Therefore,

$\mathbb{P}$(j^th smallest observation X_t,m > U)

$$=\mathbb{P}\left(\sum _{t=1}^T\sum _{m=1}^M{Y}_{t,m}\le j-1\right)=\sum _{\mathcal{l}=0}^{j-1}\mathbb{P}\left(\sum _{t=1}^T\sum _{m=1}^M{Y}_{t,m}=\mathcal{l}\right)\le \sum _{\mathcal{l}=0}^j\sum _{y\in {\mathcal{Y}}^{\mathcal{l}}}\mathbb{P}(Y=y).$$

Here we define $Y_{t,m}\triangleq 1\left\{X_{t,m}\le U\right\}$, and ${\mathcal{Y}}^{\mathcal{l}}=\left\{y\in {\{0,1\}}^{M\times T}|{\sum }_{t=1}^T{\sum }_{m=1}^M{y}_{t,m}=\mathcal{l}\right\}$. We then condition the values of Y_t on all previous values of Y and then understand this as a marginal of the joint distribution over Y_t and X_t−1. Below we use the notation Y_1:t to denote all the time indices of Y from 1 to t, and similarly for y.

$$\begin{gathered} \mathbb{P}(Y=y) \\ =\prod _{t=1}^T\mathbb{P}\left(Y_t=y_t|Y_{1:t-1}=y_{1:t-1}\right) \\ =\prod _{t=1}^T\sum _{x_{t-1}}(\mathbb{P}\left(Y_t=y_t|Y_{1:t-1}=y_{1:t-1},X_{t-1}=x_{t-1}\right)\mathbb{P}\left(X_{t-1}=x_{t-1}|Y_{1:t-1}=y_{1:t-1}\right)) \\ =\prod _{t=1}^T\sum _{x_{t-1}}\left(\left(\prod _{m=1}^M\mathbb{P}\left(Y_{t,m}=y_{t,m}|X_{t-1}=x_{t-1}\right)\right)\mathbb{P}\left(X_{t-1}=x_{t-1}|Y_{1:t-1}=y_{1:t-1}\right)\right) \end{gathered}$$

In the last line we use the fact that conditioned on X_t−1, Y_t is independent across dimensions m, and independent of previous values Y_1:t−1. We now make the observation that $\mathbb{P}\left(X_{t,m}>U|X_{t-1}=x_{t-1}\right)$ is exactly the probability that a Poisson random variable with rate exp(${\nu }_m+a_m^{*\top }{x}_{t-1}$) is greater than U, which can be upper-bounded by the probability that a Poisson random variable with rate exp(ν_max) is greater than U because we have assumed all values of a $a_m^{*}$ are non-positive. Call this probability p_νmax. Thus we have $\mathbb{P}(Y=y)\le p_{{\nu }_{\text{max}}}^{MT-{\sum }_{t=1}^T{\sum }_{m=1}^M{y}_{t,m}}$ and therefore,

$$\begin{gathered} \mathbb{P}\left(\sum _{t=1}^T\sum _{m=1}^M{Y}_{t,m}\le j-1\right) \\ \le \sum _{\mathcal{l}=0}^j\left(MT\mathcal{l}\right)p_{{\nu }_{\text{max}}}^{MT-\mathcal{l}} \\ ={\left(1+p_{{\nu }_{\text{max}}}\right)}^{MT}-\sum _{\mathcal{l}=0}^{MT-j-1}\left(MT\mathcal{l}\right)p_{{\nu }_{\text{max}}}^{\mathcal{l}} \\ \le \left(MTMT-j\right){\left(1+p_{{\nu }_{\text{max}}}\right)}^j{p}_{{\nu }_{\text{max}}}^{MT-j} \\ \le {\left(\frac{MTe}{MT-j}\right)}^{MT-j}{\left(1+p_{{\nu }_{\text{max}}}\right)}^j{p}_{{\nu }_{\text{max}}}^{MT-j}. \end{gathered}$$

The second inequality is from the application of Taylor’s Remainder Theorem, and the third is from the fact that $\left({}_k^n\right)\le {\left(\frac{ne}{k}\right)}^k$. Now use the fact that j = αMT as stated in the Lemma, to give

$$\begin{gathered} \mathbb{P}\left(\sum _{t=1}^T\sum _{m=1}^M{Y}_{t,m}\le j-1\right) \\ \le {\left(\frac{p_{{\nu }_{\text{max}}}e}{1-\alpha }\right)}^{(1-\alpha )MT}{\left(1+p_{{\nu }_{\text{max}}}\right)}^{\alpha MT} \\ \le {\left[{\left(\frac{p_{{\nu }_{\text{max}}}e}{1-\alpha }\right)}^{1-\alpha }{2}^{\alpha }\right]}^{MT}. \end{gathered}$$

By using Lemma 4 in a similar way as was used in the proof of Lemma 1 part 1, p_νmax can be controlled by U in the following way,

$$\begin{gathered} p_{{\nu }_{\text{max}}}=\mathbb{P}(X>U) \\ \le \text{exp}\left(-\frac{U-e^{{\nu }_{\text{max}}}}{4}\text{log}\left(1+\frac{U-e^{{\nu }_{\text{max}}}}{2e^{{\nu }_{\text{max}}}}\right)\right) \\ \le \text{exp}\left(-\frac{U-e^{{\nu }_{\text{max}}}}{4}\right), \end{gathered}$$

when U ≥ e^νmax(2e − 1). Plugging the result back into the bound gives $\mathbb{P}\left(\text{at least }\alpha MT\text{ observations\hspace{0.17em} }{X}_{t,m}\le U\right)\ge 1-e^{-cMT}$

When $U>4+e^{{\nu }_{\text{max}}}+\frac{4\alpha \text{log}(2)}{1-\alpha }-4\text{log}\left(1-\alpha \right)$ and additionally greater than e^νmax (2e − 1) the condition from above, then the probability of this event is decaying in M and T. Therefore, for $c=\left(1-\frac{U-e^{{\nu }_{\text{max}}}}{4}-\text{log}(1-\alpha )\right)(1-\alpha )-\alpha \text{log}(2)$, have the inequality

$\mathbb{P}$ (at least αMT observations X_t,m ≤ U) ≥ 1 – e−^cMT ■

C. Proof of Lemma 2

Proof: To prove the form of the stationary distribution we show that

$$\pi (y)={\int }_x\pi (x)P(x,y),$$

where

$$\text{P}(\text{x},\text{y})=\text{exp}\left({\nu }^{\top }y+y^{\top }{A}^{*}x-\sum _{m=1}^{M}Z\left({\nu }_m+a_m^{\top }x\right)\right)\prod _{m=1}^{M}h\left(y_m\right).$$

Plugging in π(x) as specified,

$$\begin{gathered} {\int }_x\pi (x)P(x,y) \\ =C_{\nu ,A^{*}}{\int }_x\text{exp}({\nu }^{\top }x+\sum _{m=1}^{M}Z\left({\nu }_m+a_m^{*\top }x\right)+{\nu }^{\top }y+y^{\top }{A}^{*}x-\sum _{m=1}^{M}Z\left({\nu }_m+a_m^{*\top }x\right))\prod _{m=1}^{M}h\left(x_m\right)h\left(y_m\right) \\ =C_{\nu ,A^{*}}\text{exp}\left({\nu }^{\top }y\right)\prod _{m=1}^M\left(h\left(y_m\right)\right){\int }_x\text{exp}\left({\nu }^{\top }x+y^{\top }{A}^{*}x\right)\prod _{m=1}^{M}h\left(x_m\right) \\ =C_{\nu ,A^{*}}\text{exp}\left({\nu }^{\top }y\right)\prod _{m=1}^M\left(h\left(y_m\right)\right){\int }_x\text{exp}\left({\nu }^{\top }x+x^{\top }{A}^{*}y\right)\prod _{m=1}^{M}h\left(x_m\right) \\ =C_{\nu ,A^{*}}\text{exp}\left({\nu }^{\top }y\right)\prod _{m=1}^M\left(h\left(y_m\right){\int }_{x_m}\text{exp}\left({\nu }_m{x}_m+x_m{a}_m^{*\top }y\right)h\left(x_m\right)\right) \\ =C_{\nu ,A^{*}}\text{exp}\left({\nu }^{\top }y+\sum _{m=1}^{M}Z\left({\nu }_m+a_m^{*\top }y\right)\right)\prod _{m=1}^{M}h\left(y_m\right) \\ =\pi (y) \end{gathered}$$

The second to last equality uses the definition of Z as the log partition function, and the third uses the assumption that A* = A^*⊤.

To prove the upper bound on total variation distance for Markov chains on countable domains, we define two chains, one chain Y_t begins at the stationary distribution and the other independent chain starts at X_t begins at some arbitrary random state x, both with transition kernel P. These two chains are said to be coupled if they are run independently until the first time where the states are equal, then are equal for the rest of the trial. The notation P^t(x, y) denotes the probability of transitioning from state y to state x in exactly t steps. Theorem 5.2 of [70] asserts that:

$${\Vert P^t(x,\cdot )-\pi (\cdot )\Vert }_{TV}\le {\mathbb{P}}_x\left({\tau }_{couple}>t\right),$$

where ${\tau }_{\text{couple}}:=\left\{\underset{{}_{t>0}}{\text{min}}:X_t=Y_t\right\}$. Note first that $\mathbb{P}\left({\tau }_{\text{couple}}>t\right)\le \prod _{\tau =0}^t\left(1-\mathbb{P}\left(X_{\tau }=Y_{\tau }=0\right)\right)$. Since the chains are independent until ${\tau }_{\text{ couple }},\mathbb{P}\left(X_{\tau }=Y_{\tau }=0\right)=\mathbb{P}\left(X_{\tau }=0\right)\mathbb{P}\left(Y_{\tau }=0\right)$. Note also that:

$$\begin{gathered} \mathbb{P}\left(X_{\tau }=0|X_{\tau -1}=x\right) \\ =h{\left(0\right)}^M\text{exp}\left(-\sum _{m=1}^{M}Z\left({\nu }_m+a_m^{*\top }x\right)\right) \\ \ge h{\left(0\right)}^M\text{exp}\left(-\sum _{m=1}^{M}Z\left({\nu }_m\right)\right) \\ \ge h{\left(0\right)}^M\text{exp}\left(-MZ\left({\nu }_{\text{max}}\right)\right), \end{gathered}$$

where the first inequality is due to the fact that Z is an increasing function, and from the assumption that A_i,j ≥ 0. Hence. $\mathbb{P}\left({\tau }_{couple}>t\right)\le {{\prod }_{\tau =0}^t\left(1-h{(0)}^{-2M}\text{exp}\left(-2MZ\left({\nu }_{\text{max}}\right)\right)\right)=\left(1-h{\left(0\right)}^{-2M}\text{exp}\left(-2MZ\left({\nu }_{\text{max}}\right)\right)\right)}^t$. ■

D. Empirical processes for martingale sequences

To concretely define the martingale, let (X_t)_t≥1 be a sequence of random variables adapted to the filtration ${\left({\mathcal{A}}_t\right)}_{t\ge 1}$. First we present a bounded difference inequality for martingales developed by van de Geer [65].

Theorem 4

(Theorem 2.6 in [65]). Fix T ≥ 1 and let Z_T be an ${\mathcal{A}}_{\mathcal{T}}$ -measurable random variable, satisfying for each t = 1, 2, …, t,

$$L_t\le \mathbb{E}\left[Z_T|{\mathcal{A}}_t\right]\le U_t,$$

almost surely where L_t < U_t are constants. Define $C_T^2={\sum }_{t=1}^T{\left(U_t-L_t\right)}^2$. Then for all α > 0,

$$\mathbb{P}\left(Z_T-\mathbb{E}\left[Z_T\right]\ge a\right)\le \text{exp}\left(-\frac{2a^2}{C_T^2}\right).$$

The second important result we need is a notion of sequential Rademacher complexity for martingales that allows us to do symmetrization, an important step in empirical process theory (see e.g. [71]). To do this we use machinery developed in [66]. Recall that (X_t)_t≥1 is a martingale and let χ be the range of each X_t. Let $\mathcal{F}$ be a function class where for all $f\in \mathcal{F},f:\chi \to ℝ$.

To define the notion of sequential Rademacher complexity, we first let ${\left({ϵ}_t\right)}_{t=1}^T$ be a sequence of independent Rademacher random variables (i.e. $\mathbb{P}\left({ϵ}_t=+1\right)=\mathbb{P}\left({ϵ}_t=-1\right)=\frac{1}{2})$). Next we define a tree process as a function of these independent Rademacher random variables.

A χ-valued tree x of depth T is a rooted complete binary tree with nodes labelled by elements of χ. We identify the tree x with the sequence (x₁, x₂, …, x_T) of labeling functions $x_t:{\{\pm 1\}}^{t-1}\to \chi$ which provide the labels for each node. Here x₁ ∈ χ is the label for the root of the tree, while xt for t > 1 is the label of the node obtained by following the path of length t − 1 from the root, with +1 indicating “right” and −1 indicating “left.” Based on this tree, x_t is a function of (ϵ₁, ϵ ₂, …, ϵ _t−1).

Based on this, we define the sequential Rademacher complexity of a function class $\mathcal{F}$.

Definition 1

(Definition 3 in [66]). The sequential Rademacher complexity of a function class $\mathcal{F}$ on a χ-valued tree x is defined as

$${\mathcal{R}}_T(\mathcal{F})\triangleq \underset{x}{\text{sup}}\mathbb{E}\left[\underset{f\in \mathcal{F}}{\text{sup}}{ϵ}_{t}f\left(x_t\left({ϵ}_1,{ϵ}_2,\dots ,{ϵ}_{t-1}\right)\right)\right]$$

where the outer supremum is taken over all χ-valued trees. Importantly note that (ϵ_tf(x_t(ϵ₁, ϵ₂, …, ϵ_t−1))_t≥1 is a martingale. Now we are in a position to state the main result which allows us to do symmetrization for functions of martingales.

Theorem 5

(Theorem 2 in [66]).

$$\mathbb{E}\left[\underset{f\in \mathcal{F}}{\text{sup}}\frac{1}{T}\sum _{t=1}^T\mathbb{E}\left[f\left(X_t\right)|{\mathcal{A}}_{t-1}\right]-f\left(X_t\right)\right]\le 2{\mathcal{R}}_T(\mathcal{F}).$$

For further details refer to [66].