High-contrast and reversible polymer thermal regulator by structural phase transition

An average thermal switching ratio of ~8× and maximum switching ratio of ~10× is achieved within a temperature range of 10 K.

Abstract

In comparison with the advancement of switchable, nonlinear, and active components in electronics, solid-state thermal components for actively controlling heat flow have been extremely rare. We demonstrate a high-contrast and reversible polymer thermal regulator based on the structural phase transition in crystalline polyethylene nanofibers. This structural phase transition represents a dramatic change in morphology from a highly ordered all-trans conformation to a combined trans and gauche conformation with rotational disorder, leading to an abrupt change in phonon transport along the molecular chains. For five nanofiber samples measured here, we observe an average thermal switching ratio of ~8× and maximum switching ratio of ~10×, which occurs in a narrow temperature range of 10 K across the structural phase transition. To the best of our knowledge, the ~10× switching ratio exceeds any reported experimental values for solid-solid and solid-liquid phase transitions of materials. There is no thermal hysteresis observed upon heating/cooling cycles.

INTRODUCTION

Active control of thermal transport is of substantial interest for a broad range of applications including heating and cooling, energy conversion, materials processing, and data storage. However, compared with the remarkable success for manipulating electrons using switchable, nonlinear, and active electrical components, a similar degree of control over heat flow has never been realized by mankind, although both heat conduction and electrical conduction are two fundamental energy transport mechanisms in solids (1, 2). Consequently, the development of advanced thermal components in an analogy of electronics, such as thermal switches, thermal diodes, and thermal regulators, has been extremely limited (3–6).

Although several mechanisms based on external stimuli, electrochemical tuning, phase transition, and desiccation-hydration of materials were demonstrated for developing thermal switches or regulators, it has remained a challenge to achieve a large thermal switching ratio of materials that is defined as the ratio between the “on-state” high and the “off-state” low thermal conductance (or thermal conductivity) values. Here, a thermal regulator is a two terminal component that can thermally switch between a high-conductance and a low-conductance state across a critical temperature, whereas a thermal switch is a two terminal component enabling thermal switching based on a nonthermal control parameter, such as an electric field, magnetic field, or applied pressure (6). Liquid crystal networks exhibited a ~1.5× thermal switching ratio due to magnetic field–induced molecular orientation (7). By manipulating the nanoscale ferroelastic domains in lead zirconate titanate thin films under external electric fields, a ~1.1× thermal switching ratio was achieved (8). The desiccation-hydration of boron nanoribbons and tandem repeat proteins led to thermal switching ratios of ~1.5× and ~4×, respectively (9, 10). Under electrochemical tuning, the delithiation of lithium cobalt oxide gave rise to a ~1.5× thermal switching ratio, whereas the lithium intercalation in molybdenum disulfide resulted in 8 to 10× thermal switching ratios (11, 12). Through thermally induced martensitic transition, a ~1.5× thermal switching ratio was observed in Ni-Mn-In alloys (13). Recently, a 3.5× thermal switching ratio has been achieved in light-responsive azobenzene polymers by modulation of chain alignment, which results from the conformational transition between nonplanar (cis) and planar (trans) azobenzene groups under green and ultraviolet light illumination (14).

Without changing the chemical composition of materials, solid-state phase transition such as solid-liquid or solid-solid phase transition has been proposed as a promising mechanism for thermal switches or regulators, yet the modulation of thermal transport properties occurring across phase transition is usually minimal for almost all the materials (6, 15). Here, we report high-contrast, abrupt, and reversible thermal conductance change in crystalline polyethylene (PE) nanofibers induced by structural phase transition, which enables an unprecedented ~10× thermal switching ratio beyond any previously reported experimental values for solid-solid and solid-liquid phase transitions (6, 15–17). We also show that the demonstrated reversible thermal regulators based on the PE nanofibers can sustain temperatures up to ~450 K and have no degradation after multiple thermal cycles. This control of heat flow at the nanoscale opens up new possibilities for developing switchable thermal devices for autonomous thermal management, solid-state refrigeration, waste heat scavenging, thermal circuits, and phononic computing.

RESULTS

In an orthorhombic PE crystal with extended chains (Fig. 1A), its molecular structure is highly anisotropic with strong carbon-carbon bonds along the chain but weak van der Waals interactions between chains. While these strong carbon bonds give rise to high energy constants for bond stretching (E_r = ~300 kcal mol⁻¹) and bond bending (E_α = ~40 kcal mol⁻¹), the dihedral angle energy (E_θ = ~0.2 kcal mol⁻¹) is two to three orders of magnitude lower (Fig. 1A, inset) (18). As a result, the PE chains are stiff in terms of bond stretching and bending degrees of freedom, but soft in the rotational degree of freedom, leading to a unique platform for thermal transport control. At a low temperature, they have an intrinsic high thermal conductivity along the chain direction due to the aligned and highly ordered carbon segmental arrangement (Fig. 1A) (19–21). However, when temperature increases to allow the atomic kinetic energy to overcome the weak dihedral energy barrier, segmental rotations of PE chains occur, which introduces a structural phase transition from a highly ordered all-trans conformation to a combined trans and gauche conformation with rotational disorder (Fig. 1B) (18, 22). Such a marked change in morphology can drastically induce phonon scattering along the chains, resulting in a low thermal conductivity after the phase transition. However, it has been challenging to synthesize bulk PE crystals with extended chains to take full advantage of their intrinsic abrupt change in thermal transport. Here, by fabricating highly crystalline PE nanofibers with extended chains (see the Supplementary Materials), we demonstrate a high-contrast polymer thermal regulator at the nanoscale. Figure 1C shows the transmission electron microscopy (TEM) micrograph of a PE nanofiber sample that typically has a diameter of ~100 nm. In Fig. 1D, selected area electron diffraction (SAED) pattern illustrates an orthorhombic crystal structure with lattice constants a = 7.350 Å, b = 4.920 Å, and c = 2.550 Å, which are consistent with the values in the literature (18).

Fig. 1. Structural phase transition in crystalline PE nanofibers.

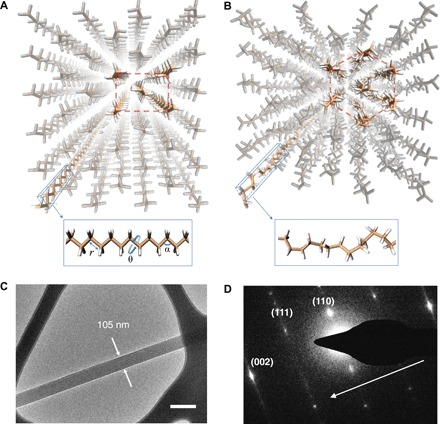
(A) Highly ordered all-trans conformation of an orthorhombic PE crystal before the phase transition. Inset in (A) shows an aligned and ordered PE molecular chain, where r, α, and θ represent bond length, bond angle, and dihedral angle, respectively. (B) Combined trans and gauche conformation after the phase transition, which corresponds to a rotationally disordered hexagonal phase. Inset in (B) shows a PE molecular chain with random segmental rotations. (C) Transmission electron microscopy (TEM) micrograph of a typical crystalline PE nanofiber sample. Scale bar, 200 nm. (D) Selected area electron diffraction (SAED) pattern of the PE nanofiber taken using low-dose TEM at cryogenic temperature. The arrow in (D) indicates the c axis.

In Fig. 2A, we measure the temperature-dependent thermal conductance of a PE nanofiber in high vacuum (2 × 10⁻⁶ Torr) using a suspended platinum resistance thermometer microdevice that consists of heating and sensing measurement islands (23–25). In the experiment, a dc current is applied to raise the temperature of one of the suspended islands. By exerting a small ac current on both islands to monitor the resistance change, we can measure the temperature difference between the two islands as well as the heat flow through the nanofiber crossing the islands. The temperature difference between the two islands for thermal conductance measurements is ~3 K. In all the measurements, the dc current increases from 0 to 20 μA, with the step of 0.2 μA. At each step, we collect the experimental data after the whole device reaches thermal equilibrium.

Fig. 2. High-contrast and reversible polymer thermal regulator based on PE nanofibers.

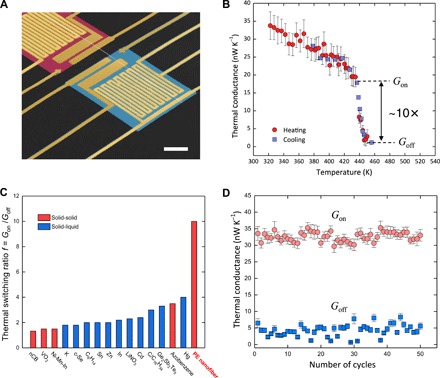
(A) False-colored SEM micrograph of a suspended platinum resistance thermometer microdevice. A PE nanofiber crosses its heating and sensing islands. Scale bar, 10 μm. (B) Temperature-dependent thermal conductance G(T) of nanofiber #1 from 320 to 455 K. An abrupt and reversible thermal conductance change is observed around 440 K due to the structural phase transition. (C) Thermal switching ratio f of PE nanofibers compared with the solid-solid or solid-liquid transition in some existing materials. The values are summarized in table S1. The associated references are as follows. nCB (31); VO₂ (26); K, Zn, Cd, and Hg (32); c-Se (33); Ni-Mn-In alloy (13); C₆H₁₄ (34); Sn, In, and LiNO₃ (15); C/C₁₆H₃₄ composite (17); Ge₂Sb₂Te₅ (27); azobenzene polymers (14). (D) Multiple on/off thermal cycles of nanofiber #2 around the phase transition temperature of 440 K.

To enhance the thermal contact between the PE nanofiber and the measurement device, we apply an isopropanol drop on top of the thermal device when placing the nanofiber onto the measurement islands. The capillary force from the evaporating liquid then pulls the nanofiber to intimately contact the measurement islands. With this strategy, the contact resistances are estimated to be less than 10% of the total thermal resistance of the sample (see the Supplementary Materials). Figure 2B shows the measured thermal conductance of nanofiber #1 in the environmental temperature range of 320 to 455 K. As the temperature increases (the “heating” data in Fig. 2B), the thermal conductance of the nanofiber first gradually decreases due to the well-known Umklapp scattering of phonons in crystals and abruptly drops from 17.8 nW K⁻¹ (~20 Wm⁻¹ K⁻¹) to 1.79 nW K⁻¹ (~2 Wm⁻¹ K⁻¹) within a small temperature range of 435 to 445 K due to the structural phase transition in Fig. 1 (A and B). This corresponds to a thermal switching ratio f = 9.9 ± 1.8, where f = G_on/G_off is defined as the ratio of the on-state high thermal conductance G_on to the off-state low thermal conductance G_off (fig. S1). An average f ~ 8 is achieved over five nanofiber samples (see table S2). To the best of our knowledge, the observed high switching ratio exceeds by far any experimental values of the solid-solid or solid-liquid phase transition in typical phase change materials such as VO₂ (26), Ge₂Sb₂Te₅ (27), and other conventional materials (15), as shown in Fig. 2C and table S1. Moreover, the demonstrated thermal conductance change in PE nanofibers is found to be reversible, as shown by the “cooling” data in Fig. 2B, where the temperature decreases, which is quite different from the hysteresis of that observed in PE microfibers (fig. S2). This reversibility can be maintained without observable degradation over many “on/off” thermal cycles (e.g., 50 cycles in Fig. 2D for nanofiber #2) around the phase transition temperature.

To further investigate the thermal stability and temperature limit of the phase transition in PE nanofibers, we slowly heat nanofiber #3 and hold it for 10 hours at 450 K, which is ~10 K above its phase transition temperature. Upon cooling, the measured thermal conductance overlaps the original heating data of the specimen, as shown in Fig. 3A. When heating a nanofiber sample beyond 500 K, we measure the thermal conductance of nanofiber #4 up to 530 K (Fig. 3B) in the first run. After cooling the sample back to 380 K, we reheat the sample and measure its thermal conductance up to 560 K in the second run. In Fig. 3B, the nanofiber still shows partial phase transition even though the temperature has reached 530 K in the first run. This partial phase transition indicates that the nanofiber does not break at 530 K but loses some crystallinity due to the high temperature. In the third run, after cooling the sample from 560 to 320 K, we remeasure its thermal conductance with the increasing temperature, and there is no phase transition observed, in which the nanofiber shows a slightly increasing thermal conductance trend with temperature like that of an amorphous specimen. The measured thermal conductance value (~1 nW/K) in the third run is much lower than the original values in the first run, but still larger than the background signal (~0.2 nW/K), which indicates that the nanofiber does not break even at 560 K. Thus, the PE nanofibers turn out to be stable up to ~560 K, which is more than 100 K higher than the equilibrium melting temperature of bulk PE (~400 K). Such excellent thermal stability stems from the high crystallinity of the PE nanofibers, the small test length scale (~5 μm gap between the two measurement islands in Fig. 2A) compared with the length of a PE molecule (30 to 50 μm), and the capillary force–assisted clamping of the nanofiber ends to the measurement device, all of which limit the relaxation of the PE molecules. On the other hand, strain effects on the fiber can affect the measured switching ratio (fig. S9). However, because of the high mechanical compliance of the suspended thermal device, the stress applied on the fiber during our experiment is negligible.

Fig. 3. Thermal stability and temperature limit of the phase transition in PE nanofibers.

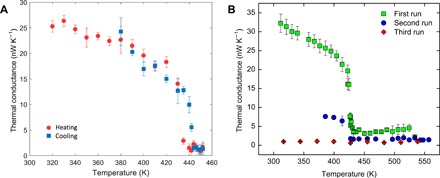
(A) Thermal conductance of nanofiber #3 before and after holding the specimen at 450 K for 10 hours. The thermal conductances of this nanofiber in the heating and the cooling processes overlap and, thus, show the complete reversibility when the temperature is ~10 K higher than the phase transition temperature. (B) High-temperature stability of nanofiber #4. The nanofiber shows the partial phase transition at ~430 K when the temperature reaches 530 K. This phase transition disappears, and the crystalline PE nanofiber becomes amorphous when the temperature increases up to 560 K.

The observed high-contrast, abrupt, and reversible thermal conductance change is attributed to the phase transition from a highly ordered orthorhombic phase to a rotationally disordered hexagonal phase in PE nanofibers (28, 29). This disordered hexagonal phase has been described in constrained PE microfibers using in situ x-ray diffraction and Raman scattering (22), but the phase transition in the PE microfibers is only partially reversible (fig. S2) compared with the PE nanofibers. Here, we conduct micro-Raman measurements of PE nanofibers for direct characterization of the structural phase transition. As shown in Fig. 4A, the peak representing the CH₂ bending mode shifts from 1418 to 1440 cm⁻¹ when the temperature increases from 420 to 430 K, indicating that the original orthorhombic phase disappears (30). Meanwhile, the degree of crystallinity drops during the phase transition. The intensity peak of the skeletal bond stretching mode at 1130 cm⁻¹ remains at 430 K but disappears at 440 K, indicating that the chain alignment still retains at 430 K (22). These observations from the micro-Raman measurements show that the nanofiber is in the hexagonal phase at 430 K but melts at 440 K. Thus, orthorhombic-hexagonal phase transition occurs at a temperature between 420 and 430 K. Note that the phase transition temperature reported from the Raman measurements is lower than that measured in Fig. 2B. This difference is mainly due to the variation of the nanofiber samples and the laser heating in the Raman measurements.

Fig. 4. Micro-Raman measurements and MD simulations of PE nanofibers before and after the phase transition.

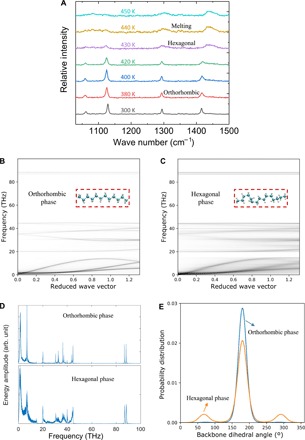
(A) Temperature-dependent micro-Raman measurements of a PE nanofiber. All Raman spectra are normalized with respect to the intensity of the Raman peak at ~1128 cm⁻¹ at 300 K. (B and C) Phonon dispersions of the orthorhombic phase and the hexagonal phase of a PE nanofiber. The less blurry (cleaner) lines of the phonon dispersion in (B) suggest less phonon scattering. (D) Corresponding vibrational power spectra at the reduced wave vector value of k = 0.33. (E) Corresponding dihedral angle θ distributions.

We perform molecular dynamics (MD) simulations to further understand this effect. From the thermal transport point of view, the segmental rotations in the disordered hexagonal phase pose structural defects along the chains and cause substantial phonon scattering and, thus, the reduced thermal conductance (Fig. 2B). We calculate the phonon dispersion relation from the MD trajectory (see the Supplementary Materials). In Fig. 4 (B and C), the dispersion relation of the hexagonal phase in the along-chain direction is much more blurred than that in the orthorhombic phase, which indicates that the CH₂ segments become less ordered along the chain due to rotations. In Fig. 4D, where a selected reduced wave vector of k = 0.33 is displayed, since the scattering rates of phonons are proportional to the broadening of these peaks (linewidth), the broadened peaks directly indicate the enhanced scattering in the disordered hexagonal phase (fig. S5). The degree of segmental rotation is also characterized by calculating the dihedral angle distribution. In Fig. 4E, the population of the gauche conformation, corresponding to dihedral angles of 70° and 290°, increases greatly in the hexagonal phase. In the low-temperature phase, however, the population of the gauche conformation is almost eliminated with a single peak at 180° in Fig. 4E, displaying an all-trans conformation. In addition, we use Fourier transform analysis to quantitatively characterize the phonon group velocity, the phonon lifetime, and the heat capacity (see the Supplementary Materials). From the orthorhombic phase to the hexagonal phase, both the volumetric heat capacity and the phonon group velocity change by only 5%, but the phonon lifetime dramatically drops from 3.3 to 0.72 ps. Hence, the dominant reason for the high thermal switching ratio (5.44) is the longer phonon lifetime in the orthorhombic phase (4.58 times).

CONCLUSIONS

In summary, we report a high-contrast, abrupt, and reversible polymer thermal regulator. An unprecedented thermal switching ratio f ~ 10 is observed on the basis of the reversible structural phase transition in crystalline PE nanofibers, which exceeds any reported experimental values of solid-state phase transition of materials. The reversibility of the demonstrated polymer thermal regulator can be maintained without observable degradation over many thermal cycles. MD simulations are performed to quantitatively understand the phonon scattering induced by the structural phase transition. The advanced nanoscale thermal regulators demonstrated in this work can potentially perform as fundamental building blocks for regulating heat flow and provide a new platform for thermal transport control, which enables new applications for efficient thermal management and energy harvesting.

MATERIALS AND METHODS

Fabrication of crystalline PE nanofibers

The fabrication of the crystalline PE nanofibers follows a similar procedure presented in (21). To form a PE gel, we mixed 0.8 weight % ultrahigh molecular weight PE powder (average molecular weight, 3 × 10⁶ to 6 × 10⁶ g mol⁻¹; Sigma-Aldrich) with decalin (Sigma-Aldrich). Then, the mixture was heated up to 145°C inside an argon-filled glove box to avoid oxidation and molecular degradation. A glass rod was used to constantly stir and uniformly heat the solution. After the PE powder completely dissolves, the transparent and viscous solution was quenched to room temperature in a water bath to form the gel. The PE gel was then used to draw PE nanofibers in a two-step process. First, we used a tip drawing method to produce PE microfibers. In this process, a small drop of PE gel was placed onto a 5 mm by 5 mm thin film heater and heated up to 120° to 130°C. The ambient was maintained at a temperature of 90°C by a hot plate placed underneath the thin film heater. As the gel was melted around 130°C, a sharp glass tip (10 μm in diameter) was used to first draw a hundreds-of-microns-long PE microfiber. After the solvent was fully evaporated, the PE microfiber was further drawn to a length of ~1 cm and quenched to the room temperature. This minimizes the relaxation of the extended chain molecules. A sample collector, a bulk micromachined silicon frame with a square hole, was used to store the PE microfiber under tensile stress. The prestressed PE microfiber was locally heated near the melting point by a tungsten micro heater, during which the tensile stress quickly stretches a section of the microfiber to a diameter ranging from 10 to 150 nm.

Micro-Raman measurements of PE nanofibers

Micro-Raman spectroscopy was performed using a Horiba LabRAM HR Evolution spectrometer in a 180° backscattering configuration with 532-nm laser excitation and a long working distance 50× objective (numerical aperture, 0.45). It is found that higher laser powers can result in laser-induced damage or premature failure of the fibers; therefore, to minimize structural damage, a low laser power (~1.5 mW) and acquisition time (60 s for microfiber, 90 s for nanofiber) were used. Multiple accumulations were used to remove spikes in the Raman spectra and increase the signal-to-noise ratio. Temperature-dependent Raman measurements were conducted using a Linkam TMS 94 temperature-controlled stage. Since the ends of the fibers were attached to a carrier substrate (Si) via epoxy, increasing the stage temperature induced tensile stress in the fibers due to thermal expansion of the carrier substrate. Therefore, a low ramp rate for the stage temperature was adopted to avoid premature failure of the fibers. Through experimentation, a maximum ramp rate of 1 K/min was used. Each microfiber or nanofiber was individually placed on separate Si carrier substrates. As mentioned, epoxy was used to attach the ends of the microfibers and nanofibers to the substrate. Raman measurements were performed at the center of each fiber and in the direction perpendicular to the fiber direction.

MD simulations of PE nanofibers

Here, MD simulations were used to understand the phase transition phenomena in PE nanofibers. The polymer-consistent force field was used, which can accurately simulate the structural, vibrational, and thermophysical properties (e.g., phase transition temperature) of PE in both isolated and condensed phases. Standard nonequilibrium MD was used to calculate the thermal conductivity of PE structures by adding two Langevin thermostats applied at the ends of the simulation domain to establish a temperature gradient across the sample.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/12/eaax3777/DC1

Supplementary Text

Table S1. Data of the switching ratios of the thermal switches in Fig. 2C.

Table S2. Data of the switching ratios of multiple samples.

Table S3. Thermal conductivity, volumetric heat capacity, phonon group velocity, and phonon life time.

Fig. S1. Determination of G_on and G_off.

Fig. S2. Thermal conductance measurement of a PE microfiber in two heating/cooling cycles.

Fig. S3. Heat flow versus temperature bias at different heating rates.

Fig. S4. Multiple temperature sweeps of a PE nanofiber.

Fig. S5. The vibrational power spectra at three wave vectors before and after the phase transition of crystalline PE nanofibers.

Fig. S6. Thermal conductivity of PE from 300 to 500 K.

Fig. S7. Spectral energy density of PE at different k-points.

Fig. S8. Phonon dispersion and group velocity of PE.

Fig. S9. Volume as a function of temperature when fibers are under stretching stress.

Fig. S10. Thermal contact resistance between the PE nanofiber and one suspended island as a function of the axial thermal conductivity of the PE nanofiber.

Fig. S11. The height map of a suspended nanofiber measured using atomic force microscopy.

Fig. S12. Raman spectra in the temperature range from 300 to 420 K.