Ordered colloidal clusters constructed by nanocrystals with valence for efficient CO₂ photoreduction

Anisotropic nanocrystals express “valence” when assembling into functional colloidal clusters, which demonstrate high catalytic activity.

Abstract

The ability to construct discrete colloidal clusters (CCs) as complex as molecular clusters is limited due to the lack of available colloidal building blocks and specific directional bonds. Here, we explore a strategy to organize anisotropic Prussian blue analog nanocrystals (NCs) toward CCs with open and highly ordered structures, experimentally realizing colloidal analogs to zeolitic clathrate structures. The directional interactions are derived from either crystallographic or morphological anisotropy of the NCs and achieved by the interplay of epitaxial growth, oriented attachment, and local packing. We attribute these interparticle interactions to enthalpic and entropic valences that imitate hybridized atomic orbitals of sp³d² octahedron and sp³d³f cube. Benefiting from the ordered multilevel porous structures, the obtained CCs exhibit greatly enhanced catalytic activity for CO₂ photoreduction. Our work offers some fundamental insights into directional bonding among NCs and opens an avenue that promises access to unique CCs with unprecedented structures and applications.

INTRODUCTION

Structural, chemical, and physical natures of materials depend primarily on the state and degree of aggregation. Clusters, namely, finite aggregate systems encompassing as few as two to thousands of particles, provide platforms to explore novel properties and investigate transitional phenomena bridged between single particle and condensed matter (1). In the past decades, we have witnessed the flourishing of molecular clusters, particularly those with atomic precision [fullerene (2), “magic size” metal clusters (3), and supramolecular cages (4)] as well as the assembly of these clusters (5, 6). The cluster concept also bewitches nanoscientists to program the assembly of colloidal building blocks into discrete structures at multiple levels to rival the complexity of molecular clusters (7–16). The fascination of this field comes from the ability to access not only aesthetic structures by precisely manipulating the placement of each specific component but also the exotic properties. For instance, strong magnetic and Fano-like plasmon resonances can emerge in close-packed colloidal clusters (CCs) (8). However, the CCs remain in the infancy stage, whereas a wide spectrum of relatively infinite colloidal assemblies (17), such as dense packings (18, 19), superlattices (20–24), and mesoscale supercrystals (25, 26), has been made. Recent advances in the fabrication of CCs are limited to three-step approaches based on silica or polystyrene spheres: synthesize, functionalize, and then assemble these building blocks (27). Some of these approaches are engaged with templates (12) or external force fields (14–16). Exploring building blocks with other structural features (composition or shape) to build sophisticated CCs in simplified routes is highly challenging but promising to enrich the synthetic methodology and extend the potential applications, thus pushing the frontiers of this field. Furthermore, high yield of uniform CCs is also difficult but desirable for the next level of assembly (11, 27).

The key to constructing complex colloidal assemblies lies in the ability to build highly directional interactions among building blocks (28). One innovative means is to create anisotropy in colloids to express “valence” (10, 29), inspired by a chemistry concept established to depict the directional assembly behavior of atoms and molecules. This strategy of concept translation from atomic to colloidal regime is conceptually simple, yet challenging to realize. In general, decorating anisotropic patches, such as deoxyribonucleic acid (DNA) strands (10), sticky spots (30), or hydrophobic domains (31), on the surface of colloids could deliver enthalpic valence. This definition arises from the fact that such directional attraction among the colloids, for example, DNA hybridization, can minimize the enthalpy of the systems. A complementary concept to the enthalpic valence is the entropic valence, which concerns the realization of oriented colloid assembly through the anisotropic shape-induced entropy maximization (32–35). Therefore, both of these two valences can describe the specific connectivity of the colloidal building blocks and predict the geometric motifs of the resulting structures, yet from different thermodynamic considerations. The combination of these two valences is expected to provide opportunities for enhancing particularly desired particle alignment or produce competitive forces that may give rise to structures of high complexity (34). However, compelling demonstrations of this valence combination in the colloidal assembly are still rare (36, 37).

Here, we demonstrate a facile one-pot synthesis of highly uniform CCs with a precise number of colloids and the feasibility of assembly of these CCs into a larger dimension. Specifically, we directionally arrange Prussian blue analog (PBA) nanocrystals (NCs) into three-dimensional (3D) superstructures that are ordered, cube symmetric, and single crystalline, with a high degree of similarities to those complex supramolecular clusters within the proposed zeolite structures. Comprehensive investigations allow us to recognize unique enthalpic and entropic valences of the NCs that mimic atomic multivalences derived from sp³d² and sp³d³f hybridized orbitals. Directional assembly of NCs can be achieved by either a combination of these two valences or an exclusive usage of one of them. Also, we show that PBA CCs can transform to corresponding oxide CCs with preserved architectures but hollow interior by a simple thermal treatment. When used as the catalysts for carbon dioxide (CO₂) photoreduction, PBA and oxide CCs exhibit promising activities and structure-dependent catalytic properties.

RESULTS

Characterization of the PBA CCs

X-ray powder diffraction (XRD) pattern and energy-dispersive x-ray spectroscopy (EDX) spectrum reveal that the product is Co-Fe PBA with a typical face-centered cubic (fcc) structure (fig. S1) and rich alkali cations are embedded in the molecular framework (fig. S2). Highly uniform particles with an average size of ca. 400 nm and cubic architecture can be observed from a field-emission scanning electron microscopy (FESEM) overview image (fig. S3). Each particle is a discrete cluster constructed of smaller nanoparticles (NPs), hereafter denoted as CC-1. Closer FESEM inspection and corresponding schematic models of representative particles from different directions (Fig. 1, A to F) show the distinctive architectural features as follows: (i) A typical CC-1 particle comprises precisely eight truncated cuboctahedron-shaped components with 200 nm in size that are arranged at the corners of a cube; (ii) each nanoscale truncated cuboctahedron (NTC) acts as a tritopic building block (4) to attach orderly toward neighboring NTCs; and (iii) the void space makes each CC-1 particle a distinguishable open superstructure. The architectures detected by the FESEM technique (Fig. 1, A, C, and E) can also be found in transmission electron microscopy (TEM) images from similar orientations (Fig. 1, G, I, and K), further confirming that the NTC-knitted CC-1 particles have open 3D structures. These superstructures appear as single crystals, as evidenced by the selected-area electron diffraction (SAED) patterns (Fig. 1, H, J, and L). The slight arcs observed in the diffraction spots indicate a nearly perfect crystallographic alignment for the attached NTCs. An integrated analysis of all the experimental data above allows us to confirm that the NTCs are dominated by 6 {100}, 12 {110}, and 8 {111} facets that correspond to octagon (Fig. 1B), tetragon (Fig. 1D), and hexagon (Fig. 1F), respectively, in conformity with an fcc crystal habit. Therefore, these NTC single crystals establish ordered connection via a face-to-face ({100} facets) attaching manner. We notice that the architectural features of CC-1, including the geometry of the building blocks and topological structure, share high similarities with those of the Linde Type A (LTA) zeolitic structure. As can be seen in Fig. 1 (M to O), supramolecular α-cage in the LTA unit cell also presents a geometry of truncated cuboctahedron (symbol: [4¹²6⁸8⁶]). In a (2 × 2 × 2) supercell, eight α-cages assemble into the cubic supramolecular framework by sharing T₈O₈ (T = Al/Si) rings. A further comparison between CC-1 and the supramolecular framework is illustrated in Fig. 1P. The void space within a CC-1 particle is shaped by a combination of one truncated octahedron and six cubes. This unique structural geometry is also similar to that of the compensated cage for the α-cage assembly within the LTA clathrate.

Fig. 1. Identification of Co-Fe PBA CC-1.

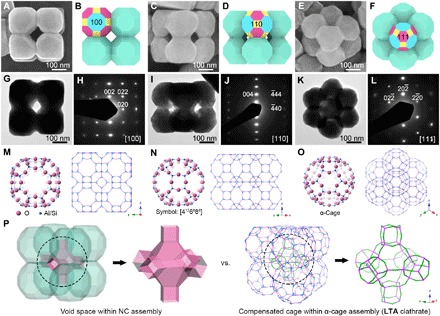
(A, C, and E) FESEM images, (B, D, and F) schematic models, (G, I, and K) TEM images, and (H, J, and L) SAED patterns of typical CC-1 particles from three directions of (A, B, G, and H) [100], (C, D, I, and J) [110], and (E, F, K, and L) [111]. Specific colors in the schematic models: blue, {100} facets; yellow, {110} facets; magenta, {111} facets. (M to O) Molecular frameworks of the LTA zeolite structure represented from different directions. The unit cell represented by the “ball & stick” model shows a supramolecular architecture of the α-cage. The “stick” models show a (2 × 2 × 2) supercell, displaying a typical LTA clathrate assembled from the α-cage building blocks. Na atoms and H₂O molecules are omitted for clarity. (P) Comparison of the architecture between CC-1 and LTA clathrate.

By using hexadecyltrimethylammonium bromide (CTAB) into the reaction system, we can access another type of ordered CCs, hereafter denoted as CC-2. The product is also a Co-Fe PBA material, and each piece of the particles contains a greater number of NPs that are displayed as a porous framework architecture (figs. S4 and S5). Therefore, CC-2 has not only micropores constructed by the molecular framework in PBA NCs but also ordered macropores in the NC-assembled colloidal framework, endowing it as a multilevel porous material (fig. S6) (38). The single crystal feature of CC-2 (fig. S7A) implies that the NC building blocks surprisingly accommodate the same crystallographic orientation even when they are registering into a larger domain. Figure 2 (A to C) exhibits the CC-2 structures from different directions by FESEM images and corresponding schematic models. The primary components in CC-2 are nanoscale truncated octahedrons (NTOs) with 200 nm in size and enclosed by six tetragons ({100} facets) and eight hexagons ({111} facets). The attachment facets of the NTOs within CC-2 are also the {100} facets. We can occasionally find eight-NTO constructed CCs in the sample of CC-2 (fig. S7, B to D), suggesting that this structure could be the secondary building blocks to fabricate the frameworks of CC-2. Low-dimensional crystallographic defects are detected in CC-2, such as dislocations (Fig. 2, A and B) and vacancies (Fig. 2C), similar to those observations for NC superlattices (17). When comparing the architectures of CC-2 with the sodalite (SOD) zeolitic clathrate (Fig. 2, D to F), one can easily find their resemblance. For example, the building blocks of the SOD clathrate are also shaped as the truncated octahedron (β-cages, symbol: [4⁶6⁸]). This geometry is special as it makes the shape of the compensated cage within β-cages assembly the same, similar to that of the void space within CC-2 (Fig. 2G). Although CC-1 and CC-2 have different structures concerning the assembly dimension and the shape of building blocks, they share many similarities (table S1). For instance, they both own primitive cubic (pc) unit cell when regarded as crystals and demonstrate the same type of topological networks. The edge lengths of the unit cell for these two samples are both around 200 nm, as revealed by small-angle x-ray scattering (SAXS) measurements (fig. S8), which are in good agreement with the aforementioned FESEM observations.

Fig. 2. Identification of Co-Fe PBA CC-2.

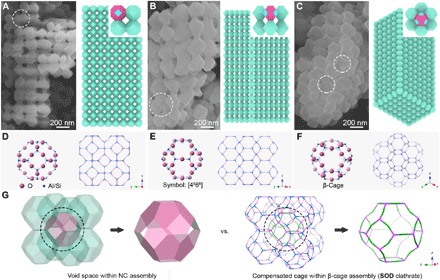
(A to C) FESEM images and corresponding schematic models of the typical CC-2 particles from different directions. Specific colors in the schematic models: blue, {100} facets; magenta, {111} facets. Some defects in the colloidal superlattices are located by white dotted circles in the FESEM images. (D to F) Molecular frameworks of the SOD zeolite structure represented from different directions. The unit cell represented by the “ball & stick” model shows a supramolecular architecture of the β-cage. The “stick” models show a (2 × 2 × 2) supercell, displaying a typical SOD clathrate assembled from the β-cage building blocks. Na atoms and H₂O molecules are omitted for clarity. (G) Comparison of the architecture between CC-2 and SOD clathrate.

Formation process and mechanism

To gain insights into the formation mechanism of the Co-Fe PBA CCs, we first monitor reaction products at different stages of CC-1 (fig. S9). We observe that nanocubes with truncated corners first form. As the reaction time goes, small NCs preferentially generate on the corners of the nanocubes as eight satellites symmetrically distributed around each core. These satellite NCs (SNCs) would then gradually grow up to be larger and anisotropic. They orderly get closer along the edges of the cores and then attach to form cubic architectures by taking advantage of the anchoring effect supplied from the cores. Simultaneously, these cores would be dissolved and completely removed, transforming the core@satellite structures to open CCs. Eventually, the cubic CC-1 is obtained as the SNCs ripen to NTCs (route I in Fig. 3A). XRD patterns show that CC-1 and nanocubes can be assigned to the K₂CoFe and Co₃Fe₂ phase, respectively (fig. S10). It indicates that a phase transition occurs during the nanocube-to-CC evolution process, accompanied with which the amount of alkali ions increases and the cyanide-related bonds vary, as revealed by the EDX (figs. S1B and S11) and Fourier transform infrared (FTIR) spectra (fig. S12 and table S2), respectively.

Fig. 3. Schematic illustration of the formation of Co-Fe PBA CCs.

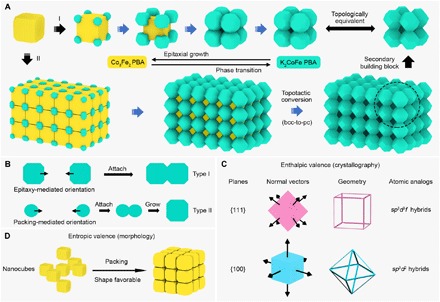
(A) Routes for the formation of CC-1 (route I) and CC-2 (route II) with the structural evolution and phase transition. (B) Two pathways toward the orientation of the SNCs for the following attachment. (C) Illustration of the enthalpic valence of NCs and their atomic analogs. (D) Illustration of the entropic valence of NCs.

Control experiments imply that the addition of a proper amount of sodium dodecyl sulfate (SDS) in this system is important for the formation of well-defined CCs (fig. S13). With the absence of the SDS, nanoframes rather than CCs are obtained due to the complete coalescence of SNCs that grow on both the edges and corners of the cores (fig. S14) (13). This means that the SDS might prefer to adsorb on the edges of the PBA materials, while the citrate ions have been indicated to cap on the side faces (13). As a result, only the corners of the cores are highly reactive since they are uncovered, and these are the regions available for nucleation of the SNCs. Regarding the SNCs, their geometry would be shaped as the NTC by the site-selected adsorbed SDS. Moreover, the high viscosity of the SDS molecules could reduce the mass transport rate to avoid the full fusion of the SNCs. We also find that the SDS could be replaceable by other anionic surfactants to fabricate CC-1, but not by nonionic or cationic ones (fig. S15). These results further indicate the crucial role of the SDS-type anionic surfactants in regulating the growth kinetics of the nanostructures in the present system. In PBA materials, one can grow on another via epitaxial growth (EG) due to their similar crystal structures (39). In our case, the acceptable lattice mismatch between the K₂CoFe and Co₃Fe₂ phase (for example, 2.1% for the {111} planes) grants the feasibility of EG (40). Besides, the morphological and crystallographic alignments (fig. S16) of the K₂CoFe SNCs and the Co₃Fe₂ core further suggest the SNCs epitaxially grow on the corners of the cores along the <111> directions. The epitaxy here leads to a template-confined assembly of the anchored SNCs for the subsequent attachment. After the attachment, a further coarsening could extend the fusing interface of the adjacent SNCs to make a robust architecture. Apparently, free-standing NTCs rather than NTC-assembled CCs would be obtained if there is no attachment involved. TEM characterizations show that the lattice fringes around the attachment region of adjacent NTCs share a common crystallographic orientation in a continuous manner and have an identical interplanar spacing (fig. S17). These are typical features from the result of oriented attachment (OA) (41). In conventional OA processes, the NCs are free-floating in the solution and will undergo successive approach and orientation procedures by movement and rotation, respectively, to find an optimal configuration before attaching (41). In our case, the “optimal configuration” is achieved instead by the epitaxy. Although the anchored SNCs are under physical (movement and rotation) constraints, epitaxy impels these SNCs to align crystallographically from their initial formation to the final attachment (type I in Fig. 3B). Besides, the anisotropy of the nanocube cores guarantees that the SNC approaches along the directions parallel with the edges of the cores (<100> orientations) and can then attach by the prealigned {100} facets. Therefore, the assembly pathway of the NCs in this OA process is quite different from the conventional one. The structural evolution of the SNCs is also found to be interesting. They are asymmetric when epitaxially growing on the cores (fig. S18) but are developed to be symmetric and solid NTCs after the removal of the core (fig. S19). In a few cases, the final NTCs are ³/₄ solid but ¹/₄ hollow, manifesting unprecedented architectures with symmetric exterior and asymmetric interior (fig. S20).

Experimental investigations for the formation of CC-2 indicate that it holds similar features in structure evolution to that of CC-1 (figs. S10, S12, and S21): the phase transition and the epitaxy-mediated OA. Furthermore, we observe a short-range local packing of the nanocube cores in a face-to-face ({100} facets) manner at the early stage of the reaction (fig. S21B). The packing of the cores creates both the crystallographic orientation and sufficient proximity to the SNCs for their upcoming OA (type II in Fig. 3B), whose assembly pathway is like neither of the aforementioned epitaxy-mediated nor conventional OA. As the reaction time goes, this packing-mediated OA process will take place on the SNCs from different but adjacent cores along the <100> directions while leaving the cores separated with an observable interparticle gap (fig. S22). After further growing, these attached SNCs will develop to be larger units to participate in the following epitaxy-mediated OA to form a body-centered cubic (bcc) superlattice (route II in Fig. 3A). Eventually, CC-2 is obtained when the cores are totally removed, accompanied by a bcc-to-pc topotactic conversion of the superlattice (23). Therefore, the framework architecture of CC-2 can also be regarded as the assembly of the eight-NTO constructed CCs (secondary building blocks in Fig. 3A and fig. S7, B to D) by sharing NTOs, further confirming our inference mentioned above. Note that this eight-NTO constructed CC is a topological equivalence of CC-1 (Fig. 3A). The observed crystallographic defects in CC-2 (Fig. 2, A to C) could be originated from some assembly imperfections during the packing process (fig. S23).

“Valence” delivered by NCs for assembly

On the basis of the above observations, we here provide an attempt to discern the valence from the NC building blocks and elucidate how it governs the directional assembly of the NCs for particular configurations in the ordered CCs. Unlike the existing enthalpic bonds that rely on the surface modification of colloids (27), we propose that the enthalpic valence here concerns the anisotropy in crystallography, which dictates the preferred orientation of the NC assembly (Fig. 3C). The aforementioned EG and OA should then be two typical processes that express the directional interactions by the enthalpic valence of NCs (42). To be specific, the normal vector geometry of {111} planes is a cube, mimicking that of the sp³d³f hybrids of atomic valence. Therefore, the nanocube cores can offer an enthalpic valence with a cubic symmetry for the directional organization of the SNCs on their corners, realized by the EG along the <111> directions. On the other hand, the normal vectors of {100} planes constitute an octahedral geometry that is analogical to the atomic valence derived from sp³d² hybrids. Using this enthalpic valence, the SNCs can assemble directionally through the OA along the <100> directions. The {100} facets of the SNCs that fail to participate in the OA can be regarded as those pairs of nonbonding electrons in the atomic regime. For the enthalpic valence in this work, the inherent preferences of the directional binding motifs are encoded in certain building blocks depending on the crystal system. With the well-established formulas for calculating interplanar angles in hand, one can predict the relative angle for an incoming building blocks in the enthalpy-involved assembly if the specific crystal planes are given and vice versa. Another type of the NC valence is the morphology-created entropic valence, which means that the anisotropic shape of the NCs contributes to the directional packing (Fig. 3D). Note that although the packing here is short range, it shares the same rule as that of dense packing (33, 34). In the synthesis of CC-2, the entropic force, which relies on the CTAB micelle-induced depletion interactions (43), drives the nanocube cores to maximize alignment of their six {100} facets, demonstrating an octahedron-configurational valence with similar operations to those of the enthalpic one (Fig. 3C). The binding preference of the entropic valence could be predicted by using the enthalpic valence as reference (table S3). One can also find clues for the entropic valence from some recent theoretical findings, where the packing configurations of the NPs are investigated and the attractive force is quantified (32–34).

We can conclude that single crystals from the same material or materials with matched lattice is the key requirement in our work for the NCs that can demonstrate the enthalpic valence, regardless of whether they have distinguishable shapes. In contrast, aside from the single crystals, those NPs in polycrystalline or amorphous status could theoretically embody the entropic valence as long as they have anisotropic shapes (44). Nevertheless, the strategy we demonstrate here, that is, the employment of anisotropy-shaped single crystals, should be an effective approach to access a combination of the enthalpic and entropic valences of colloids to create sophisticated and ordered structures.

Derivatives of the PBA CCs

By simple annealing in air, we convert the Co-Fe PBAs to corresponding Co-Fe mixed oxides (hereafter denoted as Co-Fe-O), as revealed by the XRD and EDX data (figs. S24 and S25). FESEM images show that the uniform, cubic, cluster-like structures of CC-1 can be well retained after the annealing (Fig. 4, A and B, and fig. S26A). Notably, we observe a hollow interior within the structures from the TEM images (Fig. 4, C and D, and fig. S26, B and C), thus acquiring Co-Fe-O hollow CCs (HCC-1). The concave surface seen on the HCC-1 particles (Fig. 4B) suggests that the hollowing mechanism could be driven by a heterogeneous contraction, where mass and volume lost during the thermal treatment (45). Similar with HCC-1, Co-Fe-O HCC-2 inherits all the external architectural features of its mother structure (Co-Fe PBA CC-2), for example, the macroporous framework structures, yet exhibits a hollow interior (figs. S24, S25, and S27).

Fig. 4. Morphology and structural characterization of Co-Fe-O HCC-1.

(A and B) FESEM and (C and D) TEM images.

CO₂ photoreduction performance

Converting CO₂ to value-added carbon products, particularly by a reduction reaction using solar energy, represents a promising solution for the increasing energy demand and global warming (46–53). Reticular materials, for example, metal-organic frameworks (MOFs), have recently been emerging as ideal platforms for CO₂ photoreduction. This is because their microporous structures are beneficial to the CO₂ capture and the open transition-metal sites (Co, Ni, or Cu) act as the CO₂ activators (54). PBAs, a type of reticular materials, however, have limited success as catalysts for the CO₂ photoreduction thus far. Motivated by this limitation, we evaluate the catalytic performance of Co-Fe PBA CC-1 in a visible light–driven CO₂ reduction system (λ ≥ 400 nm), where [Ru(bpy)₃]Cl₂·6H₂O (abbreviated as Ru, bpy = 2′2-bipyridine) and triethanolamine (TEOA) are used as the photosensitizer and sacrificial agent, respectively (55). Figure 5A displays the performance of the CO₂ catalysis under various reaction conditions. Impressively, the normal reaction (Fig. 5A, column 1) can afford a high CO production rate of 11,700 μmol h⁻¹ g⁻¹ with a good selectivity of 77.5% over competitive H₂ generation. No hydrocarbon products are detected from this system. The apparent quantum efficiency of Co-Fe PBA CC-1 is determined to be 0.97% under monochromatic light irradiation of 420 nm, which is comparable to those values in recent reports (56, 57). Without CC-1 (Fig. 5A, column 2), the evolution of CO reduces significantly. This result suggests that CC-1 can efficiently catalyze the CO₂-to-CO conversion by a considerable contribution to the activity. The inactivation of the CO₂ reduction with the absence of Ru or light irradiation (Fig. 5A, columns 3 and 4) proves that this system is a photosensitized process. Only H₂ yields but no CO when replacing CO₂ with N₂ to perform the reaction (Fig. 5A, column 5), which indicates that the generated CO is from the CO₂ substance. By comparison of the variation tendency of gas production and the optical absorption spectrum of Ru in Fig. 5B, we can further conclude that the CO₂ reduction is driven by the photons harvested by Ru rather than by CC-1 (fig. S28). The time courses show that CO can be continuously produced to reach a yield of 13,300 μmol g⁻¹ in a 2-hour measurement (Fig. 5C). The gradual activity loss of the system after 1 hour could be attributed to the photobleaching of the Ru photosensitizer (58). The photostability tests indicate that the Co-Fe PBA CC-1 catalyst is stable for the CO₂ photoreduction reaction (fig. S29). Moreover, FESEM and XRD analyses for the Co-Fe PBA CCs further reveal their high structural stability, even after the photocatalysis test or long-time storage in air (figs. S30 and S31). Figure 5D summarizes the catalytic performance of Co-Fe PBA CC-1 and other catalysts, including Co-Fe PBA NPs (fig. S32), Co-Fe PBA CC-2, Co-Fe-O HCC-1, and HCC-2. It can be seen that the CCs manifest higher CO₂ photoreduction activities than the NPs and the HCCs. In particular, the CO production rate of CC-2 can reach as high as 14,200 μmol h⁻¹ g⁻¹, which is comparable to and even better than some recently reported catalysts for the CO₂ photoreduction (table S4), such as the Co-based MOF (59), the Co₃O₄ platelets (56), and the enzyme/TiO₂ composite (60).

Fig. 5. Photocatalysis for CO₂ reduction.

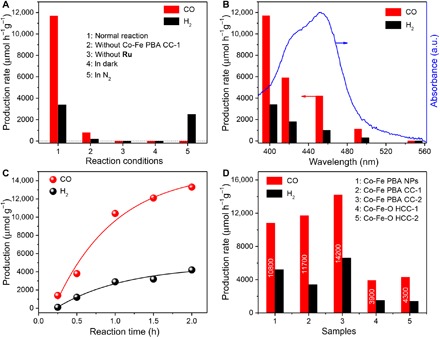
(A) Production rates of CO and H₂ for the Co-Fe PBA CC-1 catalyst under various reaction conditions. (B) Wavelength dependence of the yields of CO and H₂ for the Co-Fe PBA CC-1 catalyst and the light absorption spectrum of the Ru photosensitizer. The wavelength of incident light is controlled by applying appropriate long-pass cutoff filters. a.u., arbitrary units. (C) Evolution of CO and H₂ as a function of reaction time for the Co-Fe PBA CC-1 catalyst. (D) Production rate of CO and H₂ from diverse catalysts.

The photo(electro)chemical (PEC) characterizations are conducted to study the mechanism of the CO₂ photoreduction reaction. The electrochemical analysis (fig. S33) reveals that Co-Fe PBA CC-1 is an n-type semiconductor with conduction band and valence band potentials of around −0.59 and 1.10 V, respectively [versus normal hydrogen electrode (NHE)]. The conduction band potential of Co-Fe PBA CC-1 is negative than the redox potential of CO₂/CO (−0.53 V versus NHE) and positive than the redox potential of Ru(bpy)₃²⁺/Ru(bpy)₃⁺ (−1.09 V versus NHE) (61, 62). As a result, the catalyst is able to meet the thermodynamic requirement to accept the photoexcited electron from the reduced photosensitizer to operate the CO₂-to-CO reduction catalysis (61). Furthermore, the room temperature photoluminescence (PL) shows that the employment of the Co-Fe PBA CC-1 catalyst into the system would cause obviously reduced PL emission (fig. S34). This PL quenching indicates the enhanced separation of the charge carriers, thus demonstrating a favorable charge transfer from the reduced photosensitizer to the catalyst. On the basis of these PEC results, the possible mechanism of the photosensitized CO₂ reduction catalysis is proposed (fig. S35). Under visible light irradiation, the Ru(bpy)₃²⁺ photosensitizer is motivated to the excited state Ru(bpy)₃^2+*, which will be reductively quenched by the electron donor TEOA to form the reduced state Ru(bpy)₃⁺. Afterward, the excited electrons of the reduced photosensitizer would delocalize and transfer to the porous CCs that act as cocatalysts (51), and then reduce the adsorbed CO₂ molecules to form CO. During this process, the electron donor TEOA is oxidized to aldehydes (fig. S36) (63), thus accomplishing the redox cycle of the CO₂ photoreduction catalysis.

DISCUSSION

It should be mentioned that no obvious FTIR signals of the alkane chains (coming from the SDS and CTAB) can be detected for the PBA CCs (fig. S12). Thus, the influence of the possible organic surfactant residue on the CO₂ photoreduction performance of the catalysts could be neglected. We observe that the PBA materials have an order of magnitude higher catalytic activity than the oxides regarding the CO production rate, which could be attributed to the catalytically friendly structure and chemical environment within the PBAs. The N₂ adsorption measurements show that the PBA CCs have higher Brunauer-Emmett-Teller (BET) surface areas than their oxide derivatives (fig. S37). This result confirms that the molecular frameworks of PBAs could provide open channels for the migration of the CO₂ to access more Co sites within the materials (54) rather than just on the surface as those for the oxides (56). Besides, the active Co sites are usually coordinated by water ligands in PBAs and may facilitate a proton-coupled electron transfer process (13, 64), which could accelerate the CO₂-to-CO conversion kinetics (58). After the thermal annealing, the molecular frameworks within the PBAs would be destroyed completely, thus greatly reducing the amounts of the open active sites, which may be another reason for the relatively poor photoactivity of the oxides. Among the PBAs, the CCs have better catalytic performance than the NPs. This could be explained by the higher BET surface areas (fig. S37) as well as enhanced CO₂ capture ability (fig. S38) of the ordered macroporous structures of the CCs constructed by the hierarchical assembly of the NCs. Compared with the discrete NPs, a collective effect from the strong interaction of the attached NCs in the assembled structure of the CCs might also help to enhance the catalytic performance. Regarding the PBA CCs, CC-2 shows higher CO₂ photoreduction activity than CC-1, which may be attributed to its higher Co content that would provide more catalytically active sites for the reaction. On the other hand, the CO selectivity calculated from the competitive H₂ evolution of CC-1 (77.5%) is higher than that of CC-2 (68.3%). The exposure of diverse crystal facets with different reactivities on the primary building blocks of CC-1 and CC-2 (that is, NTC versus NTO) might account for this selectivity difference (51). It is believed that enhanced activity and selectivity of the CO₂ photoreduction catalysis may be realized by further optimization of the photoelectronic and textural properties of the CCs.

In summary, we have successfully developed a hierarchical assembly strategy to organize anisotropic NCs toward CCs with open and highly ordered structures, experimentally creating colloidal analogs to complex molecular clusters within zeolites. The number of colloids within an individual cluster can be controlled as precise eight or up to dozens. As a demonstration, the fabrication of Co-Fe PBA and Co-Fe-O CCs extends the diversity of the motifs of colloidal assemblies and the toolbox of available building blocks in terms of composition, shape, and interior (hollow) structure. The directional interactions among NCs are realized by EG, OA, or local packing, where the former two manners are identified as the enthalpic valence, while the latter one is recognized as the entropic valence. The present work provides fundamental insights into directional bonding among NCs that mimic atomic valence, and opens an avenue that promises access to unique CCs by deliberate engineering of these underlying colloidal valences. The established rules here might help to understand the relation between the anisotropy attributes of the NC building blocks and the motifs of their potential assembled structures. In virtue of the multilevel porous structures and the ordered assembly, the Co-Fe PBA CCs exhibit excellent catalytic activity for the CO₂ photoreduction, where the highest CO production rate can reach 14,200 μmol h⁻¹ g⁻¹. We believe that our work will encourage more efforts on the construction of finite and ordered CC systems using anisotropic NC building blocks, where unprecedented materials and structural complexities could be accessible, and new properties can then be contemplated.

MATERIALS AND METHODS

Synthesis of Co-Fe PBA CCs

In a typical synthetic procedure of CC-1, 0.150 g of cobalt(II) acetate tetrahydrate, 0.147 g of trisodium citrate dihydrate, and 1.0 g of SDS were dissolved in 40 ml of deionized (DI) water to form solution A. Potassium hexacyanoferrate(III) (0.132 g) was dissolved in 60 ml of DI water to form solution B. Then, solution B was added into A under magnetic stirring in 15 s. After continuously stirring for 1 min, the obtained mixed solution was heated to 80°C under an oil bath and stirring for 3 hours. The precipitate was collected by centrifugation, washed with DI water and ethanol, and dried at 70°C overnight. The synthesis of CC-2 is similar to that of CC-1, except with the additional 0.5 g of CTAB in solution A, and the mixed solution was aged at 80°C without stirring.

Synthesis of Co-Fe PBA NPs

In a typical synthetic procedure, 0.30 g of cobalt(II) acetate tetrahydrate and 0.588 g of trisodium citrate dihydrate were dissolved in 40 ml of DI water to form solution A. Potassium hexacyanoferrate(III) (0.264 g) was dissolved in 60 ml of DI water to form solution B. Then, solution B was added into A under magnetic stirring in 15 s. After continuously stirring for 1 min, the obtained mixed solution was aged at 80°C for 3 hours. The precipitate was collected by centrifugation, washed with DI water and ethanol, and dried at 70°C overnight.

Synthesis of Co-Fe-O HCCs

In a typical synthesis, the as-prepared Co-Fe PBA CCs were annealed in a muffle furnace at 350°C for 6 hours with a heating rate of 2°C min⁻¹ in air.

Materials characterization

XRD patterns were collected on the Bruker D2 Phaser X-Ray Diffractometer with Ni-filtered Cu Kα radiation (λ = 1.5406 Å) at a voltage of 30 kV and a current of 10 mA. The morphology and structure of the products were characterized using FESEM (JEOL, JSM-6700F) equipped with EDX and TEM (JEOL, JEM-1400/JEM-2010). FTIR spectra were collected using PerkinElmer FTIR spectrometers. SAXS measurements with a wavelength of 0.177 nm were carried out at the beamline BL16B1 in Shanghai Synchrotron Radiation Facility. In each experiment, hundreds of frames of x-ray scattering patterns were collected to monitor the structural evolution with a PILATUS 2M detector (1475 × 1679 pixels and pixel size of 172 μm). The distance between the detector and the sample was set to 5260 mm. N₂ and CO₂ adsorption isotherms were collected on an ASAP2020M apparatus. The samples were degassed in vacuum at 120°C for 4 hours and then measured at 77 K and 0°C to determine N₂ and CO₂ adsorption, respectively. PL spectra of the reaction systems were acquired on Edinburgh Analytical Instruments FL/FSTCSPC920 coupled with a time-correlated single-photo counting system at room temperature under an excitation wavelength of 520 nm. The BAS Epsilon Electrochemical System was used to perform the electrochemical analyses in a three-electrode cell (Pt plate as the counter electrode and Ag/AgCl as the reference electrode). For the Mott-Schottky experiment, the used frequency was 1.0 kHz. Before all electrochemical measurements, the electrolyte (0.2 M Na₂SO₄ solution) was purged with N₂.

Photocatalytic CO₂ reduction

Typically, catalyst (1 mg; for example, Co-Fe PBA CC-1), [Ru(bpy)₃]Cl₂·6H₂O (10 μmol), solvent [5 ml; 2:3 (v/v) H₂O/acetonitrile], and TEOA (1 ml) were added in a gas-closed glass reactor (80 ml in capacity). Then, high-purity CO₂ was introduced to the reactor with a partial pressure of 1 atm. A 300-W Xe lamp with a 400-nm long-pass cutoff filter was used as the light source. During the photocatalytic process, the reaction system was vigorously stirred with a magnetic stirrer. After reaction for a certain time, the generated products were sampled and quantified by an Agilent 7890B gas chromatograph.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/12/eaax5095/DC1

Fig. S1. Characterization of Co-Fe PBA CC-1.

Fig. S2. The molecular framework of the Co-Fe PBA materials.

Fig. S3. FESEM overview image of Co-Fe PBA CC-1.

Fig. S4. Characterization of Co-Fe PBA CC-2.

Fig. S5. FESEM overview image of Co-Fe PBA CC-2.

Fig. S6. Schematic models of Co-Fe PBA CC-2.

Fig. S7. TEM characterization of Co-Fe PBA CC-2.

Fig. S8. SAXS data of the samples.

Fig. S9. FESEM and TEM images of the intermediate products for the synthesis of Co-Fe PBA CC-1.

Fig. S10. XRD patterns of different products.

Fig. S11. EDX spectrum of the nanocubes.

Fig. S12. FTIR spectra of different samples.

Fig. S13. FESEM images of the control samples with different amounts of SDS.

Fig. S14. FESEM images of the intermediate products for the synthesis of the sample with the absence of SDS (as seen in fig. S13A).

Fig. S15. FESEM images of the control samples with different surfactants.

Fig. S16. TEM and SAED images of a typical core@satellite superstructure obtained at the reaction time of 45 min for the synthesis of Co-Fe PBA CC-1.

Fig. S17. Characterization of a typical Co-Fe PBA CC-1 particle.

Fig. S18. Characterization of some isolated SNCs that fall off the core at the reaction time of 1 hour for the synthesis of Co-Fe PBA CC-1.

Fig. S19. TEM images of the typical particle obtained at different reaction times for the synthesis of Co-Fe PBA CC-1.

Fig. S20. TEM images of some occasionally observed particles in the sample of Co-Fe PBA CC-1.

Fig. S21. FESEM images of the intermediate products for the synthesis of Co-Fe PBA CC-2.

Fig. S22. Characterization of the core@satellite superstructures obtained at the reaction time of 45 min for the synthesis of Co-Fe PBA CC-2.

Fig. S23. A FESEM image shows the assembly imperfections in the packing of the core@satellite superstructures.

Fig. S24. XRD patterns of the Co-Fe-O HCCs that derived from the Co-Fe PBA CCs.

Fig. S25. EDX spectra of the Co-Fe-O HCCs derived from the Co-Fe PBA CCs.

Fig. S26. Characterization of Co-Fe-O HCC-1.

Fig. S27. Characterization of Co-Fe-O HCC-2.

Fig. S28. Light absorption spectrum of the Co-Fe PBA CC-1 catalyst.

Fig. S29. Stability tests of the Co-Fe PBA CC-1 catalyst for CO₂ photoreduction.

Fig. S30. Characterizations of the Co-Fe PBA CC-1 catalyst after the photocatalysis.

Fig. S31. Characterization of the Co-Fe PBA CCs after storage as powder in air for more than 6 months.

Fig. S32. Characterization of the Co-Fe PBA NPs as a catalyst without colloidal assembly.

Fig. S33. Electrochemical measurements of the Co-Fe PBA CC-1 catalyst.

Fig. S34. Room temperature PL spectra of the reaction systems with and without the Co-Fe PBA CC-1 catalyst.

Fig. S35. Proposed mechanism for the photocatalytic conversion of CO₂ to CO.

Fig. S36. Liquid chromatography–mass spectrometry analyses of the oxidation species.

Fig. S37. N₂ adsorption measurements of diverse catalysts.

Fig. S38. CO₂ adsorption isotherms of Co-Fe PBA CC-2 and Co-Fe PBA NPs.

Table S1. Some parameters of the Co-Fe PBA CCs.

Table S2. The position of FTIR peaks of the samples and their assignment.

Table S3. Similarities of the entropic and enthalpic valence of NCs and their operations in the assembly.

Table S4. Comparison of the photocatalytic CO₂ reduction performance of the Co-Fe PBA CCs prepared in this work with some recently reported advanced catalysts.