Significance
Contrary to our intuition, even a single-component substance may have more than 2 liquid states. The transition between them is called “liquid–liquid transition (LLT).” Recently, we have accumulated evidence for the presence of LLT. This transition may have a strong influence on crystallization, if it exists below the melting point of the crystal. Here we show that crystal nucleation rate can indeed be enhanced by many orders of magnitude near the spinodal point of LLT. This may be used not only for the control of crystalline morphology but also for searching LLT in a metastable state, which is hidden behind crystallization. Our finding also sheds light on how crystallization and other liquid-state transitions can be coupled.
Keywords: crystal nucleation, critical-like fluctuations, liquid–liquid transition, interface tension, order parameter
Abstract
Crystallization is one of the most familiar and fundamental phase transition phenomena. There is a possibility that crystallization may be enhanced by critical-like fluctuations associated with another nearby phase transition if the order parameter of the former is coupled to that of the latter; however, the mechanism of such order parameter coupling and its generality remain elusive due to the lack of experimental studies. Here we report experimental evidence for a nontrivial coupling between crystallization and liquid–liquid transition (LLT) for a molecular liquid, triphenyl phosphite. We find that the crystal nucleation frequency is drastically enhanced by short-time preannealing near but above the spinodal temperature of LLT. By successfully separating the thermodynamic and kinetic factors governing crystal nucleation, we show that this enhancement is induced by the lowering of the crystal–liquid interfacial energy due to the presence of critical-like order parameter fluctuations. This finding may be regarded as a fingerprint of the presence of LLT below the melting point. Thus, it may allow us not only to control the crystal nucleation frequency by LLT but also to unveil LLT hidden behind crystallization. This enhancement of nucleation frequency by critical-like fluctuations of another ordering phenomenon may be general to a variety of combinations of phase transitions. It would provide a way to control a crystal grain structure, which is a crucial control factor of mechanical and thermal properties of crystalline materials.
Crystallization is a nonequilibrium transformation process from a disordered liquid state to an ordered crystalline state. The resulting final crystalline structure is basically controlled by 2 kinetic factors, the nucleation frequency and the growth speed of crystals. The phenomenon of crystallization and its control are important not only in condensed matter physics but also in biology and in many industrial applications, including the phase-change memory of calcogenides, nanocrystalline materials for magnetic applications, protein crystallization, and cryopreservation. After long and intensive research, the essential physics of nucleation and growth of crystals in a macroscopic scale has been reasonably understood in the framework of the classical nucleation theory (CNT) (1–5); however, even now, there still remain many fundamental open issues such as many orders of magnitude differences in the crystal nucleation rate between experiments and numerical simulations (see, e.g., refs. 6–10).
According to CNT (1–4, 6), the crystal nucleation frequency is given by
| [1] |
where is a prefactor, is the characteristic time of material transport, is the Boltzmann factor, and is the temperature. Here is the free-energy barrier for the formation of a critical nucleus, and it is a key thermodynamic factor governing . According to CNT, assuming the spherical shape of a nucleus, the critical nucleus size is estimated as , where is the chemical potential difference between the supercooled liquid and the crystal per molecule, is the interfacial tension between them, and is a volume per molecule. Then, is obtained as
| [2] |
Note that is an increasing function of the degree of supercooling , where is the melting point. We may assume that near , where is the enthalpy of fusion per molecule. Note that is often assumed to be temperature-independent in CNT. In reality, it may depend on temperature and nucleus size (6, 8, 11). On the other hand, the kinetic factor governing is , which is the characteristic time of material transport controlling crystallization. We note that the nucleation kinetics is controlled not by the viscosity (or rotational diffusion) but by the translational diffusion (see, e.g., refs. 12–14). We stress that the decoupling in the temperature dependence between the viscosity and the translational diffusion coefficient becomes more and more significant with an increase in , which is known as the violation of the Stokes–Einstein relation. After nucleation, a crystal grows with the growth velocity given by
| [3] |
where is a constant. It is worth mentioning that is independent of . Unlike the nucleation frequency, experimental results of the crystal growth speed are rather well described by Eq. 3, (15).
The liquid-to-crystal transformation can be described by the change in the relevant order parameters. The most obvious important order parameter is translational order (or density). CNT assumes that a crystal nucleus has exactly the same structure as the bulk equilibrium crystal and the only difference between the nucleus and the bulk crystal is the surface energy contribution. Since the breakdown of orientational symmetry is automatically accompanied by that of translational symmetry upon crystallization, CNT completely ignores the role of the orientational ordering. Recently, however, the important role of bond orientational order has been revealed on the basis of numerical (12, 16–19) and experimental (20) studies of crystallization. More specifically, precursors with high crystal-like bond-orientational order, which are spontaneously formed as fluctuations in a supercooled liquid, reduce the liquid–crystal interfacial tension and thus promote crystal nucleation: The friendliness of the precursor structure to the crystal one controls the ease of crystallization. Although the presence of an extra order parameter other than translational order parameter is not considered in CNT, these studies have shown that, even for ordinary crystallization, a coupling between translational and orientational orderings has a drastic impact on crystal nucleation. In general, this scenario should work if there is a coupling between crystallization and another type of ordering phenomena such as phase separation (21) and liquid–liquid transition (LLT).
In a seminal paper, ten Wolde and Frenkel (22) showed that density fluctuations near a gas–liquid critical point in a supercooled state can significantly increase the crystal nucleation frequency by many orders of magnitude. More specifically, they studied, by using numerical simulations, how the presence of the gas–liquid critical point of a colloidal suspension affects crystal nucleation. In the first stage of the process, density fluctuations grow without accompanying translational ordering. Then, in the next stage, crystal ordering proceeds selectively in high-density regions. They showed that this 2-step kinetic pathway drastically reduces the liquid–crystal interfacial tension, because of preferential wetting of higher-density regions to the crystal, indicating that the presence of critical density fluctuations drastically enhances the nucleation frequency of colloid crystals (22). Then this scenario was supported theoretically (23–25). Here we note that the underlying physics is the same between the impact of density fluctuations linked to a gas–liquid criticality and that of the above-mentioned bond-orientational order fluctuations in a supercooled liquid.
This problem was also studied experimentally in protein solutions, and the enhancement of the nucleation rate was indeed observed near the binodal line (26, 27); however, the maximum of the nucleation rate is located several degrees above the spinodal temperature , but not at . Considering that the above-described thermodynamic argument at the mean field level predicts the nucleation frequency to be maximized at , the deviation of the maximum from has cast some doubt on the origin of the crystal nucleation enhancement. For example, this discrepancy might be explained by the slowing down of the kinetics, or the increase in : An increase in the viscosity of dense liquid droplets may decrease the nucleation rate (26, 27). Possible glassiness of the intermediate metastable phase was also suggested (28). In addition, the role of the temperature dependence of may not be ruled out. At this moment, thus, there is no firm consensus on the origin of the discrepancy (see, e.g., ref. 18 for a review). For elucidating the very origin of the enhancement, thus, it is crucial to disentangle the thermodynamic ( and ) and kinetic factors ().
The key to crystal nucleation enhancement due to criticality is the reduction of the crystal–liquid interfacial tension due to fluctuations of an extra order parameter in the liquid state. For this to happen, the order parameter with criticality must be coupled to crystalline order parameter(s). Then the next questions are how strong the coupling is and how large the order parameter fluctuations are. Criticality is crucial for the realization of large amplitude and long correlation length of the fluctuations. This consideration leads to a conclusion that this physical mechanism of crystal nucleation enhancement should be valid universally to any phase ordering, provided that it is located below the melting point and fluctuations of its order parameter efficiently reduce the crystal–liquid interfacial tension .
Here we take, as such an example of phase-ordering phenomena, LLT that is a phase transition between multiple liquid states in a single-component liquid (2). Recently, there are many pieces of experimental and theoretical evidence for the existence of LLT in single-component systems (2, 29–35). Polyamorphic transitions were suggested for water (34). Furthermore, the existence of LLT has also been suggested for important atomic elements, such as Si, C, S, and Se (29, 31, 33). However, for many of these liquids, including water, LLT is expected to occur in their metastable supercooled liquid states, often far below (29, 33, 34); that is, LLT is hidden behind crystallization. This makes experimental investigations of the phenomena quite challenging. Thus, the influence of the presence of LLT on crystallization is also important for studying LLT itself.
It might be a bit counterintuitive to accept 2 liquid states for a pure substance. We argued that LLT is controlled by a new order parameter , which is the fraction of locally favored structures (12, 36). According to this 2-order-parameter model, LLT can be viewed as a gas–liquid transition of this order parameter (i.e., the 2 liquids are -rich and -poor liquids in our model), whereas the normal gas–liquid transition is a transition of the density order parameter. The density is conserved in a system, and thus its change at a certain position must be accompanied by a change in nearby density. On the other hand, locally favored structures can be created and annihilated rather independently, and thus the order parameter is a nonconserved order parameter (37).
Some time ago, we found experimental evidence for LLT in a molecular liquid, triphenyl phosphite (TPP) (12) (see Fig. 1 for the key temperatures of TPP). We identified 2 types of transformation from liquid I to liquid II, nucleation growth (NG) and spinodal decomposition (SD) type. For TPP, NG-type transformation takes place between the spinodal temperature K and the binodal temperature K, while the transformation is SD-type below K (38, 39). Since the melting point is located at 295 K, LLT always takes place in a metastable supercooled state. We found that the transition between NG-type and SD-type LLT is rather sharp, indicative of the mean field nature of the transition. This is suggestive of enhancement of critical-like fluctuations of near . This is because, when approaching from above, the metastable state approaches an unstable state. Such enhancement is known to be more significant for a system with stronger mean field nature. The mean field nature is stronger for a system with longer bare correlation length. This is known as the Ginzburg criterion (3). In ordinary gas–liquid phase transition, for example, the bare correlation length is roughly given by the size of a molecule. On the other hand, for liquid–liquid transition, the size of locally favored structures, which are made of several molecules, is larger than the size of a single molecule. For TPP, for example, we estimated the size to be about 3 nm (40). This longer bare correlation length should lead to stronger mean field nature, or stronger enhancement of the order parameter () fluctuations toward . Indeed, we found experimental indications for the presence of critical-like order parameter fluctuations near the spinodal temperature (12, 36), including spatial confinement effects on LLT (41) and wetting effects on LLT (42). Furthermore, the longer characteristic length should lead to the longer lifetime of fluctuations, which is proportional to the cube of the correlation length. This slow relaxation allows us to use a special protocol we use in our experiments (see below). In this article, we study the impact of fluctuations near but above on crystal nucleation in TPP.
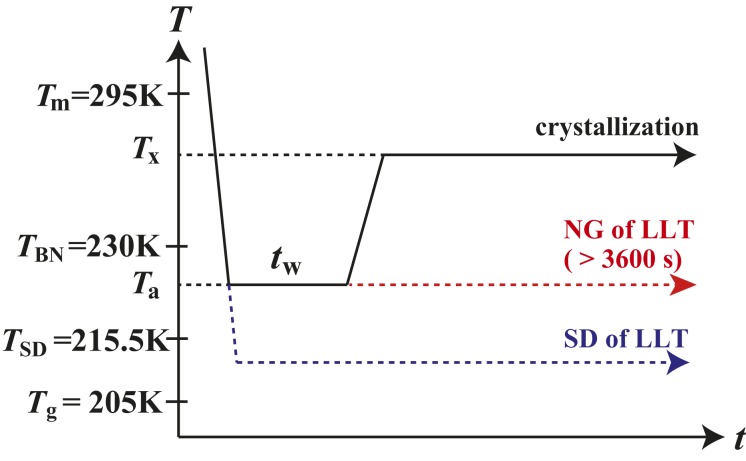
Fig. 1.
Key temperatures of TPP and a special temperature protocol used in our experiments. The melting point of TPP is located at 295 K. LLT takes place below the binodal temperature K. The transformation kinetics of LLT from liquid I to liquid II can be classified into 2 types: NG and SD type. NG-type transformation takes place between K and the spinodal temperature K, whereas SD-type one takes place below K. Since is located below (295 K), LLT always takes place in a metastable supercooled state. We anneal TPP for at in order to create fluctuations near but above . Then we heat it to for crystallization under influence of fluctuations. The glass transition temperature is located at 205 K slightly below .
One might think that we may study this problem simply by measuring the crystal nucleation rate as a function of the crystallization temperature . But we cannot take this strategy: Since the nucleation barrier of the liquid II phase rapidly decreases while approaching (38), NG-type LLT takes place before crystallization occurs, below 225 K (or near ). This prevents us from studying the crystallization behavior in this temperature region with the ordinary temperature protocol. Thus, we design a special experimental protocol, as shown in Fig. 1 (see SI Appendix, section 1 for the details), in which the crystal nucleation rate is measured at a fixed above , where LLT never takes place, after a short-time annealing of the melt at a temperature over near but above . During annealing at , fluctuations may grow near before NG-type LLT takes place. Then, after heating to , if the fluctuations remain until crystal nucleation, they might help the nucleation by reducing . This is our expectation based on our previous study (19), in which only is affected by order parameter fluctuations whereas and are not so much. This protocol relies on a specific relationship between the growth and decay time of fluctuations, the incubation time for crystal nucleation, the kinetics of NG-type LLT, and the characteristic time of the temperature change (see below and SI Appendix, section 1). It allows us not only to separate the activation energy of crystal nucleation from the kinetic one (Eq. 1) but also to separate the effect of from that of (Eq. 2). Note that, in this temperature protocol, the dependencies of and on fluctuations are negligible for different annealing conditions (see below). So, if there is no LLT, or in the absence of the effect of fluctuations, then should also be the same, and thus the crystallization behavior should not depend on . We indeed confirmed this experimentally for 4 molecular liquids without LLT (see below).
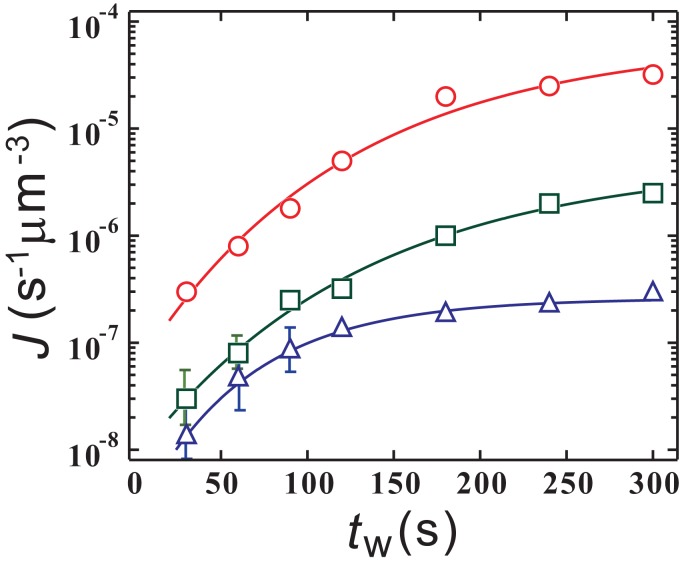
First, we discuss the growth of fluctuations at and their fate after rapid heating to the crystallization temperature (). Fig. 2 shows the dependence of the crystal nucleation rate at K on the annealing time for K (circles), 218 K (squares), and 220 K (triangles) (SI Appendix, section 2). There we can see the increase of with an increase in for the 3 s, and the amount of the increase is larger near . We stress that should not depend on if the liquid already reaches its equilibrium state with little fluctuation at just after being heated to this . We also note that, above but near , the nucleation of liquid II droplets occurs only after a rather long induction time (900 s), and our annealing time is much shorter than this incubation time. In other words, liquid II nuclei rarely exceed the critical nucleus size, in this protocol. Thus, there can be only fluctuations of the order parameter as long as s. Thus, the above result clearly indicates that 1) thermal fluctuations of grow by annealing near and are more enhanced when is closer to but above the spinodal line , 2) they remain for a reasonably long time (at least for s [SI Appendix, section 2 and Fig. S1 ]) after being heated from to until crystal nuclei are formed at , and 3) their presence assists the crystal nucleation. This enhancement of fluctuations near may be due to the mean field-like nature of LLT.
Fig. 2.
The crystal nucleation rate at as a function of the annealing time for K (circles), 218 K (squares), and 220 K (triangles). For 300 s, almost becomes constant, meaning that fluctuations are quasi-equilibrated at . We note that an incubation time for NG-type LLT at is much longer than 300 s. Thus, the fact that the crystal nucleation rate increases when is closer to indicates that fluctuations are more enhanced near (see also the main text and Methods). The solid lines are fits by , where , , and are the fitting parameters (see the main text). To reduce the statistical errors, we took an average over 10 independent experiments for each . The error bars are shown in the plot only when they exceed the size of the symbols.
We also find that the dependence of on can be well described as
| [4] |
where is the final crystal nucleation rate after the establishment of quasi-equilibrium fluctuations, which we denote , for long enough at , and thus it should be given by
| [5] |
where is the free-energy barrier for a liquid with fully developed fluctuations, , at . On the other hand, at , there are no fluctuations, and the free-energy barrier should be given by , where 0 means the absence of fluctuations. Thus, we obtain
| [6] |
Thus, has a clear physical meaning of the thermal energy-scaled free-energy barrier difference between a liquid without and with fluctuations. The is then the characteristic time of the growth of fluctuations. In this way, Eq. 4 has a clear physical meaning.
From the fitting, is estimated to be 146 s at 216 K, 128 s at 218 K, and 82 s at 220 K, and, thus, much longer than the structural (density order parameter) relaxation time [ s at 216 K measured by dielectric spectroscopy (43)]. This result indicates that 1) it takes a longer time for fluctuations to grow near and 2) once they are formed, they have a rather long lifetime. These 2 facts allow us to equilibrate fluctuations at and keep it at with little decay even after heating from to until crystals are nucleated. We note that it is difficult to directly access fluctuations experimentally. The origin of such slow growth and relaxation of fluctuations is an important problem, but we leave it for future research.
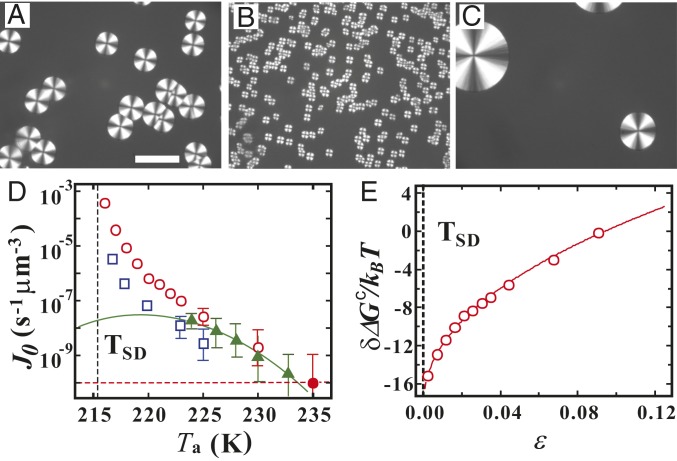
Now we show how the fluctuations formed at and still remaining at affect crystal nucleation. Using the above-mentioned protocol, we first annealed TPP at K (Fig. 3A), 217 K (Fig. 3B), and 150 K (Fig. 3C) for the annealing time s, and then heated it with a rate of 100 K/min to the target temperature K, where crystallization takes place. Fig. 3 A–C shows images of crystalline spherulites observed with polarizing microscopy after waiting for 20 min at . We can clearly see that the number of crystal nuclei is very different between the 3 cases (Fig. 3 A–C), despite the fact that all crystallization processes take place at the same temperature and thus and should be the same between them. We note that the cases in Fig. 3 A and C are far from , whereas the case in Fig. 3B is near .
Fig. 3.
Enhancement of the crystal nucleation frequency near the spinodal temperature of LLT, . (A–C) Images show crystals observed with polarizing microscopy in TPP samples, which were first quenched to (A) K, (B) 217 K, and (C) 150 K and annealed there for 5 min, then heated to K with a rate of 100 K/min and annealed for 20 min. We stress that the crystallization always takes place at K. (Scale bar: , 20 ; also applies to and .) () The crystal nucleation rate at K (circles) and 240 K (squares) as a function of for a sample with fluctuations, which is annealed at for 5 min. The for the ordinary crystallization protocol is also shown by green triangles, together with the CNT prediction (green solid curve) (SI Appendix, section 3 and Fig. S3). This without fluctuations obeys the CNT prediction, as expected. The vertical black dashed line indicates the location of . For both s, for crystallization of a sample with fluctuations increases very steeply when . The filled red circle corresponds to for a sample directly quenched to 235 K from melt; that is, it corresponds to in absence of fluctuations at K. The horizontal red dashed line is the value of expected in the absence of LLT. For K, the number of crystal nuclei becomes very small, leading to a larger statistical error. The data are the crystal nucleation rate averaged over 10 times. The error bars are shown in the plot only when they exceed the size of the symbols (SI Appendix, section 2) () The difference between at 235 K and that at as a function of . The solid curve is a fit by with (see text).
Next, we estimate the crystal nucleation rate as a function of , where is the value of for the equilibrated state after long enough (for the method to estimate , see SI Appendix, section 2 and Fig. S1), for K as a function of . The enhancement of by many orders of magnitude when is observed for both s. We stress that this increase far exceeds the maximum nucleation frequency () expected for the ordinary quench protocol (see the green solid line in Fig. 3D). The filled red circle in Fig. 3D corresponds to the nucleation rate for a liquid which is quenched directly to 235 K from melt; that is, it corresponds to in the absence of fluctuations at K. As will be shown below, if there is no LLT, the crystal nucleation rate is not affected by annealing, contrary to the case of TPP.
The crucial feature is the positive curvature of the temperature dependence of the crystal nucleation frequency . This can never be explained by the ordinary classical nucleation frequency scenario, which predicts the negative curvature due to the steep decrease toward both and (SI Appendix, section 3 and Fig. S3). The only possible explanation may be crystallization of 2 polymorphs with different melting points. Although there is a systematic deviation, we can somehow fit the data with CNT assuming the 2 types of polymorphs (SI Appendix, section 3 and Fig. S4). However, this scenario is unlikely by the single melting behavior of only one type of crystal.
We also calculate at K, which is the difference in between the liquid without fluctuations and the one with fluctuations formed at (Eq. 6). Fig. 3E plots as a function of the reduced temperature ( ). We find that the free-energy barrier decreases by 16 toward . This is a comparable reduction reported by ten Wolde and Frenkel (22) for colloidal suspensions near a gas–liquid critical point. We can express as , where , , and 0.10 when , but the physical meaning of the value of the exponent is not clear at this moment.
Here we discuss the physical origin of the drastic enhancement of the crystal nucleation rate by our protocol. The crucial point is that the enhancement of S fluctuations may influence and , but the effects should be minor. For example, since contributes to the nucleation frequency as a prefactor (Eq. 1), its small change can never lead to many orders of magnitude change in the crystal nucleation frequency. We also note that our measurements of dielectric spectroscopy show that the influence of fluctuations on the structural relaxation time is very minor if it even exists (43). Furthermore, the enthalpy change of liquid detected by differential scanning calorimetry (DSC) measurements is also negligibly small (SI Appendix, section 4 and Fig. S5), indicating that the influence of fluctuations on should also be minor. Thus, we may assume that depends only on . This is consistent with the fact that the growth velocity is independent of (note that depends only on [Eq. 3]). Thus, we may conclude that any dependence of the crystal nucleation rate, or, more specifically, , on should originate mainly from the influence of fluctuations formed at on .
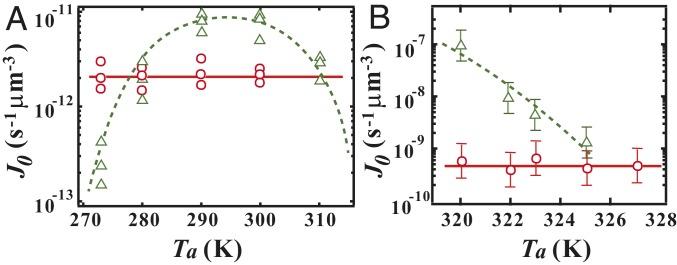
To confirm the crucial role of LLT in the observed drastic enhancement of the crystal nucleation rate by annealing near the spinodal temperature , here we study the effect of annealing on the rate of crystal nucleation in ordinary liquids without LLT. Fig. 4A shows the protocol dependence of for D-sorbitol. The triangle corresponds to when the liquid D-sorbitol is annealed and crystallized at . The dashed line in Fig. 4A is the CNT fitting of the data, which are consistent with the results reported in ref. 44. On the other hand, the circle symbols shown in Fig. 4A correspond to at a fixed temperature K after the liquid is annealed at for 1 h. These results clearly indicate that the nucleation rate of D-sorbitol is not affected by the annealing treatment at all. We also obtain the same conclusion for poly(-caprolactone) (PCL) (Fig. 4B), triphenyl phosphine (TPPN), and polyethylene glycol (PEG) (SI Appendix, section 5 and Fig. S6). Here it is worth noting that TPPN is a glass-forming material, which has a molecular structure similar to TPP. Thus, we may conclude that, for ordinary liquids that do not have LLT, there is no effect of such annealing on the crystal nucleation rate. Contrary to these ordinary liquids, for TPP, the nucleation rate is drastically enhanced by nearly 7 orders of magnitude with a decrease of from 235 K to 215 K. This strongly indicates that the presence of LLT and the resulting enhancement of fluctuations toward are responsible for such a drastic increase in the nucleation rate of crystals toward .
Fig. 4.
Effects of annealing on the crystal nucleation rate for ordinary liquids without LLT. () The rate of crystal nucleation in D-sorbitol. The triangles correspond to when the sample is crystallized at an annealing temperature . The dashed curve is the CNT fitting of the data, which are consistent with the results in ref. 44. On the other hand, the circle symbols represent the nucleation rates for a protocol in which a sample is annealed at for 1 h and then heated and crystallized at K. () The rate of crystal nucleation in PCL. The dashed curve is a guide to eye. The triangles correspond to when the sample is crystallized at . The circle symbols correspond to at K after the sample is annealed at for 10 min. In both systems, the crystal nucleation rate is not affected by the annealing at temperatures below .
One might think that the enhancement of crystal nucleation for TPP can be due to formation of invisible crystal nuclei during annealing at . But this scenario is unlikely because of the following reasons: 1) The size of nuclei should be smaller than the critical nucleus size at . This is because, otherwise, we should see their continuous growth, but this was never observed before the formation of liquid II nuclei below 223 K (38). Then, on noting that the critical nucleus size should be larger at 235 K than around 215 K, this scenario cannot explain the observed enhancement. 2) For this scenario, the crystal nucleation rate should be constant with , but this is clearly inconsistent with the results shown in Fig. 1. Furthermore, the incubation time for crystallization at shown in SI Appendix, section 2 and Fig. S1 should not be observed, and instead their immediate growth from should be observed. 3) This scenario cannot explain a much higher nucleation rate at after annealing at than the rate predicted by CNT (green solid curve in Fig. 3D). 4) We compare between at K and 235 K (Fig. 3D). We can see that decreases at higher . If invisible yet large crystal nuclei are already formed during annealing at , should be larger for higher temperature, since a higher growth rate at 240 K (0.2 m) than at 235 K (0.1 m) (38) (SI Appendix, section 2 and Fig. S2). This clearly contradicts our observation. In our scenario, we can naturally explain the lower crystal nucleation rate at higher as a consequence of weaker fluctuations there. 5) As shown in SI Appendix, section 4 and Fig. S5A, peak L in the DSC curve continuously shifts to lower temperature. If we suppose that preexisting nuclei are formed in the annealing process, we expect that crystal growth should start at the same temperature for different annealing periods and thus the DSC peak position should be the same. This contradicts our observation. 6) We also note that, if such a scenario is relevant, we should see similar behaviors in D-sorbitol, PCL, TPPN, and PEG, but we do not see any such indications, as shown in Fig. 4 and SI Appendix, section 5 and Fig. S6. From considerations 1 through 6, we conclude that the steep increase of toward is due to the enhancement of fluctuations.
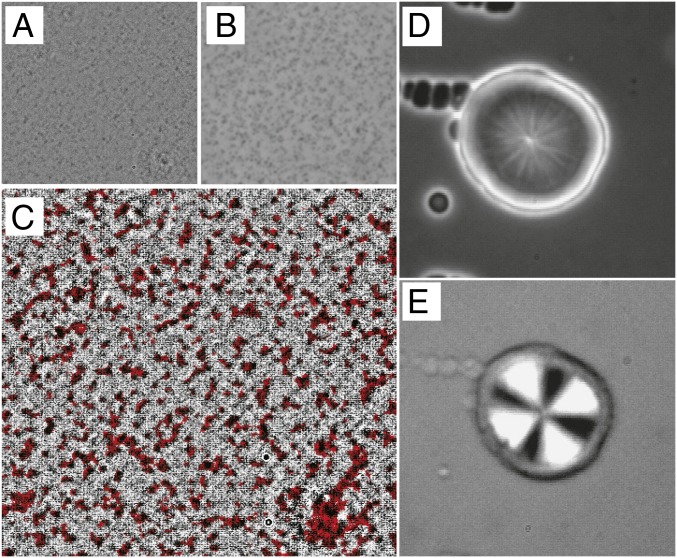
Next we study the spatial correlation between crystal nucleation sites and fluctuations to check the coupling between the order parameters of crystallization and LLT, including its sign. To do so, we anneal TPP below to enhance fluctuations by SD-type LLT, since fluctuations cannot be directly observed above with optical microscopy but can be observed below (38). This, although not a direct proof, reveals the nature of the coupling between the order parameter of LLT () and that of crystallization. We show, in Fig. 5A, a phase-contrast microscopy image of SD-type LLT observed after annealing at 214 K () for min, where dark regions correspond to high- regions. Then, we heat the sample to K with a rate of 20 K/min. Fig. 5B shows an optical microscopy image of crystal nuclei observed after annealing for 5 min at 235 K in exactly the same region as Fig. 5A. To see the spatial correlation between fluctuations and crystal nuclei, we superimpose the 2 images, fluctuations (Fig. 5A) (appeared black) and crystal nuclei (Fig. 5B) (appeared red), in Fig. 5C. We can clearly see that crystal nucleation preferentially occurs in higher- regions with darker contrast, suggesting 1) the survival of fluctuations after heating to and 2) lower in higher regions. To be more quantitative, we estimate the probability of crystal nuclei being formed in high- regions and find that about 93% of crystal nuclei are formed in high- dark regions.
Fig. 5.
Coupling between crystallization and fluctuations. () Spatial fluctuations of observed with phase-contrast microscopy in a sample quenched to 214 K (below ) after annealing there for 120 min. The darker regions correspond to higher regions. () Crystal nuclei (dark droplets) observed with phase-contrast microscopy in the same area as panel , after heating the sample to 235 K with a rate of 20 K/min and annealing there for 5 min. () Superposition of images from (gray) and (red). We can see a clear spatial correlation between high- regions (black) and crystal nuclei (red). () A crystal spherulite that is wet by liquid II. First the crystal was formed at 235 K, and then the sample was quenched to 220 K to initiate NG-type LLT. The image is taken 80 min after the quench. We can see that the wetting layer of liquid II is preferentially formed on the surface of the spherulite in the middle of the image. Dark small droplets of liquid II are also nucleated in bulk. () Polarizing microscopy observation of the same sample as in . We can see the nonbirefringent wetting layer around the crystal spherulite with Maltese cross. The size of all images is 120 120 .
To further confirm this conclusion that the crystal–liquid interfacial free energy is a decreasing function of , we also observe how LLT proceeds under an influence of a preexisting crystal. First, we prepare a crystalline spherulite by annealing TPP at a temperature above K but below K. Note that, under this condition, only crystallization takes place without accompanying LLT. Then we quench the system below to initiate NG-type LLT. We find that liquid II is preferentially nucleated on the surface of the preexisting crystal to form the wetting layer, as shown in Fig. 5 D and E. This unambiguously indicates that liquid II is more wettable for crystals than liquid I, or the crystal–liquid interfacial tension is a decreasing function of (see also ref. 42). We also show other supporting evidence for the reduction of the crystal nucleation barrier by fluctuations from DSC measurements in SI Appendix, section 4 and Fig. S5.
To summarize, we find the enhancement of crystal nucleation by order parameter fluctuations associated with LLT. This is clear experimental evidence that the crystal nucleation is enhanced thermodynamically near the spinodal temperature of LLT. Our study suggests the universality of the scenario proposed by ten Wolde and Frenkel (22) in relation to various types of phase transitions such as phase demixing and liquid–liquid transition. This scenario is originally proposed for phase demixing or gas–liquid transition, where the order parameter is conserved. On the other hand, the order parameter of LLT can be changed locally, or it is of nonconserved nature (12). Thus, our finding indicates that the scenario does not depend upon whether the order parameter is conserved or not, and the only crucial factor is the presence of its coupling to the crystal order parameter and the resulting reduction of the crystal–liquid interfacial tension. With the help of critical-like fluctuations, we may attain a large nucleation frequency far beyond its maximum in the ordinary quench protocol, providing a way to decrease the crystal grain size and its variance that are important factors controlling the physical properties of crystalline materials (45, 46).
This phenomenon may also be used to reveal any phase transition that is located in a supercooled state metastable against crystallization and thus hidden behind crystallization. For example, there are many candidates of LLTs, which are expected to occur far below but hidden by crystallization: They include water, Si, Ge, and metallic liquids (29, 33, 34, 47). Our finding provides an experimental method to detect order parameter fluctuations associated with a hidden LLT in such systems by using crystallization behavior as a probe. The enhancement of the crystal nucleation frequency as a function of the preannealing temperature at a constant crystallization temperature can be used as a fingerprint for the presence of a hidden phase transition. We also reveal the difference in crystallization dynamics between liquid I and liquid II (SI Appendix, section 4 and Fig. S5). This is related to another interesting subject of research, that is, a link between crystallization behavior and LLT (see, e.g., refs. 48 and 49). For example, our study may shed light on LLT in water: For example, our study may provide insight into a recent interest in how the kinetic pathway of ordering is affected by an interplay between crystallization and LLT in a metastable supercooled water (35). Finally, we note that the physical scenario is not limited to crystallization, but may be universal to nucleation of an ordered phase under the influence of critical fluctuations associated with another phase ordering.
Methods
The sample used is TPP purchased from Aldrich Chemical Co., Inc., and used after extracting only a crystallizable part and filtering it to remove impurities that may act as nucleators for crystallization. We observed the liquid–liquid transformation process with phase-contrast and polarizing microscopy. For these observations, a sample was sandwiched between 2 cover glasses, and its thickness was controlled to be 10 m by using monodisperse glass beads as spacers (see SI Appendix, section 2 for effects of the sample thickness on crystal nucleation). We confirmed that this level of spatial confinement does not affect the behaviors significantly (41). The temperature was controlled within 0.1 K by a computer-controlled hot stage (Linkam LK-600PH) with a cooling unit (Linkam L-600A). We note that, in our phase-contrast microscopy observation, a region having a higher refractive index (or the higher density) appears with darker contrast. We also used D-sorbitol, PCL (molecular weight: 60,000), TPPN, and PEG (molecular weight: 6,000) purchased from Aldrich Chemical Co., Inc., to clarify whether the annealing at low temperatures affects crystallization for systems without LLT or not. We measured the nucleation rate of the so-called polymorph E of D-sorbitol ( K) (44). In SI Appendix, section 4 and Fig. S5, we report results of our heat experiments. In the experiments, we measured the heat flux during the transformation with a differential scanning calorimeter (DSC-822e; Mettler Toledo).
Supplementary Material
Acknowledgments
H.T. acknowledges support from Grants-in-Aid for Scientific Research (S) and (A) (Grants JP21224011 and JP18H03675, respectively), and Specially Promoted Research (Grant JP25000002) from the Japan Society of the Promotion of Science. R.K. acknowledges support from a Grant-in-Aid for Scientific Research (B) (Grant JP17H02945).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1909660116/-/DCSupplemental.
References
- 1.Binder K., Theory of first-order phase transitions. Rep. Prog. Phys. 50, 783–859 (1987). [Google Scholar]
- 2.Debenedetti P. G., Metastable Liquids (Princeton University Press, Princeton, NJ, 1997). [Google Scholar]
- 3.Onuki A., Phase Transition Dynamics (Cambridge University Press, Cambridge, United Kingdom, 2002). [Google Scholar]
- 4.Turnbull D., Under what conditions can a glass be formed? Contemp. Phys. 10, 473–488 (1969). [Google Scholar]
- 5.Statt A., Virnau P., Binder K., Finite-size effects on liquid-solid phase coexistence and the estimation of crystal nucleation barriers. Phys. Rev. Lett. 114, 026101 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Kelton K., Greer A. L., Nucleation in Condensed Matter: Applications in Materials and Biology (Elsevier, 2010), vol. 15. [Google Scholar]
- 7.Neilson G. F., Weinberg M. C., A test of classical nucleation theory: Crystal nucleation of lithium disilicate glass. J. Non-Cryst. Solids 34, 137–147 (1979). [Google Scholar]
- 8.Gránásy L., James P. F., Non-classical theory of crystal nucleation: Application to oxide glasses: Review. J. Non-Cryst. Solids 253, 210–230 (1999). [Google Scholar]
- 9.Sear R. P., Nucleation: Theory and applications to protein solutions and colloidal suspensions. J. Phys. Condens. Matter 19, 033101 (2007). [Google Scholar]
- 10.Gasser U., Crystallization in three- and two-dimensional colloidal suspensions. J. Phys. Condens. Matter 21, 203101 (2009). [DOI] [PubMed] [Google Scholar]
- 11.Fokin V. M., Zanotto E. D., Crystal nucleation in silicate glasses: The temperature and size dependence of crystal/liquid surface energy. J. Non-Crystal Solids 265, 105–112 (2000). [Google Scholar]
- 12.Tanaka H., Bond orientational order in liquids: Towards a unified description of water-like anomalies, liquid-liquid transition, glass transition, and crystallization. Eur. Phys. J. E 35, 113–196 (2012). [DOI] [PubMed] [Google Scholar]
- 13.Ediger M., Harrowell P., Yu L., Crystal growth kinetics exhibit a fragility-dependent decoupling from viscosity. J. Chem. Phys. 128, 034709 (2008). [DOI] [PubMed] [Google Scholar]
- 14.Zanotto E. D., Cassar D. R., The race within supercooled liquids—Relaxation versus crystallization. J. Chem. Phys. 149, 024503 (2018). [DOI] [PubMed] [Google Scholar]
- 15.Weinberg M. C., Poisl W. H., Gránásy L., Crystal growth and classical nucleation theory. C. R. Chimie 5, 765–771 (2002). [Google Scholar]
- 16.Kawasaki T., Tanaka H., Formation of a crystal nucleus from liquid. Proc. Natl. Acad. Sci. U.S.A. 107, 14036–14041 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Russo J., Tanaka H., The microscopic pathway to crystallization in supercooled liquids. Sci. Rep. 2, 505 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Russo J., Tanaka H., Crystal nucleation as the ordering of multiple order parameters. J. Chem. Phys. 145, 211801 (2016). [DOI] [PubMed] [Google Scholar]
- 19.Russo J., Romano F., Tanaka H., Glass forming ability in systems with competing orderings. Phys. Rev. X 8, 021040 (2018). [Google Scholar]
- 20.Tan P., Xu N., Xu L., Visualizing kinetic pathways of homogeneous nucleation in colloidal crystallization. Nat. Phys. 10, 73–79 (2014). [Google Scholar]
- 21.Tanaka H., Nishi T., New types of phase separation behavior during the crystallization process in polymer blends with phase diagram. Phys. Rev. Lett. 55, 1102–1105 (1985). [DOI] [PubMed] [Google Scholar]
- 22.ten Wolde P. R., Frenkel D., Enhancement of protein crystal nucleation by critical density fluctuations. Science 277, 1975–1978 (1997). [DOI] [PubMed]
- 23.Talanquer V., Oxtoby D. W., Crystal nucleation in the presence of a metastable critical point. J. Chem. Phys. 109, 223–227 (1998).
- 24.Sear R. P., Homogeneous nucleation of a noncritical phase near a continuous phase transition. Phys. Rev. E 63, 066105 (2001). [DOI] [PubMed] [Google Scholar]
- 25.Shiryayev A., Gunton J. D., Crystal nucleation for a model of globular proteins. J. Chem. Phys. 120, 8318–8326 (2004). [DOI] [PubMed] [Google Scholar]
- 26.Galkin O., Vekilov G., Control of protein crystal nucleation around the metastable liquid–liquid phase boundary. Proc. Natl. Acad. Sci. U.S.A. 97, 6277–6281 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Galkin O., Vekilov G., Nucleation of protein crystals: Critical nuclei, phase behavior, and control pathways. J. Cryst. Growth 1-4, 63–76 (2001). [Google Scholar]
- 28.Evans R. M. L., Poon W. C. K., Cates M. E., Role of metastable states in phase ordering dynamics. Europhys. Lett. 38, 595–600 (1997). [Google Scholar]
- 29.Deb S. K., Wilding M., Somayazulu M., McMillan P. F., Pressure-induced amorphization and an amorphous-amorphous transition in densified porous silicon. Nature 414, 528–530 (2001). [DOI] [PubMed] [Google Scholar]
- 30.Angell C. A., Formation of glasses from liquids and biopolymers. Science 267, 1924–1935 (1995). [DOI] [PubMed] [Google Scholar]
- 31.Poole P. H., Grande T., Angell C. A., McMillan P. F.. Polymorphic phase transitions in liquids and glasses. Science 275, 322–323 (1997). [Google Scholar]
- 32.Katayama Y., Mizutani T., Utsumi W., Shimomura O., Yamakata M., A first-order liquid-liquid transition in phosphorus. Nature 403, 170–173 (2000). [DOI] [PubMed] [Google Scholar]
- 33.Brazhkin W., Lyapin A. G., High-pressure phase transformations in liquids and amorphous solids. J. Phys. Condens. Matter 15, 6059–6084 (2003). [Google Scholar]
- 34.Mishima O., Stanley H. E., The relationship between liquid, supercooled and glassy water. Nature 396, 329–335 (1998). [Google Scholar]
- 35.Palmer J. C., Poole P. H., Sciortino F., Debenedetti P. G., Advances in computational studies of the liquid–liquid transition in water and water-like models. Chem. Rev. 118, 9129–9151 (2018). [DOI] [PubMed] [Google Scholar]
- 36.Kurita R., Tanaka H., Critical-like phenomena associated with liquid-liquid transition in a molecular liquid. Science 306, 845–848 (2004) [DOI] [PubMed] [Google Scholar]
- 37.Tanaka H., General view of a liquid-liquid phase transition. Phys. Rev. E 62, 6968–6976 (2000). [DOI] [PubMed] [Google Scholar]
- 38.Tanaka H., Kurita R., Mataki H., Liquid-liquid transition in the molecular liquid triphenyl phosphite. Phys. Rev. Lett. 92, 025701 (2004). [DOI] [PubMed] [Google Scholar]
- 39.Kobayashi M., Tanaka H., The reversibility and first-order nature of liquid–liquid transition in a molecular liquid. Nat. Commun. 7, 13438 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Murata K., Tanaka H., Microscopic identification of the order parameter governing liquid–liquid transition in a molecular liquid. Proc. Natl. Acad. Sci. U.S.A. 112, 5956–5961 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kurita R., Tanaka H., Control of the liquid-liquid transition in a molecular liquid by spatial confinement. Phys. Rev. Lett. 98, 235701 (2007). [DOI] [PubMed] [Google Scholar]
- 42.Murata K., Tanaka H., Surface-wetting effects on the liquid-liquid transition of a single-component molecular liquid. Nat. Commun. 1, 16 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Murata K., Tanaka H., Link between molecular mobility and order parameter during liquid–liquid transition of a molecular liquid. Proc. Natl. Acad. Sci. U.S.A. 116, 7176–7185 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Huang C., et al. , Crystal nucleation rates in glass-forming molecular liquids: D-sorbitol, d-arabitol, d-xylitol, and glycerol. J. Chem. Phys. 149, 054503 (2018). [DOI] [PubMed] [Google Scholar]
- 45.Yip S., Nanocrystals: The strongest size. Nature 391, 532–533 (1998). [Google Scholar]
- 46.Uchic M. D., Dimiduk D. M., Florando J. N., Nix W. D., Sample dimensions influence strength and crystal plasticity. Science 305, 986–989 (2004). [DOI] [PubMed] [Google Scholar]
- 47.Sheng H. W., et al. , Polyamorphismin ametallic glass. Nat. Mater. 6, 192–197 (2007). [DOI] [PubMed] [Google Scholar]
- 48.Bhat M. H., et al. , Vitrification of a monoatomic metalic liquid. Nature 448, 787–790 (2007). [DOI] [PubMed] [Google Scholar]
- 49.Angell C. A., Glass-formers and viscous liquid slowdown since David Turnbull: Enduring puzzles and new twists. MRS Bull. 33, 544–555 (2008). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.