Significance
In October 2017, most European networks involved in the monitoring of atmospheric radioactive contamination measured small 106Ru air concentrations. One of the particularities of the event was that the location and the magnitude of the source were unknown at the time when the first detections were reported. This paper describes the use of inverse modeling techniques combining an atmospheric transport model with environmental measurements in order to identify the origin of the 106Ru detections and to assess the magnitude of the 106Ru emissions. The method, easily embedded for operational use, made it possible to quickly point out the southern Urals in the Russia Federation as the most likely geographical origin of the release.
Keywords: inverse modeling, ruthenium detection, atmospheric dispersion modeling, source reconstruction
Abstract
In October 2017 unusual 106Ru detections across most of Europe prompted the Institut de Radioprotection et de Sûreté Nucléaire (IRSN) to analyze the event in order to locate the origin and identify the magnitude of the release. This paper presents the inverse modeling techniques used during the event to achieve this goal. The method is based on a variational approach and consists of using air concentration measurements with the ldX long-range dispersion model included in the IRSN’s C3X operational platform. The method made it possible to quickly identify the southern Urals as the most likely geographical origin of the release. Despite uncertainties regarding the starting date of the release, calculations show that it potentially began on 23 September, while most of the release was emitted on 26 September. Among the nuclear plants identified in the southern Urals, the Mayak complex is that from which the dispersion of the 106Ru plume is most consistent with observations. The reconstructed 106Ru source term from Mayak is ∼250 TBq. In total, it was found that for 72% of the measurements simulated and observed air concentration agreed within a factor of 5. In addition, the simulated deposition of 106Ru agrees with the observed deposition. Outside the southern Urals, the simulations indicate that areas with highest deposition values are located in southern Scandinavia and southeastern Bulgaria and are explained by rainfall events occurring while the plume was passing over.
A rare episode of low levels of particulate radioactive ruthenium (106Ru) was observed in the atmosphere of most European countries between late September and mid-October 2017. The concentrations reported were in the range of several microbequerels per cubic meter to more than 100 mBq/m3 (1). As for the 131I detection event in January/February 2017 (2), no elevation in gamma dose rate was reported by measurement networks around known nuclear sites in Europe. While this makes a major accidental release scenario unlikely, analyzing only activity measurements in the air, for which the observed values are usually weekly averaged, cannot identify either the origin or the magnitude of the release. For such situation, the Institut de Radioprotection et de Sûreté Nucléaire (IRSN) uses modeling techniques to analyze the event in more detail. The aim is, in particular, to identify the origin and to assess the duration and the magnitude of the releases.
The first methods used to estimate the source location of a nuclear release were empirical and consisted of the analysis of back-trajectories and retro-plumes (3). The current methods, which are more efficient, are based on inverse modeling techniques, which combine environmental measurements with atmospheric dispersion modeling and are based on a rigorous mathematical formalism. Inverse methods include Bayesian approaches in which probabilistic considerations may be introduced into the problem in order to account for uncertainties for the input data. Very popular Bayesian techniques are random search algorithms such as Markov chain Monte Carlo (MCMC) methods (4–6). MCMC methods can be applied to major accident situations such as the Fukushima and Chernobyl accidents. In that context, the aim is to estimate how the releases will evolve with time (7), since the location is known. MCMC methods are also relevant for radionuclide detection events of smaller magnitude where the release location is unknown. As regards the problem of source identification, an MCMC method was applied to the Algeciras incident (8) that occurred at the end of May 1998 and led to a radioactive release following the fusion of a 137Cs radioactive medical source. In fall 2011, 131I was detected at several monitoring stations in central Europe following a 131I release from the Institute of Isotopes in Budapest. The source location, the magnitude, and the temporal evolution of the release are retrieved in ref. 9 assuming no prior information. A Bayesian method was used for source reconstruction for real-world activity concentration data measured by the International Monitoring System radionuclide network maintained under the auspices of the Comprehensive Nuclear-Test-Ban Treaty Organization (10). Variational inverse modeling methods (11–16) are a variant of Bayesian methods since they draw on the Bayes formula but consist only of estimating the optimal solution and not obtaining the probability density function of the estimated source parameters. A variational method was applied to identify the origin of 131I detected in Europe between January and February 2017 (2). As no information on the source was available, several potential releases sites were considered to reduce the size of the inverse problem. Compared to variational approaches, MCMC Bayesian methods may be not suitable for operational use because of their prohibitive computational costs, especially where there is a large number of source parameters to sample. Another type of inverse modeling method is maximum entropy on the mean (17–19). It is based on a formalism which is a variant of the Bayes approach, enabling prior information, for example the source positivity, to be taken into account. Maximum entropy of the mean offers a general framework in which the information input prior to inversion is used in a flexible and controlled way. The inversion is shown to be equivalent to the minimization of an optimal cost function, expressed in the dual space of observations. It has been shown that such techniques are efficient in the case of an accidental event like Chernobyl (20).
In this paper, a variational inverse modeling method is used to determine the most probable 106Ru source location and its magnitude using 106Ru air concentration measurements. The decision to use a variational inverse technique was based on its ease of implementation and the fact that the computing time is less prohibitive than with Bayesian methods. We first describe the observations reported in Europe. Then, the methodology of the inverse method is presented and applied to identify the 106Ru source location and the quantities released in the atmosphere from the most reliable location. The main results obtained by inverse modeling are discussed and validated by performing a model-to-data comparison.
Observations
Air Concentration Measurements.
The available dataset of 106Ru air concentrations (for further details see ref. 1) was mainly compiled by Ro5 reports and was completed with data from the Roshydromet website (21), the Typhoon Association website (22), and the EGASMRO website (23, 24). Ruthenium-106 was observed between the end of September and mid-October 2017 in the atmosphere of 31 countries on the European continent at levels ranging from a few microbequerels per cubic meter to more than 170 mBq/m3. Only stations located in western Europe (Portugal, Spain, Great Britain, Benelux, and Northern Ireland) did not report detections of 106Ru above detection limits. Outside Europe, 106Ru was also detected at very low levels (microbequerels per cubic meter) in Guadeloupe, Kuwait, Florida, the eastern part of the Russian Federation, and Mongolia. The detection limit of the measurements also varied significantly between stations depending on airborne concentration, sampling equipment, and measurement capabilities. As outlined in ref. 1, maximum air concentration values were measured in Romania (176 mBq/m3), which was explained by the variability of air sampling duration in various countries. The air sampling periods differ from one country to another, ranging from half a day to several weeks. In addition, a given result may correspond to the compilation of several subperiod filters leading to a composite filter sample corresponding up to several months. Hence, it was not possible to identify the source release location solely via the average value over a given sampling period.
Deposition Measurements.
In addition to the air concentration measurements, deposition was also measured in a number of European countries (see ref. 1). They were either samples taken after the releases were over, giving the cumulative 106Ru deposit at a particular location, or samples showing the total quantity of 106Ru deposited in a single day. The daily samples are of greatest interest because they make it possible to work out the period when the 106Ru was deposited. A number of daily deposition observations were recorded in the Russian Federation, between the Urals and the regions further west, as well as in the rest of Europe.
Although the number of deposition reports is much smaller than the number of air concentration measurements, analysis of the daily deposit observations identifies southern Ural as the first region to have detected the presence of 106Ru. Daily samples on 23 September in Kyshtym, on 25 September in Argayash, and on 26 September in Bugulma, Dema-Ufa, Metlino, and Novogornyy indicate that 106Ru deposits reached several hundred bequerels per square meter. Several samples were also taken in December 2017 around the Mayak site in southern Ural. One of the samples situated around 15 km southwest of Mayak confirmed the presence of 106Ru with deposits of between 500 and 1,200 Bq/m2 (25). The levels of 106Ru deposits were much lower at locations west of the Urals (maximum of 17 Bq/m2 in Morozovsk, 17 Bq/m2 in Dema-Ufa, and 30 Bq/m2 in Bugulma). Elsewhere in Europe, the highest deposits were recorded in Scandinavia with levels of up to 90 Bq/m2 in Finland and 45 Bq/m2 in Sweden (26). Deposition of 106Ru was also reported from Poland, Austria, Italy, and the Czech Republic, with a few bequerels per square meter of 106Ru (1).
Source Reconstruction Methodology
In this section, we introduce the methodological framework of the source reconstruction used in this study, enabling the geographical origin of the emissions and the 106Ru quantities emitted in the environment to be determined. The method is based on variational inverse modeling techniques and inspired by that of ref. 27. Although daily deposition measurements provide useful information about the starting date of the release, these are few and are not used during the inversion process. Inverse modeling approaches combining air activity and deposition measurements simultaneously have already been implemented to reconstruct the source term from the Fukushima accident (13, 15). However, these methods require the estimation of additional parameters quantifying the confidence level associated with each type of measurement, which makes their real-time use difficult. Therefore, only air concentration measurements are used in this study. The implementation of the source reconstruction methodology consists of 3 main steps.
A Priori Information
Because 106Ru is not normally detected in the environment, it is reasonable to think that one single source of release caused the detections of 106Ru. The hypothesis of concomitant releases of 106Ru was therefore not taken into account in this study. Because of apparent west-to-east gradient in 106Ru detections, it is assumed that the release occurred somewhere between western Europe and the Russian Federation. Dimensions of the domain containing the source are [10W, 70E], [34N, 70 N], covering the majority of the detections of 106Ru (except those situated outside Europe). For computation time reasons, the initial domain is subdivided into regular mesh cells of resolution 2° × 2°, leading to a total of 720 mesh cells. Each cell center is then considered to be a potential source of release. With no prior on the geographical origin of the 106Ru detections, the probability that the source comes from one particular cell is the same for all cells of the domain.
Inverse Modeling Method
For each potential source contained in [10W, 70E], [34N, 70 N] related to the cell center , the source term is assessed by inverse modeling using the following variational approach.
Source–Receptor Relationship.
The variational approach used estimates the source term using field observations and atmospheric dispersion and deposition modeling. The method is described in several publications (see, for instance, ref. 14). It assumes that the measurement vector in can be described as a linear model with a source–receptor matrix (11) and unknown source term vector in :
| [1] |
The in source–receptor matrix is the Jacobian matrix of the transport model computed in forward mode under the approach proposed in ref. 28. Each column of represents the dispersion model’s response to a unitary release emitted from the cell center . In view of the period of the 106Ru detections, we aim to estimate the daily release rates from 22 September to 13 October. The number of components of (i.e., release rate per day in bequerels per second) is therefore equal to n = 21 (number of columns of ). The vector in represents a combined model–representativity–instrumental error, hereafter called the observation error.
In general, the source–receptor relationship Eq. 1 constitutes an ill-posed inverse problem and its resolution may fail, particularly when the number of observations is limited. A background (or a priori) term is therefore taken into account when resolving the inverse problem in order to incorporate available knowledge of the source term to be estimated (28). For the present study, 290 air sampling stations have been considered in the inversion procedure, that is, more than 1,100 measurements. Among all of the stations, some of them did not report 106Ru traces in the atmosphere. Nonetheless, they provide important information and ensure the inverse problem to be solved is better constrained. The number of air concentration measurements taken into account in the inversion procedure is therefore much higher than the number of the source vector components , suggesting that the background term can be omitted (28).
Modeling Errors.
Observation errors defined in Eq. 1 are usually assumed to be Gaussian, following a normal distribution:
| [2] |
where is the observation error covariance matrix and its determinant. A strong disadvantage of Gaussian observation errors is that they give more weight to the high concentration values than to the low values, as it is the value of the model-to-measurement difference that is considered in the probability density function (pdf). One possibility for overcoming this difficulty is to choose a log-normal distribution of observation errors (29) with the following pdf:
| [3] |
Assuming log-normal observation errors, the application of Bayesian inference leads to
| [4] |
| [5] |
From this inference, to obtain the maximum a posteriori estimate , one should maximize the likelihood , which is equivalent to maximizing and minimizing the following cost function :
| [6] |
measures the log differences between the model predictions and the real measurements . As described in ref. 7, the main drawback of log-normal observation errors is that they ascribe too much importance to very low concentration values. One way to mitigate the influence of small concentration values is to introduce a threshold in the cost function as follows:
| [7] |
This tempers the values of if there are large differences between the observed and simulated concentrations, particularly for low concentrations with values just above the detection limits. In this paper, we have chosen to consider log-normal observation errors whereas simple parameterization for matrix is used. It is assumed that is diagonal and the error variance is the same for all diagonal elements (homoscedasticity property):
| [8] |
Indeed, minimizing is equivalent to minimizing
| [9] |
However, the choice of homoscedasticity assumption is not the most appropriate since, theoretically, one should include correlations induced by observation error. More sophisticated approaches are possible (29). The impact of the homoscedasticity assumption will be discussed later in more detail. Furthermore, as in ref. 30, the parameter is manually selected large enough to prevent the lowest air concentration values from dominating the inverse problem (7, 30). Several values of were tested: , , and mBq/m3. is minimized using the L-BFGS-B limited-memory quasi-Newton minimizer (31). The positivity of the source is enforced in L-BFGS-B and no upper bound is used.
Statistical Indicators
For each potential release at the cell center , the simulated concentrations at each station i are trivially given by the product . Then, the agreement between simulated and observed air concentration measurements is assessed using the following statistical indicators:
-
•
The reduction factor of the cost function (RFJ) per cell center: Since the initial contribution of each grid center to the cost function has the same value, the RFJ obtained after minimization provides a good indication of the most relevant cells centers for the source location.
-
•
The percentage within a factor of 2 (fac2) per cell center: This is the proportion of the simulated activity concentrations calculated using the reconstructed source vector that are within a factor of 2 of the observed values. The fac2 indicator is complementary to RFJ since all of the concentration values have the same weight.
The probability that a cell center is the source location increases with the value of the statistical indicator and therefore the level of agreement between the simulated and observed concentrations. The individual performances of each potential source are projected by linear interpolation on a map enabling the relevance of the potential release areas to be viewed.
Sensitivity Analysis
Sensitivity to Observation Error.
The inverse method based on the likelihood maximization only provides an optimal solution without quantifying the associated uncertainties. One way to quantify this uncertainty is to use a Monte Carlo sensitivity analysis (14). To compute a sample n, the observation vector is perturbed such as , , and r follows a log-normal law , where is the SD of the related Gaussian law . Then, for each sample n, an optimal solution is obtained by performing the minimization of the cost function .
Sensitivity to the Spatial Distribution of Stations.
Assuming that the matrix is diagonal suggests that the measurements are not correlated in time and space. In order to quantify the impact of this hypothesis and to evaluate the robustness of the reconstructed source, inverse modeling was applied using n random subsets of stations with different sizes. The random process used ensures that each station selected is sufficiently far from the others to mitigate the effects of spatial and temporal correlations. Measurements can be therefore considered independent, which is consistent with the assumption of homoscedasticity.
To interpret the results related to sensitivity analysis, the maps of average and SD of the indicators previously defined are plotted.
Application to 106Ru Source Reconstruction
The aim is to apply the inverse method previously described in order to locate the most probable origin of the 106Ru detections and the quantities released into the atmosphere between 22 September and 13 October.
Atmospheric Dispersion Modeling
Seven hundred twenty source–receptor matrixes are computed in accordance with the domain [10W, 70E], [34N, 70 N] of 2° × 2° resolution. In view of the number of columns of , it requires launching 21 × 720 forward simulations using the Eulerian atmospheric dispersion model ldX. This model is part of IRSN’s C3X operational platform (32). It is based on the Polair3D chemistry transport model (33) and has been validated in past nuclear accidents (16, 34, 35). ldX takes into account dry and wet deposition as well as radioactive decay and filiation. Dry deposition is modeled by a simple scheme with a constant deposition velocity: vdep = 2.10−3 m/s. For wet scavenging, the parameterization used is in the form , where h/(mm⋅s) and p0 is the rainfall intensity in millimeters per hour (36). The simulations are carried out by forcing ldX with three-hourly operational meteorological data from the ARPEGE model provided by Météo France. The spatial resolution of these data is 0.5° × 0.5°. The spatial domain of the ldX simulations is [20W, 90E], [20N, 80N], thus encompassing most of the detections. The time resolution is 10 min and the ldX model provides hourly instantaneous concentrations. The spatial resolution is that of the meteorological data (0.5° × 0.5°) and 11 vertical levels between 0 and 4,400 m are considered. The release height is taken to be the first level of the model, that is, between 0 and 40 m.
Discussion of the Results
Location of the 106Ru Release.
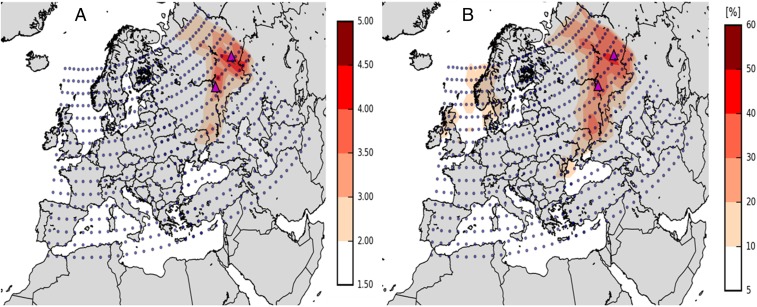
The inverse modeling results show that the values of the parameter have a small influence upon the assessed release location (SI Appendix, Fig. S1). For the sake of simplicity, we have chosen to present the results with . Fig. 1 shows a gridded map of the fac2 and the RFJ attached to each potential source. The higher fac2 is, the higher the agreement between modeled and observed air concentrations. The fac2 values are above 40% in a small area in the Russian Federation along the southern Ural Mountains, consistent with ref. 37. Further west, between Ukraine and Volga, the fac2 values are lower and range from 30 to 40%. In addition, analysis of the simulations, considering a source situated in this area, indicates that it is not possible to reproduce the observations in southern Ural between 26 September and 1 October, when several tens of millibequerels per cubic meter were observed at the Argayash and Novogornyy stations. The winds were blowing from Ural toward Europe throughout this period, so a release situated between Ukraine and Volga, or further west, could not have been carried to Ural. Similarly, a release from Ukraine or further west is not consistent with the detections in Siberia (12).
Fig. 1.
(A) Reduction factor of the cost function. (B) Percentage of simulated air concentrations that are within a factor of 2 of the observed values. Inversion procedure is performed using . Purple triangles represent the location of the Mayak and Dimitrovgrad sites. Blue dots are the 720 potential source locations.
Even though the inverse modeling results show that the northern Ural region is also a potential source region (fac2 > 30%), the number of air concentration measurements available in this area is not sufficient to confirm the relevance of this result. Moreover, the Beloyarsk station situated 150 km north of the Mayak nuclear complex (southern Ural area) did not report the presence of 106Ru between 18 and 25 September, which is not consistent with a release from the northern Ural region. Therefore, the hypothesis of a release emitted from the southern Ural region remains at this step the most relevant because it better explains all of the measurements. Similar results are obtained when a domain of 0.5° × 0.5° resolution is considered (SI Appendix, Fig. S2).
Beyond this geographical area, the fac2 values decrease rapidly down to below 30% at the Russia–Ukraine border. We also notice that the fac2 values range from only 5 to 20% in Romania, even though the highest air concentration activities were measured in the country. Even further west, the fac2 values fall below 5% nearing Poland, Germany, Spain, and France. This means that a release from western Europe is an unlikely hypothesis. The calculations performed using RFJ indicators restrict the most reliable area of the potential release to the southern Ural region (RFJ > 4.5). In this area, the reduction factor is close to 5, whereas it is close to 2 in the Russia–Ukraine border area. It confirms the results obtained using the fac2 indicator.
The Monte Carlo analysis performed for n = 1,000 samples using realistic value of the SD indicates that perturbations in observations have a negligible impact on the source reconstruction. Indeed, the highest averaged RFJ values from the 1,000 samples are located in the southern Urals (SI Appendix, Fig. S3). In addition, the SD calculated from the RFJ indicator (SI Appendix, Fig. S3) is particularly low in the southern Urals, which highlights the robustness of the result.
To assess the effect of the temporal and spatial correlation between stations, the method previously described is applied by considering n = 1,000 random subsets of respectively 10, 20, 50, and 100 stations. A random subset is constructed imposing a minimal distance of 200 km between stations. Then, we applied inverse modeling on each of the random subsets. Since the initial value of the cost function may vary significantly depending on the measurements including in a subset, the use of the RFJ indicator is not suitable to interpret the results. Only the mean and SD of fac2 for subsets of 10, 20, 50, and 100 stations are therefore plotted in SI Appendix, Figs. S4 and S5. SI Appendix, Figs. S4 and S5 show that the southern Urals is identified as the most relevant release area for all subsets considered, including those containing a small number of stations. The higher the size of subset is, the lower the SD of fac2. For example, the SD of fac2 is lower than 5% for a subset of 100 stations, which highlights the robustness of the source location assessment.
Candidate Sites.
In the area where the fac2 values exceed 30%, to our knowledge 2 nuclear facilities have the capacity to produce sufficiently large quantities of 106Ru to be detected thousands of kilometers away. They are the Research Institute of Atomic Reactor (RIAR) in Dimitrovgrad (Volga region, 800 km east of Moscow), a factory producing isotopes for medical use, and the Mayak Production Association in Ozyorsk (south of the Urals, 2,000 km east of Moscow), a spent fuel reprocessing facility.
The Mayak site is in the area where the fac2 and cost function reduction factor values are highest (Fig. 1 and SI Appendix, Fig. S2). The Dimitrovgrad site is located on the western edge of the most reliable area where the values of fac2 and the factor reduction of the cost function do not exceed 35% and 3.5, respectively. These lower scores are explained partly by the fact that a simulated release from the area of the Dimitrovgrad site does not reproduce the air concentrations in southern Ural measured between 26 September and 1 October. Moreover, the release reconstructed by inverse modeling from the area of the Dimitrovgrad site occurs mainly on 27 September, which is not compatible with the daily deposit observations at Kychtym indicating the presence of 106Ru from 23 September.
Source Term Assessment.
For the most relevant area of release defined by fac2 > 30%, the quantity of 106Ru released estimated by inverse modeling ranges from 100 to 1,000 TBq (SI Appendix, Fig. S6). In this area, the release would have started between 23 September in the northern Ural and to a lesser extent 28 September close to the Ukrainian border. In the southern Ural area, identified as the most reliable source location taking account of all of the calculation results, the quantity of 106Ru ranges from 200 to 600 TBq, consistent with the estimate in refs. 38 and 39. Table 1 describes the estimated quantities from the Mayak site as a function of values of the parameter.
Table 1.
Evolution of the source term, fac2, and the error diminution obtained after minimizing the cost function depending on the value of and assuming that Mayak is the release location
| , mBq/m3 | Error reduction of J, % | fac2, % | Source term, TBq |
| 10−3 | 75.2 | 24 | |
| 10−2 | 76.8 | 37 | |
| 10−1 | 77.9 | 43 | |
| 1 | 75.8 | 40 |
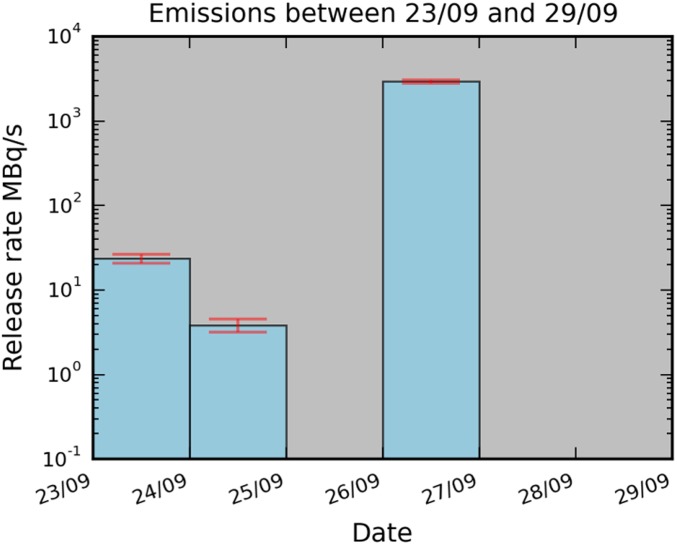
We notice that the source term varies moderately depending on the values of and the maximum estimated quantities are 260 TBq for. In addition, the value of leads to the highest fac2 score (43%) and the maximum error reduction of the cost function (around 78%). The value of is a compromise which avoids giving too much weight to very low concentration values, close to the detection limits, but also avoids giving too much weight to the highest concentrations. In the rest of the paper, we will therefore consider the inversions obtained with as the reference results. In this case, the source term from the Mayak site is 252 ± 13 TBq. Fig. 2 highlights that most of the release occurred on 26 September and very-low-level releases also occurred on 23 and 24 September. Monte Carlo analysis (n = 1,000 inversions using are performed) ascertains that the quantities estimated between 23 and 25 September do not exceed 2 TBq, whereas the reconstructed quantities released on 26 September are around 250 TBq.
Fig. 2.
Mean and SD range of the reconstructed release rates (megabequerels per second) from Mayak computed using Monte Carlo analysis (n = 1,000 samples). Inversion procedure is performed using .
Model-to-Data Comparison
In this section, the source term from the Mayak Production Association is validated by comparing the environmental measurements with the atmospheric dispersion simulation obtained using the ldX model. The agreement between the simulations and the observations over time, the geographical areas, and the type of statistics is evaluated and analyzed.
Plume Dispersion Analysis.
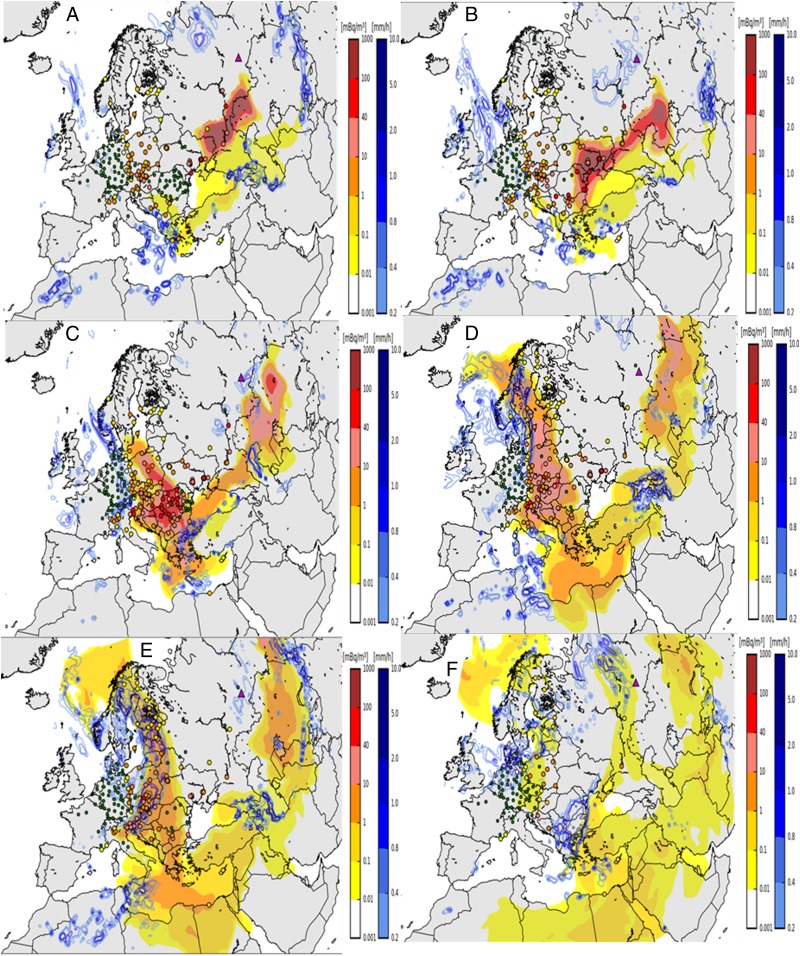
The simulation of the plume dispersion from the Mayak site is shown in Fig. 3 at different dates between 28 September and 7 October. At the start of this period, the meteorological situation was characterized by the presence of a huge anticyclone centered on northeastern Scandinavia (SI Appendix, Fig. S7), encouraging the establishment of an easterly wind between the Urals and a large part of Europe. Following the small releases on 23 September, the first plume reached southeast Europe between 25 and 28 September. The simulated concentration levels in this plume rarely exceed 1 mBq/m3 throughout the period. A second plume is then emitted as a result of the large releases on 26 September. Between 26 and 28 September, again driven by the east winds, this plume headed for the Republic of Tartastan in the Russian Federation, which is consistent with the daily deposit measurements in Bugulma indicating the presence of 106Ru on 26 and 27 September.
Fig. 3.
Dispersion of the 106Ru plume assuming a release from the Mayak site. (A) 28 September 1200, (B) 29 September 1200, (C) 1 October 0000, (D) 2 October 1200, (E) 3 October 1200, (F) 7 October 1200. The dots represent the observed concentrations. Measurements under detection limit are represented by green dots. Precipitations are ranged from 0.2 and 10 mm⋅h−1.
No rain is modeled in this geographical area because of the anticyclonic conditions in the region at the time. The plume then reached the Rostov Oblast in southwest of the Russian Federation on 28 September, when the deposits of 106Ru measured at Morozovsk were about 20 Bq/m2, then Ukraine. The plume was over Romania on 29 September. In the middle of the day on 29 September, the highest simulated hourly concentrations exceeded 100 mBq/m3 between Ukraine and Romania. During the day on 30 September, the simulated plume split in two: One part spread toward Central Europe and the other moved eastwards toward Siberia. Significant precipitation is modeled in southeast Bulgaria, northern Greece, and the westernmost part of Turkey when the simulated air concentrations become significant (>40 mBq/m3). Daily readings from several Bulgarian and Turkish meteorological stations confirm the occurrence of precipitation on 30 September, which agrees with the ARPEGE meteorological model. On 1 October, the main plume was over central Europe and southeastern Europe (Turkey and Greece). The simulated hourly concentrations exceed 40 mBq/m3 in the Czech Republic, Serbia, and Bulgaria but were generally lower in Greece and Turkey (between 1 and 10 mBq/m3). Hourly simulated concentration levels also exceed 40 mBq/m3 in northern Kazakhstan, although no data are available to confirm the simulated concentration levels. On 2 October, the main part of the plume went northward toward Scandinavia and reached the eastern part of Italy, where the simulated levels were up to 40 mBq/m3. Because the anticyclone over Scandinavia subsided (SI Appendix, Fig. S7), the plume’s progress westward was halted. The anticyclone was replaced by a more oceanic weather pattern reflected in the presence of a large rainy front stretching from Germany to Norway at a time when the simulated hourly concentrations were falling but remained close to 30 mBq/m3 in southern Sweden. Between 2 and 3 October, the eastern part of the plume continued to move eastward toward Siberia. The simulated concentrations are much more significant (>10 mBq/m3) further west toward Kazakhstan. From 3 October, westerly winds settled in over a large area of western Europe after the rainy front had passed, causing the plume to spread eastward and have an impact again on several stations in eastern Europe. Levels gradually fell in Europe as the plume spread to North Africa (Libya and Egypt) and the Middle East. Finally, small precipitations are reproduced by the ARPEGE models in the western part of the Russian Federation on 6 and 7 October, when the simulated concentrations are below 1 mBq/m3.
Comparison with 106Ru Air Concentration Measurements.
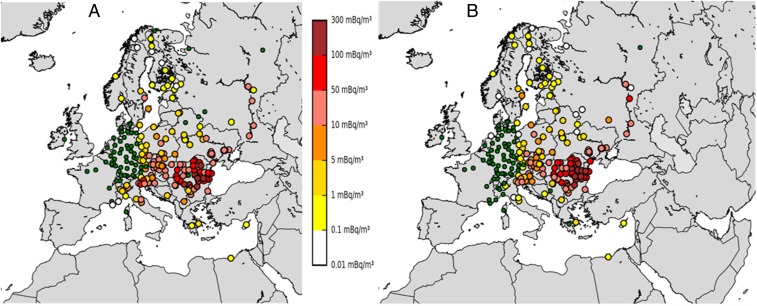
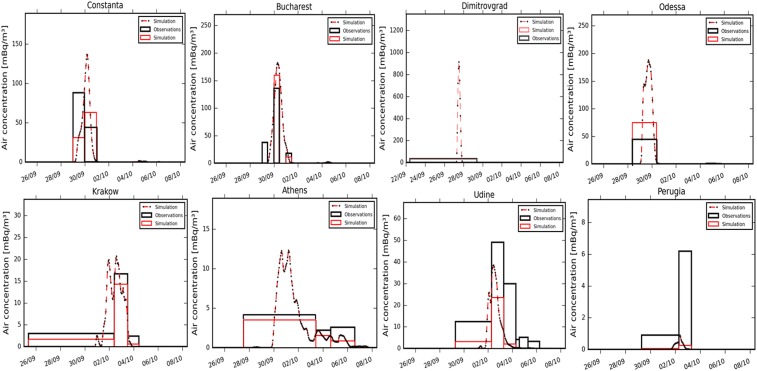
The objective is to study the ability of the simulations to reproduce the observed concentrations and therefore the realism of the assessed source terms. Fig. 4 shows the maximum concentrations observed and simulated by station using the reconstructed source term from the Mayak complex. According to Fig. 4, the simulations clearly distinguish the area delimiting, on the one hand, the stations that did not detect 106Ru, in the western part of Europe and, on the other the stations further east that measured higher levels of 106Ru. This area extends from southeastern France to Denmark, passing through Germany. The maximum observed concentrations are generally well reproduced by the simulations, as shown by the fac2 values presented in Table 1. Fig. 5, which provides examples of comparisons between simulated and observed concentrations at different stations, confirms that the simulation performed using the reconstructed source term satisfactorily reproduces all of the observations. The scores obtained are, for example, higher than for other accident situations such as the Fukushima accident (40). In the Russian Federation, the Dimitrovgrad station indicates that the residence time of the plume evaluated by simulation is less than 24 h. However, the simulated hourly concentration reaches values between 500 mBq/m3 and 1 Bq/m3 on 27 September, 5 times higher than the maximum simulated in Romania (Bucharest and Constanta stations). The sampling period at the Dimitrovgrad station, which lasts for 10 d, explains the much lower levels measured there than in Romania.
Fig. 4.
Maximum 106Ru air concentrations for each monitoring station. (A) Observations. (B) Forward simulation forced using reconstructed source term from Mayak. Green dots represent air concentration measurements below the detection limit.
Fig. 5.
Comparisons between simulated and observed air concentrations at several stations in Europe. A black rectangle shows the activity observed and the red rectangle the simulated air concentration for the observation period. The red dash represents the simulated hourly concentration.
At the stations in Romania, the country where the highest concentrations were measured, the level of agreement between the simulations and the observations is satisfactory even though the observed maximum concentrations are slightly underestimated in the western part of Romania.
Daily or twice-daily sampling at the Romanian stations makes it possible to realistically evaluate the residence time of the plume, which did not exceed 48 h. The simulations manage to reproduce this residence time fairly accurately. It can be seen that the simulated arrival time of the plume at the Bucharest station is several hours late, which may be related to the daily resolution of the reconstructed source term. In central Europe, the simulations show that the plume stayed for ∼72 h between 1 and 4 October (Krakow station in Poland). The vast majority of the simulated and observed concentrations are within a factor of 5. The simulated hourly concentrations vary between 20 and 50 mBq/m3.
In Greece, the Athens station (Fig. 5) indicates that the simulated plume was present between 9 and 11 d. The simulated hourly concentrations, although lower in central Europe, reach 20 mBq/m3. Finally, further west in Europe, the highest concentrations are reported in Italy and sometimes exceed 50 mBq/m3 at the Udine station during the day on 3 October. At this station, the event is relatively well reconstructed by the simulations, although the plume residence time and concentrations are slightly underestimated. At the Perugia station and at other Italian stations further west, the underestimation of the concentration levels observed becomes very large (by a factor of 3 to 10). This underestimate could be induced by the effects of the Alpine relief insufficiently accounted for by the meteorological model at a spatial resolution of 0.5°. It should also be added that the dispersion error increases the further one moves from the potential source of the release.
Comparison with 106Ru Deposition Measurements.
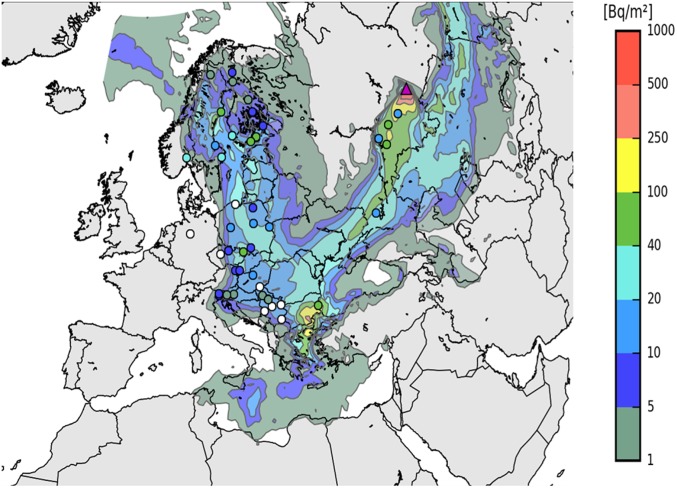
A deposition measurement is generally subject to more variability than a measurement of air concentration because of wet or dry deposition patterns. Its use in models also requires realistic modeling of physical processes such as the deposition of radionuclides by wet scavenging. The deposition measurements were not used to estimate the inverted source term. As a result, comparing the simulated deposits with these observations is a relevant way of validating the source term, especially the total amount assessed. A direct analysis of the observations for deposition indicates that southern Ural is the first region where 106Ru was detected on 23 September. This corroborates the results obtained by inverse modeling targeting southern Ural as the source area of the 106Ru and identifying a small release on 23 September. The simulation of total deposits of 106Ru, based on the reference source term, is shown in Fig. 6.
Fig. 6.
Map of simulated cumulative 106Ru deposition using the reconstructed source term from Mayak. Dots represent the observed cumulative 106Ru deposition. White dots represent measurements under detection limit.
According to Fig. 6, the most significant simulated deposits were concentrated in southwestern Ural, southern Scandinavia, and southeastern Bulgaria, with cumulative quantities sometimes higher than 100 Bq/m2.
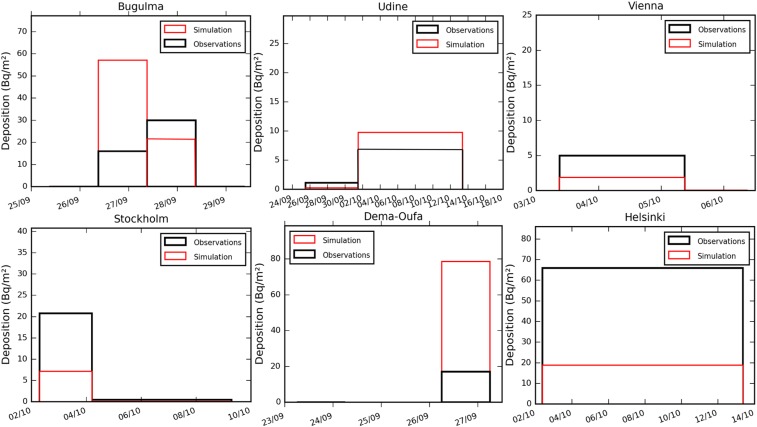
Fig. 7 compares the observed surface activity of 106Ru with the temporal evolution of the simulated deposition. Since the ldX model is performed using 0.5° spatial resolution, several deposition measurements in southern Ural, located in the mesh grid containing the source location, were not exploited. Therefore, only stations located beyond a distance of 200 km from the Mayak site have been taken into account in the model-to-data comparison. Several of these stations are located in western Ural (Bugulma and Dema-Ufa stations) around 500 km west-southwest of the Mayak site. The simulations have a tendency to overestimate the observed deposits by about a factor of 3, particularly in Dema-Ufa. However, the data are incomplete at this station, since daily deposition values are available only for 26 September. Other Russian stations are situated on the edge of the most significant deposits in an area of steep gradients (Fig. 6), which explains the difficulty of reproducing the deposits observed at these stations. Low deposit levels are recorded at several Russian stations including Dimitrovgrad at the beginning of October, despite somewhat limited air concentrations levels. The deposition simulations have difficulty in reproducing this event, despite simulated air concentrations that coincide rather well with the observed air concentrations. The simulated deposits in southeast Bulgaria are > 100 Bq/m2. These simulated deposition values are sometimes greater than those simulated in western Ural. The origin of these larger deposits is explained by the occurrence of precipitation in southeastern Bulgaria as the plume was passing over between 30 September and 1 October. No rainfall is modeled at the Russian stations in southwest Ural when the main plume passed over between 26 and 28 September. To confirm the pertinence of the simulated deposits in Bulgaria, plant and soil samples were taken in several villages in southeast Bulgaria (1) at the start of October 2018. All plant samples and especially litter attest of the presence of 106Ru deposition. However, because of the difficulty to convert bequerels per kilogram into bequerels per square meter, only the soil sample was used, and it confirmed the presence of 106Ru with measured deposits of between 50 and 500 Bq/m2, which is consistent with the simulations. Southern Scandinavia is characterized by measured deposits of nearly 100 Bq/m2, particularly in southern Finland (Helsinki station). These deposits seem to be due to heavy rainfall as the plume was passing over during daytime on 2 October. Although the observed air concentrations are reproduced satisfactorily throughout Scandinavia by the simulations, the observed deposits are underestimated by the simulations, especially in southern Finland.
Fig. 7.
Comparisons between simulated and observed deposits at several stations in Europe. A black rectangle shows the cumulated observed activity over a period and a red rectangle the simulated deposition for the observation period.
In western Europe, the agreement between simulated and observed deposits is more satisfactory (Udine station, Italy), despite the air concentrations’ being underestimated. Finally, low deposition values (<5 Bq/m2) were reported in the Czech Republic and Serbia; these deposits were overestimated by the simulations. The scores are not as good as for air concentration since the proportion of the simulated deposition that is within a factor of 5 of the observed values is 52%.
Conclusion
In this paper, we used an inverse modeling method to identify the origin of 106Ru detections measured in Europe in fall 2017 and to estimate the total amount released into the atmosphere. The method is part of a variational approach, which remains the most appropriate one for operational use. More than 1,100 air concentration observations were used in the inverse modeling process. The observation errors were modeled using log-normal statistics, whereas the background errors were assumed to be Gaussian by enforcing source positivity. The obtained results indicate that a release of about several hundred terabequerels, emitted from the southern of the Urals region, is the most likely hypothesis. It is a release from the southern Urals that manages to consistently explain all of the observations. The meteorological conditions, mainly dominated by the presence of an anticyclone over northeastern Scandinavia, encouraged the dispersion of the 106Ru from southern of the Urals toward western Europe between the end of September and the very beginning of October. Of the known nuclear facilities in this region that are likely to release large quantities of 106Ru, the Mayak site is the most pertinent. Forward simulation of a release from Mayak consistently reproduces observations of air concentrations in Europe and it is the only identified site compatible with the deposition observations made in the southern Urals. The source term evaluated from the Mayak site is about 250 TBq. The density of the observations means that a regularization term is not necessary when resolving the inverse problem, guaranteeing a robust estimate. The simulations made using the source term from Mayak indicate that the percentage of observed and simulated concentrations within a factor of 2 exceeds 40%. The percentage of observed and simulated observations within a factor of 5 is greater than 70%. It can be seen, however, that the observations made furthest from the release point, in Italy, are the most difficult for the simulations to reproduce. Comparisons of the simulations with the deposition measurements, not taken into account in the inversion process, are also realistic. The simulations identify the occurrence of several rainfall events, which are the cause of the higher 106Ru deposits measured in Bulgaria and Scandinavia. Several samples taken in Bulgaria confirmed the presence of 106Ru in proportions similar to those calculated by simulation. However, the deposit is sometimes underestimated by the simulations, particularly in southern Scandinavia. The majority of the release would have occurred during the day on 26 September. Other smaller releases could also have occurred from 23 September, consistent with positive deposition measurements from 23 September in the southern Urals. In future, the use of meteorological fields with a finer spatial and temporal resolution is envisaged, so that observations within a 50-km radius of the release location can be used. Integrating a more realistic wet deposition model (41) could also improve the reconstruction of the 106Ru deposition observed in southern Scandinavia. Finally, IRSN is currently working on the development of probabilistic MCMC methods (42). This type of approach complements the variational approach because it enables the uncertainties of the result of inverse modeling obtained using a variational approach to be quantified.
Supplementary Material
Acknowledgments
We thank V. Durand for helpful discussions and Météo-France for providing the meteorological data.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data deposition: All data discussed in the paper will be made available to readers.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1907823116/-/DCSupplemental.
References
- 1.Masson O., et al. , Airborne concentrations and chemical considerations of radioactive ruthenium from an undeclared major nuclear release in 2017. Proc. Natl. Acad. Sci. U.S.A. 116, 16750–16759 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Masson O., et al. , Potential source apportionment and meteorological conditions involved in airborne 131I detections in January/February 2017 in Europe. Environ. Sci. Technol. 52, 8488–8500 (2018). [DOI] [PubMed] [Google Scholar]
- 3.Stohl A., Computation, accuracy and applications of trajectories–A review and bibliography. Atmos. Environ. 32, 947–966 (1998). [Google Scholar]
- 4.Keats A., Yee E., Lien F. S., Bayesian inference for source determination with applications to a complex urban environment. Atmos. Environ. 41, 465–479 (2007). [Google Scholar]
- 5.Yee E., Lien F. S., Keats A., D’Amours R., Bayesian inversion of concentration data: Source reconstruction in the adjoint representation of atmospheric diffusion. J. Wind Eng. Ind. Aerodyn. 96, 1805–1816 (2008). [Google Scholar]
- 6.Lucas D. D., Simpson M., Cameron-Smith P., Baskett R. L., Bayesian inverse modeling of the atmospheric transport and emissions of a controlled tracer release from a nuclear power plant. Atmos. Chem. Phys. 17, 13521–13543 (2017). [Google Scholar]
- 7.Liu Y., et al. , Uncertainty quantification of pollutant source retrieval: Comparison of Bayesian methods with application to the Chernobyl and Fukushima Daiichi accidental releases of radionuclides. Q. J. R. Meteorol. Soc. 143, 2886–2901 (2017). [Google Scholar]
- 8.Delle Monache L., et al. , Bayesian inference and Markov chain Monte Carlo sampling to reconstruct a contaminant source on a continental scale. J. Appl. Meteorol. Climatol. 47, 2600–2613 (2008). [Google Scholar]
- 9.Tichý O., et al. , Bayesian inverse modeling and source location of an unintended I-131 release in Europe in the fall of 2011. Atmos. Chem. Phys. 17, 12677–12696 (2017). [Google Scholar]
- 10.Yee E., Hoffman I., Ungar K.. Bayesian inference for source reconstruction: A real-world application. Int. Sch. Res. Notices 2014, 1–12 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Seibert P., Frank A., Source-receptor matrix calculation with a Lagrangian particle dispersion model in backward mode. Atmos. Chem. Phys. 4, 51–63 (2004). [Google Scholar]
- 12.Kovalets I. V., Andronopoulos S., Venetsanos A. G., Bartzis J. G., Identification of strength and location of stationary point source of atmospheric pollutant in urban conditions using computational fluid dynamics model. Math. Comput. Simul. 82, 244–257 (2011). [Google Scholar]
- 13.Stohl A., et al. , Xenon-133 and caesium-137 releases into the atmosphere from the Fukushima Dai-ichi nuclear power plant: Determination of the ST, atmospheric dispersion, and deposition. Atmos. Chem. Phys. 12, 2313–2343 (2012). [Google Scholar]
- 14.Winiarek V., Bocquet M., Saunier O., Mathieu A., Estimation of errors in the inverse modeling of accidental release of atmospheric pollutant: Application to the reconstruction of the cesium-137 and iodine-131 STs from the Fukushima Daiichi power plant. J. Geophys. Res. Atmos. 117, D05122 (2012). [Google Scholar]
- 15.Winiarek V., et al. , Estimation of the caesium-137 source term from the Fukushima Daiichi nuclear power plant using a consistent joint assimilation of air concentration and deposition observations. Atmos. Environ. 82, 268–279 (2014). [Google Scholar]
- 16.Saunier O., et al. , An inverse modeling method to assess the source term of the Fukushima Nuclear Power Plant accident using gamma dose rate observations. Atmos. Chem. Phys. 13, 11403–11421 (2013). [Google Scholar]
- 17.Bocquet M., Reconstruction of an atmospheric tracer source using the principle of maximum entropy. II: Applications. Q. J. R. Meteorol. Soc. 131, 2209–2223 (2005). [Google Scholar]
- 18.Krysta M., Bocquet M., Brandt J., Probing ETEX-II data set with inverse modelling. Atmos. Chem. Phys. 8, 3963–3971 (2008). [Google Scholar]
- 19.Krysta M., Bocquet M., Source reconstruction of an accidental radionuclide release at European scale. Q. J. R. Meteorol. Soc. 133, 529–544 (2007). [Google Scholar]
- 20.Davoine X., Bocquet M., Inverse modelling-based reconstruction of the Chernobyl source term available for long-range transport. Atmos. Chem. Phys. 7, 1549–1564 (2007). [Google Scholar]
- 21.Federal Service for Hydrometeorology and Environmental Monitoring , Roshydromet - Typhoon Association. http://www.rpatyphoon.ru/. Accessed 29 October 2019.
- 22.Roshydromet , Report on the causes and source of ruthenium-106 on the territory of Russia in September-October 2017 (Отчет по определению причин и источника рутения-106 на территории России в сентябре-октябре 2017 года) [in Russian]. (2017). http://egasmro.ru/files/documents/reports/report_28_12_2017.pdf. Accessed 29 October 2019.
- 23.EGASMRO , БЮЛЛЕТЕНЬ о радиационной обстановке на территории России в сентябре 566 2017 г [in Russian]. http://egasmro.ru/files/documents/ro_bulletins/byulleten_rorf_09_2017.pdf. Accessed 29 October 2019.
- 24.EGASMRO , БЮЛЛЕТЕНЬ о радиационной обстановке на территории России в октябре 569 2017 г [in Russian]. http://egasmro.ru/files/documents/ro_bulletins/byulleten_rorf_10_2017.pdf. Accessed 29 October 2019.
- 25.CRIIRAD , Contamination par le ruthénium 106 [in French]. (2018). http://www.criirad.org/accident-et-pollutions/Note_CRIIRAD_N_18-21_Ru_106_Mayak.pdf. Accessed 29 October 2019.
- 26.Ramebäck H., et al. , Measurements of 106Ru in Sweden during the autumn 2017: Gamma-ray spectrometric measurements of air filters, precipitation and soil samples, and in situ gamma-ray spectrometry measurement. Appl. Radiat. Isot. 140, 179–184 (2018). [DOI] [PubMed] [Google Scholar]
- 27.Seibert P., Methods for source determination in the context of the CTBT radionuclide monitoring system. (2000). http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.540.265&rep=rep1&type=pdf. Accessed 29 October 2019.
- 28.Winiarek V., Vira J., Bocquet M., Sofiev M., Saunier O., Towards the operational estimation of a radiological plume using data assimilation after a radiological accidental atmospheric release. Atmos. Environ. 45, 2944–2955 (2011). [Google Scholar]
- 29.Abida R., Bocquet M., Targeting of observations for accidental atmospheric release monitoring. Atmos. Environ. 43, 6312–6327 (2009). [Google Scholar]
- 30.De Meutter P., Camps J., Delcloo A., Termonia P., Source localisation and its uncertainty quantification after the third DPRK nuclear test. Sci. Rep. 8, 10155 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Liu D. C., Nocedal J., On the limited memory method for large scale optimization. Math. Program. B. 45, 503–528 (1989). [Google Scholar]
- 32.Tombette M., et al. , C3X: A software platform for assessing the consequences of an accidental release of radioactivity into the atmosphere. (2014). http://venus.iis.u-tokyo.ac.jp/english/workshop/Poster/3rd%20March/Damien%20Didier.pdf. Accessed 29 October 2019.
- 33.Boutahar J., et al. , Development and validation of a fully modular platform for the numerical modeling of air pollution: POLAIR. Int. J. Environ. Pollut. 22, 17–28 (2004). [Google Scholar]
- 34.Quelo D., et al. , Validation of the Polyphemus platform on the ETEX, Chernobyl and Algeciras cases. Atmos. Environ. 41, 5300–5315 (2007). [Google Scholar]
- 35.Mathieu A., et al. , Atmospheric dispersion and deposition of radionuclides from the Fukushima Daiichi nuclear power plant accident. Elements 8, 195–200 (2012). [Google Scholar]
- 36.Baklanov B., Sørensen J. H., Parameterisation of radionuclides deposition in atmospheric long-range transport modelling. Phys. Chem. Earth B Hydrol. Oceans Atmos. 26, 787–799 (2001). [Google Scholar]
- 37.Bossew P., et al. , An episode of Ru-106 in air over Europe, September-October 2017–Geographical distribution of inhalation dose over Europe. J. Environ. Radioact. 205-206, 79–92 (2019). [DOI] [PubMed] [Google Scholar]
- 38.Kovalets I. V., Romanenko an detection of ruthenium-106 in 2017: Meteorological analysis of the potential sources. (2017). https://www.linkedin.com/pulse/detection-ruthenium-106-2017-meteorological-analysis-sources-ivan/. Accessed 29 October 2019.
- 39.Sørensen J. H., Method for source localization proposed and applied to the October 2017 case of atmospheric dispersion of Ru-106. J. Environ. Radioact. 189, 221–226 (2018). [DOI] [PubMed] [Google Scholar]
- 40.Kitayama K., et al. , Atmospheric modeling of 137 Cs plumes from the Fukushima Daiichi nuclear power plant-evaluation of the model intercomparison data of the science council of Japan. J. Geophys. Res. Atmos. 123, 7754–7770 (2018). [Google Scholar]
- 41.Querel A., Roustan Y., Quelo D., Benoit J. P., Hints to discriminate the choice of wet deposition models applied to an accidental radioactive release. Int. J. Environ. Pollut. 58, 268–279 (2018). [Google Scholar]
- 42.Dumont Le Brazidec J., Bocquet M., Saunier O., Roustan Y., MCMC methods applied to the reconstruction of the autumn 2017 Ru-106 atmospheric contamination source. Atmos. Environ. (2019). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.