Extensive free-energy simulations identify water as the base in nucleotide addition by DNA polymerase

Significance

The microscopic chemical mechanism of adding a base to a growing strand of DNA during DNA replication is unknown. The chemistry requires multiple proton transfers in a complex active site, and experimental probes have been unable to distinguish among the many plausible reaction pathways. This work uses an efficient computational approach to systematically survey the many plausible chemical mechanisms for the reaction and concludes that a water molecule in the active site plays a crucial role. The work also clarifies the catalytic role played by a controversial third metal cation that appeared in the active site during crystallographic studies. The new mechanistic understanding will guide studies of medically and technologically vital questions on DNA replication, gene expression, and gene editing.

Abstract

Transphosphorylation of nucleotide triphosphates is the central reaction in DNA replication by DNA polymerase as well as many other biological processes. Despite its importance, the microscopic chemical mechanism of transphosphorylation of nucleotide triphosphates is, in most cases, unknown. Here we use extensive simulations of DNA polymerase η to test mechanistic hypotheses. We systematically survey the reactive space by calculating 2D free-energy surfaces for 10 different plausible mechanisms that have been proposed. We supplement these free-energy surfaces with calculations of pK_a for a number of potentially acidic protons in different states relevant to the catalytic cycle. We find that among all of the conditions that we test, the smallest activation barrier occurs for a reaction where a Mg²⁺-coordinated water deprotonates the nucleophilic 3′-OH, and this deprotonation is concerted with the phosphoryl transfer. The presence of a third Mg²⁺ in the active site lowers the activation barrier for the water-as-base mechanism, as does protonation of the pyrophosphate leaving group, which is consistent with general acid catalysis. The results demonstrate the value of simulations, when used in conjunction with experimental data, to help establish a microscopic chemical mechanism in a complex environment.

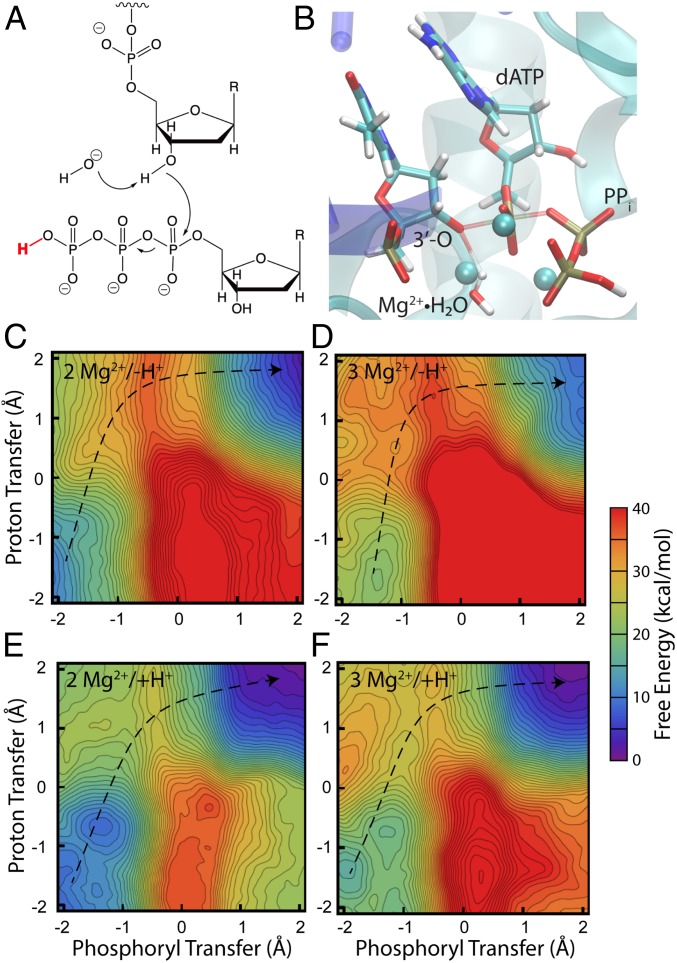
One of the most vital biological reactions is the transphosphorylation of nucleotide triphosphates (NTPs), where the triphosphate is cleaved at either P_α-O-P_β or P_β-O-P_γ (Fig. 1). Transphosphorylation of NTPs drives processes ranging from the work done by motor proteins, to signal transduction by G protein coupled receptors, to gene expression and replication by nucleic acid synthases (1, 2). Despite this ubiquitous role, the chemical and physical mechanisms of transphosphorylation of NTPs have been opaque to experimental and computational probes (3). A range of factors contribute to the challenge of elucidating these mechanisms, including complex active sites that contain metal cations and are often exposed to solvent (Fig. 2). Solvent exposure may implicate participation of water molecules in multiple roles, including nucleophilic attack and shuttling of protons throughout the active site. Furthermore, the triphosphate moiety possesses a rich electronic nature that overwhelms typical computational methods—particularly when metals are present—which limits the aid that computational work can provide. On top of that, the many imaginable mechanisms and many imaginable protonation states within each mechanism present a daunting challenge to those interested in a methodical search of mechanistic space. Here we present steps toward overcoming these obstacles through an efficient hybrid quantum mechanics/molecular mechanics (QM/MM) exploration of the nucleotide addition cycle by a DNA polymerase.

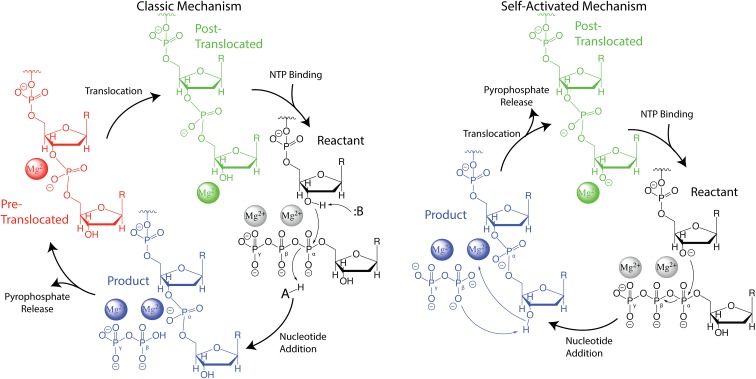
Fig. 1.

Mechanistic proposals for the nucleic acid elongation cycle by nucleic acid polymerases. Each of the states along the proposed cycles is colored differently (e.g., reactant, product, pre-translocated, and post-translocated). One of the key differences between the 2 mechanisms is the protonation state of the 3′-OH, which serves as the nucleophile for nucleotide addition. In the classic mechanism the 3′-OH is deprotonated by some base immediately prior to or concerted with nucleophilic attack. In the self-activated mechanism, the pyrophosphate leaving group deprotonates the 3′-OH, which leaves the 3′-O deprotonated in the post-translocated state, prior to binding of the next NTP. One of the Mg²⁺ ions is bound principally by the NTP and is thought to be released when pyrophosphate is released. Additionally, recent work indicated that a third Mg²⁺ plays some role in catalysis (11). We have omitted the third Mg²⁺ from this figure for clarity, but when appropriate, our simulations include it to explore its role in the reaction.

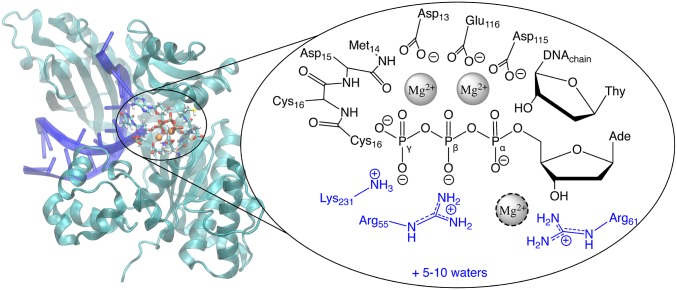
Fig. 2.

The structure of DNAP, highlighting the active site groups that were treated at the QM level during simulations. We have shown the reactant state here; other states used the same protein residues in the QM region, but the details of the nucleotide/DNA and protonation states differed depending on the particular objective. QM link atoms were placed between C_α and C_β for most protein residues. Link atoms in the backbone between the carbonyl C and C_α allowed us to include the backbone from M14-C16; the side chains of D15 and C16 were omitted with link atoms between C_α and C_β. The Mg²⁺ surrounded by a dotted line was only present at all in models based on the crystal structure of the product. The protein residues colored blue were not included in the QM region in simulations that used the small QM region, and the small QM region contained only 2 QM waters. The 2D free-energy surfaces used the small QM region.

Nucleic acid polymerases, including DNA and RNA polymerases, as well as reverse transcriptase, DNA primase, etc., processively elongate nucleic acids by adding nucleotides to the 3′-O of the growing polymer (4, 5). Overall structures of nucleic acid polymerases vary widely, ranging from small monomers to large multisubunit complexes, but their active site architectures are strikingly similar (6, 7), suggesting that evolution may have converged on similar nucleotide addition mechanisms (5, 6, 8, 9). In general, these enzymes are known to require at least 2 divalent metal ions to activate the terminal 3′-OH of the growing polymer for nucleophilic attack at the α-phosphate of the NTP substrate. The nucleophilic attack at the α-phosphate displaces a pyrophosphate leaving group as a byproduct. Important mechanistic questions persist, though, particularly in terms of acid–base chemistry and the role(s) of the metal cations.

Most proposals for the mechanism of nucleotide addition (6, 9, 10) suggest that deprotonation of the nucleophilic 3′-OH occurs after an incoming NTP has bound, which allows the nucleophilic displacement to occur immediately following, or even concerted with, the deprotonation (Fig. 1, classic mechanism). Furthermore, that deprotonation is usually proposed to be accomplished by either an active site residue or by a water present in the active site. A recent study by De Vivo and coworkers (7), though, proposed an intriguing alternative after the authors noticed a conspicuous proximity of the pyrophosphate leaving group to the 3′-OH of the just-added nucleotide. In the self-activated mechanism that they proposed, the pyrophosphate serves as the base to deprotonate the 3′-OH of the just-added nucleotide (Fig. 1, self-activated mechanism). This proton abstraction occurs concurrently with translocation, which is the process of polymerase shifting registers along the template DNA to prepare to add the next nucleotide. Thus, the 3′-OH is deprotonated and ready for nucleophilic attack as soon as the next NTP binds to the active site.

Here we test a number of mechanistic proposals for nucleotide addition by DNA polymerase using a variety of simulation methods, including calculations of the free-energy profiles for different steps in the reaction and calculations of the pK_a of potentially deprotonated oxygens. We find that the 3′-OH is unlikely to be deprotonated by the pyrophosphate, and regardless of what serves as the base, the 3′-OH is unlikely to be deprotonated in the post-translocated complex, as implied by the self-activated mechanism. Instead, we find more plausible energetics for mechanisms where a base deprotonates the nucleophile only after binding of the incoming NTP. In each mechanistic proposal, including the self-activated mechanism, we test the role of a third Mg²⁺ which was observed in time-resolved crystal structures of the reaction (11, 12). We also test the role of protonating the pyrophosphate leaving group which was suggested by proton inventory studies (6, 9). By comparing the computed energetics of each mechanism against available experimental data, we reach the conclusion that the only energetically plausible pathway is one in which an active site water molecule deprotonates the 3′-OH, which attacks the α-phosphate in a concerted step. We find that the presence of a third Mg²⁺ contributes to lowering the activation barrier as well as to stabilizing the product. Overall, our work illustrates how experimental results and atomistic simulations, only when used together, can help distinguish among many plausible microscopic chemical mechanisms in a complex environment.

Results and Discussion

Tests of the Self-Activated Mechanism.

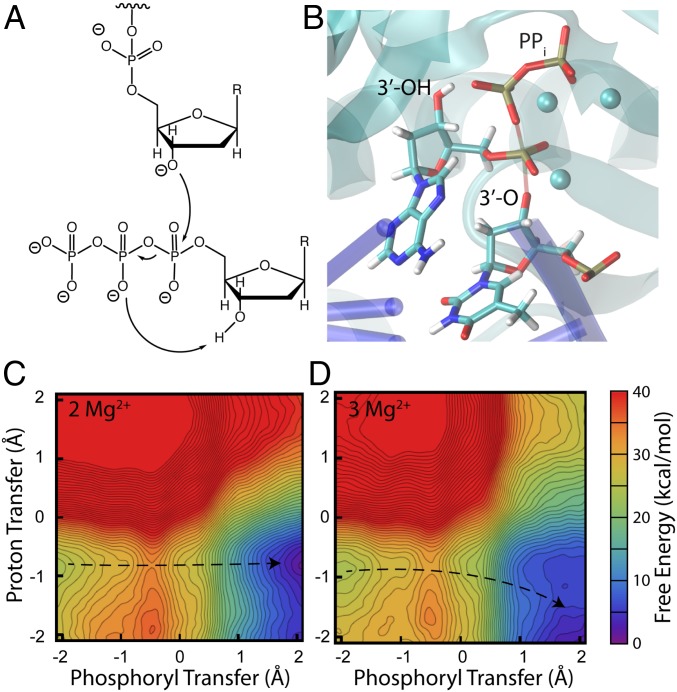
The recently proposed self-activated mechanism for nucleotide addition (7) has several distinguishing features versus the classic mechanism. Two of the most important of these are 1) following nucleotide addition, the pyrophosphate leaving group deprotonates the 3′-OH of the just-added nucleotide and 2) that 3′-O remains deprotonated throughout the subsequent kinetic steps, up until its nucleophilic attack on the next NTP. We initially tested these features by calculating a free-energy surface for the nucleotide addition step assuming that the nucleophilic 3′-OH is already deprotonated in the reactant state and that the pyrophosphate leaving group deprotonates the 3′-OH of the just-added nucleotide (Fig. 3). For the mechanism with 2 Mg²⁺, the nucleophilic attack has a small barrier (∆G^‡ = 10.7 kcal/mol) and is quite exergonic (∆G_reaction = −22.2 kcal/mol); the subsequent proton transfer, though, is quite endergonic and does not, in fact, exhibit a product well. Adding a third Mg²⁺ to the active site stabilizes the transition state for phosphoryl transfer, reducing the barrier height (∆G^‡ = 7.9 kcal/mol), and the reaction remains highly exergonic (∆G_reaction = −22.0 kcal/mol). Still, as with 2 Mg²⁺, any proton transfer from the 3′-OH to the pyrophosphate is unfavorable, and we observe no product well for that process. Thermodynamic parameters for these surfaces and all others in this study are listed in Table 1. The relatively small barrier we observe qualitatively agrees with the small barrier found by a hybrid density functional theory method (B3LYP/6-31G**), which is much more computationally costly and only allowed for much more limited MD sampling (13). That work observed a more substantial effect of the third Mg²⁺: with only 2 Mg²⁺, ∆G^‡ increased by ∼15 kcal/mol, and ∆G_reaction increased by 25 to 30 kcal/mol. However, we note that the contribution of an active site Mg²⁺, which was not resolved in the original crystal structure, to peptide bond formation in the ribosome was estimated by QM/MM calculations (14) to be ∼2-3 kcal/mol on the barrier height. The surprisingly large effect of a third Mg²⁺ in ref. 13 tempts us to speculate that it is partially attributable to limited MD sampling. Calculations with 3 Mg²⁺ start from a structure of the product, while those with 2 Mg²⁺ start from a structure of the reactant. The initial conformations, therefore, favor either the reactant or the product, meaning an overly exergonic reaction with 3 Mg²⁺ and an overly endergonic reaction with 2 Mg²⁺. That bias cannot be overcome without extensive simulation time to allow the environment to adapt to electronic changes in the reacting groups. The tradeoff between QM reliability and simulation timescale remains a challenge for complex systems such as this.

Fig. 3.

Mechanism (A), transition state structure (B), and free-energy surfaces for nucleotide addition in the self-activated mechanism with either 2 Mg²⁺ (C) or 3 Mg² (D). The proximity of the pyrophosphate leaving group to the 3′-OH of the just-added nucleotide suggested that the pyrophosphate could deprotonate the 3′-OH (7). The phosphoryl transfer coordinate is defined as the difference in length of the breaking and forming O–P bonds, and the proton transfer coordinate is defined as the difference in length of the breaking and forming O–H bonds. The structure in B is representative of the transition state region for the reaction with three Mg²⁺, with the breaking and forming bonds shown as transparent. The third Mg²⁺ ion lowers the barrier for phosphoryl transfer (∆G^‡ = 10.7 kcal/mol vs. 7.9 kcal/mol for 2 and 3 Mg²⁺). In neither case, though, is subsequent proton abstraction by the pyrophosphate a plausible next step; that process is steeply endergonic regardless of the number of metals. While there is a short hydrogen bond between the leaving group and the 3′-OH of the nucleotide being added, the leaving group cannot abstract that proton. We note that in these surfaces, as well as all others in the main text, the simulations sampled the entirety of the displayed reaction space; the free-energy scale was truncated at +40 kcal/mol for all surfaces for clarity of individual surfaces and to simplify comparisons among the various mechanisms. The dotted lines guide the eye along the minimum free-energy path from reactant to product; the transition state corresponds to the location of the maximum free energy along this minimum path.

Table 1.

Reaction energetics (kcal/mol) for each mechanism

Base	Metals	Leaving group	∆G‡	∆Greaction
Pyrophosphate*	2 Mg2+	Deprotonated*	10.7	−22.2
	3 Mg2+	Deprotonated*	7.9	−22.0
Asp115	2 Mg2+	Deprotonated	27.3	+5.0
		Protonated	24.2	+0.6
	3 Mg2+	Deprotonated	25.4	−2.1
		Protonated	25.8	+5.4
Mg2+-bound water	2 Mg2+	Deprotonated	28.6	−7.5
		Protonated	18.2	−7.7
	3 Mg2+	Deprotonated	16.8	−12.6
		Protonated	12.9	−15.9

^*The self-activated mechanism. In principle, the mechanism involves protonation of the leaving group, but our simulations show this to be unfavorable, and the parameters for ∆G_reaction for that mechanism use the product well with proton still bound to the just-added nucleotide (Fig. 3).

In any case, our simulations and the previous ones find quite small barriers for the reaction. While one might be tempted to conclude that the small barriers, especially with the third Mg²⁺, lend credence to this mechanism, we caution against that because the simulation starts with a deprotonated 3′-O. There is some energetic cost associated with deprotonating the 3′-O, and Fig. 3 demonstrates that the pyrophosphate cannot accomplish this. To be fair, ref. 7 suggested that the proton transfer from the 3′-OH to pyrophosphate is concerted with the process of translocation and release of the pyrophosphate. Testing this possibility is particularly challenging because it requires a method that can reliably model proton transfers in this setting while simultaneously simulating the large structural changes of translocation (15). The simulation time necessary to directly test this process with a suitable QM method is prohibitively expensive, as indicated by the minimally sampled free-energy surface of ref. 7. To overcome this issue, rather than attempting to simulate translocation at the QM/MM level, we calculated the free-energy profile for H⁺ transfer in the post-translocated state (SI Appendix, Fig. S3) to complement the pre-translocated calculation (Fig. 3). We reasoned that regardless of any potential coupling between translocation and H⁺ transfer, in order to be a thermodynamically favorable process, the H⁺ transfer needs to be exergonic in either the pre-translocated state or the post-translocated state. SI Appendix, Fig. S3, shows that even in the post-translocated state, H⁺ transfer from the 3′-OH to the pyrophosphate is endergonic.

Although our results show that proton transfer from the just-added 3′-OH to the pyrophosphate is disfavorable, Fig. 3 indicates that protonation of the leaving group is not required for phosphoryl transfer to be favorable. This result is surprising in the context of experiments that suggested a general acid protonates pyrophosphate in other polymerases (6). Our finding does not eliminate the possibility of protonation of pyrophosphate by a general acid but hints that it is not required, which may be why mutants of proposed general acids retained enzymatic activity (6). We also note that a recent study of RNA polymerase indicated that general acid catalysis may not be universal (10). We explore the effect and need for protonating the leaving group in more detail for other mechanisms below. In the self-activated mechanism the thermodynamics of the phosphoryl transfer are presumably made more favorable by the initial condition, namely, a deprotonated 3′-OH. The deprotonated form is perhaps not the most stable form of the nucleophile, and to test its stability we calculated its pK_a in various states.

An important point made by ref. 7 is that in the self-activated mechanism, after pyrophosphate abstracts the proton, the proton can quickly transfer among the oxygens of the pyrophosphate. That is to say, the ultimate proton acceptor is not rigorously defined, particularly once the pyrophosphate dissociates from the active site and is dissolved in the enzyme’s buffered surroundings. Thus, the free-energy profile for the proton transfer may not be the most direct test of when and how the 3′-OH is deprotonated. A test that gets to the crux of the self-activated mechanism is to determine what the state of the 3′-OH is following dissociation of the pyrophosphate but prior to binding of the incoming NTP (cf. Fig. 1). Does the 3′-OH lose its proton prior to or after binding of the incoming NTP? The central issue, then, is how the active site perturbs the pK_a of the 3′-OH (13). If the 3′-OH is deprotonated in the apo state at physiological pH, this would indicate that the active site environment of DNAP lowers the pK_a of that hydroxyl by nearly 10 pH units, which would be a surprising result, although not unprecedented. Human carbonic anhydrase II (CAII) (16), for example, is known to lower the pK_a of an active site water to around 7, and some researchers (17, 18) have suggested that an active site serine in Escherichia coli alkaline phosphatase (AP) has a pK_a ≤ 5.5. To test the protonation state of the 3′-OH, we calculated how the active site perturbs its pK_a in various states that are relevant to either the self-activated mechanism or the classic mechanism (Table 2). Since the 3′-OH is a secondary alcohol, we used isopropanol in water (pK_a = 16.5) as a reference point for determining the perturbation in the active site. Isopropanol may not be a perfect reference (19), but it generally mimics the chemical nature of the 3′-OH to achieve substantial cancellation of any errors. We found that the pK_a shifts substantially in models of the pre-translocated and post-translocated state and with or without pyrophosphate and a third Mg²⁺ in the active site. The lowest pK_a, as one would intuitively expect, is in the post-translocated state where pyrophosphate has dissociated but the incoming NTP has not yet bound. We generated this state based on crystal structures of both the reactant and product, by deleting the NTP or the added nucleotide, respectively. The pK_a values for the 2 models of the post-translocated state are 9.0 and 12.0, respectively. Measurements of pH indicate that in the nucleus of mammalian cells the pH is 7.5 to 8.0 (20), implying that the 3′-OH is predominantly protonated in the post-translocated state. We note that the pK_a calculations all included at least 2 Mg²⁺, but the second Mg²⁺ is tightly bound to the pyrophosphate and dissociates at the same time that the pyrophosphate does. The loss of positive charge in the active site would increase the pK_a of the 3′-OH, further disfavoring the deprotonated species. Thus, pK_a = 9.0 should be regarded as a lower limit of the true pK_a in the post-translocated state, and the following tests demonstrate the reliability of our calculated values.

Table 2.

Calculated vs. experimental pK_a values

Proton and environment	Charge*	∆pKa†	pKa (calc)	pKa (exp)	Ref. (exp)
DNAP post-translocated 3′-OH
Reference: isopropanol				16.5
3Mg2+/+pyrophosphate/large QM‡	+2	−1.5	15.0
3Mg2+/+pyrophosphate/small QM‡	−1	−1.5	15.0
2Mg2+/-pyrophosphate/product‡	+1	−7.5	9.0
2Mg2+/-pyrophosphate/reactant§	+1	−4.5	12.0
DNAP reactant Mg2+-H2O
Reference: water				14.0
2Mg2+/dATP	+1	+15.0	29.0
3Mg2+/dATP	+2	+2.6	16.6
2Mg2+/dATP•H+	+2	+8.0	22.0
3Mg2+/dATP•H+	+3	−0.4	13.6
Test Cases
Reference: water				14.0
Zn2+•H2O (aqueous)	+2	−6.2	7.8	9.0	(54)
Mg2+•H2O (aqueous)	+2	−1.3	12.7	11.2	(54)
Zn2+•H2O (WT CAII)	+2	−6.5	7.5	6.8	(16)
Zn2+•H2O (H94D CAII)	+1	−3.2	10.8	≥9.6	(16)
Reference: ethanol				16.0
Zn2+•OHSer102 (AP)	+2	−4.2	11.8	≤5.5	(17)

^*Total charge of the QM region in the protonated state.

^†Change in pK_a value relative to the italicized reference species in water. The reference species were chosen to represent the local bonded environment of the acidic proton, such that the shift in pK_a captures only the effects of changing the surrounding environment.

^‡Generated from the crystal structure of the product.

^§Generated from the crystal structure of the reactant.

We have shown that our DFTB3/MM free-energy perturbation method (21) is accurate to within 1 to 2 pH units for calculating the relative pK_a of a series of alcohols in water (22) and metal-coordinated water in solution (23), but we have still not fully calibrated the effects of metals on pK_a in enzyme active sites. To do such a calibration, we have calculated shifts in pK_a for systems with analogous metal-induced perturbations on -OH groups. We find that our calculations accurately reproduce the shift in pK_a induced by metal cations to within 1 to 2 pH units (Table 2). This includes both metals in solution and in the active sites of CAII (WT and H94D). A discrepancy appears in our calculation of the pK_a of the nucleophillic serine of AP. The experimental work suggested that the pK_a of serine is lowered by over 10 pH units, to ca. 5. The pK_a of the water in CAII lends plausibility to that value, but closer comparison of CAII—and its mutants—with AP suggests that there may be reason to reexamine the measurements in AP. In particular, mutation of CAII showed how the ligands coordinating Zn²⁺ affect the active site water’s pK_a. In wild-type CAII, the Zn coordination is His₃(H₂O), leaving an overall charge of +2, and the pK_a is ∼7.5. In His→Asp mutants, though, the coordination is His₂Asp(H₂O), and the charge lowers to +1, which shifts the pK_a upward by at least 3 pH units (H94D has a pK_a ≥ 9.6) (16). The relevant Zn²⁺ in AP has an additional Asp, making the coordination HisAsp₂(Ser) and the overall charge neutral. There are additional cations in the vicinity, including another Zn²⁺, a Mg²⁺, and an Arginine, but these cations are also neutralized by anionic protein side chains. Altogether, therefore, we believe additional studies are necessary to measure the pK_a of AP’s nucleophilic serine and how it is activated. Otherwise, our test cases lend confidence to our calculated pK_a values in DNAP.

The primary source of uncertainty in our pK_a calculations, then, seems to be in how we generated the model of the post-translocated state. That uncertainty is highlighted by the discrepancy between our 2 models of that state (pK_a = 9.0 vs. pK_a = 12.0). As mentioned, though, these models both contain 2 Mg²⁺, but the true post-translocated state probably contains only 1 (24), which will leave the deprotonated 3′-OH even less favored than in our models. Thus, we maintain that pK_a = 9.0 can be viewed as a lower limit for the post-translocated state, meaning that in contrast to the self-activated mechanism, the 3′-OH is only transiently deprotonated, either immediately prior to nucleophilic attack or concerted with the nucleophilic attack. That transient deprotonation would be consistent with various flavors of the classic mechanism.

Tests of the Classic Mechanism.

The general framework of the classic mechanism allows for a variety of specific mechanisms (8). The base that deprotonates the 3′-OH and the acid that protonates the pyrophosphate (if, indeed, that occurs) are yet to be conclusively identified; when those processes occur and when the third Mg²⁺ binds and what its role might be are all open questions. Many of these questions are opaque even to the most sophisticated experimental probes. An exhaustive computational search of this vast mechanistic space is daunting and requires a QM/MM method that balances speed and reliability. In what follows, we find that the DFTB3/MM method is poised for such a challenge; we simulate many possible mechanisms, and after presenting the results we will discuss their reliability in the context of higher-level QM calculations as well as experiments. To test possibilities for the classic mechanism using a minimal level of MD sampling, we have calculated a series of 2D free-energy profiles that use proton abstraction and phosphoryl transfer as the reaction coordinates, similar to the profiles for the self-activated mechanism. We leave many questions about protonation of the pyrophosphate leaving group for future work, but we have examined the effect of protonating the pyrophosphate on the other 2 coordinates. The free-energy surfaces disqualify certain mechanisms based on the magnitude of the activation barrier; others have plausible activation barriers, and by interpreting the simulations in the context of experimental results we are able to conclude the nature of the microscopic mechanism of the reaction.

We first discuss the possibility of general base catalysis, by either Asp115 or Glu116, which are the most reasonable candidates for an enzymatic base. Both of those residues are 3.2 Å from the 3′-O in the crystal structure. The next nearest titratable group, Asp13, is 4.5 Å from the 3′-O, and a Mg²⁺ is directly in the middle. To test the propensity for either Asp115 or Glu116 to deprotonate the 3′-OH, we calculated a free-energy surface using a reaction coordinate based on the center of excess charge (i.e., the position of the proton) (25) along a path from Asp to 3′-O to Glu (SI Appendix, Fig. S4). The free-energy profile indicates that Asp115 may be a suitable base to transiently deprotonate the 3′-OH, but Glu116 appears unlikely to serve as a base. Thus, our next simulations focused on a mechanism where Asp115 deprotonates the 3′-OH to prepare it for nucleophilic attack.

We have calculated the Asp115-catalyzed mechanism in 4 different contexts: with and without a third Mg²⁺ and with and without a protonated pyrophosphate leaving group. The free-energy surfaces for that mechanism (Fig. 4) indicate that Asp115 is not proficient at abstracting the proton. The free-energy barrier is significantly higher than the experimental value (11), regardless of whether a third Mg²⁺ is present or if a general acid plays a role. Using transition state theory, for example, the experimentally measured k_cat of 62 min⁻¹ for nucleotide addition would correspond to a barrier of ca. 18 kcal/mol vs. our calculated barrier of at least 24 kcal/mol (Table 1). The overall reaction is roughly neutral thermodynamically, but the minimum free-energy path is such that the 3′-O is deprotonated only after nucleophilic attack. A mechanism where nucleophilic attack occurs prior to proton transfer is reminiscent of the preferred mechanism of phosphate hydrolysis in some recent studies (26), but in the present case it results in an insurmountable barrier, highlighting the potential limits of generalizing results to different environments. The cases where such a mechanism is favorable are those where there is no explicit base and the proton transfers directly from the nucleophile to the phosphate under attack (27). This is more likely for situations where nucleophilic attack occurs at P_γ, as it does in GTPases and ATPases, because in those reactions the phosphate under attack is en route to becoming an inorganic phosphate. In the case of nucleotide addition, the attacked phosphate is en route to becoming a phosphate diester, which is a significantly worse base. In any case, the presence of a third Mg²⁺ has a minimal effect in altering the free-energy surface for this pathway, and the large activation barrier suggests this pathway is unlikely. Additionally, protonation of the leaving group in this mechanism has little effect, which would contradict the notion that general acid catalysis plays a role (6). Altogether, we conclude that Asp115, which is itself ligated to a Mg²⁺, is not the base that abstracts the proton from the 3′-OH, and there is no other more suitable candidate for an enzymatic base.

Fig. 4.

Mechanism (A), transition state structure (B), and free-energy surfaces for nucleotide addition using Asp115 as a general base under 4 different conditions (C–F). The 4 conditions are: 2 Mg²⁺ and deprotonated leaving group (C), 3 Mg²⁺ and deprotonated leaving group (D), 2 Mg²⁺ and protonated leaving group (E), 3 Mg²⁺ and protonated leaving group (F). The large barrier heights under all 4 conditions indicate that this mechanism is unlikely. The structure in the Upper Right is representative of the transition state region for the reaction with 2 Mg²⁺ and a protonated leaving group, with the breaking and forming bonds shown as transparent. The phosphoryl transfer coordinate is defined as the difference in length of the breaking and forming O–P bonds, and the proton transfer coordinate is defined as the difference in length of the breaking and forming O–H bonds. The proton shown in red is only present in the Bottom simulations. The dotted lines guide the eye as to the minimum free-energy path from reactant to product; the transition state corresponds to the location of the maximum free energy along this minimum path.

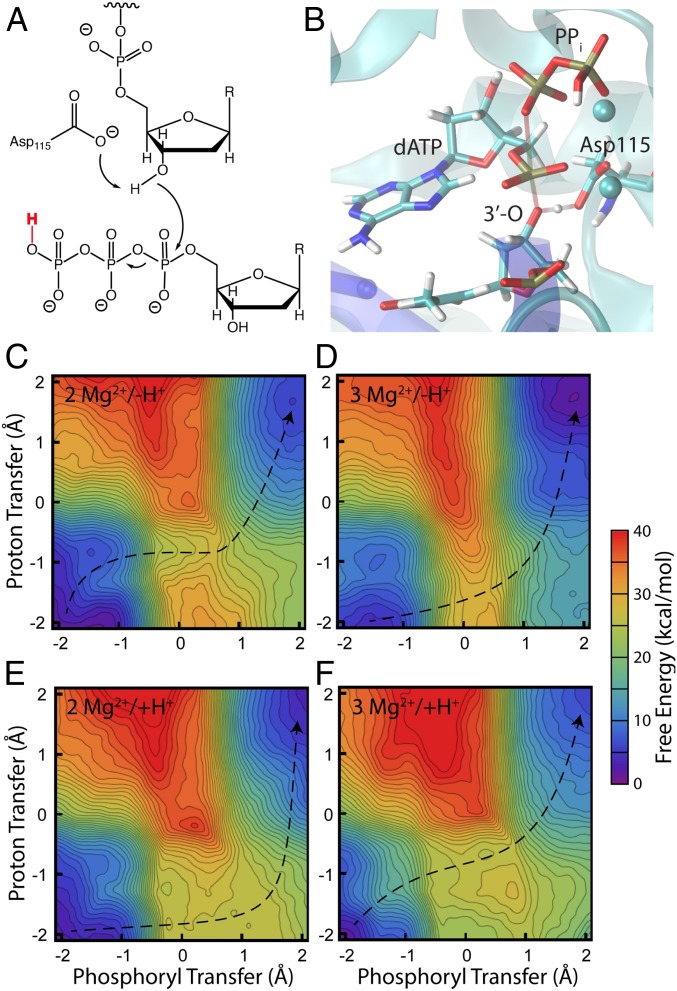
Finally, we tested the efficacy of a Mg²⁺-bound hydroxide serving as the base to deprotonate the 3′-OH (Fig. 5). We find that the energetics (Table 1) and characteristics of this mechanism are congruent with experimental results, both qualitatively and semiquantitatively: participation of a third Mg²⁺ lowers the activation barrier substantially, as does protonation of the leaving group. Thus, the reaction with a third Mg²⁺ and a protonated leaving group has a barrier height of 12.9 kcal/mol and is exergonic by 15.9 kcal/mol. The minimum free-energy path is such that motion along the proton transfer coordinate is nearly complete at the transition state, and motion at the transition state is almost exclusively along the phosphoryl transfer coordinate. We caution against an attempt to partition between these processes in the energetic cost of reaching the transition state, though, because the approach to the transition state includes substantial motion along both coordinates. The processes are still concerted even if the proton transfer finishes prior to reaching the transition state. We note that this pathway is opposite to the pathway for the Asp-catalyzed mechanism. We propose that this difference in pathway contributes to the difference in whether positive charge (either a third Mg²⁺ or protonated leaving group) affects the barrier height. When the proton remains on the 3′-O during nucleophilic attack, less electron density is deposited into the triphosphate moiety at the transition state. Thus, positive charge that interacts with the triphosphate is less effective at stabilizing the transition state. While the proton transfer is essentially complete at the transition state, there is no intermediate where the proton has been abstracted but nucleophilic attack has yet to occur; i.e., the 2 processes are concerted. A deprotonated 3′-OH with bound NTP is not a stable state of this system. We did, in fact, calculate the pK_a of the 3′-OH for that state (2 Mg²⁺, deprotonated leaving group) and found that it is shifted as much as +21 pH units relative to isopropanol, making the population of the deprotonated form astronomically small. Even that value, though, is in some sense contrived because the O–H bonds of nearby waters were constrained during the simulation by SHAKE. The surfaces in Fig. 5 demonstrate that at equilibrium, if the 3′-OH becomes deprotonated, a proton will spontaneously transfer, with no activation barrier, from the Mg²⁺-bound water to the 3′-OH.

Fig. 5.

Mechanism (A), transition state structure (B), and free-energy surfaces for a mechanism with a Mg²⁺-coordinated hydroxide as the base under 4 different conditions (C–F). The 4 conditions are: 2 Mg²⁺ and deprotonated leaving group (C), 3 Mg²⁺ and deprotonated leaving group (D), 2 Mg²⁺ and protonated leaving group (E), 3 Mg²⁺ and protonated leaving group (F). This mechanism achieves all the characteristics of the mechanism suggested by experiments, including rate acceleration by a third Mg²⁺ (11) and by protonation of the leaving group (6). Furthermore, when combined with estimates of pK_a (see text), the overall barrier height for the condition with a third Mg²⁺ and a protonated leaving group compares well with experiment (21 kcal/mol vs. 18 kcal/mol in experiment). The structure in the Upper Right is representative of the transition state region for that reaction with the breaking and forming bonds shown as transparent. See also Movie S1 for a representation of that mechanism. The phosphoryl transfer coordinate is defined as the difference in length of the breaking and forming O–P bonds, and the proton transfer coordinate is defined as the difference in length of the breaking and forming O–H bonds. The proton shown in red is only present in the Bottom simulations. The dotted lines guide the eye along the minimum free-energy path from reactant to product; the transition state corresponds to the location of the maximum free energy along this minimum path.

A limitation to interpreting the thermodynamic parameters for the surfaces in Fig. 5, of course, is our initial reactant state, namely, a hydroxide ion as the base. Is that Mg²⁺-coordinated water indeed deprotonated in the active site? Despite all of the negative charge associated with the triphosphate of the incoming NTP, Table 2 shows that with a third Mg²⁺ and a protonated leaving group, the active site water has a pK_a of 13.6. From the Henderson–Hasselbach equation, this pK_a indicates that under physiological conditions (pH = 7.5 to 8.0) (20) the fraction of deprotonated waters is ca. 10⁻⁶, suggesting an additional effective thermodynamic cost of ca. 8 kcal/mol to the barrier height and to the exergonicity. Thus, our simulations estimate the overall reaction barrier as 21 kcal/mol and the exergonicity as −8 kcal/mol. The goal of DFTB3/MM simulations here is primarily to use semiquantitative results to compare mechanisms and trends; one cannot generally expect absolute quantitative accuracy from these sorts of simulations. Nonetheless, our estimated barrier height of 21 kcal/mol compares quite well with the 18 kcal/mol barrier estimated from measured rates (11).

A few challenges exist in evaluating our confidence in the comparison between calculated and measured barriers. First, there is some uncertainty in the statistical convergence of the simulations. SI Appendix, Fig. S1, shows that our simulations ran long enough that the reaction parameters have converged to within 1 to 2 kcal/mol. Other uncertainty arises from the DFTB3/MM potential energy surface, which is not expected to yield perfect quantitative accuracy (SI Appendix, Figs. S5 and S6). We have calibrated these methods against experimental measurements in the pK_a calculations, for example, and against high-level quantum methods in similar reactions (22, 28, 29). The inherent errors we observed in those tests are likely to be consistent across the many mechanisms we have modeled, suggesting that we can count on some cancellation of error when comparing the mechanisms with one another. Together, these sources of potential error and uncertainty indicate error bars in the values in Table 1 that could be as large as 4 to 5 kcal/mol. When comparing those values with one another, though, the cancellation of systematic error suggests reduced overall errors, perhaps to 2 to 3 kcal/mol. This indicates that the computed barrier height of 24 kcal/mol for the Asp-catalyzed mechanism may be within error of the barrier height for the water-catalyzed mechanism (21 kcal/mol). The barrier height for the Asp-catalyzed mechanism, however, is beyond the margin of error of the experimentally measured barrier (18 kcal/mol). Similarly, the estimated error bars cannot rescue the self-activated mechanism; proton abstraction by the pyrophosphate is too costly, and the 3′-OH cannot remain deprotonated throughout the catalytic cycle. Thus, after ruling out the other plausible mechanisms, the agreement between measured and computed barrier heights of the water-as-base mechanism supports this mechanism as most likely.

The Role of the Third Mg²⁺.

The presence of a third Mg²⁺ substantially accelerates the water-as-base mechanism, both by directly lowering the barrier to phosphoryl transfer (Table 1) and by lowering the pK_a of the Mg²⁺-coordinated water (Table 2). The positive charge on the metal stabilizes the hydroxide form of the water and stabilizes negative charge accumulation on the phosphoryl group at the transition state. To be clear, the water serving as a base is coordinated to a different Mg²⁺ than the one whose role is in question. We have not directly tested when and how the third Mg²⁺ binds, but our inability to find a plausible reaction barrier without a third Mg²⁺ implies that the ion binds prior to nucleophilic attack. This contrasts with a recent reanalysis of occupancies from the time-resolved crystallography, which concluded that formation of the pyrophosphate precedes the appearance of a third metal (30). Tsai, though, cautioned against overinterpretation of occupancies due to the vastly different timescales involved in the chemical step, metal binding/release, and time-resolved crystallography (31). The precise timing of Mg²⁺ binding and release may require further study, but we reiterate the point made recently (32) that transition state theory assumes a closed system, where the same chemical composition is used in comparing reactants with transition states. In this case, the difference in timescale involved in binding of a divalent metal ion—or binding of anything else, for that matter—make it unlikely to be concerted with the nucleophilic attack.

In contrast to the water-as-base mechanism, the third Mg²⁺ contributes little in the Asp-catalyzed mechanism. The different effects of the third Mg²⁺ for different mechanisms may be some of the source of disagreement over its role in the reaction (11, 13, 32, 33). One study found a dramatic effect of the third Mg²⁺ in catalyzing the mechanism we show in Fig. 3, when the 3′-OH begins deprotonated (13), while another study found that a third Mg²⁺ primarily stabilizes the product and does not lower the activation barrier (32). Unfortunately, the latter study did not identify which particular mechanism they simulated, so comparison to our work is difficult. Stabilization of the product is consistent with what we find for the water-catalyzed mechanism, but our simulations of that mechanism also indicate rate acceleration by the third Mg²⁺. Still another study found that a third Mg²⁺ catalyzes the reverse reaction, namely, pyrophosphorolysis, and was inhibitory to the forward reaction (33). The authors of that study cautioned, though, that they did not use dynamics at all along the reaction coordinate, making the results challenging to interpret. Reactions of phosphates and their accompanying proton transfers introduce significant changes in electronic structure. While enzymes evolve to be preorganized to catalyze their reactions (34), substantial environmental reorganization must still occur along the way from reactant to transition state to product; extensive MD simulations are necessary to capture this behavior. Additional studies may be required to reach agreement on the role of the third Mg²⁺, and we hope the trend toward more extensive MD simulations will lead the many viewpoints to reach a converged model.

Connection to Experiments.

In addition to more extensive simulations, additional experiments can guide our understanding and test the predictions implied by computational models. Measured rate constants are an important quantitative check on the veracity of a computational model, but as mentioned, the inherent errors in QM/MM simulations limit any expectation of quantitative agreement with experiment. Trends in qualitative behavior, though, can be implied by a QM/MM model and ought to be taken as more firm predictions. Our model, for example, is consistent with multiple proton transfers occurring during the rate-limiting step, including deprotonation of the nucleophile, protonation of the leaving group, and possibly deprotonation of the Mg²⁺-coordinate water. Proton inventory studies indicated that at least 2 protons are transferred in the rate limiting step (6, 9), which supports our model but adds to the evidence contradicting the self-activated mechanism, which has just a single proton transfer during the entire catalytic cycle. Our model further indicates that the proton abstraction is concerted with the nucleophilic attack. Thus, it predicts an observable isotope effect on the nucleophilic oxygen, which can be measured using 3′-¹⁸O-dNTP as substrate, as well as isotope effects on the oxygens surrounding P_α. Additional tests of the role of a third metal may be achievable through rapid mixing experiments, given that the intrinsic reaction is relatively slow (∼1 s⁻¹). If one could prepare a ternary complex in the presence of limited metal concentration and then rapidly add some additional divalent metal, one could test the ability of that metal to bind and catalyze the reaction after the substrate has bound. Further, since our model proposes that the third metal affects the pK_a of the Mg²⁺-coordinated water, it could be tested by measuring the pH dependence of how the rapidly added metal affects catalysis. We hope experimental laboratories will continue to test computational models of nucleotide addition and further reduce the mechanistic space that must be covered by computational work.

Conclusions

Taken together, the qualitative and semiquantitative aspects of the 3 classes of mechanisms (self-activated, enzyme as base, and water as base) and each of their instantiations favor a Mg²⁺-bound water serving as a base to deprotonate the 3′-OH. The activation barrier for the self-activated mechanism was lower, but that mechanism relies on a 3′-OH to remain deprotonated throughout the catalytic cycle, and our pK_a calculations show that to be implausible. Moreover, simulations of other mechanisms demonstrate that there is no stable state with deprotonated 3′-OH and bound NTP. Of the mechanisms where the 3′-OH is deprotonated only transiently, the lowest activation barrier occurs for the water-as-base mechanism. When the barrier height is adjusted to account for the pK_a of the Mg²⁺-coordinated water, the barrier agrees well with measured kinetics. The Asp-catalyzed mechanism has a barrier that is substantially larger than experiments indicate. Altogether, the results best support water as the base in the classic mechanism.

Our conclusions are still limited in some respects. We have not identified the general acid and have not examined when the leaving group is protonated. If this proton transfer is concerted with the deprotonation of the nucleophile and the phosphoryl transfer, as implied by proton inventories (9), it could affect the dynamics of nucleotide addition in ways that are not captured in our simulations. While we have examined the 2D free-energy surfaces in the beginning and end states for protonation of the leaving group, a full accounting will require simulations of 3D surfaces (14) that test proton transfers originating from a variety of candidates for active site acids. Other subtleties in the dynamics could arise if the deprotonation of the Mg²⁺-coordinated water is concerted with deprotonation of the 3′-OH, through a Grotthuss-type mechanism. While there are still open questions regarding the nucleotide addition cycle, we expect the overall conclusion that water is the base will stand up to further clarifications of other aspects.

This conclusion is the result of extensive MD simulation of each of 10 distinct microscopic mechanisms as well as many pK_a calculations and other free-energy calculations that disqualify certain pathways. The need for such extensive simulation highlights one of the challenges of elucidating mechanisms using computational methods and the need for tools that combine speed with semiquantitative accuracy. Even after accounting for experimental constraints, established rules of reactivity, and chemical intuition, one is left with a wide range of plausible mechanistic space: each imaginable placement of a proton, for example, requires a separate simulation. Experiments, on the other hand, can reliably test broad regions of mechanistic space in single experiments—for example, measurements with and without a mutation can test the role of a general acid in the reaction and thus rule out all classes of mechanisms that do not qualitatively conform to that experimental result. Experiments, though, can have ambiguous interpretations and are generally unable to test a specific microscopic mechanism. Only by combining information obtained from experiments with that obtained from simulation can we obtain microscopic answers to questions of chemical reactivity in complex settings.

Methods

All simulations were done using Chemistry at HARvard Macromolecular Mechanics (CHARMM) (36, 37) and followed the general methods we have used in other recent studies of enzymatic phosphate chemistry (22, 28, 29, 35, 38–41). Briefly, initial models of both the reactant and product states were taken from a single crystal structure of DNA Polymerase η generated through time-resolved crystallography (Protein Data Bank ID 4ECV) (12). Simulations used the generalized solvation boundary potential (42, 43), which treats an inner region of a system as flexible during molecular dynamics simulations while outside of this region the atoms are frozen and treated with an implicit solvation scheme. Active site atoms were treated with QM at the DFTB3 level (Fig. 2) (23, 45–47). Atoms outside of the QM region used the Charmm36 force field (48–50) with a modified TIP3P water (51).

To calculate free-energy surfaces we used multiwalker metadynamics (52) with the program PLUgin for MolEcular Dynamics (PLUMED) (53) interfaced with CHARMM. Sampling of 1D surfaces typically used 5 to 10 walkers, while 2D surfaces used as many as 50 to 100 walkers. Simulation of each walker continued for ca. 500 ps, depending on sampling goals, apparent convergence, and how many parallel walkers the system contained (SI Appendix, Table S1 and Fig. S1). Thus, each of the 2D free-energy surfaces above include data from a minimum of 25 ns of total MD sampling and are the sum of at least 250,000 Gaussian potentials. To calculate pK_a values, we employed the free-energy perturbation method developed in ref. 21. Additional details are available in SI Appendix.

Data Availability.

All input files, protein coordinates, and relevant trajectory files are available from authors upon request.