Model-based physiological noise removal in fast fMRI

Abstract

Recent improvements in the speed and sensitivity of fMRI acquisition techniques suggest that fast fMRI can be used to detect and precisely localize sub-second neural dynamics. This enhanced temporal resolution has enormous potential for neuroscientists. However, physiological noise poses a major challenge for the analysis of fast fMRI data. Physiological noise scales with sensitivity, and its autocorrelation structure is altered in rapidly sampled data, suggesting that new approaches are needed for physiological noise removal in fast fMRI. Existing strategies either rely on external physiological recordings, which can be noisy or difficult to collect, or employ data-driven approaches which make assumptions that may not hold true in fast fMRI. We created a statistical model of harmonic regression with autoregressive noise (HRAN) to estimate and remove cardiac and respiratory noise from the fMRI signal directly. This technique exploits the fact that cardiac and respiratory noise signals are fully sampled (rather than aliasing) when imaging at fast rates, allowing us to track and model physiology over time without requiring external physiological measurements. We then created a joint model of neural hemodynamics, and physiological and autocorrelated noise to more accurately remove noise. We first verified that HRAN accurately estimates cardiac and respiratory dynamics and that our model demonstrates goodness-of-fit in fast fMRI data. In task-driven data, we then demonstrated that HRAN is able to remove physiological noise while leaving the neural signal intact, thereby increasing detection of task-driven voxels. Finally, we established that in both simulations and fast fMRI data HRAN is able to improve statistical inferences as compared with gold-standard physiological noise removal techniques. In conclusion, we created a tool that harnesses the novel information in fast fMRI to remove physiological noise, enabling broader use of the technology to study human brain function.

Introduction

Recent technological advances in fMRI have enabled neuroscientists to investigate brain function at a higher temporal resolution. In particular, the increasingly widespread use of ultra-high field magnets coupled with methods for simultaneous multi-slice (SMS) imaging offer enhanced sensitivity and an order of magnitude increase in the sampling frequency of fMRI measurements (Barth et al., 2016; Feinberg and Setsompop, 2013; Feinberg and Yacoub, 2012; Hennig et al., 2007; Larkman et al., 2001; Lin et al., 2006; Moeller et al., 2010b, 2010a; Narsude et al., 2016; Setsompop et al., 2012, 2016; Zahneisen et al., 2011), enabling imaging of blood-oxygenation-level-dependent (BOLD) signals at rapid (repetition times (TR) <500 ms) timescales. Using fast fMRI, researchers have been able to detect and precisely localize neurally-driven activity on the order of hundreds of milliseconds (Lewis et al., 2016), investigate functional connectivity networks at higher frequencies than those conventionally examined (Boubela et al., 2013; Chen and Glover, 2015; Lee et al., 2013; Lin et al., 2015; Sahib et al., 2018; Trapp et al., 2018), and resolve variable temporal dynamics in the hemodynamic response function (Lewis et al., 2018; Lin et al., 2018; Smith et al., 2012).

While fast fMRI offers enormous potential as a research tool, novel challenges also emerge in the analysis of rapidly acquired data (Chen et al., 2019). Fast (>0.1 Hz) neurally-driven BOLD signals are very low in amplitude, due to the filtering properties of the hemodynamic response (Bandettini, 2014; Dale, 1999; Lewis et al., 2016). These signals may therefore be obscured by physiological noise associated with rhythmic respiratory (~ 0.2 Hz) and cardiac (~ 1 Hz) activity, which are of much larger amplitude than the signal. Furthermore, physiological noise scales with the sensitivity of fMRI measurements (Hutton et al., 2011; Krüger and Glover, 2001; Triantafyllou et al., 2005). This relative increase in physiological noise limits the ability of fast fMRI to detect subtle changes in rapid, neurally-driven activity, as increasing sensitivity to these small neural signals will in turn also increase physiological noise. A related concern in fast fMRI analysis is the enhanced autocorrelation, which conventional models of fMRI are unable to account for (Bollmann et al., 2018; Corbin et al., 2018; Eklund et al., 2012; Mathiak et al., 2016; Olszowy et al., 2019). Incorrect models of the physiological noise (Chen et al., 2016; Chen and Glover, 2015; Hallquist et al., 2013; Lund et al., 2006; Murphy et al., 2009; Weissenbacher et al., 2009) or of the autocorrelation (Bollmann et al., 2018; Corbin et al., 2018; Eklund et al., 2012; Honari et al., 2019; Mathiak et al., 2016; Olszowy et al., 2019) can lead to important errors in interpretation of the fMRI signal, suggesting that unique analysis strategies are necessary for fast fMRI.

Numerous physiological noise removal techniques, designed for conventional fMRI, are currently widely used. These techniques can be broadly grouped into reference-based models and data-driven approaches (for a more complete list see (Kasper et al., 2017). Reference-based models make use of external reference signals such as electrocardiography (EKG), pulse oximetry, and respiratory belts to estimate and remove physiological noise. For instance, the widely used algorithm RETROICOR estimates the phases of cardiac and respiratory periods from external reference signals relative to fMRI acquisition and models physiological noise using a Fourier expansion of the phases (Glover et al., 2000; Harvey et al., 2008). The external physiological recordings can also be used to model the cardiac and respiratory response functions, which are lower frequency fluctuations (Birn et al., 2008b, 2008a, 2006; Chang et al., 2009; Chang and Glover, 2009). These techniques often perform very well – however, they require the collection of external signals, which can be technically difficult, particularly in patient populations, and prone to noise in an MR environment. In addition, these methods do not explicitly account for time-varying amplitude changes present in physiological noise signals, or the altered autocorrelation structure of fast fMRI.

Due to the added complexity of acquiring external physiological signals, many studies now employ data-driven approaches which estimate physiological noise from the fMRI data directly, often using component analysis techniques (Behzadi et al., 2007; Beissner et al., 2014; Churchill and Strother, 2013; Perlbarg et al., 2007; Thomas et al., 2002). For example, CompCor estimates physiological noise regressors by applying principal component analysis on voxels with the highest temporal standard deviation or from anatomical regions with no assumed neurally-relevant signal, such as the cerebrospinal fluid (CSF) or white matter (Behzadi et al., 2007). While these techniques have improved detection of neurally-driven responses, they also come with limitations that can prove problematic in fast fMRI studies. Unlike model-based approaches which isolate physiological noise in specific frequency bands, the estimated physiological noise components from data-driven approaches are broadband. Particularly with the enhanced frequency resolution of fast fMRI, subtracting these broadband components from voxels across the brain may in fact introduce artifactual noise into frequency bands >0.1 Hz (Chen et al., 2017; Chen and Glover, 2015). Similarly, data-driven approaches are unable to account for the temporal lag of physiological noise across the brain as effectively as model-based approaches, which can limit their performance.

We hypothesized that fast fMRI could enable an alternative approach to physiological noise removal. Specifically, if the TR is sufficiently low (~<0.5s) then the fundamental frequencies of cardiac and respiratory activity can be sampled directly, rather than aliasing into lower-frequency bands (Aslan et al., 2019). Fast fMRI data therefore contain new information - high amplitude and non-aliased physiological noise signals - that can in turn inform the noise removal technique. This additional information present in fast fMRI data could potentially be used to more accurately detect and model physiological noise.

An ideal noise removal technique would selectively remove the narrowband physiological noise while preserving the full spectrum of the neurally-driven BOLD signal. Lowpass filtering therefore cannot sufficiently remove these artifacts, as it would remove the fast neural signals as well. In addition, as illustrated in (Chen et al., 2019), simply notch filtering this quasi-periodic physiological noise may fail to remove higher order harmonics and can also remove neurally-relevant signals. Moreover, the data also contain background autoregressive noise that should be accounted for. We therefore investigated whether a model-based approach could be derived from the fast fMRI data directly, which would obviate the need for external reference signals, account for the underlying neural signal and autocorrelation, and prevent artificial introduction of broadband noise components into the fMRI signal.

We aimed to develop a physiological noise removal algorithm that leverages the new information in fast fMRI to overcome these challenges. Our approach is based on a model of Harmonic Regression with Autoregressive Noise (HRAN) and estimates physiological noise directly from the fast fMRI data. Our technique also uses a general linear model, and can therefore be easily integrated with commonly used analysis streams in the fMRI community. We first constructed a mathematical basis for fast fMRI data and defined the physiological and autoregressive noise parametrically. Next, we used efficient likelihood-based regression techniques to estimate the fundamental physiological frequencies from physiologically noisy regions of the brain. With these determined frequencies, our method estimates both the physiological and autocorrelated noise in addition to the neurally-relevant signal in each voxel or region of interest (ROI), and selectively removes the physiological noise. To assess our model performance, we constructed simulated datasets to show that our technique can accurately detect physiological noise in the presence of autoregressive noise, and can effectively remove it even when its phase and amplitude is time-varying. Finally, we applied our technique to fast fMRI data collected in a visual task, compared its performance to other gold standard physiological noise removal techniques, and found that our approach enables improved statistical inferences.

Methods

Model Motivation and Structure

In conventional fMRI, physiological noise resulting from cardiac and respiratory cycles is aliased into the same band as the neurally-relevant signals, due to the slow (< 0.5 Hz) sampling rate. In contrast, the temporal resolution of fast fMRI (> 2-3 Hz) allows direct observation of the fundamental respiratory frequency and its lower harmonics (e.g. ~0.25 Hz, 0.5 Hz, 0.75 Hz) and the fundamental cardiac frequency (e.g. ~1 Hz), although its harmonics may alias (e.g. 2 Hz, 3 Hz). For example, the spectrogram of the 4th ventricle obtained during a resting-state scan of fast fMRI (Experiment A, TR = 0.367s) shows high-power activity in typical respiratory and cardiac frequency bands (Fig 1A). The EKG and respiratory belt data show the high-power oscillations seen in the spectrogram have the same period as respiratory and cardiac cycles (Fig 1B). In data acquired from a separate subject at higher sampling rates (Experiment B, TR=0.227s), spectrograms of three different brain regions show that the physiological noise varies spatially (as observed from the differences in signal across the spectrograms) and temporally (as observed from the differences in signal within each spectrogram) (Fig 1C); however, the fundamental physiological frequencies and overall harmonic structure are preserved.

Figure 1: Physiological noise sampled directly in fast fMRI.

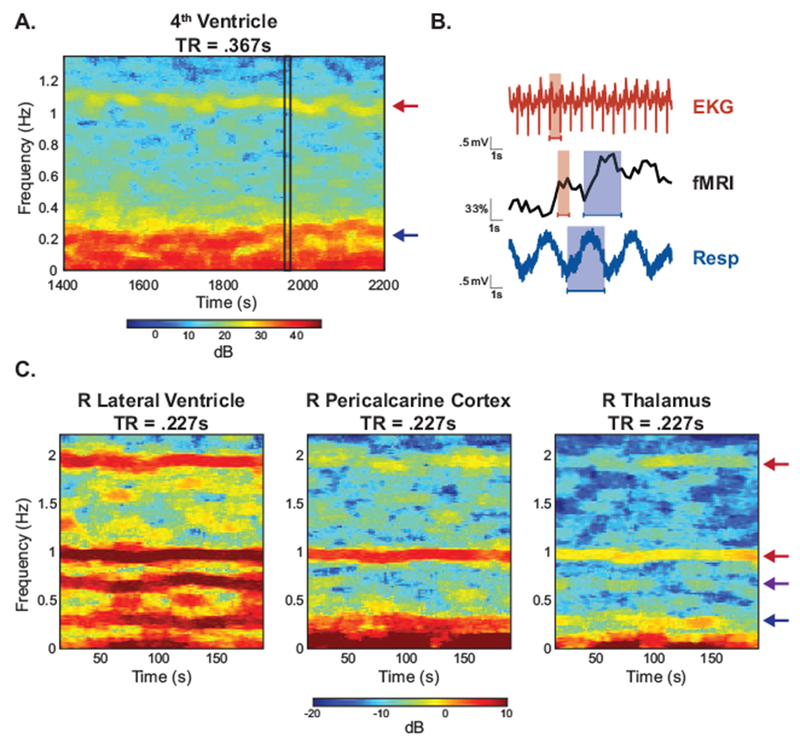
Unlike conventional fMRI, physiological noise can be resolved without aliasing in fast fMRI. (A) A spectrogram of the 4th ventricle from a subject in Experiment A shows high power oscillations in the cardiac (red arrow) and respiratory (blue arrow) frequency range. (B) A zoomed-in time series from (A) (black rectangle) shows that the high-power oscillations correspond to cardiac (red) and respiratory (blue) cycles obtained from external physiological recordings. (C) Spectrograms from ROIs in Experiment B manifest the harmonic structure of the physiological noise. In the right lateral ventricle (left) one respiration term (blue arrow), two cardiac terms (red arrow), and one interaction term (purple arrow) are observed. These components are also present to varying degrees in pericalcarine cortex (middle) and the thalamus (right).

These observations suggest that physiological noise in fast fMRI may be modeled by an appropriately designed harmonic regression model. For a given time segment t₁, t₂, …, t_T of length T we model the physiological noise related to cardiac activity c = [c_t1, c_t2, …, c_tT]′ and respiration r = [r_t1, r_t2, …, r_tT]′ as:

$$c_{t_i}=\sum _{k=1}^K(A_{c_k}\cos (k{\omega }_c{t}_i)+B_{c_k}\sin (k{\omega }_c{t}_i))$$

$$r_{t_i}=\sum _{l=1}^L(A_{r_l}\cos (l{\omega }_r{t}_i)+B_{r_l}\sin (l{\omega }_r{t}_i))$$

Where c_ti and r_ti are the cardiac and respiratory noise at time t_i respectively. In this model, ω_c is the fundamental cardiac frequency, A_ck and B_ck define the amplitude and phase of the k’th harmonic of cardiac activity, and K specifies the number of cardiac harmonics. Similarly, ω_r is the fundamental frequency of respiration, A_rl and B_rl define the amplitude and phase of the l’th harmonic of respiratory activity, and L specifies the number of respiratory harmonics.

In addition to the physiological noise, the fMRI data may consist of low frequency drift, neurally-relevant signals, and un-modeled activity, typically represented using an autoregressive (AR) process.

To model the drift d = [d_t1, d_t2, …, d_tT]′ in the fMRI signal, we use a linear term:

$$d_{t_i}={\mu }_0+{\mu }_1{t}_i$$

Where d_ti is the linear drift at time t_i with coefficients μ₀ and μ₁.

To model the neurally-relevant signals n = [n_t1, n_t2, …, n_tT]′, we use a standard fMRI approach and convolve the applied neural stimulus with a hemodynamic response function (HRF):

$$n_{t_i}=\kappa \sum _{k=1}^{T}s(t_i-t_k)h(t_k)$$

Where n_ti is the neurally-relevant signal at time t_i, s is the applied neural stimulus, h is the chosen HRF, and κ is a weighting coefficient.

Finally, we use an AR process to capture the remaining elements of the fMRI signal that we have not explicitly modeled, which may include spontaneous, un-modeled neural activity (Bianciardi et al., 2009; Bollmann et al., 2018). An AR(1) process can sufficiently explain any un-modeled activity in conventional fMRI (Purdon and Weisskoff, 1998; Woolrich et al., 2001; Worsley et al., 2002). However, in fast fMRI, even with physiological noise correction, a higher order AR process or more elaborate model is required to fully explain the data (Bollmann et al., 2018; Corbin et al., 2018). We therefore model the remaining fMRI signal ε = [ε_t1, ε_t2, …, ε_tT]′ as:

$${\epsilon }_{t_i}=\sum _{p=1}^P{\alpha }_p{\epsilon }_{t_i-p}+{\eta }_{t_i}$$

$${\eta }_{t_i}~\mathcal{N}(0,{\sigma }^2)$$

Where ε_ti depicts an autoregressive process of order P (which may be greater than one) at time t_i, α_p is the autoregressive coefficient at lag p, and η_ti is Gaussian noise with a mean of zero and variance σ². Alternatively stated, ε can be represented as a vector of Gaussian noise with a mean of zero and covariance Q(α, σ²), where Q(α, σ²) is the AR covariance matrix associated with parameters α = [α₁, α₂, …, α_P] and σ².

Gathering all of these components of our model together, we can represent the data segment y = [y₁, y₂, …, y_T]′ (e.g. from a voxel or region of interest) as the sum of cardiac noise c, respiratory noise r, drift d, neurally-relevant signal n, and autoregressive noise ε.

$$\mathit{y}=\mathit{c}+\mathit{r}+\mathit{d}+\mathit{n}+\mathit{\epsilon }$$

We can also rewrite this model compactly using matrix notation. We specify a matrix Z(ω_r, ω_c) and parameter vector β as:

$$\mathbf{Z}({\mathit{\omega }}_{\mathit{r}},{\mathit{\omega }}_{\mathit{c}})=\left[\stackrel{\mathbf{d}}{\overbrace{\begin{array}{cc}1& t_1\\ 1& t_2\\ ⋮& ⋮\\ 1& t_T\end{array}}}\stackrel{\mathbf{n}}{\overbrace{\begin{array}{c}{\sum }_{j=1}^{T}s(t_1-t_j)h(t_j)\\ {\sum }_{j=1}^{T}s(t_2-t_j)h(t_j)\\ ⋮\\ {\sum }_{j=1}^{T}s(t_T-t_j)h(t_j)\end{array}}}\stackrel{\mathbf{c}}{\overbrace{\begin{array}{ccc}\mathit{cos}({\omega }_c{t}_1)& \dots & \mathit{sin}(K{\omega }_c{t}_1)\\ \mathit{cos}({\omega }_c{t}_2)& \dots & \mathit{sin}(K{\omega }_c{t}_2)\\ ⋮& \ddots & ⋮\\ \mathit{cos}({\omega }_c{t}_T)& \dots & \mathit{sin}(K{\omega }_c{t}_T)\end{array}}}\stackrel{\mathbf{r}}{\overbrace{\begin{array}{ccc}\mathit{cos}({\omega }_r{t}_1)& \dots & \mathit{sin}(L{\omega }_r{t}_1)\\ \mathit{cos}({\omega }_r{t}_2)& \dots & \mathit{sin}(L{\omega }_r{t}_2)\\ ⋮& \ddots & ⋮\\ \mathit{cos}({\omega }_r{t}_T)& \dots & \mathit{sin}(L{\omega }_r{t}_T)\end{array}}}\right]$$

$$\beta ={\left[{\mu }_0{\mu }_1\kappa A_{c_k}\dots B_{c_k}{A}_{r_l}\dots B_{r_l}\right]}^{\prime }$$

such that our full model becomes:

$$\mathit{y}\mathit{(}{\omega }_r,{\omega }_c,\mathit{\beta },\mathit{\alpha },{\sigma }^2\mathit{)}=\mathit{Z}\mathit{(}{\mathit{\omega }}_{\mathit{r}}\mathbf{,}{\mathit{\omega }}_{\mathit{c}}\mathit{)}\mathit{\beta }+\mathit{\epsilon }$$

Our model specifies a parametrically defined basis for the physiological noise that is separable from the remaining components of the fMRI signal. Importantly, our model also allows for time and frequency overlap between physiological sources of noise (represented by the harmonic regression) and any un-modeled, spontaneous neural activity (represented by the autoregressive noise), which prevents over-estimation of the physiological noise and preserves the underlying fMRI signal.

Estimating parameters with cyclic descent algorithm

In order to estimate and remove the physiological noise, we must estimate the parameters ω_r, ω_c, β, α, and σ² defined in our model. Our model consists of harmonic regression with autoregressive noise, for which parameter estimation methods using maximum likelihood techniques have been developed and implemented in a wide variety of models, including ballistocardiogram artifacts (Krishnaswamy et al., 2016), two-photon calcium imaging data (Malik et al., 2011), and circadian rhythms (Brown et al., 2004; Brown and Schmid, 1994). In particular, (Krishnaswamy et al., 2016) employ an efficient cyclic descent algorithm that addresses the specific challenges of our parameter estimation. First, the cyclic descent algorithm handles the non-linearity resulting from the unknown physiological frequencies ω_r and ω_c through sequential minimizations (Krishnaswamy et al., 2016). Second, the algorithm uses a local likelihood framework to accommodate time-varying parameter estimates (e.g. variable amplitude or frequency of respiration over time) (Krishnaswamy et al., 2016).

Here, we adapt the approach taken by (Krishnaswamy et al., 2016) to 1) estimate the physiological frequencies from a manually defined brain region with high physiological noise and 2) use the estimated physiological frequencies to regress out physiological noise in each voxel. The implementation of our model and algorithm, which we refer to as Harmonic Regression with Autoregressive Noise (HRAN), is described below. Step 1 is performed once to estimate physiological frequencies, and Step 2 involves fitting the model across voxels and time windows.

Estimating physiological noise

First, we select an anatomically defined brain region known to manifest high levels of physiological noise (e.g. the ventricles, see “Physiological ROI selection”), from which we will estimate the physiological frequencies. We advance through the extracted data in moving time windows, to account for variable physiological frequencies over time. For a given time window (which in our experiments ranged from 24s – 45s, see “Time window selection”) we assume a constant cardiac and respiratory frequency. As in (van der Meer et al., 2016), we also apply a Hann window to each data window (see “Time window selection”).

To estimate the cardiac and respiratory frequencies in each windowed data segment y of length T, we generate matrices Z(ω_r, ω_c) by iterating through a range of physiologically plausible frequencies and generating regressors for each cardiac and respiratory frequency pair. For example, ω_r may range from .15 Hz - .35 Hz (9-21 breaths per minute), and ω_c may range from .8 - 1.6 Hz (48-96 beats per minute). For each Z(ω_r, ω_c), we then determine the negative log likelihood in a particular time window using a recursive fitting procedure.

Specifically, we apply the same Hann window we applied to the data segment to the design matrix Z(ω_r, ω_c), and compute the generalized least squares estimate as:

$$\widehat{\mathit{\beta }}({\mathit{\omega }}_{\mathit{r}},{\mathit{\omega }}_{\mathit{c}})={(\mathit{Z}({\mathit{\omega }}_{\mathit{r}},{\mathit{\omega }}_{\mathit{c}}{)}^{\prime }\widehat{\mathit{Q}}{({\mathit{\omega }}_{\mathit{r}},{\mathit{\omega }}_{\mathit{c}})}^{-1}\mathit{Z}({\mathit{\omega }}_{\mathit{r}},{\mathit{\omega }}_{\mathit{c}})+\mathit{W}{({\mathit{\omega }}_{\mathit{r}},{\mathit{\omega }}_{\mathit{c}})}^{-1})}^{-1}\mathit{Z}({\mathit{\omega }}_{\mathit{r}},{\mathit{\omega }}_{\mathit{c}}{)}^{\prime }\widehat{\mathit{Q}}{({\mathit{\omega }}_{\mathit{r}},{\mathit{\omega }}_{\mathit{c}})}^{-1}\mathit{y}$$

where $\widehat{\beta }({\omega }_{\mathit{r}},{\omega }_{\mathit{c}})$ is the amplitude estimate, $\widehat{\mathit{Q}}({\omega }_{\mathit{r}},{\omega }_{\mathit{c}}{)}^{-1}$ is the inverse AR covariance estimate initialized as the identity matrix I_TxT, and W(ω_r, ω_c) is an estimate of the prior covariance computed using the multitaper power spectrum. W(ω_r, ω_c) is defined as a diagonal matrix with the difference in power at the given physiologic frequency and its harmonics in each column and a moving average of the multitaper power spectrum. Including an estimate of the prior covariance W(ω_r, ω_c) helps to guide the first few iterations of the cyclic descent as $\widehat{\mathit{Q}}({\omega }_{\mathit{r}},{\omega }_{\mathit{c}}{)}^{-1}$ is estimated.

Next, we compute the residual of the generalized least squares estimation, which is our estimate of the autoregressive noise:

$$\widehat{\epsilon }({\omega }_r,{\omega }_c)=\mathit{y}-\mathit{Z}({\omega }_r,{\omega }_c)\widehat{\beta }({\omega }_r,{\omega }_c)$$

Using the Burg algorithm, a recursive set of operations that minimize the least squares forward-backward prediction error, we can estimate $\widehat{\alpha }({\omega }_{\mathit{r}},{\omega }_{\mathit{c}})$ and $\widehat{{\alpha }^2}({\omega }_r,{\omega }_c)$ (Box et al., 2008; Kay, 1988) from $\widehat{\epsilon }({\omega }_{\mathit{r}},{\omega }_{\mathit{c}})$. Levinson-Durbin recursions can then be used to efficiently compute the inverse AR covariance matrix $\widehat{\mathit{Q}}({\omega }_{\mathit{r}},{\omega }_{\mathit{c}}{)}^{-1}$, which can be made increasingly computationally efficient through block multiplication (Box et al., 2008; Kay, 1988; Krishnaswamy et al., 2016; Malik et al., 2011).

The generalized least squares estimate is then recomputed, informed with the inverse AR covariance matrix $\widehat{\mathit{Q}}({\omega }_{\mathit{r}},{\omega }_{\mathit{c}}{)}^{-1}$, and the Burg algorithm and Levinson-Durbin recursions are once again used to estimate the autoregressive parameters from the residual. This process is cycled until subsequent $\widehat{{\sigma }^2}({\omega }_r,{\omega }_c)$ converge to within .01%. At this point, the weighted mean square error $\widehat{S_T}({\omega }_r,{\omega }_c)$ is computed as:

$$\widehat{S_T}({\omega }_r,{\omega }_c)=(y-Z({\omega }_r,{\omega }_c)\widehat{\beta }({\omega }_r,{\omega }_c){)}^{\prime }\widehat{\mathit{Q}}{({\omega }_r,{\omega }_c)}^{-1}(y-Z({\omega }_r,{\omega }_c)\widehat{\beta }({\omega }_r,{\omega }_c))$$

and the negative log likelihood of the selected parameters (in particular, ω_r and ω_c) is computed as:

$$-\mathit{log}(L({\omega }_r,{\omega }_c,\widehat{\mathit{\beta }},\widehat{\mathit{\alpha }},\widehat{{\sigma }^2}|\mathit{y}))\propto T\mathit{log}(\widehat{{\sigma }^2})-\mathit{log}(|\widehat{{\mathit{Q}}^{-1}}|)+\widehat{S_T}/\widehat{{\sigma }^2}$$

This negative log likelihood is computed for each pair of physiologically plausible ω_r and ω_c (i.e. for each of the Z(ω_r, ω_c) matrices we generated) for a given data window. Then, the negative log likelihood is minimized to determine the optimal ω_r and ω_c for the given data window. This cyclic descent algorithm is then repeated across the subsequent, overlapping Hann time windows to determine the optimal physiological frequencies in each window across time.

Removing physiological noise

As noted earlier, the physiological frequencies are conserved throughout the brain (Fig 1). Therefore, the full cyclic descent algorithm only needs to be completed once to identify ω_r and ω_c. Once these quantities are known, the parameter estimation becomes linear and far more computationally efficient as a sequential optimization is no longer required (Malik et al., 2011). As a result, once the physiological frequencies are determined we can efficiently remove physiological noise from each voxel by performing the same moving-windowed, recursive fitting procedure in each voxel, thereby accounting for phase and amplitude variation across the brain. This fitting approach parallels how noise is removed in a GLM if an autoregressive model has also been included (for example, with RETROICOR, HRV, or RVT). However, a distinction is that we calculate these model fits in sliding windows to also allow for varying dynamics over time.

Specifically, for a given time window in a given voxel, we can determine the maximum likelihood estimate of beta $\widehat{\beta }({\omega }_{\mathit{r}},{\omega }_{\mathit{c}})$ using recursive fitting as described above. We can then remove the physiological noise (associated with specific columns in Z(ω_r, ω_c)) from that particular data segment as:

$$y-Z_{\mathit{p}}\mathit{(}{\mathit{\omega }}_{\mathit{r}},{\mathit{\omega }}_{\mathit{c}}\mathit{)}\widehat{{\mathit{\beta }}_p}\mathit{(}{\mathit{\omega }}_{\mathit{r}},{\mathit{\omega }}_{\mathit{c}}\mathit{)}$$

where ω_r and ω_c have been previously determined, Z_p(ω_r, ω_c) contains the subset of columns in Z(ω_r, ω_c) associated with physiological noise, and $\widehat{{\beta }_p}({\omega }_{\mathit{r}},{\omega }_{\mathit{c}})$ is the amplitude associated with each respective column Z_p(ω_r, ω_c). This method can be efficiently applied on a voxel-to-voxel basis to account for spatial and temporal variations in amplitude and phase of physiological noise. Notably, we also obtain an estimate of the drift, neural signal, and autoregressive noise for each time window and each voxel. In this study, we choose to only remove the physiological noise and keep the estimated autoregressive noise and drift terms in the data. However, one could also choose to remove the estimated autoregressive noise and drift at this step, for instance, if they wished to obtain white residuals.

Simulated Data

In order to test the ability of HRAN to estimate and remove physiological noise, we created two simulated time series of 300s with TR=0.250s.

The first simulated data set, used to test whether HRAN can track physiological noise frequencies, depicts a region of interest with high physiological noise (e.g. the ventricles). It consists of (a) respiratory noise simulated as a sinusoid centered at 0.3 Hz and its first harmonic at 0.6 Hz with variable amplitude (ranging from 3 to 16 arbitrary units) and frequency (ranging from 0.27 to 0.33 Hz) over time, (b) cardiac noise simulated as a sinusoid centered at 1 Hz with variable amplitude (ranging from 2 to 8 arbitrary units) and frequency (ranging from 0.92 to 1.08 Hz) over time, and (c) AR(1) background noise (with alpha = 0.9, sigma squared = 5).

The second simulated data set, used to test performance of HRAN in detecting neural signals, depicts a region of interest with neurally-relevant activity (e.g. visual cortex), represented by a 0.1 Hz sinusoid (with amplitude 25 arbitrary units) and the same AR(1) background noise as the first simulation. It also contains simulated physiological noise of the same amplitude and frequency as in the first simulation, but with the cardiac noise phase shifted by 90 degrees.

Data Acquisition

Study participants

We analyzed data collected from three separate experiments. The first two experiments were performed at Massachusetts General Hospital. All subjects provided informed written consent and all experimental procedures were approved by the Massachusetts General Hospital Institutional Review Board. We analyzed one subject collected as part of a previous study that acquired long-duration resting state data (Experiment A) and four subjects performing a visual task (Experiment B). Of these five subjects, three identified as female and two identified as male, with an age range of 22-27.

The third experiment (Experiment C) was performed at Boston University. All subjects provided informed written consent and all experimental procedures were approved by the Boston University Institutional Review Board. Four subjects were enrolled (one identified as female, three identified as male), with an age range of 25 – 32.

Data acquisition

Experiment A – resting-state data

In Experiment A, we analyzed a long duration resting-state scan with external physiological recordings in one subject, which enabled us to assess how well HRAN was able to estimate the physiological frequencies over a large time range.

The subject was imaged in a 3T Prisma scanner with a 64-channel head coil, with the neck channels turned off (remaining=48 channels). An initial anatomical multi-echo MPRAGE scan was acquired (van der Kouwe et al., 2008) with 1 mm isotropic resolution. Functional imaging consisted of a single-shot gradient echo blipped-CAIPI SMS EPI (Setsompop et al., 2012). The resting-state functional scan was acquired with a TR of 0.367s, 2.5mm isotropic resolution, TE=32 ms, multiband factor=8, FOV=230×230, shift factor=FOV/4, flip angle=35°, VERSE factor=1, no in-plane acceleration, number of slices=40, and number of repetitions = 8000. External physiological recordings included EKG and a respiratory belt, as well as electroencephalography recorded for a separate study. Physiological recordings were acquired at 1000 Hz, synchronized with the scanner, and downsampled to 200 Hz prior to analysis.

Experiment B – 7T visual task

In Experiment B, we analyzed data from four subjects who were presented with visual stimuli to determine whether HRAN was able to improve detection of visually-responsive voxels in 7T data acquired without physiological recordings. The visual stimuli consisted of flickering radial checkerboards with sinusoidally varying luminance contrast. The oscillation frequency was fixed within each run, and varied from 0.1 to 0.3 Hz across runs (as in (Lewis et al., 2018, 2016)). A red dot was also located at the center of the checkerboard and changed brightness according to a uniform distribution. Subjects were instructed to press a button when they observed this brightness change to ensure they remained attentive.

Imaging was performed in a 7T Siemens scanner with a custom-built 32-channel head coil. An initial anatomical multi-echo MPRAGE scan was acquired (van der Kouwe et al., 2008) with 0.75 mm isotropic resolution. Each functional run lasted 254 s and used a TR of 0.227s, 2 mm isotropic resolution, TE=24ms, multiband factor=3, FOV=240x240, shift factor=FOV/3, flip angle=30°, VERSE factor=1, R=2 acceleration, number of slices=15, and number of repetitions = 1119. Due to the limited field of view, the functional acquisition was positioned along the calcarine sulcus to target primary visual cortex, using the anatomical image for guidance. A whole brain reference scan with the same slice orientation as the functional runs was also performed to assist with registration of functional scans to anatomical scans. No external physiological data were acquired.

Experiment C – 3T visual task with isometric force hold

In Experiment C, we collected data from four subjects at 3T replicating the visual experimental paradigm of Experiment B, but with a) an additional task designed to alter physiology, b) external physiological recordings, and c) different TRs in order to compare HRAN with other physiological removal techniques. First, one localizer run was performed with the identical stimulus paradigm of Experiment B and used to identify visually-responsive voxels. For each subsequent run, subjects were also instructed to perform an isometric hand grip of a force gauge half-way through the run (signaled by the red dot at the center of the checkerboard turning blue).

Imaging was performed on a 3T Prisma scanner with a 64-channel head coil, with the neck channels turned off (remaining=48 channels). An initial anatomical multi-echo MPRAGE scan was acquired (van der Kouwe et al., 2008) with 1 mm isotropic resolution. The functional scans were acquired with TRs of 0.347s, 0.520s, and 0.720s for 254s, with 2.5mm isotropic resolution, TE=30ms, multiband factor=2, FOV=190x190, shift factor=FOV/3, VERSE factor=1, no in-plane acceleration, and number of slices=10. For each TR (.347s, .520s, and .720s), the flip angles were 37°, 49°, and 56° respectively. As in Experiment B, a whole brain reference scan with the same slice orientation as the functional runs was also performed to assist with registration of functional scans to anatomical scans. External physiological recordings included pulse oximetry and a respiratory belt (BIOPAC) recorded at 2000 Hz. One subject had slightly longer runs (an additional 45, 20, and 10 volumes at each respective TR) and these additional images were excluded to maintain consistent analysis across subjects.

Data Analysis

fMRI preprocessing and statistical analysis

All fMRI data was first slice time corrected using FSL 5.0.11 (fsl.fmrib.ox.ac.uk/fsl/fslwiki/) and motion corrected using AFNI (https://afni.numh.nih.gov/) (Cox J.S., 1996) using the middle frame in the time series as the reference. The data were then smoothed in FSL using a 5mm full-width-at-half-maximum Gaussian kernel. Functional runs were registered to the anatomical image using boundary-based registration (Greve and Fischl, 2009). Anatomical segmentations were generated automatically from the anatomical image using Freesurfer (Fischl, 2012). Anatomical regions of interest (e.g. primary visual cortex) for each run were then extracted from the automatic segmentation, and transformed to each individual subject’s native space. All subsequent analyses were performed within the individual subject space. Additional analyses (including implementation of HRAN) were performed in MATLAB 9.5 (2018b).

For analysis of Experiment B data, the initial thirty seconds (132 volumes) and final thirty seconds (132 volumes) of each run were excluded. The first thirty seconds were excluded as our analysis used oscillating stimuli to induce a neural signal with a known frequency, and we therefore restricted our analysis to the time expected to contain this induced oscillation (i.e. after the large onset transient subsided), as in (Lewis et al., 2016). The final thirty seconds were excluded as motion artefact was present in a handful of our subjects in a subset of runs towards the end of the run, likely related to fatigue from multiple runs of the visual stimulus, and we opted to slightly truncate the runs to consistently remove this issue. To examine visual-evoked activation of individual voxels, a general linear model (GLM) was implemented in FSL consisting of a sine function and cosine function at the stimulus frequency. The GLM was then solved in FSL using the default settings for pre-whitening, a high-pass filter of 100s, and a voxel-wise corrected significance threshold of .05. Each subject had one localizer run with a stimulus frequency of 0.1 Hz, which was used to create a region-of-interest (ROI) for comparison of activation across stimulus frequencies. The ROI was defined as voxels that were anatomically located in primary visual cortex, based on the Freesurfer segmentation, and exhibited a significant F-test of the neural regressors in the localizer run. To compare activation maps with and without physiological noise regression, the median z-score was computed across all voxels in this ROI for each run, and a Wilcoxon signed-rank test of the median z-scores was performed across runs. Three runs spanning a broad stimulus frequency range were analyzed for each subject leading to a total of 12 runs.

For analysis of Experiment C data, the initial thirty seconds of each run were excluded to examine the steady-state responses (86 volumes for TR=0.347s, 58 volumes for TR=0.520s, 42 volumes for TR=0.720s). All other analysis steps were identical to the analysis of Experiment B, including an initial run with a stimulus frequency of 0.1 Hz for each subject to create an ROI of task-responsive voxels in visual cortex, and the comparison of median z-scores for each of the physiological noise removal methods using the Wilcoxon signed-rank test across runs. With a TR of 0.347s, one run was collected for Subject 1, and six runs were collected for Subjects 2-4. The pulse oximeter fell off for the second subject during the first run, so no analysis of these physiological recordings were performed for this subject. With a TR of 0.520s, one run was collected for Subject 1 and two runs were collected for Subjects 2 – 4. With a TR of 0.720s, one run was collected for each subject.

Physiological recordings analysis

To assess whether our model accurately estimates model parameters (in particular, heart rate and respiration rate), we collected simultaneous external physiological recordings in Experiment A and Experiment C. We computed heart rate using the algorithm presented in (Barbieri et al., 2004), which treats heart beats as a point process and therefore overcomes challenges of using moving window or instantaneous estimate approaches. As a similar technique does not exist for respiration, we computed respiration rate as the reciprocal of the time interval between subsequent breaths.

To obtain RETROICOR regressors in Experiment C, we processed our external physiological recordings using the PhysIO Toolbox (Kasper et al., 2017).

Model order selection

Our model requires specification of the following three parameters: the number of cardiac harmonics K, the number of respiratory harmonics L, and the AR order P. These parameters can be defined separately for estimating the physiological frequencies from a region of interest with high physiological noise (K_freq, L_freq, P_freq), and for physiological noise regression throughout the brain (K_Z, L_Z, P_Z).

In the majority of fast fMRI scans, only the fundamental cardiac frequency and the fundamental respiratory frequency along with its lower harmonics can be observed directly (Fig 1A). With this in mind, we specify K_freq = 1 and L_freq = 1 in Experiment A and Experiment C, which are appropriate model orders in general. However, we note that with at least one subject in Experiment B (7T, TR=0.227s) both a second cardiac harmonic and interaction effect between cardiac and respiratory activity are discernible (Fig 1C). While we could similarly set K_freq = 1 and L_freq = 1, the enhanced physiological noise provides additional information to improve parameter estimates. Therefore, we specify K_freq = 2 and L_freq = 1 for Experiment B, and include interaction terms as described in (Harvey et al., 2008):

$$\mathit{x}=\sum _{m=1}^M(D_m\mathit{sin}(A_{x_m}{\omega }_{c}t+B_{x_m}{\omega }_{r}t)+E_m\mathit{cos}(A_{x_m}{\omega }_{c}t+B_{x_m}{\omega }_{r}t)+F_m\mathit{sin}(A_{x_m}{\omega }_{c}t-B_{x_m}{\omega }_{r}t)+G_m\mathit{cos}(A_{x_m}{\omega }_{c}t-B_{x_m}{\omega }_{r}t))$$

where x = [x₁, … x_T] is the sum of the interaction effects, A_xm and B_xm are integers less than or equal to the number of cardiac harmonics (K) and the number of respiratory harmonics (L), D_m, E_m, F_m, and G_m define the amplitude and phase of the interaction effects, and M is the order of the interaction terms. For all experiments, we specified P_freq = 1 as we found changing P_freq did not greatly affect physiological frequency estimates (Fig S3 A–B).

Given prior literature (Bollmann et al., 2018; Chen et al., 2019; Harvey et al., 2008) and using the Bayesian Information Criterion (BIC) as a guide (see Supplemental Information), we specified K_z = 3, L_z = 2, and included no interaction terms for all experiments to capture higher order harmonics of the cardiac and respiratory noise without overfitting our signal. As suggested by the BIC, we specified P_z = 2 for all experiments.

Physiological ROI selection

Many anatomically defined brain areas are known to manifest high levels of physiological noise, including the ventricles, white matter, and brainstem, and individuals may manifest varied levels of physiological noise in each region. We used Freesurfer (Fischl, 2012) to generate anatomical segmentations, and for all subjects estimated physiological noise from either the ventricles (left lateral ventricle, right lateral ventricle, 3^rd ventricle, or 4^th ventricle) or white matter ROIs, depending on which regions were included in our acquisition window (which had a limited field of view). We chose the ventricles and white matter, and not the brainstem, because they are less likely to contain neurally-relevant signals, which may impact our estimates of the physiological noise. In these analyses, the size of these ROIs ranged from a couple dozen voxels (e.g. using the 4^th ventricle) to a few thousand voxels (e.g. using white matter). In general, estimating physiological noise from ROIs as compared with single voxels is beneficial as averaging across voxels enhances the relative proportion of physiological to thermal noise (Triantafyllou et al., 2005); however, one could estimate physiological noise from any single voxel (including voxels with neural activity if this is appropriately modelled), as long as inspection verified that the voxel contained large-amplitude physiological noise.

Time window selection

HRAN requires specification of a moving time window. In general, we found that with shorter TRs we are able to use smaller time windows (e.g. closer to 24s) without a reduction in accuracy, and with longer TRs larger time windows (e.g. closer to 45s) may lead to slightly improved performance. However, these parameters are subject to not only TR, but also individual physiology and experimental condition. For example, if a subject is performing a task with behavioral state changes, like sleep, a shorter time window may be important to capture transient physiological dynamics. While the length of these time windows may be optimized for a particular experiment, we found that parameter estimates were fairly consistent across window lengths (Fig S3 C–F). We selected a 30 s window for Experiment A (TR=0.367s), a 24s moving time window for Experiment B, (TR=0.227s) and windows of lengths 30s, 36s, and 45s for each of the respective TR’s in Experiment C (TR=0.347s, TR=0.520s, TR=0.720s). For all experiments, we specified a 75% overlap of Hann windows. The windows are overlapping and tapered to prevent artificial “jumps” that may occur in non-tapered, sequential windows (Figure S4).

Physiological frequency range

HRAN requires specification of the expected cardiac and respiratory frequency ranges. These values may be set broadly as ranging from cardiac frequencies = [40…120] bpm and respiratory frequencies = [8…24] bpm to capture large variations in physiology across the population, or could be set based on the individual subject’s estimated heart rate and respiration rate. We visually inspected spectrograms of the ventricles and estimated the mean heart rate and respiration rate from these spectrograms, if they could be sampled directly. We then initialized the physiological frequency ranges as the mean heart rate +/− 12 and the mean respiration rate +/− 6, which allowed for more computationally efficient frequency estimation. For higher TRs (0.520s, 0.720s), a broader range of 40 – 120 bpm and 8 – 24 bpm were used for cardiac and respiratory frequencies respectively.

Spectral Analysis

All power spectra and spectrograms were computed using the Chronux toolbox (chronux.org) (Bokil et al., 2010) using five tapers and three tapers respectively. A moving window of 60s was used for Experiment A, and 30s moving windows were used for both Experiment B and C.

Comparison to other physiological noise methods

In simulated data, we compared HRAN performance with a simulated reference-based model approach (which we term simRETROICOR) and a simulated data-driven approach (which we term simPCA). For simRETROICOR, we modeled the physiological noise as a Fourier expansion of the simulated cardiac and respiratory frequencies (with 1 cardiac term and 2 respiratory terms as in the simulation) and used a GLM to remove the estimated physiological noise. This approach is similar to that of RETROICOR, and models a best-case scenario with perfect estimation of the cardiac and respiratory signals from the external recordings. For simPCA, we first replicated the simulated physiological noise region ten times with added white noise (to reflect, for example, individual voxels of the ventricles). We next performed principal component analysis (PCA) on these ten simulated physiological noise voxels, incorporated the first three principal components into a design matrix, and used GLM to remove them from our simulated data. This approach is similar to many data-driven approaches, which use component analysis on physiologically noisy voxels to estimate individual physiological noise components.

In Experiment C, we compared HRAN to widely used physiological noise regression techniques in fast fMRI data. We implemented RETROICOR with our acquired external physiological reference signals and the PhysIO toolbox (Kasper et al., 2017). In both HRAN and RETROICOR, we used 3 cardiac terms, 2 respiratory terms, and no interaction terms. We also implemented a data driven approach modeled after aCompCor (Behzadi et al., 2007), which we simply term anatomical PCA (aPCA). First, we extracted masks of white matter and cerebrospinal fluid (including the ventricles), eroding by one voxel. For each voxel in this mask, we detrended the functional time series by removing the mean and linear drift and normalized the variance by dividing the time series by the temporal standard deviation. We then examined the correlation between the voxel time series and our neural regressors (consisting of a sine and cosine at the stimulus frequency). If either correlation had a p-value less than 0.2, we excluded the voxel. We conducted PCA using singular value decomposition on all voxels that satisfied the above criteria and selected the first five principal components from white matter and the first five principal components from CSF as physiological regressors. For HRAN, RETROICOR, and aPCA, we removed the estimated physiological noise from each voxel before performing statistical analysis in FSL.

Results

HRAN accurately estimates cardiac and respiratory dynamics and explains fast fMRI data

We first validated that our model is able to provide faithful estimates of the fundamental cardiac and respiratory frequencies directly from the fast fMRI signals, without requiring external physiological recordings. In resting-state data in which heart rate and respiratory rate varied over time, we used HRAN to estimate the physiological frequencies from the 4th ventricle (Fig 3A). We found that these estimated physiological frequencies accurately tracked the heart rate and respiration rate computed from simultaneously collected EKG and respiratory belt data (Fig 3B). In particular, our model estimates of heart rate and respiration were each within the range of the heart rate and respiration rate obtained from external recordings in 96% of analyzed time windows (n = 100 thirty-second windows). Furthermore, the median root-mean-squared-error (RMSE) of our model estimates and the heart rate and respiration rate obtained from physiological recordings were 2.8 bpm (+/− standard error of 0.27) and 2.0 bpm (+/− standard error of 0.14) respectively. These errors in our model estimates are similar to the median RMSE of the heart rate and respiration rate obtained from physiological recordings with their averages in a given time window, which were 2.7 (+/− standard error of 0.10) and 1.7 (+/− standard error of 0.09) respectively, suggesting that the errors reflect the variability of cardiac and respiratory activity within the time window. These results demonstrate that HRAN can be used to determine cardiac and respiratory frequencies directly from fast fMRI data, without requiring external reference signals.

Figure 3: HRAN accurately estimates physiological frequencies.

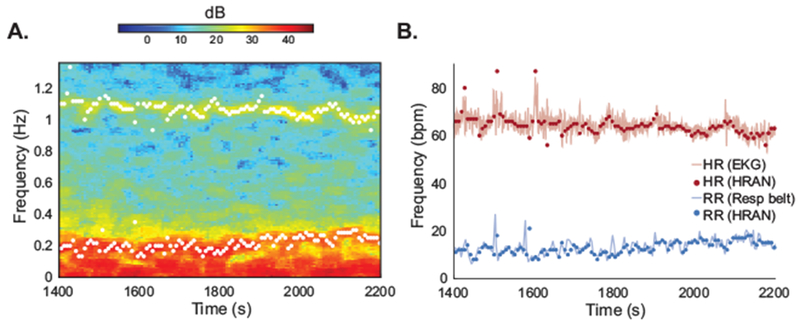
Estimates of cardiac and respiratory frequencies derived from fast fMRI data using HRAN track estimates derived from external physiological reference signals. (A) A spectrogram of the 4th ventricle from a subject in Experiment A. The 4th ventricle was used to generate estimates of the fundamental physiological frequencies (white dots). (B) These estimated cardiac (red dots) and respiratory (blue dots) frequencies correspond to the heart rate obtained from EKG (red line) and respiratory rate obtained from a respiratory belt (blue line).

Given this accurate estimation of physiological frequencies, we next examined how well our full model (including physiological noise, drift, autoregressive components, and neural signal) fits fast fMRI data. Assessing the goodness-of-fit of our model is critical to ensure that we do not underestimate or overestimate the physiological noise, along with the autoregressive components, thereby leaving correlated noise in the residuals and skewing statistical inferences. This step is especially important for fast fMRI data, where both the autocorrelation structure and magnitude of physiological noise vary substantially across voxels. For example, the power spectra of a white matter voxel, a grey matter neocortical voxel, and a brain stem voxel (Fig 4A) in a run from Experiment B manifested a variable number of physiological harmonics of differing amplitude and low-frequency correlated noise, and our model must be able to accommodate these differences.

Figure 4: HRAN explains fast fMRI data across tissue type.

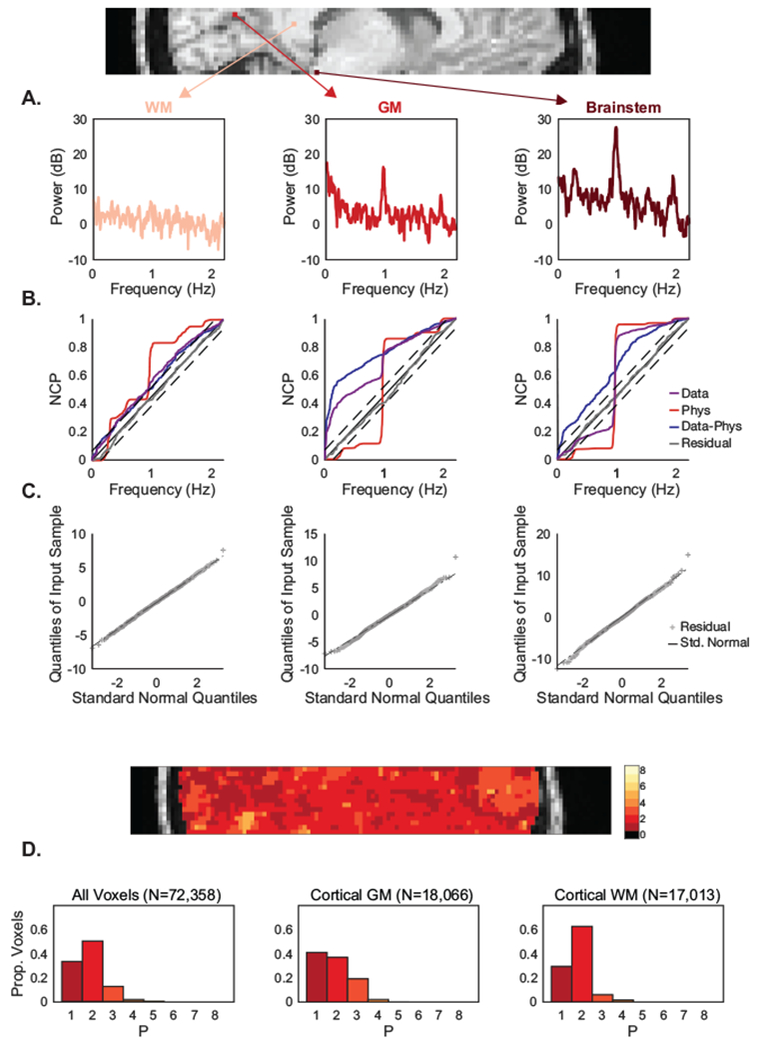
HRAN satisfies goodness-of-fit criteria across voxels with varied noise properties. (A) The power spectra of three exemplar voxels are shown from a subject in Experiment B: a cortical white matter voxel (left), a cortical grey matter voxel (middle), and a brainstem voxel (right). Each voxel manifests differing levels of physiological and autocorrelated noise. (B) The normalized cumulative periodograms (NCP) demonstrate that the residuals (grey line) in each voxel lie within a 95% confidence interval of ideal white noise (dashed black lines). (C) Quantile-quantile plots show that the residuals are also approximately normally distributed. (D) Goodness-of-fit criteria were similarly examined across the brain, and histograms of all voxels (left), cortical grey matter voxels (middle), and cortical white mater voxels (right) demonstrate that HRAN satisfies goodness-of-fit criteria across the majority of voxels in the brain.

To confirm that HRAN explains data across voxels, we performed HRAN and checked standard goodness-of-fit criteria in one run acquired with our shortest TR (Experiment B). We first calculated the normalized cumulative periodogram (NCP) of the estimated HRAN components in each voxel. The NCP depicts the cumulative power at each frequency – for example, ideal white noise contains equal power at each frequency and would therefore increase linearly across all sampled frequencies (Fig 4B). NCP demonstrated that the white matter voxel was relatively similar to white noise, the grey matter voxel contained a combination of both low frequency and physiological noise, and the brainstem voxel was dominated by physiological noise (Fig 4B). Notably, the residuals of HRAN in each of these voxels lay within a 95% confidence interval of ideal white noise, indicating that the residuals of our model do not significantly differ from white noise. Furthermore, we created a quantile-quantile plot of each of the residuals which demonstrate that they are approximately normally distributed (Fig 4C). These two findings suggest that HRAN is able to appropriately model the data in each voxel, despite their differing ratios of physiological and correlated noise.

We computed the NCP across all brain voxels and found that the residuals lie within the 95% confidence interval of pure white noise in 84% of all voxels (N = 72,358), 92% of neocortical white matter voxels (N = 17,013, Fig 4L), and 78% of neocortical grey matter voxels (N= 18,066) using an AR(2) model as indicated by the BIC (Fig 4D) (see Model Order Selection). We also increased the AR order until the residuals remained within the 95% confidence interval of ideal white noise and found that with an AR(3) model, HRAN residuals remained within the 95% confidence of ideal white noise in 97% of all voxels, 98% of neocortical white matter voxels, and 97% of neocortical grey matter voxels.

Taken together, these results suggest that HRAN is able to 1) accurately estimate the cardiac and respiratory frequencies from fast fMRI data directly and 2) satisfy goodness-of-fit criteria in voxels with varied physiological noise and autocorrelation structure.

HRAN accurately removes time-varying physiological noise in simulated data

We next examined whether HRAN could accurately remove physiological noise while preserving neural signal in a simulated dataset. A challenge for many physiological noise removal methods is that the amplitude and frequency of respiratory and cardiac signals are often not stable throughout a run, but rather vary dynamically over time. We therefore included variable amplitude and frequency noise in this simulation, to create a difficult test case for each method.

First, we generated simulated fast fMRI data with cardiac and respiratory noise of variable amplitude and frequency, representing the ventricles. We then simulated cortical fMRI data as a neurally-driven oscillation at 0.1 Hz contaminated with physiological noise. Notably, the physiological noise in the simulated cortex has the same amplitude and frequency as in the simulated ventricles; however, the phase of the cardiac noise is shifted, representing temporal delays of physiological noise across the brain which are often present in real data.

To test the performance of our method, we used HRAN to estimate the physiological frequencies from the simulated ventricle data, and then regress out the physiological noise from the simulated cortex data. We also compared HRAN to (a) a simulated reference-based modeling approach, in which the frequencies are known (due to external reference signals) but the amplitude remains constant (simRETROICOR), and (b) a simulated data-driven approach, in which principal component analysis is used to estimate and remove the physiological noise from the data directly (simPCA).

Visual examination of the cleaned simulated spectrograms demonstrated that HRAN was the most effective in removing the simulated physiological noise (Fig 5A). The de-noised simRETROICOR spectrogram contained high amplitude physiological noise not only when the original signal had relatively high amplitude physiological noise, but also when the original signal had relatively low amplitude physiological noise. A time-series plot of simulated physiological noise with the estimated physiological noise from simRETROICOR overlaid shows that the method overestimated the physiological noise in the original signal when it had low amplitude (Fig 5B). This resulted in the artificial introduction of noise into these segments (Fig 5A,C). In fact, by examining only the de-noised data one is unable to discern whether the residual physiological noise results from failure to remove high amplitude physiological noise present in the original data or its artificial introduction. These challenges arise because simRETROICOR assumes a fixed amplitude of cardiac and respiratory noise across time, which, especially in longer duration scans, may not hold true.

Figure 5: HRAN removes simulated physiological noise with variable amplitude and frequency.

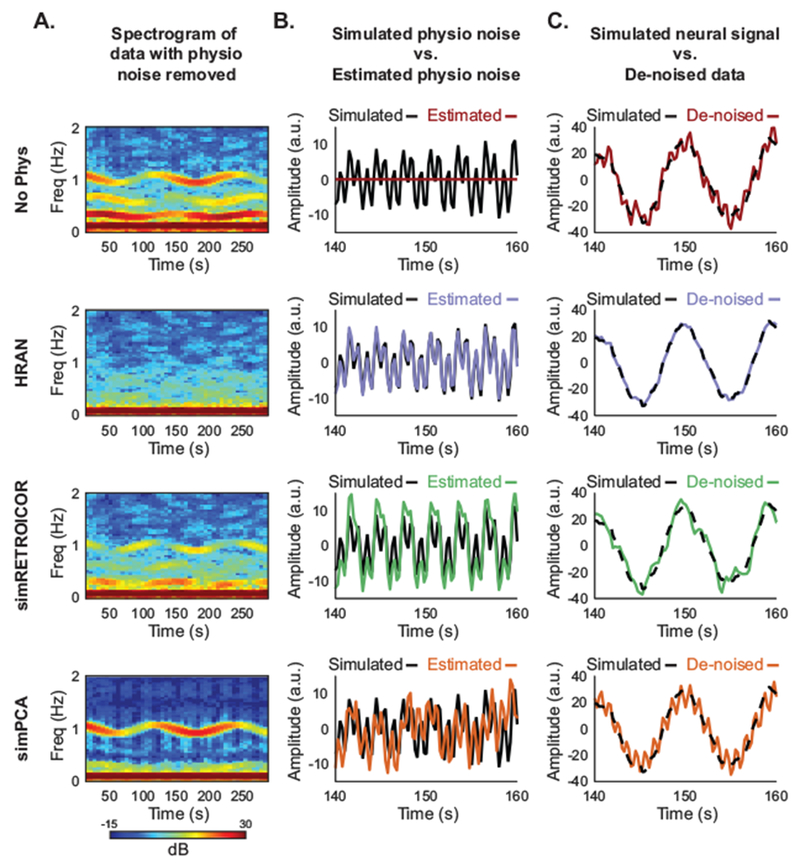
Each row displays the results of physiological noise removal using a different technique (row 1 no physiological noise removal, row 2 HRAN, row 3 simRETROICOR, and row 4 simPCA). Spectrograms of the simulated data with each of the physiological noise removal methods performed are shown in (Column A). The simulated physiological noise (black lines) and estimated physiological noise using each method (colored lines) are displayed in (Column B). The simulated data with physiological noise removed using each method (colored lines) are displayed on top of the simulated neural signal (black dashed lined) in (Column C). HRAN effectively accounts for and removes the physiological noise from the simulated data (second row). As simRETROICOR cannot accommodate variations in amplitude, physiological noise is both left in and introduced into the simulated data (third row). While the simPCA approach accounts for amplitude variations, it is unable to address the 90° phase delay of the cardiac noise and leaves it in the simulated data (fourth row).

While the simPCA approach successfully removed the simulated respiratory noise, the cardiac noise, which was phase-shifted relative to the simulated ventricle data, was still present (Fig 5A,C). This PCA-based approach is unable to account for the phase difference between the cardiac noise in the two simulated data sets, and is therefore unable to successfully remove the physiological noise. Furthermore, because the estimated components are broadband, the structure of the background AR noise was also affected. Unlike model-based methods, estimated regressors derived from component analysis based approaches depend on the timeseries from which they are extracted, and therefore do not necessarily generalize across the brain.

Conversely, HRAN was able to accurately estimate the amplitude and frequency changes of the physiological noise (Fig 5A–C). As a result, HRAN was most effective in removing the physiological noise from the simulated neurally-relevant activity, reducing the root mean squared error of the original data by 86% (9.42 to 1.34), a 64% improvement compared to simRETROICOR (1.34 vs 3.70), and an 80% improvement compared to simPCA (1.35 vs 6.74). These simulations therefore demonstrate that HRAN can accurately model and remove physiological noise in multiple challenging settings: when the amplitude and frequency of the noise vary over time, and when the phase of the noise varies over space.

HRAN improves detection of stimulus-driven neural activity

After confirming that HRAN can accurately detect and remove physiological noise in simulated data, we examined whether it was able to improve statistical detection of task-related activity in a fast fMRI experiment. In Experiment B, we presented subjects with visual stimuli oscillating at specific frequencies (ranging from 0.1 to 0.3 Hz). We selected an ROI that was within primary visual cortex and driven by the lowest frequency stimulus (0.1 Hz), which elicited the largest amplitude fMRI response, in order to identify a region that is expected to exhibit task-driven signals. In this ROI, we compared the median change in z-scores with and without physiological noise removal using HRAN. By selecting our ROI in a run with a higher signal-to-noise ratio without any noise removal, we prevented bias in the ROI selection due to the performance of any particular cleaning method.

We found that even in this visual task known to evoke a strong response, HRAN increased the median z-scores in the ROIs as compared with no physiological noise removal (Fig 6A, median change of 0.10, Wilcoxon signed rank, p < 0.002). Notably, a median-increase in z-scores of these task relevant voxels does not necessarily imply appropriate physiological noise removal. In fact, if one were to simply bandpass filter the data around the frequency of interest, this would also result in an overall increase in z-scores, but would remove much more of the signal than just the physiological noise. We therefore also examined spectral content of the fMRI signals. Spectrograms (Fig 6B,C) and power spectra (Fig 6 D,F) of two example runs suggested that HRAN was able to selectively remove the respiratory and cardiac noise from the signal, including their harmonics, despite the variations in amplitude and frequency across time (particularly the respiration). Importantly, in both runs the background power spectra were kept intact, suggesting that HRAN also preserved the neurally-relevant signal as well as the autoregressive noise, and did not introduce additional noise into the original data.

Figure 6: HRAN improves detection of task-driven voxels.

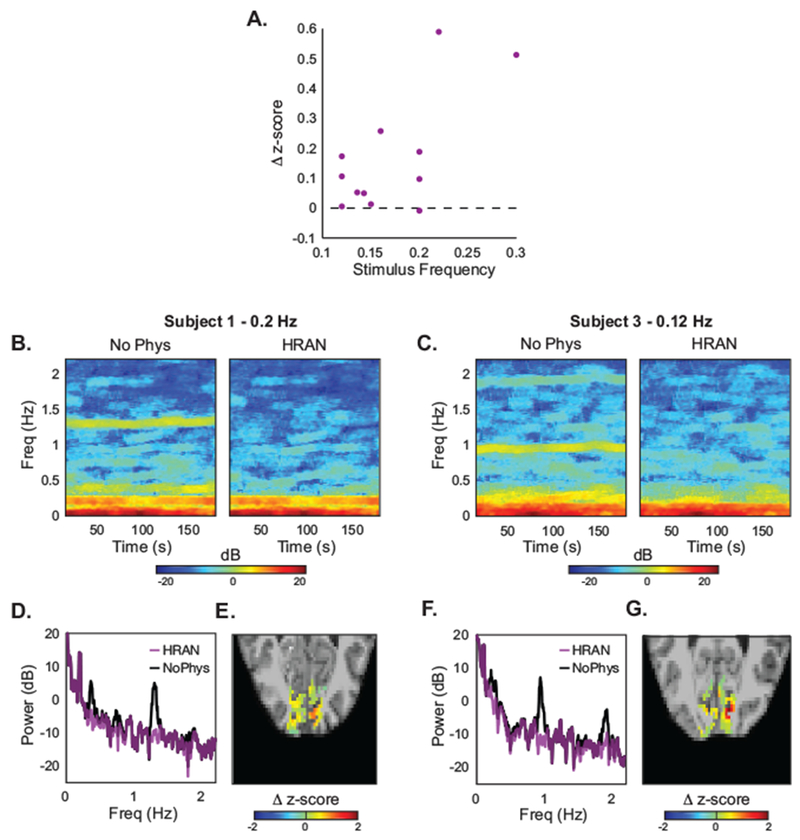
(A) As compared with no physiological regression, HRAN increases the median z-scores of anatomically and functionally defined ROIs in visual cortex across four subjects and twelve runs. Autoregressive noise was not removed. (B, C) Spectrograms of this ROI are shown with and without physiological noise removal in two exemplar runs, demonstrating that respiratory and cardiac frequencies are selectively removed. (D, F) Power spectra in these two exemplar runs further illustrates that these physiological peaks are removed, while the signal and background noise is preserved. (E, G) Maps of the differences in z-scores in each voxel of an example slice with and without HRAN, showing broad increases in statistical detection of activation across the visual cortex when HRAN is applied.

These results suggested that HRAN was able to successfully estimate and remove physiological noise in fast fMRI data, thereby improving detection of task-driven voxels. Furthermore, HRAN was particularly effective in improving the z-scores at faster stimulus frequencies, which have lower amplitude neural signals and in turn lower overall z-scores, indicating that HRAN would be beneficial for single-subject imaging of fast BOLD dynamics or more complex cognitive studies seeking to characterize relatively small effects.

HRAN performs as well as gold-standard physiological noise removal methods without requiring external physiological recordings

We next designed an experiment (Experiment C) to compare HRAN with other widely used physiological noise removal approaches: RETROICOR (which we take as gold standard due to its accurate noise estimation from external physiological recordings) and an anatomical PCA based approach (aPCA), where physiological noise components were estimated using principal component analysis on the CSF and white matter. In the experiment, subjects viewed an oscillating visual stimulus (as in Experiment B). Halfway through each run, subjects performed an isometric hand grip, maintaining force for the second half of each run. An isometric hand grip is known to induce a greater afterload on the heart, or increase systemic vascular resistance, which may impact heart rate and cerebral blood flow (Lilly, 2011). Therefore, this experiment contains a task-driven response (induced by the visual stimulus) with time-varying physiological noise (induced by the hand grip).

The task elicited both the expected stimulus-driven response and dynamic physiological noise over time (Fig 7A). The spectrograms and power spectra suggested that both HRAN and RETROICOR effectively accounted for the physiological noise (Fig 7A,B), whereas aPCA had mixed results. Specifically, aPCA removed a substantial amount of the low-frequency components present in the signal, but also introduced high-frequency noise which obscured the cardiac and respiratory peaks (Fig 7A,B). Inspecting the time series further demonstrated this high-pass filtering and introduction of high-frequency noise in aPCA, while both HRAN and RETROICOR tracked the original signal well (Fig 7C).

Figure 7: Comparison of noise removal methods in one subject.

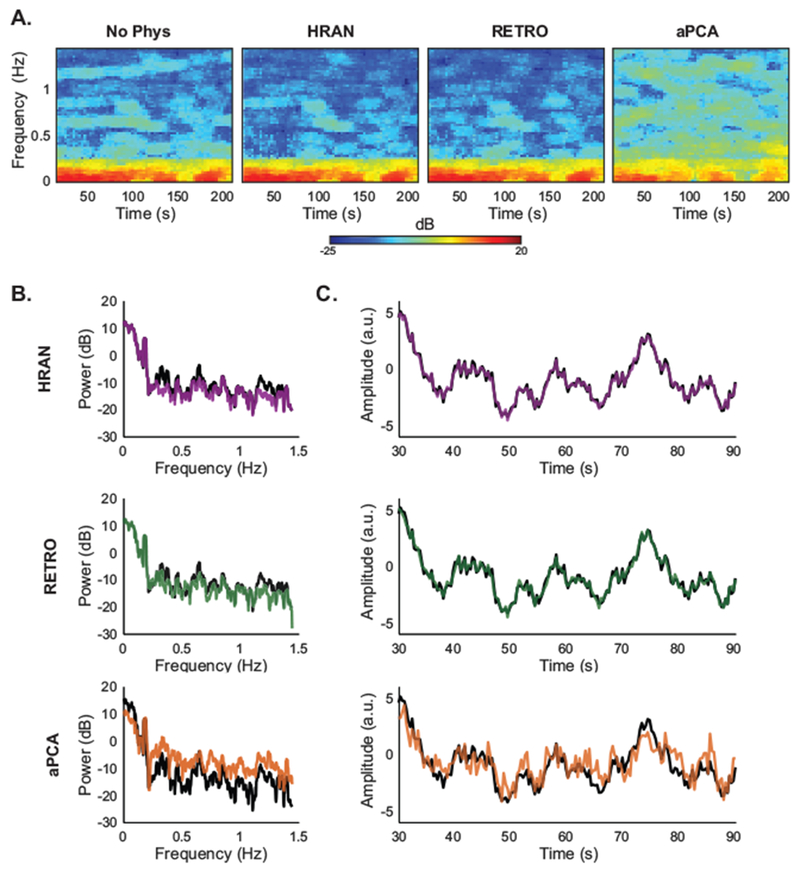
HRAN removes physiological noise while preserving fMRI signal. (A) Spectrograms of the ROI in one run from Experiment C (Subject 4) show that cardiac noise is appropriately removed by HRAN and RETROICOR, but not by aPCA. (B) Power spectra of the same ROI show that HRAN and RETROICOR account for time-varying physiological noise, while aPCA removes low-frequency noise and introduces high-frequency noise. (C) Timeseries of the ROI demonstrate that HRAN and RETROICOR track the original data, whereas aPCA introduces substantial high-frequency fluctuations.

We found that all physiological noise removal methods increased the median z-scores in the majority of runs. In particular, HRAN increased the median z-score in 12/13 runs (median change of 0.216, Wilcoxon signed rank, p = .001), RETROICOR increased the median z-score in 11/13 runs (median change of 0.023, Wilcoxon signed rank, p = 0.049), and aPCA increased the median z-score in 10/13 runs (median change of 0.278, Wilcoxon signed rank, p = 0.048). However, this performance of aPCA was not consistent across stimulus types. Notably, aPCA manifested the greatest increase in z-scores only in the lower stimulus frequencies, and actually decreased the z-score when higher stimulus frequencies were presented, whereas HRAN and RETROICOR increased the z-scores for both low and high stimulus frequencies (Fig 8B).

Figure 8: Comparison of noise removal methods across subjects.

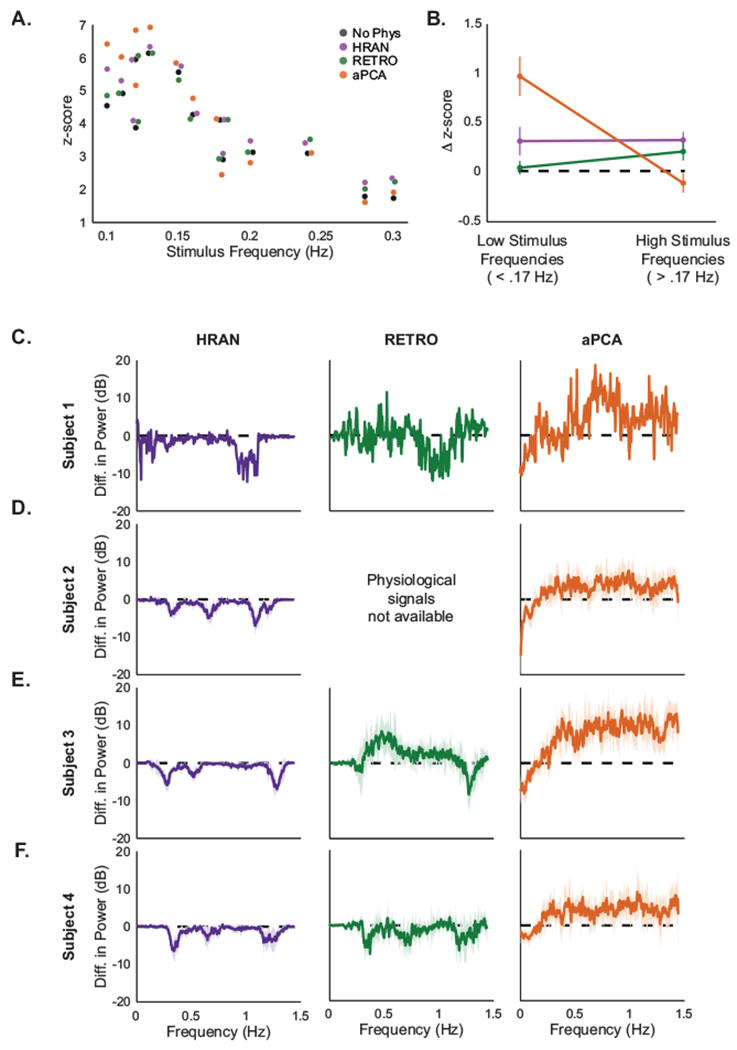
HRAN selectively removes physiological noise and improves z-scores across stimulus frequencies. (A) Median z-scores across the ROI with no physiological noise removal (black), HRAN (purple), RETROICOR (green), and aPCA (orange) across all subjects. Stimulus frequency is jittered for display. At lower stimulus frequencies aPCA demonstrates the greatest increase in z-scores, but at higher stimulus frequencies only HRAN and RETROICOR improve detection. (B) Average difference of median z-scores with each method and no physiological regression grouped by stimulus frequency: low frequency (<0.17 Hz, n = 7 runs) and high frequency (>0.17 Hz, n = 6 runs). Error bars depict standard error. (C-F) Difference in mean power spectra between each physiological noise removal method and no physiological noise removal in the ROI. Negative values indicate that power at that frequency has been reduced (or noise has been removed), and positive values indicate that power has been increased (or noise has been introduced). Shading represents the standard deviation across runs for each subject. One run was collected for Subject 1, and six runs were collected for Subjects 2-4.

Notably, it is possible that these observed increases in z-scores may have resulted from the removal of variance in the fMRI signal that is not directly related to physiological noise. To characterize how well each method selectively removed physiological noise, we examined the average difference in power spectra before and after physiological noise removal across runs for each subject (Fig 8C–F). We expected that successful physiological noise removal techniques would manifest a power difference only in physiological frequency bands, leaving the rest of the signal intact.

We found that both HRAN and RETROICOR effectively removed physiological noise in distinct frequency bands associated with cardiac and respiratory activity (as indicated by the negative differences in power), while preserving neural signal. A notable exception was present in one subject (Fig 8E), where increased noise was present in the first harmonic of respiration. We found that this increased noise was related to a low frequency component present in only one of the RETROICOR regressors, which may have resulted from irregular breathing patterns that can lead to sub-optimal fitting. On the other hand, aPCA primarily removed low frequency noise, and though it also demonstrated relative reductions of noise in the cardiac and respiratory frequency bands, it was with a background of overall increased high-frequency noise. This high-pass filtering effect likely contributed to the observed increase in z-scores at lower stimulus frequencies, while the broadband noise may have impeded detection of more rapid neurally-driven responses (Fig 8B). In other words, although aPCA increased the z-scores in a majority of runs, this result may have been driven by the reduction of variance at lower frequencies (<0.1 Hz) rather than removal of noise in respiratory and cardiac frequency bands.

These results demonstrated that HRAN can selectively remove physiological noise as effectively as the gold standard technique, RETROICOR, but without requiring external reference signals.

HRAN performance at lower sampling rates

While we have shown that HRAN performs well at TRs where respiratory and cardiac frequencies can be unambiguously identified, we next aimed to determine how HRAN performs when these physiological signals are aliased. For example, a TR of 0.500s is required to track a typical heart rate of 60bpm (or 1 Hz), but it is not clear how HRAN estimates would vary if the subject’s heart rate increased slightly above the Nyquist limit. In Experiment C, we also collected runs with TRs of 0.520s and 0.720s with external physiological recordings to investigate whether HRAN could correctly identify the fundamental physiological frequencies at lower sampling rates.

In one run, we observed that the heart rate varied from slightly below highest observable frequency (58 bpm with a TR of .520s) at 53 bpm to well above it at 71 bpm (Fig 9A). We found that while HRAN could not track these heart rate dynamics directly, the aliased cardiac estimates from HRAN accurately tracked the aliased heart rate. As expected, HRAN was not able to distinguish between the true heart rate and aliased heart rate as the fast fMRI data lack sufficient information; however, HRAN was able to successfully account for and remove the aliased cardiac noise in the fast fMRI data (Fig 9B). In other words, because the cardiac noise aliased into a distinct frequency band, HRAN was able to appropriately estimate and remove the noise despite not sampling it directly. We compared HRAN (using only 1 cardiac term and 1 respiratory term as higher harmonics may not be correctly determined) with RETROICOR (using 3 cardiac terms and 2 respiratory terms), and found that both HRAN and RETROICOR removed physiological noise from the ROI in visual cortex (Fig 9B,C) and improved the median z-score in this ROI as compared with no physiological regression (no physiological regression: 6.36, HRAN: 6.53, RETROICOR: 6.47). In the five runs we collected with TR = 0.520s, HRAN improved the z-score in 5/5 cases with a median increase of 0.16 and RETROICOR improved the z-score in 4/5 cases with a median increase of 0.02.

Figure 9: Performance of HRAN varies with TR and physiology.

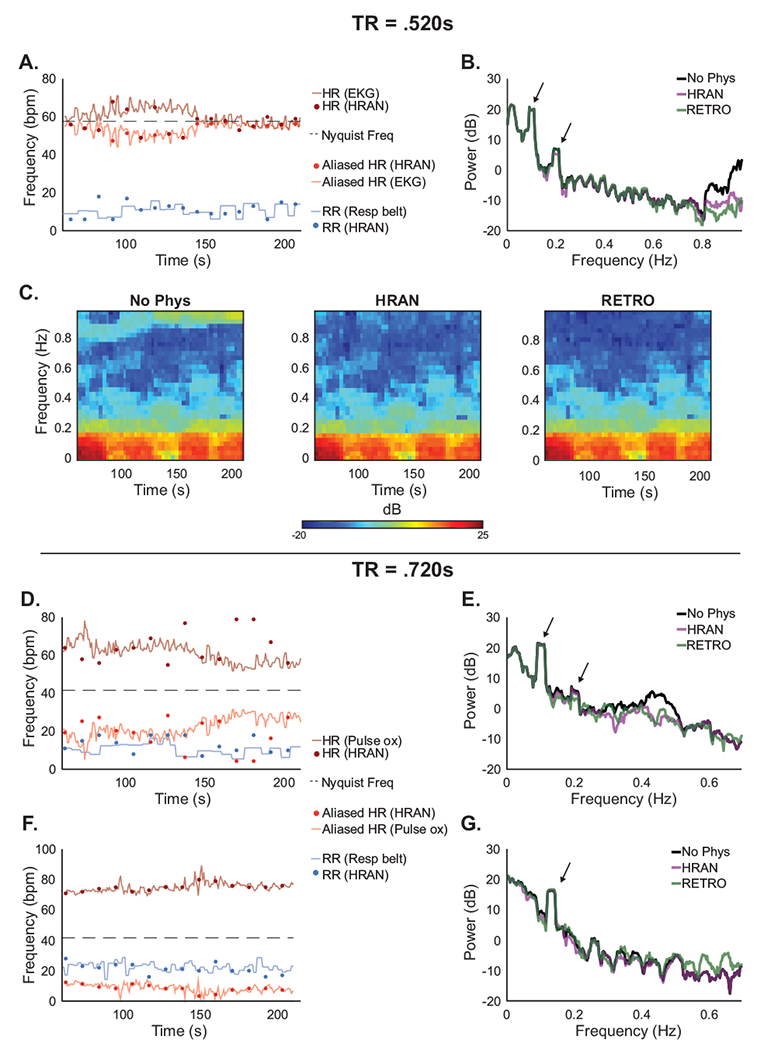
HRAN may be effective even if fMRI data is sampled below the Nyquist frequency, though to a limited extent. (A) With TR = .520s, the respiratory frequencies estimated by HRAN (blue dots) track the respiration rate obtained using external recordings (blue line), though the cardiac estimates (dark red dots) do not always track the heart rate (dark red line) directly; however, the aliased HRAN cardiac estimates (light red dots) track the aliased heart rate (light red line). (B-C) Power spectra and spectrograms of the ROI demonstrate removal of physiological noise. Neurally-relevant peaks indicated by arrows. (D,F) The cardiac frequencies may alias into respiratory frequency bands and limit HRAN estimation, or into a distinct frequency band where HRAN still performs well (examples have TR = .720s). (E,G) Power spectra demonstrate removal of the physiological noise to varying degrees. Neurally-relevant peaks indicated by arrows.

With a TR of 0.720s the highest observable frequency is much lower (42 bpm), and the cardiac noise may alias more broadly across sampled frequencies. For example, in one run the heart rate varied from 52 bpm to 78 bpm, and aliased into the respiratory frequency range (Fig 9D). HRAN was therefore unable to distinguish between cardiac and respiratory frequencies (as seen by the HRAN respiratory estimates tracking the heart rate, and HRAN cardiac estimates tracking the respiration). As a result of the aliasing, HRAN lacked a defined cardiac frequency range and essentially treated any oscillatory signal in the ventricles as physiological noise. In a separate run, the cardiac noise aliased into a distinct frequency band, and therefore HRAN was able to accurately estimate the cardiac and respiratory frequencies from the aliased signal (Fig 9F).

In the three runs we collected with a TR of 0.720s, we found that HRAN was able to remove noise in similar frequency bands as RETROICOR (Fig 9E,G), and both HRAN and RETROICOR improved the z-scores in all three cases with a median increase of 0.62 and 0.57 respectively. However, these results must be interpreted with caution as it is possible that HRAN (like conventional data-driven methods) may have also removed noise not directly associated with cardiac and respiratory activity. Together, these results suggest that HRAN may be useful even at slightly higher TRs which cannot directly resolve physiological frequencies, but must be applied more carefully.

Discussion

We created a model of harmonic regression with autoregressive noise to estimate and remove physiological noise in fast fMRI. Our model determines the fundamental cardiac and respiratory frequencies from the fMRI data directly, and removes the physiological noise from neurally-relevant signals and autocorrelated noise without requiring external physiological recordings.

Before performing any inference with our model, we first confirmed that our model sufficiently explains fast fMRI data. Importantly, we achieved a balance between model complexity and goodness-of-fit using standard model comparison criteria as a guide and validating that the residuals were not biased to any particular frequency (Fig 3,4,S1). While we found the specified model orders (i.e. the number of cardiac terms, the number of respiratory terms, and autoregressive order) were sufficient to explain fast fMRI data across a wide range of acquisition parameters (e.g. field strengths of 3T and 7T, TRs of 0.227s to 0.720s), they can also be adapted depending on experimental paradigm, preprocessing, and acquisition. For example, we focused on visual cortex, but studies investigating regions known to manifest higher levels of physiological noise, such as the brainstem, may choose to include higher physiological harmonics or interaction terms (Harvey et al., 2008). Similarly, we did not incorporate realignment regressors into our estimates of physiological noise, which may help to account for respiratory artifacts related to motion (Bollmann et al., 2018; Fair et al., 2018). Our data were also smoothed, which amplified the magnitude of the signal and physiological noise, relative to thermal noise. Unsmoothed data may create a more distinct separation of optimal AR orders between tissue type (Bollmann et al., 2018), and reduce the detection of the higher physiological harmonics. Our model is therefore able to perform well across a wide range of conditions, and can adapt as investigators continue to expand the capabilities of fast fMRI.

Another important aspect of HRAN is that although it estimates physiological noise from the data, it is a model-based approach designed specifically for fast fMRI. In particular, it avoids removing neural signals at high (>0.15 Hz) frequencies, preserving information that may be of interest in fast fMRI studies (Fig 6–8). Recent studies have discovered neurally-driven signals an order of magnitude larger than predicted by the canonical hemodynamic response function up to 0.75 Hz (Lewis et al., 2016) and high-frequency fMRI signals have also been reported in the resting state (Lee et al., 2013); therefore, approaches to remove physiological noise that also remove signal or enhance noise in these higher frequency bands may not be appropriate for fast fMRI. For example, while temporal low-pass filtering removes non-aliased physiological noise, it also removes all fast neurally-driven signals. In addition, as suggested by previous work (Chen et al., 2017), we found that data-driven methods in fast fMRI often estimate broadband physiological noise regressors which are driven by low-frequency components. Regressing these components across the brain introduced high frequency noise into the data and obscured detection of the faster neural signals. Notably, our tested data-driven method, aPCA, does lead to an improvement in z-scores at lower stimulus frequencies. However, as evident from the difference in power spectra in Fig 8, the improvement in z-scores is not related to physiological noise removal, but rather is related to removal of variance in the signal not associated with physiological noise (in this particular case, high-pass filtering). Given that z-scores improve with removal of any non-task-related variance, we recommend examining the power spectra before and after physiological noise removal as an effective quality control measure to ensure proper physiological noise removal. Certain pre-processing steps including pre-whitening, filtering, manual classification, or even performing HRAN on the estimated physiological regressors could help to prevent this introduction of noise, but come with their own challenges (Bright et al., 2017; Carp, 2013; Chen et al., 2017; Hallquist et al., 2013). Unlike data-driven methods, model-based approaches are informed with biological intuition about the properties of the noise. Therefore, they selectively remove physiological noise in distinct frequency bands and preserve the higher-frequency signals, which is important as these low-amplitude, high-frequency signals can overlap with the physiological frequency range.

While HRAN was most effective at TRs where physiological noise is sampled directly, we found that it also was able to remove physiological noise in longer TR scans in which the cardiac rhythm was aliased (Fig 9). In fact, in this undersampled case HRAN is similar to many data-driven approaches which estimate physiological noise from anatomically defined regions, except with the additional constraint that the noise must be periodic. As a result, at longer TRs HRAN has the potential to introduce noise into the data, for example, if the physiological frequencies are estimated inaccurately. This limitation could be overcome if external physiological recordings are collected by combining RETROICOR with HRAN. Specifically, the estimated physiological regressors in RETROICOR could be incorporated into the cyclic descent algorithm to ensure that physiological frequencies were accurately tracked (even if undersampled in the fMRI), the amplitude was allowed to vary, and the autocorrelated noise was appropriately accounted for. Alternatively, a slice-based approach as in (Aslan et al., 2019) could potentially be used to sample the physiological noise. A second limitation is that HRAN does not currently model low-frequency changes in respiratory volume or heart rate variability (Birn et al., 2008b, 2008a, 2006; Chang et al., 2009; Chang and Glover, 2009). Future work could examine how to incorporate these variables into HRAN, either through direct measurements, or through exploring whether these low-frequency fluctuations may in fact be captured by the dynamic amplitude measures fit with HRAN in each time window. A related limitation of HRAN is that it assumes fixed parameters for a given time window, but physiological frequencies and amplitude can vary even within a time window. In addition, HRAN assumes a periodic structure to the physiological noise. While this prevents the artificial introduction of noise potentially seen in data-driven approaches, it also limits the potential ability of HRAN to remove physiological noise that deviates from the model. State-space approaches, such as DRIFTER (Särkkä et al., 2012), are better able to accommodate these dynamic changes, and could perhaps be integrated with HRAN to optimally account for temporally and spatially varying physiological and autocorrelated noise in fast fMRI. Finally, HRAN currently estimates noise parameters from each voxel independently, though a regularization procedure as in (Purdon et al., 2001) could be implemented to produce smoother noise estimates.

In conclusion, we harnessed the enhanced information in fast fMRI to estimate and remove physiological noise directly from the data, while preserving the underlying signal. Notably, the faster signals detectable in fast fMRI overlap with physiological noise, and the statistical structure of the noise is altered, making accurate noise removal particularly important -- especially in patient populations or long duration scans where physiological noise may be variable, and external physiological recordings are difficult to collect. We demonstrate that while analysis of fast fMRI data poses novel challenges, it also contains unique and meaningful information, and our technique could be broadly useful for future studies that aim to examine and exploit this abundance of new information in fast fMRI signals. The full software is available at https://github.com/LewisNeuro/HRAN.

Supplementary Material

1

Figure S1: Optimal model orders. Selection of the model orders (number of cardiac terms K, number of respiratory terms L, and autoregressive order P) was performed using the Bayesian Information Criterion (BIC). (A) The power spectra of three exemplar voxels are shown from a subject in Experiment B: a cortical white matter voxel (left), a cortical grey matter voxel (middle), and a brainstem voxel (right). Each voxel manifests differing levels of physiological and autocorrelated noise. (B) The BIC (indicated by co/orbai) was first determined by setting P as 1 and varying K and L. Optimal BICs are indicated by the white star. (C) For the optimal K and L, the optimal P was determined (minimum of line). (D-F) This procedure was repeated for each voxel in the brain, and displayed in one sagittal slice and as histograms. The optimal K are shown in red, optimal L are shown in blue, and optimal P are shown in purple with intensity of color representative of increasing model order.

2

Figure S2: Interaction terms well localized to ventricles. In one subject from Experiment B, we examined the magnitude of the interaction terms across the brain. We fit HRAN including interaction terms and display a heat map of the estimated interaction (left), cardiac (middle), and respiratory (right) components in axial slices (A-C). Hotter colors indicate that an increasing percent of a voxel’s total variance is explained by a given component. Only a small fraction of a voxel’s total variance is explained by the interaction terms across all axial slices, and these interaction effects are well localized to the ventricles.

3

Figure S3: HRAN estimates relatively insensitive to parameter selection. In the subject from Experiment A we varied the autoregressive order (A-B) and the moving time window length (D-F) to see how selection of these parameters effected HRAN estimates of physiological frequencies. In all plots, HRAN frequency estimates are indicated as dots (cardiac in red and respiratory in blue), and heart rate and respiration rate obtained from external recordings are shown as lines with corresponding colors. An autoregressive order choice of 2 or 3 had little effect on HRAN estimates (A-B), shown using a 30s window as in Figure 3. In general, smaller time windows led to more dynamic but sometimes unreliable estimates (for example, (C)), and longer time windows led to less dynamic but slightly more accurate estimates (for example, (D)).

4

Figure S4: Harm windowing prevents artificial jumps. (A) For an arbitrary data segment from Experiment B, we plotted the estimated model components with Hann windowing (B, left) and rectangular windowing (B, right). The estimated cardiac (C), respiratory (D), and trend terms (E) are all continuous across consecutive Hann windows, but not rectangular windows (discontinuities in black). As a result the de-noised data (F) is continuous using Hann windows, but not rectangular windows.

Figure 2: Cyclic Descent Algorithm.

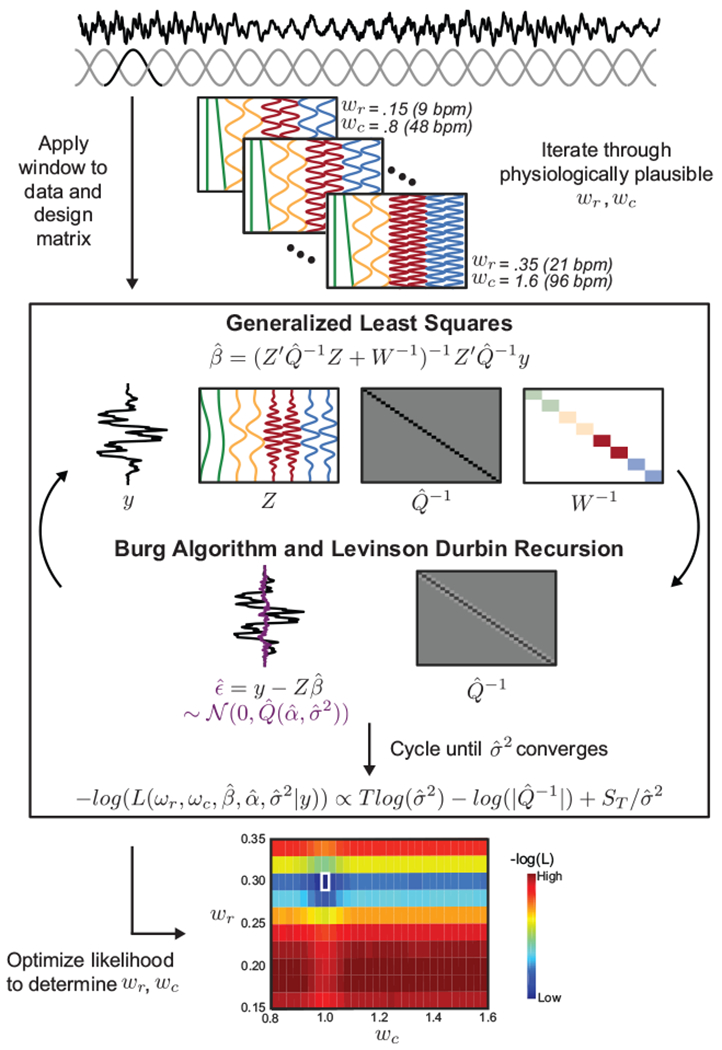
HRAN uses an efficient cyclic descent algorithm to estimate model parameters. First, a windowed data segment y is selected from a physiological noise ROI (e.g. the ventricles). Second, windowed design matrices Z are generated by iterating through physiologically plausible cardiac and respiratory frequencies. Third, β^ for a given data segment y and design matrix Z is computed using Generalized Least Squares. Fourth, α^ and σ^² are determined using the Burg Algorithm and Levinson Durbin Recursion on the residuals. Steps three and four are cycled until σ^² converges, and the likelihood for the given parameters is computed. Finally, the likelihood is optimized across all tested physiological frequencies, yielding estimates of the fundamental cardiac and respiratory frequencies.