A maximum likelihood approach to electronic health record phenotyping using positive and unlabeled patients

Abstract

Objective

Phenotyping patients using electronic health record (EHR) data conventionally requires labeled cases and controls. Assigning labels requires manual medical chart review and therefore is labor intensive. For some phenotypes, identifying gold-standard controls is prohibitive. We developed an accurate EHR phenotyping approach that does not require labeled controls.

Materials and Methods

Our framework relies on a random subset of cases, which can be specified using an anchor variable that has excellent positive predictive value and sensitivity independent of predictors. We proposed a maximum likelihood approach that efficiently leverages data from the specified cases and unlabeled patients to develop logistic regression phenotyping models, and compare model performance with existing algorithms.

Results

Our method outperformed the existing algorithms on predictive accuracy in Monte Carlo simulation studies, application to identify hypertension patients with hypokalemia requiring oral supplementation using a simulated anchor, and application to identify primary aldosteronism patients using real-world cases and anchor variables. Our method additionally generated consistent estimates of 2 important parameters, phenotype prevalence and the proportion of true cases that are labeled.

Discussion

Upon identification of an anchor variable that is scalable and transferable to different practices, our approach should facilitate development of scalable, transferable, and practice-specific phenotyping models.

Conclusions

Our proposed approach enables accurate semiautomated EHR phenotyping with minimal manual labeling and therefore should greatly facilitate EHR clinical decision support and research.

INTRODUCTION

The adoption of electronic health records (EHRs) by healthcare systems has the potential to enable implementation of comprehensive, computational clinical decision support and clinical research.^1–4 However, EHRs have been designed primarily to support documentation for medical billing rather than being intricately embedded in clinical diagnostic processes,^5–7 so that patients’ complex, clinical phenotypes are not natively represented in an accurate, precise format.^8–11 To overcome this limitation, a variety of heuristic rules and statistical methods have been developed for phenotyping patients using EHR data.^12–15 The vast majority of these existing methods require a large, curated dataset of patients who are completely and accurately labeled with regard to the presence or absence of a phenotype. Such methods require experts to retrospectively review EHR charts or prospectively evaluate patients. For many phenotypes, the labor and cost of these processes limit the achievable sample size, compromising the accuracy of potential phenotyping models.

Such approaches can be improved on by appreciating that clinical practice workflows are often not symmetric with regard to cases and controls. In practice, for most diseases, only specific patients are actively evaluated based on clinical suspicion. There are very few phenotypes for which everyone is actively screened, so clinical practice data is frequently insufficient to identify a large set of gold-standard controls. As a result, for many phenotypes, the most readily accessible annotations are an incomplete set of gold-standard cases and few or no gold-standard controls. It is highly desirable to develop new phenotyping methods that efficiently and accurately leverage such incomplete phenotyping, or “positive-only” data.

One application for which a phenotyping method that learns from positive-only design is advantageous is identifying patients with and estimating the prevalence of primary aldosteronism (PA). PA is the most common cause of secondary hypertension, thought to affect ∼5% of hypertensive patients and up to 20% in specific subgroups of hypertension patients, including hypertension with hypokalemia and resistant hypertension.^16–18 PA can be treated effectively by unilateral adrenalectomy or targeted medications. Previous methodological work has tried to improve the diagnostic evaluation for PA.^19–21 Unfortunately, PA is not recognized or not treated optimally in many affected patients,²² so methods for EHR phenotyping have the potential to dramatically improve care for these patients.

Over the past decade, several methods have been proposed in the machine learning and biostatistics literature for analyzing data arising from such “positive-only” design.^23–28 Under this design, one special case with extremely desirable consequences is when the labeled cases are a random subset of the full set of cases. This set of cases could be identified through an active labeling process as part of existing clinical care or research. However, a more generalizable strategy that has the potential to decrease the requirement for manual chart review is the use of binary “anchor variables”²⁹ that summarize clinical domain expertise for classifying patients’ phenotype. By definition, an anchor variable has perfect positive predictive value (PPV) but is not required to have high sensitivity. That is, anchor positivity indicates presence of the phenotype, but anchor negativity is nondeterministic of the true phenotype status. The second requirement for an anchor variable is that its sensitivity is independent of all phenotype model predictors. An ideal anchor variable is a structured data element in the EHR that is only present in cases, such as the result of a diagnostic confirmatory test or an order that only follows a definitive diagnosis. For example, a pathologic diagnosis of cancer will in most scenarios have a very high PPV, but perhaps an imperfect sensitivity because of variability in practice or documentation, variability in diagnostic categories, or data incompleteness. For many phenotypes, such definitive diagnostic information may not be available, so surrogates such as diagnosis codes, medications, or note concepts must be considered. Expert knowledge is necessary to select a variable or a composite variable that meets the high PPV and predictor independence requirements.²⁹

The algorithm for learning with positive anchors proposed by Halpern et al²⁹ was initially introduced by Elkan and Noto.²³ Their method predicted the probability of phenotype presence through estimating the probability that a subject is anchor positive, motivated by a lemma that the 2 probabilities differ by a constant factor, anchor sensitivity. This method trains a classifier for the anchor variable in a random subset of patients, then applies the classifier on the rest of patients to estimate the anchor sensitivity. Unfortunately, it yields a consistent estimate of phenotype prevalence only when the predictor distributions for cases and controls are completely separable,³⁰ and the estimated phenotype probability may fall outside of the [0, 1] range otherwise.

To enable more efficient and accurate EHR phenotyping and estimation of phenotype prevalence in the setting of incomplete clinical training phenotypes, we hereby propose a maximum likelihood (ML) method to develop a logistic regression prediction model using positive-only EHR data using cases identified by chart review or anchor variables. We have demonstrated, via extensive simulation studies, development of phenotyping models for hypokalemia requiring oral supplementation among primary care patients with hypertension using a simulated anchor variable, and development of a PA phenotyping model for patients screened for PA using 2 different real-world sets of cases, that this method develops models that accurately identify unlabeled cases and yields consistent estimate of phenotype prevalence.

MATERIALS AND METHODS

Positive-only data

Let Y denote the latent binary label for the phenotype (1: case; 0: control), X denote the predictor variables of Y, and S denote the binary anchor variable (1: positive; 0: negative). Here $(\mathit{X},Y,S)$ are considered as random variables from which EHR patients, including both anchor-positive cases and unlabeled patients, are randomly drawn, with only $(\mathit{X},S)$ observed. For a well-chosen anchor variable, Y takes value 1 whenever $S=1$, that is, $p\left(Y=1|S=1\right)=1$. But Y can take either value 1 or 0 when $S=0$. The anchor sensitivity being independent of X can be formalized as²⁴

$$p\left(S=1|Y=1,\mathit{X}\right)=p(S=1|Y=1)\equiv c,$$ (1)

where c is a constant between 0 and 1. We use a logistic working model to relate Y and X which is commonly implemented in the EHR setting, although our method is applicable for any parametric model that is reasonable for modeling binary outcome variables:

$$\mathrm{logit}\mathrm{ }p\left(Y=1|\mathit{X};\mathit{\beta }\right)={\mathit{X}}^T\mathit{\beta }.$$ (2)

Here, we allow X to include a vector of 1 so that the intercept parameter is implicitly included in the logit function ${\mathit{X}}^{\mathit{T}}\mathit{\beta }$. For notational simplicity, we use $P(\mathit{X};\mathit{\beta })$ to denote $p\left(Y=1|\mathit{X};\mathit{\beta }\right)$. Let $F\left(\mathit{X}\right)$ denote the cumulative distribution function of X, $f\left(\mathit{X}\right)$ the corresponding probability density function, and q the phenotype prevalence, $q=p\left(Y=1\right)=\int P(\mathit{X};\beta )\mathit{dF}\left(\mathit{X}\right)$. Let h be the probability of anchor being positive, $h=p(S=1)$. It is easy to show that anchor sensitivity $c=h/q$ by applying (1).

Algorithms for learning with positive-only data

In this section we describe 2 methods for fitting model (2) and estimating parameters c and q from positive-only data, an algorithm developed by Elkan and Noto,^23,29 which to our best knowledge is the only available method to date (EN algorithm), and an ML method that we here propose (ML method). We also describe a “naive” logistic modeling referred to as naive logit, which simply treats the unlabeled patients as controls and has largely been the standard method for analyzing positive-only data.

EN algorithm

The EN algorithm^23,29 learns from positive-only data by building on a lemma relating the models for predicting outcome status Y and anchor status S, $p\left(Y=1|\mathit{X}\right)=p\left(S=1|\mathit{X}\right)/c$. This method requires the positive-only data to be randomly separated into 2 parts, the training set and validation set. It can be summarized into 3 steps. First, a logistic regression model is developed for predicting anchor status S, $g\left(\mathit{X}\right)=p\left(S=1|\mathit{X}\right)$, by fitting the model directly to the training set with S being the outcome variable. Second, the anchor sensitivity c is estimated using the validation set. They proposed that c be estimated as $\widehat{c}={\sum }_{i=1}^{n^v}g\left({\mathit{X}}_{\mathit{i}}\right)I({\mathit{S}}_{\mathit{i}}=1)/{\sum }_{i=1}^{n^v}I({\mathit{S}}_{\mathit{i}}=1)$ with n^v being the size of the validation set. Third, the probability of the outcome status is estimated for an unlabeled patient as $p\left(Y=1|\mathit{X}\right)=p\left(S=1|\mathit{X}\right)/\widehat{c}$. The algorithm is intuitive and easy to implement. But the proposed estimator of $c$ is often biased unless the predictor distributions for cases and controls are completely separable,³⁰ thereby leading to biased estimation of $p\left(Y=1|\mathit{X}\right)$ and prevalence q. When the estimated $c$ is biased toward 0, the estimated $p\left(Y=1|\mathit{X}\right)$ could exceed 1.

ML method

We hereby propose to use the ML method for fitting model $p\left(Y=1|\mathit{X};\mathit{\beta }\right)$ and estimating anchor sensitivity $c$ simultaneously. The likelihood function for the observed data for all N patients is as follows,

$$\begin{array}{c}L\left(\mathit{\beta },c\right)=\prod _{i=1}^N{p\left({\mathit{X}}_{\mathit{i}},{\mathit{S}}_{\mathit{i}}=1\right)}^{{\mathit{S}}_{\mathit{i}}}{p\left({\mathit{X}}_i,S_i=0\right)}^{{1-\mathit{S}}_{\mathit{i}}}\\ \mathrm{ }\propto \prod _{\mathit{i}=1}^{\mathit{N}}{\{\mathit{cp}({\mathit{X}}_{\mathit{i}};\mathit{\beta })\}}^{S_i}{\{1-\mathit{cp}{(\mathit{X}}_i;\mathit{\beta })\}}^{{1-S}_{\mathit{i}}}\end{array}$$

As shown in Supplementary Appendix A, $\left(\mathit{\beta },\mathrm{ }c\right)$ are identifiable with positive-only data. Thus we can obtain the ML method estimates $(\widehat{\mathit{\beta }},\widehat{c})$ by maximizing the log likelihood function $\log L\left(\mathit{\beta },\mathrm{ }c\right)$. The large sample variance-covariance matrix of these estimates can be established from the inverse of the information matrix. We propose 2 methods for estimating phenotype prevalence q. Because q can be expressed as $h/c$, it can be estimated as $\widehat{q}=\widehat{h}/\widehat{c}$, where $\widehat{h}$ is the ML estimate of $p(S=1)$ and equal to the sample fraction of those with $S=1$. Alternatively, it can be estimated as the average of the estimated phenotype probabilities, $N^{-1}{\sum }_{i=1}^{N}P({\mathit{X}}_i;\widehat{\mathit{\beta }})$. In Supplementary Appendix B, we described an extension of this method by allowing c to vary with respect to a small number of prespecified strata.

Naive logit

This method simply fits a logistic regression model to the positive-only data, treating the unlabeled patients as controls. That is, the anchor status S was used as if it were the truth label Y.

Simulation studies

We carried out extensive simulation studies to evaluate the performance of the ML method relative to the EN algorithm and naive logit for phenotyping using positive-only data. We also included results from the ideal learning in which fully labeled data is used to fit standard logistic regression models with the true labels Y as the outcome variable. The ideal learning, feasible only for simulation studies, was used as the comparison benchmark. Given that anchor-positive patients are classified as cases by definition, we assess classification accuracy only among the unlabeled patients, using measures true positive rate $\left({\mathit{TPR}}_v\right)$, false positive rate $\left({\mathit{FPR}}_v\right)$, positive predictive value $\left({\mathit{PPV}}_v\right)$, and negative predictive value $\left({\mathit{NPV}}_v\right)$ at a decision threshold v and area under the $\mathit{ROC}$ curve $\left(\mathit{AUC}\right)$. We also demonstrated statistical consistency for the ML estimators $\widehat{\mathit{\beta }}$, $\widehat{\mathit{c}}$, and $\widehat{\mathit{q}}$ across a range of prevalence and anchor sensitivities in Supplementary Appendix C & D.

Simulation settings

To mimic the complex data structure in EHR, we generated the binary outcome variable Y from a logistic regression model with 9 predictors:

$$\mathrm{logit}\mathrm{ }p(Y=1|\mathit{X};\mathit{\beta })={\beta }_0+\sum _{k=1}^9{\beta }_k{\mathit{X}}_k,$$ (3)

with ($X_1,X_2,X_3$), ($X_4,X_5,X_6$), ($X_7,X_8,X_9$) representing weak, moderate and strong predictors, respectively, by setting the corresponding parameter coefficients at ${(\beta }_1,{\beta }_2,{\beta }_3)=(0.2,\mathrm{ }0.4,\mathrm{ }0.6)$, ${(\beta }_4,{\beta }_5,{\beta }_6)=(-1.0,-1.4,\mathrm{ }1.8)$, and ${(\beta }_7,{\beta }_8,{\beta }_9)=(-2.0,\mathrm{ }2.4,\mathrm{ }2.8)$. The 9 predictors were independently distributed, with $X_1$, $X_4$, and $X_7$ generated from normal distribution N(5, 10), $X_2$, $X_5$, and $X_8$ from Bernoulli distribution with success rate 0.5 and $X_3$, $X_6$, and $X_9$ from the logit transformed standard uniform distribution.

The value of ${\beta }_0$ was varied accordingly to achieve the phenotype prevalence at 5%, 10%, 15%, and 20%. The anchor sensitivity $c$ was fixed at 0.5. For each case ($Y=1$), the anchor variable $S$ was generated according to a Bernoulli distribution with success rate $c$. For each control ($Y=0$), $S$ was always set to 0. In each Monte Carlo simulation, we drew a random sample of size 10 000 as the training set, and a disjoint testing set of 5000. To implement the EN algorithm, 20% of the training set was put aside as the validation set to estimate c. For each parameter combination, we iterated the simulation 1000 times. Below we focus our discussion on the results when the phenotype prevalence was set as 10%. Results for the other 3 prevalence values were similar and included in the Supplementary Appendix C & D.

RESULTS

Simulation results

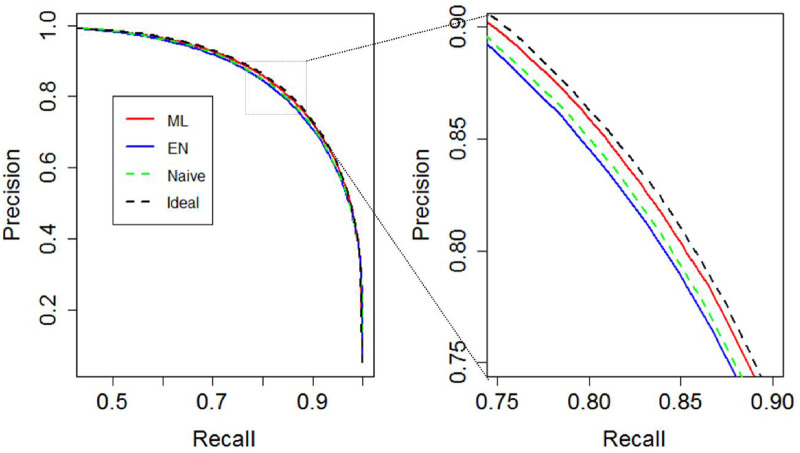
As shown in Table 1, our ML method yielded consistent estimates of the anchor sensitivity c and the phenotype prevalence q that were nearly identical to that of the ideal logistic regression using the truth labels. EN algorithm underestimated anchor sensitivity c as 0.37 with empirical standard error (ESE) 0.04, with the bias potentially caused by the overlapping of predictor distributions, leading to overestimation of prevalence q as 0.14 (ESE: 0.01). Among the unlabeled patients, 4% (ESE: 0.5%) of the EN algorithm-predicted probabilities $\widehat{p}\left(Y=1|\mathit{X}\right)$ were >1. The EN algorithm estimates remained nearly identical when we increased the size of the validation set to 5000. As demonstrated in Table 2 and Figure 1, ML method achieved comparable predictive accuracy to that of ideal learning among the unlabeled patients, with similar AUC (0.994 and 0.994, respectively) and precision-recall curve, which is a plot of PPV (y-axis) and TPR (x-axis) for different risk thresholds. EN algorithm and naive logit achieved identical AUC of 0.993. However, at their respective threshold for 80% sensitivity (TPR), ML method achieved higher specificity, with PPV and FPR estimated as 86% and 0.7%, compared with 84% and 0.9% for the EN algorithm and 83% and 0.9% for naive logit, respectively. Similarly, at thresholds for 80% PPV, ML method yielded higher TPR than did the EN algorithm and naive logit (Table 2, Figure 1).

Table 1.

Estimates of $c$ and $q$

	Anchor sensitivity c	Phenotype prevalence q
True value	0.5 (—)	0.1 (—)
Ideal learning	—	0.10 (0.0003)
Naive logit	—	0.05 (0.002)
EN algorithm	0.37 (0.04)	0.14 (0.01)
ML method	0.50 (0.021)	0.10 (0.004)

Values are mean (empirical standard error) over 1000 iterations.

EN: Elkan and Noto.

Table 2.

Phenotyping accuracy measures at thresholds selected to achieve TPR = 0.8 or PPV = 0.8

	TPR = 0.8				PPV = 0.8
	Threshold	FPR	PPV	NPV	Threshold	TPR	FPR	NPV
Ideal learning	0.63	0.007 (0.001)	0.86 (0.02)	0.99 (0.002)	0.50	0.90 (0.02)	0.01 (0.002)	0.99 (0.001)
Naive logit	0.15	0.009 (0.002)	0.83 (0.03)	0.99 (0.002)	0.14	0.84 (0.03)	0.01 (0.002)	0.99 (0.002)
EN algorithm	0.42	0.009 (0.003)	0.84 (0.05)	0.99 (0.003)	0.38	0.84 (0.04)	0.01 (0.004)	0.99 (0.002)
ML method	0.63	0.007 (0.002)	0.86 (0.03)	0.99 (0.002)	0.50	0.89 (0.03)	0.01 (0.002)	0.99 (0.002)

Values are mean (empirical standard error) over 1000 iterations.

EN: Elkan and Noto; FPR: false positive rate; ML: maximum likelihood; NPV: negative predictive value; PPV: positive predictive value; TPR: true positive rate.

Figure 1.

Precision-recall curve of the 4 methods from simulation study with 10% prevalence. EN: Elkan and Noto; ML: maximum likelihood.

As shown in Supplementary Table S1, the averaged ML parameter estimates ($\widehat{\mathit{\beta }},\mathrm{ }\widehat{c},\mathrm{ }\widehat{q}$) appeared very close to the true values. The negligibly small biases (<4%) indicated statistical consistency of the proposed ML estimators. The variances of the ML method estimates can be well approximated by the asymptotic standard errors (ASEs), as their average across simulated data and the ESE were very close, with a difference <6%. The ML method therefore is superior to EN algorithm also because the variance of the estimates ($\widehat{\mathit{\beta }},\mathrm{ }\widehat{c},\mathrm{ }\widehat{q}$) can be obtained conveniently.

Method validation using real-world EHR data and a simulated anchor variable

Next we sought to validate the ML method using real-world EHR data and a simulated, perfect anchor variable. We compared the performance of the proposed ML method to that of the EN algorithm, naive logit and ideal learning for identifying a patient population that should be screened for PA, those with hypokalemia requiring oral supplementation, from among 10 000 Penn Medicine primary care patients with hypertension. Patients (≥18 years of age) were randomly selected from among those with ≥5 office visits over ≥3 distinct years, including ≥2 at 1 specific primary care practice, between 2007 and 2017. The population was restricted to patients with hypertension by filtering for ≥2 outpatient encounters with a hypertension diagnosis code (International Classification of Diseases-Ninth Revision [ICD-9]: 401.*, 405.*; International Classification of Diseases-Tenth Revision: I10.*, I15.*). We defined the phenotype status Y for each patient as whether the patient had ≥3 outpatient orders for oral potassium supplementation. The resulting dataset contained 796 (8%) cases and 9204 controls. As our goal was to demonstrate the performance of the positive-only phenotyping methods when a good anchor variable is available, we artificially created an anchor variable S with sensitivity 0.2 by randomly setting S to 1 for 20% of all cases (Y = 1), and to 0 for the remaining 80% of cases and for all controls. The predictors of interest, X, were selected by clinical experts from among diagnosis codes, medication prescriptions, laboratory results, vital signs, encounter meta information (Supplementary Table S4). We emphasize that the ML method and the EN algorithm only need S and Xfor model training. The true label Y was only used for ideal learning. For the EN algorithm, we randomly set aside 20% of the dataset for estimating anchor sensitivity. We performed 10-fold cross-validation for estimating all predictive accuracy metrics based on phenotype status Y. The proposed ML method estimated anchor sensitivity c as 0.17 (ASE: 0.04), which was much closer to the true value 0.2 than the EN algorithm estimate of 0.05. Consequently, the ML method estimate of prevalence q, 0.09 (ASE: 0.02), was much closer to the true value 0.08 than was the EN algorithm estimate, 0.32.

For phenotyping accuracy, ideal learning achieved the highest AUC of 0.86, which is the best discrimination since it used the Y truth labels. The ML method and naive logit both achieved AUC as 0.85, which was slightly higher than that of the EN algorithm, 0.83. At their respective thresholds for reaching 70% TPR, the ML method achieved a PPV of 23%, which was identical to that of ideal learning (23%) and naive logit (23%), and slightly higher than that of the EN algorithm (20%) (Figure 2). Furthermore, FPRs of the ML method and ideal learning were also identical (16%), which were lower than those of the EN algorithm (19%). The NPV was comparable for all four methods. At their respective threshold for achieving 50% PPV, the ML method achieved a TPR of 44%, which was comparable to that of ideal learning (45%) and higher than that of naive logit (38%) and the EN algorithm (39%). In addition, 5% of the EN algorithm–predicted probabilities $\widehat{p}\left(Y=1|\mathit{X},S=0\right)$ were greater than 1.

Figure 2.

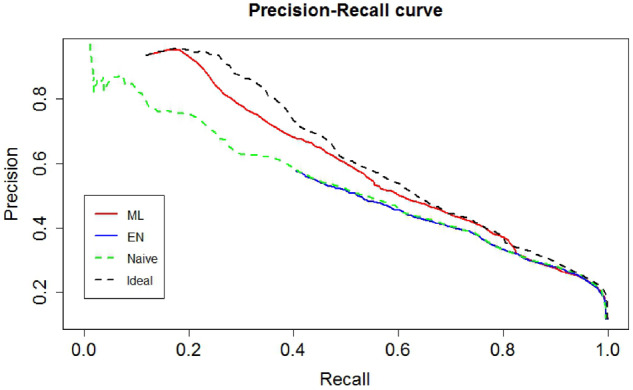
Precision-recall curve of the 4 methods for identifying patients with hypokalemia requiring potassium supplementation among Penn Medicine primary care patients with hypertension. EN: Elkan and Noto; ML: maximum likelihood.

A preliminary phenotyping model for PA using real-world predictors and cases

We then applied the proposed ML method to develop a preliminary model for identifying PA patients using a dataset derived from the Penn Medicine EHR containing 6319 patients who had an order for a PA screening laboratory test. Predictor variables, listed in Supplementary Tables S5 and S6, were selected by clinical experts. Because lab test ordering is nonrandom and potentially informative of phenotype status, we created binary variables indicative of result presence and included these binary indicators as well as the original lab test variables, with missing values replaced by zero. Missing values in variables other than laboratory results were imputed with respective mean values. In addition, variables with highly positively skewed distributions were log-transformed, and all continuous variables were standardized. Since the focus of this work is on demonstrating the performance of the ML method with a wisely chosen set of cases, we leveraged an existing expert-curated PA research registry³¹ in which every patient was a definitive PA case (case set A: n = 149, 2.4%). The patients were identified for the registry because they underwent a diagnostic procedure, adrenal vein sampling, which in our practice is only performed on patients definitively diagnosed with primary aldosteronism. We later supplemented this set using an anchor variable strategy to include patients with a laboratory test order for adrenal vein cortisol, which is only performed as part of this the adrenal vein sampling procedure (set B). This anchor variable labeled an additional 47 patients, increasing the set of cases to a total of 196 (3.1%). The additional patients included many who were tested after 2015 and some that were missing from the registry for unknown reasons. We evaluated the predictive accuracy of the models using TPR and PPV. TPR was estimated using the case set via 10-fold cross-validation for models developed by each of the 3 methods. This was plausible because the independence property of anchor variable implied that TPR among all PA cases can be estimated by TPR among anchor-labeled cases, $\mathit{TPR}=p(\widehat{p}>v|Y=1)$=$\mathrm{ }p\left(\widehat{p}>v|S=1\right).\mathrm{ }$To estimate PPV, charts for patients receiving longitudinal care and $\widehat{p}\left(Y=1|\mathit{X}\right)\ge 0.2$ by each model were reviewed by a clinician I.A. and ambiguous cases were further reviewed by D.S.H. There were 185 charts reviewed and were adjudicated with respect to PA as 132 positive, 5 unknown, and 48 negative. The final models were included in Supplementary Table S7.

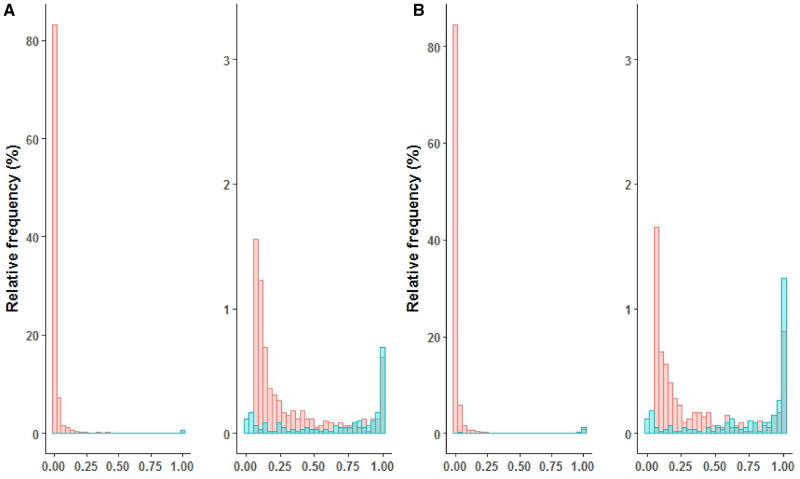
Using case set A, the ML method estimated the label sensitivity c as 0.56, compared with 0.35 of EN algorithm. Consequently, it estimated phenotype prevalence q as 4% (95% confidence interval [CI], 3%-5%), compared with 7% by the EN algorithm. For both case sets, the ML method–fitted model appeared to have high discriminatory power, indicated by the double-peaked histogram of $\widehat{p}(Y=1|\mathit{X})$, with anchor-positive cases mostly having high predicted probabilities (Figure 3). The ML method achieved consistently higher TPR than did the other 2 methods. For example, at threshold 0.5, TPR was estimated as 0.66, 0.59, and 0.28 for the ML method, EN algorithm, and naive logit, respectively (Table 3). In addition, 0.6% of the EN algorithm–predicted probabilities $\widehat{p}\left(Y=1|\mathit{X},S=0\right)$ were greater than 1. Results using case set B were similar, with c estimated as 0.62 and 0.41 by the ML method and EN algorithm, respectively, and q estimated as 5% (95% CI, 4%-6%) by the ML method and 8% by the EN algorithm. Again, TPR of ML method was consistently higher than that of the other 2 methods (Table 3), and 0.7% of the EN algorithm–predicted probabilities $\widehat{p}\left(Y=1|\mathit{X},S=0\right)$ were >1.

Figure 3.

Histogram of estimated probabilities of PA, p (Y=1|X) based on (A) case set A and (B) case set B. The left panels display the probability histogram with the range of y-axis being 0%-100%. The right panels display the zoomed-in probability histogram with y-axis limited to 0%-3%. Labeled cases (blue) and unlabeled patients (red) are indicated.

Table 3.

PA model TPR estimated using labeled patients

Threshold	Case set A			Case set B
	ML method	EN algorithm	Naive logit	ML method	EN algorithm	Naive logit
0.1	0.85	0.85	0.73	0.89	0.86	0.77
0.2	0.79	0.74	0.60	0.85	0.80	0.63
0.3	0.74	0.70	0.49	0.83	0.71	0.56
0.4	0.70	0.64	0.35	0.80	0.64	0.47
0.5	0.66	0.59	0.28	0.78	0.61	0.41
0.6	0.62	0.55	0.26	0.72	0.57	0.34
0.7	0.56	0.48	0.21	0.66	0.55	0.30
0.8	0.52	0.42	0.15	0.60	0.49	0.24
0.9	0.41	0.40	0.10	0.54	0.45	0.16

EN: Elkan and Noto; ML: maximum likelihood; PA: primary aldosteronism; TPR: true positive rate.

According to the chart review results, the models based on case set A and B achieved similar PPVs at threshold 0.2 (75% and 76% respectively) and threshold 0.5 (78% and 77%, respectively). Notably, the ML method identified 7 unlabeled PA patients that do not meet PA heuristic rules ≥2 PA diagnosis codes (ICD-9: 255.10, 255.11, 255.12; International Classification of Diseases-Tenth Revision: E26.01, E26.02, E26.09, E26.9) or PA laboratory testing results that meet conservative diagnostic criteria (aldosterone ≥15 ng/dL, plasma renin activity < 0.5 ng/mL/h, aldosterone: plasma renin activity ≥30).

To assess the sensitivity of our method with respect to the independence requirement of anchor variables, we performed stratified analyses as described in Supplementary Appendix B by allowing anchor sensitivity to vary with the encounter variables. Specifically, for each variable, we allowed anchor sensitivity to differ between the 2 strata, above or below the median. The phenotype prevalence estimates were nearly identical to those presented earlier where the independence assumption was imposed, and differences between the 2 stratum-specific anchor sensitivity estimates were minor (Supplementary Table S8). The estimated regression coefficients were very similar as well (Supplementary Tables S9).

DISCUSSION

A key step to comprehensive and accurate EHR phenotyping is the development of accurate approaches that efficiently leverage clinical expertise and available data. Currently, to train phenotyping algorithms, most existing methods require a complete set of expert-annotated cases and controls or naively treat unlabeled patients as definitive controls. Our proposed ML method builds accurate model classifiers based upon a random sample of positive cases and a large number of unlabeled patients. To identify a random sample of cases, the method can leverage domain expertise summarized in the form of an anchor variable, with modest upfront effort from clinical experts.²⁹ Compared with standard strategies, this method dramatically decreases the need for labor-intensive chart annotation and prospective phenotyping.

Our ML method appeared to consistently outperform EN algorithm and naive logit in all numerical studies according to predictive accuracy metrics considered and estimates of anchor sensitivity and phenotype prevalence. Another notable feature of our ML method is transferability to other practices. The anchor concept may itself be more easily transferred rather than the full model.³² Model validation with respect to calibration and predictive accuracy classically requires annotated labels for a random set of patients. However the anchor variable framework and ML method allow the development of novel methods for internally assessing model calibration and predictive accuracy using positive-only data (which we are currently working on), precluding the need for external model validation. Thus to generalize our method to secondary sites, chart review need only be performed to confirm that the anchor has very high PPV for the phenotype of interest, which is considerably less burdensome validation of a classically fit or transferred model. Recent work has considered phenotyping methods that take advantage of both noisy labels with random error and anchor variable framework.¹⁹ Our method can similarly be extended in this regard.

The model performance relies on the independence of labeled cases, or anchor sensitivity, and model predictors. This necessitates meticulous selection of the anchor based on clinical expertise. If unclear, the appropriateness of an anchor could be supported by explicitly validating the estimated phenotype prevalence, model sensitivity, or the conditional independence assumption. We refer readers to the work of Halpern et al³² for methods to support defining potential anchors. The phenotyping models for PA based on the 2 case sets were similar, which to a certain extent suggests the robustness of the ML method with respect to anchor selection. We also extended the current implementation of anchor variables to allow anchor sensitivity to vary across a fixed number of discrete strata that are predefined by patient EHR data (Supplementary Appendix B). We then applied this approach in our PA modeling to exclude major predictor-anchor dependence.

In this work, we applied our method to develop models to identify patients with PA. In selecting as cases PA patients who underwent a subtyping diagnostic procedure, we targeted patients with more severe and actionable disease rather than all PA patients. Thus, based on the conditional independence assumption, our models suggest that among patients screened for PA, including primary care and specialty referral populations, the prevalence of PA eligible for adrenal vein sampling is approximately 5%. To validate the prevalence estimation, it would be ideal to have expert annotation for a random sample of patients. Because the prevalence of PA is low, a large number of patients would need to be annotated. Unfortunately, since the diagnosis of PA requires specific diagnosis testing (measurement of blood aldosterone and plasma renin activity), chart review is not sufficient to identify all PA patients in a cohort. Therefore, it is implausible to obtain a sufficient annotated validation set. That said, our prevalence estimates were reasonable based on the literature: ∼5% for the prevalence of all PA in primary care populations³³ and ∼10% for prevalence of PA in tertiary care settings.³⁴ One recent Dutch study³⁵ that has a similar study design demonstrated a 3% (95% CI, 1.4%-4.9%) prevalence of PA confirmed by provocative testing among patients newly diagnosed with hypertension and screened for PA.

Our ML method demonstrated good sensitivity and PPV for identifying PA patients. However, as this was merely a proof-of-concept analysis, there is considerable room for improvement. We focused on specific predictors selected by domain experts, and did not exhaustively explore feature selection and engineering. Our current method is suitable for developing phenotyping models when the number of potential predictors is far less than the number of records. It is of interest to explore additional predictors across high dimensional EHR data, which we expect would lead to models with improved accuracy and more precise estimates of anchor sensitivity. We plan to extend our current method to facilitate variable selection in building the prediction model. For example, Yu et al¹⁵ proposed a surrogate-assisted feature extraction method for high-throughput EHR phenotyping. It reduces the needed number of gold-standard labels by selecting a candidate set of predictors that are correlated with ICD-9 codes or natural language processing-extracted concept counts. Potentially, a surrogate-assisted feature extraction–like approach could be applied to generate candidate predictors for use in our ML method–based anchor learning method. The resultant reduction in the need for manual variable selection would yield improved phenotyping efficiency and scalability. Similarly, we would expect considerable further gains from more extensive modeling, including exploration of alternative missing data approaches.

CONCLUSION

The incompleteness and asymmetry of EHR data limits its use for clinical decision support and research. We have developed a novel likelihood-based method that uses labeled cases and unlabeled patients to simultaneously enable accurate model development and identification of unlabeled cases. We expect this method will facilitate phenotype model development and transferability for a wide variety of EHR clinical decision support and research applications.

FUNDING

This work was supported by University of Pennsylvania, Penn Medicine Precision Medicine Accelerator Grant, and NIH grants R56-HL138306 and R01-HL138306.

AUTHOR CONTRIBUTIONS

LZ, DSH, and JC designed the studies. LZ and JC developed the biostatistical methods. XD and DSH collected, wrangled, and transformed the clinical data. LZ performed the statistical analyses. IA and DSH performed the chart review. LZ, DSH, and JC wrote the manuscript. All authors approved the final manuscript.