Ensuring electronic medical record simulation through better training, modeling, and evaluation

Abstract

Objective

Electronic medical records (EMRs) can support medical research and discovery, but privacy risks limit the sharing of such data on a wide scale. Various approaches have been developed to mitigate risk, including record simulation via generative adversarial networks (GANs). While showing promise in certain application domains, GANs lack a principled approach for EMR data that induces subpar simulation. In this article, we improve EMR simulation through a novel pipeline that (1) enhances the learning model, (2) incorporates evaluation criteria for data utility that informs learning, and (3) refines the training process.

Materials and Methods

We propose a new electronic health record generator using a GAN with a Wasserstein divergence and layer normalization techniques. We designed 2 utility measures to characterize similarity in the structural properties of real and simulated EMRs in the original and latent space, respectively. We applied a filtering strategy to enhance GAN training for low-prevalence clinical concepts. We evaluated the new and existing GANs with utility and privacy measures (membership and disclosure attacks) using billing codes from over 1 million EMRs at Vanderbilt University Medical Center.

Results

The proposed model outperformed the state-of-the-art approaches with significant improvement in retaining the nature of real records, including prediction performance and structural properties, without sacrificing privacy. Additionally, the filtering strategy achieved higher utility when the EMR training dataset was small.

Conclusions

These findings illustrate that EMR simulation through GANs can be substantially improved through more appropriate training, modeling, and evaluation criteria.

INTRODUCTION

Electronic medical record (EMR) systems provide opportunities for healthcare organizations to enhance patient safety,^1–3 improve the efficiency of healthcare delivery^4,5 and aid in clinical training.^6,7 Originally designed to support the primary objectives of the clinical domain, EMRs hold great promise for reuse in secondary endeavors^8,9 including policy evaluation,^10,11 the development and refinement of clinical decision support technologies,^12–14 and large-scale biomedical research investigations.^15–17 As such, healthcare organizations are incentivized, and sometimes required, to make such data available beyond the initial point of collection, by, for example, the National Institutes of Health Final Data Sharing Policy.¹⁸ However, concerns over patient privacy¹⁹ often limit EMR data-sharing activities.²⁰

A wide array of computational approaches has been developed to balance the utility achieved through sharing real EMR data against various types of privacy intrusions.^16,17 For instance, to prevent identity disclosure attacks (ie, maintain patient anonymity), one class of approaches focuses on manipulating the features of individuals that can allow a data recipient to link to a patient’s identity (eg, residential zip code or date of birth).^21–23 A second class of approaches aims to prevent attribute disclosure attacks (ie, maintain patient confidentiality) by perturbing the EMR data,^24,25 as well as the aggregate statistics based on such data. Typical approaches to realizing these privacy principals are k-anonymity^22,23,26 and differential privacy,^27,28 respectively. While popular, these approaches function directly on the data to be shared, which induce an inherent tradeoff between utility and privacy.^29–31

The research community has attempted to resolve this tension by simulating synthetic EMR data through models based on clinical knowledge published in the literature^32,33 and the data documented in real EMRs.³⁴ Multiple contributions can be categorized into knowledge-oriented EMR synthesis, in which knowledge is extracted from either real EMR data or external data.^35–38 For instance, Buczak et al³⁹ generated synthetic EMRs of tularemia patients by mining real EMR records to obtain patients’ care patterns, frequencies of billing codes, and syndromes. Dube and Gallagher⁴⁰ leveraged both public statistics (eg, disease prevalence) and clinical practice guidelines to build synthetic EMRs. These approaches are appropriately designed based on the extracted knowledge and can account for static as well as temporal aspects of a patient’s status and the evolution of disease. However, there are several limitations common to these approaches: (1) the knowledge merged into the generation process is often incomplete (or biased); (2) the generation mechanisms are specific to a particular phenotype or process, which lacks generalization ability; and (3) sharing patient-level synthetic data may be vulnerable to another privacy intrusion, namely the membership attack. In this situation, the data recipient is able to correctly predict if a real record is part of the training dataset that led to synthetic records. This attack may leak information about features (eg, diagnoses) of a real patient.

More recently, the machine learning community has focused on the development of advanced generative models that automatically extract the inherent knowledge within (or between) data in real records. Among various techniques, generative adversarial networks (GANs) have shown a remarkable ability to generate synthetic data with a realistic feel,^41–43 while simultaneously protecting privacy. This is because the artificial nature of the data has the potential to mitigate the concerns of reidentification. GANs are also empirically resistant to the attribute disclosure and membership attack.⁴⁴ In general, GANs are notable in that they are designed to address an adversarial environment in which a generator is forced to produce increasingly realistic instances, such that an evolving discriminator cannot distinguish them from real data. To date, the applications of GANs have been successful in the domains of imaging, natural language text, and audio generation.^45–47

Over the past several years, GANs have been customized to generate structured and categorical EMR data (eg, sets of billing codes).^34,44,48,49 GANs in this domain adopt the following pipeline. Initially, the system selects a training dataset of EMRs that satisfies the definition of a target population (eg, type 2 diabetics). Next, the system encodes and decodes the records via an autoencoder to learn their latent representations. Then, the system optimizes for an objective function based on the distance between the distributions of synthetic and real data. Finally, the system evaluates the GAN with respect to data utility and privacy risks. GAN learning is usually accomplished by characterizing both the distributional similarity of features and predictive similarity on a simple task between the real and synthetic data.

However, this approach to EMR simulation has several drawbacks. First, the autoencoder pretraining (which was designed to address the challenge of discrete approximation for the output) may introduce noise and, thus, induce a barrier in the learning task. Second, current measures of data utility fail to characterize if the generated data retain key structural properties of real data in the original and the latent space. Third, relying solely on the EMRs of a population of interest as the training data may cause a loss of certain statistical properties of the real data.

Given the limitations of the current simulation pipeline, we hypothesized that the utility of the data could be enhanced, without scarifying privacy, through a refinement of the learning process and models. Specifically, we aimed to enhance the learning model of GANs through removing the autoencoder, incorporating additional utility measures of key structural properties, and refining the filtering strategy for selecting training data. We demonstrate the plausibility of this hypothesis by applying the new GAN pipeline with approximately 1 million real EMRs from Vanderbilt University Medical Center.

MATERIALS and Methods

The data in this study is derived from the Vanderbilt University Medical Center Synthetic Derivative (SD), a de-identified warehouse of over 2.2 million EMRs. We extracted all International Classification of Diseases-Ninth Revision diagnosis codes for each patient, which were rolled up to their subcategories by removing the portion of the codes to the right of the “.” and retained the distinct set codes. This process led to 944 codes. We refer to this dataset as the SD dataset.

Summary statistics for this dataset, including age and sex, are provided in Table 1. Note that we discretized age into 4 groups (0-17, 18-44, 45-64, and >64 years of age) based on U.S. Census 2010 criteria⁵⁰ for presentation purposes (more fine-grained age groups could be applied). In doing so, we treat the dataset categorically, facilitating the evaluation of training strategies.

Table 1.

Summary statistics of the EMR datasets

	SD Dataset	CSD Dataset
Patients	2 246 444	1 045 634
Number of ICD-9 codes	944	854
Age distribution, %
0-17 y	21	17
18-44 y	32	29
45-64 y	24	26
>64 y	23	28
Male/female, %	47/53	47/53
Codes per patient	8.11	14.76
Patients per code	19 298	18 080

CSD: clean Synthetic Derivative; EMR: electronic medical record; ICD-9: International Classification of Diseases-Ninth Revision; SD: Synthetic Derivative.

It was observed that a portion of the records, as well as a subset of the billing codes, were not suitable for EMR synthesis. For example, EMRs with too few codes may not be informative during learning and, instead, may lead to biased (or even incorrect) models. The same is true for International Classification of Diseases-Ninth Revision codes with very low prevalence. As such, we refined the data (details in Supplementary Appendix A) to compose a cleaner dataset, which we refer to as the CSD dataset. This dataset is composed of 854 billing codes. It has approximately half the patients in the SD dataset, but maintains roughly the same distribution of age and sex. The number of distinct codes per patient and the number of patients per code is approximately 15 and 18 000, respectively, compared with 8 and 19 300 for the SD dataset.

Each patient’s record is represented as a binary vector over the codes, in which a cell value is 1 if the corresponding code is in an EMR and 0 otherwise.

GANs in the Medical Domain

To contextualize this research, we provide a brief tutorial on the foundations of GANs in Supplementary Appendix B. We specifically review the general framework of GANs and 2 frequently adopted distance functions: Jensen-Shannon (JS) divergence and Wasserstein divergence.

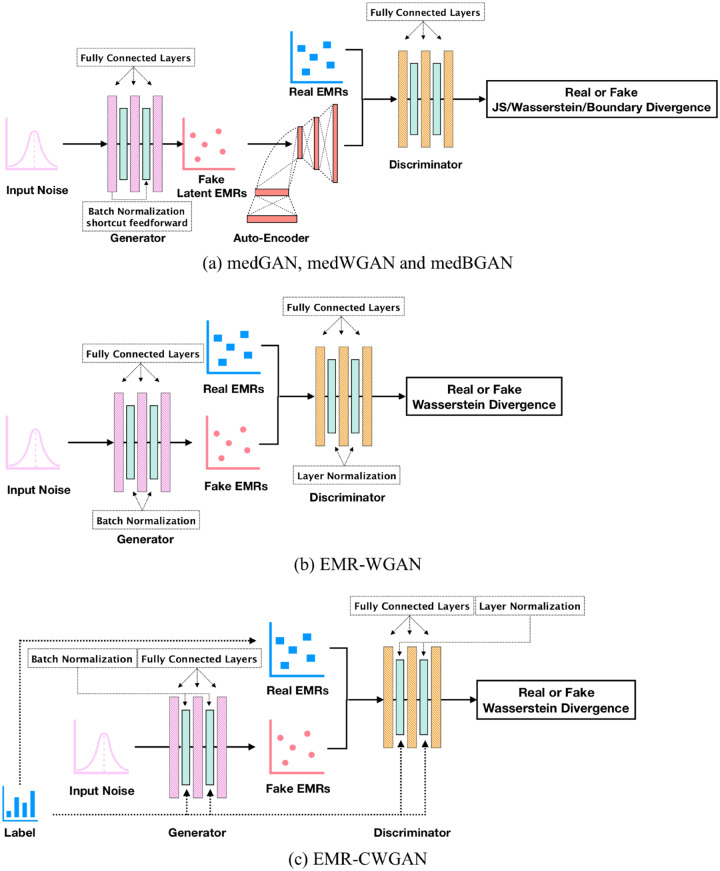
In the medical domain, several variations of GANs have been developed to generate realistic EMRs of diagnosis and procedure codes. These include medGAN,⁴⁴ medBGAN, and medWGAN.⁴⁸ These GANs have several commonalities and their architecture is shown in Figure 1a. First, they are all based on a framework that combines the GAN architecture with an autoencoder (which projects the original data into a low-dimension space and then reconstructs them), as shown in Figure 1a. The autoencoder is incorporated to address the limitation that the original GAN cannot generate discrete outputs. This is achieved by concatenating the generator with the pretrained decoder, which is fine-tuned during the training process. Another common characteristic is that they all apply batch normalization⁵¹ and a shortcut technique⁵² to the generator to accelerate learning. Yet, these GANs differ in their distance measures between the distributions of real and synthetic data.

Figure 1.

Architecture of (a) current and (b, c) new generative adversarial network (GAN) models. BGAN: boundary-seeking generative adversarial network; EMRs: electronic medical records; JS: Jensen-Shannon; WGAN: Wasserstein generative adversarial network.

medGAN applies JS divergence, which makes it susceptible to mode collapse, in which the generator learns to map different inputs to the same output, and mode drop, in which the generator only captures certain regions of the underlying distribution of the real data.³ To stabilize GAN training and solve the mode challenges, medBGAN and medWGAN adopt the distance measures introduced in boundary-seeking GAN⁵⁴ and Wasserstein GAN,^55,56 respectively. The objective function of medBGAN pushes the generator to match the distribution of the real data by continuing to generate samples near the boundary of the discriminator in each optimization iteration. By contrast, medWGAN applies Wasserstein divergence to formulate the objective function in a manner that the divergence between the distributions can be more accurately measured. However, as these GANs rely on an autoencoder, they may be led to a biased model because noise is introduced into the learning process.

EMR Wasserstein GAN

EMR Wasserstein GAN (EMR-WGAN), whose architecture is shown in Figure 1b, refines the learning model. It uses the basic structure of the original GAN model introduced in Goodfellow et al⁴¹ but removes the autoencoder. Owing to the drawbacks of JS divergence, EMR-WGAN, similar to medWGAN, adopts the Wasserstein divergence. To mitigate the effect of an exploding gradient, a phenomenon in which gradients accumulate large amounts of error (resulting in unstable training), and a vanishing gradient, a phenomenon in which the gradient of the loss function becomes zero (resulting in an inability to appropriately update the network), we apply 2 normalization techniques, both of which ensure values are in a common range. To formally explain the normalization, in each layer, let $x_j^i$ denote the input value of neuron $i$ with respect to data instance $j$, ${\mathbf{x}}_j$ denote the input vector of in this layer with respect to instance $j$, and ${\mathbf{x}}^i$ denote the input batch vector on neuron $i$. Note that the set of data instances is often randomly partitioned into batches for convenience in training. Additionally, let $\mathrm{\mu }$() and $\mathrm{\sigma }\left(\right)$ denote the mean and standard deviation, respectively. In the generator, we apply batch normalization,⁵¹ which revises the input of each neuron, according to the batch of data that passes through it, by ${y_j^i=\mathrm{ }(x}_j^i-\mathrm{\mu }\left({\mathbf{x}}^i\right))/\mathrm{\sigma }({\mathbf{x}}^i)$. For the discriminator, we apply layer normalization,⁵⁷ which revises the input of each neuron, according to the data that pass through the layer in which the neuron is situated, by ${y_j^i=\mathrm{ }(x}_j^i-\mathrm{\mu }\left({\mathbf{x}}_j\right))/\mathrm{\sigma }({\mathbf{x}}_j)$. Batch normalization is not applied to the discriminator because it would change the training objective from penalizing the norm of the discriminator’s gradient with respect to each input independently to penalizing the gradient’s norm of the entire batch. By contrast, layer normalization maintains its computation within each single input, which is suitable for the discriminator to mitigate the training obstacles incurred by unexpected gradient updates.

Evaluation Measures

In this section, we describe the utility and privacy measures of GANs for generating categorical EMR data.

Standard utility measures include dimension-wise statistics (DWS) and dimension-wise prediction (DWP).⁴⁴ DWS investigates the degree to which the distribution of each code among the generated records is similar to real data, whereas DWP evaluates the degree to which a generative model captures the interdimensional relationships of real data. The details of their implementation in our setting are in Supplementary Appendix C. These methods provide some insights into GAN utility; however, it is difficult to reach a solid conclusion on the performance of GANs by these measures alone because neither assesses if the structural properties of real data have been maintained. To address this issue, we introduce 2 new utility measures to characterize the statistical similarity between real and synthetic data.

Novel utility measures

Latent space representation

This measure evaluates the ability of a generative model to capture the latent factorized representations of real data. It is natural to assume that each real record is generated from a distribution $\mathrm{p}\left(\mathbf{x}\right|\mathbf{w})$, where $\mathbf{w}$ represents data generative factors in the latent space ${\mathbb{R}}^{\mathrm{d}}$ with m independent and d-m dependent dimensions. We utilize the $\mathrm{\beta }$ variational autoencoder ($\mathrm{\beta }$-VAE)⁵⁸ to discover, among ${\mathbb{R}}^{\mathrm{d}}$, the efficient representation ${\mathbf{w}}^{\mathrm{\text{'}}}\in {\mathbb{R}}^{\mathrm{k}}(d>k>m)$ of real data. $\mathrm{\beta }$-VAE rewrites the objective function of VAE⁵⁹ by inserting a weight $\mathrm{\beta }$ to the Kullback-Leibler divergence regularization:

$$\mathcal{L}\left(\theta ,\mathrm{ }\phi ;\mathbf{x},\mathbf{z},\mathrm{\beta }\right)={\mathbb{E}}_{{\mathrm{q}}_{\varphi }\left(\mathbf{z},\mathbf{x}\right)}\left[\log p_{\theta }\left(\mathbf{x}||\mathbf{z}\right)\right]-\mathrm{\beta }{\mathrm{D}}_{\mathrm{KL}}\left(q_{\varphi }\left(\mathbf{z}|\mathbf{x}\right)\right|\left|p\right(\mathbf{z}\left)\right),$$

where ${\mathbf{z}\in \mathbb{R}}^{\mathrm{d}}$ satisfies the standard Gaussian distribution. A larger $\mathrm{\beta }$ value encourages more dimensions in $q_{\varphi }\left(\mathbf{z}|\mathbf{x}\right)$ to approach their corresponding dimensions in $p\left(\mathbf{z}\right)$. In other words, the mean of the variance distribution in each of these dimensions is forced to approach 1. At the same time, the remaining dimensions (ie, ${\mathbf{w}}^{\mathrm{\text{'}}}$) can be thought of as efficient latent dimensions to characterize, and then reconstruct, the input data. We interpret each of these dimensions as a latent mode. A useful generative model is expected to yield synthetic data with a variance distribution for each latent mode that is similar to real data.

We train a $\mathrm{\beta }$-VAE model over the CSD dataset and retain the set of latent modes with a threshold for the mean of the variance distribution <0.5. We provide a synthetic dataset of the same size as the CSD dataset into this $\mathrm{\beta }$-VAE model. In doing so, we record the variance distributions of the latent modes. We measure the distance between the mean of each mode’s variance distribution and the mean of its counterpart in real data. A smaller distance indicates a greater similarity in synthetic and real data.

First-order proximity

This measure investigates whether synthetic data retains the local structure of real data. To do so, we build an undirected code graph $\mathit{FOP}(·)$ from a population (with a format of adjacency matrix), where the weight of an edge between codes corresponds to their co-occurrence frequency in the population. First-order proximity (FOP), denoted by edge weights, is widely adopted to characterize adjacent structures of networks.⁶⁰ We measure the difference in FOP between the synthetic data $s$ and real data r. Formally, this is calculated as

$$\sum h\left(\frac{\left|\mathit{FOP}\left(s\right)-\mathit{FOP}\left(r\right)\right|}{\mathit{FOP}\left(s\right)+\mathit{FOP}\left(r\right)}\right)$$

Here, the denominator serves as a normalization term and function $h(·)$ computes an element-wise transformation. The CSD dataset and the synthetic dataset of the same size are used to make the assessment. As a baseline, we measure the distance between an equal-sized random partition of the CSD dataset.

Privacy measures

Membership inference

An attacker committing a membership attack could be motivated in numerous ways. Here, provide several as an illustration of the potential problems. First, the attacker may execute the attack to gain new knowledge about a known person. It is often the case that a training dataset is composed of a cohort based on some rigorously defined criteria (eg, all patients have HIV or share a certain sexual orientation). In this case, if this knowledge is not known to the attacker a priori, then proving a targeted individual’s membership would lead to a clear disclosure about the individual. Even if the attacker had some prior belief about the status of the targeted individual, proving their membership would provide absolute certainty, which would be a boost in their knowledge. Second, the attacker might not be interested in targeting the individuals in the dataset, but rather, discrediting the organization that shared the simulated data. Consider, it is likely that healthcare organizations will claim that such simulated data is de-identified. At the same time, they may promise the individuals to whom the real data corresponds that their inclusion in such a dataset will not be made evident. However, if the attacker can prove the presence of 1 or more targeted individuals, then they may claim that the organization is failing to adhere to its promises and might be in violation of federal regulation (particularly if they did not obtain consent from the patients before creating the synthesizer).

We assume that an attacker is in possession of the complete set of diagnosis of a set of real patients. The attacker will attempt to infer which patients are in the training dataset. We calculate the Hamming distance between each known and synthetic record. Given a distance threshold, the attacker claims that all records less distant to any real one than the threshold are the targeted real patient. We assess the precision and recall of this claim.

Attribute inference

This attack is accomplished by inferring an unknown attribute value of a set of compromised patients via the generated data. Attribute inference may infringe upon a patient’s privacy when an attacker gains knowledge that is only accessible in the training dataset. We assume that the attacker possesses a subset of attributes of some real records and attempts to infer the value of the missing attribute. This is accomplished by applying a k-nearest neighbors algorithm, in which for each real record, the k nearest neighbors in synthetic data help decide the feature value of interest. We measure the F1 score of attribute inference as a function of k.

Reproduction rate

The portion of reproduced records among synthetic records helps evaluate the risk of identity disclosure, as well as the ability of a generative model to create new instances rather than memorizing the training data.

Training Strategy

For the purposes of generating EMR data with a specific concept, it is straightforward to train a GAN model on real records with the same concept. We refer to such a filtering strategy as simple training. However, simple training may cause a loss of certain statistical properties when the size of available real data is small.

We introduce a conditional training strategy, in which we use a conditional version of GANs over the EMR data with various concepts to generate synthetic records of a single concept. For example, when the target concept is “Male, age 18–44,” and the CSD dataset is the real dataset, then conditional training will use the real records of all 8 concepts (according to Table 1) as the training data.

Conditional training needs to explicitly figure out the concept label of each record, and thus we build the conditional version of EMR-WGAN, EMR-CWGAN, whose architecture is shown in Figure 1c. We incorporate the concept labels of records as part of the generator and the discriminator. Specifically, we apply conditional batch normalization and conditional layer normalization⁶¹ to the generator and discriminator, respectively. In particular, each label is denoted by a set of embeddings, each of which corresponds to a normalization layer in the generator and discriminator. After training EMR-CWGAN with different populations and their labels, one can apply the set of embeddings associated with the label of the desired population along with random noise to obtain the synthetic records.

To investigate the performance of these 2 training strategies, we train EMR-WGAN and EMR-CWGAN by varying the size of the available training set and then compute the utility measures as discussed earlier.

RESULTS

Experimental setup

To compare the GANs, we learn the hyperparameters of the medGAN, medWGAN, and medBGAN and then set EMR-WGAN and EMR-CWGAN accordingly. All generators and discriminators use a network structure of (128, 128, 128, 854) and (854, 256, 128, 1), respectively. All generative models were trained with 500 epochs. The autoencoder module of medGAN used a network structure of (854, 128, 854) and was trained with 200 epochs. We applied the Adam optimizer with a learning rate of 10⁻⁴ and a weight decay 10⁻⁴.

Evaluating EMR-WGAN

Dimension-wise statistics

The results of DWS are shown in Figure 2. The original system is shown in Figure 2a. In all other subfigures, the x-axis corresponds to the original system, while the y-axis corresponds to the synthetic system. There are several notable findings. First, as expected, the results of DWS in the real vs real setting (Figure 2a) are the most stable. Second, as shown in Figure 2b, medGAN poorly represents the probabilities of codes with frequency smaller than 0.01. Third, as shown in Figures 2c and 2d, medBGAN outperforms medWGAN. This is evident as a large portion of the codes, with probabilities smaller than 0.01, in synthetic data generated by medWGAN demonstrate a more unstable pattern. Fourth, there is an obvious bias in EMR-WGAN in comparison with medBGAN, as shown in Figure 2e. However, this is a superficial result and, as will be shown in the following set of experiments, EMR-WGAN achieves superiority in utility with respect to more structural aspects of the data in the latent space.

Figure 2.

Dimension-wise statistics. Bernoulli success probabilities for 854 International Classification of Diseases-Ninth Revision codes. BGAN: boundary-seeking generative adversarial network; EMR: electronic medical record; GAN: generative adversarial network; WGAN: Wasserstein generative adversarial network.

Dimension-wise prediction

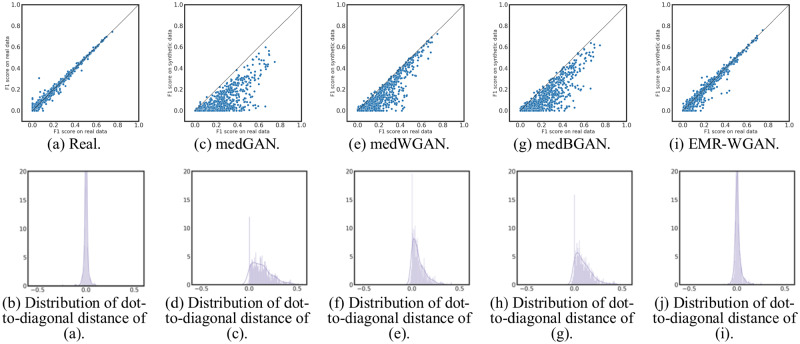
The results for DWP are shown in Figure 3. There are several findings worth highlighting. In Figures 3a and 3b, it can be seen that the F1 scores for billing codes in the real vs real setting are close to the diagonal without obvious bias. Additionally, the distribution of dot-to-diagonal distances is roughly symmetric, which indicates the stability of the interdimensional relationship in the original system. As depicted in Figures 3c and 3d, the distribution of dot-to-diagonal distances are heavily biased toward real data, which suggests that medGAN fails to capture the interdimensional relationship of real data. Third, Figures 3f and 3h show that medWGAN and medBGAN achieve similar performance, but are still biased in a manner similar to medGAN. Fourth, EMR-WGAN outperforms all alternatives demonstrate similar patterns as the real vs real setting, as presented in Figures 3i and 3j. As such, it appears that EMR-WGAN is more apt at simulating the interdimensional relationships in real data.

Figure 3.

Dimension-wise prediction. (a) F1 scores of logistic regression classifiers in real vs real setting. (c, e, g, i) Results of real vs synthetic setting of 4 generative adversarial networks (GANs). (b, d, f, h, j) Distributions of perpendicular distances from dots to the diagonal line for panels a, c, e, g, and i, respectively. BGAN: boundary-seeking generative adversarial network; EMR: electronic medical record; WGAN: Wasserstein generative adversarial network.

Latent space representation

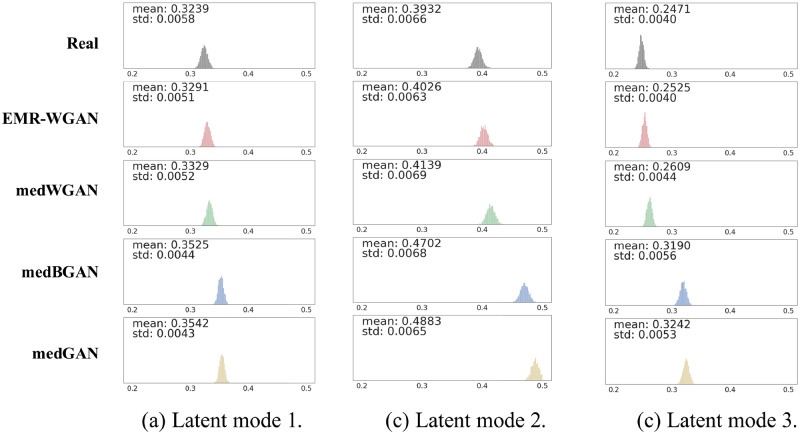
Figure 4 shows the latent space representation (LSR) results in all 3 latent modes. The generative models are sorted according to the mean of the variance distributions. EMR-WGAN achieves the smallest distance to real data. By contrast, there are relatively large gaps between the medBGAN and medGAN distributions and real data. To assess the reproducibility of this finding, we generated data 10 times for each generative model and confirmed that EMR-WGAN had a smaller mean than each of the alternative methods at a .01 significance level (via t test). This result suggests that EMR-WGAN can better capture the latent structural properties of the data. It is notable that such a result contradicts the one of the DWS results (medBGAN is better than EMR-WGAN).

Figure 4.

Latent space representation. Each subfigure illustrates the distribution of the variances in one latent dimension (with mean <0.5). The first row corresponds to real data. Each subsequent row corresponds to synthetic data generated by a particular type of generative adversarial network (GAN). BGAN: boundary-seeking generative adversarial network; EMR: electronic medical record; WGAN: Wasserstein generative adversarial network.

First-order proximity

Figure 5 shows the FOP graph distances between synthetic and real data. EMR-WGAN clearly achieves the smallest distance and outperforms all other approaches. medWGAN and medBGAN are less likely to capture the patterns of local structures in real data. Similar to LSR, the result of FOP graph distance conflicts with the DWS result as well. The new measures illustrate that the standard utility measure—DWS—appears to be less capable of sufficiently characterizing the utility of a GAN.

Figure 5.

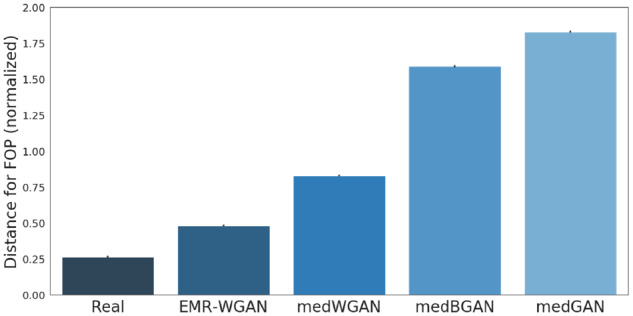
First-order proximity. The normalized graph distances between the billing code networks learned from real and synthetic data with respect to first-order proximity (FOP). We compute the graph distances in 4 settings: real vs real, medGAN vs real, medWGAN vs real, medBGAN vs real and EMR-WGAN vs real. We sort the generative models according to the normalized distance values. BGAN: boundary-seeking generative adversarial network; EMR: electronic medical record; GAN: generative adversarial network; WGAN: Wasserstein generative adversarial network.

Privacy risk measurement

We evaluated the 8 populations in the CSD dataset (formed by age group and sex defined in Table 1). The results of membership inference, attribute inference and reproduction rate for the 8 CSD subpopulations are shown in Supplementary Appendix D. The main finding is that EMR-WGAN achieves similar privacy risk level with the state-of-the-art approaches, which are limited.

According to the evaluation results, the new learning model, EMR-WGAN, outperforms medWGAN and medBGAN by generating synthetic EMR records with higher data utility but assumes no greater privacy risks. The new utility measures provide more evidence than DWS on the degree that a GAN captures the structural properties of real data. Thus, applying EMR-WGAN, as well as the utility measures including DWP, LSR and FOP, can improve the EMR generation tasks.

Evaluating the training strategy

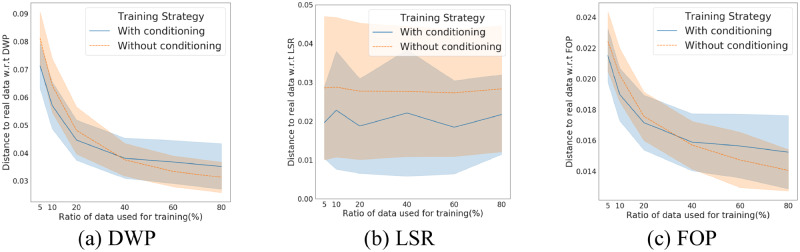
We compare the simple training (based on EMR-WGAN) and conditional training strategy (based on EMR-CWGAN) by assessing utility (including DWP, LSR, and FOP). We varied the training set to determine how it influenced the utility. The results are in Figure 6, where we present the average and standard deviation of each utility measure across each subpopulation.

Figure 6.

A comparison of 3 utility measures on 2 training strategies: (a) Dimension-wise prediction (DWP), (b) latent space representation (LSR), and (c) first-order proximity (FOP).

In Figure 6a, we report the difference in the mean of the dot-to-diagonal distribution between the simulated and real data in DWP. For LSR, as shown in Figure 6b, we report the difference in the mean of variance distribution between the simulated and real data. In Figure 6c, we show the FOP distance between simulated and real data.

As can be seen, when the training dataset is small (toward the left of the figures), conditional training outperforms traditional training. Specifically, when the size of available data for training is <35% of the original, conditional training can achieve higher data utility with respect to DWP and FOP. With respect to LSR, conditional training leads to a better utility than simple training.

We believe that this is because the complex associations between diseases may cross the boundary of populations with different concept labels. In other words, when the available training dataset size is small, real EMR records with their concept labels different from the simulation task can help strengthen the signals characterizing the statistical properties between code features.

DISCUSSION

This study has several notable implications for the design and deployment of GAN pipelines.

First, applying Wasserstein divergence as well as the affiliated optimization techniques provides a medical GAN model with the ability to solve the problem of generating categorical data. As a result, adding an autoencoder into a GAN using such a distance function only introduces noise and degrades performance.

Second, this work illustrates the importance of utility measures that capture structural aspects of the data. Utility measures that characterize basic distributions can lead to biased or incorrect conclusions.

Third, conditional training is more useful in generating EMR data than simple training strategy, especially when real data for training are small. Such finding makes a clear suggestion for the EMR generation tasks in the application domain, in which the volume of real data is often a bottleneck for learning.

Despite the merits of this work, there are several limitations that should be acknowledged. First, we focused on only binary features (eg, positive assertion or lack of a diagnosis). Further investigation is needed into EMR simulation when continuous features are taken into account. Second, we modeled the EMR in a static manner, yet the trajectory of a disease evolves, often punctuated by various interventions. For example, in the event lab test results should be generated, then time should be considered and modeled accordingly. Finally, we note that this analysis considered only the statistical validity of the synthetic records. It is possible that the synthetic records conflict with known phenomena that a clinical specialist might recognize in the data. It is critical for the data from such synthesis methods to be adjudicated by clinically knowledgeable individuals to aid in their uptake in practice, though it should be recognized that EMR data is inherently noisy, such that generating records that are not in alignment with clinical expectations would not necessarily imply that the proposed methodology has failed to accomplish its goal of creating EMR data.

CONCLUSION

Here, we improved the pipeline of EMR data simulation through GANs through 3 aspects: (1) the learning model, (2) the training strategy, and (3) the utility measures. In doing so, we engineered a new generative model, defined a conditional training strategy, and evaluated new utility measures that account for the latent basis of medical data. Our experimental results with over 1 million EMRs illustrate that the updated pipeline outperforms state-of-the-art GANs without sacrificing the privacy provided by such models.

FUNDING

The research has sponsored in part by National Science Foundation grant 1418504 (BAM) and National Institutes of Health grants R01HG006844 (BAM) and U2COD023196 (BAM).

AUTHOR CONTRIBUTIONS

ZZ, CY, and BAM contributed to the idea of the work. CY performed the data collection. ZZ and CY designed the methods. ZZ carried out experiments. CY drafted the article. CY, ZZ, DAM, JS, and BAM interpreted the results, editing, reviewing, and approving the final manuscript. DAM and JS contributed to editing and reviewing the manuscript.

Conflict of interest statement

None declared.