Learned sensing: jointly optimized microscope hardware for accurate image classification

Abstract

Since its invention, the microscope has been optimized for interpretation by a human observer. With the recent development of deep learning algorithms for automated image analysis, there is now a clear need to re-design the microscope’s hardware for specific interpretation tasks. To increase the speed and accuracy of automated image classification, this work presents a method to co-optimize how a sample is illuminated in a microscope, along with a pipeline to automatically classify the resulting image, using a deep neural network. By adding a “physical layer” to a deep classification network, we are able to jointly optimize for specific illumination patterns that highlight the most important sample features for the particular learning task at hand, which may not be obvious under standard illumination. We demonstrate how our learned sensing approach for illumination design can automatically identify malaria-infected cells with up to 5-10% greater accuracy than standard and alternative microscope lighting designs. We show that this joint hardware-software design procedure generalizes to offer accurate diagnoses for two different blood smear types, and experimentally show how our new procedure can translate across different experimental setups while maintaining high accuracy.

1. Introduction

Optical microscopes remain an important instrument in both the biology lab and the clinic. Over the past decade, the incorporation of the digital image sensor into the microscope has transformed how we analyze biological specimens. Many standard tasks, such as microscopic feature detection, classification, and region segmentation, for example, can now be automatically performed by a variety of machine learning algorithms [1]. For example, it is now possible to automatically predict cell lineage and cycle changes over time [2,3], examine a patient’s skin to automatically identify indications of cancer [4], rapidly find neurons in calcium imaging data [5], and search across various biological samples for the presence of disease [6].

Despite the widespread automation enabled by new post-processing software, the physical layout of the standard microscope has still changed relatively little - it is, for the most part, still optimized for a human viewer to peer through and inspect what is placed beneath. This paradigm presents several key limitations, an important one being that human-centered microscopes cannot simultaneously image over a large area at high resolution [7]. To see a large area, the sample must typically be physically scanned beneath the microscope, which is time consuming and can be error prone, even when scanning is automated with a mechanical device [8]. In addition, even in the absence of scanning, it is still challenging to resolve many important phenomena using the traditional transmission optical microscope. Biological samples are transparent, contain sub-cellular features, and can cause light to scatter, all of which limit what we can deduce from visible observations.

The diagnosis of malaria offers a good example of the challenges surrounding light microscopes in the clinic. Human-based analysis of light microscope images is still the diagnostic gold standard for this disease in resource-limited settings [9]. Due to their small size (approximately 1 $\mu$m diameter or less), the malaria parasite (Plasmodium falciparum) must be visually diagnosed by a trained professional using a high-resolution objective lens (typically an oil immersion objective lens [10]). Unfortunately, it is challenging to create high-resolution lenses that can image over a large area. The typical field-of-view of a 100X oil-immersion objective lens is 270 $\mu$m in diameter [11], which is just enough area to contain a few dozen cells. As the infection density of the malaria parasite within a blood smear is relatively low, to find several examples for a confident diagnosis, a trained professional must scan through 100 or more unique fields-of-view (FOV) [12,13]. A typical diagnosis thus takes 10 minutes or more for an expert, leading to a serious bottleneck at clinics with a large number of patients and few trained professionals. While the analysis process can be automated, for example by developing algorithms, such as a convolutional neural network, to detect abnormalities within digitally acquired images [6,14], a significant bottleneck still remains in the data acquisition process - human-centered microscope designs still must mechanically scan across the sample to capture over 100 focused images, which each must then be processed before it is possible to reach a confident diagnosis.

Alternative methods are available to speed up and/or improve microscope-based image diagnosis. For example phase imaging [15], lensless imaging [16] and flow cytometry [17] can all help improve automated classification accuracies and/or speed. In general, while these alternative methods show promise, many of such new technologies often tend to fall short of their goal of altering diagnostic workflows at hospitals and clinics, especially in resource-limited areas.

Here, we suggest a simple modification to the standard light microscope that can improve the speed and accuracy of disease diagnosis (e.g., finding P. falciparum within a blood smear, or tuberculosis bacilli within a sputum smear), without dramatically altering the standard image-based diagnosis process. In our approach, we 1) add a programmable LED array to a microscope, which allows us to illuminate samples of interest under a wide variety of conditions, and 2) employ a convolutional neural network (CNN) that is jointly optimized to automatically detect the presence of infection, and to simultaneously generate an ideal LED illumination pattern to highlight sample features that are important for classification. While a number of different works have applied deep CNNs to achieve impressive results with novel types of microscopes, from augmenting microscopic imagery [18,19] to creating 3D tomographic images at high resolution [20], we hypothesize that the use of a deep CNN to physically alter how image data is acquired for each task at hand can lead to critical performance gains.

Since this approach relies on machine learning to co-optimize the microscope’s sensing process, we refer to it as a “learned sensing” paradigm. Here, we are optimizing the microscope to sense, for example, the presence or absence of a malaria parasite, as opposed to forming a high-resolution image of each infected blood cell. By learning task-optimized hardware settings, we are able to achieve classification accuracies exceeding 90 percent using large field-of-view, low-resolution microscope objective lenses, which can see thousands of cells simultaneously, as opposed to just dozens of cells seen in the current diagnostic methods using a high-resolution objective lens. This removes the need for mechanical scanning to obtain an accurate diagnosis, suggesting a way to speedup current diagnosis pipelines in the future - in principle, from 10 minutes for manually searching for the malaria parasite, to 10 seconds for snapshot capture and automatic classification. It also suggests a new way to consider how to jointly design a microscope’s physical sensing hardware and post-processing software in an end-to-end manner.

2. Approach

Our approach is based on the following hypothesis: while standard bright-field microscope images are often useful for humans to interpret, these images are likely sub-optimal for a computer to use for automated diagnosis. Transparent samples like blood cells will exhibit little contrast under bright-field illumination and can likely be examined with greater accuracy using alternative illumination schemes. Techniques such as dark-field illumination, differential phase contrast imaging [21], multispectral imaging [22] and structured illumination [23] can help extract additional information from such samples and can thus increase the accuracy of automated processing. However, it is not obvious what particular form of illumination might be optimal for a particular machine learning task. For example, the detection of P. falciparum within blood smears might benefit from one spectral and angular distribution of incident light, which will likely differ from what might be required to optimally find tuberculosis within sputum smears or to segment a histology slide into healthy and diseased tissue areas.

2.1. Deep learning for optimal illumination

To address this problem, we created a machine learning algorithm to jointly perform image classification and determine optimal illumination schemes to maximize image classification accuracy. Our learned sensing approach (Fig. 1) consists of a CNN that is enhanced with what we term “physical layers,” which model the physically relevant sensing parameters that we aim to optimize - here, the variable brightness of the LEDs within a programmable array placed beneath the sample plane of a standard microscope. The physical layer concept proposed here has the potential to generalize to help optimize a variety of different experimental parameters, such as the imaging system pupil, polarization properties, spatial and spectral sampling conditions, sensor color filters [24], etc. In our first demonstration here, for simplicity, we limited our optimization to the brightness of the individual LEDs in the array and their 3 spectral channels (i.e., blue, green and red LED active areas). Once these weights are optimized, they define the best distribution of LED brightness and color for illuminating a sample to achieve a particular inference task (e.g., classification of the malaria parasite). The latter weights within our network make up its “digital layers” and perform this specific task - here, the mapping of each of the uniquely illuminated images to a set of classification probabilities. The weights within both the physical and digital layers are jointly optimized using a large training dataset via standard supervised learning methods (see Appendix).

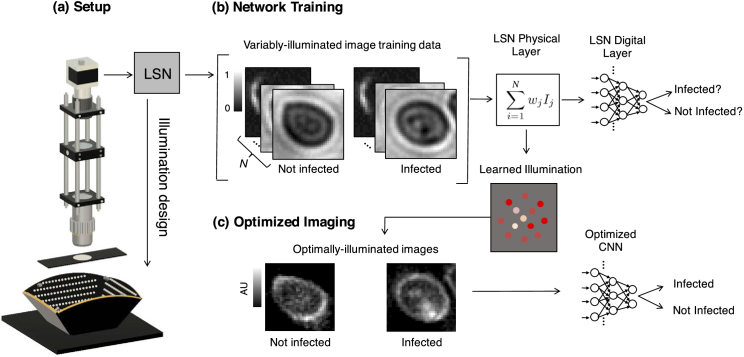
Fig. 1.

We present a learned sensing network (LSN), which optimizes a microscope’s illumination to improve the accuracy of automated image classification. (a) Standard optical microscope outfitted with an array of individually controllable LEDs for illumination. (b) Network training is accomplished with a large number of training image stacks, each containing $N$ uniquely illuminated images. The proposed network’s physical layer combines images within a stack via a weighted sum before classifying the result, where each weight corresponds to the relative brightness of each LED in the array. (c) After training, the physical layer returns an optimized LED illumination pattern that is displayed on the LED array to improve classification accuracies in subsequent experiments.

There are several recent works that also consider how to use machine learning algorithms to jointly establish hardware and software parameters for imaging tasks. Example applications include the “end-to-end” design of a camera’s optical elements and post-processing software for extended depth-of-field imaging [25], target classification [26], depth detection [27], and color image reproduction [24], the latter of which was one of the first examples employing this class of technique. While our learned sensing approach here is conceptually similar to the end-to-end learning approaches listed above, we chose here to use slightly the broader “learned sensing” term to refer to our microscope-based implementation, which includes dynamically controllable hardware and is thus not coupled to a fixed optimized optical design. In other words, the optimized illumination pattern in our microscope can change to better highlight different samples under inspection. This may be important to allow the microscope to capture category-specific sample features either of the P. falciparum malaria parasite, or of tuberculosis bacilli, for example, as each exhibits a different volumetric morphology and often appears within a unique spatial context. Since the LED array is programmable, the optimal illumination pattern can be easily changed without the need to physically replace hardware, which is not the case for previously reported literature.

For microscopic imaging, similar concepts to our approach have been applied to co-optimize a spatial light modulator to improve multi-color localization of fluorescent emitters [28–30]. In addition, several works have also optimized the illumination in a microscope via machine learning to improve imaging performance, primarily for the task of producing a phase contrast or quantitative phase image [31–33], but also for improving resolution-enhancement methods like Fourier ptychography [34–36]. A useful review of similar machine learning methods in microscopy is presented in Ref. [37]. These prior goals are distinct from the present effort of learning the illumination (or sensing parameters in general) for context-specific decisions (e.g., for classification, object detection, image segmentation) in an integrated pipeline. We note that this current work is a revised version of an earlier investigation of ours [38] posted on arXiv, which was one of the earlier works to propose illumination optimization for context-specific decisions. Here, we now examine the problem of joint optimization over the LEDs’ position and spectrum, using multiple larger datasets, which provide us with a more complete picture of our proposed network’s performance. We also now test the robustness of our approach to collecting and processing data across multiple unique optical setups.

As noted above, while the physical layers of our learned sensing network may take on a variety of different forms, our implementation for LED illumination optimization requires one simple physical layer. In the absence of noise, the image formed by turning on multiple LEDs is equal to the digitally computed sum of the images formed by turning on each LED individually (since the LEDs in the array are mutually incoherent). Similarly, the image of a sample illuminated with a broad range of colors (i.e., different optical wavelengths) can be formed by summing up images where each color was used to separately illuminate the sample. Thus, we can digitally synthesize images under a wide range of illumination conditions by computing a weighted sum of images captured under illumination from each and every colored LED within our array. If the brightness of the $n$th LED in the array is denoted as $w_n$, and the associated image formed by illuminating the sample with only this LED at a fixed brightness is $I_n$, then the image formed by turning on a set of $N$ LEDs at variable brightness levels and/or spectral settings is,

$$I\prime =\sum _{n=1}^N{w}_n{I}_n.$$ (1)

Accordingly, our physical layer contains a set of learned weights $w_n$, for $n\in [1,N]$, that are each multiplied by their associated image and summed. A 4-layer CNN, connected within the same network, subsequently classifies this summed image into one of two categories (infected or not infected). Our complete learned sensing CNN for illumination optimization is summarized in Algorithm 1.

Algorithm 1. Learned sensing based network for optimized microscope illumination.

1:	Input: {Ij,n} with n ∈ {1, …, N} uniquely illuminated images of the jth object, object labels {yj}. Number of iterations T. An image classification model F parametrized by θ.
2:	Randomly initialize the LED weights $\mathit{w}={\left\{w_n\right\}}_{n=1}^N$.
3:	for iteration t = 1 … , T do
4:	Sample a minibatch of $({\{I_{j,n}\}}_{n=1}^N,y_j)$,
5:	Generate each pattern-illuminated image $I_j^{\prime }$ via the weighted sum $I_j^{\prime }={\sum }_{n=1}^N{w}_n{I}_{j,n}$
6:	Take a gradient descent step on CrossEntropy($F(I_j^{\prime }),y_j$ ) with respect to w and θ.
7:	end for
8:	Output: the optimized LED weights w and the model parameters θ.

Unlike standard classification methods, which typically train with images under uniform illumination, our network here requires a set of $N$ uniquely illuminated images ${\{I_n\}}_{n=1}^N$ per training example. Once network training is completed, the inference process requires just one or two optimally illuminated low-resolution images. Multiplexed image acquisition [39] or other more advanced methods [40,41] might be used in the future to reduce the total amount of acquired training data per example. At the same time, we also note that capturing this data overhead is only required once, for the training dataset. After network training, the optimized physical parameters (the LED brightnesses and colors) can then be used on the same or on different setups (as we will demonstrate) to improve image classification performance.

2.2. Experimental setup

To experimentally test our learned sensing approach, we attempt to automatically detect the P. falciparum parasite in blood smear slides. We examine two types of smears commonly used in the clinic: “thin” smears, in which the blood cell bodies remain whole and are ideally spread out as a monolayer onto a microscope slide, and “thick” smears, in which the cell bodies are lysed to form a nonuniform background. For each sample category, we captured data with a slightly different microscope and LED array configuration. We imaged thin blood smears with a 20X microscope objective lens (0.5 NA, Olympus UPLFLN) and a CCD camera (Kodak KAI-29050, 5.5 $\mu$m pixels). Variable illumination was provided by a flat LED array, using 29 LEDs arranged in 3 concentric rings placed approximately 7 cm from the sample (maximum LED illumination angle: 40 degrees). Each LED contained 3 individually addressable spectral channels, creating $N=87$ unique spectral and angular channels for thin smear illumination.

For thick smears, in which the infections were slightly easier to identify, we used a 10X objective lens (0.28 NA, Mitutoyo), a CMOS camera (Basler Ace acA4024-29um), and variable illumination from a custom-designed LED array [42] (Spectral Coded Illumination, Inc.) containing approximately 1500 individually addressable LEDs arranged in a bowl-like geometry that surround the sample from below (see Fig. 1). This bowl-like geometry helps maximize the amount of detectable light from LEDs that are at a large angle with respect to the optical axis. We used 41 LEDs distributed across the bowl (maximum LED illumination angle of approximately 45 degrees) with 3 spectral channels per LED (480 nm, 530 nm and 630 nm center wavelength), making $N=123$. We limited our attention to a subset of 29 LEDs for the thin smear, and 41 LEDs for the thick smear, instead of using all of the 1000+ LEDs available within each array, based upon memory constraints in our network. In principle, it is possible to optimize patterns consisting of thousands of LEDs, using thousands of uniquely illuminated images, with a computational pipeline for optimization that has sufficient memory. We selected a particular spatial distribution of LEDs for each case to help balance the number of LEDs in the bright-field and dark-field channels, which was desired for our initial tests.

In both imaging setups, our objective lenses offer a much lower resolution than an oil immersion lens, what is typically required by a trained expert to visually identify the P. falciparum parasite. This allowed us to capture a much larger FOV (25-100X larger area), but at the expense of a lower image resolution. By illuminating the sample at a variety of angles, up to 45 degrees, it is possible to capture thin-sample spatial frequencies that are close to the maximum cutoff of an oil-immersion lens [21]. Our aim here is to determine whether an optimized illumination strategy can help overcome the limited resolution and contrast (and thus classification performance) of our low NA objective lenses, which can potentially lead to accurate diagnosis over 25-100X more cells per snapshot in an oil-free imaging setup.

2.3. Thin smear dataset

To classify cells infected with the malaria parasite in thin blood smears, we captured images of approximately 15 different slides with monolayers of blood cells. Some cells within each slide were infected with P. falciparum while the majority of cells were not infected. Of the infected cells, the majority were infected with P. falciparum at ring stage. Much fewer (~1%) of the infected cells are trophozoites and schizonts, to help test how well the classifier generalizes to different stages of infection. Each slide has been lightly stained using a Hema 3 stain.

To create our classification data set, we first used the image illuminated by the on-axis (center) LED to identify cells with non-standard morphology. We then drew small bounding boxes around each cell and used Fourier ptychography (FP) [11] to process each set of 29 images (under green illumination) into an image reconstruction with higher resolution. The FP reconstructions provide both the cell absorption and phase delay at 385 nm resolution (expected Sparrow limit), which approximately matches the quality of imaging with an oil-immersion objective lens [21]. We then digitally refocused the FP reconstruction to the best plane of focus and visually inspected each cell to verify whether it was uninfected or contained features indicative of infection. Since the human annotation process heavily relied on the image formed by the center LED, we decided to not use the center LED image for algorithm training and instead used $N=84$ uniquely illuminated images (28 LEDs with 3 colors per LED) per training/testing example. This helped minimize any potential effects of per-image bias that could impact the generality of our optimized illumination patterns. We chose an image size of 28×28 pixels, which is slightly larger than the size of an average imaged blood cell, to ensure that there is one complete blood cell within the field-of-view of each example. Individual blood cells were cropped from the full field-of-view image and when necessary, we performed cubic resizing to create 28 × 28 pixel images to make all cropped images the same size. Each $28\times 28\times 84$ data cube and its binary diagnosis label (infected or uninfected) form one labeled training example.

Our total thin smear training dataset consisted of approximately 1,025 cropped example cells, where 330 of the example cells contained an infection and 795 examples contained no infection. We applied data augmentation (factor of 32) separately to the training and testing sets. Each final training set contained 25,000 examples. Each final test set was approximately 25% of the size of its associated training set, with 6,000 examples. We ensured that each test dataset included 50% uninfected examples and 50% infected examples, which simplified our statistical analyses. Mixtures of 4 different transformations were tested for data augmentation: image rotation (90 degree increments), image blurring (3×3 pixel Gaussian blur kernel), elastic image deformation and the addition of Gaussian noise. These transformations align with the following experimental uncertainties that may arise in future experiments: arbitrary slide placement, slight microscope defocus, distortions caused by different smear procedures and varying amounts of sensor readout noise.

To ensure the quality of this dataset, a trained human expert, not involved in the sample preparation or imaging experiments, re-examined a random selection of 50 of the labeled examples (0.5 probability uninfected, 0.5 infected). For each randomly selected example, we displayed 4 images to the expert: one generated by the center LED, a bright-field off-axis LED, a dark-field off-axis LED, and the FP-reconstructed magnitude. Based on these 4 images, the expert made a diagnosis that matched the assigned label with an accuracy of 96% (48 matched, 2 mismatched as false positives). Diagnosis errors can be partially attributed to the low resolution of each raw image and artifacts present in the FP reconstruction.

2.4. Thick smear dataset

To test how well our learned sensing approach generalized across microscope setups and classification tasks, we captured thick smear malaria data on a new microscope, with a bowl-like arrangement of LEDs. The thick smears included the P. falciparum infection at ring stage with a 0.002%-0.5% concentration. Each slide also included early trophozoites at a much lower concentration, as well as a large background of red blood cells that were partially lysed and contributed a substantial amount of debris to each slide. We captured our data from 5 different slides and followed a similar classification and segmentation pipeline as explained for the thin smear data, again using cubic resizing to 28 × 28 pixel images when necessary. We captured data from $N=123$ unique LEDs in total (41 red, green and blue LEDs), and again chose to remove the 3 center LED images from the training dataset (since they were heavily relied upon during the annotation process) to create labeled examples each $28\times 28\times 120$ in size. We identified 694 examples of suspected infection using the center LED-illuminated images across all 5 slides, while we cropped 1,432 regions containing no infection from various image plane locations, leading to 2,126 total examples. 16X augmentation led to a final training dataset with 24,000 examples. Due to the more obvious features of the parasite in the thick smear, FP was not used to aid annotation. Furthermore, due to the lysing of the red blood cell bodies, each uninfected example is not necessarily of a cell body and primarily contains cell body debris.

3. Experimental results, thin smear

Table 1 presents our experimental classification results for thin-smear malaria. Our network consisted of the 5-layer CNN detailed in the Appendix, using the physical layer for illumination optimization described in Section 2. In this table, we compare the classification accuracy for a variety of different illumination schemes, including our network’s optimized illumination method, which outperforms each of the tested alternatives. Each entry within the table includes 1) an average accuracy from 15 independent runs, 2) a ’majority vote’ that selects the mode of classification category across the 15 trials to establish the final classification for each test example, and the standard deviation of the classification accuracy for the 15 trials.

Table 1. Learned sensing classification of P. falciparum infection, thin smear.

		Illumination Type & Classification Score
Data	Value	PC Ring	Off-axis	PC +/-	All	Random	Optim.
Red-only	Average	0.827	0.782	0.718	0.711	0.749	0.852
	Majority	0.847	0.804	0.728	0.724	0.797	0.862
	STD	0.008	0.012	0.007	0.008	0.026	0.010
	Precision	0.922	0.917	0.845	0.822	0.860	0.926
	Recall	0.715	0.619	0.532	0.534	0.593	0.765
Green-only	Average	0.859	0.746	0.699	0.705	0.760	0.873
	Majority	0.878	0.756	0.707	0.719	0.807	0.892
	STD	0.008	0.015	0.014	0.011	0.040	0.017
	Precision	0.936	0.863	0.837	0.804	0.858	0.944
	Recall	0.769	0.582	0.498	0.542	0.621	0.791
Blue-only	Average	0.842	0.748	0.735	0.731	0.758	0.853
	Majority	0.872	0.771	0.744	0.751	0.825	0.884
	STD	0.015	0.011	0.013	0.011	0.029	0.018
	Precision	0.932	0.867	0.869	0.845	0.868	0.920
	Recall	0.737	0.585	0.554	0.566	0.610	0.773
RGB	Average	0.847	0.768	0.726	0.707	0.753	0.882
	Majority	0.872	0.788	0.747	0.722	0.833	0.908
	STD	0.018	0.010	0.020	0.020	0.039	0.019
	Precision	0.907	0.835	0.822	0.808	0.841	0.939
	Recall	0.772	0.669	0.579	0.544	0.625	0.818

"PC ring" illuminates with a ring of 20 dark-field LEDs for the first image and then the 8 central bright-field LEDs for the second image and subtracts the two images for phase contrast. "Off-axis" illuminates with one LED at a small angle with respect to the optical axis. "PC +/-" illuminates with a bright-field LED at an angle for the first image and the LED at equal and opposite angle for the second image before subtracting these two images. "All" sets all LEDs to a uniform brightness. "Random" sets the LEDs’ brightness to random values for the illumination. "Optim." is the learned pattern.

The alternative illumination schemes that we tested include spatially incoherent illumination from “all” LEDs within the array, “off-axis” illumination from one LED at small angle with respect to the optical axis, “random” illumination from all of the LEDs set at randomly selected brightness levels, and then two “phase contrast” (PC) methods that rely on using both positive and negative LED weights to form the final image. It is important to note our optimizer solves for weights $w_n$ that can be either positive or negative. To implement these positive and negative LED weights experimentally, we capture and subtract two images - the first with positively-weighted LEDs illuminated at their respective brightness and the second with the negatively weighted LEDs, and subtract the second from the first to form the final image that will be fed into the classification network. It is certainly possible to use more than two optimized LED patterns to capture more than two images for improved classification, potentially with another slightly modified learned sensing optimization framework. As our current approach can only optimize for either one or two illumination patterns, we focus our attention on this limited subset of imaging configurations for comparison.

Accordingly, for the “PC +/-” configuration’s positive and negative illuminations, we set the brightness of an angled LED within the bright-field cutoff to 1, and set the brightness of the LED at an equal and opposite angle to -1. This generates a final image that shares properties with a large class of differential phase contrast illumination techniques [43], which capture and subtract two images under angled illumination. There are a large variety of differential phase contrast techniques that use more than two captured images [44–47], which are, as noted above, challenging to directly compare to this limited learned sensing network. Second, the PC Ring illumination scheme consists of using a ring of 20 LEDs within the dark-field channel to illuminate and capture one image, and a set of 8 LEDs within the bright field channel to illuminate and capture a second image, and subtracts the two images to create phase contrast. This type of illumination scheme has been previously investigated in Ref. [44]. We selected this particular phase contrast LED pattern to generally match the optimized LED illumination pattern structure that we consistently observed during classification optimization (see details below).

The classification scores in Table 1 indicate that our optimized illumination pattern results in classification accuracies that exceed all other tested illumination methods. Improvement over the naive approach of using uniform Köhler-type illumination with "all" LEDs on, which is a primary illumination scheme for clinicians and for acquisition of most microscope image data, can be greater than 15%. In general, we observed that a higher classification accuracy is achieved when the illumination provides some sort of phase contrast. The best alternative option is provided by PC Ring illumination.

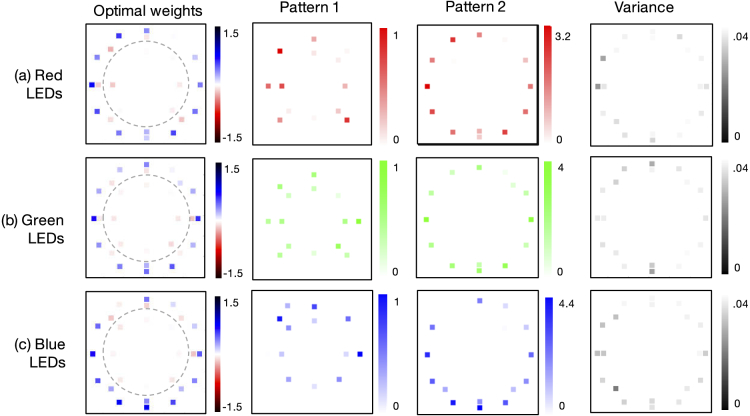
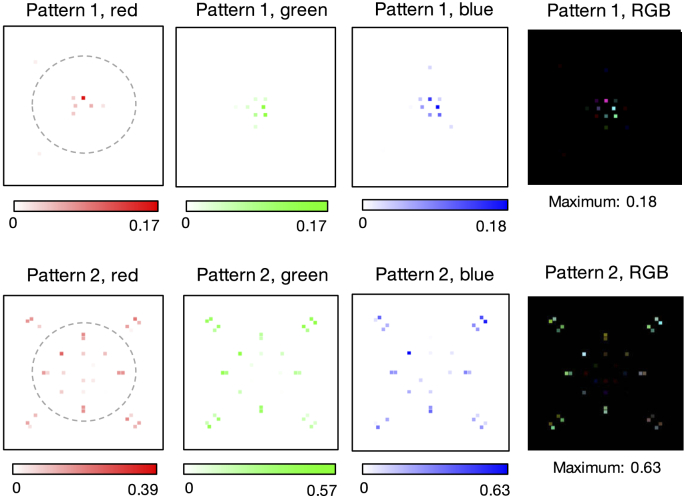
Our variably-illuminated data allows us to test how well our learned sensing network improves classification accuracy with both angularly varying illumination, as well as spectrally varying illumination. First, we examined the performance of each spectral channel (i.e., the red, green and blue LEDs) separately. To do so, we optimized for single-color illumination patterns by training our algorithm with only the image data captured from each respective LED color. The classification accuracies obtained from this exercise, of using just one color at a time, are listed in the first three sections of Table 1. These results highlight that the spatial pattern established for the green channel is slightly better at resulting in correct classification of the malaria parasite in thin smears. Example optimized LED illumination patterns determined by our network for each single-color case are shown in Fig. 2. Here, we observe that the CNN converges to similar optimized LED patterns for each color channel considered individually, albeit with slight differences (e.g., see Pattern 1 green versus blue). The average variance of optimized LED weights (with normalized brightness) across 15 independent trials was 0.010. The primary observation here is that, independent of LED color, our CNN’s physical layer consistently converged to a very similar distribution of weights that were negative for LEDs along the outer-most ring (beyond the bright-field/dark-field cutoff) and were positive elsewhere, establishing a particular illumination pattern that was close to but not quite circularly symmetric to optimally classify the malaria parasite. There are a number of possible causes of an observed asymmetry, including the fact that all tested blood samples exhibited a similar preferential smear direction, as well as possible influences of data augmentation. We plan to investigate the specific properties of these optimized illumination patterns and hope to uncover causes of asymmetry in the near future.

Fig. 2.

Optimal single-color illumination patterns determined by our network for thin-smear malaria classification (average over 15 trials). (a) Optimized LED arrangement determined using only the red spectral channel exhibits negative (Pattern 1) and positive (Pattern 2) weights that lead to two LED patterns to display on the LED array, recording two images which are then subtracted. Variance over 15 independent runs of the network’s algorithm shows limited fluctuation in the optimized LED pattern. (b-c) Same as (a), but using only the green and blue spectral channels, respectively, for the classification optimization. Dashed line denotes bright-field/dark-field cutoff.

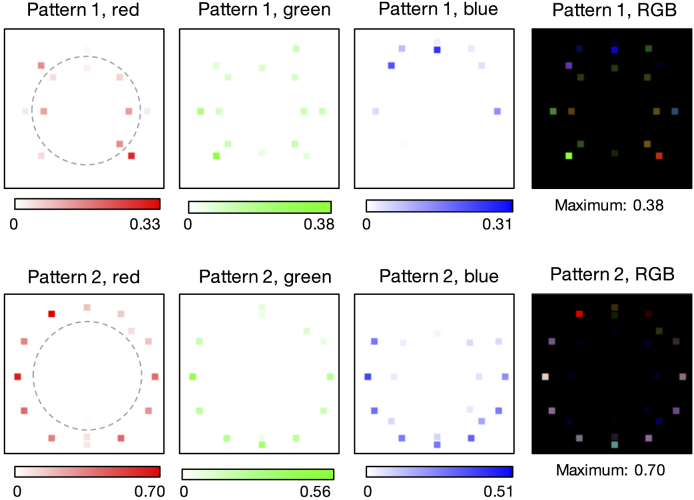
Second, we examined the classification performance of our network while jointly optimizing over LED position and color, using all $N=84$ images per example during the model training. The results of this optimization exercise are at the bottom of Table 1. Joint spatio-spectral optimization produced the highest classification accuracy observed with the thin smear data (91 percent). This exceeds the accuracy of standard white illumination from an off-axis LED (79 percent), from the phase contrast ring pattern (87 percent), and from optimized illumination using only the green LEDs (89 percent). The average optimal color illumination patterns are in Fig. 3. We observe here that the optimized LED array pattern for all colors considered jointly exhibits a spatially varying spectral profile (that is, the spatial distribution of the colors within the patterned illumination appears to be important for increasing the final classification accuracy). The average variance of normalized LED brightness during multispectral optimization across 15 independent trials was 0.008.

Fig. 3.

Optimal multispectral illumination patterns determined by our network for thin-smear malaria classification (average over 15 trials). Learned sensing optimization is jointly performed here over 3 LED colors and 28 LED locations simultaneously, yielding 2 unique spatio-spectral patterns that produce 2 optimally illuminated images for subtraction.

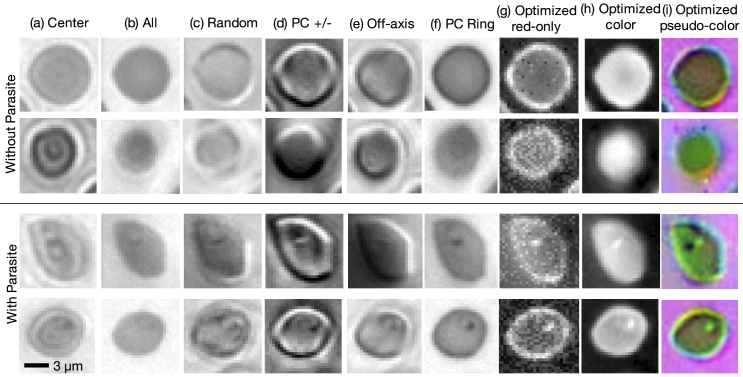
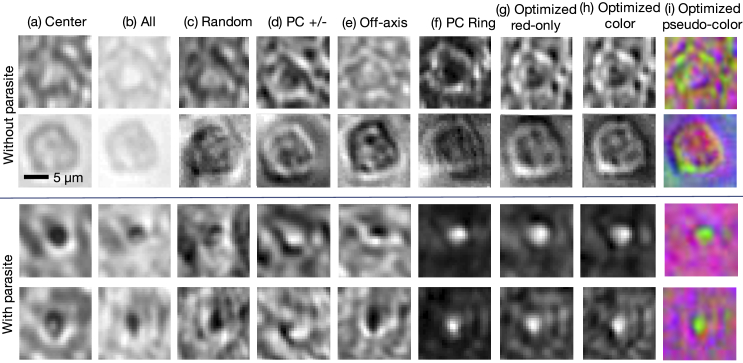
Images of several randomly selected cells under each tested illumination pattern, including the optimized illumination patterns, are shown in Fig. 4. As noted above, images under illumination from positively and negatively weighted LEDs were formed by capturing and subtracting the two images. The PC Ring and optimized illumination schemes yield images with little background and a noticeable bright spot at the location of each parasite. We note that the single-color optimized patterns patterns for the red channel exhibit the lowest signal-to-noise ratio out of all three spectral channels, due to our use of lower power for the red LEDs and the relative low-contrast of the blood cells in red, which mostly disappears when we additionally optimize over the green and blue spectral channels. The average false positive rate and false negative rate breakdown for the single-color optimized results was 2.91% and 11.14%, respectively (averaged over 15 independent trials and 3 separate colors). For the jointly optimized LED position and color results, the false positive/false negative rates were 2.96% and 8.87%, respectively. While our test datasets were a 50 percent split between infected and uninfected examples, our training data consisted of a larger number of uninfected examples, which may be one reason why we observe a slightly larger number of false negatives in our results. Future work will aim to better understand how the optimized illumination pattern distinctly impacts false positive and false negative rates.

Fig. 4.

Example images of individual thin-smear blood cells under different forms of illumination. Top two rows are negative examples of cells that do not include a malaria parasite, bottom two rows are positive examples that contain the parasite. Example illuminations include from (a) just the center LED, (b) uniform light from all LEDs, (c) all LEDs with uniformly random brightnesses, (d) a phase contrast-type (PC) arrangement, (e) an off-axis LED, (f) a phase contrast (PC) ring, (g) optimized pattern with red illumination, (h) optimized multispectral pattern, and (i) the same as in (h) but showing response to each individual LED color in pseudo-color, to highlight color illumination’s effect at different locations across the sample.

4. Experimental results, thick smear

We repeated the same experimental exercise with our labeled images of thick smear preparations of malaria-infected blood smears. The resulting classification accuracies for the same set of 6 different possible illumination schemes are shown in Table 2, once again for 15 independent trials of the network. For our thick smears, the classification accuracies for all illumination schemes are much higher than for the thin smear - approximately $10-15$ percent higher across the board. We hypothesize that this gain is most likely due to the use of heavier staining on the thick smear slides, which caused parasites in these slides to be more absorptive and thus stand out with higher contrast from the background.

Table 2. Learned sensing classification of P. falciparum infection, thick smear.

		Illumination Type & Classification Score
Data	Value	PC Ring	Off-axis	PC +/-	All	Random	Optim.
Red-only	Average	0.976	0.972	0.910	0.972	0.947	0.982
	Majority	0.977	0.975	0.918	0.974	0.975	0.982
	STD	0.002	0.002	0.013	0.002	0.022	0.001
	Precision	0.988	0.993	0.977	0.984	0.974	0.987
	Recall	0.962	0.950	0.837	0.961	0.917	0.977
Green-only	Average	0.993	0.969	0.918	0.986	0.932	0.995
	Majority	0.994	0.974	0.926	0.988	0.959	0.995
	STD	0.001	0.004	0.008	0.001	0.009	0.001
	Precision	0.998	0.980	0.980	0.995	0.984	0.994
	Recall	0.988	0.958	0.854	0.975	0.878	0.995
Blue-only	Average	0.988	0.975	0.938	0.989	0.970	0.994
	Majority	0.988	0.977	0.943	0.991	0.981	0.996
	STD	0.002	0.003	0.004	0.002	0.007	0.002
	Precision	0.999	0.998	0.990	0.994	0.992	0.999
	Recall	0.976	0.953	0.886	0.984	0.948	0.990
RGB	Average	0.990	0.970	0.941	0.981	0.965	0.990
	Majority	0.991	0.976	0.948	0.983	0.980	0.990
	STD	0.003	0.006	0.008	0.003	0.020	0.001
	Precision	0.998	0.990	0.988	0.994	0.994	0.999
	Recall	0.981	0.950	0.892	0.900	0.936	0.981

"PC Ring" illuminates with a ring of 26 dark-field LEDs for the first image and then 14 central bright-field LEDs for the second image and subtracts the two images for phase contrast. "Off-axis" illuminates with one LED at a small angle with respect to the optical axis. "PC +/-" illuminates with a bright-field LED at an angle for the first image and the LED at equal and opposite angle for the second image before subtracting these two images. "All" sets all LEDs to a uniform brightness. "Random" sets the LEDs’ brightness to random values for the illumination. "Optim." is the learned pattern.

Although all tested LED patterns yielded higher accuracy than with thin smear data, thus making differential performance analysis slightly more challenging, we still consistently obtained the highest classification accuracy using optimized illumination. Once again, PC Ring illumination produced, on average, the second highest classification scores. Unlike the thin smear case, uniform Köhler-type illumination also led to high classification accuracies. We hypothesize that the higher amount of absorption caused by each thick smear provided sufficient contrast for strong performance under uniform lighting from all LEDs.

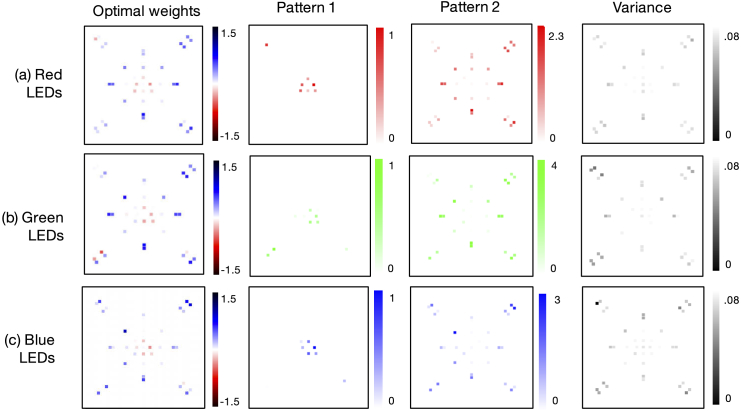
While high (95-99%) classification accuracies make it more challenging to draw conclusions about our network’s optimization performance, for each LED color ($N=40$) versus joint optimization across all colors, one observation is that patterns using green and blue light outperformed those using red light. This matches expectations for the red-stained thick smears, which include parasites that absorb more green and blue light. It is also verified by the optimized patterns obtained from joint optimization across LED location and color ($N=120$), shown in Fig. 5, which are more heavily blue-green. Optimized LED patterns for each individual color channel exhibit a similar structure, as shown in the Appendix (see Fig. 8). Furthermore, we note that the slight drop in classification accuracy of the joint location and color optimization, versus just the single-color results, is likely due to to the size of the augmented training dataset for each case (14,000 for the former, 24,000 for the latter), which was due to memory constraints encountered during network training.

Fig. 5.

Optimal multispectral illumination patterns determined by the learned sensing network for thick-smear malaria classification. Network optimization is jointly performed over 3 LED colors and 40 locations simultaneously. Dashed line denotes bright-field/dark-field cutoff. Optimized pattern uses a similar phase contrast mechanism as with the thin smear, but converges towards a distinctly unique spatial pattern and multispectral profile.

As with the thin smear case, our network converged to an optimal LED arrangement that included negatively-weighted LEDs distributed beyond the dark-field cutoff, and positively-weighted LEDs within the bright-field area, once again utilizing a phase contrast mechanism to boost classification performance that is structurally similar to the PC Ring scheme that we test performance against. However, the particular spatial arrangements and multispectral distributions of the optimized patterns for thin and thick smears are uniquely distinct, pointing towards our modified network’s ability to create task-specific optimized illumination patterns. It should be noted that the LED arrays used in the thin and thick smear experiments each have a slightly different physical layout, but both provide similar Fourier space coverage. Each array has a similar split of bright-field and dark-field LEDs (9/20 and 12/29 bright-field/dark-field LEDs, respectively, for the thin and thick smear setups). Thus, by examining the optimized patterns, we can conclude that, for the first snapshot, more direct and slightly asymmetric bright-field illumination was preferred for thick-smear classification, whereas more tilted and symmetric bright-field illumination was preferred for thin-smear classification. Both sample types preferred ring-like dark-field illumination for the second snapshot, but with obvious color differences.

Figure 6 highlights the effects of the various illumination methods, including the optimized pattern, on several example areas with and without a parasite in the thick smear data. The optimized LED patterns were slightly less consistent than with the thin smear, but were still very repeatable - the average variance across LEDs trained during multispectral optimization was 0.012 (15 independent trials). Single-color optimization yielded an average false positive/false negative rate of 0.31% and 0.66%, respectively, while the multispectral optimization yielded rates of 0.05% and 0.94%, respectively, on the thick smear data. Once again, we currently attribute this imbalance to our uneven training data and are currently investigating how the learned sensing network’s physical layers impact this split.

Fig. 6.

Example images of thick-smear locations under different forms of illumination. Top two rows are negative examples of areas that do not include a malaria parasite, bottom two rows are positive examples that contain the parasite. Example illuminations for (a)–(f) mirror those from Fig. 4, while the optimized patterns used for (h)–(i) are shown in Fig. 5.

4.1. Transfer across experimental setups

As a final exercise, we tested the robustness of our network’s optimized illumination patterns to different experimental conditions and setups. A primary goal of our experimental efforts here is to establish whether our learned sensing technique can be eventually applied across a large number of devices. We would ideally like to apply the same set of learned patterns across multiple microscopes distributed at different clinics and laboratories. A prerequisite to effectively achieve this goal will be to ensure that an optimal illumination pattern established using training data captured by one microscope at one location (e.g., a dedicated laboratory), can be used with a second microscope at a different location (e.g., in the field) while still offering accurate performance. This would imply that the optimized patterns are not coupled to a specific setup, but instead can generalize to different experimental conditions. At the same time, we aim for these optimized patterns to remain effective for their specific sample category. While we only test robustness for one sample category here, we aim to understand the interplay and trade-offs between these two related goals in future work.

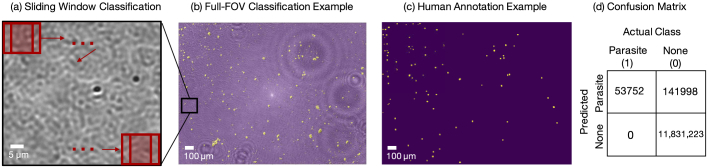
Accordingly, we trained a learned sensing network first using a labeled thick smear experimental dataset collected as described above, in Erlangen, Germany. Training resulted in a set of optimized classification CNN weights and an optimized illumination pattern similar to that shown in Fig. 5. Next, a new microscope with a similar configuration was set up in Durham, North Carolina, which used similar components to match key specifications (0.28 NA, 10X objective lens, LED array bowl and the CMOS camera). For other components (sample stage, tube lens, LED array mount etc.), different model parts were used. There were also some small variations present in the setup due to tolerances in the construction. We used the new setup to capture new images of unseen thick-smear slides (Fig. 7(a)). Finally, we input these new images into the previously trained network, one image patch at a time via a sliding window technique [48,49] shown in Fig. 7(a), and evaluated the classification performance. In this sliding window method, a 28x28 pixel patch around a given pixel in the 10X raw image is chosen and sent to the network to get a classification score, which is then assigned to the corresponding pixel on the classification map. This is repeated for all pixels in the 10X image to create the final classification map. An example sliding window classification map, overlaid on its associated 10X raw image, is shown in Fig. 7(b).

Fig. 7.

Full-slide classification performance using a pre-trained learned sensing network with a new experimental setup. (a) Zoom-in of a thick smear image captured in Durham, NC with sliding window classification process depicted on the top. (b) Classification map (in yellow) overlayed on top of the experimental image of the thick smear. Here the classification map for the entire thick smear image was generated by the sliding-window technique, using the learned-sensing CNN trained on the data captured in Erlangen, Germany. (c) Human annotation map of same thick smear. (d) Confusion matrix of classification performance.

To obtain the ground truth for performance evaluation, we also captured high-resolution images (40X objective lens) of the same thick-smear samples in Durham, NC over the full 10X objective lens FOV. A human annotator used the 40X images to create "true map" images of the location of infections in the 10X images. An example human annotation map is in Fig. 7(c). Comparing the predicted map to the true annotation map of the parasites, we obtained an average accuracy of 0.988. The associated Intersect-over-Union metric was 0.284, which is relatively low. We observed that classification results in this set of tests were affected by the presence of artifacts created by dust or other debris not associated with the blood smear itself, which led to a relatively large number of false positives. However, we observed a perfect true positive rate (i.e., we did not miss any parasites). For completeness, we also trained a CNN using data captured in Germany under uniform Köhler-type illumination, and performed the same classification task using the sliding window technique on uniformly illuminated images captured in Durham, NC. In this case, we obtained an average accuracy of 0.975 ($19,876$ True Positives and $11,711,364$ True Negatives). The associated Intersect-over-Union metric was 0.055. It is evident that optimized illumination maintains superior performance over standard uniform illumination when results are translated to different setups.

As noted above, future work will attempt to better understand the interplay between different types of classification error, and to reduce the number of false positives in these translated results. At the same time, it is important to note that the final quantity that we are eventually interested in is a single diagnosis for each entire blood smear. Accordingly, we will eventually aim to aggregate classification statistics from thousands of different image patches from the same slide, which will allow us to significantly reduce the impact of false positive errors to increase confidence in final decisions and diagnoses.

5. Discussion and conclusion

We have presented a method to improve the image classification performance of a standard microscope, by adding a simple LED array and jointly optimizing its illumination pattern within an enhanced deep convolutional neural network. We achieved this joint optimization by adding what we refer to as a “physical layer” to the first components of the network, which jointly solves for weights that can be experimentally implemented in hardware. Since the LED array offers full electronic control over the brightness and the color of each LED, this results in the ability to use a wide variety of illumination patterns that are optimized for different sensing tasks. In this case, we considered two specific sensing tasks - classifying the malaria parasite within thin blood smears and within thick blood smears, which resulted in two notably different optimal illumination patterns.

With minimal modification, the network presented here directly optimizes for either one or two illumination patterns - depending upon the use of a non-negativity constraint on physical layer weights during optimization. Capturing more than 2 images with more than 2 unique illumination patterns would most certainly help improve the classification accuracy. This topic is a current line of investigation within the microwave regime [50], and can likely extend to the optical domain as well. Such an effort will likely benefit from an adaptive illumination strategy, whereby reinforcement learning can be used to establish a feedback loop between captured images and optimal subsequent illumination patterns. This leads to the interesting future aim of creating an “intelligent” microscope, whose sensing parameters (illumination angle and color, sample position, lens settings) are dynamically established during image acquisition, via a task-specific policy, to increase inference accuracy.

Future work might also aim to improve the experimental hardware used for imaging. With the selected objective lenses, we observed that chromatic aberrations, especially at the edges of the image FOV, caused the acquired image data from different colored LEDs to not align perfectly. While this effect will be present in nearly all experimental microscopes, such as the one used here, future tests should work towards minimizing or accounting for this effect. Future work might also examine our network’s performance as a function of the number of illumination LEDs - a larger number will require additional training overhead, but might yield a smoother illumination distribution in the source plane, and thus offer further insight into how illumination can help maximize classification accuracies for various sample categories.

Finally, this preliminary investigation is a first step towards a broader aim to create a simple, inexpensive and portable microscopic imaging system that can accurately detect and identify various infectious diseases across a large FOV. A low-cost portable microscope with an LED array illumination was recently reported [51] using a Raspberry Pi as the computer. Despite not having a high-power graphics card, the computational power on such single-board computers is sufficient to perform classification with the co-optimized LED illumination and the CNN that was trained on a lab setup. In addition, we hope to increase the size and diversity of our labeled dataset of P. falciparum, both in terms of examining the parasite at different stages within its life cycle, as well as under different stains and smear preparations. Transfer learning [52] may also be used to help broaden our future datasets to include images of blood smears from significantly different microscope setups. We also hope to perform learned sensing-based optimization with other sample categories - for example, tuberculosis bacilli within sputum smears or filaria parasites within blood samples. Finally, we aim to apply our approach to improve the performance of alternative machine learning goals - for example, for object detection [53] and image segmentation [54]. In short, there are many possible extensions of the learned sensing technique, and we encourage others who work with deep networks to simultaneously consider how to jointly optimize their data sensing hardware, in addition to their machine learning software, for improved system performance.

Appendix

Network optimization: All machine learning optimization was performed with Tensorflow. To process each type of data, we used the cross-entropy metric, trained with 25k iterations with a batch size of 50 and applied dropout before the final layer. We primarily used Gaussian random weight initialization for all weights, except for optimization of RGB weights with the thin smear data, where we found slightly better performance by initializing with zeros. All reported results used Adam Optimization with a step size of ${10}^{-3}$ and the following parameters: ${\beta }_1=0.9$, ${\beta }_2=0.999$ and $\mathit{ϵ}={10}^{-8}$.

Our CNN contained 5 layers, where layers proceeded as follows: layer 1 (physical layer) is a tensor product between a $28\times 28\times N$ input and a $1\times N$ weight vector $w$, layer 2 uses a $5\times 5$ convolution kernel, 32 features, ReLU activation and $2\times 2$ max pooling, layer 3 uses a $5\times 5$ convolution kernel, 64 features, ReLU activation and $2\times 2$ max pooling, layer 4 is a densely connected layer with 1024 neurons and ReLU activation and layer 5 is densely connected readout layer. We apply dropout with a probability of 0.5 between layers 4 and 5. For the thin-smear case, $N=28$ for the single-color optimization trials and $N=84$ for the multispectral optimization, while $N=40$ for the single-color optimization trials and $N=120$ for the thick smear case. This code will be made available at the following project page: deepimaging.io.

Fig. 8.

Optimal single-color illumination patterns determined by our network for thick-smear malaria classification (average over 15 trials). (a) Optimized LED arrangement determined using only the red spectral channel has (Pattern 1) negative and (Pattern 2) positive weights that lead to two LED patterns to display while capturing and subtracting two images. Variance over 15 independent runs. (b-c) Same as (a), but using only the green and blue spectral channels, respectively, for optimization.

Funding

Deutsche Forschungsgemeinschaft10.13039/501100001659.

Disclosures

The authors declare that there are no conflicts of interest related to this article.