Morphological changes of human crystalline lens in myopia

Abstract

Ocular biometric parameters, including full shape crystalline lens, were assessed in myopes and emmetropes using 3-D optical coherence tomography. The anterior chamber depth, the radius of the curvature of the anterior cornea, anterior lens, and posterior lens, lens thickness, lens equatorial diameter, surface area, equatorial position, volume, and power, were evaluated as functions of refractive errors and axial lengths while controlling for age effects. The crystalline lens appears to change with myopia consistent with lens thinning, equatorial, and capsular stretching while keeping constant volume. Axial elongation appears counteracted by a crystalline lens power reduction, while corneal power remains unaffected.

1. Introduction

Myopia is a common refractive error condition that affects a growing number of people worldwide [1,2]. Understanding the underlying causes for myopia and the changes undergone by the myopic eye is important for finding new strategies for myopia control.

The refractive error is determined by the relationship between the axial length of the eye and its optical power. The interplay of axial dimensions and surface curvatures of the cornea and crystalline lens (which determine the eye’s optical power) is important for focusing an image on the retina in an emmetropization, and in its disruption leading to the development of refractive errors [3,4]. Although the emmetropization mechanism is not fully understood, data from animal models indicate that eye growth is actively controlled, being driven by blur in the retinal image [5,6]. Human studies show that during the first years of life there is a significant shift in refraction of the eye, generally from hyperopic refraction toward emmetropia, [7,8], with the axial elongation being compensated mostly by a decrease of crystalline lens power [4]. A study by Mutti et al [9] showed that rapid emmetropization due to optical and structural development happens in the first two years of life and slows down later on. Disruption of this balance by excessive eye elongation or imbalance in the power of cornea and lens results in myopia [10].

The potential differences in corneal power across different refractive error groups have been often studied [11–15]. Some works have not found correlations between the corneal radius of curvature and refractive error [13,14], while other studies have reported steeper corneas in longer eyes [11,12,15]. Also, higher axial length/corneal radii of curvature ratio has been associated to higher risk of myopia development [16].

Reports on the changes in the crystalline lens with myopia are scarce. The lens radii of curvature have been shown to flatten throughout childhood, and studies have found more lens thinning in myopic children [8]. From the relation given by Bennet and Rabbets [17], Garner et al. [4] found that myopic subjects exhibit lower crystalline lens power compared to their emmetropic counterparts. Mutti et al [18] reported in a longitudinal study in children that myopic subjects exhibited thinner crystalline lens and lower lens power compared to emmetropic subjects. On the onset of myopia, the crystalline lens stopped thinning and flattening compared to the subjects who remained emmetropic, suggesting that the crystalline lens stops adapting to the eye’s continued growth. In a similar study by Rozema et al [19] on children, they found that new myopes show higher lens power loss before myopia compared to emmetropes. These changes were speculated to arise from enlarged ciliary muscles in the developing eye that restricts equatorial expansion of the lens, resulting in an attenuation of crystalline lens thinning.

Most studies have quantified the crystalline lens morphological changes with age and accommodation using optical techniques such as Purkinje-imaging [20,21], Scheimpflug imaging [22–25] and Optical Coherence Tomography (OCT) [26–31]. However, these techniques are not able to image the full shape of the crystalline lens because the iris blocks the incident light and only the information through the eyes natural pupil (the central part of the lens) is available. Ultrasound biomicroscopy (UBM) [32] and Magnetic Resonance Imaging (MRI) [33–35] have also been used to characterize the crystalline lens without obstruction by the iris, but UBM requires contact with a probe and MRI resolution and speed are lower than the ones of optical techniques. These works generally provide axial measurements or 2-D information, along a crystalline lens meridian [20–26,28].

Optical Coherence Tomography (OCT) in combination with fan and optical distortion correction [36,37] has proved to produce fully 3-D anterior segment quantification, including the central part of the crystalline lens. Furthermore, we have recently presented and validated a method to estimate the full shape of the crystalline lens from its central part [38]. This method was successfully applied to assess changes of the crystalline lens full shape with accommodation [39] and with age [40] in vivo, to improve the estimation of the intraocular position in a cataract surgery [41] and to quantify the crystalline lens in animal models of myopia [42].

In this study we used 3-D OCT imaging to evaluate the anterior segment biometry (including the full shape of the lens) as a function of refractive error/axial length (RE or AL). This allowed us to study the involvement of the crystalline lens in both the fine tuning of optical elements and AL leading to emmetropization and in the balance loss resulting in myopia. Particularly we have been able to assess the open question whether the changes in the crystalline lens morphology are a mere result of the overall growth of the entire eye globe (passive) or if those changes are the result of lens actively trying to emmetropize (active). Although the study is cross-sectional and performed in young adults, it likely reflects the underlying compensatory changes undergone by the crystalline lens during emmetropization and the development of RE. To our knowledge this is the first work evaluating the full shape of the crystalline lens of myopes using OCT.

2. Methods

2.1. Subjects

The study was conducted on 21 subjects (11 males, 10 females), of which 13 were myopic (-6.25 to -0.5 D of sphere) and 8 were emmetropic (-0.5 to 0.5 D of sphere), with cylinders from -1.25 D to 0 D. Refractive errors were obtained by cyclopleged subjective refraction. For each subject, the right eye was measured if astigmatism was below 1.25 D. Otherwise, the contralateral, less astigmatic eye, was measured. Myopic and emmetropic groups were similar in age (27 ± 4.29 y/o and 28 ± 4.94 y/o, respectively). All subjects signed a consent form approved by the Institutional Review Boards after they had been informed on the nature and possible consequences of the study, in accordance to the tenets of the Declaration of Helsinki.

2.2. OCT system

Images were acquired using a custom developed spectral Optical Coherence Tomography (sOCT) system described elsewhere [29,43–45]. The system is based on a fiber optic Michelson interferometer configuration with a superluminiscent diode (λ0 = 840 nm, Δ = 50 nm). The spectral interference fringes are captured by a 12-bit line scan CMOS camera (4096 pixels) coupled with a spectrometer. The effective acquisition speed was 25000 A-Scans/s. The axial range of the OCT system was 7 mm in air resulting in a pixel size of 3.4 µm. The axial resolution estimated from spectral width of the light source was 6.9 µm in tissue and sensitivity roll off over the entire axial range was 19.5 dB. In order to compensate for the defocus, an external channel was incorporated to the system containing a motorized Badal Optometer. A fixation stimulus (E letter) was projected on a black background with the help of a Digital Light Processing (DLP) projector at far point of each individual subject (0D accommodation).

2.3. Experimental protocol

AL was measured using a commercial non-contact low-coherence tomography based biometer (Lenstar LS 900). Keratometry was measured using auto-refractometry (NIDEK ARK 1), under natural viewing conditions. Three-dimensional images of the anterior segment of the eye were acquired using the custom sOCT system described in previous section. Since the specifications of the spectrometer and light source limited the axial range to 7 mm (in air), three sets of images were captured sequentially by axially shifting the plane of focus: (1) cornea, (2) anterior lens surface, and (3) posterior lens surface [31]. All OCT images were taken in an 11 × 11 mm scanning area containing 50 B-scans and 300 A-scans per B-scan. The acquisition time for an entire 3-D volume was 0.6 s.

Measurements were conducted with and without mydriasis, used depending on the measured pupil diameter under photopic lighting conditions. If the pupil diameter was < 5 mm, one drop of phenylephrine was applied, which allowed measuring through a larger pupil diameter without affecting the lens’ state of accommodation, surface topography or geometry [38].

All subjects were stabilized with a custom-made bite bar. The alignment of the subject in both horizontal and vertical meridians was done with respect to corneal specular reflection, visible on the OCT’s user interface [46]. Prior to imaging, the pupillary axis of the eye was aligned to the optical axis of the instrument, so that the iris appeared flat in the preview OCT images [31]. This was achieved by moving the fixation stimulus in 5 pixel steps horizontally and vertically. For each eye, 5 repeated sets of anterior segment volumes were obtained.

2.4. Full crystalline lens shape quantification

The quantification of the full shape of the lens included image segmentation, registration, distortion correction, full shape estimation and quantification.

Image segmentation (i.e., detection of the different surfaces within the eye) and registration (i.e., setting the cornea, anterior and posterior lens surface images in the same coordinate system) were performed using algorithms described in earlier publications [39,47]. Fan distortion, arising from the scanning architecture, was corrected by using a series of 3-D volumes of a calibrated grid at different axial positions within the axial range of the sOCT [37,44]. Optical distortion, arising from refraction at the interocular surfaces, was corrected using ray tracing routines [36]. The full shape of the lens was estimated from the information visible through the pupil using a parametric model that had been trained using human ex-vivo lenses [38,39,41].

In the quantification process, biometric parameters were estimated from the 3-D reconstructed models: Anterior chamber depth (ACD), lens thickness (LT), radius of curvature of anterior (RAL) and posterior lens (RPL), lens equatorial diameter (DIA), lens surface area (LSA), equatorial plane position (EPP), and lens volume (VOL) were calculated from the model. Definition and detail on the calculations for LSA, DIA, VOL and EPP can be found in earlier literature [38]. The lens surfaces were fitted to the best sphere in a 6 mm diameter after 6th order Zernike polynomial approximation.

2.5. Crystalline lens power estimation

The crystalline lens paraxial power (P_L) was estimated using the lensmaker equation from the measured radii of curvature of the anterior and posterior lens (RAL and RPL), lens thickness, and indices of refraction

$$P_L=(n_L-n)\left(\frac{1}{RAL}-\frac{1}{RPL}\right)+\frac{{(n_L-n)}^2\times LT}{RAL\times RPL\times n_L}$$ (1)

where ${\text{n}}_{\text{L}}$ is the lens equivalent refractive index, taken as a constant (${\text{n}}_{\text{L}}$=1.422) within our age range [48]; and $\text{n}$ is the aqueous and vitreous humor refractive indices ($\text{n}$ = 1.336) taken from previous literature [49,50]. The eye equivalent power was estimated from the radius of curvature of the anterior surface of the cornea (RAC), axial length (AL), anterior chamber depth (ACD) and crystalline lens paraxial power (P_L) [50].

2.6. Data analysis

All lens parameters and ACD were obtained as the mean of five different measurements. We analyzed linear relationships of the parameters and of several ratios between parameters with RE and with AL. We included in this paper the ratios AL/RAC, LT/AL and RAC/RPL because they were significantly correlated with RE or AL and they had a direct interpretation. AL/RAC indicates a compensating association between both AL and RAC during the emmetropization process. LT/AL represents the proportion of length occupied by the lens over the entire AL of the eye and reveals potential compensatory effect of the crystalline lens. RAC/RPL represents a shape factor between cornea and lens.

Although there was no correlation between age and RE in the sample (r = 0.138, p = 0.55), partial correlations (r) were obtained in order to measure the degree of association between parameters and RE and AL while controlling for age. The p-value for testing the hypothesis of no correlation was also obtained. Statistical significance was defined as a p-value lower than 0.05. SPSS 25.0 for Windows (IBM SPSS, Chicago, Illinois, USA) was used for statistical analysis.

3. Results

3.1. Crystalline lens images and refractive error

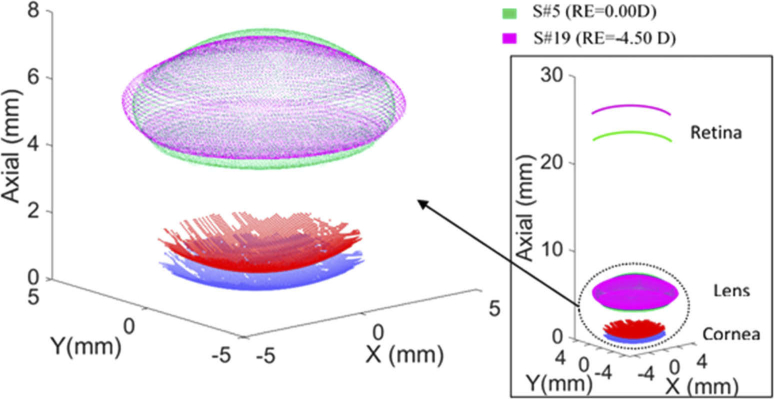
Figure 1 shows the changes on the lens shape with RE, exemplified by subjects S#5 (RE = 0.00D of sphere) and S#19 (RE=-4.50D of sphere). For simplification purposes, only the corneal surfaces of subject #5 are presented in blue (anterior) and in red (posterior).

Fig. 1.

Differences in the 3D eye biometry between an emmetropic eye (S#5, 23 y/o) and a myopic eye (S#19, 24 y/o). The right graph includes axial length; the left graph a blown up version of the anterior segment. The blue and red surfaces represent the anterior and posterior surfaces of the cornea of S#5. The green and magenta surfaces represent the crystalline lens of both subjects. Myopic eye shows thinner and flatter lens with deeper anterior chamber depth compared to emmetropic eye. Registration of both models is performed with respect to the anterior corneal apex.

3.2. Ocular biometry and refractive error

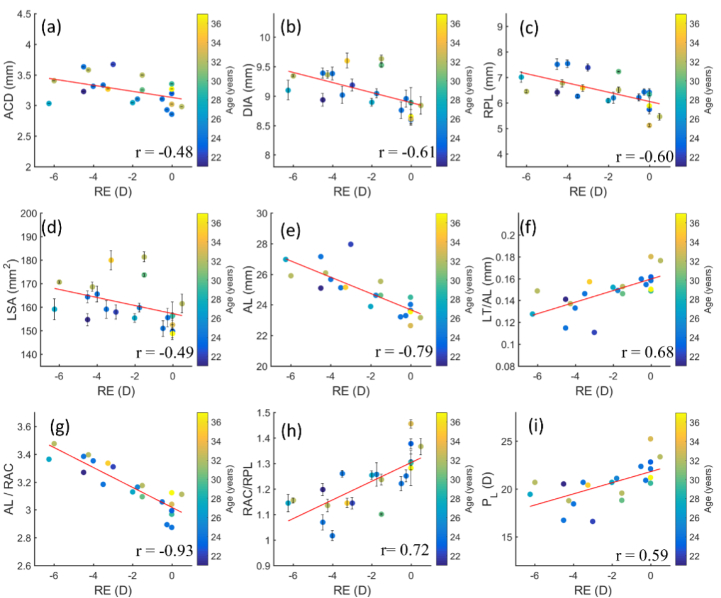
We investigated linear relationships between ocular biometry and RE. Figure 2 shows the scatter plots and corresponding regression lines for the parameters whose partial correlation (i.e., age-adjusted correlation) with RE was statistically significant, namely: ACD, DIA, RPL, LSA, AL, LT/AL, AL/RAC, RAC/RPL and P_L. Age is color-mapped as indicated by the color bar. Error bars on each point represent the standard deviation across the 5 different measurements. The partial correlation coefficient (r) is superimposed in the figures. The slope of the regression line (m), r, and the p-value of the correlations are summarized in Table 1.

Fig. 2.

Biometric parameters as a function of refractive error. (a) anterior chamber depth (b) lens equatorial diameter, (c) posterior lens radius of curvature, (d) lens surface area, (e) axial length, (f) ratio of lens thickness to axial length, (g) ratio of axial length to corneal radius of curvature, (h) ratio of radius of curvature of cornea to posterior lens, (i) lens power. Color bar/coding represents the age. Solid red lines are regression fits to the data (correlation coefficient is shown in the lower right corner; p-values and slopes for all parameters are shown in Table 1).

Table 1. Partial correlation coefficient (r), p-value and the slope of the regression line (m) for the linear regression of the biometric parameters with the refractive error. Asterisks indicate statistically significant correlations.

Biometric Parameters	Partial correlation coefficient (r)	p-value	Slope (m)
LT	0.44	0.054	0.054 mm/D
ACD	−0.48	0.034*	−0.05 mm/D
DIA	−0.61	0.005*	−0.09 mm/D
EPP	0.2	0.4	0.013 mm/D
RAL	−0.4	0.09	−0.34 mm/D
RPL	−0.60	0.005*	−0.182 mm/D
RAC	0.16	0.51	0.01 mm/D
LSA	−0.49	0.028*	−1.71 mm2/D
VOL	−0.2	0.41	−0.51 mm3/D
AL	−0.79	3.3 E-05*	−0.53 mm/D
LT/AL	0.68	0.001*	0.054 D−1
AL/RAC	−0.93	5.6 8E-09*	−0.072 D−1
RAC/RPL	0.72	3 E-04*	0.037 D−1
PL	0.59	0.006*	0.58

As expected from previous studies, AL was significantly correlated with the RE. ACD, DIA, RPL and LSA also increased significantly with increased (more negative) RE. We did not observe a statistically significant change in LT, EPP, RAL, VOL or RAC with RE. However, LT/AL, AL/RAC and RAC/RPL ratios were highly correlated with RE. P_L decreased significantly from emmetropia to myopia.

3.3. Ocular biometry and axial length

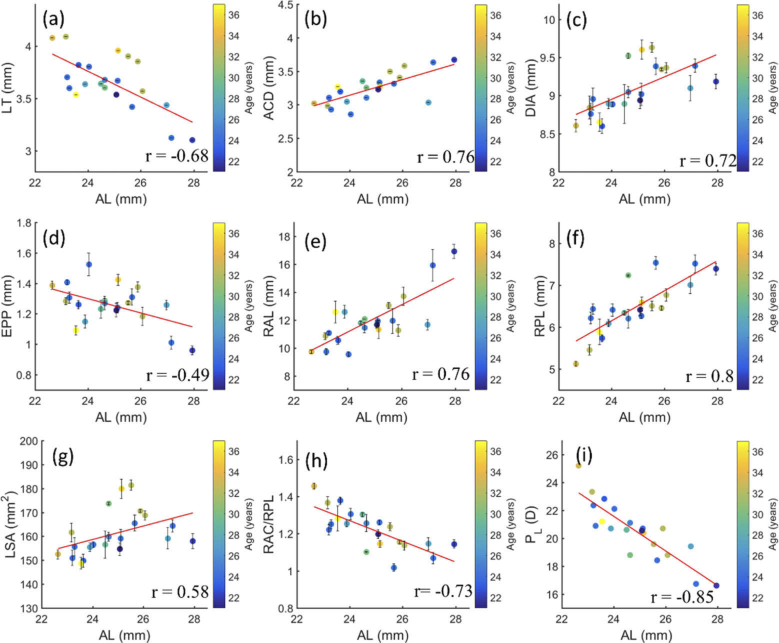
Figure 3 shows the scatter plots and corresponding linear regression lines for the parameters whose partial correlation (age-adjusted correlation) with AL was statistically significant, namely: LT, ACD, DIA, EPP, RAL, RPL, LSA, RAC/RPL and P_L. The slope of the regression line (m), the partial correlation coefficient (r), and the p-value of the regressions are summarized in Table 2. ACD, DIA, RAL, RPL and LSA increased significantly with AL, while LT, EPP, RAC/RPL ratio and P_L decreased significantly with AL. VOL and RAC did not show significant changes with AL.

Fig. 3.

Biometric parameters as a function of axial length. (a) lens thickness, (b) anterior chamber depth, (c) lens equatorial diameter, (d) equatorial plane position, (e) anterior lens radius of curvature, (f) posterior lens radius of curvature, (g) lens surface area, (h) ratio of radius of curvature of cornea to posterior lens, (i) lens power. Color bar/coding represents the age. Solid red lines are regression fits to the data (correlation coefficient is shown in the lower right corner; p-value and slopes of all parameters are shown in Table 2).

Table 2. Partial correlation coefficient (r), p-value and the slope of the regression line (m) of the biometric parameters with axial length. Asterisks indicate statistically significant correlations.

Biometric Parameters	Partial correlation coefficient (r)	p-value	Slope (m)
LT	−0.68	1 E-03*	−0.12
ACD	0.76	1.1 E-04*	0.12
DIA	0.72	3.7 E-04*	0.15
EPP	−0.49	0.03*	−0.05
RAL	0.76	8.7 E-05*	0.97
RPL	0.8	2.3 E-05*	0.36
RAC	0.35	0.13	0.09
LSA	0.58	0.008*	2.82 mm
VOL	0.14	0.56	−0.06 mm2
LT/AL	0.91	3.91 E-8*	−0.12 mm−1
RAC/RPL	−0.73	2.4 E-04*	−0.06 mm−1
PL	−0.85	2 E-06*	−1.24 D/mm
Eye Power	−0.7	0.001*	−1.21 D/mm

4. Discussion

This study provides estimates of the relationship between biometric parameters (including crystalline lens full shape geometry) with refractive error in a young cohort of myopes. To our knowledge, these geometrical parameters have been obtained, for the first time, from 3-D OCT images.

4.1. Corneal and crystalline lens power in myopia development

Prior literature shows conflicting data regarding corneal shape in myopic and hyperopic eyes. Scott et al found steeper corneas in myopic eyes [15], while Mainstone et al. [14] did not find association between RAC and RE. Some of the differences in corneal shape across refractive groups appear to occur in other corneal parameters, such as asphericity. For example Llorente et al. [51] showed more positive asphericity in hyperopes than in myopes, leading to a higher spherical aberration, but no differences in corneal power across groups. In the current study, we did not find statistically significant correlations of RAC with either AL or RE. Similarly to Grosvenor et al. [16], we have observed that AL/RAC shows a higher association to myopia than the AL and RAC individually, suggesting the importance of the correct coupling between AL and RAC in proper emmetropization.

In a comparative study of the ocular dimensions in age-matched myopes and emmetropes, Garner et al. [4] did not find differences in corneal radius of curvature between the two groups, but there was a significant difference in crystalline lens power of 2.30 D, suggesting that a greater compensation for axial elongation of the eye was achieved by the decrease in crystalline lens power than by corneal flattening. Our study, where lens power is directly estimated from measurements of the lens shape, supports the conclusion that lens power is strongly correlated with both RE and AL. In fact, the rate of power decrease with AL is similar for the lens to the rate for the whole eye (−1.24 D/mm and −1.21 D/mm respectively, see Table 2), confirming a primary role of the lens in the myopic eye’s refraction.

4.2. Anterior segment axial distances and myopia

Our data reveal deeper anterior chamber depth and thinner lenses in longer (and more myopic) eyes. This thinning is also evident by the decreased value of LT/AL in myopes, as the relative length occupied by the crystalline lens to the length of the eye in myopes is smaller compared to emmetropes. These findings agree with results from McBrien et al. [52] in late onset myopes, who showed deeper anterior chamber depths and thinner lenses than emmetropes. A deeper ACD has been found in children who eventually became myopic, as well as steeper slope in the growth curve of ACD with age than in persistent emmetropes [53]. The combined data and the fact that the ratio ACD/AL is constant suggest that increased ACD in myopes is a result of geometrical scaling during axial elongation. However, the consistent lens thinning found in previous [52–54] and the current study indicates an independent behavior of the lens to an axial scaling model.

4.3. Relationships between crystalline lens parameters

Several reports have documented the change in the crystalline lens morphology (and gradient refractive index [55,56]) with age in vivo and ex vivo, particularly addressing the changes occurring in presbyopia [55,57–59]. Some studies in donor eyes also include crystalline lenses from an early age, which provides insights into the lens growth during emmetropization. Martinez-Enriquez et al. [40] have shown that from birth to adolescence, the crystalline lens experiences a sharp increase in radii of curvature, in lens equatorial diameter, and in lens surface area, and a decrease in lens thickness, while volume increases at a constant rate with age. Although, it is expected that a large fraction of these changes occur by the reduction of the accommodation amplitude with age, it appears clear that the lens undergoes dramatic remodeling during emmetropization and eventually myopia development. Our data set only comprises adult eyes, and being a cross-sectional data with RE, we can only speculate on the longitudinal changes undergone by these eyes with myopia development. The age range in our study was sufficiently narrow to (statistically tested) not represent a confounding factor to the correlations with RE or AL. In any case, we used partial correlations (age-adjusted correlation) for avoiding the effects of age.

We found an increase in RAL with AL (in agreement with previous literature [60]) as well as an increase in RPL with increasing myopia and AL. From paraxial power calculations it was concluded that RPL had a primary contribution in the total lens power. A ± 20% change in the RPL changed lens power by −2.18 D to 3.27 D while a similar change in RAL changed the lens power by −1.16 D to 1.73 D., suggesting that RPL may be a key factor in the decrease of lens power with myopia.

The increase in DIA with axial elongation is consistent with equatorial stretching. Stretching is also indicated by the increase in lens surface area as the eye elongates. Interestingly, the VOL was not significantly different across RE or AL, suggesting that lens thinning and flattening, equatorial expansion, and capsular stretching occur through a remodeling of the lens without any significant expansion of lens contents.

4.4. An active or a passive crystalline lens growth?

Our study on the quantification of the full shape of the crystalline lens in myopia sheds light into the question whether the lens undergoes a geometric scaling as a result of axial elongation (overall eye growth-passive), or, alternatively, if the lens actively attempts to emmetropize, reshaping and decreasing its refractive power to compensate for axial elongation [61,62]. Note that, in the context of this paper, both passive and active changes may occur in parallel to axial elongation. For example, although there should be more physical constraints in equatorial elongation of the eye ball produced by the bony orbital walls, than in other dimensions [63], we found that in fact the lens expands equatorially, but gets thinner in myopia. It is not clear whether this increase in diameter is related with the global expansion of the entire eye globe or related to the changes occurring in the ciliary muscle. However, the lens does not appear to gain volume with myopia as it may happen if growth factors would be released during axial elongation which would make the lens grow larger. Indeed, the lens reshapes, in a way similarly occurring with disaccommodation, i.e., lens flattening, thinning and a stretched capsule. This change in lens dimensions results in a change of lens power, while corneal power remains almost constant with eye growth. The effective decrease in lens power while the eye elongates appears to be an indication of the lens trying to actively control the eye’s RE, in an attempt to emmetropize.

5. Conclusion

The changes in ocular biometry during myopia development is not just elongation in axial direction, there are indeed significant changes happening in the anterior segment especially in the lens biometry. It is clear that the combined effect of geometrical changes is reflected in the total dioptric power of the lens, where lower power lenses are observed in subjects with higher refractive error.

Funding

European Research Council10.13039/501100000781 (ERC-2011-AdG- 294099, H-2020-MSCA-COFUND-2015 Ref. 713694, H-2020-MSCA-ITN-2015-ETN-MyFUN No: 675137); Ministerio de Ciencia, Innovación y Universidades10.13039/100014440 (FIS 2017-84753 R MYOPT).

Disclosures

Spanish patent: Procedure to calibrate and correct the scan distortion of an Optical Coherence Tomography system, P201130685 (Sergio Ortiz, Susana Marcos, Damian Siedlecki and Carlos Dorronsoro).

USA patent application: Method of estimating a full shape of the crystalline lens from measurements taken by optic imaging techniques and method of estimating an intraocular lens position in a cataract surgery, US201662329392P (Eduardo Martínez-Enríquez, Susana Marcos, and Carlos Dorronsoro).