Automated plaque characterization using deep learning on coronary intravascular optical coherence tomographic images

Abstract

Accurate identification of coronary plaque is very important for cardiologists when treating patients with advanced atherosclerosis. We developed fully-automated semantic segmentation of plaque in intravascular OCT images. We trained/tested a deep learning model on a folded, large, manually annotated clinical dataset. The sensitivities/specificities were 87.4%/89.5% and 85.1%/94.2% for pixel-wise classification of lipidous and calcified plaque, respectively. Automated clinical lesion metrics, potentially useful for treatment planning and research, compared favorably (<4%) with those derived from ground-truth labels. When we converted the results to A-line classification, they were significantly better (p < 0.05) than those obtained previously by using deep learning classifications of A-lines.

1. Introduction

Coronary heart disease is a known leading cause of morbidity and mortality for both sexes in developed countries [1], so imaging is needed to plan and assess treatments. Atherosclerosis leads to different kinds of lesions (e.g., fibrotic tissues, lipid-filled necrotic pools, calcifications) [2]. Non-invasive X-ray, computed tomography, or magnetic resonance imaging with contrast agents of the coronary arteries mostly shows the lumen, which allows only limited identification of arterial wall tissues. Principal methods for intracoronary imaging are intravascular ultrasound (IVUS) and intravascular optical coherence tomography (IVOCT). Although IVUS can provide significant insights into plaque composition, it has two significant limitations. First, the technique has a limited axial resolution of 150–250 μm and a lateral resolution of 150–300 μm, which is unable to detect thin fibrous caps (≈ 65 μm). Second, the technique also hinders determination of the depth of calcification because of acoustic shadowing. Compared with IVUS, IVOCT has higher image axial (12–18 μm) and lateral (20–90 μm) resolution [3] depending on the light source specifications. IVOCT has shown high accuracy and reproducibility in identifying thin cap fibroatheroma and different plaque components, such as calcium and lipid. Therefore, significantly improved clinical capabilities have led to increasing application of IVOCT for percutaneous coronary intervention, which is the most widely performed surgical treatment for coronary heart diseases [3].

Major calcifications are of great concern when performing stent intervention as they can restrict stent expansion. Lipidous lesions also may hinder stent deployment because the edge of a stent must not land in a lipidous region to avoid causing a probable arterial dissection or rupture. One of the challenges of real-time treatment planning is that each IVOCT pullback includes >500 image frames, which is an image data overload. Manual analysis of every frame is labor intensive, time consuming, and suffers from high inter- and intra-observer variability. Previously, our group reported ≤5% intra- and 6% interobserver variability among skilled cardiologists for detecting stent struts in IVOCT images [4]. This finding indicates the need for a quick and fully automated plaque characterization method.

To overcome such limitations, previous studies have developed promising semi-automatic and fully automatic plaque characterization approaches. An automatic classification method based on the optical attenuation coefficient of the tissues was introduced to characterize plaque constituents [5–8]. Athanasiou et al. [9] extracted a set of traditional texture- and intensity-based features in gray-scale IVOCT images and classified the atherosclerotic plaques by using a random forest classifier. Ughi et al. [7] developed an automated characterization method for atherosclerotic tissues based on well-known attenuation coefficient (μ_t), geometrical, and textural features. This method also classified each voxel by using a random forest classifier, and the overall accuracy was 81.5%. Shalev et al. [10] proposed a technique using microscopic cryo-imaging to classify fibrocalcific tissue as a method to validate their ground-truth labels. They implemented one-class support vector machine. Methods using linear discriminant analysis and decision trees also have been developed to classify plaque components [11,12]. Prabhu et al. [13] developed machine learning method to characterize fibrolipidic and fibrocalcific A-lines in IVOCT images using a comprehensive set of hand-crafted features. They found that the morphological and 3-D features were very useful for plaque classification and obtained an overall accuracy of 81.6% on a held-out test set. Recently, some researchers have attempted to implement deep learning techniques, such as a convolutional neural network (CNN) for tissue characterization. Abdolmanafi et al. [14,15] used a pre-trained AlexNet model [16] as a feature generator by removing the output layer and fine-tuned each step by modifying the learning rate. Then, arterial borders and plaques were successfully segmented by using random forest and support vector machine classifiers. He et al. [17] proposed a CNN-based method to automatically characterize plaques in IVOCT images. The algorithm was validated with a total of 269 images acquired from 22 patients, and the overall accuracy for five tissue types was 86.6%. To classify each A-line from raw IVOCT images in the polar (r,θ) domain, Kolluru et al. [18] implemented a simple CNN model comprising two convolutional and max-pooling layers. After classification, they applied a fully-connected conditional random field (CRF) as a post-processing step, improving classification sensitivity by 10%–15%. Similarly, Yong et al. [19] proposed a linear-regression CNN to automatically segment the lumen in IVOCT images. Abdolmanafi et al. [20] distinguished between normal and diseased arterial wall structure, and identified multiple lesions (e.g., calcification, fibrosis, macrophage, and neovascularization) using VGG-based fully convolutional network. The previous approaches have three main limitations. First, the size of the image data sets is relatively small, and classifier performance and generalizability can deteriorate with small sample sizes. Second, previous studies attempted to segment one or two tissues, such as fibrous, lipid, or calcium. However, to select an appropriate interventional strategy, it is necessary to simultaneously identify both lipidic and calcific tissues. Third, existing studies used textural or optical feature-based traditional machine learning methods or simplified CNN models. Studies did not perform a semantic segmentation using deep learning in IVOCT images.

The main contribution of this study is that we implement and compare the fully-automated deep learning models (SegNet and Deeplab v3+) for plaque characterization in terms of both the pixel-wise and A-line-based classifications. In previously reported studies, these deep learning methods have provided the outstanding results in terms of segmentation in various medical images [21–27]. There are multiple sub-contributions. First, we determined a rational approach for training/testing of pixels when the back border of a lipidous plaque is not evident due to absorption of light, giving indeterminate pixels in an image. Second, in addition to standard performance metrics (e.g., Dice), we computed clinically relevant measures (e.g., arc angle and depth) from automated outputs and compared them to those from analyst’s labels. Third, we performed a visual clinical score assessment to determine potential impact of the proposed method on clinical decision making. Fourth, we created a method for reporting A-line based classifications (e.g., fibro-lipidic and fibro-calcific A-lines) and compared against previous A-line based classifiers.

In this study, we present a new plaque characterization method for automated identification of lipidous and calcified plaques from grayscale IVOCT images. We present pixel-wise and A-line-based classification results based on a SegNet deep learning network [28] and compared them with those based on a Deeplab v3+ network [29]. Instead of using standard images in the Cartesian domain, raw images in the polar (r,θ) domain are used to prevent potential distortion due to interpolation. Since plaques are widely distributed in the arterial wall, a fully connected CRF is implemented for post-processing to compensate segmentation errors over larger regions.

2. Image analysis methods

The processing pipeline consisted of pre-processing, CNN for semantic segmentation using SegNet, and noise reduction using CRF. Segmentation results were assessed by using ten-fold cross validation.

2.1. Pre-processing

A modified and optimized version of pre-processing described previously by our group [18] was applied to IVOCT image data in the polar (r,θ) domain to simplify further calculations. Pre-processing extracted the appropriate region of interest (ROI) and reduced noise in each image. First, the lumen boundary was detected by using dynamic programming, as proposed by our group [30]. Briefly, the method computed the gradient in the (r,θ) image and identified the lumen boundary as the contour with the highest cumulative edge strength across θ. Second, the guidewire and corresponding shadow regions were automatically removed [31] because these regions are indeterminate. Third, each A-line of the resulting images was pixel shifted to the left so that all rows had the same starting point along the radial direction. This step not only aligned the tissues more properly (see Discussion), it also enabled creation of a smaller rectangular ROI, which simplified processing. Fourth, we used only the first 200 pixels (∼1 mm) in r since IVOCT has limited penetration depth. Consequently, the input image size (968 × 496 pixels) was reduced to 200 × 496 pixels for processing. Fifth, image data were log transformed to change multiplicative speckle into an additive form. Sixth, a non-local mean filter [32] was employed to reduce the speckle artifact with search and comparison windows of 21 and five pixels, respectively. The degree of smoothing was set to the estimated standard deviation of noise estimated from the image.

2.2. SegNet convolutional neural network architecture

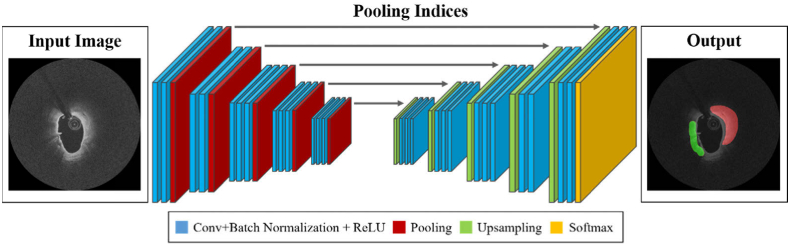
We used a SegNet convolutional neural network classifier, as reported by Badrinarayanan et al. [28], composed of five encoding and five corresponding decoding steps, followed by a final pixel-wise classification layer (Fig. 1). The encoder had 13 convolutional layers comprising a “3 × 3-convolution-batch normalization-rectified linear unit” structure [28], which corresponds to the VGG 16 network [33]. Therefore, we were able to initialize the weights of each layer by transferring the weights pre-trained on large datasets [34]. For downsampling, a 2 × 2-max-pooling operation with a stride of two was added between each encoding step, and the output was sub-sampled by a factor of two. We used maximum pooling to prevent translation variance over small spatial shifts in the input image. On the other hand, a 2 × 2-max-unpooling followed by a convolution was applied after each decoding step for upsampling. Each decoder upsampled the input feature map based on the stored max-pooling indices from the corresponding encoder feature map inducing a sparse feature map. At the final layer, a 1 × 1 convolution with the softmax activation function was used to produce class probabilities for each pixel independently. Consequently, the SegNet classifier included 91 layers, including 26 convolutional layers, five max-pooling, and five max-unpooling layers. The receptive field is one of the crucial factors for determining the classification performance of the SegNet classifier because the field of view relies on the input image. The field can be defined as the input image space region that affects a particular unit of the classifier. In this study, the SegNet architecture had a receptive field of 211 pixels and one pixel was padded for each convolution step. Since the IVOCT images are continuous in each pullback, misclassification (edge effect) might occur if the padding values are set to 0 or the nearest pixel value. To solve this problem, we used different padding values for the top, bottom, left, and right positions based on the continuous image information. The left and right padding values were set to 0 since these regions belonged to the lumen and background, respectively, and provided no meaningful tissue information. On the other hand, the top and bottom paddings were set to the previous frame’s last row and the next frame’s first row, respectively. For the first frame, the current image’s last row was used as the top padding, and the first row was used as the bottom padding for the last frame. Training and implementation details of the classifier are provided in Section 3.2.

Fig. 1.

SegNet architecture. The SegNet classifier comprises five encoding and five decoding steps. Each encoder includes 3 × 3 convolution, batch normalization, and rectified linear unit (ReLU) structures, followed by max-pooling, whereas max-unpooling is applied followed by convolution in the decoding step. The left and right figures indicate the original IVOCT image and predicted label, respectively. The input and output images sizes are exactly the same. Actual processing is done in the (r, θ) view, but the (x, y) view is shown here.

2.3. Post-processing using the fully connected conditional random field (CRF)

To reduce classification errors, we used a fully-connected CRF method [35] that establishes pairwise potentials on all pairs of pixels for each pixel classification (x,y) of the SegNet classifier. CRF assigns a new label, which has more spatial characteristics similar to surrounding pixels, on the basis of the neural network-generated probability estimates.

For random variables over data and corresponding label sequences, a CRF model is characterized by a Gibbs distribution, and the corresponding energy of labeling is given by:

$$E(L)={\sum }_i{\delta }_i(L_i)+{\sum }_{i<j}{\delta }_i(L_i,L_j)$$ (1)

where L is an assigned label for all pixels, δ_i(L_i) is the unary potential computed by a classifier over the assigned labels, and δ_i(L_i,L_j) is the pairwise potential connecting all pixel pairs in the image. The pairwise potential can be described as follows:

$${\delta }_i(L_i,L_j)=\gamma (L_i,L_j){\sum }_{b=1}^B{W}^{(b)}{G}^{(b)}(V_i,V_j)$$ (2)

where γ and W indicate a label compatibility function and linear combination weight, respectively. G is a Gaussian kernel, and V is the feature vector for each pixel. Here, the contrast-sensitive two kernel potentials representing appearance and smoothness kernels were used for multi-class classification that can be described by color vectors (C_i,C_j) and positions (P_i,P_j).

$$G(V_i,V_j)=\left[W_1{e}^{\left(-\frac{{|P_i-P_j|}^2}{2{\sigma }_{\alpha }^2}-\frac{{|C_i-C_j|}^2}{2{\sigma }_{\beta }^2}\right)}\right]+\left[W_2{e}^{\left(-\frac{{|P_i-P_j|}^2}{2{\sigma }_{\rho }^2}\right)}\right]$$ (3)

The appearance kernel performs optimization based on the assumption that the adjacent pixels containing similar intensity characteristics have a higher probability to be included in the same class. For example, if most pixels in a neighborhood look similar in the image, they are likely to be in the same class. Parameters σ_α and σ_β control the degrees of nearness and similarity. On the other hand, the smoothness kernel effectively reduces the small isolated regions [36]. More specifically, this term considers the small regions that are isolated from main tissue regions as the classification errors.

The optimization algorithm of CRF used in this study is based on a mean field approximation to the CRF distribution. A mean field approximation calculates Q(X) minimizing the Kullback–Leibler divergence between P and Q rather than computing the distribution P(X). It is also possible to perform highly efficient approximation by using Gaussian filtering during each message passing.

3. Experimental methods

3.1. Data acquisition

The IVOCT dataset used in this study consisted of 57 pullbacks from 55 patients with 89 volumes of interest (VOIs) having calcification (32 VOIs), lipidous regions (36 VOIs) or both (12 VOIs), and 9 VOIs consisting of regions without calcification or lipidous regions. IVOCT imaging was performed by using a frequency-domain ILUMIEN IVOCT system (St. Jude Medical Inc., St. Paul, Minnesota, USA). The IVOCT system includes a tunable laser light source sweeping from 1,250 to 1,360 nm at a frame rate of 180 fps with a pullback speed of 36 mm/s and an axial resolution of approximately 20 μm. A total of 4,892 frames were used for further image analysis in this work. The raw data comprised 968 × 496 pixels in 16-bit gray scale.

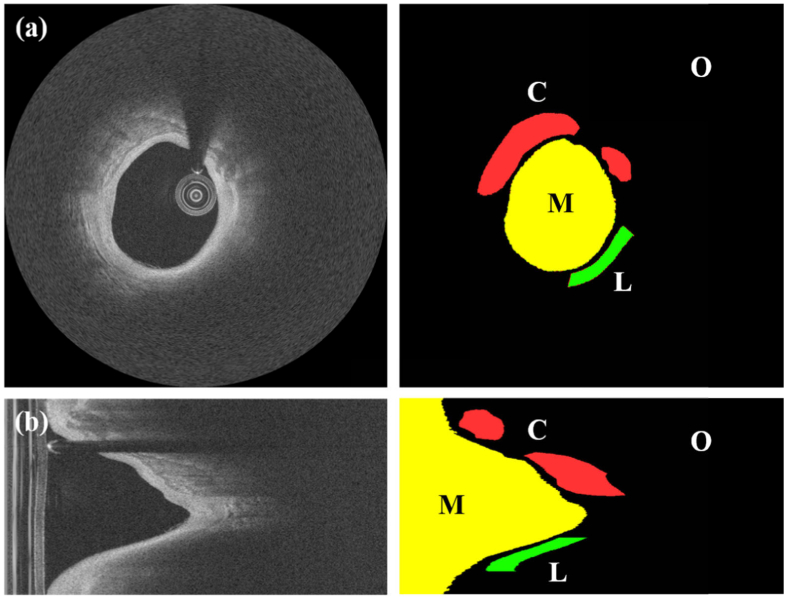
Raw (r,θ) images were converted to the standard (x,y) Cartesian domain for pixel-wise ground-truth annotations. Annotations were manually performed by consensus of two expert readers from the Cardiovascular Imaging Core Laboratory, Harrington Heart and Vascular Institute, University Hospitals Cleveland Medical Center, Cleveland, OH, USA. According to the definitions described previously [37], the lipidous and calcified regions were annotated for all IVOCT images, and the resulting masks were transformed back to the polar domain. In addition to these two categories, an additional class “other” was used to include residual pixels that did not meet the criteria of the above classes. Typically, it is impossible to measure the thickness of lipidous tissue in IVOCT images because of the quick drop-off in IVOCT signal. To address this limitation, we fixed the lipidous region depth to a consistent thickness of 350 μm (Fig. 2). The pixels beyond this criterion were not considered during the plaque characterization. Consequently, a total of over 800 million pixels were labeled and each divided into one of three classes. Lipidous and calcified classes comprised nearly 30 and 50 million pixels, respectively, with the remaining pixels belonging to the other class. Figure 2 shows example annotations for each class in both (x,y) and (r,θ) views.

Fig. 2.

Example annotations for IVOCT images in (x, y) (a) and (r, θ) (b) views. The left and right columns show IVOCT images and expert annotations, respectively, with labels (M: lumen, L: lipid, C: calcium, and O: other). Because lipids are highly absorbing, we do not know their actual depth and assigned this class a consistent thickness of 350 μm. Here and in other figures, IVOCT images are shown following log transformation for improved visualization.

After acquiring pixel-wise ground-truth annotations, we also created additional ground-truth labels for A-lines. Since the size of IVOCT images was 968 × 496 in (r,θ), each IVOCT image included 496 A-lines. The appropriate A-line label was determined by counting the number of pixels in A-line in each class and then creating fibrolipidic, fibrocalcific, or other A-line classes as reported previously [18]. If an A-line contained ≥3 pixels of either lipidous or calcified tissues, it was not “other”. A-line classification was then assigned based upon which of lipidous or calcified classes was in the majority.

3.2. Network training and testing

The learning parameters of each layer in the encoder were initialized by transferring weights from a VGG 16 [33] network, pre-trained on the ImageNet dataset [34]. Network weights were fine-tuned one layer at a time starting from the last layer using backpropagation. Network was sequentially fine-tuned by changing the learning rates of the next layers until performance on validation set stopped improving. We used adaptive moment estimation (ADAM) optimization [38] for network training. The ADAM optimization method is straightforward to implement and requires little memory. Moreover, this method can provide reliable segmentation results for medical images because of the robust performance in a wide range of non-convex optimization problems. We empirically set the initial learning rate of the ADAM optimizer to 0.001 and gradually reduced the learning rate. The drop factor and drop period were set to 0.2 and 5, respectively. We multiplied the initial learning rate by a drop factor every drop period. The maximum number of epochs was 50. The class weights were computed as the inversed median frequency of class proportions because the training data set were unbalanced. For each encoder and decoder subnetwork, convolutional layer weights were initialized using the MSRA method [39]. The energy function for network was computed by using a cross entropy loss function over the softmax outputs. The softmax function is a generalization of the logistic function that squashes a vector v of arbitrary real values to a vector φ(v) of real values that sum to unity. The standard softmax function is given by applying an exponential function to each coordinate divided by the sum of all the coordinates as follows:

$$\phi {(v)}_j=\frac{e^{v_j}}{{\sum }_{k=1}^K{e}^{v_k}}\text{for}j=1,\dots ,K$$ (4)

where K is the number of classes, e^v denotes the activation in feature channel k, and φ(v) is the approximated maximum function. The cross entropy was subsequently used as a loss function to quantify the segmentation performance with a probability input value between 0 and 1 [40].

Typically, deep learning networks are prone to overfitting, especially when the network is trained with a large number of iterations (epochs). To avoid overfitting, we validated the network and stopped the training when the validation loss did not improve over 5 successive epochs or when a maximum number of epochs was reached. All processing was done using MATLAB (R2018b, MathWorks Inc.) on a NVIDIA GeForce GTX 1080 Ti GPU (64 GB RAM) installed in a Dell Precision T7600.

3.3. Performance evaluation

The proposed method was evaluated by using ten-fold cross validation to prevent the potential influence caused by similar tissue characteristics within a VOI. All VOIs were divided into ten independent subgroups and assigned for training (80%), validation (10%), and testing (10%). Subgroups were based on VOIs rather than images because it is possible to have very similar images from a lesion in the training and test sets. This process was repeated ten times so that all pullbacks were utilized as either training, validation, or test sets. We ensured that each VOI was in only one group. To improve comparisons, the exact same ten-fold data sets were used to compare all processing methods. In addition, nine VOIs without any identified lipidous and calcified plaques were used as the held-out data for testing. These images were neither used for training nor testing during cross validation. We compared segmentation/classification results based on a SegNet deep learning network with those based on a Deeplab v3+ model [29].

Segmentations were evaluated in multiple ways. We first calculated the sensitivity, specificity, Dice, and Jaccard coefficient. Sensitivity quantifies the proportion of actual positives that are correctly classified as such. The Dice coefficient evaluates the spatial overlap between two regions [41] as follows:

$$\text{DC}(A,B)=\frac{2\cdot |A\cap B|}{|A|+|B|}$$ (5)

where DC(A,B) is the Dice coefficient between the predicted (A) and labeled (B) regions. The JC(A,B) measures the Jaccard coefficient between two segmented regions of A and B and is defined as the size of the overlapped region divided by the size of the union [42]:

$$\text{JC}(\text{A, B})=\frac{|A\cap B|}{|A\cup B|}=\frac{|A\cap B|}{|A|+|B|-|A\cap B|}$$ (6)

For both metrics, a higher value implies better segmentation performance in both the pixel-wise and A-line based approaches.

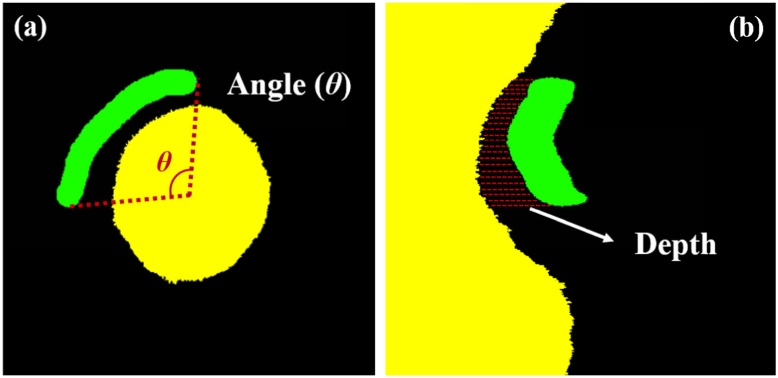
In addition to standard metrics, we used more clinically meaningful ones. We measured clinical lesion attributes (i.e., arc angle and depth) used previously in clinical research studies [43,44]. As shown in Fig. 3, the arc angle was measured from the center of lumen to the left- and right-most points. The depth was the mean distance from the lumen boundary to the tissue. The arc angle was measured in the (x,y) domain, and the depth was obtained in the (r,θ) domain. Manual and automated lesion attributes were compared. We also asked three cardiologists to compare manual and automated results with regard to clinical decision making; they compared en face segmentation and individual image results, and responded to the statement, “The automated result does not change my clinical decision making as compared to the manually derived counterpart.” Responses were scaled from 1–5 as strongly disagree, disagree, unsure, agree, and strongly agree, respectively.

Fig. 3.

Clinical plaque attributes include (a) angle and (b) depth. Panel (a) is in (x, y) whereas panel (b) is in (r, θ). Yellow, green, and black indicate lumen, lipidous plaque, and other, respectively. For better visualization, only the lipidous plaque is shown, and images were cropped from their original size.

4. Results

The pre-processing results are shown in Fig. 4. We previously determined the superiority of using polar (r,θ) IVOCT data. The lumen boundary (Fig. 4(a)) and indeterminate guidewire and its shadow regions (Fig. 4(b)) are accurately identified. Image data were pixel shifted (Fig. 4(c)) and filtered to reduce noise (Fig. 4(d)). Pixel shifting normalizes the lesion appearance across training data, and noise reduction reduced the effect of speckle noise.

Fig. 4.

Pre-processing results for a representative IVOCT image frame. Panels are: (a) original (r, θ) image showing lumen segmentation in red as obtained by dynamic programming, (b) removal of A-lines corresponding to the guidewire and its shadow, (c) pixel-shifted data, and (d) speckle noise reduction.

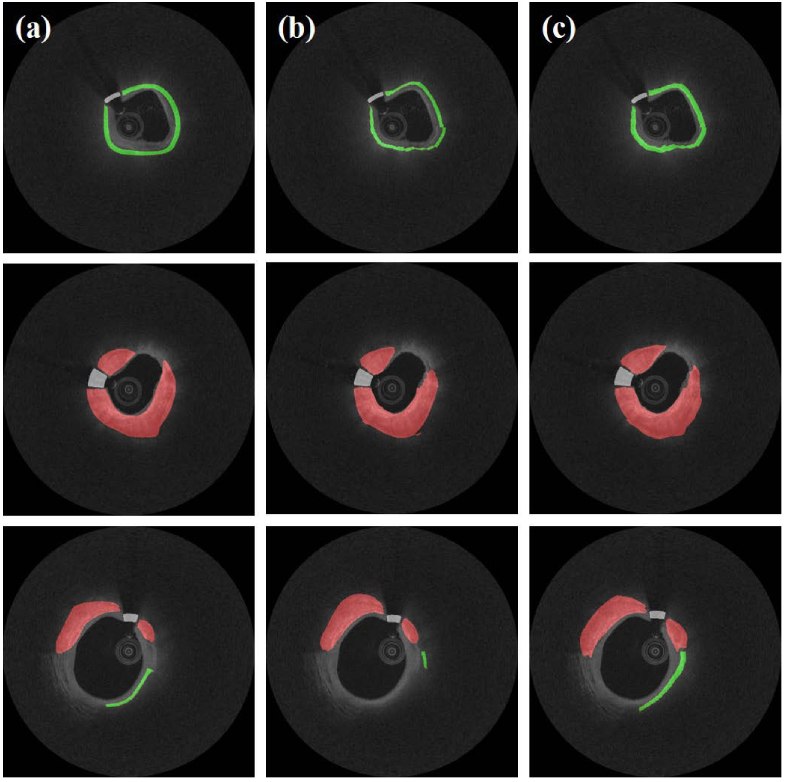
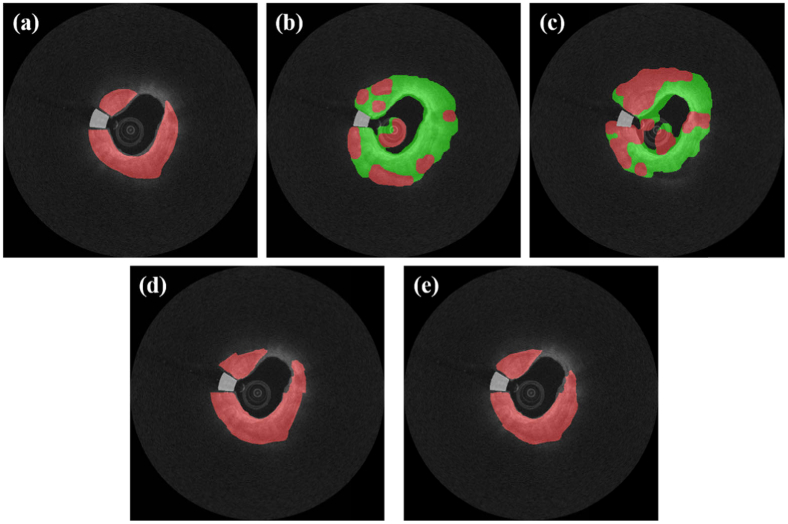
Using our baseline methods (i.e., SegNet), we obtained deep learning semantic segmentation results and compared them with those using Deeplab v3+ network (Fig. 5). Interestingly, in these images, the Deeplab v3+ method underestimated fibrolipidic and fibrocalcific plaques. Table 1 compares performance metrics for Deeplab v3+ and SegNet across folds. Although Dice/Jaccard coefficients were statistically similar, SegNet had improved sensitivities for fibrolipidic and fibrocalcific plaques, and differences were significant (p < 0.05). The CRF method visually improved results (e.g., small islands were removed), but results across folds were insignificantly different (Fig. 6 and Table 2). Both networks showed remarkable results (sensitivity > 99.0% and Dice coefficient > 0.995) on a held-out test set without any identified plaques (Table 3). This suggests that processing of an entire pullback should create minimal false-positive plaque identifications.

Fig. 5.

Comparison of classification results between Deeplab v3+ and SegNet mapped to (x,y) view for three images. Panels show: (a) ground truth, (b) results obtained using Deeplab v3+, and (c) results obtained using SegNet. Colors are green (lipid), red (calcium), and white (guidewire).

Table 1. Mean performance metrics over folds, including sensitivity, specificity, Dice, and Jaccard coefficients, between Deeplab v3+ and SegNet. With SegNet, the sensitivities of fibrolipidic and fibrocalcific plaques were significantly improved (*p < 0.05). For statistical analysis, the Wilcoxon signed-rank test was performed.

Classes		Sensitivity (%)	Specificity (%)	Dice	Jaccard
Deeplab v3+	Fibrolipidic	82.3 ± 10.3	92.1 ± 3.6	0.799 ± 0.048	0.693 ± 0.056
	Fibrocalcific	77.7 ± 9.9	97.4 ± 1.3	0.742 ± 0.058	0.621 ± 0.067
	Other	89.7 ± 4.3	82.8 ± 6.5	0.903 ± 0.023	0.832 ± 0.035
SegNet	Fibrolipidic	87.4 ± 7.2*	89.5 ± 4.6	0.801 ± 0.044	0.690 ± 0.058
	Fibrocalcific	85.1 ± 7.2*	94.2 ± 2.4	0.734 ± 0.085	0.594 ± 0.064
	Other	87.2 ± 3.2	81.5 ± 7.1	0.908 ± 0.031	0.837 ± 0.052

Fig. 6.

Classification results (SegNet) before and after CRF noise cleaning mapped to (x,y) view. Panels show: (a) ground truth, (b) results prior to CRF noise cleaning, and (c) results after CRF noise cleaning. Colors are green (lipid), red (calcium), and white (guidewire).

Table 2. Mean performance metrics (SegNet) over folds, including sensitivity, specificity, Dice, and Jaccard coefficients, before and after CRF noise cleaning. With CRF noise cleaning, the overall metrics were slightly increased but statistically insignificant (p > 0.05). For statistical analysis, the Wilcoxon signed-rank test was performed.

Classes		Sensitivity (%)	Specificity (%)	Dice	Jaccard
Lipidous	before CRF	88.7 ± 7.2	88.3 ± 5.0	0.794 ± 0.045	0.681 ± 0.058
	after CRF	87.4 ± 7.2	89.5 ± 4.6	0.801 ± 0.044	0.690 ± 0.058
Calcified	before CRF	85.8 ± 7.0	93.6 ± 2.8	0.726 ± 0.088	0.578 ± 0.066
	after CRF	85.1 ± 7.2	94.2 ± 2.4	0.734 ± 0.085	0.594 ± 0.064
Other	before CRF	86.7 ± 3.2	81.9 ± 6.9	0.905 ± 0.032	0.833 ± 0.053
	after CRF	87.2 ± 3.2	81.5 ± 7.1	0.908 ± 0.031	0.837 ± 0.052

Table 3. Mean performance metrics measured on a held-out test sample without any identified calcification or lipidous regions, including sensitivity, Dice, and Jaccard coefficients between Deeplab v3+ and SegNet. A held-out data set was composed of 600 IVOCT images from nine VOIs. Results shows that both methods are highly suitable for discriminating non-plaques. CRF noise cleaning did not significantly improve results (p > 0.05). For statistical analysis, the Wilcoxon signed-rank test was performed.

Method	Sensitivity (%)	Dice	Jaccard
Deeplab v3+	99.4	0.997	0.994
SegNet	99.0	0.995	0.990

To better understand their impact on performance, we compared results obtained using SegNet with and without pre-processing steps (pixel shifting and noise reduction). In general, pixel shifting had a large, significant effect on results (Fig. 7). In Table 4, although the sensitivity was relatively high (85.4%) without pre-processing, both the lipidous and calcified classes had very low Dice and Jaccard coefficients (<0.21). Noise reduction alone improved results across the board, but changes were statistically insignificant for each instance. Interestingly, noise reduction did not bring significant improvement on lipidous class but showed a substantial increase on calcified class. Compared with no pre-processing, combined noise reduction and pixel shifting gave significant improvements.

Fig. 7.

Effects of pre-processing steps on classification segmentation. Panels are: (a) ground truth, (b) no pre-processing, (c) noise reduction but no pixel shifting, (d) pixel shifting but no noise reduction, and (e) pixel shifting and noise reduction. Colors are green (lipid), red (calcium), and white (guidewire). In general, pixel shifting had a very significant effect on results.

Table 4. Metrics assessed over folds with and without pre-processing (pixel shifting and noise reduction). We found that pixel shifting helped significantly improve classification performance. Statistically significant differences (p < 0.05) compared with no pre-processing are indicated by an asterisk (*). The Wilcoxon signed-rank test was performed. To improve comparisons, all folds were exactly the same for all instances. All metrics were obtained after CRF noise cleaning.

Classes		Sensitivity (%)	Specificity (%)	Dice	Jaccard
Lipidous	no pre-processing	85.4 ± 6.9	91.5 ± 2.2	0.131 ± 0.113	0.080 ± 0.074
	noise reduction, but no pixel-shifting	86.5 ± 11.4	90.5 ± 5.0	0.119 ± 0.095	0.071 ± 0.061
	pixel-shifting, but no noise reduction	87.1 ± 6.1*	94.3 ± 1.3	0.798 ± 0.054*	0.685 ± 0.066*
	pixel shifting and noise reduction	87.4 ± 7.2*	89.5 ± 4.6	0.801 ± 0.044*	0.690 ± 0.058*
Calcified	no pre-processing	40.2 ± 18.1	92.4 ± 2.5	0.207 ± 0.084	0.124 ± 0.057
	noise reduction, but no pixel-shifting	43.2 ± 27.2	95.5 ± 1.9	0.243 ± 0.125	0.150 ± 0.093
	pixel-shifting, but no noise reduction	79.7 ± 8.7*	94.1 ± 0.8	0.682 ± 0.087*	0.552 ± 0.102*
	pixel shifting and noise reduction	85.1 ± 7.2*	94.2 ± 2.4	0.734 ± 0.085*	0.594 ± 0.064*
Other	no pre-processing	85.8 ± 2.7	87.7 ± 5.9	0.922 ± 0.016	0.856 ± 0.027
	noise reduction, but no pixel-shifting	87.5 ± 3.9	83.7 ± 8.4	0.931 ± 0.022	0.872 ± 0.039
	pixel-shifting, but no noise reduction	86.9 ± 1.3	79.3 ± 8.6	0.900 ± 0.012*	0.824 ± 0.020
	pixel shifting and noise reduction	87.2 ± 3.2	81.5 ± 7.1	0.908 ± 0.031*	0.837 ± 0.052

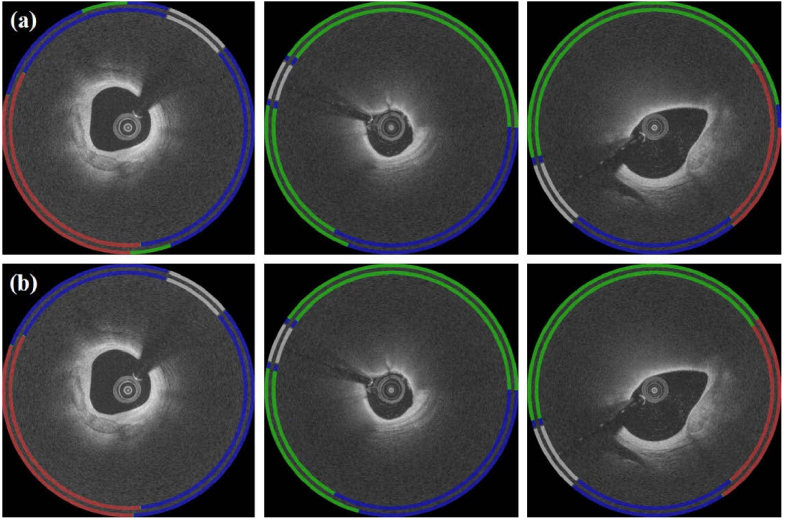
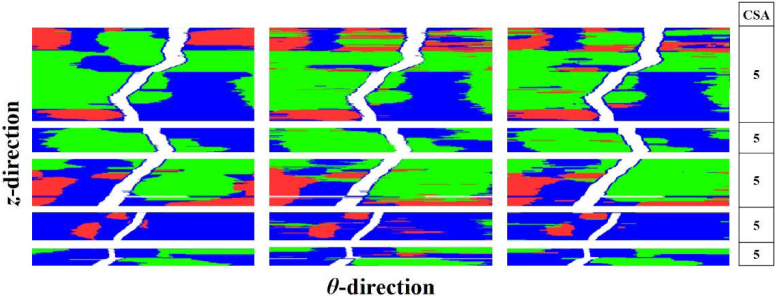
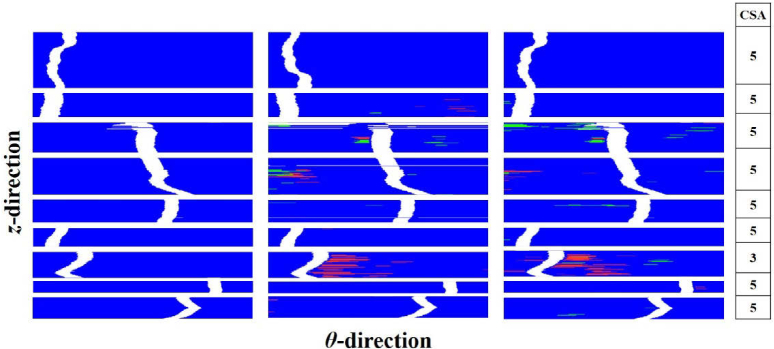
Given that A-line classification is suitable for angular metrics of calcifications and lipidous regions, and removes the confusion associated with the depth of unseen lipidous regions, we analyzed results of both of the current networks in terms of A-lines. As shown in Fig. 8, Deeplab v3+ gave a relatively large number of false negatives for both plaques (particularly fibrolipidic) as compared to SegNet. En face classification arrays allow one to evaluate an entire lesion in the (θ,z) view (Fig. 9). Deeplab v3+ shows more small islands of error than does SegNet. When analyzed across folds, SegNet performed better than Deeplab v3+ with a statistically significant difference for all plaques (p < 0.05) (Table 5). We also analyzed A-line classification results on nine held-out VOIs without any identified calcification or lipidous plaques (Fig. 10). Results of both networks were very nearly devoid of these plaque types, indicating an extremely small number of false-positive classification. Particularly, the sensitivities approached 100%, and the Dice coefficients were extremely high (0.972 for Deeplab v3+ and 0.975 for SegNet).

Fig. 8.

A-line classification results obtained by processing pixel-wise results (Methods). Note that an A-line is labeled according to its predominant tissues, starting from the lumen (e.g., fibrocalcific indicates an A-line with fibrous tissue followed by calcification). Panels show: (a) results obtained using Deeplab v3+ and (b) results obtained using SegNet. For each figure, the inner ring is the ground-truth label, and the outer ring is the predicted result. Red, green, and blue indicate fibrocalcific, fibrolipidic, and other classes, respectively. White is the guidewire.

Fig. 9.

A-line classification results in en face (θ,z) view. Panels in columns are (left) ground truth, (center) results obtained using Deeplab v3+, and (right) results obtained using SegNet. Red, green, and blue indicate fibrocalcific, fibrolipidic, and other A-line classes, respectively. White is the guidewire. Results are from one test fold data, including five VOIs (479 image frames). Cardiologists scored lesion results by performing a clinical score assessment (CSA), with the following rating scale: 1: strongly disagree, 2: disagree, 3: unsure, 4: agree, and 5: strongly agree. All three cardiologists agreed that the automated results will not change clinical decision making.

Table 5. Mean performance metrics over folds, including sensitivity, specificity, Dice, and Jaccard coefficients measured from A-line-based classification between Deeplab v3+ and SegNet. With SegNet, the sensitivity of fibrolipidic class increased by nearly 16% (from 74.2% to 90.1%) relative to that for the Deeplab v3+, whereas fibrocalcific tissue yielded an improvement of approximately 12%. Statistically significant differences (p < 0.05) compared with each class of Deeplab v3+ are indicated by an asterisk (*).

Classes		Sensitivity (%)	Specificity (%)	Dice	Jaccard
Deeplab v3+	Fibrolipidic	74.2 ± 10.9	93.8 ± 4.4	0.780 ± 0.077	0.646 ± 0.099
	Fibrocalcific	81.1 ± 11.1	96.1 ± 3.9	0.818 ± 0.074	0.698 ± 0.103
	Other	91.1 ± 5.3	82.9 ± 6.1	0.888 ± 0.029	0.800 ± 0.047
SegNet	Fibrolipidic	90.1 ± 3.9*	84.3 ± 6.6*	0.827 ± 0.057*	0.733 ± 0.073*
	Fibrocalcific	92.9 ± 4.5*	76.4 ± 6.2*	0.897 ± 0.038*	0.827 ± 0.057*
	Other	87.9 ± 3.2	80.0 ± 6.9	0.907 ± 0.023	0.836 ± 0.036

Fig. 10.

En face (θ,z) view of A-line classification results on a held-out test sample including 600 IVOCT images with nine VOIs without any identified calcification or lipidous region. Panels show: (left) ground truth, (center) result obtained using Deeplab v3+, and (right) result obtained using SegNet. See Fig. 8 for details.

In addition to standard segmentation metrics, we assessed segmentation results of SegNet and Deeplab v3+ using clinically meaningful lesion metrics (i.e., arc angle and depth). Table 6 shows small differences in mean arc angle and depth in both classes. Anecdotally, when expert cardiologists reviewed results on individual images, the deemed differences below what would influence clinical decision making.

Table 6. Mean clinical plaque attributes over folds, including arc angle and depth. Both networks gave values close to those derived manually; i.e., the difference values (mean arc angle, depth) of Deeplab v3+ were (13.5°, 0.03 mm) and (11.3°, 0.004 mm) for lipidic and calcific lesions, respectively, while SegNet showed the values of (8.6°, 0.03 mm) and (9.4°, 0.005 mm), likely within the range of clinical relevance. Metrics were obtained after CRF noise cleaning. Despite differences being small relative to clinical impact, a Student’s t-test rejected the null hypothesis of no difference (*p < 0.05 and **p < 0.001).

	Lipidous Plaque		Calcified Plaque
	Arc Angle (°)*	Depth (mm)**	Arc Angle (°)**	Depth (mm)
Ground Truth	146.0 ± 44.1	0.151 ± 0.035	85.0 ± 35.5	0.050 ± 0.013
Deeplab v3+	157.5 ± 47.8*	0.121 ± 0.057**	93.0 ± 72.1*	0.048 ± 0.036
SegNet	152.3 ± 41.0*	0.121 ± 0.024**	88.6 ± 39.1**	0.049 ± 0.012

To determine the potential impact on clinical decision making, we performed a clinical score assessment based on the en face (θ,z) and individual image results. The data of both networks contained residual misclassifications as shown in the plaque (Fig. 9) and non-plaque (Fig. 10) cases. Despite this, the three cardiologists unanimously scored results with a 5 for both methods, indicating strong agreement that clinical decision making would be the same for automated and manually obtained results. In the case of the 7^th VOI in Fig. 10, the automated results showed a number of misclassified A-lines, but the cardiologists were not concerned because the arc angles were small.

The proposed method (SegNet) was compared with our previous A-line CNN-based approach [18] in Table 7. We trained/tested on the exact same folds. For standard “regional segmentation” metrics (Dice and Jaccard), the new approach performed much better that the previous method for all plaque classes, giving statistically significant differences (p < 0.05). Interestingly, for A-line metrics, sensitivity improved but specificity degraded for the current method as compared to the previous one. This effect is likely due to the loss functions which were differently optimized. The current method uses the weighted cross entropy over pixels in the image while the previous method was optimized over A-lines themselves.

Table 7. Comparison of the proposed method (SegNet) to the previously reported A-line CNN-based approach [18]. In almost all cases, the new method outperformed, with particularly large improvements in sensitivity, Dice, and Jaccard. Using the Wilcoxon signed-rank test, we determined statistically significant differences (p < 0.05) between the two methods in many instances, as indicated by an asterisk (*).

Classes		Sensitivity (%)	Specificity (%)	Dice	Jaccard
Fibrolipidic	Previous Method	69.3 ± 15.7	92.3 ± 4.3	0.737 ± 0.103	0.593 ± 0.124
	Current Method	90.1 ± 3.9*	84.3 ± 6.6*	0.827 ± 0.057*	0.733 ± 0.073*
Fibrocalcific	Previous Method	75.1 ± 16.2	94.4 ± 3.6	0.721 ± 0.120	0.576 ± 0.147
	Current Method	92.9 ± 4.5*	76.4 ± 6.2*	0.897 ± 0.038*	0.827 ± 0.057*
Other	Previous Method	89.2 ± 3.6	79.2 ± 7.4	0.866 ± 0.034	0.766 ± 0.053
	Current Method	87.9 ± 3.2	80.0 ± 6.9	0.907 ± 0.023*	0.836 ± 0.036*

5. Discussion

Our method for automated semantic segmentation of plaques is very promising both with regards to clinical treatment planning and research applications. Results were very similar to those of analyst’s ground-truth labels for both the pixel-wise (Fig. 5) and A-line-based (Fig. 8) approaches. Good traditional metrics, such as Dice and sensitivity/specificity (Tables 1, 3, and 5), were obtained. Since errors of a few pixels are really not relevant to clinical decision making, we performed more clinically relevant evaluations. First, we created en face analysis of A-lines to allow visualization of entire lesions. The predicted classification maps agreed favorably with the manually annotated counterparts. Second, we performed a clinical lesion score assessment based on the en face and individual image results. We obtained strong agreement that the automated results would not change clinical decision making from that of manual annotations. Third, we assessed clinically relevant lesion metrics (i.e., arc angle and depth), which have been applied in clinical research studies [43,44]. The results were encouraging with small differences likely within the range of relevance. The current processing time is realistic for clinical and research applications. On our computer system with non-optimized code, the computation time is only about 0.27 sec per image (0.05 sec for pre-processing, 0.02 sec for segmentation, and 0.2 sec for post-processing classification noise reduction). Currently, the proposed method can process an entire pullback of 300–500 frames in 80–135 sec, which is suitable even for clinical application. With post-processing optimization, time could be greatly reduced.

SegNet had better segmentation/classification performance than Deeplab v3 + . Although the Dice/Jaccard coefficients were similar, SegNet gave significantly better sensitivities than Deeplab v3+ for pixel-wise classification (Table 1). For A-line-based classification, most metrics (e.g., sensitivity, Dice, and Jaccard coefficients) were significantly improved when the SegNet network was used (Table 5). One possible reason is the difference in the number of trainable parameters between two networks. Although SegNet (pre-training dataset: vgg16) and Deeplab v3+ (pre-training dataset: ResNet18) have very similar depths, SegNet (138 million parameters) has 10 times more parameters than Deeplab v3+ (11.7 million parameters), indicating a possibility of better training and generalization. Deeplab v3+ trained faster than SegNet, but testing times were similar (0.018 sec and 0.02 sec, respectively per image).

The current A-line segmentation results were improved relative to those from our previous studies, i.e., Kolluru et al. [18] and Prabhu et al. [13]. Table 7 shows that regional segmentation metrics (i.e., Dice, and Jaccard coefficients) of fibrolipidic and fibrocalcific classes are significantly improved by the current method as compared to the deep learning A-line method of Kolluru et al., when exactly the same data and folds were used. The improvement is likely due to multiple-processing differences. First, we used an advanced deep learning model (SegNet) having 91 layers, rather than a simpler CNN architecture used previously. Second, we used the entire pixels for processing giving us a great opportunity for learning the spatial similarities of plaques. The previous method used the A-line (200 × 1), which limited the ability to learn spatial relationships. In addition, current results are better than those in our recent A-line machine learning-based approach (Prabhu et al. [13]) for all plaques on similar, but not identical datasets. That is, Dice coefficients ordered (current, values from Prabhu et al. [13]) are (0.827, 0.672), (0.897, 0.785), and (0.907, 0.870) for fibrolipidic, fibrocalcific, and other plaques, respectively. Interestingly, the CRF noise cleaning showed only a small improvement in pixel-wise classification as opposed to our previous A-line classifications [13,18], likely due to the greater base of support in the current method. Nevertheless, CRF remains a desirable step. Unfortunately, it is difficult to compare results with those of other researchers because there is no public image database for comparison. Any comparison on different datasets would greatly depend on the mix of cases.

We found that pre-processing steps (noise reduction and pixel shifting) were important for improving segmentation results. As shown in Table 4, when pre-processing (particularly pixel shifting) was not used, the classifier was very much degraded. We believe that pixel shifting makes plaques look more “similar,” enhancing learning. That is, without pixel shifting, plaques appear very dissimilar depending on the catheter’s location within the artery, possibly requiring many more cases for training. In addition, redundant regions having no meaningful information (e.g., lumen, catheter, and shadow) degraded training performance. In some cases, these regions were falsely classified as plaques (Fig. 7(b–c)). With pre-processing, these were efficiently determined in advance and excluded from learning process. Particularly, pixel shifting enabled focusing only on the specific regions having meaningful information. One potential disadvantage of pixel shifting is the inevitable loss of lumen and physics features. For example, if the IVOCT light beam strikes the lumen obliquely, the detectable reflected signal can be reduced. This additional information cannot be “learned” from pixel-shifted data. In addition, with calcifications, the lumen can be irregular, a characteristic that cannot be recovered from pixel-shifted data. Noise reduction filtering led to a significant but smaller improvement than that of pixel shifting (Table 4). This result is surprising because deep learning semantic segmentation is expected to be relatively immune to noise and because speckle contains information about tissue structure. Improvement was obtained even though we used a deep network (SegNet, 91 layers) and a large amount of training data. Regardless, performance was improved, which suggested that the reduced “noise” provided more consistent data for training.

There are limitations of this study. First, we trained on manually annotated images. Although we learned how experts segment data, this was training to an imperfect gold standard. This limitation could be circumvented in the future by using cryo-imaging, which is proposed by our group [45]. Second, although we used a large dataset, even more lesions would ensure that we are training for the variety of lesions one will find in clinical practice. Third, there are numerous other deep learning models that might give even better results.

In summary, deep learning semantic segmentation on (r,θ) images works well and is fast, suggesting that this might be an appropriate approach for automated IVOCT analysis. The proposed method enables highly automated, objective, repeatable, and comprehensive plaque analysis. The method is promising for both research and clinical applications.

Funding

NIH (R21HL108263, R01HL114406, R01HL143484, C06 RR12463).

Disclosures

Dr. Bezerra has received consulting fees from Abbott Vascular.