Identification of Neuronal Lineages in the Drosophila Peripheral Nervous System with a “Digital” Multi-spectral Lineage Tracing System

SUMMARY

Elucidating cell lineages provides crucial understanding of development. Recently developed sequencing-based techniques enhance the scale of lineage tracing but eliminate the spatial information offered by conventional approaches. Multi-spectral labeling techniques, such as Brainbow, have the potential to identify lineage-related cells in situ. Here, we report nuclear Bitbow (nBitbow), a “digital” version of Brainbow that greatly expands the color diversity for scoring cells, and a suite of statistical methods for quantifying the lineage relationship of any two cells. Applying these tools to the Drosophila peripheral nervous system (PNS), we determined lineage relationship between all neuronal pairs. This study demonstrates nBitbow as an efficient tool for in situ lineage mapping, and the complete lineage relationship among larval PNS neurons opens new possibilities for studying how neurons gain specific features and circuit connectivity.

In Brief

Veling et al. report a multi-color labeling system and statistical methods for mapping cell lineages. They identify the lineage relationship of all neurons in the peripheral nervous system of Drosophila larvae and show the utility of this technique in mapping neurons in the CNS.

Graphical Abstract

INTRODUCTION

Cell lineage, which denotes the developmental history of a cell, provides the conceptual framework for understanding organism formation (Papaioannou, 2016; Stent, 1985). For example, identifying the lineage relationship among neurons is essential for understanding how neurons gain specific physiological, morphological, and neurochemical features and proper circuit connectivity (Hobert and Kratsios, 2019; Lacin et al., 2019; Lee, 2017). Modern molecular genetic techniques have led to evolutionary improvement in lineage tracing from classic techniques involving dye filling or cell transplantation (Woodworth et al., 2017). For instance, sequencing-based methods can distinguish hundreds to thousands of uniquely barcoded lineages (Raj et al., 2018; Schmidt et al., 2017; Spanjaard et al., 2018). However, sequencing-based methods do not offer in situ spatial relationships of these lineages, because they require tissue disassembly. Moreover, the birth timing of cells within a lineage is difficult to resolve. In contrast, imaging-based methods, such as Brainbow, can preserve the spatial information in situ and permit live imaging, but their efficiencies are still limited by labeling diversities and lack of statistical tools for unambiguous lineage tracing (Boulina et al., 2013; Cachero and Jefferis, 2011; Cai et al., 2013; Hadjieconomou et al., 2011; Hampel et al., 2011; Livet et al., 2007; Pan et al., 2013). Hence, there is an urgent need to create novel labeling, detection, and quantification methods that allow highly efficient lineage tracing while preserving spatial information.

Brainbow, a multi-spectral labeling technology, is designed to randomly express one of three or four fluorescent proteins (FPs) from a single cassette, thus creating stochastic labeling colors in neighboring cells or cell lineages (Boulina et al., 2013; Cachero and Jefferis, 2011; Cai et al., 2013; Hadjieconomou et al., 2011; Hampel et al., 2011; Livet et al., 2007; Pan et al., 2013). When more color variants are needed to uniquely label many cell lineages, more than one Brainbow cassette can be used to create differential expression levels of FPs. However, using color shades for lineage tracing is not always reliable. Distinguishing two color variants differing by subtle FP expression levels (e.g., color A generated from 2 YFP + 1 RFP + 1 CFP compares to color B generated from 1 YFP + 2 RFP + 1 CFP) can be challenging because of imaging noise (Cai et al., 2013). When applying Brainbow to trace cell lineages, daughter cells in the same lineage are assumed to inherit the same color generated in the mother stem cell. However, protein synthesis levels in daughter cells can be quite different. A more robust color generation mechanism would address these concerns and provide more reliable lineage tracing.

One way to generate more robust Brainbow lineage labels is to localize the same FPs to different subcellular compartments. Cytoplasmic membrane-targeted and nucleus-targeted FPs, expressed through genome integration by electroporated transposase, have been used to differentiate neighboring neuronal lineages in chick and mouse embryonic brains (García-Moreno et al., 2014; Loulier et al., 2014). However, transposase integrates varying numbers of targeting cassettes in different cells, making it difficult to estimate the probability of each label combination for quantitative analysis. Generating transgenic animals with a fixed number of labeling cassettes would solve this problem. For instance, the Raeppli strategy used 4 FPs to create up to 4 × 4 = 16 membrane and nucleus color combinations in transgenic Drosophila (Kanca et al., 2014). Another recombination mechanism, implemented in the CLoNe and the MultiColor FlpOut (MCFO) Drosophila lines, generates random colors by stochastic removal of the expression stops from each FP module (García-Moreno et al., 2014; Nern et al., 2015). For instance, a MCFO fly integrates 3 different stop-spaghetti monster GFPs (smGFPs) modules into 3 distinct genomic loci and generates up to 2³ – 1 = 7 smGFP combinations. However, expanding the color pool requires inserting more FP modules to additional genomic loci to prevent inter-module recombination. In addition, the optimal color outcome can be difficult to obtain from CLoNe and MCFO animals. This is because while low FLP activity results in simple single-marker colors, high FLP activity often results in expressing all FPs in most cells (Nern et al., 2015). In conclusion, the small unique color pools generated by the previously mentioned methods result in frequent observations that neighboring cells or lineages are labeled with the same color.

To overcome these limitations, we introduced a “digital” format of Brainbow for robust lineage tracing, which we call nuclear Bitbow (nBitbow). A single nBitbow cassette composites binary switches to independently determine an ON/OFF state of 5 FPs to generate up to 2⁵ ‒ 1 = 31 color variants. To facilitate the detection of the FPs independent of their intensities, the FPs are tagged for nuclear localization. We applied nBitbow to trace neuronal lineages in the Drosophila peripheral nervous system (PNS). We chose the fly PNS as a model because (1) individual PNS neurons are identifiable by their soma locations and neurite patterns; (2) PNS neuronal lineages reported in previous studies can serve as references for result comparison (Brewster and Bodmer, 1995, 1996); and (3) previous neuronal lineage mapping in PNS was incomplete because of technical challenges. Because there is a lack of statistical methods for color-based lineage tracing, we developed a lineage-relatedness test to determine the likelihood of two cells being lineage related based on their colors. Using this statistic test, we confirmed and rejected previously determined lineages, as well as revealing previously unidentified lineages. Moreover, applying nBitbow labeling at different developmental time points, we revealed the proximate birth timing of many PNS neuronal lineages. Furthermore, we demonstrated the feasibility of using nBitbow for lineage mapping in other systems by applying it to determine the lineage relationship of a subset of interneurons in the CNS.

RESULTS

nBitbow Design and Characterization

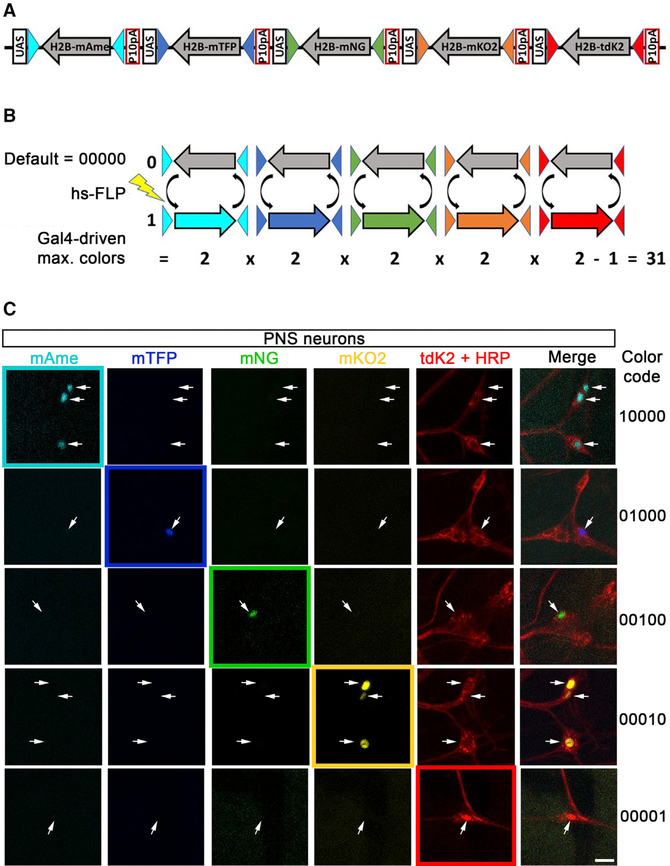
As opposed to previous Brainbow designs that expand color variations by recombining multiple cassettes to mix different intensity levels in each spectral channel, Bitbow, a digital form of Brainbow, use several (N) FPs and randomly assign each to an ON or OFF expression state upon FLP-mediated recombination (Figure 1A). As a result, Bitbow generates N-bit (2^N – 1, minus the all-OFF state) colors from a single cassette. We further optimized Bitbow for lineage tracing and generated a nuclear Bitbow (nBitbow) cassette containing 5 FPs (mAmetrine, mTFP, mNeonGreen, mKusabira-Orange2, and tdKatushka2), each of which was fused to a human histone H2B (hH2B) for nuclear tagging. The cDNA of each nuclear FP was positioned in the inverse direction and flanked by a pair of incompatible FLP recognition target (FRT) sites, thus permitting spinning the FPs in forward or inverse orientation upon FLP recombination (Cai et al., 2013; McLeod et al., 1986; Schlake and Bode, 1994; Turan et al., 2010; Volkert and Broach, 1986). Unlike previous Brainbow designs, recombination of each nuclear FP in nBitbow was independent of each other, resulting in up to 2⁵ – 1 = 31 unique colors by a single cassette (Figure 1B). Finally, an upstream activating sequence (UAS) and a p10 baculovirus poly-adenylation sequence were placed upstream and downstream, respectively, to each of the five FP recombination units to allow strong FP expression when driven by a Gal4 driver (Pfeiffer et al., 2012). We chose FPs whose native signals are bright and stable so that immunostaining is not required. In addition, spectral imaging and linear unmixing were applied and optimized for separating the five fluorescent signals to avoid signal bleed-through (Figure 1C).

Figure 1. Design and Color-Coding Principles of nBitbow.

(A) Schematic of the nBitbow spinning design The H2B fusion nuclear FP (nucFP) open reading frames are positioned in the reverse direction as a default non-detectable color in the absence of FLP.

(B) Schematics of color-coding in nBitbow. Upon heat shock-induced FLP expression, which causes recombination of FRT sites, each H2B-FP module can stochastically and independently spin into a forward (1, visible) or reversed (0, nondetectable) expression state. A maximum of 31 visible colors can be detected in the presence of a Gal4 driver.

(C) Spectral imaging and linear unmixing are performed to identify the five-bit nBitbow color code for each cell, in which 1s represent the FPs that are turned on and 0s represent those that are not turned on. Images shown are PNS neurons. HRP, anti-HRP immunostaining, which specifically labels PNS neurons. Scale bar: 10 mm.

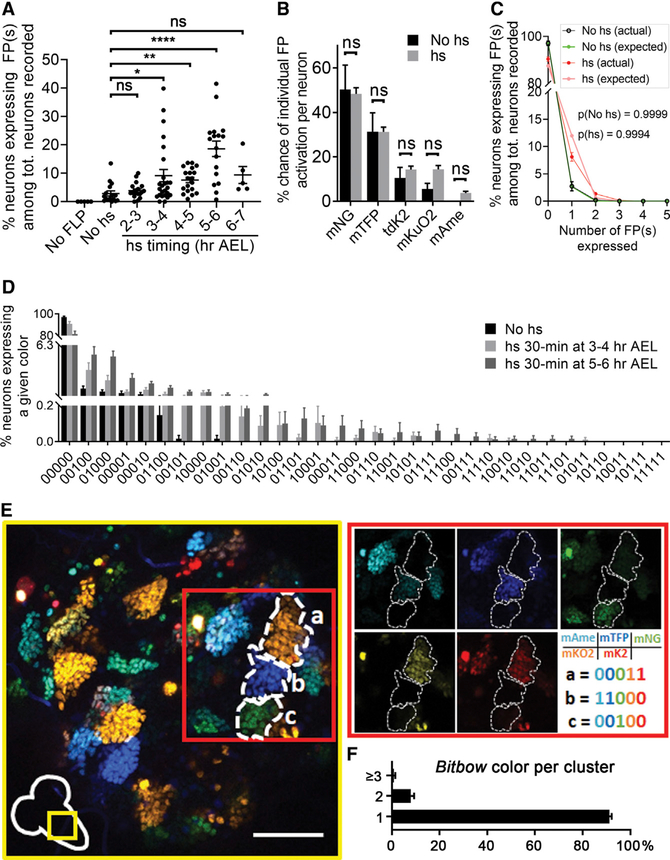
To evaluate the labeling efficiency of nBitbow in the Drosophila larval PNS, we first combined a transgene encoding heat shock-inducible flippase (hsFLP) and the pan-neuronal driver elav-Gal4 to determine how often neurons expressed colors in the third-instar larvae. Without heat shock (no hs), an average of 2.89% ± 0.90% (mean ± SEM) of PNS neurons showed colors when the larvae were raised at 23C (Figure 2A), likely due to leaky FLP expression, because we did not observe FP expression in the absence of the FLP transgene (no FLP) (Golic and Lindquist, 1989). Lowering the developmental temperature to 18C did not reduce this leaky FLP activity (data not shown). Induction of FLP expression by a 30-min heat shock at 37C that started at 3, 4, or 5 h after egg laying (AEL) led to significant increases of the number of PNS neurons that expressed colors (up to 18.62% ± 2.74%) (Figure 2A). Heat shock that started at 2 h AEL turned on color expression in a similar number of neurons compared with the non-heat shock condition (Figure 2A), possibly because of either low levels of FLP expression or poor accessibility of FLP to the nBitbow construct at very early stages of embryogenesis. Interestingly, we observed that the efficiency of turning on colors at 6 h AEL decreased to the level of non-heat shock condition. This may indicate a lower efficiency of FLP recombination in the post-mitotic cells (detailed later).

Figure 2. Labeling and Lineage Tracing Efficacy of nBitbow in the Drosophila Nervous System.

(A) Quantification of the labeling coverage of nBitbow by heat shock FLP induction in the PNS at various time points during early embryonic development. Sample numbers (larvae): no FLP, 5; no hs, 16; 2–3 h AEL, 18; 3–4 h AEL, 25; 4–5 h AEL, 19; 5–6 h AEL, 17; 6–7 h AEL, 5. The p values were calculated by Dunn’s multiple comparison test. ns, p > 0.05; *0.01 < p ≤ 0.05; **0.001 < p ≤ 0.01; ***0.001 < p ≤ 0.001; and ****p < 0.0001.

(B) Comparison of the turn-on efficiency of each FRT-nucFP-FRT module in the PNS. Heat shock (hs) data are the combined data from hs at 2–3, 3–4, 4–5, 5–6, and 6–7 h AEL. Sample numbers (larvae): no hs, 16; hs, 81. The p values were calculated by multiple comparison using the Holm-Sidak method.

(C) The actual FP frequency distribution is not different from the theoretical distribution (expected) as the number of activated FP increases in the PNS. This indicates that the recombination of each FRT-nucFP-FRT module is independent of each other. Sample numbers (larvae): no hs, 15; hs, 81. The p values were calculated by the chi-square goodness-of-fit test for Poisson distribution.

(D) 27 color codes were observed with different frequencies in the PNS from a Drosophila line that carries only one nBitbow cassette. Sample numbers (larvae): no hs, 15; 3–4 h AEL, 25; 5–6 h AEL, 17.

(E) Representative images of nBitbow labeling in thoracic segments in the CNS of the third-instar larvae with embryonic heat shock FLP induction. Most cell clusters (i.e., lineage clones) were labeled with the same color. 193 clusters were analyzed. Scale bar: 50 μm.

(F) Proportion of thoracic lineage clones labeled by one, two, or more Bitbow color tags, quantified across n = 193 clusters. The p values were calculated using unpaired two-tailed t test, and α of 0.05 is used as the cutoff for significance. Error bars: SEM.

Because different FRT sites exhibit different efficiencies of FLP-induced recombination (Schlake and Bode, 1994; Turan et al., 2010), we quantified the expression frequency of individual FPs. mNeonGreen displayed the highest expression frequency, followed by mTFP, mKusabira-Orange2, tdKatushka2, and mAmetrine (Figure 2B). Next, we quantified the frequency of neurons expressing one, two, three, four, or all five FPs. We found that such frequency followed a Poisson distribution from expressing one FP to five FPs. Chi-square goodness-of-fit test confirmed that such distribution (actual) had no significant difference from the theoretical distribution (expected) (Figure 2C). Thus, the expression of one FP does not appear to increase the chance of expressing other FPs, suggesting that the recombination of distinct FRT sites is independent of each other. Finally, the expression frequencies of all FP combinations (i.e., color variants) are quantified for our lineage-relatedness test (Figure 2D) (detailed later). Despite that different combinations exhibited different frequencies, we observed 27 of the 31 expected colors after heat shock-induced FLP expression.

One potential drawback of nBitbow for lineage tracing is that the spinning recombination design may cause color changes over time if the leaky FLP activity is persistent in a cell. As a result, cells with altered colors in the same lineage may be mis-identified as being in distinct lineages. To test this, we applied the same heat shock protocol and examined nBitbow color labeling in the CNS, because neuroblasts (NBs) in the CNS divide many more times than the sensory organ precursors (SOPs) in the PNS to generate cell clusters with clear boundaries (Birkholz et al., 2015; Truman and Bate, 1988). We found that most cells in each cluster were labeled in the same nBitbow color (Figure 2E). We occasionally observed a few scattered cells labeled by different colors in a cluster and rarely observed a cell cluster that was labeled by two distinctly colored clones (Figure 2F). This result is surprising, because every neuroblast division generates a ganglion mother cell (GMC) that produces 2 daughter cells. As a consequence, similar numbers of neuroblast clones and 1- or 2-cell clones are expected. We observed a very small number of 1-cell or 2-cell clones, which indicates that for unknown reasons, the nBitbow labeling induced by embryonic heat shock mostly happens in neural stem/progenitor cells and that color changes caused by persistent FLP activity are minimal. We also observed that nBitbow had lower labeling efficiency in the PNS when heat-shocked at 6 h AEL (Figure 2A), a stage that has more post-mitotic cells. Altogether, these results suggest that nBitbow provides more unique colors from a single cassette than previous variants of Brainbow and is reliable for lineage tracing in the Drosophila nervous system.

Identification of Neuronal Lineages in the Drosophila Larval PNS by nBitbow

Drosophila PNS neurons are generated through lineages that repeat in the abdominal hemisegments (Figure 3A) (Hartenstein and Campos-Ortega, 1984; Hartenstein et al., 1987). The SOPs in each hemisegment are born and delaminated from ectoderm around 3.5–7.5 h AEL to eventually give rise to 45 PNS neurons (Bodmer et al., 1989; Ghysen and O’Kane, 1989; Younossi-Hartenstein and Hartenstein, 1997). We therefore induced nBitbow recombination in PNS neurons by 30-min heat shock at 3–4 or 5–6 h AEL and recorded their colors in the third-instar larvae (Figure 3B). We expect to observe a significantly higher probability of two neurons being labeled in the same colors if they belong to the same lineage (i.e., inheriting the same colors from their SOP) (Figure 3C) than if they belong to different lineages (i.e., acquiring the same colors by chance).

Figure 3. nBitbow Efficiently Identifies Neuronal Lineages of Drosophila PNS Neurons.

(A) Schematic drawing of the distribution of PNS neurons in one hemisegment of the larval body wall. In the PNS, multipolar neurons include the md, da, bipolar dendrite (bd), and td types, whereas bipolar neurons include the es and chordotonal (ch) types.

(B) Schematic drawing of the experimental steps.

(C) Representative fluorescent images that show matching color codes of pairs of neurons previously thought to be independent of each other. These neuronal pairs are the five es neurons (desC, lesC, v’esA, vesA, and vesB) and their lineage-related da or td neurons. These es neurons have been previously reported as the only neuron from individual SOPs (Brewster and Bodmer, 1995). Larvae were heat-shocked at 3–4 h AEL. Scale bar: 10 μm.

(D) Statistical analysis confirms that these neuron pairs are lineage related. The κ values calculated based on experimental observations (red arrows) are significantly higher (i.e., closer to 1) than those calculated based on a random color distribution (blue).

See also Figures S1 and S2.

The different expression frequencies of the color variants call for statistical methods that weigh these variants appropriately in their strengths for deducing the lineage relationship between two neurons (Figure 2D). Based on Cohen’s kappa (k) statistics (Cohen, 1960; Dwass, 1957; Nichols and Holmes, 2002, 2007), which calculates the above-background match rate in non-uniform distributions like ours, we designed a randomized lineage-relatedness test—with the frequencies of each nBitbow color weighed in—to determine whether two neurons in a pair are lineage related. Ranging from −1 to 1, κ = 1 indicates the two neurons are always labeled by the same colors, κ = 0 indicates the neurons are labeled with the same colors by chance, and κ = −1 indicates the two neurons are always labeled with different colors. We calculated the κ value of every pair of PNS neurons in Drosophila larvae and determined whether each κ value is significantly different from the probability of labeling the same neuron pair with the same colors by chance in a randomization test (Figure 3D, and see STAR Methods for further details). Finally, a ≤2% false discovery rate (FDR) based on the Benjamini-Hochberg method was applied to confirm any pair of neurons that are lineage related (Benjamini and Hochberg, 1995).

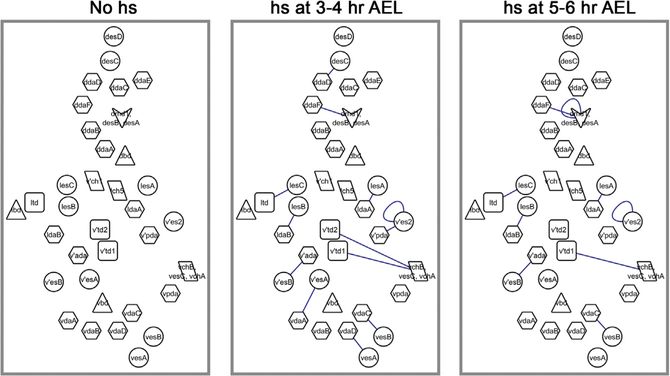
Because some neurons are labeled at the third-instar larval stage without heat shock, we first examined how this leaky FLP activity would affect the outcomes of our color-based lineage analysis. From the non-heat shock experiments, our lineage-relatedness test determined that all neurons appear to be in distinct lineages (Figure 4, left panel). This indicates that the leaky FLP activity is unlikely to recombine the nBitbow cassette in any SOP until accumulation to a sufficiently high level to recombine in the post-mitotic neurons. This also suggests that our lineage-relatedness test is reliable to avoid the false-positive assignment of two cells being lineage related.

Figure 4. PNS Lineage Maps Revealed by nBitbow at Different Developmental Times.

Neurons in a hemisegment are shown. These maps are based on the lineage relationships of all neurons determined by their calculated κ values from experiments with no heat shock (left), heat shock at 3–4 h AEL (middle), and heat shock at 5–6 h AEL (right). Each line connects a pair of lineage-related neurons with ≤2% false discovery rate (FDR). Three groups of neurons that cannot be identified individually (dotted boxes in Figure 3A) are presented as single symbols in these maps: the arrowhead includes four neurons—dmd1, desB, and 2 desA—that are located close together; the parallelogram labeled as lch5 includes 5 ch neurons; and the parallelogram labeled as vchA, vchB, and vesC includes the three neurons indicated.

See also Figure S3.

Previous studies used heat shock to sparsely induce lacZ expression at early developmental time points and referred cell clusters that are located nearby to be in the same SOP lineages (Brewster and Bodmer, 1995, 1996). We started nBitbow lineage tracing with 30-min heat shock at 3–4 h AEL. The lineage-relatedness test led to some of the same conclusions as previous studies: 4 distinct lineages give rise to a pair of ldaA-lesA, ldaB-lesB, v’ada-v’esB, or v’pda-v’es2 neurons, respectively (Figure S1).

The lacZ-based lineage tracing approach may incorrectly determine neurons in different lineages as being in the same lineage if they are easily labeled at the same heat shock time point. However, nBitbow labels the lineage-unrelated neurons in distinct colors even if their progenitors are labeled at the same heat shock time point. For instance, prior studies suggested that some dendritic arborization (da) neurons in the dorsal multidendritic (dmd) cluster were generated from one SOP and those in the ventral multidendritic (vmd) cluster were generated from another SOP (Figure 3A, shaded clusters) (Brewster and Bodmer, 1995, 1996). In contrast, our results showed that none of the da neurons from either the dmd or the vmd cluster are lineage related (Figure S2). The lacZ-based lineage tracing approach may also incorrectly determine neurons in the same lineage as being in different lineages if they migrate away from each other. However, nBitbow relies on color identify, not spatial proximity, and thus avoids this type of error. For instance, the 5 external sensory (es) neurons (desC, lesC, v’esA, vesA, and vesB) had been previously concluded to be the only neurons generated from 5 SOPs. Our lineage-relatedness test revealed that each of the 5 es neurons was lineage related to either a da or a tracheal dendrite (td) neuron (ddaD-desC, ltd-lesC, vdaA-v’esA, vdaC-vesB, and vdaD-vesA) (Figures 3C and 3D). This finding is in agreement with the results mentioned earlier that dda or vda neurons in the dmd or vmd clusters are not lineage related to each other but are lineage related to the des or ves neurons, respectively (Figures 3C and 3D; Figure S2).

Altogether, these results demonstrate the feasibility of using nBitbow for lineage studies in the PNS of the Drosophila larva and offer a lineage map of all larval PNS neurons.

Estimating the Birth Timing of PNS Neurons by nBitbow

One inherent benefit of using nBitbow for lineage mapping is its efficiency. nBitbow does not require sparse labeling. Indeed, all samples expressing any FP colors were used in the analysis. This allowed us to efficiently map the complete PNS lineages using only 17–25 larvae for each heat shock time point.

Comparing experiments done with 3–4 h AEL heat shock to those done with 5–6 h AEL heat shock, we found that even though many more neurons were labeled (Figure 2A), the overall percentage of neuron pairs that were labeled in matching colors decreased from 28.80% to 23.98%, respectively. Consistently, the lineage-relatedness tests indicated that the ddaD-desC, v’pda-v’es2, v’td2-vchA/vchB/vesC, v’esA-vdaA, and vdaDvesA neuron pairs no longer appeared to be lineage related when heat shock was applied at 5–6 h AEL (Figure 4, middle and right panels). Although the frequency of color matching of the v’ada-v’esB pair or the vdaC-vesB pair dropped significantly in the experiments done with 5–6 h AEL heat shock, that of the ldaA-lesA pair or the two es neurons in the v’es2 group remained unchanged (Figure S3). These observations suggest that at least one of the neurons in the v’ada-v’esB or the vdaC-vesB lineage finishes its final cell division earlier than those in the ldaA-lesA or the v’es2 lineage.

Altogether, the birth timing of individual lineages can be estimated by comparing the color matching frequency between earlier and later heat shock time points.

nBitbow Is Suitable for Studying Lineages in the Drosophila CNS

The use of nBitbow for lineage studies is not restricted to Drosophila PNS. Similar to the PNS, the ventral nerve cord (VNC) of Drosophila CNS contains repeated segments, each of which contains about 30 neuroblasts giving rise to approximately 350 neurons (Bossing et al., 1996; Doe, 1992; Schmidt et al., 1997). Although there is no marker for the identification of every CNS neuron, markers that label subsets of cells, such as Gal4 drivers that express transgenes in specific cell types, allow the application of nBitbow to trace lineages within subsets of CNS neurons. Recent studies have identified a subset of larval interneurons, called Basin neurons (Basin-1, Basin-2, Basin-3, and Basin-4), that receive synaptic inputs from nociceptors and mechanosensors (Ohyama et al., 2015). These neurons are speculated to be lineage related, based on their similar cell body locations, morphologies, and projection patterns (Ohyama et al., 2015). Using nBitbow and the Basin-specific-driver R72F11-Gal4, we found that the four Basins typically expressed the same colors induced by 1-h heat shock at 3–4 h AEL and were significantly related to each other (Figure 5). These results demonstrate the feasibility of using nBitbow for lineage studies in the Drosophila CNS.

Figure 5. Lineage Tracing of Basin Neurons in the CNS of Drosophila.

(A) Quantification of color activation frequency inBasin neurons with 1-h heat shock at 3–4 h AEL. Sample number (larvae): 13. Error bars: SEM.

(B) Representative fluorescent images that showBasin neurons expressing the same color in a cluster that is different from the adjacent cluster. Scale bar: 10 μm.

(C) κ value and random distribution of Basin neurons. Statistical analysis confirms that all four basin neurons are lineage related.

See also Figure S4

DISCUSSION

In this study, we introduced a digital version of Brainbow, termed nBitbow, for lineage tracing with enhanced efficiency and improved accuracy. Importantly, we developed statistical methods to determine the likelihood of two cells being lineage related based on their nBitbow colors. Applying nBitbow to trace neuronal lineages in the PNS of Drosophila larva, we confirmed and rejected previously determined lineages and discovered unknown lineages. Moreover, nBitbow revealed the proximate birth timing of many PNS neuronal lineages. In addition, we demonstrated the feasibility of using nBitbow for lineage studies in the Drosophila CNS.

nBitbow Enhances the Efficiency in Lineage Mapping

Mapping lineages by nBitbow is more efficient compared with previous methods. For example, a previous study examined more than 5,000 embryos to identify the lineage relationships in the Drosophila larval PNS. This is because the labeling needs to be extremely sparse to reliably determine the frequency of neighboring cells expressing a lacZ marker that was induced by heat shock in a single progenitor cell (Brewster and Bodmer, 1995, 1996). Using nBitbow, we achieved a similar goal with 40 animals (23 for heat shock at 3–4 h AEL and 17 for heat shock at 5–6 h AEL). Moreover, power analysis suggested, based on the color activation frequency with 30-min heat shock at 3–4 h AEL, that only 124 samples (e.g., hemisegments for segmentally repeated lineages) would be needed to lineage a set of 300 cells with 80% power at a 50% cell color match rate (Figure S4A, left panel; STAR Methods). In addition, taking advantage of each larval PNS neuron being identifiable by its cell body position and the morphology of proximal dendrites (Bodmer and Jan, 1987; Grueber et al., 2002; Jan and Jan, 1982), we combined neuronal morphology staining with nBitbow’s multi-color nuclear labeling to assign each identified neuron to a lineage. With these technical improvements, we were able to determine the lineage relationships in all larval PNS neurons with a small number of animals.

nBitbow Improves the Accuracy of Lineage Mapping

The ability of nBitbow to generate many more unique colors overcomes previous methods’ fundamental limitation in labeling accuracy. With limited color choices, previous monochromic or multicolor labeling methods rely on physical proximity when determining whether two or more cells belong to the same lineage. This may generate false-negative or false-positive results; for instance, cells that migrate far from their sisters may be missed as in distinct lineages, or cells located close to the cluster boundary may be included in the neighboring lineages. Our method minimizes these errors by providing reliable statistics to determine whether two cells are lineage related based solely on nBitbow color, but not on their physical locations. For instance, we discovered that even though da neurons in the vmd or dmd clusters are physically close to each other, they are all generated by distinct progenitor cells (Figure S2). Moreover, many of these da neurons were lineage related to a nonmultipolar neuron located farther away (Figures 3C and 3D). These findings support the notion that nBitbow improves the accuracy of lineage mapping.

nBitbow Reveals Proximate Birth Times of Cells

Initiating nBitbow labeling at different developmental time points permitted convenient birth-timing analysis in the context of lineage relationship among PNS neurons (Figure 4). We found that several PNS neuronal pairs that were identified as lineage related in experiments with an earlier heat shock time point were identified as lineage unrelated in experiments with a later heat shock time point. This suggests that none of the neurons in those lineages were born at the earlier time point, so they inherited the same colors from their mother SOPs when heat shock was applied. However, one of the neurons in any of these lineages came to complete its last cell division at the later time point, so its color is distinct from its sister neuron. Nevertheless, this method could not be used to determine the birth timing of those cells that are the sole neurons in their lineages. Because nBitbow expresses bright nuclear-targeted FPs, it is possible that the birth timing of such neurons can be revealed by time-lapse imaging in live tissues. As a preliminary test, we performed time-lapse imaging of CNS cells labeled by nBitbow and observed that single mother cells divided into two daughter cells expressing the same color as their mother (Figure S4B).

Comparisons with Other Multicolor Labeling Systems

Different multicolor labeling systems have advantages and limitations for specific applications (Kretzschmar and Watt, 2012; Weissman and Pan, 2015). This is true for nBitbow.

First, the availability of drivers for activating colors through recombination limits the applicability of each system. For example, dBrainbow, UAS-Brainbows, LoLLIbow, and MCFO use Cre recombinase to activate color selection, while Flybows, TIE-DYE, and our nBitbow use FLP recombinase; Raeppli uses FLP to activate an integrase, which in turn activates color selection (Boulina et al., 2013; Hadjieconomou et al., 2011; Hampel et al., 2011; Kanca et al., 2014; Nern et al., 2015; Richier and Salecker, 2015; Worley et al., 2013). Because Raeppli requires extra time to activate colors, it might not be suitable for studying lineages, at least those occurring at early developmental stages.

Second, the subcellular localization and brightness of FPs are appropriate for specific purposes. For examples, Flybows, UAS-Brainbows, LoLLIbow, and Raeppli use membrane-bound FPs, allowing the visualization of fine morphological structures, such as dendritic spines or synapse, and can be used for identifying cells in certain circumstances. By contrast, nBitbow and Raeppli use nuclear FPs. Although they do not reveal cell morphology, they generally produce brighter FP signals, eliminating the need for immunostaining. Moreover, cells expressing nuclear FPs are easier to score than those expressing membrane FPs in tissues with a high density of cells.

Third, the diversity of colors is important for successful application of multicolor labeling systems in large numbers of cells. The more color variants available, the less likely that two random cells will express the same color. dBrainbow, Flybows, UAS-Brainbows, LoLLIbow, and Raeppli provide 3 or 4 colors per construct and MCFO and TIE-DYE provide 7 colors, whereas nBitbow provides more than 20 colors per construct, making it a great candidate for lineage tracing of large numbers of cells.

Finally, the direct signal detection and stability of FPs affect suitability for live imaging. For example, although MCFO provides more colors than other Brainbow variants, it requires immunostaining to enhance FP signals, precluding its use for live imaging. In contrast, both nBitbow and LoLLIbow can be used for live imaging. nBitbow is probably more suitable for visualizing larger scales of lineage patterns and distribution because of its greater color diversity. Membrane-bound LoLLIbow is probably better for imaging fine details of cell morphology in a small number of cells because of its 3 color variants.

Applying nBitbow to Lineage Mapping in Other Tissues

One concern about applying nBitbow in other tissues is that although the nuclear Bitbow is sufficient for cell identification in the Drosophila PNS, because neurons can be readily identified by anti-horseradish peroxidase (HRP) staining, it might be difficult to use in tissues in which cells cannot be easily identified. The solution is to focus on mapping lineages within a subset of cells by using specific Gal4 drivers. In this work, we demonstrated the feasibility of this approach with 14 larvae by showing that the four Basin neurons are lineage related (Figure 5). Additional power analysis suggested that only 34 samples would be needed for determining lineage relationship of 300 cells, based on the color activation frequency with 1-h heat shock at 3–4 h AEL and the same criteria mentioned previously (Figure S4A, right panel). Although our CNS demonstration does not show the identity of individual Basins, additional cell-type-specific markers (e.g., Basin subtype-specific Gal4) (Ohyama et al., 2015) or UAS-membrane markers can be recombined with nBitbow to identify individual neurons. If a Gal4 driver is weak, increasing Gal4 copies or immunostaining FPs would enhance nBitbow signals. If the expression of a Gal4 is dynamic, a cell-type-specific FLP with temporal expression in the early developmental stage can be used in combination with a constitutive Gal4. Alternatively, other binary expression systems (e.g., LexA/LexAop and QF/QUAS) can be combined with nBitbow to serve as cell-type-specific markers. Besides the nuclear-localized Bitbow, a membrane Bitbow may be useful for cell identification.

New Opportunities Resulted from Lineage Mapping by nBitbow

The success of our PNS lineage mapping created new opportunities for studying other aspects of neuronal development related to lineage development. For instance, it lays the foundation for studying whether particular molecular mechanisms are specified in neurons arising from different lineages. These neuronal properties include morphological selection, electrophysiology, neurotransmission, and circuit connections. Furthermore, we expect these tools to greatly increase the efficiency and accuracy for studying Drosophila lineage development beyond the nervous system. These tools also bring the potential of combining lineage mapping with other fields of research to answer complex questions in developmental biology.

STAR★METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Dr. Bing Ye (bingye@umich.edu). All unique/stable reagents generated in this study are available from the Lead Contact without restriction.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

To generate UAS-nBitbow flies, the nBitbow construct cDNAs encoding the following FPs were used: mAmetrine, mTFP, mNeonGreen, mKusabira-Orange2, and tdKatushka2 (Ai et al., 2006, 2008; Sakaue-Sawano et al., 2008; Shcherbo et al., 2009; Shaner et al., 2013). Human histone 2B protein (hH2B) was fused in frame to the N terminus of individual FPs (hH2B-FP). Individual incompatible FRT sequence pairs (FRT^F3, FRT^F14, FRT⁵⁴⁵, FRT^F13, or FRT^5T2) was then placed in the opposing direction on both ends of the hH2B-FP sequence (Cai et al., 2013; McLeod et al., 1986; Schlake and Bode, 1994; Turan et al., 2010; Volkert and Broach, 1986). And then each of the five FRT-H2B-FP-invFRT cassettes were assembled into the pJFRC-MUH backbone vector (Addgene, Inc.) by standard cloning method, so that the expression of each cassette is under the control of an upstream activation sequence (UAS) and an p10 poly-adenylation (p10pA) sequence (Pfeiffer et al., 2012). The final nBitbow targeting plasmid was assembled by Gibson assembly (Gibson et al., 2009) into the same pJFRC-MUH backbone and was integrated into Drosophila melanogaster genome docking site VK00027 (BestGene, Inc.) using the FC31 integrase-mediated transgenesis systems (Bateman et al., 2006; Bischof et al., 2007; Groth et al., 2004; Markstein et al., 2008; Venken et al., 2006).

Other stocks: hs-FLP¹²² (Rangarajan et al., 1999); elav-Gal4 (BDSC, #8760); GMR72F11-Gal4 (BDSC, #39786).

METHOD DETAILS

nBitbow transgenic flies, UAS-nBitbow, was crossed with flies that carry heat-shock-inducible FLP¹²² and a Gal4 driver (elav-Gal4 for PNS and R72F11-Gal4 for Basin neurons) (Pfeiffer et al., 2008), and raised at 23C for 2 days. To induce FP expression in the larval PNS, embryos were collected within consecutive 1 hr windows on day 3, and kept at 23C until heat-shocked at 2–3, 3–4, 4–5, 5–6, or 6–7 hr AEL. To induce FP expression in Basin neurons, embryos were heat-shocked at 3–4 hr AEL. To induce FP expression in thoracic lineage clones in the larval CNS, 1^st instar larvae were heat-shocked on 1 day AEL. The heat shock was performed by heating the embryo-containing agar-plate on the surface of a 70C heat-block for 1.5 min, followed by a 30-min (or 1-hr for Basin neurons) heat chamber incubation at 37C. The plate was then transferred back to the 23C incubator for the next 4 days.

Late 3^rd instar larvae were dissected to make fillet preparations in 1× hemolymph-like 3.1 saline buffer (Feng et al., 2004), immediately followed by fixation in 4% paraformaldehyde in 1× PBS for 20 min at room temperature (RT) with gentle shaking. Larval fillets were transferred to 1.5 mL Eppendorf tubes wrapped in tinfoil to prevent possible photobleaching by ambient lights. The samples were washed 3 times with 0.1% Triton X-100 in 1× PBS, 15 min each at RT, on a nutator, and then incubated in 5% normal donkey serum containing 0.1% Triton X-100 in 1× PBS for 30 min at RT. Alexa Fluor 647 AffiniPure Goat Anti-Horseradish Peroxidase antibody (1:500, Jackson Immuno Research) was added to the samples for overnight incubation at 4C with gentle shaking. Samples were washed 3 times as described above. Fillets were placed on poly-L-lysine-coated coverslips and mounted with ProLong Diamond Antifade mountant (Invitrogen™). Samples were left dry in the dark overnight at RT and imaged by confocal imaging on the following day or kept at 4C for up to a week until imaging.

nBitbow samples were imaged with a Zeiss LSM780 laser scanning confocal microscope. PNS data were collected from abdominal segments 2 to 7 (A2-A7). Fiji with customized plugin scripts was used to process raw images for FP spectral unmixing (Schindelin et al., 2012). Individual FP signals assuming the shape of a nucleus in the soma were identified on a single z-plane. If a particular FP signal were observed in a neuron, it is recorded as an “1” in the color code; if that FP’s signal is not observed, it is then recorded as a “0.” Color code of each neuron was recorded manually to create a data sheet for each experimental condition, which were subsequently analyzed computationally and statistically.

For time-lapse imaging, embryos were collected as described above. Embryos were then manually dechorionated and incubated at 25C until heat-shock at 37C for 30-min at 4–5 hr AEL, followed by incubation at 18C for recovery. Subsequently, the embryos were placed on a poly-L-Lysine coated coverslip and covered by a drop of Halocarbon oil 700 (Sigma-Aldrich) to prevent drying. Time-lapse imaging started at 9–10 hr AEL with 30-min intervals for 12 hours. A 40x oil immersion lens (NA = 1.3) was used for imaging.

QUANTIFICATION AND STATISTICAL ANALYSIS

Quantification of lineage-relatedness

The goal of our statistical methods was to systematically identify neurons that share a common lineage versus those that do not share a common lineage. A key aspect of this test is the ability to score the lineage-relatedness for a pair of two neurons based on the color codes recorded from the nBitbow experiments. To do this, we implemented a modified version of the Cohen’s Kappa (k) to quantify the degree of color-code agreement between two neurons, which is defined as:

$$\kappa =\frac{p_0-p_e}{1-p_e},$$ (1)

where p₀ and p_e are the degree of color code agreement between the two neurons calculated by observation and by chance, respectively.

To calculate the κ value for each neuron pair, we first calculate the probability of a single neuron n expressing a particular color c, Pn, c:

$$P_{n,c}=\frac{M_c}{N},$$ (2)

where, M_c is the total observation that a neuron expresses color c, and N is the total number of neurons. As shown in Figure 2D, the chance that a neuron expressed any fluorescent color was relatively low (6% maximum). We therefore hypothesize that most of the null-color neurons were the result of no Flp recombination at all, instead of due to the same FP being recombined even times. As a result, we estimated the κ in the cases that at least one of the neurons in a comparing pair needs to express at least one FP to avoid the false identification of null-color expressing neurons being lineage related. Based on this assumption, we can estimate the p_e value between neurons i and j (i.e., $p_e^{i,j}$), in which at least one of them expresses at least one FP. The $p_e^{i,j}$ value can be calculated by summing the products of the P_{n, c} for both neurons for all the non null colors (denoted from 1 to C) then dividing by all cases where at least one neuron had color (1 – (P_{i, 0})×(P_j,0)) to account for our modified κ value ignoring double blank matches:

$$p_e^{i,j}=\frac{{\sum }_1^C\left(P_{i,c}\right)\times \left(P_{j,c}\right)}{1-\left(P_{i,0}\right)\times \left(P_{j,0}\right)}.$$ (3)

To calculate the p₀ value of the corresponding neuron pair $p_0^{i,j}$, we again, only considered the cases in which at least one of the neurons expressed at least one FP:

$$p_0^{i,j}=\frac{N_{i,j}^c}{M_{i,j}},$$ (4)

where, $N_{i,j}^c$ is the total observations that both neurons expressed a same non null colors color and M_i,j is the total observations that either neuron expressed a non null color.

Finally, we acquired the observed κ values for all the neuron pairs using their p_e and p₀ values following Equation 1. An analysis of this equation reveals that if any two neurons always have perfectly matched colors (i.e., p₀= 1), they will have a κ= 1. If two neurons’ colors are matched exactly as would be expected by chance (i.e., p₀= p_e), then they will have a κ= 0. In this way, a higher κ value indicates a higher probability that the two neurons are labeled in the same color not by chance (i.e., lineage-related).

Statistical analysis of lineage relatedness

We designed a statistical test to determine whether the experimentally observed κ value of a neuron pair is significantly higher than that by chance. To estimate the κ value distribution from labeling a particular neuron pair by random colors, we established a randomization process, starting with generating a raw color matrix where every row represents an individual PNS hemi-segment, and each column represents a neuron within that hemi-segment. The κ values were calculated for all possible combinations of neuron pairs within the data. Next, the raw color matrix was randomized by shuffling the colors each neuron expressing any non-00000 null-color. This ensures that the neurons receiving a color in the randomized data will have also had a color in the real data. We reason that this randomization process is more accurate than a total randomization process because each neuron pair remains the same total chance to match colors as in the real experiments, in which the ambiguous 00000 null-color are excluded from being assigning as a matched color (see above). After the color randomization, the κ values were calculated for all possible combinations of neuron pairs within the data. This randomization process was repeated 100,000 times for each neuron pair to generate a distribution of κ values that were compared to the κ value obtained from the experimental observation. The number of times that the random κ value was greater than or equal to the observed κ value was counted and then divided by 100,000 to generate a p value to estimate whether the experimentally observed κ value is significantly larger than those calculated by random color assignment. Finally, the p values was adjusted for multiple hypothesis testing by calculating a false discovery rate (FDR) using the Python statsmodels package (https://www.statsmodels.org/dev/generated/statsmodels.stats.multitest.multipletests.html). The Benjamini/Hochberg (non-negative) method was used for FDR evaluation (Benjamini and Hochberg, 1995).

It is important to run a separate test for each neuron pair because certain neurons expressed a color more often than others. This allowed us to normalize the high expressing neurons in a way that they did not just have a better κ value by chance.

The complete lineages map of PNS neurons was generated by the Cytoscape Software package (version 3.7.1., https://cytoscape.org/index.html).

Power analysis of lineage-relatedness test

To quantify the number of samples needed to robustly lineage a set of neurons, we performed a power analysis on our test. This analysis modeled a single neuron pair within a theoretical larger lineage. This single neuron pair was assigned a number of samples (N), a color distribution (C) and an above background match percentage (P). This above background match percentage corresponds to the effect size of this analysis and represents the chance that two neurons match due to their lineage relationship.

To model N neuron pairs from color distribution C with a match percentage P, we first randomly assigned N neurons as either “matching” or “non-matching” based on P. A random number from 0 to 1 was generated. If that number is less than P, then the neuron pair is said to be matching. If a neuron pair is assigned to be matching, a single color is selected from color distribution C. As C contains blanks, it is possible that both neurons are assigned the null-color even if they are matching. If a neuron pair is not assigned to be matching, two colors are chosen from C and assigned to the neurons separately. This process was repeated N times to generate the theoretical dataset.

This dataset containing a single neuron pair with N neurons was analyzed as described above with one important exception: the $p_e^{i,j}$ value was assigned based on the color distribution C not based on the observed colors within the small subset. This prevented wild changes to the κ value with small sample numbers and is consistent with our modeling of a pair within a larger set of neurons. A p value was calculated for this individual neuron pair using the randomization protocol described above.

To calculate the minimum number of samples (n) to obtain a power (Pr) at a given p value cutoff (α) this modeling process was repeated 1000 times. The number of times the p value was below α was divided by 1000 to obtain a power for the parameters specified in the analysis. If this power is above the desired Pr value, N is reduced. If the power is below the desired Pr, N is increased until the minimum number of samples required for the desired power is found (n).

For our analysis, we started with the 3–4 hr AEL color distribution as that is the most sparsely labeled and therefore the most conservative. We targeted Pr = 80% and calculated the minimum number of samples required to identify lineages with different effect sizes (match rates). The alpha level of our analysis was set at 0.000001, which corresponds to a 0.05 p value with a Bonferroni correction for all combinations of 300 cell pairs.

DATA AND CODE AVAILABILITY

The code for implementing the lineage-relatedness statistical model is available at https://github.com/MikeVeling/Process-Bitbow-Data

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Alexa Fluor 647 AffiniPure Goat Anti-Horseradish Peroxidase antibody	Jackson Immuno Research	Cat# 123–605-021; RRID: AB_2338967
Experimental Models: Organisms/Strains
D. melanogaster: yw;;UAS-nBitbow	This paper	N/A
D. melanogaster: hs-flp122;;	Rangarajan et al., 1999	N/A
D. melanogaster: w*;;elav-Gal4	Bloomington Drosophila Stock Center	RRID:BDSC_8760
D. melanogaster: w1118;;GMR72F11-Gal4	Bloomington Drosophila Stock Center	RRID:BDSC_39786
Recombinant DNA
Plasmid: pJRFC-MUH-nBitbow	This paper	N/A
Software and Algorithms
Fiji	NIH	RRID:SCR_002285
Cytoscape (version 3.7.1)	NIGMS	RRID:SCR_003032
Python Statsmodels	NIDA	RRID:SCR_016074
ZEN (2012 SP1 black edition, release 8.1.0)	Carl Zeiss Microscopy	RRID:SCR_013672
Leica Microsystems LAS AF (version 2.6.3)	Leica Microscopy	RRID:SCR_008960
Prism 8	GraphPad	RRID:SCR_002798
Process-Bitbow-Data	This Paper	https://github.com/MikeVeling/Process-Bitbow-Data

Highlights.

• A single nBitbow cassette generates up to 31 color variants

• nBitbow enhances the efficiency and improves the accuracy of cell lineage tracing

• nBitbow is suitable for lineage tracing in both the PNS and the CNS of Drosophila

• The lineage relationship of all PNS neurons in Drosophila larvae is determined