A Forecasting Model of Disease Prevalence Based on the McKendrick-von Foerster Equation

Abstract

A new model for disease prevalence based on the analytical solutions of McKendrick-von Foerster’s partial differential equations is developed. Derivation of the model and methods to cross check obtained results are explicitly demonstrated. Obtained equations describe the time evolution of the healthy and unhealthy age-structured sub-populations and age patterns of disease prevalence. The projection of disease prevalence into the future requires estimates of time trends of age-specific disease incidence, relative survival functions, and prevalence at the initial age and year available in the data. The computational scheme for parameter estimations using Medicare data, analytical properties of the model, application for diabetes prevalence, and relationship with partitioning models are described and discussed. The model allows natural generalization for the case of several diseases as well as for modeling time trends in cause-specific mortality rates.

Introduction

Several types of forecasting (or projection) models are currently used to predict the prevalence of a specific disease and/or the number of individuals living with the disease. The simplest approach is designed in three steps: disease prevalence is estimated in subpopulations, the estimated values are assumed to be unchanged (or changed using a predetermined pattern) in the future, and the number of sick individuals is computed by multiplying these estimates by the size of the projected population from the Census projections [1]. Recently, this approach has been applied to the study of atrial fibrillation and flutter [2], diabetes [3], and glaucoma [4]. Time-series methods such as autoregression and Lee-Carter-based approaches [5] widely used for the calculation of incidence and mortality rates can also be used to forecast disease prevalence, e.g., for prevalence of end-stage renal disease [6]. More advanced approaches use multistate models involving healthy and unhealthy states. Predictions are based on assumptions about the future dynamics of incidence, total mortality, and the death hazard ratio of being in the unhealthy state; such models have been applied to the prevalence of diabetes [7], Alzheimer’s disease [8], and atrial fibrillation [9]. Although the models currently used in projections of disease prevalence are different in assumptions, the influence of these technical assumptions on predicted prevalence has not been estimated.

In existing models, projections are constructed by assuming that parameters driving the population process such as hazard ratios or age-specific incidence and mortality rates (or their current trends) will not change with time. This is a very restrictive assumption, that is made because of i) insufficient measurements for more precise prognoses and ii) insufficient methodological developments allowing for natural incorporation of the trends of these parameters in the future. The objective of this study is to develop a new population model of disease prevalence that would i) generalize multistate models for continuous time to better reflect the nature of the dynamic processes and minimize biases from rounding of age and time measures in data, ii) be maximally analytical to provide flexibility in the analyses of dynamic properties and provide insights on these population processes, iii) provide a flexible computational framework allowing for the inclusion of specific advanced models for projecting the parameters driving population processes, and iv) be ultimately free from methodological limitations that are usually incurred when a researcher makes pure technical assumptions to simplify calculation. Application of this model to population data will allow us to significantly improve the quality of health forecasting by improving the accuracy of predictions and controlling for possible biases including the bias from incomplete data for incidence and mortality-related measures.

The model is constructed to represent changes in the age-patterns of prevalence of age-related diseases over time to reflect changes in incidence and survival in the population under study. This process is described by age dynamics in a multi-state model with transitions from healthy to one of multiple unhealthy states, between these unhealthy states, and ultimately the transition to the “deceased” state. Cohort-specific models for these transitions are integrated in the form of a system of interrelated McKendrick-von Foerster partial differential equations [10–12]. The original form of the McKendrick-von Foerster equation describes the dynamics of a cohort by means of the density of age distribution function, i.e., it allows a researcher to predict the age distribution over the time. In the standard form, the equation does not include discrete states, therefore if one needs to predict health-related outcomes (e.g., disease prevalence) respective generalization is required. We derive the equation for two (healthy and unhealthy) states in which transition to an unhealthy state is based on a diagnosis of a chronic disease for a patient. These equations describe the time evolution of population age structures and age patterns of disease prevalence. The equation can be analytically solved and the solution can be recalculated to compute disease prevalence for a specific cohort. The solution represents analytical expressions, extrapolation of which provides a forecasting model of disease prevalence. The projection for disease prevalence is obtained through summing (or averaging) over the contributions of specific cohorts. We evaluate age-adjusted prevalence, however the approach can be naturally generalized for predictions of sex- and race-adjusted prevalence as well as for inclusion of the effects of in- and out-migration.

McKendrick-von Foerster equations and the model for disease prevalence

The McKendrick-von Foerster equations for the density of age distribution of healthy $n(x,y)$ and unhealthy $p(x,y)$ subpopulations ($x$ and $y$ denote age and calendar year) are used to describe joint dynamics of related age-distributions in these subpopulations at a given time interval. The densities are normalized such that the integral over all ages gives the total number of living subjects in respective populations in year $y$. The decline in the subpopulation of healthy individuals due to death and disease diagnoses cases is described by mortality ${\mu }_n(x,y)$ and incidence $\lambda (x,y)$ rates. Similarly, the number of individuals in the unhealthy subpopulation can increase because of migration from the healthy population due to new diagnoses and decrease because of death Derivatives over time ($dx/dt=dy/dt=1$)

$$\frac{dn(x,y)}{dt}=\frac{\partial n(x,y)}{\partial x}+\frac{\partial n(x,y)}{\partial y},\frac{dp(x,y)}{dt}=\frac{\partial p(x,y)}{\partial x}+\frac{\partial p(x,y)}{\partial y}$$ (1)

result in the McKendrick-von Foerster equation for the density of age distribution of healthy and unhealthy subpopulations:

$$\begin{gathered} \frac{\partial n(x,y)}{\partial x}+\frac{\partial n(x,y)}{\partial y}=-\lambda (x,y)n(x,y)-{\mu }_n(x,y)n(x,y) \\ \frac{\partial p(x,y)}{\partial x}+\frac{\partial p(x,y)}{\partial y}=\lambda (x,y)n(x,y)-{\mu }_p(x,y)p(x,y) \end{gathered}$$ (2)

The term $-\lambda (x,y)n(x,y)$ in the first equation of (2) describes the decrease in the number of healthy individuals and, the respective term $\lambda (x,y)n(x,y)$ in the second equation of (2) describes the increase in the number of unhealthy individuals. The terms containing $-{\mu }_{n,p}(x,y)n(x,y)$ describe declines in subgroups of healthy and unhealthy individuals due to death. The equation can be solved if we determine initial/boundary conditions for the densities which represent the values of the densities in initial year and ages that can be obtained from available data. The explicit solution is presented in Appendix. The solution is:

$$\begin{gathered} n(x,y)=n({\overline{x}}_0,{\overline{y}}_0)S_h(x-{\overline{x}}_0,{\overline{x}}_0) \\ p(x,y)=p({\overline{x}}_0,{\overline{y}}_0)S_d(x-{\overline{x}}_0,{\overline{x}}_0)+n({\overline{x}}_0,{\overline{y}}_0){\int }_{{\overline{x}}_0}^x\lambda (\tau ,y-x+\tau )S_h(\tau -{\overline{x}}_0,{\overline{x}}_0)S_d(x-\tau ,\tau )d\tau \end{gathered}$$ (3)

where $({\overline{x}}_0,{\overline{y}}_0)$ is the point of the origin of the cohort (i.e., either ${\overline{y}}_0=y_{00}=1992$ or ${\overline{x}}_0=x_0=65$); $S_h(s,x_0)$ and $S_d(s,x_0)$ are the survival functions in healthy and unhealthy states with the first and second arguments showing the time period and the age of the cohort forming, respectively. We also use the survival for entire population (i.e., for $n(x,y)+p(x,y)$) or, simply, total survival $S_t(s,x_0)$ with the same arguments.

These expressions can be used for modeling of time changes in disease prevalence, that is defined as

$$P(x,y)=\frac{p(x,y)}{n(x,y)+p(x,y)}$$

Differentiation of both parts and using (3) results is (see also (13)):

$${\partial }_{xy}P(x,y)=\lambda (x,y)(1-P(x,y))+({\mu }_n(x,y)-{\mu }_p(x,y))P(x,y)(1-P(x,y))$$ (4)

The above solution for $P(x,y)$ takes the form:

$$P(x,y)=P({\overline{x}}_0,y-x+{\overline{x}}_0)\frac{S_d(x-{\overline{x}}_0,{\overline{x}}_0)}{S_t(x-{\overline{x}}_0,{\overline{x}}_0)}+{\int }_{{\overline{x}}_0}^x\lambda (\tau ,y-x+\tau )\frac{S_d(x-\tau ,\tau )}{S_t(x-\tau ,\tau )}d\tau$$ (5)

The formula for disease prevalence (5) exactly equals the expression for the disease prevalence model obtained based on another approach in [13]. One can make sure that the representation (5) satisfies equation (4) (see eq. (14)):

Estimation and Projection

Projection is constructed as a solution of the ordinal differential equation for a specific cohort. Then age-adjusted prevalence is calculated through the sum of age- and cohort-specific prevalence for a certain year. Four models are considered. The first is based on eqn. (4) rewritten for a cohort:

$$\frac{dP(x_s,y_s)}{ds}=\lambda (x_s,y_s)(1-P(x_s,y_s))+({\mu }_n(x_s,y_s)-{\mu }_p(x_s,y_s))P(x_s,y_s)(1-P(x_s,y_s))$$

where $x_s$ and $y_s$ are defined in eqn. (10). The model in brief notation is:

$$P^{\prime }(s)=\overline{\lambda }(s)+({\mu }_n(s)-{\mu }_p(s))P(s)(1-P(s))$$ (6)

Initial prevalence (i.e., $P(65)$) for all cohorts, as well as models for incidence ($\overline{\lambda }(s)=\lambda (s)(1-P(s))$) and mortality from healthy (${\mu }_n(s)$) and unhealthy (${\mu }_p(s)$) states are required for solution of (6). Often information on total (${\mu }_t(s)$) and cause-specific (${\mu }_c(s)$) mortality is accessible instead of mortality from healthy and unhealthy states. The second model uses ${\mu }_t(s)$ and ${\mu }_c(s)$ instead of ${\mu }_n(s)$ and ${\mu }_p(s)$. Both pairs of quantities are related through equations: ${\mu }_t(s)={\mu }_p(s)P(s)+{\mu }_n(s)(1-P(s))$ and ${\mu }_c(s)={\mu }_p(s)P(s)$. The second model is:

$$P^{\prime }(s)=\overline{\lambda }(s)+{\mu }_t(s)P(s)-{\mu }_c(s)$$ (7)

The third model uses the fraction of death cases for individuals with a disease among all death cases, $f_p={\mu }_c/{\mu }_t$. This measure can be estimated from the Multiple Cause of Death data without attracting information on cohort-specific population counts, usually known with poorer accuracy. The third model is:

$$P^{\prime }(s)=\overline{\lambda }(s)+{\mu }_t(s)(P(s)-f_p(s))$$ (8)

The fourth model uses hazard ratio ($h_r(s)={\mu }_p(s)/{\mu }_n(s)$) as an additional measure to the total mortality which also can be known from other studies. The model from ref. [7] used the total mortality and hazard ratio for their projections. The model rewritten to incorporate the death hazard ratio is:

$$P^{\prime }(s)=\overline{\lambda }(s)+{\mu }_t(s)\frac{1-h_r(s)}{1+(h_r(s)-1)P(s)}P(s)(1-P(s))$$ (9)

We apply the model for forecasting diabetes prevalence using 5%-Medicare data. There are more than 5M individual Medicare trajectories in these data. A Medicare trajectory represents the time-ordered collection of individual Medicare records in which each record contains ICD-9 codes for medical diagnoses and used procedures. We extract codes of diabetes mellitus type 2 (T2D) which allowed us to identify whether an individual i) had T2D at the time of Medicare enrollment/entry into the data, ii) experienced T2D onset while covered by the Medicare system (in this case the day of onset is identified), or iii) did not have T2D prior to the date of death/censoring. The empirical estimates of the epidemiologic characteristics (prevalence, incidence, mortality, and related quantities involved in eqs. (6)–(9)) are based on the analysis of individual trajectories of healthy and unhealthy patients, i.e., the sets of records before (for the healthy group) and after (for the unhealthy group) disease onset. For example, incidence and all mortality in each group are defined empirically in age groups (as the number of onset/death cases in an age group per the respective number of person-years).

To solve these equations with respect to disease prevalence we need to know the initial prevalence (i.e., $P(65)$), age-specific incidence, and two mortality related characteristics for different models. In our data, these characteristics are available untill 2012. Therefore, we need to apply a model for forecasting of all these measures after 2012. Three approaches are used. The first is the simplest one when we assume time independent patterns for these quantities after 2012. This is in accordance with assumptions made for diabetes prevalence projection in ref [7] (similar assumptions were used in refs [14–17]). The second is the autoregressive error model that includes three parameters per age group to estimate: intercept, effect of time (slope parameter), and autoregression of error terms: ${\mu }_{x,y}=u_x+b_{x}t+{\nu }_t,{\nu }_t={\alpha }_x{\nu }_{t-1}+e_t$. The third model is the Lee-Carter approach [5] that is applied for incidence and for mortalities. In this approach $\log (m_{x,y})=a_x+b_x{k}_y+e_{x,y},k_y=k_{y-1}+d+e_y$, where $a_x$ is the average (over time) log-mortality at age $x$ and $b_x$ measures the response at age $x$ to change in the overall level of mortality over time. Time series $k_y$ represents the overall level of mortality in year $y$. It is modeled by the random walk with drift $d$. This model exploits the fact that age-specific rates fluctuate together over time, though this is not a precise observation. The Lee-Carter approach models mortality age and time patterns in a quite parsimonious style. In total, the model requires only two parameters per age group and the drift parameter of time changes in the overall level of mortality. Parameters are estimated using the two-stage algorithm involved the singular value decomposition. In addition we use the approach developed by Wilmoth [18] allowing for dealing with age groups with zeroth number of cases.

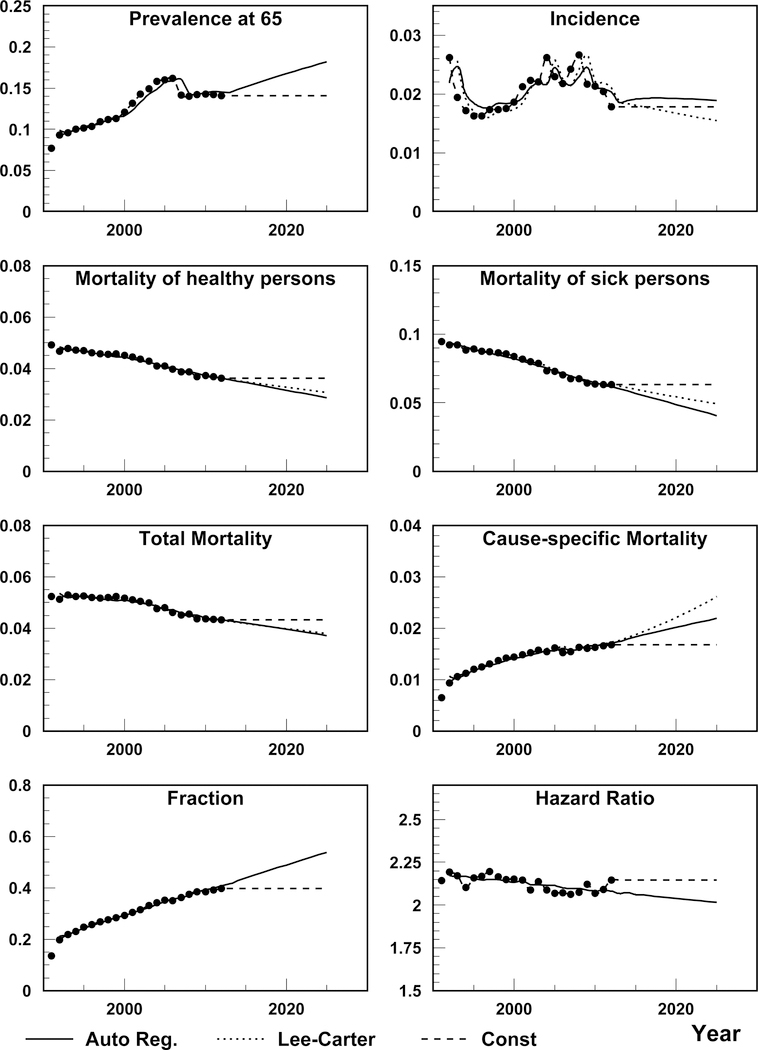
Figure 1 shows estimation and projection of all the eight measures needed for solution of eqs. (6)–(9). Note that projections are made for age-specific rates (except initial prevalence), and then age-adjusted measures are calculated. Namely age-adjusted measures are presented in Figure 1. Projections at each plot require additional visual inspection to use them for constructing projections using respective equations. Initial prevalence is presented in upper-left plot of Figure 1. The model based on autoregression predicts an increase in the initial prevalence, however this is due to the increase in period before 2005. After that empiric prevalence is almost constant. Therefore we use the constant projection in solution of (6)–(9) for the initial prevalence. The pattern of the incidence rate is not monotonic. Partly this can be explained by the effects of respective risk factors and transitions of diagnoses to younger-than-65 age group with time. We use constant models for incidence above 2012. Lee-Carter model reasonably reflects time patterns of ${\mu }_n(s)$, ${\mu }_p(s)$, and ${\mu }_t(s)$, therefore we use the Lee-Carter projection for them. Both Lee-Carter and autoregression model overestimate the cause-specific (${\mu }_c(s)$) mortality. We use the constant projection in the model (7). To be consistent, we use the constant total mortality projection when solving eqn. (7). Finally, we use constant projection for the fraction ($f_p(s)$) and autoregression projection for the hazard ratio ($h_r(s)$). The choice of specific projections described defines our base model for T2D projection. All estimated model parameters are shown in Supplementary Table 1. Solutions of eqs. (6)–(9) obtained using the projected coefficients in the base model provide four projections that are compared and discussed below. The solutions with other variants of the projected coefficients are compared in sensitivity analysis.

Figure 1.

Data (points) and projections using autoregression and Lee-Carter approach. Incidence and the four mortality hazard functions have units of year⁻¹; initial prevalence proportion, the fraction of death cases for individuals with a disease among all death cases ($f_p={\mu }_c/{\mu }_t$) and the hazard ratio are dimensionless.

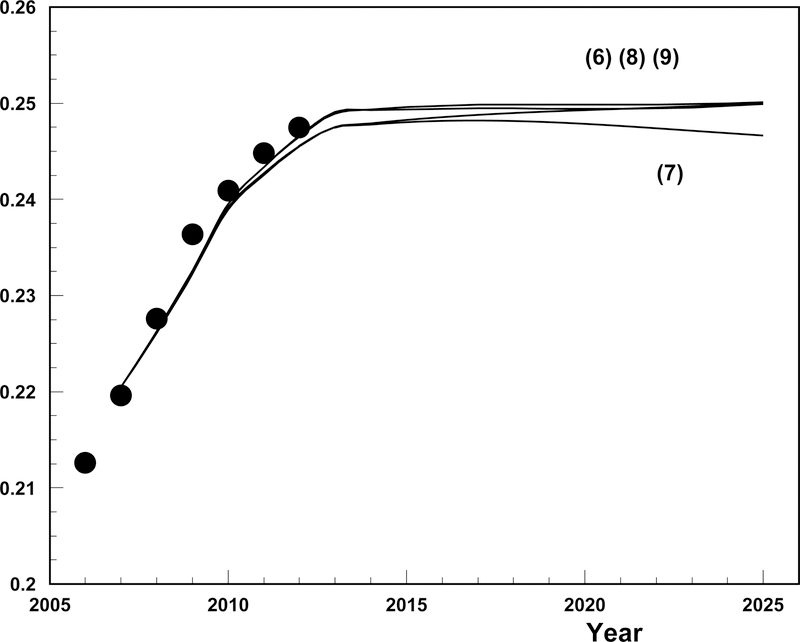
The resulting empirical estimates and future projections of T2D prevalence vs. calendar time are presented in Figure 2. The projection begins in 2008 with empiric estimates of T2D age-specific prevalence used as the initial values for eqs. (6)–(9) which generated the projection. Age-specific prevalence for the next age and year are calculated using eqs. (6)–(9) and then age-adjusted. Since we have real data until 2012 both empirical estimates and projected estimates for the 2008–2012 period are presented. Post 2012 only the projected values are available. Actual values of incidence, mortality, hazard ratios, and the fraction $f_p$ were used till 2012 and then their projections using the models selected as described above were used. The models based on eqns (6)–(9) appropriately describe the empirical data for the 2008–2012 period and then predict a leveling off in disease prevalence. Predictions of all four models are close. The lowest prevalence is predicted by the model using cause-specific mortality (i.e., eq. (7)). The model involving the fraction $f_p$ (i.e., eq. (8)) is close to the model (7) at 2008 and then increase and join the models (6) and (9) in 2020.

Figure 2.

Data (points) and projections of diabetes prevalence starting from 2008. Only data before 2008 are used for estimation. Empirical prevalence is shown by big dots. Four solid lines are projections using eqns. (6)–(9) using specifications of models for projections of coefficients: i) constant projections are used for initial prevalence, incidence, fractions $f_p(s)$, cause-specific and total (only for projections using eq. (7)); ii) Lee-Carter projections are used for mortality from healthy and unhealthy states as well as for total mortality for projections using eqs. (8) and (9); and iii) autoregression projection is used for hazard ratio. Further details and discussions of the specifications are described in the text.

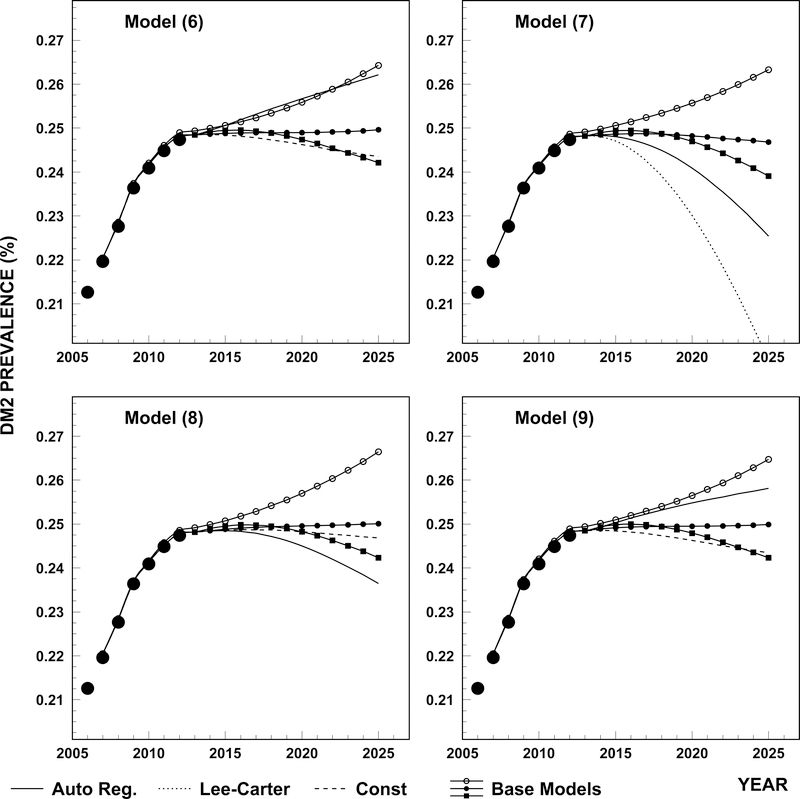
The results of sensitivity analysis are presented in Figure 3. Four plots correspond to four models given by eqs. (6)–(9). For each model we present the base model also shown in Figure 2 (solid line and closed dots) together with two alternative base models where initial prevalence is predicted using autoregression instead of the constant model (solid line with open dots) and incidence rate is predicted by the Lee-Carter model instead of the constant model (solid line with squares). Also three other curve types correspond to models in which coefficients are projected using autoregression, Lee-Carter, and constant models. We see that non-critical approach (i.e. without performing adequate sensitivity studies and cross checking the ability of the model to predict past data) for choosing the projections of coefficients could result in non-realistic projections of T2D prevalence.

Figure 3.

Projections of T2D prevalence using different models (6)–(9) and different approaches for coefficient projections: i) base model in which coefficients are chosen as in Figure 2 (solid line with closed dots); ii) the base model in which initial prevalence is predicted using autoregression instead of constant model (solid line with open dots); iii) the base model in which incidence rate is predicted by Lee-Carter model instead of constant model (solid line with squares); iv) all measures (except initial prevalence) are obtained using autoregression (solid); v) all measures are obtained using Lee-Carter (dotted model), not applicable for models (8) and (9), almost coincide with approach iii) for eq. (6); and vi) all measures are obtained using constant model.

Discussion

In this study we have developed a new approach to modeling disease prevalence for a cohort based on the interrelated McKendrick-von Foerster partial differential equations. The model provides analytical expressions for disease prevalence for the analysis of the relative contributions of incidence and survival as important components of total prevalence. Obtained analytical expressions (3) represent the forecasting model allowing for the projection of these functions into the future. They allow for the description of the time evolution of the prevalence of a specific disease and the subpopulation of individuals without this disease. Expression (5) represents the analytical solution for age- and time-specific disease prevalence involving integration over ages at diagnoses. The prevalence patterns can be also presented in the form of ordinary differential equations for cohort-specific disease prevalence that are subject for numeric solution. Four types of differential equations were proposed. Although they are mathematically equivalent, specific equations could be more convenient depending on the measurements available for model estimation.

The coefficients in the differential equations (6)–(9) are related to disease incidence and survival, and therefore time-dependent and largely unknown. In contrast to approaches currently in use[7] that assume that the incidence rate and death hazard ratios are unchanged over time, the approach developed in our paper uses well-developed time series methods to model these coefficients explicitly. We used two widely known approaches: i) autoregression––common in time series analysis, and ii) Lee-Carter widely used in forecasting age- and time-structure of mortality and other transition rates in demography.

We applied our model to the case of type II diabetes mellitus. Although data was available for the 1992–2013 period, we only used data from 1992–2008 for the model estimation and applied the resulting model to forecast of diabetes prevalence from 2008 to 2013 and beyond. We found that under our choice of time-series models for the coefficients in differential equations (6)–(9) the model predicts empiric prevalence well (Figure 2) and suggests that type II diabetes mellitus prevalence will experience a deceleration in the rate of its increase after 2013. We demonstrated that approaches with constant coefficients provide projections that strongly deviate from those in which coefficients are estimated based on time series methods and that unrealistic assumptions on the dynamics of the coefficients result in bias, the size of which can be estimated using our model (Figure 3). Thus, use of our model will reduce the levels of uncertainty currently present in health forecasting with all of the resulting benefits to health planning. Another type of uncertainties are pure statistical uncertainties that can come from sampling and from uncertainties in estimating model parameters for the coefficients in differential equations (6)–(9). Non parametric bootstrap (resampling with replacement from the data set) shows that the sampling uncertainty estimated as standard error of multiple calculations based on resampled datasets is less than 1% in respect of estimated and projected prevalence. Standard error for projected prevalence due to the coefficients in differential equations (6)–(9) is about 30% and similar for Lee-Carter and autoregression projections with the largest uncertainty coming from diabetes incidence.

The model developed in this paper represents a multistate model with two states (healthy and unhealthy) with continuous time and age. Such model formulation allows to better reflect the nature of dynamic population processes that are continuous with respect to time. In Medicare and other administrative data age and time are known at the daily level (i.e. the exact date of birth and calendar date of any given diagnosis is known), and therefore, when using our model there is no need to split variables that are continuous by nature into fairly arbitrary discrete groups. The model can be further extended to the case of several unhealthy states, recovery from unhealthy states[19] as well as the incorporation of migration if the respective transition rates of in and out migration is known. Since all projections are cohort-based, the projections for the entire population can be constructed from projections of individual subpopulations.

The analytic expression for disease prevalence developed in this paper allows for analytical manipulation that can provide important insights into the properties of the age- and time-patterns of disease prevalence which can be further used to explicitly model potential future health scenarios and other hypothesized assumptions and to identify the sources (properties) behind identified patterns. For example, the formula for disease prevalence (5) is closely related to the model for diabetes presented in a recently developed partitioning approach [13]. Although the focus of partitioning analyses is different (i.e., trend decomposition) one by-product of this approach is the model for disease prevalence. Expression (5) obtained from the solution of McKendrick-von Foerster partial differential equation exactly coincides with the expression for disease prevalence obtained within the partitioning approach. The resulting formula for prevalence dynamics provides an analytic expression for prevalence as a function of age and time and can be used in theoretical analyses to provide insights into the dynamics of prevalence and for the projection of these dynamics numerically. Another example is the analysis of the properties of age patterns of disease prevalence. If we assume constant incidence (${\lambda }_0$), initial prevalence ($P_0$) and model relative survival (i.e., $S_d/S_t\equiv S_r$ in (5)) by an exponential distribution (i.e., $S_r(x-\tau ,\tau )=\exp (-b(x-\tau ))$ and $S_r(x-x_0,x_0)=\exp (-b(x-x_0))$), the integrals in (5) are analytically calculated resulting in $P(x,y)=(P_0-{\overline{\lambda }}_0)E+{\overline{\lambda }}_0$, where ${\overline{\lambda }}_0={\lambda }_0/b$ and $E=\exp (-b(x-x_0))$. This model predicts a decrease in disease prevalence with age because of the effect of relative survival being less than one. More realistic scenarios are also analytically calculable, e.g. if the incidence is age dependent ($\lambda ={\lambda }_0+{\lambda }_{x}x$), the expression for prevalence becomes $P=(P_0+{\overline{\lambda }}_x-{\overline{\lambda }}_0-x_{0}b{\overline{\lambda }}_x)E-{\overline{\lambda }}_x+{\overline{\lambda }}_0+xb{\overline{\lambda }}_x$. This model predicts that age pattern of disease prevalence can have a maximum, and the maximal age is: $x_{max}=x_0+b^{-1}\log (1-b{x}_0+(p_0-{\overline{\lambda }}_0)/{\overline{\lambda }}_x)$ if the argument of the logarithm is positive.

Appendix. Solution of McKendrick-von Foerster equations

Observational data are usually available within a certain region over age and time. For example, the Medicare Administrative Data used in this study provides individual heath related information on U.S. Medicare beneficiaries after age 65 and after a certain year (1991). The panel length and level of detail provided by such data allow us to determine if a certain individual has the disease of interest and therefore calculate the densities. The disease indicator of disease presence at any time points is usually defined through occurrence of disease-specific ICD-9 codes during a certain look-back period (usually 12 months). Figure 1 presents the Lexis diagram in the plane over age (in years; denoted by $x$) and calendar time (in years; denoted by $y$). Each of the dashed lines in the Lexis diagram uniquely corresponds to a birth cohort with the birth time $y_b=y-x$ for any point $(x,y)$ belonging to the cohort-specific dashed line. Therefore, epidemiologic characteristics at a given point of time are defined by the history of the cohort represented by a leftward move along the respective line in the Lexis diagram down to bounds of the available region. The bound is defined by an initial year ($y_{00}$) or minimal age ($x_0$) observed in the data. These two subareas are separated by the bisecting line defined as $y=y_{00}+x-x_0$. Above the bisecting line, the starting point is defined by the initial conditions y = y₀₀ with various ages while below the line the initial point is defined by boundary condition $x=x_0$ with various years. The cohort-specific bounding point is defined as ${\overline{x}}_0=\max (x_0,y_{00}-y_b)$ and ${\overline{y}}_0=y_b+{\overline{x}}_0$. The values of the densities in points $({\overline{x}}_0,{\overline{y}}_0)$ completely define boundary and initial conditions: $n_0({\overline{x}}_0,{\overline{y}}_0)$ and $p_0({\overline{x}}_0,{\overline{y}}_0)$. Specifically, the boundary conditions, $n_{x0}(x)=n(x,y_{00})$ and $p_{x0}(x)=p(x,y_{00})$, represent the densities at $y_{00}$. Integration over $x$ gives the number of individuals in $y_{00}$. Also, we use $n_{00}=n(x_0,y_{00})$ and $p_{00}=p(x_0,y_{00})$. Respectively, the initial conditions are $n_{0y}(y)=n(x_0,y)$ and $p_{0y}(y)=p(x_0,y)$. The generalized initial conditions, i.e., $n_0({\overline{x}}_0,{\overline{y}}_0)$ and $p_0({\overline{x}}_0,{\overline{y}}_0)$, equal $n_{x0}(x)$ and $p_{x0}(x)$ for $y\le y_{00}+x-x_0$ or $n_{0y}(y)$ and $p_{0y}(y)$ for $y>y_{00}+x-x_0$.

The standard approach for solving partial differential equations is the method of characteristics. The characteristic is a curve in the plane $(x,y)$ along which the partial differential equations are reduced to an ordinary differential equation. The equation of the characteristics is specified from the condition that the left-hand side (LHS) of these equations represent the full derivative:

$$\frac{dn(x(s),y(s))}{ds}=\frac{\partial n}{\partial x}\frac{dx}{ds}+\frac{\partial n}{\partial y}\frac{dy}{ds}$$

Therefore, the equation for the characteristic curves is defined by $dx/ds=1$ and $dy/ds=1$ resulting in

$$\begin{gathered} x=x_0+s\equiv x_s \\ y=y_{00}+s\equiv y_s \end{gathered}$$ (10)

For the characteristic line going through the origin $(x_0,y_{00})$

$$\frac{dn(x_s,y_s)}{ds}=-\lambda (x_s,y_s)n(x_s,y_s)-{\mu }_n(x_s,y_s)n(x_s,y_s)$$

The solution is straightforward

$$\begin{gathered} n(x_s,y_s)=n_{00}\exp \left(-{\int }_0^s(\lambda (x_{\overline{s}},y_{\overline{s}})+{\mu }_n(x_{\overline{s}},y_{\overline{s}}))d\overline{s}\right)=n_{00}\exp \left(-{\int }_{x_0}^{x_0+s}(\lambda (u,y_{00}+u-x_0)+{\mu }_n(u,y_{00}+u-x_0))du\right) \\ =n_{00}{S}_h(s,x_0) \end{gathered}$$

A survival function with two arguments, S_h(s, x₀), denotes the survival probability in the time period shown in the first argument for the cohort forming at the age shown in the second argument. Subscript h in survival function shows healthy survival that is the fraction of individuals staying in the healthy state. Respective equation for unhealthy subpopulation becomes

$$\frac{dp(x_s,y_s)}{ds}=\lambda (x_s,y_s)n_{00}{S}_h(s,x_0)-{\mu }_p(x_s,y_s)p(x_s,y_s)$$

Through the solution of homogeneous equation (i.e., without the first term in the right-hand side (RHS)) we search the solution in the form

$$p(x_s,y_s)=C(s)\frac{S_d(x_0+s)}{S_d(x_0)}$$

resulting in an ordinary differential equation for $C(s)$

$$\frac{dC(s)}{ds}{S}_d(s,x_0)=\lambda (x_s,y_s)n_{00}{S}_h(s,x_0)$$

Final solution for the cohort line going through the origin $(x_0,y_{00})$ is

$$\begin{gathered} p(x_s,y_s)=p_{00}{S}_d(s,x_0)+n_{00}{\int }_0^s\lambda (x_{\overline{s}},y_{\overline{s}})S_h(\overline{s},x_0)S_d(s-\overline{s},x_0+\overline{s})d\overline{s}= \\ =p_{00}{S}_d(x_s-x_0,x_0)+n_{00}{\int }_{x_0}^{x_s}\lambda (\tau ,y_s-\tau +x_0)S_h(\tau -x_0,x_0)S_d(x_s-\tau ,\tau )d\tau \end{gathered}$$

The above solution is true for the characteristic line $y=y_{00}+x-x_0$ (the diagonal line in the plot in Figure 1). For $y\le y_{00}+x-x_0$ (above the diagonal) the solution is constructed from the above expression by using other characteristic lines

$$\begin{gathered} n(x,y)=n_{x0}({\overline{x}}_0)S_h(y-y_{00},{\overline{x}}_0) \\ p(x,y)=p_{x0}({\overline{x}}_0)S_d(y-y_{00},{\overline{x}}_0)+n_{x0}({\overline{x}}_0){\int }_{{\overline{x}}_0}^x\lambda (\tau ,y-x+\tau )S_h(\tau -{\overline{x}}_0,{\overline{x}}_0)S_d(x-\tau ,\tau )d\tau \end{gathered}$$

where ${\overline{x}}_0=x-y+y_{00}$ is age for $y=y_{00}$.

Finally, we need to find solution for $y>y_{00}+x-x_0$. Similarly, the solutions are:

$$\begin{gathered} n(x,y)=n_{0y}({\overline{y}}_0)S_h(x-x_0,x_0) \\ p(x,y)=p_{0y}({\overline{y}}_0)S_d(x-x_0,x_0)+n_{0y}({\overline{y}}_0){\int }_{x_0}^x\lambda (\tau ,y-x+\tau )S_h(\tau -x_0,x_0)S_d(x-\tau ,\tau )d\tau \end{gathered}$$

where ${\overline{y}}_0=y-x+x_0$.

We can write the solution in the general form appropriate for both areas:

$$\begin{gathered} n(x,y)=n_0({\overline{x}}_0,{\overline{y}}_0)S_h(x-{\overline{x}}_0,{\overline{x}}_0) \\ p(x,y)=p_0({\overline{x}}_0,{\overline{y}}_0)S_d(x-{\overline{x}}_0,{\overline{x}}_0)+n_0({\overline{x}}_0,{\overline{y}}_0){\int }_{{\overline{x}}_0}^x\lambda (\tau ,y-x+\tau )S_h(\tau -{\overline{x}}_0,{\overline{x}}_0)S_d(x-\tau ,\tau )d\tau \end{gathered}$$ (11)

The straightforward check shows that these functions satisfy the eqs. (2). Indeed, it can be seen if we use the following explicit derivatives (denoting the differential operator ${\partial }_{xy}=(\partial /\partial x+\partial /\partial y)$):

$$\begin{gathered} {\partial }_{xy}{n}_0({\overline{x}}_0,{\overline{y}}_0)={\partial }_{xy}{p}_0({\overline{x}}_0,{\overline{y}}_0)=0, \\ {\partial }_{xy}{S}_h(x-{\overline{x}}_0,{\overline{x}}_0)=-(\lambda (x,y)+{\mu }_n(x,y))S_h(x-{\overline{x}}_0,{\overline{x}}_0) \\ {\partial }_{xy}{S}_d(x-{\overline{x}}_0,{\overline{x}}_0)=-{\mu }_p(x,y)S_d(x-{\overline{x}}_0,{\overline{x}}_0) \end{gathered}$$

and

$$\begin{array}{r}{\partial }_{xy}{\int }_{{\overline{x}}_0}^x\lambda (\tau ,y-x+\tau )S_h(\tau -{\overline{x}}_0,{\overline{x}}_0)S_d(x-\tau ,\tau )d\tau =\lambda (x,y)S_h(x-{\overline{x}}_0,{\overline{x}}_0)\\ -{\mu }_p(x,y){\int }_{{\overline{x}}_0}^x\lambda (\tau ,y-x+\tau )S_h(\tau -{\overline{x}}_0,{\overline{x}}_0)S_d(x-\tau ,\tau )d\tau \end{array}.$$

Model for Disease prevalence

Prevalence probability is defined in terms of the densities as

$$P(x,y)=\frac{p(x,y)}{n(x,y)+p(x,y)}$$ (12)

Applying the operator ${\partial }_{xy}$ to this equation and using the original McKendrick-von Foerster equations (2) we obtain the partial differential equation for the prevalence probability:

$$\begin{gathered} {\partial }_{xy}P(x,y)=\frac{{\partial }_{xy}p(x,y)(n(x,y)+p(x,y))-p(x,y)({\partial }_{xy}n(x,y)+{\partial }_{xy}p(x,y))}{{(n(x,y)+p(x,y))}^2}= \\ =\frac{\lambda (x,y)n(x,y)-{\mu }_p(x,y)p(x,y)}{n(x,y)+p(x,y)}+\frac{p(x,y)({\mu }_n(x,y)n(x,y)+{\mu }_p(x,y)p(x,y))}{{(n(x,y)+p(x,y))}^2} \end{gathered}$$ (13)

resulting in eq. (4). The above solution for $P(x,y)$ takes the form (5), in which $S_t(x-{\overline{x}}_0,{\overline{x}}_0)$ is the total survival with ${\partial }_{xy}{S}_t(x-{\overline{x}}_0,{\overline{x}}_0)=-(P(x,y){\mu }_p(x,y)+(1-P(x,y)){\mu }_n(x,y))S_t(x-{\overline{x}}_0,{\overline{x}}_0)$.

One can make sure that the representation (5) satisfies equation (4):

$$\begin{gathered} {\partial }_{xy}P(x,y)=P(x_0,y-x+x_0)\frac{S_d(x-x_0,x_0)}{S_t(x-x_0,x_0)}(-{\mu }_p(x,y)+P(x,y){\mu }_p(x,y)+(1-P(x,y)){\mu }_n(x,y))+\lambda (x,y) \\ +(-{\mu }_p(x,y)+P(x,y){\mu }_p(x,y)+(1-P(x,y)){\mu }_n(x,y)){\int }_{x_0}^x\lambda (\tau ,y-x+\tau )\frac{S_d(x-\tau ,\tau )}{S_t(x-\tau ,\tau )}d\tau = \\ =\lambda (x,y)(1-P(x,y))+({\mu }_n(x,y)-{\mu }_p(x,y))P(x,y)(1-P(x,y)) \end{gathered}$$ (14)