An efficient multi-locus mixed model framework for the detection of small and linked QTLs in F₂

Abstract

In the genetic system that regulates complex traits, metabolites, gene expression levels, RNA editing levels and DNA methylation, a series of small and linked genes exist. To date, however, little is known about how to design an efficient framework for the detection of these kinds of genes. In this article, we propose a genome-wide composite interval mapping (GCIM) in F₂. First, controlling polygenic background via selecting markers in the genome scanning of linkage analysis was replaced by estimating polygenic variance in a genome-wide association study. This can control large, middle and minor polygenic backgrounds in genome scanning. Then, additive and dominant effects for each putative quantitative trait locus (QTL) were separately scanned so that a negative logarithm P-value curve against genome position could be separately obtained for each kind of effect. In each curve, all the peaks were identified as potential QTLs. Thus, almost all the small-effect and linked QTLs are included in a multi-locus model. Finally, adaptive least absolute shrinkage and selection operator (adaptive lasso) was used to estimate all the effects in the multi-locus model, and all the nonzero effects were further identified by likelihood ratio test for true QTL identification. This method was used to reanalyze four rice traits. Among 25 known genes detected in this study, 16 small-effect genes were identified only by GCIM. To further demonstrate GCIM, a series of Monte Carlo simulation experiments was performed. As a result, GCIM is demonstrated to be more powerful than the widely used methods for the detection of closely linked and small-effect QTLs.

Introduction

Most complex traits are controlled by a few major genes with large effects plus a series of undetectable genes with small effects. When markers are introduced, some genes will be captured by the markers in recombinant or linkage disequilibrium with quantitative trait loci (QTLs). Among these reported QTLs, most have small effects on complex traits and some are closely linked QTLs [1,2], for example, flowering time in maize [3] and growth rate in Arabidopsis [4]. Although QTL mapping has proven to be useful for detecting major QTLs with relatively large effects, it may lack power in accurately modeling small-effect QTLs [5]. Additionally, closely linked QTLs might be mistakenly estimated as a single QTL with a larger effect at the wrong position if they have the same direction in effects, or they might be missed if their effects are in opposite directions [6]. We are now in the era of omics, which enables us to incorporate genetic variation in omics phenotypes into a QTL mapping framework. In expressional QTL (eQTL) mapping, most are trans-eQTLs with small effects [7,8]. Similar results have been observed in the mapping of metabolites [9], RNA editing levels [10] and DNA methylation [11]. Because of the difficulty in detecting small-effect and closely linked QTLs, the genetic foundations of most complex and omics-related traits are not well understood.

To overcome the above issue, many attempts have been made during the past several decades. In biology, accurate phenotypes and high-density molecular genotypes are needed for many thousands of individuals to map small-effect and closely linked QTLs [2]. In statistics, many approaches have been proposed. In early studies, some markers associated with complex traits of interest were selected to control polygenic background in composite interval mapping (CIM) and its derivatives [12–16]. Subsequently, controlling polygenic background via the selection of markers in the CIM was replaced by estimating all the marker variances or effects in one model [17–21]. To estimate these effects in one model, many penalization methods have been developed, for example, least absolute shrinkage and selection operator (lasso) [22], smoothly clipped absolute deviation [23] and empirical Bayes [24]. Although these penalization methods can handle a number of markers several times larger than the sample size, they will fail when the number of markers is significantly larger than the sample size, especially for extremely high marker density. Recently, controlling polygenic background in linkage analysis has been replaced by estimating polygenic variance in genome-wide association studies [25–27]. However, this method cannot be directly applied in F₂.

Goddard et al. [28] have proposed a method to treat marker effects as random and described several advantages of the random model approach over the fixed model treatment. This viewpoint has been further confirmed by Wang et al. [27,29]. If marker effects in F₂ are treated as random, five variance components must be estimated in genome scanning. Although Wang et al. [27] have proposed a new method for the detection of small and closely linked QTLs in the backcross generation, this method does not work in F₂. This is because there are five variance components to be estimated. Clearly, this increases the difficulty of parameter estimation and the calculation burden in genome scanning.

In this study, we propose a rapid and efficient multi-locus mixed linear model to detect small and linked QTLs in F₂. To decrease the number of variance components estimated in genome scanning, three measures were used. The first is to separately scan additive and dominant effects. The second is to fix the polygenic-to-residual variance ratio [30], and the last is to use the algorithm of Wen et al. [31]. To increase the power in the detection of small and linked QTLs, all the peaks in the negative logarithm P-value curve against genome position for additive or dominant effects were viewed as potential QTLs, and these potential QTLs were placed into one model for true gene identification. To confirm the benefit of the new method proposed in this study, yield and yield component traits in an ‘immortalized F₂’ (IMF₂) population derived from an elite rice hybrid [32] were reanalyzed by the new method, while a series of simulation studies were conducted to show the advantage of the new method over those currently used.

Results

Mapping QTLs for yield and yield component traits in an IMF₂

In this study, we reanalyzed four rice traits described in Zhou et al. [32] using four methods. The four traits are yield per plant (YIELD), tillers per plant (TILLER), grains per panicle (GRAIN) and thousand grain weight (KGW). The four methods were genome-wide composite interval mapping (GCIM)-random, GCIM-fixed, CIM and inclusive CIM (ICIM). GCIM-random and GCIM-fixed are the GCIM under the situations of random and fixed QTL effects, respectively. All the results are listed in Table 1, Supplementary Tables S1–S2 and Figure 1, Supplementary Figures S1–S3.

Table 1.

Previously reported genes for yield/plant (YIELD), tillers/plant (TILLER), grains/panicle (GRAIN) and thousand grain weight (KGW) in rice using GCIM-random, GCIM-fixed, ICIM and CIM methods

Trait	Gene	MSU_locus	Chr	Pos (Mb)	Marker associated	GCIM-random (A)				GCIM-fixed (B)				ICIM (C)				CIM (D)				Reference
						LOD	Add	Dom	r 2 (%)	LOD	Add	Dom	r 2 (%)	LOD	Add	Dom	r 2 (%)	LOD	Add	Dom	r 2 (%)
YIELD	Gn1a	LOC_Os01g10110	1	5.667	Bin40	10.52	−1.29	0.00	1.13													Ashikari et al. [37]
	1OsLSK1, LSK1	1LOC_Os01g47900	1	28.397	Bin135	12.79	1.47	0.00	1.71													1Zou et al. [38]
	2NOG1	2LOC_Os01g54860
																						2Huo et al. [39]
	GW2	LOC_Os02g14720	2	8.810	Bin268	3.00	0.00	−0.58	0.13													Song et al. [40]
	AFD1, OsG1L6, TH1	LOC_Os02g56610	2	34.340	Bin339	12.82	0.00	1.40	0.77													Li et al. [41]
				34.738	Bin344	10.68	0.00	−1.28	0.64
	GUDK, OsRLCK103	LOC_Os03g08170	3	4.894A, B	Bin378A, B, D	5.41	0.00	−0.84	0.28	5.91	0.00	−1.86	2.20	4.72	0.18	−3.06	7.23	4.33	0.78	−3.17	6.44	Ramegowda et al. [36]
				4.9D, 5C	Bin378∼Bin379C
	GS3	LOC_Os03g29380	3	15.597	Bin433	6.21	0.86	0.00	0.58													Fan et al. [33]
	GIF1	LOC_Os04g33740	4	19.644	Bin617	13.39	0.00	−1.51	0.90													Wang E et al. [42]
	GW5/qsw5	LOC_Os05g09520	5	3.438	Bin722	5.38	0.87	0.00	0.60													Liu et al. [34]
	d3	LOC_Os06g06050	6	3.291	Bin855	6.23	0.93	0.00	0.68													Ishikawa et al. [43]
	1OsglHAT1, GW6a	1LOC_Os06g44100	6	24.309	Bin936	12.39	0.00	−1.37	0.74													1Song et al. [44] 2Kyoko et al. [45]
	2OsAPO1, SCM2	2LOC_Os06g45460
	PROG1	LOC_Os07g05900	7	2.817	Bin989	10.58	1.31	0.00	1.36													Tan et al. [46]
	Ghd7	LOC_Os07g15770	7	8A, C	Bin1003∼Bin1004A, C	44.84	2.79	3.41	10.75	7.38	2.05	2.21	8.44	3.29	−0.22	2.52	5.10	6.91	−2.32	2.63	17.17	Xue et al. [35]
				12B	Bin1007∼Bin1008B
				12.4D	Bin1007D
	PAY1	LOC_Os08g31470	8	20.696	Bin1143	8.85	−1.10	0.95	1.31													Zhao et al. [47]
TILLER	d3	LOC_Os06g06050	6	4A	Bin859∼Bin860A	8.18	0.00	−0.56	2.44	8.28	0.00	−0.63	3.64					6.51	−0.26	−0.84	0.47	Ishikawa et al. [43]
				5.164B, 5.2D	Bin867B, D
	OsLIC, OsC3H46, 66LIC	LOC_Os06g49080	6	24.666	Bin938	2.86	0.25	0.00	0.93													Wang L et al. [48]
	TAC1, OsTAC1, Spk	LOC_Os09g35980	9	19.55A, B	Bin1262A, B	4.34	0.24	0.80	5.81	3.39	0.00	0.35	1.15									Yu et al. [49]
				5.761B	Bin42B
GRAIN	Gn1a	LOC_Os01g10110	1	6C	Bin43∼Bin44C	5.45	4.06	−2.88	3.31	5.44	4.66	−1.18	3.04	6.11	−6.00	−2.69	6.00	5.58	−6.01	−3.08	3.11	Ashikari et al. [37]
				6.04A, 6.2D	Bin44A, D
	NOG1	LOC_Os01g54860	1	28.442	Bin136	4.76	3.23	0.00	1.68													Huo et al. [39]
	PROG1	LOC_Os07g05900	7	7	Bin998∼Bin999									10.65	−8.53	2.46	10.89					Tan et al. [46]
	Ghd7	LOC_Os07g15770	7	8.4D, 8.407A	Bin1003D, Bin1004A	15.22	−3.40	5.13	3.96	14.48	6.79	5.72	8.45					10.81	−8.20	5.37	18.14	Xue et al. [35]
				8.756B	Bin1005B
KGW	GS3	LOC_Os03g29380	3	16.224A, 16.7D	Bin437A, Bin438D	15.02	−0.54	0.00	4.30	6.39	0.33	−0.38	2.63	28.06	−0.98	−0.15	16.00	21.06	−1.19	−0.30	16.83	Fan et al. [33]
				17B, C	Bin440∼Bin441B, C
	GW5/qsw5	LOC_Os05g09520	5	5A, B, C, 5.3D	Bin728∼Bin729A, B, C, Bin729D	33.11	1.00	0.00	14.76	33.56	0.97	−0.01	13.84	25.01	0.96	−0.16	13.78	13.65	0.96	−0.23	15.94	Liu et al. [34]
	IPA1	LOC_Os08g39890	8	25C	1Bin1151∼Bin1152C									15.75	0.40	0.15	2.87					Jiao et al. [50]
				28C	2Bin1175∼Bin1176C	5.08	−0.25	0.00	0.96	8.25	−0.38	0.00	2.13	210.11	−0.15	−0.17	4.80
				28.118A, B	Bin1176A, B

The individuals with missing phenotypes were excluded. The critical value for significance was $LOD\ge 2.5$ for all the methods. The data set was derived from Zhou et al. (2012). chr: chromosome; LOD: logarithm of odds.

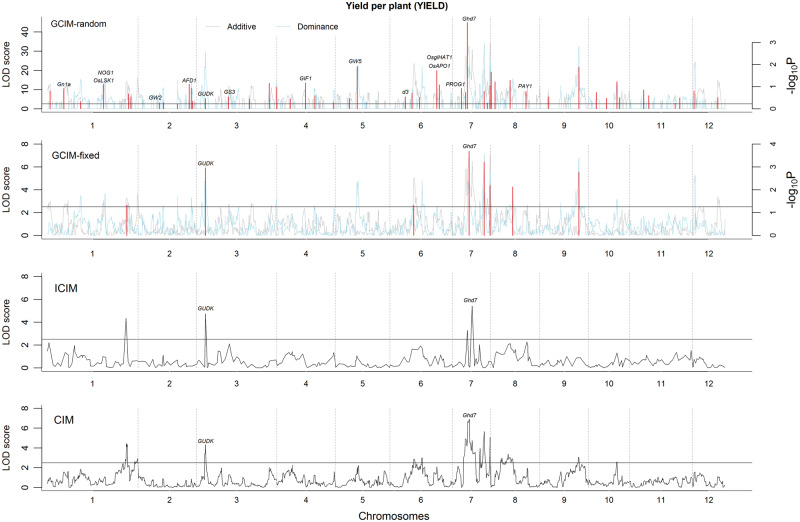
Figure 1.

Multi-locus QTL mapping for yield per plant (YIELD) in rice using CIM, ICIM, GCIM-random and GCIM-fixed methods. The data set is derived from Zhou et al. [32].

A total of 104, 56, 20 and 46 QTLs for the aforementioned four traits were detected by GCIM-random, GCIM-fixed, ICIM and CIM, respectively (Supplementary Table S1). Clearly, the number of QTLs identified by the new methods (GCIM-random and GCIM-fixed) was much higher than that identified by the current ICIM and CIM methods. For example, 24 and 21 QTLs for GRAIN were detected, respectively, by GCIM-random and GCIM-fixed while only 4 and 10 QTLs were identified, respectively, by ICIM and CIM. The same trend was also observed for the other traits. Among all the 226 QTLs, 176 (78%) had <5% proportions of phenotypic variance explained by each QTL. Among the 50 large QTLs, 11 were detected simultaneously by several methods. The QTL genotypic information for each trait was used to conduct a multiple linear regression analysis, and the corresponding Akaike’s information criteria (AIC) values were calculated. A smaller AIC value indicates a better model fit. As a result, the minimum AIC value for each trait was from GCIM, and the current methods had the maximum AIC values (Supplementary Table S2). For example, the AIC value for TILLER was 838.44 for GCIM-random, 850.17 for GCIM-fixed, 853.41 for CIM and 913.91 for ICIM.

In the proximity of the QTLs detected by GCIM-random, GCIM-fixed, ICIM and CIM methods, a total of 24, 9, 7 and 7 previously reported genes were found to be associated with the aforementioned four traits, respectively (Table 1, Figure 1, andSupplementary Figures S1–S3). Clearly, GCIM detected more previously reported genes when compared with all the other methods. Among the aforementioned genes, five genes were simultaneously detected by all the four methods, i.e. GS3 [33] and GW5 [34] for KGW, Ghd7 [35] and GUDK [36] for YIELD, Gn1a [37] for GRAIN and Ghd7 [35] for GRAIN were identified by GCIM-random, GCIM-fixed and CIM. Note that all the five genes have almost large effects (r² > 5%), and the other genes have small effects (r² < 2.5%) with an exception of gene TAC1 (r² = 5.81). More importantly, all the small-effect known genes were detected by GCIM-random rather than by the current methods (CIM or ICIM). For example, Gn1a [37], OsLSK1 [38], NOG1 [39], GW2 [40], AFD1 [41], GS3 [33], GIF1 [42], GW5 [34], d3 [43], OsglHAT1 [44], OsAPO1 [45], PROG1 [46] and PAY1 [47] for YIELD; d3 [43], OsLIC [48] and ATC1 [49] for TILLER; NOG1 [39] for GRAIN and IPA1 [50] for KGW. This means that GCIM-random has high power for the detection of small-effect QTLs or genes.

Monte Carlo simulation studies

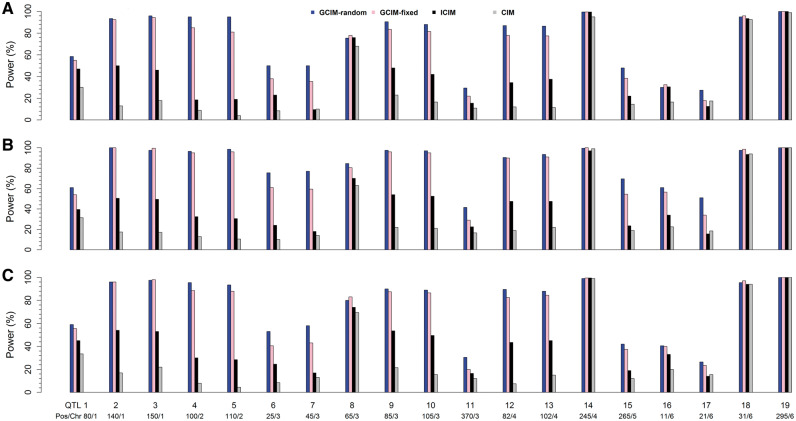
To validate the new method, a series of Monte Carlo simulation experiments was carried out. In the first experiment, 19 QTLs were simulated in an F₂ population of 400 individuals, each with 481 markers. All the interval lengths between adjacent markers were 5 cM and the number of replicates was 200. Each sample was analyzed by GCIM-random, GCIM-fixed, ICIM and CIM. As a result, the average power for the four methods was 73.42%, 67.71%, 43.39% and 29.97%, respectively (Figure 2 and Supplementary Table S3). When additive polygenic background (r² = 0.05) was added to the first simulation experiment, the average power for the four methods in the second simulation experiment was 83.63%, 78.42%, 47.47% and 33.16%, respectively (Figure 2 and Supplementary Table S3). When normal distribution for residual error in the first experiment was replaced by log-normal distribution in the third simulation experiment, average power for the four methods was 74.89%, 71.11%, 47.03% and 30.95%, respectively (Figure 2 and Supplementary Table S3). Clearly, GCIM-random has the highest average power in all three simulation experiments. If a paired t-test was used to test the significance of statistical power between new (GCIM-random and GCIM-fixed) and current (CIM and ICIM) methods, the new methods were significantly better than the current methods; GCIM-random was significantly better than GCIM-fixed, indicating the highest power from GCIM-random (Table 2).

Figure 2.

Comparison of statistical powers of QTL detection in the first (A), second (B) and third (C) simulation experiments using CIM, ICIM, GCIM-random and GCIM-fixed methods.

Table 2.

The P-values in paired t-tests of differences for power and mean absolute deviation (MAD) between the new (GCIM-random and GCIM-fixed) and current (ICIM and CIM) methods

QTL	GCIM-random (A) and GCIM- fixed (B)			GCIM-random (A) and ICIM (B)			GCIM-random (A) and CIM (B)			GCIM-fixed (A) and ICIM (B)			GCIM- fixed (A) and CIM (B)
	Power	MAD (Add)	MAD (Dom)	Power	MAD (Add)	MAD (Dom)	Power	MAD (Add)	MAD (Dom)	Power	MAD (Add)	MAD (Dom)	Power	MAD (Add)	MAD (Dom)
The first simulation experiment (phenotype = mean + 19 main-effect QTLs + residual error with normal distribution)
All	3e-04*** (5.711)	0.9645 (−0.001)	0.0000*** (0.033)	1e-04*** (30.026)	0.9046 (0.007)	0.011* (−0.141)	0.0000*** (43.447)	0.0232 (−0.211)	4e-04*** (−0.328)	1e-04*** (24.316)	0.9020 (0.008)	0.0043** (−0.174)	0.0000*** (37.737)	0.0240* (−0.211)	2e-04*** (−0.361)
Small	0.0606 (6.833)	0.0729 (0.016)	0.0293* (0.063)	0.0617 (17.167)	0.1564 (−0.138)	0.0047** (−0.258)	0.0260* (26.833)	0.0732 (−0.302)	0.0026** (−0.452)	0.080 (10.333)	0.1302 (−0.154)	0.0031** (−0.321)	0.0473* (20.000)	0.0671 (−0.318)	0.0011** (−0.515)
Large	1.0000 (0.000)	0.2078 (0.018)	0.2406 (0.023)	1.0000 (0.000)	0.7253 (0.168)	0.4038 (0.200)	0.3608 (2.750)	0.7512 (0.161)	0.4245 (0.271)	1.0000 (0.000)	0.7477 (0.150)	0.4617 (0.176)	0.3608 (2.750)	0.7732 (0.143)	0.4663 (0.247)
Linked	0.0016** (6.286)	0.6592 (−0.007)	0.0014** (0.028)	1e-04*** (37.071)	0.8206 (0.015)	0.0088** (−0.164)	0.0000*** (52.821)	0.0288 (−0.245)	2e-04*** (−0.386)	2e-04*** (30.786)	0.759 (0.022)	0.0053** (−0.192)	1e-04*** (46.536)	0.0348* (−0.238)	1e-04*** (−0.414)
The second simulation experiment (phenotype = mean + 19 main-effect QTLs + polygenic background + residual error with normal distribution)
All	0.0029** (5.211)	2e-04*** (0.039)	2e-04*** (0.059)	0.0000*** (36.158)	0.8896 (0.009)	0.0289* (−0.122)	0.0000*** (50.474)	0.0415* (−0.242)	4e-04*** (−0.345)	0.0000*** (30.947)	0.6424 (−0.03)	0.0018** (−0.181)	0.0000*** (45.263)	0.0179* (−0.280)	1e-04*** (−0.404)
Small	0.0397* (11.500)	0.0394* (0.054)	0.0517 (0.092)	0.0788 (28.833)	0.1865 (−0.156)	0.0098** (−0.220)	0.0469* (35.000)	0.1055 (−0.363)	0.0049** (−0.430)	0.1382 (17.333)	0.1405 (−0.211)	8e-04*** (−0.312)	0.0717 (23.500)	0.0908 (−0.417)	0.0085** (−0.522)
Large	0.5000 (−0.250)	0.3454 (0.060)	0.3431 (0.150)	0.5000 (1.250)	0.7323 (0.187)	0.0726 (0.325)	0.5000 (0.250)	0.8306 (0.140)	0.1576 (0.421)	0.5000 (1.500)	0.7957 (0.127)	0.4003 (0.175)	0.5000 (0.500)	0.8945 (0.080)	0.3997 (0.270)
Linked	0.0207* (4.643)	0.0075** (0.032)	3e-04*** (0.039)	0.0000*** (42.714)	0.7784 (0.018)	0.0052** (−0.164)	0.0000*** (60.964)	0.0615 (−0.270)	0.0000*** (−0.436)	0.0000*** (38.071)	0.8481 (−0.014)	0.0018** (−0.203)	0.0000*** (56.321)	0.0367* (−0.303)	0.0000*** (−0.475)
The third simulation experiment (phenotype = mean + 19 main-effect QTLs + residual error with log-normal distribution)
All	0.0032** (3.789)	0.7010 (−0.003)	0.0082** (0.019)	0.0000***(27.868)	0.040** (−0.123)	1e-04*** (−0.207)	0.0000*** (43.947)	0.0226* (−0.205)	3e-04*** (−0.340)	0.0000*** (24.079)	0.0534 (−0.120)	1e-04*** (−0.227)	0.0000*** (40.158)	0.0218* (−0.203)	2e-04*** (−0.360)
Small	0.1060 (6.167)	0.1147 (0.015)	0.0052** (0.024)	0.0298* (17.000)	0.0503 (−0.232)	0.0075** (−0.329)	0.0179* (24.667)	0.084 (−0.231)	0.0025** (−0.514)	0.1296 (10.833)	0.0524 (−0.247)	0.0071** (−0.352)	0.0743 (18.500)	0.0826 (−0.246)	0.0024** (−0.538)
Large	0.5000 (−0.250)	0.6107 (−0.010)	0.4001 (−0.010)	0.5000 (−0.250)	0.9015 (0.042)	0.8582 (0.061)	1.0000 (0.000)	0.7854 (0.121)	0.4751 (0.262)	1.0000 (0.000)	0.8839 (0.053)	0.8406 (0.071)	0.5000 (0.250)	0.7772 (0.131)	0.4727 (0.271)
Linked	0.0152* (3.857)	0.5446 (−0.005)	0.0176 (0.023)	0.0000*** (34.214)	0.0856 (−0.123)	1e-04*** (−0.22)	0.0000*** (54.357)	0.0281* (−0.246)	2e-04*** (−0.389)	0.0000*** (30.357)	0.1109 (−0.118)	0.0000*** (−0.242)	0.0000**** (50.5)	0.0263* (−0.241)	1e-04**** (−0.412)

Note: *, ** and ***: significance at the 0.05, 0.01 and 0.001 levels, respectively.

Note: Small QTL: QTL₁, QTL₁₁ and QTL₁₅; large QTL: QTL₁₄ and QTL₁₉; linked QTL: QTL₂∼QTL₁₀, QTL₁₂∼QTL₁₃ and QTL₁₆∼QTL₁₈. The differences (A−B) were in the brackets.

The accuracy of QTL effect estimation was measured by mean absolute deviation (MAD). Smaller MAD means higher accuracy of parameter estimation. As a result, the average MADs for the four methods were 0.427 ± 0.351 (additive) and 0.266 ± 0.304 (dominant), 0.429 ± 0.361 and 0.231 ± 0.314, 0.421 ± 0.225 and 0.405 ± 0.105 and 0.639 ± 0.376 and 0.592 ± 0.288, respectively, in the first simulation experiment; 0.548 ± 0.401 and 0.316 ± 0.336, 0.509 ± 0.410 and 0.254 ± 0.331, 0.538 ± 0.208 and 0.437 ± 0.150 and 0.789 ± 0.389 and 0.661 ± 0.343, respectively, in the second simulation experiment; and 0.403 ± 0.330 and 0.245 ± 0.291, 0.404 ± 0.348 and 0.223 ± 0.308, 0.529 ± 0.255 and 0.452 ± 0.152 and 0.611 ± 0.372 and 0.585 ± 0.287, respectively, in the third simulation experiment (Supplementary Table S4). Clearly, GCIM-random and GCIM-fixed have relatively small average MADs in all three simulation experiments. If a paired t-test was used to test the significance of the aforementioned accuracies between new (GCIM-random and GCIM-fixed) and current (CIM and ICIM) methods, the new methods had significantly lower MADs than the current methods, especially for dominant effects; GCIM-fixed had significantly lower MADs than GCIM-random (Table 2). This indicates that GCIM has higher accuracy in the estimation of QTL effects than the current methods.

The false positive rate (FPR) can be used to assess the performance of a method. The FPR results in the first simulation experiment are shown in Figure 3. The significance level (α) was set from 1e-8 to 1e-2.5, and the FPR slightly increased with the increase in the α value (Figure 3). When α was set at 0.0032 (1e-2.5), the FPR values for GCIM-random, GCIM-fixed, ICIM and CIM were 0.4404%, 0.1722%, 0.1000% and 0.0211%, respectively.

Figure 3.

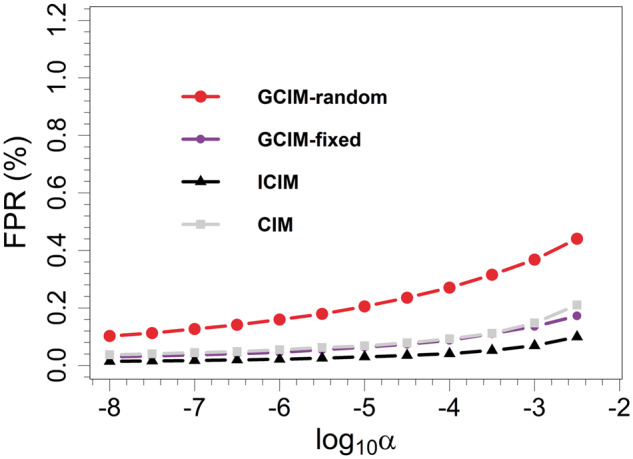
FPRs of QTL detection in the first simulation experiment plotted against Type I error (in a log10 scale) for CIM, ICIM, GCIM-random and GCIM-fixed methods.

In the three simulation experiments and real data analysis, the running times for the four methods were recorded and are listed in Supplementary Table S5. The results show that ICIM has the minimum running time followed by GCIM-fixed and GCIM-random, and CIM has the maximum running time in real data analysis, indicating the moderate running time of the GCIM. Note that GCIM-fixed is faster than GCIM-random. This is reasonable, because four variance components in GCIM-random need to be estimated while only three variance components in the GCIM-fixed need to be estimated.

We used the IMF₂ population of an elite rice hybrid as a real example to demonstrate the several methods, while we conducted Monte Carlo simulation studies on the F₂ population to compare their differences. In reality, the genome structures of both IMF₂ and F₂ are not exactly the same in all respects. If IMF₂ is derived from doubled haploid lines, named IMF₂-DH, there are no differences between them, because the recombinant rate (r) between two adjacent markers in F₂ is the same as that in IMF₂-DH. If IMF₂ is derived from recombinant inbred lines, named IMF₂-RIL, however, the differences exist, because the recombinant rate between two adjacent markers is 2r/(1 + 2r) in IMF₂-RIL rather than r in F₂. More recombinant in IMF₂-RIL will increase the power and accuracy of QTL detection. To validate the aforementioned deduction, we performed an additional simulation experiment to compare the results of QTL mapping in F₂ and IMF₂. All the results are listed in Supplementary Tables S6–S9. We found almost no significant differences between F₂ and IMF₂-DH (Supplementary Table S6). However, the powers for linked QTLs in IMF₂-RIL were significantly higher than those in both F₂ and IMF₂-DH (Supplementary Table S6), and the FPR in IMF₂-RIL was slightly less than those in both F₂ and IMF₂-DH (Supplementary Table S9).

Discussion

Genetic reasons why GCIM-random has high power in the detection of QTLs

The 19 simulated QTLs mentioned above can be divided into three types: small (QTL₁, QTL₁₁ and QTL₁₅), large (QTL₁₄ and QTL₁₉) and linked (QTL₂ ∼ QTL₁₀, QTL₁₂ ∼ QTL₁₃ and QTL₁₆ ∼ QTL₁₈). As described above, GCIM-random has 5.71%, 30.03% and 43.45% higher power than GCIM-fixed, ICIM and CIM, respectively, in the first simulation experiment (Figure 2, Table 2, andSupplementary Table S3). To make clear the reasons that result in significant difference in statistical power across various methods, we summarized the results from small, large and linked QTLs. We found that, for large-effect QTLs, GCIM-random has 0.0%, 0.0% and 2.75% higher power than GCIM-fixed, ICIM and CIM, respectively; for small-effect QTLs, GCIM-random has 6.83%, 17.17% and 26.83% higher power than GCIM-fixed, ICIM and CIM, respectively; for linked QTLs, GCIM-random has 6.29%, 37.07% and 52.82% higher power than GCIM-fixed, ICIM and CIM, respectively. This indicates the similar power of the four methods for large-effect QTLs, significantly different values between the current methods and GCIM-random for small-effect QTLs, and very significantly different values between the current methods and GCIM-random for linked QTLs. The same trends are also found in the other two simulation experiments. These results are further confirmed by real data analysis in this study. For example, five large-effect QTLs are detected simultaneously by the four methods (Table 1); among all the QTLs identified from GCIM-random and GCIM-fixed, 147 (91.88%) are small-effect (<5%) (Supplementary Table S1). In conclusion, the high power for the GCIM-random is derived from its high power in the detection of small and linked QTLs.

The advantages of GCIM-random are favorable in the mapping of gene expression levels, metabolites and epigenetic inheritance indicators. As we know, one of the most remarkable findings in eQTL mapping is that the most strong eQTLs are found to be near the target gene [8], and the proportion of these cis-acting eQTLs is approximately one third [7]. This means that most trans-eQTLs have small effects. Similar conclusions can be found in the mapping of metabolites [9] and epigenetic inheritance indicators [10,11]. Thus, GCIM-random can improve the power in the detection of expressional, metabolic and epigenetic QTLs.

The advantages of GCIM-random over the current methods

As described in Kroymann and Mitchell-Olds [4] and Mackay et al. [2], it is difficult for the widely used QTL mapping methods to detect small and linked QTLs. However, this situation has been significantly changed in this study; for example, a large number of small-effect QTLs have been identified in rice real data analysis by GCIM-random. The reasons are as follows. First, all the peaks in the negative logarithm P-value curve against genome position for additive or dominant effects are viewed as potential QTLs and placed into a multi-locus genetic model for true QTL identification. In the widely used QTL mapping methods, the peaks of small or linked QTLs in the LOD curve exist. Although their LOD scores may be less than the critical value of significant QTL, putting all the potential QTLs in one genetic model can increase the possibility of detecting small and linked QTLs. The results are consistent with those in Kao et al. [14], Xu [18], Wang et al. [51] and Wang et al. [27]. Then, controlling polygenic background via selecting markers in QTL mapping is replaced by estimating polygenic variance in a genome-wide association study (GWAS). Although CIM and ICIM can control the background of polygenes with large and individual moderate effects, GCIM-random may control the background of polygenes with large, moderate and small effects. Note that polygenic background control has been adopted in Bernardo [25], Xu [26] and Wang et al. [27]. However, GCIM-random is based on the new algorithm of Wen et al. [31], multi-locus genetic model and adaptive lasso.

In the ICIM and CIM, additive and dominant effects for each putative QTL in the genome are simultaneously estimated. However, the two effects are separately detected in this study. In doing so, the number of variance components to be estimated in GCIM-random will decrease from five to three so that the algorithm of Wen et al. [31] can be directly adopted. This solves the difficulty of parameter estimation in F₂. This is reasonable because the two effects in F₂ are orthogonal. In addition, real data analysis and simulation studies provide the evidence for this treatment. In addition, we find one unexpected phenomenon in real data analysis. That is, two falsely linked QTLs (Bin1004 and Bin1006∼Bin1007 on chr 7) are found by GCIM-random in one neighborhood to be associated with YIELD. This is because only one QTL is detected by CIM and ICIM. To make clear the position and effects of the true QTL, we scanned this neighborhood by CIM [52] (http://cran.r-project.org/web/packages/qtl/). As a result, this QTL is located between Bin1003 and Bin1004. This kind of treatment has been incorporated into our GCIM software.

In the CIM, we frequently find several peaks around one true QTL. In this situation, we cannot distinguish one QTL from multiple linked QTLs. In the GCIM-random, this situation can be avoided. This is because all the potential QTLs are placed into one genetic model, and their effects are estimated by shrinkage estimation (adaptive lasso). If there is only one true QTL in one neighborhood, only one nonzero effect estimate is obtained.

As compared with GCIM-random, GCIM-fixed has slightly higher accuracy in the estimation of QTL effects and takes less running time. However, GCIM-random has higher power in the detection of small and linked QTLs. The Monte Carlo simulation studies and real data analysis in this study provide the evidence for the detection of more small and linked QTLs (Supplementary Tables S1, S3 and S4). Thus, we recommend GCIM-random. Note that maximum likelihood (ML) and restricted maximum likelihood (REML) can be used to estimate the parameters in GCIM-random and GCIM-fixed. Thus, users may adopt both methods to analyze real data sets and to select the better one as the final results.

When adaptive lasso is used to estimate all the effects in a multi-locus model, a random number is needed. In GCIM-random, its seed is uncertain. This may produce slightly different results across the replicated calculations. To solve this issue, users can select the best result of several calculations as the final result.

We investigated the influence of the selection of distance (2 and 5 cM) on the power in the first simulation experiment. The results from paired t-tests are listed in Supplementary Table S10. In Supplementary Table S10, the power of detected QTL within 5 cM of the simulated QTL is higher at the 0.01 significance level than that within 2 cM. Similar results are shown in Supplementary Figure S4. In Supplementary Figure S4, most unlinked QTLs were identified within 2 cM of the simulated one. However, some linked QTLs were within 5 cM of the simulated one. Clearly, the significance is derived from linked QTLs rather than unlinked QTLs (Supplementary Table S10 and Supplementary Figure S4).

The prospects of the GCIM-random method

The results in this study have indeed shown the high FPR of GCIM-random over the other three methods. This means that it is possible to decrease the GCIM-random FPR in the future. However, GCIM-random has identified a series of true QTLs in simulation studies (Figure 2) and previously reported genes in real data analysis (Table 1). Moreover, some approaches can be used to obtain reliable and significant QTLs. In biology, the QTLs, detected commonly either in multiple environments (locations or years) in an IMF₂ or across multiple F₂ populations, are viewed as reliable QTLs. More importantly, the advances in modern omics can distinguish reliable candidate genes around significant QTLs, for example, gene annotation, expression, KEGG (Kyoto Encyclopedia of Genes and Genomes) and network analyses. Thus, more candidate genes related to the traits of interest can be mined.

Detecting small and linked QTLs has been a thorny issue in analyzing complex traits. Although the major contribution of this study is to propose a statistical framework jointly using CIM, random model and lasso techniques to tackle this issue for general usage, the new method is not limited to the F₂ population and can be expanded to the analysis of data from other experimental populations. Additionally, this framework can be also used to detect QTL-by-environment and QTL-by-QTL interactions, which are underway and will be reported in a subsequent paper.

Conclusion

Based on the FASTmrEMMA (fast multi-locus random-SNP-effect efficient mixed model association) algorithm, the GCIM-random method is proposed for detecting small and linked QTLs in F₂. First, FASTmrEMMA is used to separately conduct genome scanning for additive or dominant effects in F₂. For each kind of effect, all the peaks of negative logarithm P-value curve are viewed as potential QTLs, which are included into one multi-locus model. Then, adaptive lasso is used to estimate all the effects in the model, and all the nonzero effects are further identified by the likelihood ratio test (LRT) for true QTL identification. Finally, a series of Monte Carlo simulation studies and real data analysis are used to validate the GCIM-random. As a result, GCIM is more powerful for detecting closely linked and small-effect QTLs than the widely used methods. Among 25 known genes detected in this study, 16 small-effect genes were identified only by GCIM.

Materials and methods

Materials

Phenotypic and bin genotypic values in a rice IMF₂ population were downloaded from Zhou et al. [32] (http://www.pnas.org/content/suppl/2012/09/07/1214141109.DCSupplemental). The sample size was 278 and the number of bins was 1619. These bins were treated as markers for QTL mapping. The bin map was constructed by its RIL genotypes [53]. The traits analyzed in this study were yield per plant (YIELD), tillers per plant (TILLER), grains per panicle (GRAIN) and thousand grain weight (KGW). The phenotypic values of the two replicates in 1998 and 1999 were pooled for each cross after removing the year effects using $y_j=\frac{\mathbf{1}}{2}[(y_{j\mathbf{1}}-{\overline{y}}_{\mathbf{1}})+(y_{j2}-{\overline{y}}_2)]$, where ${\overline{y}}_{\mathbf{1}}$ and ${\overline{y}}_2$ are the averages of the trait measured in 1998 and 1999, respectively [26]. We inserted one or more pseudo markers at intervals larger than 1 cM to make sure that the entire genome is evenly covered by pseudo or true markers with no intervals larger than 1 cM. Thus, the number of all the pseudo or true markers was 1981. For the pseudo markers, the genotype indicator variable is missing for each individual. In this case, the missing variable was replaced by their conditional expectations, which are calculated from the R function calc.genoprob in R package qtl (http://cran.r-project.org/web/packages/qtl/).

Single-locus genetic model in F₂

We consider the following single-locus mixed linear model:

$$\mathbf{y}=\mathbf{1}\mu +{\mathbf{X}}_a{\beta }_a+{\mathbf{X}}_d{\beta }_d+{\mathbf{u}}_a+{\mathbf{u}}_d+\epsilon$$ (1)

where $\mathbf{y}$ is an $n\times \mathbf{1}$ phenotypic vector of quantitative trait, and $n$ is the number of individuals; $\mathbf{1}$ is a $n\times \mathbf{1}$ vector of 1; $\mu$ is overall average; ${\beta }_a\sim N(0,{\sigma }_a^2)$ and ${\beta }_d\sim N(0,{\sigma }_d^2)$ are random additive and dominant effects of a putative QTL, respectively; ${\mathbf{X}}_a$ and ${\mathbf{X}}_d$ are the dummy variable matrix defined as 1 and 0 for genotype AA, 0 and 1 for genotype Aa and −1 and 0 for genotype aa; ${\mathbf{u}}_a\sim \text{MVN}(0,{\sigma }_{ag}^2{\mathbf{K}}_a)$ and ${\mathbf{u}}_d\sim \text{MVN}(0,{\sigma }_{dg}^2{\mathbf{K}}_d)$ are the $n\times \mathbf{1}$ vector of additive and dominant polygenic effects, respectively; ${\mathbf{K}}_a$ and ${\mathbf{K}}_d$ are the known $n\times n$ kinship matrices for additive and dominant polygenic effects, respectively, are inferred from marker information and are defined as ${\mathbf{K}}_a=\frac{\mathbf{1}}{d_a}{\sum }_{i=\mathbf{1}}^p{X}_{ai}{X}_{ai}^T$ and ${\mathbf{K}}_d=\frac{\mathbf{1}}{d_d}{\sum }_{i=\mathbf{1}}^p{X}_{di}{X}_{di}^T$ [26,54], where $d_a=\left(\mathbf{1}/n\right)tr\left({\sum }_{i=\mathbf{1}}^p{X}_{ai}{X}_{ai}^T\right)$ and $d_d=\left(\mathbf{1}/n\right)tr\left({\sum }_{i=\mathbf{1}}^p{X}_{di}{X}_{di}^T\right)$ are normalization factors, $p$ is the number of QTLs excluding pseudo markers; and $\epsilon \sim {\text{MVN}}_n(0,{\sigma }_e^2{I}_n)$ is an $n\times \mathbf{1}$ vector of residual errors, ${\sigma }_e^2$ is the variance of residual error, and ${\mathbf{I}}_n$ is an $n\times n$ identity matrix, MVN denotes multivariate normal distribution, and tr denotes trace.

Although the ${\beta }_a$ and ${\beta }_d$ are treated as fixed in the CIM and ICIM methods, in this study we treat them as random to make the model more realistic [28,29,31,54]. In this case, five variance components need to be estimated. Thus, the variance of $\mathbf{y}$ in Model (1) is:

$$\begin{array}{c}Var(\mathbf{y})={\sigma }_a^2{\mathbf{X}}_a{\mathbf{X}}_a^T+{\sigma }_d^2{\mathbf{X}}_d{\mathbf{X}}_d^T+{\sigma }_{ag}^2{\mathbf{K}}_a+{\sigma }_{dg}^2{\mathbf{K}}_d+{\sigma }_e^2{\mathbf{I}}_n\\ ={\sigma }_e^2({\lambda }_a{\mathbf{X}}_a{\mathbf{X}}_a^T+{\lambda }_d{\mathbf{X}}_d{\mathbf{X}}_d^T+{\lambda }_{ag}{\mathbf{K}}_a+{\lambda }_{dg}{\mathbf{K}}_d+{\mathbf{I}}_n)\\ ={\sigma }_e^2\mathbf{H}\end{array}$$ (2)

where ${\lambda }_a={\sigma }_a^2/{\sigma }_e^2$, ${\lambda }_d={\sigma }_d^2/{\sigma }_e^2$, ${\lambda }_{ag}={\sigma }_{ag}^2/{\sigma }_e^2$ and ${\lambda }_{dg}={\sigma }_{dg}^2/{\sigma }_e^2$.

GCIM-random method in F₂

The key to solve Model (1) is to estimate five variance components (${\sigma }_a^2$, ${\sigma }_d^2$, ${\sigma }_{ag}^2$, ${\sigma }_{dg}^2$ and ${\sigma }_e^2$). For each putative QTL, we may estimate the five variance components using mixed model method. If the number of the putative QTLs on the genome is large, it takes a long time. To save running time, we may scan separately additive or dominant effect for each putative QTL along the genome. This method is named as GCIM-random. The details are as follows.

Estimation of four variance components. First, we estimate ${\widehat{\lambda }}_{ag}$ and ${\widehat{\lambda }}_{dg}$ by the reduced model with only polygenic background:

$$\mathbf{y}=\mathbf{1}\mu +{\mathbf{u}}_a+{\mathbf{u}}_d+\epsilon ,$$ (3)

Replacing ${\lambda }_{ag}$ and ${\lambda }_{dg}$ in $\mathrm{var}(\mathbf{y})={\sigma }_e^2\left({\lambda }_{ag}{\mathbf{K}}_a+{\lambda }_{dg}{\mathbf{K}}_d+{\mathbf{I}}_n\right)$ of (3) by ${\widehat{\lambda }}_{ag}$ and ${\widehat{\lambda }}_{dg}$, we obtain $\mathbf{B}={\widehat{\lambda }}_{ag}{\mathbf{K}}_a+{\widehat{\lambda }}_{dg}{\mathbf{K}}_d+{\mathbf{I}}_n$. Using the FASTmrEMMA algorithm of Wen et al. [31], the spectral decomposition for $\mathbf{B}$ is B = QΛQ^T, the model transformation matrix is $C=Q{\Lambda }^{-\mathbf{1}/2}{Q}_{}^T$, where $\mathbf{\Lambda }$ is a r × r diagonal matrix with positive eigenvalues, $\mathbf{Q}$ is the n × r block of an orthogonal matrix and $r=Rank(\mathbf{B})$.

Then, we may separately scan each kind of effect for all the putative QTLs. In the scanning of additive effect, the transferred single-locus mixed linear model is

$${\mathbf{y}}_c={\mathbf{1}}_c\mu +{\mathbf{X}}_{c.a}{\beta }_a+{\epsilon }_c,$$ (4)

where ${\mathbf{y}}_c=\mathbf{C}\mathbf{y}$, ${\mathbf{1}}_c=\mathbf{C}\mathbf{1}$, ${\mathbf{X}}_{c.a}=\mathbf{C}{\mathbf{X}}_a$ and ${\epsilon }_c=\mathbf{C}\left({\mathbf{u}}_a+{\mathbf{u}}_d+\epsilon \right)\sim {\text{MVN}}_n(0,{\sigma }_e^2{\mathbf{I}}_n)$. Then

$$Var({\mathbf{y}}_c)={\sigma }_e^2({\lambda }_a{\mathbf{X}}_{c.a}{\mathbf{X}}_{c.a}^T+{\mathbf{I}}_n)$$ (5)

In the scanning of dominant effect, similarly, the transferred single-locus mixed linear model is:

$${\mathbf{y}}_c={\mathbf{1}}_c\mu +{\mathbf{X}}_{c.d}{\beta }_d+{\epsilon }_c,$$ (6)

where ${\mathbf{y}}_c=\mathbf{C}\mathbf{y}$, ${\mathbf{1}}_c=\mathbf{C}\mathbf{1}$, ${\mathbf{X}}_{c.d}=\mathbf{C}{\mathbf{X}}_d$ and ${\epsilon }_c=\mathbf{C}\left({\mathbf{u}}_a+{\mathbf{u}}_d+\epsilon \right)\sim {\text{MVN}}_n(0,{\sigma }_e^2{\mathbf{I}}_n)$. Then:

$$Var({\mathbf{y}}_c)={\sigma }_e^2({\lambda }_d{\mathbf{X}}_{c.d}{\mathbf{X}}_{c.d}^T+{\mathbf{I}}_n),$$ (7)

In Models (4) and (6), clearly, only two variance components need to be estimated. In this study, we adopted the FASTmrEMMA algorithm of Wen et al. [31]. All the formulae are similar to those in Wen et al. [31]. Thus, negative logarithm P-value curve against genome position for additive effect in Model (4) and dominant effect in Model (6) can be obtained. In each curve, all the peaks are viewed as putative QTLs to be included in one multi-locus model [27], their effects are estimated by adaptive lasso [55], and all the nonzero effects are further detected by LRT for true QTL identification.

Detection of true QTLs in multi-locus model. In the multi-locus model for GCIM-random:

$$\mathbf{y}=\mathbf{1}\mu +\sum _{i=\mathbf{1}}^q\left({\mathbf{X}}_{ai}{\beta }_{ai}+{\mathbf{X}}_{di}{\beta }_{di}\right)+\epsilon ,$$ (8)

where $\mathbf{y}$, $\mu$ and $\epsilon$ are the same as those in Model (1); $q$ is the number of the potential QTLs selected in the first step of GCIM-random; ${\mathbf{X}}_{ai}$ and ${\mathbf{X}}_{di}$ are the dummy variables of additive and dominant genotypes for the ith putative QTL, respectively, and ${\beta }_{ai}$ and ${\beta }_{di}$ are additive and dominant effects. In the abovementioned model, polygenic background is not included, because all the potential QTLs have been included in Model (8). We assume that the data are centered, so the intercept term is 0. Let ${\beta }_{2q\times \mathbf{1}}={\left({\beta }_{a\mathbf{1}},{\beta }_{d\mathbf{1}},{\beta }_{a2},{\beta }_{d2},\dots ,{\beta }_{aq},{\beta }_{dq}\right)}^T$, $\mathbf{Y}=\mathbf{y}-\mathbf{1}\mu$ with a zero mean, and centralizing each column in matrix ${\left(\begin{array}{ccccccc}{X}_{a\mathbf{1}}& X_{d\mathbf{1}}& X_{a2}& X_{d2}& \dots & X_{aq}& X_{dq}\end{array}\right)}_{n\times 2q}$ produces a new matrix $\mathbf{X}$ with ${\sum }_{i=\mathbf{1}}^n{x}_{ij}=0$, $j=\mathbf{1},\dots ,2q$.

We invoked the adaptive lasso algorithm of Zou [55] to estimate their effects implemented by the R package parcor of Kraemer et al. [56] (http://cran.r-project.org/web/packages/parcor/). Therefore, adaptive lasso estimates $\widehat{\beta }$ are given by

$$\widehat{\beta }=\arg \min {\Vert Y-\mathbf{X}\beta \Vert }^2+\lambda \sum _{j=\mathbf{1}}^{2q}\left({\widehat{\omega }}_j\left|{\beta }_j\right|\right),$$ (9)

Here we use the lasso estimates ${\widehat{\beta }}_{lasso}$ as initial values and define the weights ${\widehat{\omega }}_j=\mathbf{1}/\left|{\widehat{\beta }}_{j,lasso}\right|$[56]. The tuning parameter $\lambda$ of adaptive lasso is chosen by 10-fold cross-validation.

LRT for all the nonzero effects in the multi-locus model. Based on the estimates of all the effects in the multi-locus model, the effects with $\left|{\widehat{\beta }}_j\right|>{10}^{-5}$ are further selected for LRT to obtain the significantly associated QTLs. Let the selected effects be $\widehat{\theta }={\left({\widehat{\beta }}_{(a\mathbf{1})},{\widehat{\beta }}_{(d\mathbf{1})},{\widehat{\beta }}_{(a2)},{\widehat{\beta }}_{(d2)}\cdots ,{\widehat{\beta }}_{(al)},{\widehat{\beta }}_{(dl)}\right)}^T$. Note that as long as one estimate of additive or dominant effects ($\left|{\widehat{\beta }}_{(ak)}\right|$ and $\left|{\widehat{\beta }}_{(dk)}\right|$) for kth selected QTL is greater than 10⁻⁵, we selected the two effects of this QTL. Thus, the null hypothesis is $H_0:{\beta }_{(ak)}=0$, ${\beta }_{(dk)}=0$ ($k=\mathbf{1},\dots ,l$), that no QTL exists in this position. The LOD score is calculated by:

$$LO{D}_k=-2\left[L({\widehat{\theta }}_{-k})-L(\widehat{\theta })\right]/4.605,$$ (10)

where ${\widehat{\theta }}_{-k}={\left({\widehat{\beta }}_{(a\mathbf{1})},{\widehat{\beta }}_{(d\mathbf{1})},\dots ,{\widehat{\beta }}_{(a,k-\mathbf{1})},{\widehat{\beta }}_{(d,k-\mathbf{1})},{\widehat{\beta }}_{(a,k+\mathbf{1})},{\widehat{\beta }}_{(d,k+\mathbf{1})},\dots ,{\widehat{\beta }}_{(al)},{\widehat{\beta }}_{(dl)}\right)}^T$, $L(\widehat{\theta })={\sum }_{i=\mathbf{1}}^n\ln \varphi (y_i;\mathbf{1}\widehat{\mu }+{\sum }_{k=\mathbf{1}}^l\left({\mathbf{X}}_{ak}{\widehat{\beta }}_{ak}+{\mathbf{X}}_{dk}{\widehat{\beta }}_{dk}\right),{\widehat{\sigma }}_e^2)$ is log-likelihood function, $\varphi (y_i;\mathbf{1}\widehat{\mu }+{\sum }_{k=\mathbf{1}}^l\left({\mathbf{X}}_{ak}{\widehat{\beta }}_{ak}+{\mathbf{X}}_{dk}{\widehat{\beta }}_{dk}\right),{\widehat{\sigma }}_e^2)$ is normal density with mean $\mathbf{1}\widehat{\mu }+{\sum }_{k=\mathbf{1}}^l\left({\mathbf{X}}_{ak}{\widehat{\beta }}_{ak}+{\mathbf{X}}_{dk}{\widehat{\beta }}_{dk}\right)$ and variance ${\widehat{\sigma }}_e^2$ and $\mathbf{y}={\left(y_i\right)}_{n\times \mathbf{1}}$. Considering that all potential QTLs are selected in the first step, we adopt a slightly more stringent criterion of P-value = 0.00316 as significant QTL, which is converted from LOD score 2.50 using $P=Pr({\chi }_{df=2}^2>2.5\times 4.605)\approx 0.00316$.

GCIM-fixed method in F₂

If we treat QTL effects as fixed, the method is called as GCIM-fixed. The variance $\mathbf{y}$ in Model (1) could be reduced as:

$$\begin{array}{c}Var(\mathbf{y})={\sigma }_{ag}^2{\mathbf{K}}_a+{\sigma }_{dg}^2{\mathbf{K}}_d+{\sigma }_e^2{\mathbf{I}}_n\\ ={\sigma }_e^2({\lambda }_{ag}{\mathbf{K}}_a+{\lambda }_{dg}{\mathbf{K}}_d+{\mathbf{I}}_n),\end{array}$$ (11)

where ${\lambda }_{ag}={\sigma }_{ag}^2/{\sigma }_e^2$ and ${\lambda }_{dg}={\sigma }_{dg}^2/{\sigma }_e^2$.

The GCIM-fixed includes two steps. In the first step, we estimate ${\widehat{\lambda }}_{ag}$ and ${\widehat{\lambda }}_{dg}$ under pure polygenic model and fix it when scanning each putative QTL on the genome [30], as described in GCIM-random.

In the second step, we scan separately each kind of effect for each putative QTL on the genome. In the scanning of additive effect, the single-locus mixed linear model is:

$${\mathbf{y}}_c={\mathbf{1}}_c\mu +{\mathbf{X}}_{c.a}{\beta }_a+{\epsilon }_c,$$ (12)

where ${\mathbf{y}}_c=\mathbf{C}\mathbf{y}$, ${\mathbf{1}}_c=\mathbf{C}\mathbf{1}$, ${\mathbf{X}}_{c.a}=\mathbf{C}{\mathbf{X}}_a$, ${\epsilon }_c=\mathbf{C}\left({\mathbf{u}}_a+{\mathbf{u}}_d+\epsilon \right)\sim {\text{MVN}}_n(0,{\sigma }_e^2{\mathbf{I}}_n)$ and $Var({\mathbf{y}}_c)={\sigma }_e^2{\mathbf{I}}_n$. In the scanning of dominant effect, the single-locus mixed linear model is:

$${\mathbf{y}}_c={\mathbf{1}}_c\mu +{\mathbf{X}}_{c.d}{\beta }_d+{\epsilon }_c$$ (13)

where ${\mathbf{y}}_c=\mathbf{C}\mathbf{y}$, ${\mathbf{1}}_c=\mathbf{C}\mathbf{1}$, ${\mathbf{X}}_{c.d}=\mathbf{C}{\mathbf{X}}_d$, ${\epsilon }_c=\mathbf{C}\left({\mathbf{u}}_a+{\mathbf{u}}_d+\epsilon \right)\sim {\text{MVN}}_n(0,{\sigma }_e^2{\mathbf{I}}_n)$ and $Var({\mathbf{y}}_c)={\sigma }_e^2{\mathbf{I}}_n$.

In Models (12) and (13), only one variance component is included. Thus, we can quickly estimate ${\widehat{\beta }}_a$ and ${\widehat{\beta }}_d$ using ML or REML and calculate P-value for each QTL. The remaining steps are similar to those in GCIM-random.

The abovementioned two methods can be implemented by software QTL.gCIMapping, which is available at https://cran.r-project.org/web/packages/QTL.gCIMapping/index.html.

Composite interval mapping

CIM [12,13] is a commonly used method for mapping QTLs in segregating populations derived from biparental crosses. This method was implemented by WinQTLCart, which is downloaded from https://brcwebportal.cos.ncsu.edu/qtlcart/WQTLCart.htm. The CIM was performed using Model 6 in QTL cartographer with a window size of 10.0 cM and five other markers used as cofactors in the model. Significance thresholds were set at the LOD score of 2.50.

Inclusive composite interval mapping

ICIM [15] is a modified algorithm of CIM [12,13]. In ICIM, marker selection is conducted only once through stepwise regression by considering all marker information simultaneously, and the phenotypic values are then adjusted by the selected markers (or significant cofactors) except the two markers flanking the current mapping interval. The adjusted phenotypic values are finally used in interval mapping. The ICIM was conducted by QTLIciMapping v3.0, which was downloaded from http://www.isbreeding.net/. Interval mapping at 1-cM intervals along the genome was used to scan for QTLs based on the critical LOD score of 2.50.

The methodological comparison for the abovementioned four methods is listed in Table 3.

Table 3.

Comparison of four QTL mapping methods and their packages

Case	GCIM-random	GCIM-fixed	ICIM	CIM
Model	Multi-locus model	Multi-locus model	Single-locus model	Single-locus model
Model transformation	FASTmrEMMA algorithm	FASTmrEMMA algorithm	NA	Interval mapping for ${y^{\prime }}_i=y_i-\sum _{k\ne l,l+1}(x_{ik}{a}_k+z_{ik}{d}_k)$
QTL effect	Random	Fixed	Fixed	Fixed
Estimation of QTL effect	REML or ML	REML or ML	ML	ML
Polygenic background control	Polygenic additive and dominant variances via mixed model framework of GWAS	Polygenic additive and dominant variances via mixed model framework of GWAS	The associated markers (cofactors), except the two markers flanking the current mapping interval; their effects are estimated at each position of genome scanning	The cofactors except for the two markers flanking the current mapping interval; the effects for all the cofactors are estimated only one time
No. of variance components	Five	Three	NA	NA
Polygenic-to-residual variance ratio	Fixed	Fixed	NA	NA
Running time	Fast	Fast	Fast	Slow
Software	GCIM-random and GCIM-fixed: QTL.gCIMapping (https://cran.r-project.org/web/packages/QTL.gCIMapping/index.html) QTL.gCIMapping.GUI (https://cran.r-project.org/web/packages/QTL.gCIMapping.GUI/index.html)
	ICIM: QTL IciMapping (http://www.isbreeding.net/)
	CIM: Windows QTL Cartographer (https://brcwebportal.cos.ncsu.edu/qtlcart/WQTLCart.htm)

Monte Carlo simulation studies

An F₂ population of 400 individuals was simulated in the first Monte Carlo simulation experiment. Each individual had six simulated chromosomes. On the first to fifth chromosomes, each was covered by 81 evenly spaced markers, and the sixth one was covered by 76 evenly spaced markers. We placed 19 QTLs along the genome with positions and effects listed in Supplementary Table S3. Among these simulated QTLs, 14 overlapped with markers, five resided in the middle of an interval, and the proportion of phenotypic variance explained by each QTL ranged from 0.5% to 10% (Supplementary Table S3). The total average and residual variances were set at 20 and 10, respectively. The phenotype for each F₂ individual was simulated by the model: $\mathbf{y}=\mathbf{1}\mu +{\sum }_{i=\mathbf{1}}^{19}\left(x_{ai}{b}_{ai}+x_{di}{b}_{di}\right)+\epsilon$, where $\epsilon \sim {\text{MVN}}_n(0,10\times {\mathbf{I}}_n)$. The number of replicates was 200. Each sample was analyzed by four methods: GCIM-random, GCIM-fixed, ICIM and CIM. For each simulated QTL, we counted the samples in which the LOD score had passed 2.5. A detected QTL within 5 cM of the simulated QTL was considered a true QTL. The ratio of the number of such samples to the total number of replicates represented the empirical power for this QTL. To measure the bias of QTL effect and position estimates, mean squared error (MSE) and MAD were defined as $\text{MSE}=\frac{\mathbf{1}}{200}{\sum }_{i=\mathbf{1}}^{200}{({\widehat{\beta }}_i-\beta )}^2$ and $\text{MAD}=\frac{\mathbf{1}}{200}{\sum }_{i=\mathbf{1}}^{200}\left|{\widehat{\beta }}_i-\beta \right|$, respectively, where ${\widehat{\beta }}_i$ is the estimate of QTL effect (or position) in the ith sample.

In the second Monte Carlo simulation experiment, additive polygenic background (r² = 0.05) was added to the first simulation experiment to investigate the effect of polygenic background on the new method. The polygenic effect $u_a$ was simulated by multivariate normal distribution ${\text{MVN}}_n(0,{\sigma }_{pg}^2{\mathbf{K}}_a)$, where ${\sigma }_{pg}^2=3.846$, and ${\mathbf{K}}_a$ was the kinship coefficient matrix between a pair of individuals. The other parameter values were the same as those in the first experiment. All the F₂ individual phenotypes were simulated by the model: $\mathbf{y}=\mathbf{1}\mu +{\sum }_{i=\mathbf{1}}^{19}\left(x_{ai}{b}_{ai}+x_{di}{b}_{di}\right)+u_a+\epsilon$, where $\epsilon \sim {\text{MVN}}_n(0,10\times {\mathbf{I}}_n)$.

To investigate the effect of a skewed distribution on the new method, normal distribution for residual error in the first experiment was replaced by log-normal distribution with the 1.144 SD and the zero mean in the third Monte Carlo simulation experiment. The other parameter values were the same as those in the first experiment.

A series of pseudo markers was inserted in the middle of a marker interval. As a result, the total number of pseudo and true markers was 2856. For the pseudo markers, the missing genotype variable for every individual was replaced by its conditional expectation.

To verify the differences of mapping QTLs in F₂ and IMF₂ using the new methods, IMF₂-DH and IMF₂-RIL populations were simulated. All the simulation parameters were the same as those in the first experiment (Supplementary Table S7). Each simulated data set was analyzed by GCIM-random and GCIM-fixed. All the results were compared with those in the first simulation experiment.

Key Points

• QTL mapping has been widely used to identify many genes for complex traits, metabolites, gene expression levels, RNA editing levels and DNA methylation.

• Although these complex and omics-related traits are mainly controlled by a series of minor genes, studies to design an efficient framework for the detection of the minor and linked genes are limited.

• We assess four QTL mapping methodologies using both simulated and real data sets. In the newly developed GCIM-random method, QTL effects are viewed as being random, polygenic background is estimated by polygenic variance in GWAS, FASTmrEMMA is used to separately conduct genome scanning for additive or dominant effect in F₂, all the peaks of negative logarithm P-value curve against genome position are picked up as potential QTLs in a multi-locus model and all the effects in the model are estimated by adaptive lasso.

• GCIM-random is more powerful than the widely used methods for the detection of closely linked and small-effect QTLs.

Supplementary Data

Supplementary data are available online at https://academic.oup.com/bib.

Funding

The work was supported by the Fundamental Research Funds for the Central Universities (grant number KJQN201849), National Natural Science Foundation of China (grant numbers 31701071, 31571268 and U1602261), Huazhong Agricultural University Scientific and Technological Self-innovation Foundation (grant number 2014RC020) and State Key Laboratory of Cotton Biology Open Fund (grant number CB2017B01).

Biographies

Yang-Jun Wen is a PhD Candidate in State Key Laboratory of Crop Genetics and Germplasm Enhancement at Nanjing Agricultural University, Nanjing, China.

Ya-Wen Zhang is a PhD Candidate in the College of Plant Science and Technology at Huazhong Agricultural University, Wuhan, China.

Jin Zhang is an Associate Professor in State Key Laboratory of Crop Genetics and Germplasm Enhancement at Nanjing Agricultural University, Nanjing, China.

Jian-Ying Feng is an Associate Professor in State Key Laboratory of Crop Genetics and Germplasm Enhancement at Nanjing Agricultural University, Nanjing, China.

Jim M. Dunwell is a Full Professor in the School of Agriculture, Policy and Development at the University of Reading, United Kingdom.

Yuan-Ming Zhang is director of Crop Information Center and a Chutian Scholar Professor of Statistical Genomics in the College of Plant Science and Technology at Huazhong Agricultural University, Wuhan, China.