Abstract
We employ some of the machinery developed in previous work to investigate the inferential and memory functions of quantum-like neural networks. We set up a logical apparatus to implement this in the form of a Gentzen sequent calculus which codifies some of the combinatory rules for the state spaces of the neuronal networks introduced earlier. We discuss memory storage in this context and along the way find formal proof that synchronicity promotes binding and storage. These results lead to an algorithmic fragment in calculus that simulates the memory function known as pattern completion. This claim is tested by noting that the failure of certain steps in the algorithm leads to memory deficits essentially identical to those found in such pathologies as Alzheimer’s dementia, schizophrenia, and certain forms of autism. Moreover, a specific “power-of-two” wiring architecture and computational logic, which have been postulated and observed across many brain circuits, emerge spontaneously from our model. We draw conclusions concerning the possible nature of such mental processes qua computations.
Keywords: Memory, Sequent calculus, Networks, Pattern completion, Storage, Synchronicity, Tsien’s power-of-two law
Introduction
Do brains compute? And if they do, what do they compute and how do they do it? This problem has occupied the brains (computational or not) of thinkers in many disciplines since at least the advent of modern computers if not before. (For an up to date and copiously referenced review of this vast subject, see [1].) In this article, we shall identify brains with interacting collections of neural-like networks of the kind modeled in earlier work [2, 3] and consider their logic and memory-like functions in more detail. Specifically, we shall codify them in logical form and realize one such function explicitly as an algorithmic fragment. The model and its dynamics are based on the logic of “hidden variables,” the idea being that variables underlying the internal states of biological neural networks (and other highly complex systems) are generally too complex to be very realistically modeled in any comprehensible manner. Although mathematical models of complex systems, realized as computer programs, may be—and are—run to produce concrete output, such nearly isomorphic modeling of a complex system usually cannot reveal overarching structural features any more succinctly than the system itself does. Some means of lowering the resolution, or level of detail, are often more helpful in making structural properties apparent. This strategy is of course ubiquitous in pure and applied mathematics. (For example, within pure mathematics, in the case of algebraic topology, the relation of homotopical or homological equivalence has proven more useful than the finer equivalence relation of homeomorphy.)
In [2], we proposed a formalization of this process for systems whose complexity, or fine grainedness, is such that some internal states may be deemed sufficiently similar to appear to be confusable to an external observer without recourse to disrupting the system. As our primary example, we considered the set of states of an ensemble of biological units such as neuron-like cells or parts thereof, realized as the space of possible nodal membrane potentials. This led to the replacement of the usual Boolean logic of propositions defining subsets (as their extensions) of such a space by the not necessarily Boolean logic of propositions (extensionally) corresponding to subsets defined only up to “confusability” of the constituent states. This logic, called orthologic and denoted OL, differs from Boolean logic in that distribution of conjunction over disjunction (or, equivalently, vice versa) does not hold. In this, it resembles the logic of the quantum theory, and indeed the model theory of OL reveals quantum-like behavior in the systems under consideration if certain conditions are met. These conditions are in fact met for the neuron-like systems of interest to us (cf [2] and Section 2 below). Although actual quantum mechanics is surely not a theory of hidden variables, a theory of hidden variables may have certain quantum-like attributes: ours is an example of such a theory.
The upshot is a quantum-like dynamical theory of certain neural-like networks which was initiated in [3]. It differs in certain significant respects from both standard quantum theory and standard neural net theory. The operator representing the infinitesimal generator of time evolution is called there the pseudo-Hamiltonian. It resembles a generic model known to many-body physicists as being of the quasispin type, though it acts in a real Hilbert space [4]. Unfortunately, such models are generally computationally intractable. (The model resembles the familiar and simpler Ising-like attractor models of Hopfield, et al. [5, 6].) Here we aim to show that although the model is generally intractable via traditional methods, there is an inherent logic that may be formalized and exploited to extract information. The advantages of doing this are that computations in the logic, if found, would be amenable to analyses along the lines of standard computability theory and, moreover, the logical formulation can reveal structural properties that lie beyond the scope of the mathematically intractable physical models, which resemble the most complex models of many-body theory, but are even more complex, since those circumstances that ameliorate the analogous physics, such as symmetries and known force laws, are entirely absent in brain networks.
This logic is an externalized version of the underlying orthologic, expressed in the form of a fragment of a Gentzen sequent calculus which turns out to be identical to a fragment of the linear logic LL) of Girard et al., well known to computer scientists (cf [7–13] among many others). This formalism is applied to a discussion of the memory function known as pattern completion in such systems of networks which resembles that operating in an actual brain. These procedures manifest as a family of proofs in the calculus, which represent the computations performed by the neural network. Thus, we assume that neural networks have the function to produce information-carrying outputs in response to information-carrying inputs and internal states. Processes of this type constitute physical computations according to mainstream views, including an account of physical computation proposed by the second author [14, 15]. Our model invokes a Gentzen sequent calculus dubbed here GN to characterize and analyze the computational properties of neural networks, specifically the inferences and memory functions mentioned above.
An immediate consequence of our model is a significant wiring constraint applicable to connection maps described by the basic sequent. Namely, they must obey a “power-of-two” law. This law was postulated by J. Z. Tsien as the basic wiring and computational logic of cell assemblies across many brain regions, ranging from the prefrontal and association cortices to the limbic system and subcortical circuits, and confirmed by a series of careful experiments with mice and hamsters [16–19]. It is discussed in Section 7.2.
To test these hypotheses further, we investigate how pathologies might arise if the various steps in the algorithm fail. Our results are consistent with certain aspects of dementias of Alzheimer’s type, schizophrenia, and certain forms of autism, lending some credence to our model (Section 7.3).
Except for the kinematic constraints leading to the initial setup of our model, reviewed briefly below, this paper is essentially self-contained.
The layout of the paper is as follows. Section 2 is a brief review of the foundations of our model, and Section 3 reviews the kind of networks we have considered earlier. Section 4 is a fairly self-contained introduction to the fragment of computational logic that seems appropriate to the models we have posited. As noted, this calculus turns out to be equivalent to a fragment of Girard’s linear logic (LL). As such, the modal operator, of course, written !, implements a certain kind of storage which is discussed at some length. This section offers a largely self-contained and informal discussion of this calculus and its interpretation in the category of finite-dimensional vector spaces. Section 5 arranges a meeting between our model and the logic.
Our discussion up to this point has not taken into account the passage of time. This is addressed in Section 6. We argue that the axiom crucially implementing the storage operation, namely the rule of left contraction (LC), may be realized physically, that is, in the “hardware,” and therefore may be judged to take a certain time to implement, if the network involved is synchronized. Thus, synchronicity enters the picture spontaneously in connection with a certain operation related to storage. This is followed up in two theorems, which show how logic and synchronicity conspire to promote a certain notion of binding.
Section 7 is devoted to applications, the first being, as the main application of this material, an abstract proof in the calculus of the procedure to complete a pattern: that is, to recall a set of associated memories when cued by the retrieval of one of them, as in the Proustian taste of a madeleine.
In Section 7.2, we partially derive the “power-of-two” wiring law postulated by Tsien and Section 7.3 is devoted to examining the consequences of the failure of certain steps in the algorithm and identifying some of these with known anomalous behaviors. Section 8 speculates about extensions of some of these notions, and Section 9 summarizes our conclusions. There are two mathematical appendices.
Review of previous work
In this section, we briefly review some of the results of [2] and [3]. In that work, we argued that, under the hidden variable doctrine, it is only the state-based logic of propositions that is relevant to our considerations: the actual values inside the nodes at any moment are not relevant at the logical level, which is entirely structural. The state space for a collection of n nodes holding real values (read as cell membrane—or parts of cell membrane—potential values, in the cases of interest to us) may be taken to be the product of (closed) intervals where [ai, bi] denotes the range of values allowed to the i th node. The relevant associated logic of propositions is in this case modeled by the ortholattice of subsets of W that are intersections of W with subspaces of with the origin removed. The behavior of such a collection of nodes is shown in [2] to exhibit quantum-like behavior if the origin of is an interior point of W (for n > 1). That is to say, within the space of states, there is a Euclidean open set containing the origin. (The origin itself is excluded as a state in these models.) In this case, the relevant ortholattice is isomorphic with the lattice of subspaces of . This circumstance is seen to hold in the biological context where neuron membranes, and portions of membranes, may sustain potentials which are both positive and negative. (The case of a single node in isolation, n = 1, is shown in [2] to be necessarily classical, i.e., not quantum-like.) Consequently, no logical harm is done if is itself adopted as the space in which the pure states of the system are represented by rays, or equivalently, by normalized vectors. (A pure state is one which is not itself a convex superposition.) Here is considered as a real Hilbert space with the Euclidean inner product. In [3], we dubbed such Hilbert spaces extended state spaces: here we shall often drop the qualifier. The quantum-like nature of such systems manifests as the existence of superpositional states, which realize disjunction in OL. Such a system, like Schrödinger’s cat, may be in a superposition of pure states, such as dead and alive, or ON and OFF, without being “in” any component pure state. We argued in [3] that the existence of such states materially affects the stability of such systems.
In particular, a two-node system of this type will exhibit quantum-like attributes.
Neuromorphic network models
In [3], we considered two types of neuromorphic models and the dynamics of one of these types. In this section, we briefly review the models proposed there. The first type considers single nodes to represent neurons and are essentially identical to ordinary neural net models except that we allow superpositional states. The second type of model regards the neuronal element to comprise of a pair of “chambers” imitating the input/output operations of certain biological neurons. This model pre-supposes the “standard” model of a multipolar neuron whose soma can be approximately resolved as described. Owing to the vast diversity of neuron types, not all neurons conform to this standard. For instance, amacrine retinal cells, which can have axons emanating directly from their dendrites, likely cannot be so resolved. (This is true also for certain dopaminergic neurons. Such cells would be better modeled by our first unicameral type of network.) On the other hand, we conjecture that principal excitatory cells, such as pyramidal cells, do conform to this standard and this will be the cell type to keep in mind in the considerations of the bicameral case to follow.
The unicameral case
We consider our basic network to comprise a finite-directed (or oriented) graph denoted by NA, say, whose set of n, say, vertices we call nodes, and denoted by in a chosen ordering. Each node can contain a real value, and for each edge directed from to we have assigned a real-valued function αij of the value in the i th node. All of these values can change with time. We think of the nodes as modeling neurons and the edges fanning out of ni as modeling the axon terminals of the corresponding neuron, while the edges fanning into ni model the dendritic inputs into this neuron. The values in the nodes then model the membrane potential of the corresponding neuron, and the values αij represent certain “weights” associated with the characteristics of the neuron modeled by .
We shall call a network with no internal connections a cluster. The extended state space of a network NA, namely the space of vectors of possible values in the nodes, denoted by , is equipped with a corresponding basis and elements of may be expressed as linear combinations of this basis (possibly with the ranges of coefficients suitably restricted). Thus, a vector of the form is now interpreted as representing the presence of the value λ in the node . It is the state vector in with λ in the i th position and zeroes elsewhere.
One network NA can be synaptically connected to another, NB say, by connecting each node of NA via a single step axon-like link to certain nodes (or no nodes) of NB, and upon their firing, should they fire, to determine certain values in these connected nodes. Such a connection may be expressed by associating with each state of NA a superposition of states of NB of the form where the coefficients are real-valued scaling factors which are functions of the values in the i th NA nodes, which also reflect the number of connections . We note that the quantum-like imperative to superpose entails integrating nodes, in the case of quantum-like behavior. Such behavior is absent in the single -node case but we shall assume that single nodes are also integrators.
In more detail, the firing of a particular node of NA into NB entails the collapse of a superpositional state of NA onto the “classical” state and this may be interpreted as a measurement of NA by NB. The association
| 3.1 |
is then interpreted as representing the superposition of all such possible measurements. It represents possible neural-like wiring of nodes of NA to nodes of NB along which firings may take place, together with information regarding the transmitted values, should they be transmitted. The unidirectional nature of the axonal connection of one neuron to others enables mapping of each basis state of NA (in its extended state space) to a (possibly null) superposition of basis states of the NB extended state space. This determines a linear map from to the but is not itself linear in the relevant variables.
A network NA may be considered to be synaptically connected to itself via maps of the form , where (Λij) denotes the adjacency matrix of the graph NA, and here . We may dub such networks neural-like or neuromorphic.
The bicameral case
As mentioned in [3], we introduced a network model that more closely resembles networks of biological neurons than most standard models of neuromorphic networks, whose nodes are mostly monadic single entities. Specifically, we modeled the neuron as a two-node system, since actual neurons are extended in space, some of them having for instance very long axons, others having large somas, such as pyramidal cells, and this has consequences which are generally ignored in neural net models. In that work, we simulated such an extension by resolving our single node, or unicameral, neuron model into one having two “chambers.” The first is the input chamber, namely a node corresponding to that part of the soma to which the dendrites are attached, while the second is the output chamber, namely a node corresponding to the hillock (or trigger zone)–cum–axon system, or axon initial segment, along which the action potential is conducted upon its firing. In this way, we could accommodate the values of the membrane potential at the two extreme ends of the neuron, which will generally be different upon its firing. Once the graded input potential achieves the threshold value, assuming it does, the action potential is triggered and occupies the output chamber. The value, or amplitude, of this action potential will in general be different from, and independent of, the incoming somatic potential subsequent to the firing. Since the basic neuron now comprises two nodes, its state space is a two-dimensional extended state space isomorphic to , where the first term accommodates the state space of the input node and the second term accommodates the state space for the output node, and is interpreted as a two-node system. As such, its states will be generally in a superposition, and we have something very like a qubit, which is the quantum two-state analogue of the classical bit and is taken as a basic computational unit in the hopeful discipline known as quantum computing. Denoting the generic vector in the extended state space of such a two-node system by (λ, μ), we found a pair of operators
| 3.2 |
| 3.3 |
which satisfy the following anticommutation relations:
| 3.4 |
| 3.5 |
| 3.6 |
As explained in [3], this realizes the system as a fermion-like one, since irreducible representations of the algebra generated by the operators and satisfying these (so-called canonical anticommutation) relations upon finite-dimensional spaces are all equivalent to each other and represent respectively the annihilation and creation of a fermion-like quantum of one type. The operator represents the internal transfer of the current value in the input node from that node to the output node and thus represents a preparation to fire the neuron: if λ has reached the threshold value then, at that moment, it becomes a value of the action potential and moves into the trigger zone or hillock, replacing any value μ that may be there
As a space of states of the underlying b-neuron, this space has an additional algebraic structure which captures an important aspect of actual neurons. To see this, first note that insofar as the operator represents a preparation to fire the b-neuron, that fact that means that this preparation cannot be executed twice at the same time: a neuron cannot fire while it is already firing. Now consider the subspace of the algebra of operators on , namely End, generated by the identity operator I and , which may be written
| 3.7 |
Here we have explicitly written in the two generators I and . It is immediately seen that is in fact a (commutative) subalgebra of End in view of equation (3.6). Now note that the inclusion map is easily seen to satisfy the UMP of Appendix A1 so that as an algebra. If we make explicit the state representing the b-neuron’s output node, e say, then we may express the state space of the b-neuron in the form
| 3.8 |
where e2 = e ∧ e, which will be seen to express the fact that the neuron cannot fire twice simultaneously and at the same time realizes the exterior product ∧ as essentially the unique combinator modeling this property mathematically. (We note that the generator of the input node is actually the unit of the algebra namely , which is also written |0〉 in quantum parlance since it is the vacuum state or state of zero occupancy.)
We note that the operator is not an observable of the system, but rather an internal unobservable operation that in a sense stands for the complex ionic flows, etc., that physically transfer the potential across the cell body. Although there are no actual physical particles implied by our picture we note that the fermionic number operator has the two eigenvalues 0 (with eigenspace the set of vectors (λ,0) having the output node at zero: the OFF state when normalized), and 1 (with eigenspace the set of vectors of the form (0, μ) having the input node at zero: the ON, or firable, or excited state when normalized) so that quantum mechanically an array of many such b-neurons may be expected to exhibit large-scale behavior similar to that of an Ising-like model with two-state qubit-like systems at the lattice points, or more generally, that of a quasispin model. Since each such a bicameral neuron, or b-neuron, has a fermionic character, a collection of them may be expected to exhibit large-scale behavior similar to that of an Ising-like model with two-state qubit-like systems at the lattice points, or more generally, that of a quasispin model. This is the case explained in [3].
A network of the kind we are considering is then defined by an ordinary finite-directed network, of N vertices (or nodes, not to be confused with the original nodes) say, in which the spaces are thought to label the vertices and certain maps are specified for each pair (i, j) which contain information concerning the corresponding adjacency properties of the vertices as well as information concerning the strength of the graded potential induced at the receiving b-neuron upon the firing of the upstream b-neuron. As in [3], we shall assume simplified versions of the usual structural properties of such networks: many dendritic inputs to a cell model; many axonal output terminals to other such models; communication via chemical synapses and a unidirectional flow of information from dendritic arbors through the soma to a trigger zone–cum–hillock–cum–axonal initial segment, etc. (In addition, we shall as before postulate, for those networks of interest to us, the existence of substrates of interneural and other tissue, or chemical media, which promotes connectivity of the nodes (via electrical (gap) junctions in the interneural case) in addition to their principal connections via axon–dendrite synaptic action: please see Section 5.2 below and for instance [20]. The interneural substrate, for instance, has the effect in nature of inhibiting and synchronizing the firing of local groups of networked principal neurons, and we shall later find this sort of phenomenon reproduced in the logic (Section 6.1). This is one of several ways our approach differs from the classical notion of a neural net.)
The analogue of synaptic maps of the type shown in (3.1) necessarily have a different interpretation for b-neurons since, being clusters of two nodes, they have quantum-like behaviors. Moreover, the state spaces of such bicameral networks have a richer structure which will be the subject of later sections of this paper.
Logic and computation
In this section, we give a brief account of notions pertaining to the kind of computation we shall attempt to recognize in systems of networks of the kind we have considered.
The external logic of finite-dimensional vector spaces
We have seen that the appropriate logic for systems with “hidden variables” is orthologic (OL) and that it is well represented by the lattice of closed subspaces of a Hilbert space [2]. Here the propositions correspond to the closed subspaces and the logical connectives correspond to the lattice operations. This subspace lattice may be thought to embody the “internal” logic of a vector space. There is also an “external” logic of vector spaces in which the propositions correspond to the entire spaces and the logical connectives correspond to certain operations upon, and combinations of, these vector spaces. Moreover, this logic contains a version of the original “single space” logic OL in a non-trivial way. This sort of externalization of a given logic is at the heart of an important trend in modern computational logic which we shall discuss briefly below.
The main combinator of vector spaces we shall be concerned with in this paper is the tensor product, written A ⊗kB or A ⊗ B of vector spaces A, B over a field k. When the field is not in doubt, as here, the subscript is dropped. An account of this product is given in Appendix A1.
The standard way of realizing a logic suitable for implementing a computational paradigm is to interpret within a category—such as the category of finite-dimensional vector spaces—a deductive scheme known as a Gentzen sequent calculus. We digress briefly to discuss this topic.
Gentzen sequent calculi
A Gentzen sequent calculus is a metacalculus for dealing wholesale with deductions in a possibly notional underlying deductive system. It is appropriate to our endeavor here since its modus operandi is to hide the details of a possibly notional underlying deduction. Thus, the basic term, a sequent, is written
| 4.1 |
where Γ and Δ are sets of formulas, which have the informal reading as “,” where the symbol means logical conjunction (AND) and logical disjunction (OR). As metacalculi for natural deduction systems, these sequent calculi delineate certain symmetries and structural aspects of the underlying deductive system which are hidden if one remains at the lower level of the underlying system. The organizing power of the style has had a major impact on the proof theoretic aspects of deductive logic. The sequent calculus idea lends itself to other interpretations by liberating the reading of the turnstile ⊩ from its classical rôle as a stand-in for a deduction in a putative underlying natural deduction system. A revolution occurred when Girard realized that it could be used to effect an extremely refined computational theory of resource management: here, a sequent of the form (4.1) is read, roughly speaking, as the depiction of a process in which the resource Γ is consumed to produce the resource Δ. (These resources may be evanescent, being possibly changed or used up in the process of “passing through” the turnstile.) The concomitant logical rules and connectives then acquire entirely new and more general interpretations and obey new laws. These changes vitiate the simple informal reading of a sequent given above (since the conjunct on the left and the disjunct on the right are no longer the usual ones of ordinary logic). In this way, the system known as Linear Logic (LL) arose. For a good introduction, see [7], and for a selection from the vast literature on the subject, see [8–13]. Such novel interpretations of the new sequents opened the way for a large variety of applications not only to computing itself but also in such diverse areas as quantum computing [21, 22], particle physics [23], and the study of natural language [24].
Thus, one may start from the formal specification of sequent calculus, without assumptions concerning the presence or otherwise of an underlying natural deduction system, and proceed formally in abstracto to develop a theory of proofs with wide ramifications. Quite often, it is possible—by a judicious choice of term assignments—to reproduce an underlying deduction system for which this sequent calculus then represents a metacalculus, but it is not required to do so.
In [25], the first author posited a minimal sequent calculus, GQ, for quantum resources, which in fact coincides with a fragment of an intuitionistic version of linear logic as it is represented in a category like the category of finite-dimensional vector spaces (i.e., a ∗-autonomous compact category [10]). We consider only an intuitionistic sequent calculus, which means, among other things, that at most one formula is allowed in the succedent (i.e., right-hand side) of a sequent, since the disjunction implied by collections of formulas in the succedent is disruptive in an intuitionistic system. Such systems more closely reflect the paradigm of constructive proofs or programs.
The rules of the calculus
We present below the rules of calculus we have dubbed GN, which is a fragment of a well- studied calculus called intuitionistic multiplicative exponential linear logic denoted IMELL.
Here capital Greeks stand for finite sequences of formulas including possibly the empty one, and D stands for either a single formula or no formula, i.e., the empty sequence, and when it appears in the form ⊗ D, the ⊗ symbol is presumed to be absent when D is empty. If Γ denotes the sequence A1, A2,…, An then !Γ will denote the sequence !A1,!A2,…,!An. The Girard of course exponential operator ! is sometimes pronounced “bang.” The sign ⊗ should strictly speaking just be regarded as an abstract symbol though of course we shall soon interpret it as usual.
(Note that weakening in ordinary logic reflects the validity of a deduction resulting from the conjunction of a proposition to the hypotheses of a valid deduction. This may not apply in the linear case, owing to the evanescence of “resources”: the new proposition may interfere in some way with those already present. Note that contraction entails storage, which is perhaps the most important aspect of this or any other computational scheme. This is discussed further below and in Appendix A2. Thus, the calculus unadorned with the Girard of course operator ! lacks weakening and contraction (or storability, for reasons similar to those in the case of weakening), reflecting this possible evanescence of our resources (which will ultimately derive from our network structures). Applying the operator !, a model of which exists in the category of finite-dimensional vector spaces, brings these rules back.)
The rules or axioms are expressed as a set of inferences written as fractions, the denominator being inferred from the numerator, and with labels appended to the right of the inference line. Deductions, which are called proofs in this context, are written as trees of these fractions.
| 4.2 |
| 4.3 |
| 4.4 |
| 4.5 |
| 4.6 |
| 4.7 |
| 4.8 |
| 4.9 |
| 4.10 |
(As noted, these are axioms appropriate to a fragment of the logic IMELL, meaning, among other things, that only one formula is allowed in the succedent of a sequent. The set of axioms for full linear logic, also known as classical linear logic (CLL) is to be found in [7] and our axioms above correspond to those in the latter work, given the intuitionistic embargo on more than one formula in the succedents, as follows: Section 4.4.2, p. 85, (id) Ax; (exc, r) LE; (cut) Cut; (⊗, r) R⊗; (⊗, l) L⊗. Section 5.5.2, p. 115, (weak-l) LW; (contr-l) LC; (!, l) L!; (!, r) R!.)
We remark again that the rule of contraction is paradigmatic of storability of the contracted type. If a storable resource is needed twice to produce some other resource, then it is needed only once, since it can be retrieved from the putative store for use again. We shall call such a type storage capable. In this calculus, types are generally not storage capable, owing to their evanescence, but (following Girard) they become so when operated upon by the of course operator !. Please see Section 5.6 for a more detailed discussion.
This calculus may just be regarded as a set of rules with which to manipulate abstract formulas, and this would be the business of formal logicians. We shall proceed formally for a while but then apply some of the rules informally to the specific cases at hand, namely to the family determined by the extended spaces of states of the networks we are considering, using the rules of the logic as a guide.
(Cutting through the formalism, we will soon be regarding the formulas A, B, etc. as finite-dimensional vector spaces, the connectives etc. as usual in this category, and the turnstiles as linear maps.)
In applications, one adds “non-logical” axioms to the GN rules, for instance, to depict a brain as a family of linked networks, and other sorts of given sequents. The resulting family of proofs or deductions is known by logicians as a GN theory.
Note that the following interpretations are obtained for some of the rules:
- L⊗:
Both A and B together must “produce” or map to D in order for A ⊗ B also to produce D. So ⊗ is interpreted as a parallel conjunction.
- R⊗:
In this case, the two antecedents are completely independent and share no “resources” until the parallel conjunction ⊗ is applied in the conclusion.
Interpretation of the calculus in the category of finite-dimensional vector spaces
Informally, an interpretation of a logical calculus of our type in a category is a mapping of types of the calculus to objects in the category and of logical connectives to connectives in the category in such a manner that the logical inferences hold in the category. That is to say, the interpretation should preserve the inferences of the logic. The conventions of formal logic entail a notation for the interpreted formula, such as for instance for the interpretation of the formula A. Since our treatment will be informal here, we will not make this distinction but simply identify a formula with its interpretation.
A formal treatment, which may be skipped, would be along the lines laid out in the rest of this section.
Let us denote the category of finite-dimensional k vector spaces by . To carry out the interpretation of GN in , we need to specify, for each atomic GN formula, a corresponding object of . Supposing this to have been done (and it will be done below), we then obtain for each GN formula A, not involving the operator !, an object in merely by interpreting the occurrences of ⊗ in A as carrying its usual meaning in . For such formulas, GN sequents A ⊩ B are then interpreted inductively as elements of Hom(A, B), the space of linear maps of A into B, according to the interpretations specified for the inference rules. For general sequents, we replace each comma in a non-empty sequence Γ by ⊗, so that Γ is interpreted as if Γ = A1,…, An, and we replace each empty sequence by . Thus, for instance, A ⊩ A (Ax) shall be interpreted as (or by) the identity map 1A ∈Hom(A, A). The other rules not involving ! hold in the category and linear maps may be built up which interpret GN proofs in an obvious manner. Thus, for the case of cut, since Γ, etc., is going to be interpreted by the single space , etc., we may consider Γ, , to be replaced by single spaces. Then, given interpretations , , the composition
| 4.11 |
is indeed the interpretation in of the sequent given by the cut rule applied to the antecedent sequents, so we conclude that this rule may be derived in the interpreting category. The other rules not involving ! can be treated similarly, using the properties of the connectives in .
A model for the ! operator in will be treated separately. We shall introduce it informally in Section 5.3 and give a more complete mathematical discussion in Appendix A2.
The upshot is that a proof of a sequent Γ ⊩ D, say, gives rise to a linear map , such that if another equivalent proof of Γ ⊩ D is used, the same linear map is produced. Here, the notion of equivalence of proofs needs to be defined, but it is not necessary for us to do so here.
We shall adopt these lower case Romans, a, bi, etc., interpreted as state spaces of single nodes, as our syntactic atoms.
Computation with the network models
In this section, we shall attempt to arrange a meeting between the subjects of Sections 3 and 4 as a means to later (Section 7.1) exhibiting certain processes—mimicking those in brains—as proofs or computations in the formalism proposed in the last section.
The first step is to realize that certain operations on unicameral networks induce operations among their respective state spaces.
The basic sequent
To comport with logical usage, we shall now write A for the state space we had previously written , etc., and treat it as a formula in the logic. Then the basic sequent A ⊩ B is interpreted as a linear map of state spaces necessarily of the form given in equation (3.1). This generally corresponds to a synaptic connection of the nodes of the A (or upstream) network to the nodes of the B (or downstream) network but not always. We shall also include non-synaptic connections as in the case of chemical fluxes, mainly in the bicameral cases considered below (cf Section 5.4).
Tensor product
There is a possible combination of networks that will be our main concern here. Namely, an association among nodes that is by means of a substrate, or other types of connection, different and in addition to the network of axon-like synaptic connections. In nature, there are various mechanisms whereby ensembles of cells, or parts of cell membranes which are also modeled by nodes in the bicameral case, become associated co-operatively with each other, either by spatial proximity or by sharing the same neuromodulatory chemical environment, or because they are jointly orchestrated or tuned, for instance by a shared substrate of interneurons or other cells. In this kind of combination (or pairing in the case of two networks) a node of a network NA may be associated with a node of a network NB in such a way that the pair may act as a unit, which contains a single value. The state of such a unitized pair is well modeled by the tensor product of the corresponding states (cf. Appendix A1 if necessary). A value assigned to this paired state cannot be attributed to any one constituent state since , and similarly for any number of tensorial tuples. That is to say, in keeping with the doctrine of hidden variables, such a combined tuple of nodes hides the location of a value λ: for instance the state cannot distinguish between the circumstance that the value λ is in the i node and the circumstance that it is in the j node. Thus, the space generated by all possible such pairs is the tensor product of the individual spaces,
| 5.1 |
in this case, and similarly for any number of networks. In this way, the details of the microscopic computations proceeding inside each node and among an ensemble of co-acting nodes, are hidden, in keeping with our doctrine of hidden variables, while intracellular effects are taken into account. This closely mimics the way in which interneurons among other mechanisms orchestrate the activity of principal neurons. Moreover, should one of these values momentarily become zero, then the probability of the combined state being available (or firing) falls to zero. This is both synchronizing and inhibiting. It simulates in a vastly simplified but effective manner the kind of inhibitory synchronization effected by biological interneurons, a hugely diversified group including basket cells and chandelier cells, which connect local principal neurons and induce very rapid inhibitory signalling between networks of them, having synapses of both chemical and electrical types (bidirectional gap junctions). (We note that these cells have their own panoply of neurotransmitters, such as GABA in addition to the electrical connections.) Of course, the joint value could go up, and in that case there are problems for the neural applications we have in mind (cf Section 5.4 for further discussion). (The ability of this model to take such substrate or interstitial liaisons into account is one way in which the model differs from the standard neural net model.)
It would not be too abusive to write NA ⊗ NB for the network whose state space is A ⊗ B so that NA⊗B = NA ⊗ NB.
This shows that, in addition to the basic sequent, the rules of GN, when applied to state spaces of unicameral networks, may be realized by constructs at the cellular level: that is to say, in the “hardware.”
The bicameral case
It turns out that the case of bicameral networks similarly realizes the operator !.
We shall see this first for the case of a single b-neuron. In keeping with our informal approach, we will generally identify formulas as above with their interpretations as state spaces. We then claim that is a model for !a where a is interpreted as the one-dimensional space , where ea denotes the generator of the extended state space of the single node na regarded as the output node of the b-neuron. That is, it may be shown to satisfy the rules for ! in the interpreting category. This is proved more generally in Appendix A2, so we illustrate it here with only a couple of the rules for !.
LW: Consider the map given by projecting onto the first summand of (the space representing the vacuum, or OFF state). Then an interpretation of Γ ⊩ D, namely a map , may be composed with the map which is the proposed interpretation of Γ,!a ⊩ D.
LC: Consider the linear map defined by ψ(I) = I ⊗ I, . Then the sequent !a,!a, Γ ⊩ D is realized by a map , may be composed with to produce a map which is the interpretation of !a, Γ ⊩ D.
The map ψ may be interpreted as a kind of storage operator, and banged types are storage capable. For further discussion concerning this type of storability or quantum-like duplication, see Section 5.6 and Appendix A2.
We shall for the moment denote the generator (i.e., the unit in the exterior algebra) of the extended state space of the input node of a b-neuron na by so that we may write .
Thus, the ! operator, when applied to an atomic formula a (interpreted according to our conventions as a one-dimensional space), may be interpreted as an isomorph of the algebra . We may now invoke (A.9) to obtain an interpretation of !A for any A, identified as usual with the vector space it interprets, with basis , say. Namely,
| 5.2 |
| 5.3 |
| 5.4 |
so that we should interpret !A as the vector space . The first isomorphism here is an isomorphism of algebras with the exterior product on E(A) and the graded product on the tensor product (cf Appendix A1). This may be realized in the “hardware” in the presence of the kind of substrate connectivity discussed in the last subsection.
To describe the move from the unicameral situation to the more highly resolved bicameral one, we first rehearse our notational conventions. For network NA with nodes , we denoted the unicameral state space by A, with basis . In moving to the bicameral version of the network, we replace each node by a b-neuron, namely a pair of nodes , where the original node is now regarded as the output chamber of a b-neuron to which an input chamber has been appended. The state space A is replaced by . We may promote a unicameral sequent A ⊩ B to its bicameral form by applying L! and R! to obtain the sequent !A ⊩!B, which may be checked to interpret the result of applying the functor E(). This maps an OFF state of the left-hand side (or upstream) network to the OFF state of the right-hand (or downstream) network with a certain probability depending upon the coefficients, and firing patterns on the left to firing patterns on the right, again with certain probabilities. In general, both sides consist of superpositions of firing patterns.
Since the extended state space of a single b-neuron is realized as the exterior algebra of its output node’s extended state space, the whole extended state space !A, being the tensor product of those of its constituent b-neurons, is now necessarily interpretable as the appropriate state space for the whole network. In [3], we derived the dynamics for such systems, which describe the changes in time of such firing patterns.
In what follows, we shall deal almost exclusively with networks of b-neurons whose extended states spaces are exterior algebras of the form we have been writing informally as, for instance, !A. To be consistent, we are required to denote the corresponding network by N!A.
The significance of the exterior product and extracellular neurotransmission
We have interpreted a tensor of the form λei ⊗ ej = ei ⊗ λej as a state of a pair of corresponding nodes bound together by a substrate of some kind so that the bound pair registers the single value (though the actual value is hidden from us, according to the overarching doctrine of hidden variables). If this value decreases to zero, the combined state contributes nothing to any superposition: the probability of firing, in the application to follow, falls to zero. Thus, the substrate connection admits inhibitory input into nodes, and for this reason we identified it with the substrate provided in actual brains by the network of interneurons. It would appear that this kind of connection would also admit excitatory inputs since the algebra admits any real value for λ so it may increase as well as decrease. However, in this case, a problem would arise for self connection of nodes via this substrate, whose basic state would be of the form λei ⊗ ei. If a node was connected to itself in this manner and admitted excitatory input, then it would run the risk, in the application to b-neurons, of precipitating the forbidden state of double firing of the b-neuron.
It is significant that the exterior product, ∧, which, we note, arose spontaneously out of our adoption of the operator in equation (3.2) or equation (3.3), expressly excludes this possibility, since λei ∧ ei = 0, while at the same time also admitting inhibitory substrate connections, since it has the same multilinear property of sharing scalar values as the ⊗-product.
Thus, the exterior product may reflect either inhibitory binding substrates (such as those provided by a plethora of GABAergic interneurons) or excitatory substrates (such as those provided by a glutamatergic background as in mammalian cortices) or both. As a result, the use of the operator !, such as in the storage paradigms to be discussed below, allows the involvement of both kinds of modulation.
This has a bearing upon memory formation. Although the chemical environment is exceedingly complex, it seems clear that a flux of the excitatory neurotransmitter glutamate is involved in memory formation [26, 27] as is the ambiguously modulating neurotransmitter dopamine. We can crudely simulate this in a formal fashion by regarding the influx of extracellular glutamate as provoking a non-synaptic transition of the form ξ1 ⊗⋯ ⊗ ξk↦ξ1 ∧⋯ ∧ ξk. Here the ⊗-product is associated with an inhibitory substrate while the ∧-product is associated with both inhibitory and excitatory substrates such as glutamate and dopamine. For more on this, please see Sections 6.1 and 7.1.
A remark on firing patterns and the Plücker embedding
The Plücker embedding classifies subspaces of dimension p of a vector space V in terms of rays in the exterior product (Appendix A1). But in the model of orthologic, we used originally [2] subspaces corresponded one-to-one with propositions in the logic. Consequently, in our context, the Plücker embedding may be regarded as establishing a one-to-one correspondence between propositions in the logic and certain firing patterns.
Storage
In this subsection, we briefly discuss the notion of storage as it manifests in the logical paradigm.
The rule of contraction as written for instance above in GN (4.4) is generally regarded as expressing storability of the type !A: if two instances of !A are required, !A,!A, Γ ⊩ D, then only one is needed; thus, we infer !A, Γ ⊩ D. The type !A is implicitly “stored” (somewhere) and can be re-used. We have dubbed !A storage capable. This is interesting when interpreted in the category of finite-dimensional real vector spaces if we take, as above, !A := E(A). For then, with , we have as above
| 5.5 |
and thus the smallest storage capable unit is realized as , the real version of the qubit of quantum computation (and the extended state space of a single b-neuron). Moreover, every storage capable type is then necessarily interpreted as a tensor product of these, i.e., a qubit register, in quantum computing parlance. (Note that we did not start with the classical bit: it arises instead as the classical degeneration of the quantum-like qubit.)
It seems to be a remarkable and happy circumstance that the functor !() should simultaneously induce storability while also describing the space of firing patterns: i.e., firing patterns are storable commodities in this sense.
Concomitant with the idea of storage capability is the notion of infinite reproducibility or repetition. This can be proven in the logic as follows. Take k instances of the axiomatic !A ⊩!A and apply R⊗ k − 1 times to obtain . Then apply LC k − 1 times to obtain . Thus, one instance of !A “produces” any number of (undamaged) copies of itself. (Of course, the resource paradigm does not correspond exactly with our interpretation of the turnstile as arising from a (family of) connection(s) among networks.)
It is worth noting, as in [3], that 2n bits are required to store the “classical” firing patterns associated with the network labelled A, in the absence of superposition: namely the basis states comprising n tuples of ON and OFF states of the nodes. Whereas, by the right-hand side of equation (5.5), only n qubits or b-neurons are required to house these patterns in the presence of superposition. So storage capacity is greatly enhanced in the presence of superposition.
Timing
We return to our interpretation of the basic sequent A ⊩ B in the case where these are taken to be extended state spaces of unicameral networks: the extension to the bicameral case will follow immediately from the considerations above. Such a sequent is interpreted as a map of extended state spaces of networks NA and NB induced by possible firings of NA’s nodes, and since this is a process that takes place in time, such sequents come bearing implicit time stamps. At a particular time t, a configuration of networks may be determined by a collection of basic non-logical axioms of the form A ⊩ B which represents a one-step wiring of NA to NB at time t in which node ’s axon is synaptically attached directly to NB’s nodes with certain weightings, and gives rise to a map of A to B determined by assignments of the form (3.1).
Thus, a basic sequent A ⊩ B, of the type considered above, at time t, which we shall write A ⊩tB where t is a real number residing in some subinterval of the non-negative real numbers, represents in a sense a wiring-cum-firing diagram at time t. It represents a certain state of affairs relating to how the network NA is connected to the network NB at time t, which also includes information concerning the possible firing activity of NA’s nodes relative to NB’s nodes at time t. As such, it represents an eventuality, or possible outcome at time t, rather than an event. At a particular time t, a collection of such networks, such as those comprising a brain for instance, may be describable in terms of these basic irreducible one-step or singly linked sequent types, taken to be non-logical axioms added to the logic, together with the whole panoply of relations deducible from them via the rules of GN, all at time t. The use of the cut rule produces chains of these basic maps so that in general, if two basic sequents A ⊩tB, B ⊩tC obtain at t then so does the sequent A ⊩ C which represents a wiring diagram from NA to NC which also obtains at time t (and is subject to change at later times) and so we write A ⊩tC. (Of course, there may be other sequents/wiring diagrams A ⊩tC at time t). In these cases, the map depicted in equation (3.1) would involve products of the relevant adjacency matrices at t and compositions of the functions implicit in the weights.
Sequents of the form !A ⊩ B are now interpreted as maps of the firing patterns (of A) which is to say, insofar as the sequent represents a wiring diagram, it concerns only those wirings relevant to (all possible) subsets of firing b-neurons. This is what ultimately underlies the truth of Tsien’s postulate (cf Section 7.2). In the case of bicameral networks (interpretations involving banged types), we shall allow non-logical axioms in the form of sequents that do not necessarily arise from synaptic connections: these will model chemical or other indirect connective possibilities.
In all the discussions to follow, we may take the t labels to represent a finite number of points of a finite, sufficiently fine partition of a closed subinterval of , so that we are confronted with a large but finite total number of added non-logical axioms.
(It may be noted that such timed sequents are interpreted as linear maps between finite dimensional vector spaces, such maps being indexed by t, meant to be interpreted as the time variable. As such, with t taken be a continuous parameter, they may perhaps be interpreted as describing the behavior of the analogue devices now going by the general term memristor, which are being used to implement new kinds of neuromorphic neural net-like computers, in which they play the role of synapses: for one example among many cf [28]. Their inclusion in such a scheme as ours would go beyond the confines of present logical theory.)
Certain inferences of the logic may themselves take time to implement, specifically if they can be judged to be physically implementable.
We revisit the axioms to judge which of them may be deemed to be physically implementable and therefore might entail an interval of time to effect the transition from antecedent sequent to succedent sequent.
LE: This takes no time, since it represents merely a reordering of a list. So the timed rule LEt leaves the timed ⊩t in the antecedent unchanged in the succedent.
LW: Referring to the LW rule (4.3) suppose we have a synaptic connection . Then we also have such a connection from the ⊗-paired nodes of with the vacua or input nodes of , since these pairs may be assigned to the same nodes in ND that the nodes in are assigned to, by the unitizing nature of the ⊗-product. This is seen to implement the rule (Appendix A1). It clearly takes no time to implement this step since the map in the denominator is implicit in the map in the numerator.
LC: We shall argue that the fundamental operation of contraction, associated with a notion of storage, is in fact physically implementable. Let us consider the association (cf Appendix A2). Here 1 represents the generating state of the input node of the i th b-neuron (the OFF state of , despite the notation, also written |0i〉) while represents the generating state of the output node (or ON state) of the i th b-neuron. The map represents the replacement of the output node’s generating state with the generating state of the unitized ⊗-product of both constituent nodes of the b-neuron. This could happen in a real neuron only if and when the value of the membrane potential at the output chamber (i.e., the trigger zone–cum–axon region) equalizes throughout the neuron, which then operates as a unit, so that the two I/O nodes are unitized, effectively replacing , the ON state, by as above. This occurs when the neuron attains the resting state following a firing. Suppose a firing of the i th b-neuron to be in progress at time t: then it will take a certain time to reach the resting state, in which the whole membrane is at the same potential (namely the resting potential). The unitization of the I/O nodes may also be realized as the replacement of by , and these alternative realizations should be superposed to yield the (“coproduct”) map determined by . The input state will already be unoccupied prior to a putative firing so 1 is replaced under these circumstances by a copy of itself, namely 1 ⊗ 1. Let us suppose that all the b-neurons in the network that are potentially firing at t would commence firing simultaneously. Then, at time t, they would all be at the same point in the progress of their action potentials. Then the map or wiring diagram !A,!A, Γ ⊩tD at t is replaced by at time (where denotes the common value of the ) since the connection of to ND will be “re-wired” through N!A⊗!A via ψA. So, in this case
| 6.1 |
That is to say, if !A,!A, Γ ⊩tD represents a firing-cum-wiring diagram at time t (involving only the subsets of firing b-neurons, as noted above), and all the A b-neurons that are firing at that moment are at the same point of their action potentials, then this diagram may be replaced by the diagram at time . This is the time at which all the A b-neurons would reach their rest states after t. Of course, as it stands, this value will itself depend on t so we shall take it to be the average such time, pending a finer analysis. In humans, the duration of an action potential is approximately 5 ms after initiation, so the average interval between this and the attainment of the rest state is ms. The assumption that the possibly firing neurons are at the same point of their action potentials at time t means that the A neurons have fired simultaneously at the last firing, so that it is only required that the network exhibits synchrony a short time before t, i.e., locally in time. In this case, we shall say that a network is synchronized at time t. It is known that synchronization is an important component of brain behavior for the processes we wish to discuss [29]. We note that this rule of contraction may fail in nature: for instance, if there is a pathology involving the interneurons or a deficit in the supply of appropriate neurotransmitter, or some other condition that thwarts the formation of tensor products of networks. Likewise, if synchronization in N!A has not been realized at time t, this rule may fail. Thus, the use of this rule must be guarded and used with these provisos.
We may note that in this context, synchronicity promotes storage.
The non-timed nature of the cut rule has been discussed above. Likewise, the other axioms not involving ! take no time at all; they are either just rearrangements or reframings. We shall neglect the time taken to form tensor products of state spaces since this operation is a reflection of a connection of the networks to the pre-existing matrix or substrate, and we assume that this takes a very short time to effect, if any. That is to say, we shall assume, in the normal run, that the interneural connections are already in place and operational when the wiring diagrams or maps represented by the sequents involving the tensor products are posited. Here again, as in the previous rule, the formation of tensor products may itself be thwarted by abnormalities in the interneural substrate, deficits of appropriate neurotransmitters, etc.
The axiom L! also does not take any time since the projection map implementing it is just a change in resolution from finer (bicamerality) to coarser (unicamerality) while R! is just the opposite, so also takes no time to effect. These are changes of perspective only.
Thus, the only rule we shall deem at this point to require timing to effect is the fundamental storage operation of contraction, and this only in the presence of synchronization at the relevant time, as above. The other rules are either changes to the representing Hilbert spaces reflecting un-physical processes or book-keeping devices.
The picture that emerges of such a timed calculus requires, for each time t, a finite family of non-logical axioms describing the basic building blocks of (in our case) an ensemble of networks at that time, together with all the sequents generated by these axioms and those rules of GN not involving any time-sensitive rules. The conclusions of the proofs involving one or other of the time-sensitive rules will then belong to another family of sequents holding at a later time, in case these rules do not fail. We shall make the assumption in the applications to follow that none of the rules fail initially, which we take to be the state of affairs in a normally functioning biological network, and then gauge what happens when they do fail.
Synchronicity promotes binding
These rules imply stability properties of certain sequents arising from synchronicity on the left of the turnstile. In a sense, this synchronicity of the type (or network) on the left binds it forward to the type (or network) on the right [29]. We note that there is no apparent limit on the number of steps, or cuts, leading from the antecedent to the succedent (at the relevant times).
We note again that all the t labels in what follows may be taken to comprise a finite set of points in some fixed subinterval of which form a partition of the interval sufficiently fine that the typical or minimum of the τc values may be approximated by a multiple of its subintervals or time steps. Only the order structure of the set of t labels is used in the results that follow.
First we recall that in the presence of excitatory fluxes (cf Section 5.4), we may invoke non-logical axioms of the form
| 6.2 |
whose interpretation maps ξ1 ⊗ ξ2 to ξ1 ∧ ξ2.
Theorem 6.1
Suppose for some , that N!A is synchronized at t for all and (6.2) is assumed. Then for n = 1,2,3,…
Proof
For t0 in the hypothesis we have
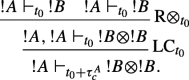 |
6.3 |
Cutting this with (6.2), we obtain
| 6.4 |
Thus, is another value satisfying the hypothesis so that we may conclude again that
| 6.5 |
that is
| 6.6 |
and so on. □
This proves the assertion.
Among the possible interpretations of this result is that part of our formalism involving tensoring and the use of the ! operator reflects well the synchronizing inhibitory nature of the implicitly assumed interneural substrate, since the banged types must keep returning to their initial sequent status, cannot run away uncontrollably, and are therefore bound in a certain sense.
Now suppose there exists a time such that, if , then !A ⊩t!B for all . Then we shall say that the sequent (or !A ⊩!B) is persistent at t0.
Theorem 6.2
Suppose !A ⊩!Bis persistent at t0, , (6.2) is assumed and N!Ais synchronized for all. Then !A ⊩t!Bfor all.
Proof
Choose any such that . Then
| 6.7 |
Consequently, by the definition, , and then by Theorem 6.1, : that is, . Thus, !A ⊩t!B for all . This argument extends by induction to any for n = 3,4,…, and this proves the assertion. □
The condition we have dubbed persistence at t0 has an interpretation in terms of non-synaptic connections of this type, and these two results have a bearing on the mechanism believed to lie behind LTP (long term potentiation). This will be investigated elsewhere.
Thus, if a persistent sequent is valid at some time t and the antecedent is synchronized at all such t, it will remain valid until synchrony fails, or equation (6.2) no longer applies, or some other disruption occurs.
We note that in the last sequent quoted in the statement of the last theorem, the actual maps implementing the sequent may themselves change in time, as may the various intervening adjacency matrices. Our formalism thus accommodates possible synaptic plasticity in the connections signified by the sequent.
As noted, in this formulation the contraction rule signifies storage. The dynamics involved in sequent proofs is thus driven by changes in “resource allocation” among the types participating in the ambient proof, these resources being essentially the storable collective states we have called firing patterns.
(We remark that this picture of the timed calculus may be likened to a fibred structure over the set of times t in which the fiber over t is the ensemble of derived sequents at t. The persistent ones then represent sections of this fibration. This interpretation will be pursued elsewhere.)
Applications: pattern completion, Tsien’s postulate, and pathological consequences
Pattern completion
We shall first outline a proof fragment in the sequent logic which implements the pattern completion function of memory in abstracto, and then specialize to possible specific functional processes. (Pattern completion refers to the process by which the Proustian taste of a madeleine brings into consciousness a flood of associated memories. It exemplifies the general notion of cued recall.)
As in the discussion in the last paragraph of Section 5.4 and equation (6.2), to effect a model of memory we may add the non-logical axiom
| 7.1 |
where we noted that the interpreted map is just multiplication in the exterior algebra !M. This may easily be generalized to a sequent interpreted for each k as the map sending firing patterns ξ1 ⊗⋯ ⊗ ξk of the corresponding bicameral network to their exterior product which is another firing pattern of the same network. This process has the property that any repeated component firing patterns are omitted, since for all ξ. This ensures that no multiple simultaneous firings of the same pattern can occur. This property will acquire a possible cognitive relevance in the development to follow (Section 7.4).
Let us assume a finite collection of persistent sequents of the form , i = 1,…, n, !M as above, and , with the Ai networks being synchronized at the relevant times. The intuition here is of incoming firing patterns of networks , representing memory fragments, or sense impressions, mutually associated in some way, possibly by time or space or emotional state, being consigned to, or encoded into, a “memory module,” or Gestalt, namely the network N!M. Then in view of the persistence of these sequents, eventually a time will come when we will have, for :
| 7.2 |
Repeated applications of R⊗t then yields the contextual sequent
| 7.3 |
for . From the discussion above, we have . Then cutting this with the last sequent yields
| 7.4 |
for any time t later than that specified above. That is to say, firing patterns of the sequence of types on the left of the turnstile are eventually “stored”—or accreted by juxtaposition—in the one on the right. Thus, N!M functions like a long term memory module (LTM). This is context formation as discussed in [3]. Now let us access or retrieve one of these stored types, say, at some time say, later than the last t. That is to say, it is “fed out” to an output network with state space , a working memory module perhaps, by some external prompt or cue, such as the Proustian taste of a madeleine, at time . This is expressed by the sequent
| 7.5 |
persistence being assumed. Then for any , we have
| 7.6 |
Thus, for , we have
| 7.7 |
Now, it is easy to show using first the axiom !M ⊩!M, and then LW, that for any t, , and similarly so for s large enough for (7.6) to be valid we may cut the sequent (7.7) with both of these last two sequents to obtain
| 7.8 |
and
| 7.9 |
which should be compared with (7.4).
To summarize, we have encoded into the formalism:
the sequential long term storage of a set of network inputs into a single memory module: (7.4);
the retrieval later of one of these stored inputs by feeding it out to a (perhaps working) memory module : (7.5).
The formalism then delivered the sequent (7.7) at a later time, which has the following interpretation. Retrieving one type from storage has the effect of a little later retrieving all of them willy-nilly: the network state space now appears on the right of the turnstile. Moreover, the circumstances of the types returned to the LTM module might now have been affected by interference and entanglement effects produced by the presence of . At the same time or later, the formalism produces the sequents (7.8) and (7.9). This shows that the memory fragments have been restored to the LTM by being copied back into it, and possibly changed by that process, while being available to working memory. The LTM is now ready to repeat this process if another memory fragment is accessed. It would seem that the order of access now must count, since the different processes may alter circumstances. This simulates contextual memory retrieval [30]. Note that each time a type is retrieved, the whole collection of them is re-established in the LTM so retrieval has a reinforcing effect. This mimics exactly the operation of memory retrieval in actual brains. Evoking one memory evokes associated memories. Moreover, the stored memories may be affected by this act of retrieval, though this retrieval reinforces their continued presence.
We remark that as an algorithm, and indeed as for any such algorithm or proof in the system, no central executive or master control “unit” is required (cf Section 8.1).
(Informally and ignoring the timings: the inputs to the storage capable (i.e., banged) memory “module” M are the A s, one at a time, as in reality. For instance, if Mchildhood is the LTM associated with the “childhood” Gestalt, then Atea could label the network enabled by the first taste of Aunt Léonie’s tea. Its affect is then “stored” in Mchildhood via !Atea ⊩!Mchildhood, and so on. In reality, there may be thousands of these. Then, one of these experiences (Amadeleine, say) is recalled (into the working memory !Dmadeleine) perhaps by tasting one again. This is expressed by !Amadeleine ⊩!Dmadeleine. Then the formalism yields the sequent (7.7): !AAuntLéonie,…,!Atea,…,!Amadeleine ⊩!Mchildhood⊗!Dmadeleine. This says: all the associated memories are recalled into !Dmadeleine, and when put back into the memory module for “childhood,” they may be changed by the presence of the ⊗!Dmadeleine on the right-hand side via possible entanglement. Note that !Amadeleine, etc., may also have been stored elsewhere, such as in the LTM for confection, !Mconfection, and therefore, memories of other kinds of confection etc. may be brought forth, resulting in an experience of great complexity.)
A wiring constraint and Tsien’s postulate
A basic sequent of the form !A ⊩ B puts a very precise constraint upon the inherent wiring architecture of the connection between the A bicameral network and the B network it represents. Namely, denoting as usual the vector space interpretation of A (B) by the same symbol, the above sequent is interpreted as a linear map
| 7.10 |
which reflects the wiring diagram of the connection. In this case, we have
| 7.11 |
where N is the number of b-neurons in the network, so dimA = N. Thus, we have output maps , , and so on. Now each b-neuron represents a different point of input which may cause a firing of those b-neurons. So, recalling that dim, there are such independent single b-neuron firing patterns (represented by the nodal basis for A), independent double b-neuron firing patterns, independent triple b-neuron firing patterns, and so on. So every possible combination of firing—or Hebbian “co-spiking”—subpatterns is accommodated and output and there are independent such firing patterns. (This can be generalized to the case in which “b-neuron” is replaced by “network or clique of co-spiking b-neurons.”) That is to say, not only does the network itself fire into the target network per neuron, as in the first map listed above (), but so also does each possible firing, or co-spiking, subpattern.
Exactly this “power-of-two” rule has been postulated by J. Z. Tsien as the basic wiring logic underlying the cell assembly-level computation involved in many brain cognitive functions, since such a structure is capable of covering all possible combinations for a given number of inputs, and might therefore be selectively advantageous. The postulate has been supported by a series of careful experiments with mice and hamsters [16–19], and has also been found serendipitously (for the case of 3 inputs) in a recent study of macaque brains [31]. In [32], the first author applies the formalism of the current paper to simulate a set of large-scale in vivo neural recording experiments Tsien and his group performed to confirm his postulated power-of-two law, and to derive the law itself.
What can go wrong?
We shall now examine each step in the process to see what our setup might say about known pathologies.
Failure of accretion via exterior multiplication: Alzheimer’s dementia
This refers to the process described in the second paragraph of Section 7.1 applied in our case here to the M-network, conjectured to reside in the neocortex. The process may fail if there is a tendency for firing patterns of the M-network to overlap, or share neurons. In this case, it is highly likely that more than a single accretion will give zero, i.e., fail, owing to the presence of repeated firing patterns. This would be devastating since in this case the process is likely to stop if more than one memory trace is accreted so newer memories cannot be registered in the neocortex. Older memories may still be recalled upon cues, since the algorithm may proceed with in place of !M, leading to the re-establishment step
| 7.12 |
in place of (7.9). If this were to happen, the re-established memoranda would be subject to scrambling owing to the massive quantum-like entanglement that is subject to. For instance, this could happen if the network is highly compact or tangled, leading to neurons shared among firing patterns. This seems to describe well the characteristics of dementias of Alzheimer’s type. Another sort of failure could occur if the substrate connection implementing the exterior product itself fails. In this case, since the exterior product implements both inhibitory and excitatory substrate involvement, we may expect its failure to entail deficits both in the interneural substrate and the (excitatory) glutamatergic complex in the cortices of Alzheimer-like dementia victims. Some support for these conclusions may be found in [33–36].
Failure of the tensoring of networks: schizophrenia
As just mentioned, the tensor product is supposed to implement connectivity at the level of the interneuron or inhibitory substrate. Tensoring, in particular the rules L⊗ and R⊗, and other sequents involving tensoring, may fail if the interneural substrate fails to operate and this could happen if the appropriate interneural neurotransmitter is defective or in short supply. Here the neurotransmitter is generally GABAergic. In case tensoring fails for the M network in Section 7.1, we may not apply the R⊗ rule there so the step (7.3) cannot be implemented. In this case, memory traces may be individually stored in the neocortex but the context, or relational structure, is lost. The owners of such networks will not be prone to as much contextual distraction as owners of typical networks would be. Meanwhile, the cued pattern completion or recall process will fail for relational information and make learning difficult. The pattern completion step may survive in piecemeal fashion though is then likely to be in error, leading to false memory recalls. Furthermore, since the interneural substrate which promotes connectivity is faulty, we would expect disruption of the networks involved in memory function.
If tensoring should fail for a (hippocampal-like) Ai-network, then the analogue of the sequent discussed in equation (7.1), namely !Ai⊗!Ai ⊩!Ai, which is interpreted as the exterior product itself, must also be abandoned. Since this product is presumed to reflect a possibly excitatory substratum, and if schizophrenia is indeed characterized by a general failure to implement tensoring, then we conclude that glutamatergic deficits should also be apparent in the hippocampi of schizophrenic patients. Moreover, the storage capacity involved is also reduced to the inefficient classical exponential form. All of these deficits characterize schizophrenia rather exactly and support the so-called GABAergic theory of this disease. For some support for these conclusions see [37–41].
Patients suffering from high-functioning autism or Asperger’s disorder (HFA/AS) have certain memory deficits which are very similar to those experienced in schizophrenia. Namely the ones described above: failure of cued recall of relational or contextual information, and concomitant difficulties with learning, though in this case it is generally milder [42].
Failure of synchronicity
Failure of synchronicity in the antecedent network of a sequent would put paid to the application of LCt such as in (7.6) but this could be intermittent and may not be noticeable in the long run.
Extending the paradigm
We briefly remark on possible extensions of some of these notions.
The Chemical Abstract Machine
This was a paradigm put forward by Berry and Boudol [43] as a means of treating asynchronous parallelism and concurrency in computing. Our logical setup using GN is similar in many respects to this abstract machine. A state of such a system resembles a chemical solution in which floating “molecules”—the networks in our case—can interact with each other according to reaction rules. These concurrent components are freely “moving” and may interact when coming into contact. A characteristic feature shared by our system is that it can operate without a central executive or control unit. Another shared feature is massive parallelism of the classical kind—namely, in our proof fragment above, each A network may belong to thousands of different contexts—in addition to quantum-like parallelism via superposition. This chemical abstract machine formalism has been translated into linear logic initially by Abramsky in [8]. We shall take this notion up as a possible refinement of GN elsewhere.
Tensor product and neurotransmitters
The ordinary tensor product of vector spaces and its related exterior product seem to have implemented the notion of an underlying modulating substratum quite successfully. However, they are not refined enough to simulate or distinguish between different types of modulation or neurotransmitting media. It may be possible to expand the category involved from that of vector spaces to more general modules over rings of functions, these functions being derived from the characteristic forms of the action potentials. This too is work for the future.
Conclusions
We have used some of the machinery built up in earlier work to gain some insight into what a quantum-like brain computation could be like. The model immediately implies a significant wiring constraint conforming to the “power-or-two” permutation logic that had already been postulated and observed in vivo by J. Z. Tsien et al. [16–19]. The use of logic in this context reveals, for instance, a causal relation between synchronicity or co-activation, a form of binding of neural assemblies, and the operation of a certain kind of storage mechanism. The setup does not predict the onset of synchronization within a network but does reveal some of its consequences in a way apparently different from the view afforded by more traditional methods. Thus, it is an approach that may complement others. We tested the fragment of proof that may simulate the operation of pattern completion, and some other related notions, by gauging how the failure of particular steps could lead to recognizable pathologies such as Alzheimer’s dementia, schizophrenia and possibly HFA/AS. The upshot, so far as computational theory is concerned, is that the computational capacities of some parts of a brain may be similar to that of an abstract chemical machine, in the terminology of Berry and Boudol. Namely, it is characterized by loosely intertwined massively parallel threads, in both classical and quantum-like interpretations of the notion of parallelism, with no central or overarching control executive or main program required. Moreover, storage may be enhanced by exploiting the quantum-like parallelism, with certain classes of neurons playing the rôle of qubit-like units.
Acknowledgments
Thanks are owed to an anonymous referee whose cogent criticism has significantly improved earlier versions of this paper, and to Jasper Brener, Eric van Buskirk, and Joe Z. Tsien for valuable input.
Appendix A: Some multilinear algebra
References for this appendix include [44–48].
A.1 Tensor products
We take vector spaces over a field (or modules over a ring) k which we may take to be , the field we will be using here. For n of them, V1, V2,…, Vn and another one W (they do not need to be finite dimensional here) one may have multilinear functions meaning that f is linear in each variable separately. Linear means it preserves vector addition and scalar multiplication. One might envisage a complicated theory of such multilinear functions generalizing the theory of linear functions of a single variable. However, such a theory is not necessary, since for any such collection of vector spaces V1, V2,…, Vn there exists a single vector space T(V1, V2,…, Vn) satisfying the following universal mapping property (UMP):
There exists a multilinear map such that for any multilinear map there exists a unique linear map such that .
It is easy to prove that such a T(V1, V2,…, Vn) must be unique up to isomorphism of vector spaces. It is called the tensor product of the vector spaces involved and written . Usually the base field or ring is appended to the tensor sign as in ⊗k since often algebraists have many fields and/or rings to deal with simultaneously. If the field is not in doubt, as here, it is omitted. In this way, multilinear maps are turned into linear ones and there is no need for a separate theory. One may think of the tensor product as the vector space generated by basis vectors of the form subject to linear additivity in each variable and the scalar multiplication property . If Vi has dimension di then dim.
Properties of tensor products may be derived entirely through the use of the UMP stated above. For instance, suppose linear maps , i = 1,…, n are given. Then is multilinear so that its composition with the linear ι -map of W1 ×… × Wn into is also multlinear so that it may be lifted to produce a linear map as in the diagram above. This map is denoted .
A.2 Exterior products
With notation as in the last section, let for . Then, a multilinear function is said to be alternating if
| A.1 |
It follows from multilinearity that interchanging any pair of adjacent variables changes the sign of the value of f and from this that the same holds for the interchange of any pair of variables. Then it follows that the repetition of any pair of variables causes the value of f to vanish. There is a UMP for alternating maps similar to the one for general multilinear maps. The unique vector space that plays the rôle of the tensor product in this case is written , and called the exterior product. It is generated by elements of the form v1 ∧ v2 ∧… ∧ vp, vi ∈ V. This element is multilinear in its arguments and alternating in the sense described above for f. Thus, for instance, v ∧ v = 0 and if v ∧ w = 0 then v and w generate the same one-dimensional subspace, i.e., are colinear. (For, if v and w were not linearly dependent, they could be included in a basis for V in which case v ∧ w would be a basis element of which could not be the zero vector.) The map corresponding to ι in the last section sends to v1 ∧ v2 ∧… ∧ vp. It is not hard to show that, if the dimension of V is n, then dim. Note that dim and that if p > n. A useful intuition is that the exterior product v1 ∧ v2 ∧… ∧ vp is a vector representing the volume of the polytope bounded by the vectors v1,…, vp normal to the surface of this polytope.
A.3 Exterior algebras
These exterior products may be assembled into a unital associative algebra (i.e., an associative algebra containing a unit) having a certain universal mapping property (UMP) with respect to linear maps into such an algebra A having the property that f(v)2 = 0 for all v ∈ V. Namely, there exists an associative unital algebra E(V ) for any vector space V, and a linear map having the property mentioned, such that if is any linear map into any associative unital algebra A having that “square free” property, then there exists a unique algebra morphism such that . E(V ) is then necessarily unique up to algebra isomorphism. One may take this algebra to be the exterior algebra of V defined by
| A.2 |
which is easily seen to satisfy the UMP. In case V is finite dimensional, of dimension n, say, this direct sum terminates to give
| A.3 |
| A.4 |
Here we take and . Note that dimE(V ) = 2n. The algebra multiplication is given by wedging together two elements of the summands—called homogenous elements—in the order given, and extending by linearity to the whole space, with elements in just acting as scalars in the usual way. The map is given by κ(v) = v considered to lie in the summand . This algebra has many interesting properties and symmetries which were understood by H. Grassmann in the middle of the nineteenth century but whose published treatment of it was famously misunderstood by his contemporaries, probably because of limitations in the notations of the time. We shall rehearse a few of these properties here. First we note that for two finite-dimensional vector spaces V and W the map
| A.5 |
given by (v1 ∧… ∧ vm) ⊗ (w1 ∧… ∧ wn)↦v1 ∧… ∧ vm ∧ w1 ∧… ∧ wn induces an isomorphism of vector spaces
| A.6 |
from which we obtain an isomorphism of vector spaces
| A.7 |
which is not an isomorphism of algebras when the ordinary tensor product algebra multiplication is used on the right-hand side of equation (A.7). There is, however, an algebra product structure on the right-hand side that does render that isomorphism above an isomorphism of algebras: it is called the graded product and it is described as follows. For homogeneous elements a, c ∈ E(V ), b, d ∈ E(W) the graded product on the algebra E(V ) ⊗ E(W) is determined by the definition:
| A.8 |
where the degree deg(f) of a homogeneous element f is the power of the exterior product to which it belongs, also called the grade of f. The graded multiplication above may be canonically extended to any number of tensor products of algebras. (The notion of grading for algebraic objects was codified in the 1950s by some of the algebraists of Paris (Bourbaki and Chevalley [44])).
Let us consider the case when V is one dimensional, with basis element e, say. Then clearly in our earlier notation, where, as an element in the algebra of , e2 = e ∧ e = 0. It is immediate that is commutative as an algebra. Now, for any finite-dimensional vector space V with basis {e1,…, en}, we have from (A.7)
| A.9 |
as vector spaces. As noted above, this is not an isomorphism of algebras with the ordinary tensor product multiplication on the right-hand side, since this would be commutative as all of the are, while the left-hand side is not. However, as mentioned, the right-hand side with graded product is isomorphic with the exterior product on the left-hand side. Thus, the exterior algebra may be described in terms of graded tensor products of algebras isomorphic with (cf. [48]). The reader may note the similarity of such tensor products to the notion of qubit registers in the parlance of quantum computation.
If is a linear map of vector spaces, there is a unique map of algebras that extends . This may be proved using the UMP for exterior algebra. It is easy to see that it is given by the linear extension of the assignments E(f)(1) = 1, E(f)(v1 ∧… ∧ vk) = f(v1) ∧… ∧ f(vk).
A.4 The Plücker embedding
For a (real) vector space V, let Gr(p, V ) denote the family of subspaces of V of dimension p, the notation Gr being in honor of Grassmann. The special case of p = 1 is called the projective space of V, and is denoted by P(V ). Exterior products may be used to obtain an explicit representation of Gr(p, V ), namely the map
| A.10 |
given, for a p-dimensional subspace , with basis {w1,…, wp}, by
| A.11 |
is well-defined. For, another basis of W is related to this basis by a matrix with a non-vanishing determinant and the corresponding exterior product is the previous one, namely w1 ∧… ∧ wp, multiplied by this determinant and so specifies the same element in . Moreover, it is not hard to see that w ∈ W if and only if w ∧ ψ(W) = 0, showing that ψ is one-to-one, or injective. It is called the Plücker embedding.
Intuitively this last result can be interpreted as follows: if the volume of the (p + 1)-dimensional polytope obtained by adding w as another side to the p-dimensional polytope with sides w1,…, wp is zero, then w must lie in the polytope, and conversely. This is easily seen when p = 2: if adding a third vector to the two-dimensional polytope with sides w1 and w2 produces a (3-dimensional) polytope of zero volume, then w must lie in the plane determined by w1 and w2, and conversely.
Appendix B: : Quantum-like storage and the ! operator in the category
B.1 A model for ! in the category
We return to a brief discussion of the exterior algebra E(V ) of a finite-dimensional k vector space V. This object has additional elements of structure we shall briefly describe. First consider the vector space maps given by , v↦(v, v) and , v↦0. As in Appendix A1, these respectively induce algebra maps
- called the coproduct which is an algebra map given on elements v ∈ V ⊂ E(V ) by
This coproduct makes E(V ) a coalgebra. Together with the algebra structure, these maps give E(V ) the structure of a graded Hopf algebra in which the product, coproduct, unit, and counit intertwine in certain ways that need not concern us here;B.1 , called the counit, given by the projection of E(V ) onto its first component.
The resulting structure has many interesting properties, but the existence of these maps, and the additional fact that E(V∗)≅E(V )∗, where W∗ denotes the space of functionals on W, will suffice for our purposes here, namely to show how E(V ) provides a model for !V in our case of . There are four rules to consider.
-
LW:
The interpretation of a sequent Γ ⊩ D is as a linear map of real vector spaces . Compose this map with the map to obtain a map . This is the required interpretation of Γ, !A ⊩ D.
-
LC:
A similar argument using . We have argued (Section 6) that this process is physically implementable at the network level and requires a time to implement.
-
L!:
A similar argument using the projection . This does not reflect a physical change at the same level of resolution but rather a change in that level of resolution so that no time is taken to effect this.
-
R!:
It suffices to show this for a single formula since, if Γ = A1,…, An, !Γ is interpreted as . Then !Γ ⊩ A is interpreted as a map . Dualizing, we get a map . From the UMP of E() this map lifts to a map . Dualizing again, we obtain a map . This is the required interpretation of !Γ ⊩!A. This is also a change in resolution so should take no time to effect.
B.2 Quantum-like storage
Returning to the rule LC, we note that in the basic case of an atomic formula a, which, according to our earlier conventions, will be interpreted by a one-dimensional space isomorphic with , we have !a interpreted as , where the first is generated by the unit 1 in the algebra, so that , and if x denotes the generator of the second component we have
| B.2 |
In quantum computing parlance the state 1, representing the vacuum state, would be written |0〉 and the state x, the state of single occupancy, would be written |1〉, so that the last equation becomes
| B.3 |
This is the map implementing the duplication operation in the rule LC:
| B.4 |
Moreover, is a maximally entangled state [49]. In actual quantum mechanics, no information about the internal constitution of the state—its preparation—can be obtained by separately performing local experiments upon the component subsystems. Thus, quantum and quantum-like duplication or storage is implemented by quantum or quantum-like entanglement. Moreover, in the actual quantum case, the conclusions of the no cloning theorem—which asserts that no quantum state can be copied per se—are avoided [49]. This is basic to the discipline known as quantum computing, and it is likely to persist in our case of quantum-like behavior.
Compliance with Ethical Standards
Conflict of interests
The authors declare that they have no conflicts of interest.
Informed consent
The authors declare that there were no human or animal participants involved in this purely theoretical study.
Research data
No data was used or generated during the course of this study.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Stephen Selesnick, Email: selesnick@mindspring.com.
Gualtiero Piccinini, Email: piccininig@umsl.edu.
References
- 1.Rescorla, M.: The computational theory of mind. In: Zalta, E. N. (ed.) The Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/archives/spr2017/entries/computational-mind/ (2017)
- 2.Selesnick SA, Rawling JP, Piccinini G. Quantum-like behavior without quantum physics I. Kinematics of neural-like systems. J. Biol. Phys. 2017;43:415–444. doi: 10.1007/s10867-017-9460-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Selesnick SA, Piccinini G. Quantum-like behavior without quantum physics II. A quantum-like model of neural network dynamics. J. Biol. Phys. 2018;44:501–538. doi: 10.1007/s10867-018-9504-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Maruhn Joachim Alexander, Reinhard Paul-Gerhard, Suraud Eric. Simple Models of Many-Fermion Systems. Berlin, Heidelberg: Springer Berlin Heidelberg; 2010. [Google Scholar]
- 5.Amit DJ. Modeling Brain Function: the World of Attractor Neural Networks. Cambridge: Cambridge University Press; 1989. [Google Scholar]
- 6.Hopfield JJ. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U. S. A. 1982;79:2554–2558. doi: 10.1073/pnas.79.8.2554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Asperti A, Longo G. Categories, Types, and Structures: an Introduction to Category Theory for the Working Computer Scientist. Cambridge: MIT Press; 1991. [Google Scholar]
- 8.Abramsky S. Computational interpretations of linear logic. Theor. Comput. Sci. 1993;111:3–57. doi: 10.1016/0304-3975(93)90181-R. [DOI] [Google Scholar]
- 9.Alexiev V. Applications of linear logic to computation: an overview. Log. J. IGPL. 1994;2(1):77–107. doi: 10.1093/jigpal/2.1.77. [DOI] [Google Scholar]
- 10.Barr M. ∗-Autonomous categories and linear logic. Math. Struct. Comput. Sci. 1991;1:159–178. doi: 10.1017/S0960129500001274. [DOI] [Google Scholar]
- 11.Blute, R., Panangaden, P., Seely, R.A.G.: Holomorphic models of exponential types in linear logic. In: Brookes, S., Main, M., Melton, A., Mislove, M., Schmidt, D. (eds.) Mathematical Foundations of Programming Semantics, Lecture Notes in Computer Science, p 802. Springer, New York and Berlin (1993)
- 12.Girard J-Y, Lafont Y, Taylor P. Proofs and Types Cambridge Tracts in Theoretical Computer Science, vol. 7. Cambridge: Cambridge University Press; 1988. [Google Scholar]
- 13.Seely, R.A.G.: Linear Logic, *–autonomous categories and cofree coalgebras. In: Gray, J., Scedrov, A. (eds.) Categories in Computer Science and Logic, Contemp. Math, p 92. American Mathematical Society, Providence (1989)
- 14.Piccinini G. Physical Computation: a Mechanistic Account. Oxford: Oxford University Press; 2015. [Google Scholar]
- 15.Piccinini G, Bahar S. Neural computation and the neural theory of cognition. Cognit. Sci. 2013;37(3):453–488. doi: 10.1111/cogs.12012. [DOI] [PubMed] [Google Scholar]
- 16.Tsien JZ. A postulate on the brain’s basic wiring logic. Trends Neurosci. 2015;38(11):669–671. doi: 10.1016/j.tins.2015.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tsien, J.Z.: Principles of intelligence: on evolutionary logic of the brain. Front. Syst. Neurosci. 9(186). 10.3389/fnsys.2015.00186 (2016) [DOI] [PMC free article] [PubMed]
- 18.Li, M., Liu, J., Tsien, J.Z.: Theory of connectivity: nature and nurture of cell assemblies and cognitive computation. Front Neural Circuits 10(34). 10.3389/fncir.2016.00034 (2016) [DOI] [PMC free article] [PubMed]
- 19.Xie, K., Fox, G.E., Liu, J., Lyu, C., Lee, J.C., Kuang, H., Jacobs, S., Li, M., Liu, T., Song, S., Tsien, J.Z.: Brain computation is organized via power-of-two-based permutation logic. Front. Syst. Neurosci. 10(95). 10.3389/fnsys.2016.00095 (2016) [DOI] [PMC free article] [PubMed]
- 20.Hjorth J, Blackwell KT, Kotaleski JH. Gap junctions between striatal fast-spiking interneurons regulate spiking activity and synchronization as a function of cortical activity. J. Neurosci. 2009;29(16):5276–5286. doi: 10.1523/JNEUROSCI.6031-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Abramsky, S., Coecke, B.: A categorical semantics of quantum protocols. arXiv:quant-ph/0402130v5 (2007)
- 22.Selesnick SA. Foundation for quantum computing. Int. J. Th. Phys. 2003;42(3):383–426. doi: 10.1023/A:1024410829713. [DOI] [Google Scholar]
- 23.Selesnick SA. Type structure and chiral breaking in the standard model. J. Math. Phys. 2007;48(7):072103. doi: 10.1063/1.2747723. [DOI] [Google Scholar]
- 24.Coecke, B., Sadrzadeh, M., Clark, S.: Mathematical foundations for a compositional distributional model of meaning. arXiv:1003.4394v1(2010)
- 25.Selesnick, S.A.: Quanta, Logic and Spacetime, Second Edition. World Scientific Publishing, London and Hong Kong (2003)
- 26.Maren S. Synaptic mechanisms of associative memory in the amygdala. Neuron. 2005;47(6):783–786. doi: 10.1016/j.neuron.2005.08.009. [DOI] [PubMed] [Google Scholar]
- 27.Lynch MA. Long-term potentiation and memory. Physiol. Rev. 2004;84(1):87–136. doi: 10.1152/physrev.00014.2003. [DOI] [PubMed] [Google Scholar]
- 28.Bayat FM, Prezioso M, Chakrabarti B, Nili H, Kataeva I, Strukov D. Implementation of multilayer perceptron network with highly uniform passive memristive crossbar circuits. Nat. Commun. 2018;9(9):2331. doi: 10.1038/s41467-018-04482-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Uhlhaas, P.J., Pipa, G., Lima, B., Melloni, L., Neuenschwander, S., Nikolić, D., Singer, W.: Neural synchrony in cortical networks: history, concept and current status. Front. Integr. Neurosci. 10.3389/neuro.07.017.2009 (2009) [DOI] [PMC free article] [PubMed]
- 30.Smith, S.M.: Environmental context-dependent memory. In: Davies, G. (ed.) Memory in Context. Wiley, New York (1988)
- 31.Morrow J, Mosher C, Gothard K. Multisensory neurons in the primate amygdala. J. Neurosci. 2019;39(19):3663–3675. doi: 10.1523/NEUROSCI.2903-18.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Selesnick, S.A.: Tsien’s power-of-two law in a neuromorphic network model suitable for artificial intelligence. IfCoLog Journal of Logics and their Applications, to appear
- 33.Palop JJ, Chin J, Roberson ED, Wang J, Thwin MT, Bien-Ly N, Yoo J, Ho KO, Yu G-Q, Kreitzer A, Finkbeiner S, Noebels JL, Mucke L. Aberrant excitatory neuronal activity and compensatory remodeling of inhibitory hippocampal circuits in mouse models of Alzheimers disease. Neuron. 2007;55:697–711. doi: 10.1016/j.neuron.2007.07.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Palop JJ, Mucke L. Network abnormalities and interneuron dysfunction in Alzheimer disease. Nat. Rev. Neurosci. 2016;17:777–792. doi: 10.1038/nrn.2016.141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mann D. Pyramidal nerve cell loss in Alzheimer’s disease. Neurodegeneration. 1996;5(4):423–427. doi: 10.1006/neur.1996.0057. [DOI] [PubMed] [Google Scholar]
- 36.Llorens-Martín M, Blazquez-Llorca L, Benavides-Piccione R, Rabano A, Hernandez F, Avila J, DeFelipe J. Selective alterations of neurons and circuits related to early memory loss in Alzheimer’s disease. Front. Neuroanat. 2014;8:38. doi: 10.3389/fnana.2014.00038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Heckers S, Konradi C. Hippocampal neurons in schizophrenia. J. Neural. Transm. 2002;109(0):891–905. doi: 10.1007/s007020200073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nakazawa K, Zsiros V, Jiang Z, Nakao K, Kolata S, Zhang S, Belforte JE. GABAErgic interneuron origin of schizophrenia pathophysiology. Neuropharmacology. 2012;62(3):1574–1583. doi: 10.1016/j.neuropharm.2011.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ragland JD, Ranganath C, Harms MP, Barch DM, Gold JM, Layher E, Tyler A, Lesh TA, MacDonald AWIII, Niendam TA, Phillips J, Silverstein SM, Yonelinas AP, Carter CS. Functional and neuroanatomic specificity of episodic memory dysfunction in schizophrenia: a functional magnetic resonance imaging study of the relational and item-specific encoding task. JAMA Psychiatry. 2015;72(9):909–916. doi: 10.1001/jamapsychiatry.2015.0276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tamminga CA, Stan AD, Wagner AD. The hippocampal formation in schizophrenia. Am. J. Psychiatry. 2010;167:1178–1193. doi: 10.1176/appi.ajp.2010.09081187. [DOI] [PubMed] [Google Scholar]
- 41.Liu Y, Liang M, Zhou Y, He Y, Hao Y, Song M, Yu C, Liu H, Liu Z, Jian T. Disrupted small–world networks in schizophrenia. Brain. 2008;13(4):945–961. doi: 10.1093/brain/awn018. [DOI] [PubMed] [Google Scholar]
- 42.Stone WS, Iguchi L. Do apparent overlaps between schizophrenia and autistic spectrum disorders reflect superficial similarities or etiological commonalities? N. Am. J. Med. Sci. (Boston) 2011;4(3):124–133. doi: 10.7156/v4i3p124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Berry G, Boudol G. The chemical abstract machine. Theor. Comput. Sci. 1992;96(1):217–248. doi: 10.1016/0304-3975(92)90185-I. [DOI] [Google Scholar]
- 44.Chevalley C. Fundamental Concepts of Algebra. New York: Academic Press; 1956. [Google Scholar]
- 45.Fulton W, Harris J. Representation Theory. A First Course. Berlin: Springer; 1991. [Google Scholar]
- 46.Knapp AW. Lie Groups, Lie Algebras, and Cohomology Mathematical Notes, vol. 34. Princeton: Princeton University Press; 1988. [Google Scholar]
- 47.Lang S. Algebra. Third Edition. Reading: Addison–Wesley; 1993. [Google Scholar]
- 48.Mac Lane S. Homology. Berlin: Springer; 1963. [Google Scholar]
- 49.Nielsen M, Chuang I. Quantum Computation and Quantum Information. Cambridge: Cambridge University Press; 2000. [Google Scholar]


