Gradual Change, Homeostasis, and Punctuated Equilibrium: Reconsidering Patterns of Health in Later-Life

Abstract

Longitudinal methods aggregate individual health histories to produce inferences about aging populations, but to what extent do these summaries reflect the experiences of older adults? We describe the assumption of gradual change built into several influential statistical models and draw on widely used, nationally representative survey data to empirically compare the conclusions drawn from mixed-regression methods (growth curve models and latent class growth analysis) designed to capture trajectories with key descriptive statistics and methods (multistate life tables and sequence analysis) that depict discrete states and transitions. We show that individual-level data record stasis irregularly punctuated by relatively sudden change in health status or mortality. Although change is prevalent in the sample, for individuals it occurs rarely, at irregular times and intervals, and in a nonlinear and multidirectional fashion. We conclude by discussing the implications of this punctuated equilibrium pattern for understanding health changes in individuals and the dynamics of inequality in aging populations.

Introduction

Two distinct and sometimes contradictory intuitions shape our thinking about health in later life. On the one hand, popular and academic discourses reinforce an image of later life as a time of progressive health decline culminating in mortality, with aging described as a set of ongoing losses in capacity and functioning. On the other hand, we recognize that varied nonmonotonic and nonlinear health histories are possible and likely: health may remain stable over long periods, and decline, if and when it occurs, may be either gradual or relatively sudden. Recoveries following spells of illness and debilitation are common, and unexpected deaths are not unheard of.

One tempting way to reconcile these two intuitions is to consider unpredictable variation in later-life health as an individual-level phenomenon, gradual health decline as a population-level process, and the two perspectives as complementary. After all, in most quantitative studies, analyses frequently draw on individual-level data, but inferences about the association between particular exposures and outcomes are made at the aggregate level. In health and aging research, empirical data on individuals’ health are routinely used to inform population models. Such models do not simply highlight personal variation: they also aim to characterize and predict systematic differences in health between groups. But what if individual-level and aggregate analyses support different intuitions about health and aging?

Research on health and aging, having long recognized that populations are not homogeneous, responded by embracing models that aim to differentiate between various forms of heterogeneity, including within individuals (over time), between individuals (in a population), and across distinct populations. Such models have increased the sophistication of research on inequality, expanding on an intuitive recognition of differences between individuals by offering a quantification of differences within and between socially stratified groups over time. These models strive to reflect the heterogeneity observed in the real world while producing tractable and parsimonious results that can inform potential policy and program interventions aimed at ameliorating health inequities.

However, longitudinal health trajectory models rarely aim to explicitly adjudicate between the two key intuitions about health and aging. Although statistical models can quantify between-person heterogeneity around population and subpopulation means, researchers who apply them to health data have primarily highlighted parameters that represent those means. These parameters are calculated by averaging over individual (within-person) trajectories in a manner reflecting an assumption of gradualism—the notion that changes accumulate slowly and by steady degrees. However, because populations comprise individuals, and individual experiences are shaped by population memberships and trends, there are questions to be asked as to whether such smooth means accurately represent a population’s heterogeneous constituents. Stated another way, longitudinal health trajectories serve as a useful case study for exploring the tension between demographic methodological individualism and a more holistic approach to understanding populations and their dynamics.

We begin by considering the extent to which influential longitudinal methods rely on an assumption of gradual change to produce inferences about population health. We then turn to widely used, nationally representative survey data on functional limitations in later life to empirically compare and contrast the documented health paths of individuals with the summaries offered by aggregate trajectory models. We show that the assumption of gradualism fits population data well. However, for most individuals in the population, the pattern of health in later life is more aptly characterized as what Eldredge and Gould (1972) termed punctuated equilibrium: long-term stability irregularly interrupted by substantial changes. We conclude by arguing that the discrepancy between the gradualist intuition and the punctuated equilibrium of individual health trajectories has important implications for our understanding of the dynamics of inequality in aging populations and for the potential impact of policies and programs that ultimately play out at an individual level.

Modeling Health Across the Life Course

Studies of aging have long emphasized the heterogeneity of health and other personal characteristics in later life (Maddox 1987; Nelson and Dannefer 1992). The influential life course perspective encourages researchers to consider health in relation to accumulated exposures to advantage and disadvantage that differentiate individuals or groups over time (Dannefer 2003; Elder 1985; Ferraro and Shippee 2009). More specifically, dynamic interactions between social structures and processes of stratification, personal traits, and contingent events are theorized to generate social and economic inequalities that are ultimately reflected in differential health and longevity. Life course research also seeks to distinguish between intraindividual and interindividual changes: that is, to differentiate between the timing, direction, and magnitude of within-person changes and the ways in which patterns of change vary across individuals and groups in a population (George 2009; Nesselroade 1991; O’Rand 1996; Wolf 2016).

Empirical studies (e.g., Ferraro et al. 2016; Haas 2008; Hayward and Gorman 2004) have tested life course hypotheses by examining the association between exposures to disadvantage in early and midlife and subsequent health outcomes. In the absence of a single comprehensive measure of health, surveys collect information about chronic illnesses, functional limitations, disability, and other indicators at multiple time points, and they record instances of mortality. Researchers depict health declines by documenting the accumulation of negative outcomes and by describing the pattern of accumulation via longitudinal models that aim to determine what changes occur, how change unfolds, and why change takes place.

A variety of statistical models are available for summarizing events over time or identifying patterns of stability and change in repeated measures. These methods vary in the extent to which they consider long-term trajectories as comprising multiple discrete snapshots or as single continuous units (Abbott 1995). Consequently, the conclusions reached by longitudinal studies of health and health disparities in older populations may be shaped by the method and unit of analysis as well as the data. In the next three sections, we review some of the most common analytic methods in the field and evaluate the extent to which they rely on the assumption that change proceeds gradually.

Growth Curve and Latent Class Models

The earliest statistical approaches to longitudinal data involved reducing repeated measures into summary indicators and calculating change as a difference between discrete endpoints (Fitzmaurice and Molenberghs 2009). Over the past three decades, however, a recognition of the need for more sophisticated models that can differentiate between various levels of heterogeneity (e.g., within- and between-person heterogeneity) has led to the rise of mixed-effects regression as a favored statistical approach to longitudinal data. Mixed-effects regressions allow researchers to use multiple data waves and model trajectories via continuous distribution functions that characterize patterns of change across ages while also recognizing differences between defined subpopulations (for a review, see Lynch and Taylor 2016). When estimated via a full-information maximum likelihood approach, these models also have the advantage of employing all available information, including on those respondents who provide incomplete information.

One major framework that guides contemporary longitudinal analyses is based on the assumption that individuals come from a single population whose change over time can be adequately described by a single parametric trajectory. Known as growth curves within the multilevel or hierarchical linear models literature (Raudenbush and Bryk 2002) or latent growth curves in the structural equation models literature (Bollen and Curran 2006), these models were first applied in education and criminology studies and have more recently been used to characterize patterns of health in later life (e.g., Bishop et al. 2016; Brown et al. 2012; Haas 2008; Quiñones et al. 2011; Shuey and Willson 2008; Warner and Brown 2011).

Although growth curve models can and do quantify between-person heterogeneity around the population mean, the researchers who employ them frequently highlight the parameters representing a mean trajectory in their interpretations. Notably, these parameters are calculated by averaging over individual (within-person) trajectories in a manner reflecting an assumption of gradualism: the notion that change occurs at a constant or constantly changing rate. Furthermore, although heterogeneity parameters capture between-person differences in the pace of change, they do not characterize discontinuities (e.g., sharp reversals or fluctuations) in the pattern of within-person change. Instead, the models depict only those changes that unfold in a gradual, continuous fashion.

Another prominent framework challenges the assumption that populations can be well characterized using a single average trajectory with random effects and instead suggests that populations comprise meaningful classes of individuals who follow distinct trajectories over time (Jung and Wickrama 2008). Latent class growth analysis (LCGA) assumes multiple internally homogeneous classes (Nagin 2005). The more computationally intensive growth mixture modeling (GMM) relaxes this assumption and models heterogeneity within distinct latent classes of trajectories (Muthén and Asparouhov 2008). Both of these group-based latent-class approaches use mixtures of probability distributions and a multinomial modeling strategy to identify unique clusters of trajectories and aim to explicitly capture interindividual differences in intraindividual trajectories. Latent class growth analysis or growth mixture models have been applied to patterns of self-rated and functional health as well as to the accumulation of limitations in activities of daily living (ADLs) and markers of frailty. They have been used to showcase differences across subpopulations and to test hypotheses about the extent to which exposure to disadvantage—such as economic hardship and discrimination based on gender, race/ethnicity, or nativity—sorts individuals into different patterns of health decline (Gill et al. 2010; Han et al. 2013; Liang et al. 2010b; Quiñones et al. 2011; Taylor and Lynch 2011; Wickrama et al. 2012).

The developers of these models have suggested that with sufficiently large statistical and computational power, such models can go beyond estimating population averages to identify more nuance in trajectories (Bollen and Curran 2006; Curran et al. 2010; Nagin 2005). This would increase the number of recommended classes, reflecting the “distinctive groupings of individual-level trajectories within the population” (Nagin and Tremblay 2001:20). In this line of thinking, latent class trajectory models could, under ideal conditions, provide a tractable and parsimonious quantitative summary of heterogeneity within a population while faithfully representing individual-level patterns. Promoters of latent methods have heralded them as “person-centered approaches” (e.g., Liang et al. 2010b, 2011) and declared that latent class methods are a means for “putting the individual back into individual growth curves” (Mehta and West 2000:23). Results from such models could, in turn, inform potential policy and program interventions that address between-group disparities by focusing on individuals with particular characteristics.

To date, however, the person-centered ideal embedded in this model has yet to be fully achieved, and latent class trajectories, like their growth curve counterparts, smooth over heterogeneous within-person patterns in generating classes with gradualist trajectories representing subpopulation means (Bollen and Curran 2006; Curran et al. 2010; Nagin 2005). This raises questions about the extent to which aggregate trajectory classes provide a meaningful basis for health equity interventions targeting individuals. Still, despite concerns about the accuracy of classification results (Warren et al. 2015), compositional bias related to nonrandom selection (Jackson et al. 2019), uncertainty about model fit (Nagin and Tremblay 2001, 2005), and ubiquitous warnings against the reification of trajectory groupings as real categories rather than heuristic devices, latent class models and their growth curve counterpart remain appealing to life course researchers because of their potential to portray a coherent pattern of longitudinal change while accounting for heterogeneity within populations.

Less examined, however, is the question of whether health survey data (and the process generating them) fit the gradualist assumptions embedded in trajectory models. In many applications of growth curves, changes in particular attributes (e.g., domains of knowledge or capacity) are indeed often monotonic, without sharp breaks or reversals. However, that is not necessarily the case for individual health trajectories. Although cumulative (dis)advantage and inequality theories recognize that risks may increase gradually as well as sporadically or nonlinearly for individuals, our models do not necessarily capture such scenarios. Thus, although trajectories estimated via mixed-regression models may vary in baseline levels and in whether the pattern of change is depicted as linear, quadratic, or exponential (DiPrete and Eirich 2006), they consistently reflect the assumption—built into both growth curve and latent class model parameters—that health change is smooth and steady.

Multistate Models

The multistate life table (Namboodiri and Suchindran 1987) is an older alternative to mixed-regression models. It models change across ages as a Markov process, allowing the calculation of transition probabilities across a finite number of predefined discrete states. The method can depict exit from and reentry into the same state, which captures both stability and change. It also accounts for competing risks, including mortality and other forms of attrition. However, the multistate life table emphasizes the occurrence of transitions rather than their timing. Although it avoids the imposition of a gradualist assumption, the model nonetheless results in a loss of information in cases when outcomes are continuous or truly accumulate slowly and gradually over time. Event-history methods (also known as time-to-event, hazard, or survival analysis) expand on the life table approach to incorporate the timing of transitions, often by building in gradualist assumptions about the smooth shape of the underlying hazard function.

Multistate life tables have been used to address a variety of social science and public health questions, including the estimation of expected duration in states of health, illness, and disability. This research has shown that increased longevity comprises years lived in both good health and disability and that the distribution of years in different health states varies by social and economic characteristics (Crimmins et al. 1994, 2009; Hayward et al. 2014). Although multistate models may provide an incomplete approximation of continuous process thought to underlie health changes, they too can be used to test hypotheses about cumulative (dis)advantage and divergent health outcomes. They thus offer a potentially instructive counterpoint to the gradualist mixed regression models.

Sequence Analysis

Sequence analysis is a method that originated in studies of protein and DNA strings and was imported into the social sciences (Abbott and Tsay 2000; Billari 2001). This method treats ordered series of discrete events or states as whole analytic units and can characterize linear progression as well as more complex patterns that allow for contingency, chance occurrences, and interdependence among states (Abbott 1995). Contemporary sequence analyses generate typologies—clusters of cases with similar trajectories—as well as measures summarizing the diversity and complexity of observed patterns (Barban and Billari 2012; Gabadinho et al. 2011).

Although sequence analysis is frequently used in life course research exploring patterns of marriage and fertility, education and employment, and criminal or deviant behavior (Billari 2001), it remains uncommon in social studies of health. An early paper identified typologies of health that differ in the timing, order, and direction of change (Clipp et al. 1992), but more recent applications in the health sciences have focused on genetic markers rather than the health measures self-reported in surveys. Sequence analysis is rich in detail and flexible enough to accommodate both gradual trajectories and less-uniform patterns of change. As such, it presents a promising tool for the study of health inequality. Although it provides less guidance for broad inferences in heterogeneous samples, it nonetheless offers a promising way to disentangle patterns of intraindividual changes from model assumptions and compositional changes that shape aggregate trajectories.

Gradualism Examined: Units of Analysis and Interpretations

The preceding review highlights gradualism as a key assumption in studies of later-life population health patterns. Although multistate analyses present an exception and sequence analysis holds potential for integrating individual- and population-level perspectives, the most prominent methods in longitudinal health research both assume and produce gradual trajectories. Gradualism is an intuitively appealing framework for health analysts because many physiological changes probably do occur in a continuous incremental fashion, albeit subclinically (Ben-Shlomo and Kuh 2002). Gradualism also has appealing statistical properties because it is easily modeled using standard functional forms that trace smooth patterns of change. Scientific hypotheses consistent with gradualist assumptions generate clear expectations about the nature of changing health in aging populations, and these hypotheses can be empirically tested and used in predictive models. But is gradualism consistent with the health data we have and the health and survey processes that generate those data?

The major studies following aging cohorts collect data from individuals in discrete increments rather than continuously. The widely used Health and Retirement Study, for example, interviews respondents over two-year intervals. More frequent assessments would likely capture more detailed individual health changes, but rather than filling in the gaps in a pattern of smooth incremental change, such finer-grained data (both in terms of time intervals and specificity of health measurements) tend to uncover brief personal spells of debilitation and recovery (Wolf and Gill 2009) that are inconsistent with the gradualism assumed by population-level trajectory models.

In studies that rely on standard survey data, the assumption of gradualism is indeed rarely tested directly largely because population health research emphasizes probabilistic interpretations of data that deliberately aggregate individual heterogeneity and chance events. The goal is not fidelity to individual cases but rather inferences to groups; prediction focuses on population averages and rates, not specific events. The logic of population analysis is based on the recognition that whereas aggregates are composed of individual members, what is highly contingent on an individual level may nonetheless be predictable at a higher level of aggregation—an emergent property of large systems, codified in the statistical law of large numbers, and observed in many studies in the physical, biological, and social sciences (Armstrong 2017; Johnson-Hanks 2015; Smith 2011). Although population and individual-level analyses are widely described as complementary approaches that reveal different dimensions of a given phenomenon, shifting between the individual and population perspectives was once a central challenge in the early development of demography as a discipline (Schweber 2006). Medical research has changed its emphasis from understanding the natural history of disease to population-based prediction (Armstrong 2017), and current epidemiologic research has indeed fully embraced its role as a group-level endeavor (Smith 2011). Still, warnings against conflating individual- and group-level explanations abound in research texts, and their presence reveals the ease with which group-level analyses get (mis)interpreted as pertaining to individual risks, and population averages are uncritically presumed to apply to the multitudes who are not average (see, e.g., Gould 1985; Rose 2016).

Our empirical analysis draws on health survey data to contrast the assumption of gradual change embedded in population trajectory models with the patterns observed in descriptive and discrete analyses of individual trajectories. We demonstrate how individual histories of functional limitations become aggregated into varied population-based summaries depending on the analytic method used, and we examine the extent to which different methods account for interindividual heterogeneity in intraindividual change. We show that individual-level data record general stability irregularly punctuated by relatively sudden change, while documented population change proceeds gradually.

Our goal here is not to criticize any particular model but rather to consider the match between models, the available data, and the processes that generate those data. By examining the individual- and population-level perspectives in the context of health trajectories, we hope to gain more insight into both their complementarity and the tension inherent in defining a populations as both the sum of individuals and a broader construct that comes to define those individuals.

Data and Methods

Data

We illustrate the contrast between the population and individual perspectives using data from the Health and Retirement Study (HRS), a nationally representative, longitudinal survey of community-dwelling middle-aged and older Americans (Juster and Suzman 1995). It is particularly well suited for our purpose because of its longitudinal design and because researchers across the social and public health sciences have relied on it extensively to learn about health in later life. We use 11 waves of data covering the period 1994–2014, when questions about functional limitations were asked in a consistent format. Our descriptive analysis also considers the first round of data, collected in 1992. The analytic sample includes members of the main HRS cohort born between 1931 and 1941, whose follow-up period encompasses the ages when health problems typically manifest and escalate.

Our analysis is based on 10,198 members of the HRS cohort. Of respondents in the initial sample, 3,505 (34 %) died during the follow-up period, and 1,781 (17 %) left the survey prior to the final wave. The full 10,198 cohort members contribute at least some information to the descriptive analysis and sequence analysis, allowing us to quantify the impact of attrition, mortality, and temporary missingness. The sample size for each analysis described later varies somewhat depending on how each method handles temporary missingness and attrition. The 9,706 individuals who have at least one measure of functional limitations are included in the latent growth curve, latent class growth analysis, and multistate models. In models that analyze change, we restrict the analytic sample to 9,141 individuals who had health outcomes observed during at least two survey rounds.

Key Variables

Our outcome is the sum (0–12) of functional limitations at survey Rounds 2–12. Functional limitations are measured via three subscales: (1) mobility (walking several blocks, walking one block, walking across the room, climbing several flights of stairs, and climbing one flight of stairs), (2) large muscle functioning (sitting for two hours, getting up from a chair, stooping or kneeling or crouching, and pushing or pulling a large object), and (3) fine motor skills (picking up a dime, eating, and dressing). For all items, 0 = no difficulty, 1 = difficulty, and higher sums indicate more limitation.

Of the health measures available in the HRS, the sum of functional limitations is arguably the best suited to capture gradual change in health over time because it contains a large number of items measuring a mix of mild and severe limitations that individuals can develop or recover from over time. Functional limitations are conceptually situated between chronic conditions and ADL limitations (Verbrugge and Jette 1994), and prior studies using the HRS have found that functional limitations gradually accumulate across survey rounds, both for the study cohort as a whole and for specific subpopulations (Brown et al. 2012; Haas 2008; Liang et al. 2010a,b). Functional limitations are more likely to fit the gradualist paradigm than other commonly used measures of health, including the number of chronic conditions or the number of limitations in ADLs. Chronic conditions, while common, accumulate more slowly than functional limitations, feature little prospect for recovery, and often require formal diagnosis by a physician. Limitations in ADLs, on the other hand, are relatively rare, and encompass only a few (five) indicators of severe disability, leaving little opportunity to capture substantial progression or recovery.

Our analyses focus on functional health trajectories and do not adjust for covariates in order to compare inferences across longitudinal techniques.

Methods

We begin by fitting a model consistent with gradualist assumptions of health change, an unconditional growth curve for repeated measures of functional limitations. The model includes a fixed effect representing a mean trajectory across all individuals in the sample and a random effect representing the variance of individual trajectories around the group mean. We test linear and quadratic specifications and choose the best-fitting model using a combination of the comparative fit index, the Tucker-Lewis index, and the root mean squared error of approximation fit statistics (Raudenbush and Bryk 2002).

Next, to allow for additional heterogeneity in health trajectories, we model the onset and accumulation of functional limitations using a latent class growth analysis (LCGA), which identifies qualitatively distinct trajectories within a population and classifies individuals into the best-fitting category (Nagin 2005). We determine the best-fitting model based on the smallest sample-adjusted BIC value combined with a significant Lo, Mendell, and Rubin likelihood ratio test (Jung and Wickrama 2008).

To evaluate the gradualist assumptions built into the aforementioned models, we conduct a descriptive analysis to estimate (1) the percentage of the sample that experiences increasing limitations, (2) the percentage of the sample with a constant (or consistently missing) number of functional limitations, and (3) the percentage of the sample that experiences decreasing limitations. Our estimates compare the first and last observed rounds and consider change and stability over the total study duration. In doing so, we can evaluate how well the gradualist models match observed respondent health experiences across survey waves.

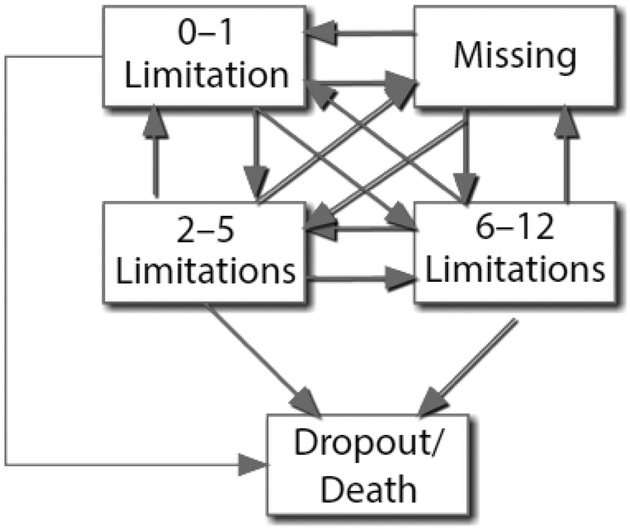
Next, we conduct analyses that relax the assumptions of gradualist models. First, we estimate a multistate model (Namboodiri and Suchindran 1987) that calculates the probability of transitions across five states: (1) 0–1 limitations, (2) 2–5 limitations, (3) 6–12 limitations, (4) temporarily missing (i.e., missing data but not attrition), and (5) lost to follow-up (including respondents who died and who dropped out of the study). The Markov-process model allows recovery, and the only absorbing state is loss to follow-up (see Fig. 1). Model fit is evaluated using the likelihood ratio test, AIC, and difference between observed and model-predicted values. The best-fitting model assumes that the probability of transitioning across states is constant between survey rounds 2–6, 6–9, and 9–12. Sensitivity analyses vary the functional limitation cut points used to classify individuals into particular health states, and our results appear robust to varying the specification of the states (see Table A7, online appendix).

Fig. 1.

Multistate model

Finally, we conduct a sequence analysis (Gabadinho et al. 2011) to identify, describe, and visualize the most commonly observed histories of functional limitation. Because the first analyses highlighted the high prevalence of static trajectories (i.e., ones where no change is experienced prior to dropout), we conduct a second sequence analysis restricted to those who experienced any increase in functional limitations.

Across analyses, no imputation is performed. Missing data are handled in the latent growth curve and LCGA using full-information maximum likelihood (FIML). FIML keeps cases in the sample until the time of attrition, allowing them to contribute all available information to estimated trajectories. However, FIML is designed for situations in which data are missing at random. For this sample, we strongly suspect that attrition and dropout are related to health selection and decidedly missing not at random (Jackson et al. 2019). In the multistate models, temporary missingness was treated as a discrete state, and individuals may transition between having any number of functional limitations to the missing state and later return to the sample. This estimation treats missingness as informative and allows us to empirically quantify the likelihood that individuals in various health states will leave and return to the sample. Subject dropout and mortality are treated as an absorbing state. Finally, in the sequence analysis, all members of the sample are included in an initial analysis that quantifies the frequency of all health patterns. This analysis distinguishes between three types of missingness—temporary missingness, attrition, and mortality—explicitly showing the contribution of different types of missing data to the cohort’s health experiences.

Analyses are conducted using Stata, R, and Mplus 7.11 (Muthén and Muthén 2013). For a more detailed description of each method, along with considerations of missing data and measurement errors, see the online appendix.

Results

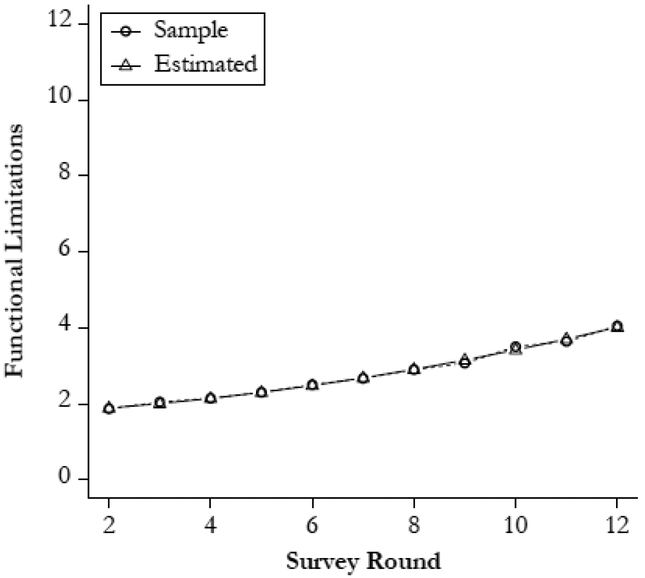
Consistent with prior analyses using the HRS, our unconditional growth curve model (Fig. 2) generates a curvilinear trajectory in which functional limitations accumulate gradually over the course of the study (see Table A2, online appendix, for model fit criteria). Although the full model results in Table 1 suggest substantial heterogeneity around the average population trajectory parameters, the main conclusion affirms common assumptions about the gradual pattern of health decline in later life. However, as subsequent analyses suggest, this gradual accumulation of functional limitations is partially driven by the model’s parameters and the relatively small proportion of individuals who experience a change in functional limitations at any particular time in the study.

Fig. 2.

Latent growth curve with quadratic slope (n = 9,706)

Table 1.

Parameters from best-fitting latent growth curve with quadratic slope (n = 9,706)

Parameter
Linear Slope With Intercept	−0.14***
Quadratic Slope With Linear Slope	−0.02***
Quadratic Slope With Intercept	0.005*
Mean
Intercept	1.89***
Linear slope	0.11***
Quadratic term	0.01***
Variance
Intercept	4.86***
Linear slope	0.26***
Quadratic slope	0.00***

^*p < .05;

^***p < .001

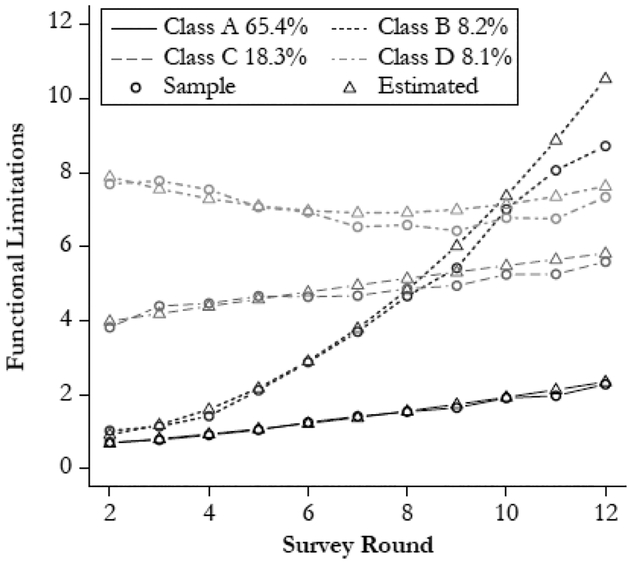
Results from our LCGA model divides the HRS cohort into four classes with qualitatively distinct health trajectories (Fig. 3). Class A (approximately 65 % of the sample) is characterized by few functional limitations at the beginning of the study and a slow, gradual accumulation of functional limitations across survey rounds. Class B displays a relatively fast pace of accumulation. Individuals in Class C begin the study with a higher number of functional limitations (four) and slowly accumulate functional limitations thereafter. Those in Class D begin with a high number of functional limitations (eight) and remain relatively constant at that level with some slight evidence of a reduction in the number of functional limitations at later rounds. Prior research casts some doubts about the accuracy of class identification (Jackson et al. 2019; Warren et al. 2015), partially because heterogeneity within classes and compositional change due to selective mortality and attrition may bias the parameters shaping each group’s trajectory. Still, the relative flatness of most class trajectories (with the striking exception of Class B) in Fig. 3 compared with the mean trajectory estimated in Fig. 2 suggests that many respondents experience stability over time and that the steeper accumulation in Fig. 2 may be partly an artifact of population composition. That said, with the exception of Class D, which depicts a slight recovery, the trajectories depicted in Fig. 3 are also characterized by a pattern of steady accumulation over time (see Table A3, online appendix, for model fit criteria).

Fig. 3.

LCGA: Four-class model with quadratic slope (n = 9,706)

Subsequent analyses further indicate that a trajectory of gradually increasing functional limitations is far from universal. Table 2 summarizes results from a simple descriptive analysis. The top panel confirms the overall health change in this sample: the average number of chronic conditions, functional limitations, and ADL limitations is higher at the last observed survey round than at the first observed one. Panel 2 describes the proportion of the sample whose health changes between their first and last observed survey rounds. Whereas 59 % of the sample reported more functional limitations at the last survey round than they did at the first round, nearly 25 % experienced no change in functional limitations, and 16 % experienced a decrease. A similar analysis of change in chronic conditions and ADL limitations reinforces the idea that the pattern of later-life health is more heterogeneous than a single trajectory of decline: 20 % of the sample reported no change in the number of chronic conditions between the first and last rounds observed, and a striking 73 % reported no change in ADL limitations between the first and last round observed.

Table 2.

Descriptive statistics on chronic conditions, functional limitations, and limitations in ADLs

	Chronic Conditions (N = 9,658)	Functional Limitations (N = 9,141)	Limitations in ADLs (N = 9,143)
Panel 1
Average number at first round observed	1.05	1.85	0.14
Average number at last round observed	2.76	3.61	0.63
Minimum number observed	1.05	0.90	0.04
Maximum number observed	2.76	4.84	0.94
Panel 2
Proportion with increase between first and last round observed	.80	.59	.24
Proportion with no change between first and last round observed	.20	.25	.73
Proportion with decrease between first and last round observed	—	.16	.03
Panel 3
Proportion with any increase across rounds observed	.80	.79	.37
Proportion with no change across rounds observed	.20	.09	.60
Proportion with any decrease across rounds observed	—	.44	.06
Panel 4
Average number of increases across successive survey rounds	1.40	2.47	0.68
Average number of successive survey rounds with no change	6.30	2.75	6.02
Average number of decreases across successive survey rounds	—	1.94	0.45

However, changes in health are somewhat more common than the prior analysis suggests. As panel 3 in Table 2 shows, although only 59 % of the sample saw increased functional limitations between their first and last observations, 79 % experienced an increase at some point. Similarly, whereas 24 % of the sample had more ADL limitations at the last round of the survey than at the first, 37 % had an increase in ADL limitations over the observation period. These findings suggest that a nontrivial proportion of the sample recovers after experiencing a health decline.

The pattern of intraindividual changes suggests that a gradual increase in functional limitations throughout the study is not common. As summarized in panel 4 of Table 2, on average across survey rounds, experiencing no change in chronic conditions, functional limitations, or ADL limitations is more common than experiencing an increase or a decrease. An individual is expected to experience 2.47 increases in functional limitations, 2.75 occasions of no change, and 1.94 decreases in functional limitations. Together, these findings suggest that although the mean number of functional limitations (as well as ADL limitations and chronic conditions) increases between the first and last rounds of observation, this population-level change reflects the experiences of only a small subset of the sample. Indeed, no individual experienced an increase in functional limitations at each follow-up survey round, and less than 1 % of the sample experienced more than three successive increases in functional limitations (see Table A4, online appendix). Declining health is not universal and does not occur in the consistent fashion assumed by gradualist models. Perhaps most importantly, on average, people spend more time not changing than they do changing.

Results from the best-fitting multistate model (Table 3) confirm that with the exception of transitions to and from a missing state, the most common pattern across survey rounds is stasis, remaining in the same functional limitation status (see Table A5, online appendix, for fit criteria). For example, individuals who had 0–1 functional limitations at Round 2 are estimated to have a 74 % chance of remaining in that state at the next round. The model also suggests a nontrivial risk of recovery: at Round 9, people with 6–12 functional limitations had a 17 % chance of transitioning to 2–5 functional limitations at Round 10. Consistent with our descriptive analysis, the multistate results suggest that a linear accumulation of functional limitations is in fact quite rare. Even at the final survey rounds, the probability of progressively moving from State 1 (0 to 1 functional limitations) to State 2 (2 to 5 functional limitations) to State 3 (6 to 12 functional limitations) is only 3.74 %.

Table 3.

Estimated transition probabilities from best-fitting multistate model (N = 9,706)

	0–1 Limitation	2–5 Limitations	6–12 Limitations	Missing	Dropout/Death
Rounds 2–5
0–1 limitation	.74	.16	.02	.03	.04
2–5 limitations	.25	.55	.13	.03	.06
6–12 limitations	.05	.22	.60	.03	.10
Missing	.26	.14	.06	.52	.01
Dropout/death	0	0	0	0	1
Rounds 6–8
0–1 limitation	.71	.20	.02	.03	.04
2–5 limitations	.21	.58	.14	.02	.05
6–12 limitations	.04	.23	.60	.02	.11
Missing	.23	.18	.09	.49	.02
Dropout/death	0	0	0	0	1
Rounds 9–12
0–1 limitation	.68	.22	.03	.01	.07
2–5 limitations	.17	.56	.17	.01	.09
6–12 limitations	.03	.17	.60	.01	.19
Missing	.27	.25	.19	.25	.05
Dropout/death	0	0	0	0	1

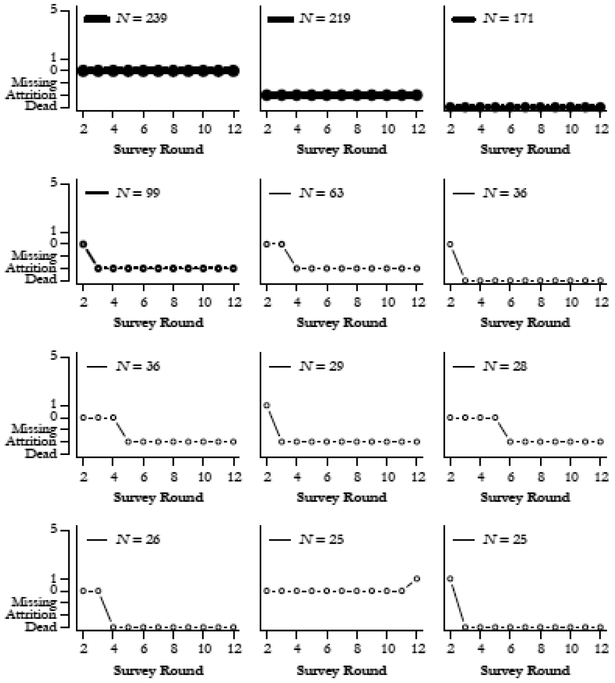
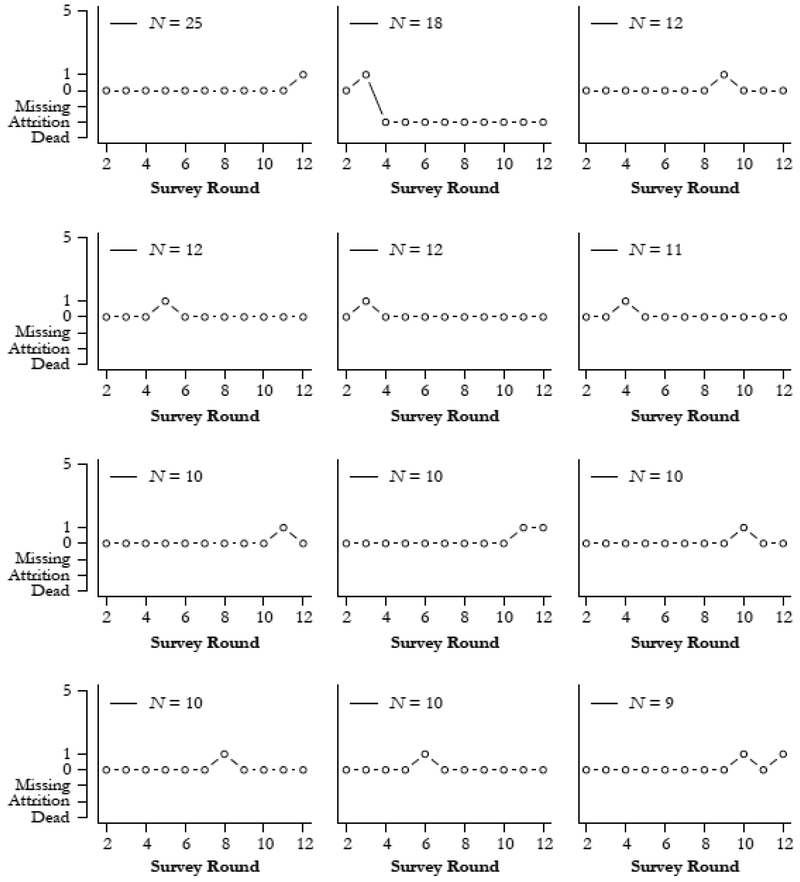
Finally, our sequence analysis identifies the most common functional limitation patterns for individual members of the HRS cohort. The line width in each panel of Figs. 4 and 5 is weighted by the number of cases who follow the particular trajectory. Sequences are shown on separate panels because they are hard to distinguish, given that most involve shifts between the state of no functional limitations and missing values (due to mortality, attrition, or temporary missingness). Notably, no single pattern characterizes more than 2 % of the sample, and none of the 12 most common trajectories in Figs. 4 and 5 involve a gradual accumulation of functional limitation. Instead, they highlight stability over time along with the influence of missing data. Although increases in functional limitations do occur, they are relatively rare and occur at varying times.

Fig. 4.

Sequence analysis: Most common trajectories (n = 10,198)

Fig. 5.

Sequence analysis: Most common trajectories with any increase (n = 7,235)

When the analysis is restricted to individuals who experience any increase in functional limitations over time (n = 7,235), the results in Fig. 5 further reinforce the conclusion that functional health over time rarely reflects the gradual accumulation of limitations. The 12 most common sequences show that an increase in functional limitations happens relatively rarely, occurs at highly variable times, and most often consists of the addition of one functional limitation between a given set of rounds rather than a gradual accumulation.

Overall, our analyses show that although examples of continuous accumulation exist, they are considerably less common than gradualist models lead us to expect. Instead, the trajectories produced by mixed regression methods are driven by parametric assumptions and compositional changes in the sample. That is, gradual trajectories are shaped by the combination of between-person differences in aging cohorts and within-person changes over time. The resulting averages are an emergent property of the population (or aggregated subgroups) but do not accurately represent the experience of most individuals.

Discussion

In longitudinal studies of health, researchers choose how to aggregate individual records into population-level summaries. The chosen models and units of analysis reflect an intuition about health and aging as well as a perspective on the relationship between the population at large and the heterogeneous individuals that constitute it. These choices also influence the inferences that can be drawn from the data. As we’ve shown here, models of gradual changes in health—albeit both intuitively and analytically appealing—depict longitudinal health change in populations that differ considerably from the vast majority of individual health histories.

Later-Life Health: Population and Individual Trajectories

By design, mixed regression models depict the pattern of health among older populations via continuous parametric trajectories. Results from our latent growth curve and LCGA models are consistent with this literature, showing a slow, gradual accumulation of functional limitations for members of the HRS cohort overall and within subgroups distinguished by their initial level of functional limitations and the pace of subsequent accumulation. Prior research has noted the importance of acknowledging within-group heterogeneity and the competing risks of attrition and has cautioned against equating the predicted smooth trajectories with the complex dynamics that trajectories imperfectly measure or reifying latent trajectory classes (Lynch and Taylor 2016; Warren et al. 2015; Wolf 2016; Zimmer et al. 2012). Still, these models have remained popular because their assumptions are biologically plausible and intuitively appealing, and their statistical properties facilitate the testing of hypotheses as well as the prediction of population health patterns. However, descriptive, multistate, and sequence analyses all underscore the distinction between gradualist population trajectories and individual health histories. Our descriptive analysis shows the discrepancy most explicitly: it demonstrates that in this sample of older adults, a pattern of gradually increasing limitations is rare rather than universal, and stasis is more common than change. The multistate and sequence analyses reinforce these conclusions: both show that even though change is common in the sample overall, for individuals it occurs only rarely, at irregular times and intervals, and in a nonlinear and sometimes multidirectional fashion.

Although the latter analyses do not impose the same parametric gradualist assumptions, they do have other drawbacks. Computational and data constraints require that individuals with different numbers of functional limitations be pooled into relatively few groups for the multistate analysis. Consequently, some health changes may not be captured by the model, although our results are robust to alternative state specifications (see the online appendix). The multistate model also flattens the temporal dimension of change, leading to the loss of some detail. The sequence analysis, in turn, preserves the full richness of the data but at the expense of parsimony. With more than 8,000 distinct sequences, it is difficult to distill findings into generalizable conclusions about population health. Still, this difficulty in reducing the data is itself informative and hints at the complexities in the relationship between individuals and the population.

The impact of missing data on inferences should also be noted. A majority of the sample is lost to attrition or mortality, raising questions about the potentially biasing impact of nonrandom compositional changes on the estimated population trajectories. Overall, individuals who drop out may experience a greater accumulation of functional limitations than those who do not, suggesting that standard analyses (including those that employ full-information maximum likelihood estimation) may underestimate the prevalence and severity of functional limitations (Jackson et al. 2019). The high prevalence of missing data also complicates the interpretation of our descriptive, multistate, and sequence analyses. Across analyses, we do not impute but instead allow the missingness to be potentially informative. Some temporary missingness, however may be random or due to illness followed by complete recovery. In the likely case that attrition and dropout are not random, however, missing data introduce an added layer of uncertainty about the ability of longitudinal models to accurately capture individual health changes.

Our results highlight stasis as a major characteristic of later-life health, with most people reporting no changes at most survey rounds, even though change occurs frequently in the sample as a whole. The analysis also highlights the diverse nature of change, with increases and declines happening at different times and intervals, yielding no single typical trajectory or clear set of naturally clustering sequence patterns. These findings are nonetheless consistent with population theory that reconciles unpredictability on the individual level with the emergence of more systematic patterns in the aggregate. The contrast we highlight means that although gradualist models may offer important insight into population-level changes, they should not be treated as straightforward aggregations of within-person changes. Both individual stochasticity and structurally influenced heterogeneity within and across subpopulations call for more caution—and perhaps alternative metaphors—in analyses of aging and health.

Gradualism, Homeostasis, and Punctuated Equilibrium

We find that individual health histories are characterized by long-term stability that is irregularly interrupted by singular, often small changes in health status or—frequently—by mortality or attrition. Inspired by a classic study in evolutionary biology, we call this pattern a punctuated equilibrium and consider it as an alternative to gradualism in analyses of health trajectories.

Paleontologists Niles Eldredge and Stephen Jay Gould introduced the concept of punctuated equilibrium in a seminal 1972 paper considering the development of new species. The prevailing gradualist view in paleontology had held that speciation unfolded as a “slow and steady transformation of entire populations” (p. 84), but Eldredge and Gould (1972) argued that a model of long-term stasis occasionally disrupted by “rapid and episodic events” more accurately describes evolutionary change as documented in the fossil record. Instead of emphasizing progressive change, the punctuated equilibrium model underscores the predominance of long spans of time without variation in key features. Eldredge and Gould acknowledged that change does take place “rather often in the fullness of time,” but it tends to be a deviation from a previously or subsequently stable trend rather than a continuous incremental process. This rereading of the fossil record as reflecting a messy, nondeterministic historical process that interweaves stability and disruption presents a compelling guide for considering how data on individual health histories is constructed into population trajectories.

Notably, Eldredge and Gould (1972) argued that the punctuated equilibrium framework is not necessarily in conflict with the gradualist one: it simply reads the available evidence on a different scale. Thus, the fundamental mechanism of change may indeed be gradual, but only changes that cross the threshold of observation are recorded in the data, yielding an observed pattern of punctuated stability. Similarly, although some changes in health may occur gradually on a subclinical level, individuals may not consciously track their health status for incremental changes until they experience a sudden change—due to either an acute event or a particular underlying health condition passing an observable threshold. Discrete survey measures, like clinical records, provide static snapshots that capture overall stability and the particular shifts in health that are significant enough to establish a new homeostasis. This perspective has long been recognized in the biological study of aging, which considers homeostasic physiological function to be the foundation of individual organismic life (Holliday 1995), and models events such as heart attacks, neoplasms, and external shocks as stochastic disturbances that challenge an individual organism’s ability to maintain or reestablish that homeostasis (Yaffee and McGee 2000). Thus, whereas gradualism may characterize both the incremental, continuous micro-level process that changes individual health in largely unobserved, subclinical ways as well as the more macro-level pattern of steady health change in populations that emerge in aggregate analyses, punctuated equilibrium appears to better capture the discrete and less predictable changes in a key intermediate level—those that are consciously experienced by individuals and documented in survey data.

Eldredge and Gould’s punctuated equilibrium model translated the idea of individual homeostasis to the population level, but our application of the concept differs from its paleontological predecessor in an important way. In evolutionary biology, punctuated equilibrium describes the emergence of new populations. Our argument here, however, is about the differences between summary statistics that apply to populations and measures of individual change. Specifically, we argue that in the case of health trajectories, the gradual change observed in population analyses is not a simple summary of individual histories but rather an emergent result of aggregating and averaging across individuals. Health gradualism is a population-level property, but it does not necessarily hold at lower levels of aggregation because it appears to be shaped by the heterogeneity and changing composition of aging cohorts as much or more than it is shaped by within-person changes (see, e.g., Vaupel et al. 1979). Thus, although the notion that functional limitations increase slowly as we age is a population-level truth, the story for most individuals is less uniform, particularly in the presence of heterogeneous structural conditions and mortality risks. If our population models of health and aging simply reflected individual trajectories in the aggregate, we might expect to see punctuated equilibrium at the population level, as Eldredge and Gould did. Empirically, however, we do not. Instead, the gradualist assumptions of mixed regression models produce gradualist results, further reinforcing that intuition as we think about how to address inequalities in health and mortality.

Implications for Health and Aging Research

Life course theories call on us to recognize heterogeneity in aging. Analyses that employ gradualist methods to link early and midlife exposures with later-life health trajectories are responsive to that call, but only partially. In particular, the built-in assumptions of mixed regression models facilitate the testing of cumulative disadvantage hypotheses, but the results reinforce common preconceptions about aging and its associated health declines, although these do not necessarily fit with the majority of individual health histories captured in survey data. Exposures to advantage and disadvantage indeed accumulate over the life course. Our findings, however, suggest that for individuals, functional limitations—and potentially other health outcomes—do not necessarily follow a gradual pattern and are instead characterized by general stability interrupted by sporadic change. Our findings are consistent with recent research that has highlighted the relatively high prevalence of recovery and health variability among nursing home residents, who may be expected to experience more serious health declines than the general population (Bolano et al. 2018). Consequently, the use of gradualist longitudinal models to link exposure to disadvantage with health disparities potentially raises both methodological and substantive complications.

In particular, several trajectory studies using the HRS (e.g., Brown et al. 2012; Gueorguieva et al. 2009; Quiñones et al. 2011) showed that certain subpopulations defined by gender, race/ethnicity, and socioeconomic status (SES) vary in baseline measures of health but found no significant differences in the slope of health change over time—a puzzling finding given the large differences in mortality between similarly defined groups (National Center for Health Statistics 2016). Rather than refuting the presence of links between early exposures and health change in later life, however, such results may reflect the poor fit of gradualist assumptions to the survey data and underscore the importance of considering the pattern of punctuated equilibrium in later-life health. The earlier death of socially and economically disadvantaged persons (who might be expected to display a cumulative health penalty) and the nonrandom nature of attrition in longitudinal surveys of health further suggest that gradual health trajectories may underestimate the accumulation of poor health outcomes in disadvantaged subpopulations (Jackson et al. 2019), contributing to an inaccurate impression of comparable health declines across heterogeneous groups. Explicitly recognizing the limitations of gradualist models and the extent of differential survey attrition and mortality selection among vulnerable individuals and subpopulations is a first step toward recognizing that current estimates of disparities in health by race/ethnicity or various indicators of SES may be too conservative.

The punctuated equilibrium perspective reorients us more explicitly to the interplay between population aggregates and the individual-level experiences that produce them. Armstrong (2017:298) recently commented on the shifting nature of the concept of population in health research:

On the one hand, the population is a sum of individual identities, but as those identities change the population provides a fluid denominator, comparator, context and analytic space. On the other hand, over the past two decades, the population has come to define those very individuals.

Over time, individuals transition in and out of various statuses and population categories, and such moves may incrementally reshape these categories themselves (Johnson-Hanks 2015). Nevertheless, some populations are defined by particular characteristics—for example, race and ethnicity, as well as gender, age, and disability, among others—that become reified, giving a sense of identity to the individuals they comprise and serving as a referent to others (Baynton 2013; Saperstein and Penner 2012). Consideration of differences across categories often illuminates inequalities, but the reification of those categories may at other times present barriers to understanding the dynamics that shape and reproduce inequalities over time. In the context of functional limitations, the application and interpretation of gradualist models have tended to blur the distinction between individual and population patterns as well as within- and between-person variation. Recognizing the punctuated equilibrium dynamic allows us to consider individual paths across particular levels of physical function while simultaneously recognizing that health categories are not necessarily fixed but are instead variable and reflective of both individual trajectories and ongoing compositional change in aging cohorts.

Notably, we do not argue that gradualist models are themselves problematic, but rather that when applied to longitudinal health survey data, these models emphasize heterogeneity and clustering across people but are less successful at describing within-person changes over time or characterizing their determinants. Thus, even while championing their potential for informing person-centered analyses and interventions, gradualist models are in fact telling us more about aggregated, heterogeneous, and changing populations—a level that is harder for classic health interventions to influence. Coarse measures of health, long intervals between survey observations, and irregular interruptions in the form of missing and censored survey data may all influence our results and the analytic challenges they highlight. To resolve them, our analysis suggests two ways forward: (1) continuing to apply gradualist models to different health data that better reflects the cumulative process of health change, or (2) analyzing health survey data with methods that do not require gradualism assumptions.

To continue with a gradualist paradigm, the ideal health data would not simply provide snapshots of broad health outcomes but rather would offer more refined measures that could be used to model truly latent (i.e., subclinical) biological processes that may be hard to detect but are known to incrementally accumulate to change health, perhaps via ongoing homeostatic adjustment. This type of individual-level data would be better suited for gradualist models because the underlying data-generating process would fit these models’ assumptions while also allowing us to more accurately translate individual trajectories to the broader population scale. Alternatively, using our existing (and ever improving) survey data infrastructures, we may consider a broader application of methods that can accommodate nonlinearities and multidirectional change and more explicitly incorporate mortality into analyses of within-person health changes. Future research should also further explore the ways in which methods that recognize the possibility of punctuated equilibrium—those discussed in this article as well as novel approaches that combine traditional mixture models with discrete transition functions (e.g., Bolano and Berchtold 2016)—may further illuminate the connection between structural inequality and the life histories that shape individual health outcomes.

In challenging the gradualist paradigm, the punctuated equilibrium perspective opens new directions for research on health inequality across the life course, although not without cost. Punctuated equilibrium approaches that emphasize the stochasticity of within-person changes in observed measures of health make it harder to characterize or predict changes in a parsimonious fashion, reintroducing the problems that population health research typically overcomes by focusing on large samples and aggregate statistics. Questions also remain about whether and how a punctuated equilibrium perspective can contribute to our ability to interpret the role of the broader, structural social conditions that shape health inequities within populations and between subpopulations. We expect that gradualist models will remain popular in studies of health changes in later life because of their alignment with our understanding of age-related physiological and cognitive changes, their statistical tractability, and their ability to give form to specific hypotheses about the determinants of population health. Nonetheless, the development of methods that can depict nonlinearity in the progression of individual health while accounting for changes in population composition over time is a particularly important avenue for future research. The need to understand both individual and population health patterns remains as strong as ever. In making inferences about later-life health, we should exercise caution in applying higher-order regularities to individuals and subgroups and consider the implications of punctuated equilibrium for our ability to accurately characterize changes in health and interventions designed to ameliorate health inequities.